Black Hole as a Quantum Field Configuration
Abstract
:1. Introduction
Strategy and Result
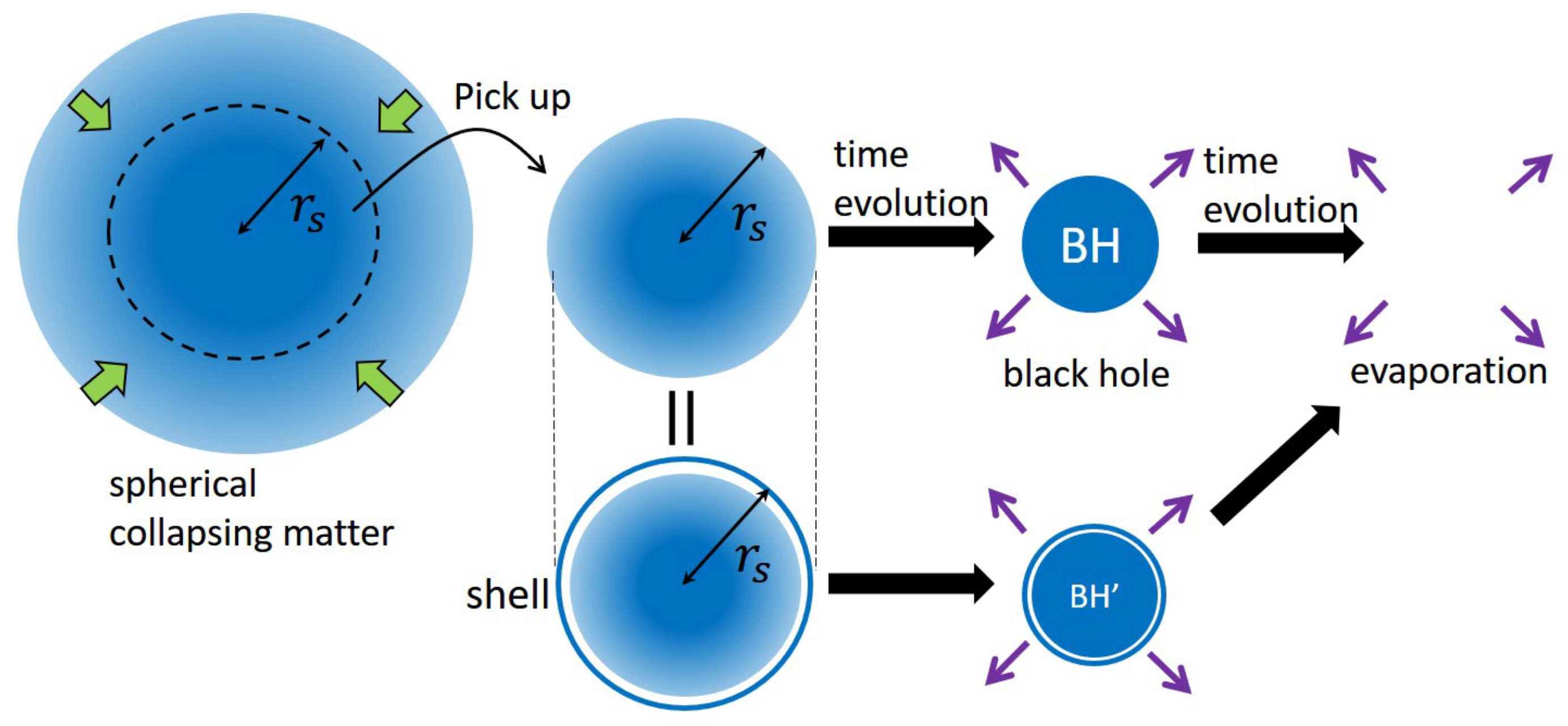
2. Basic Idea
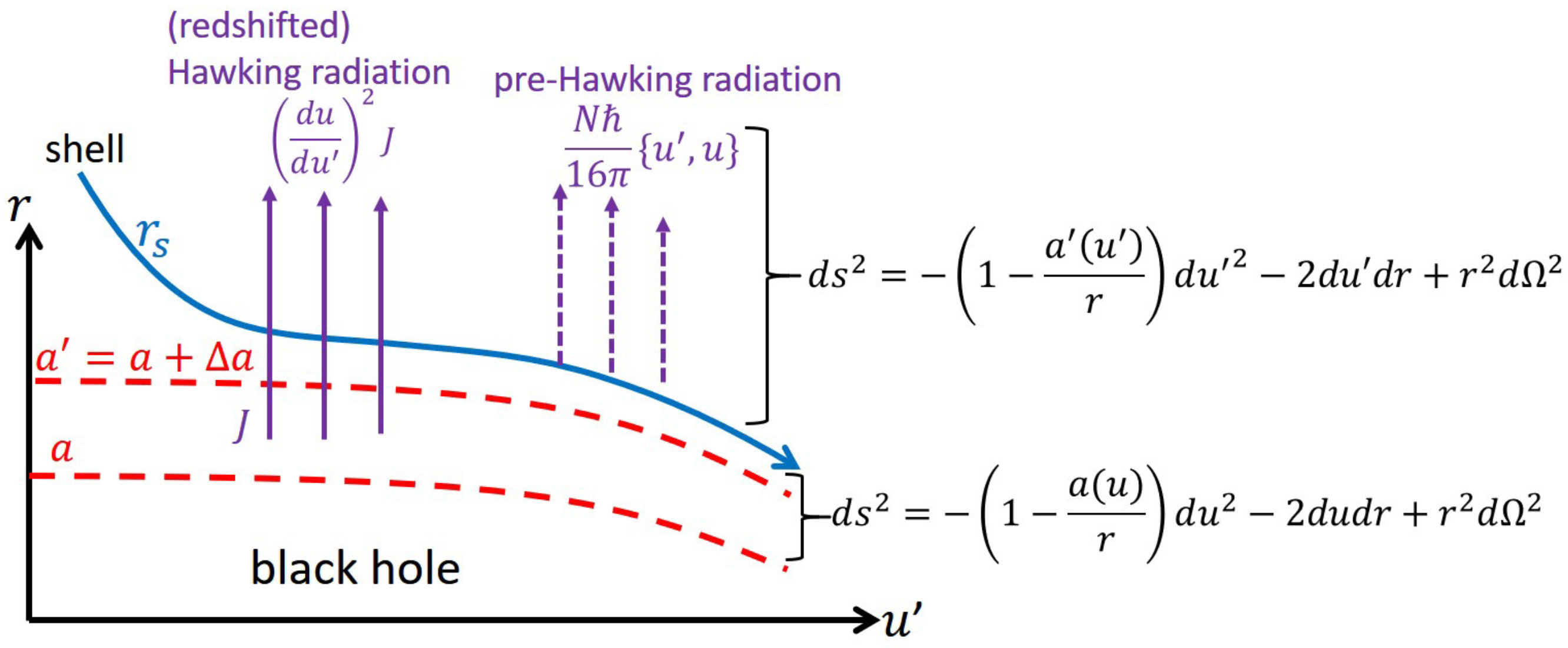
2.1. Step1: Motion of a Shell Near the Evaporating Black Hole
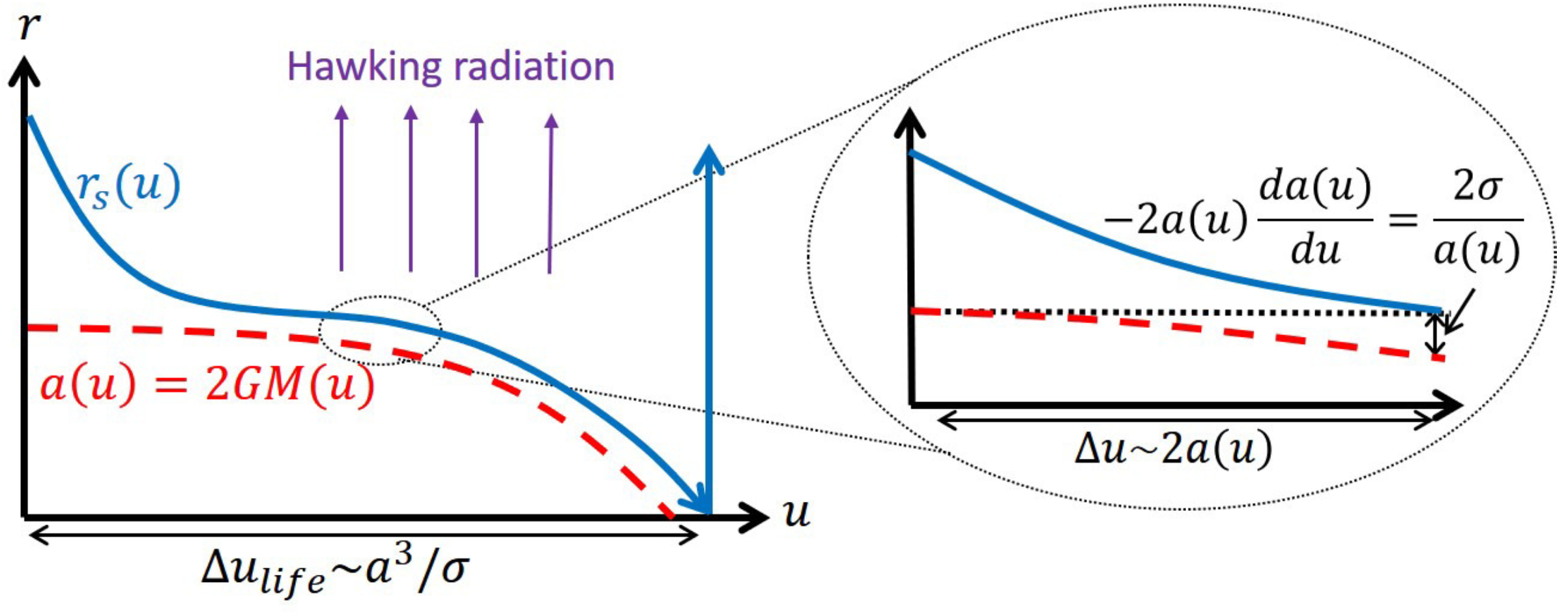
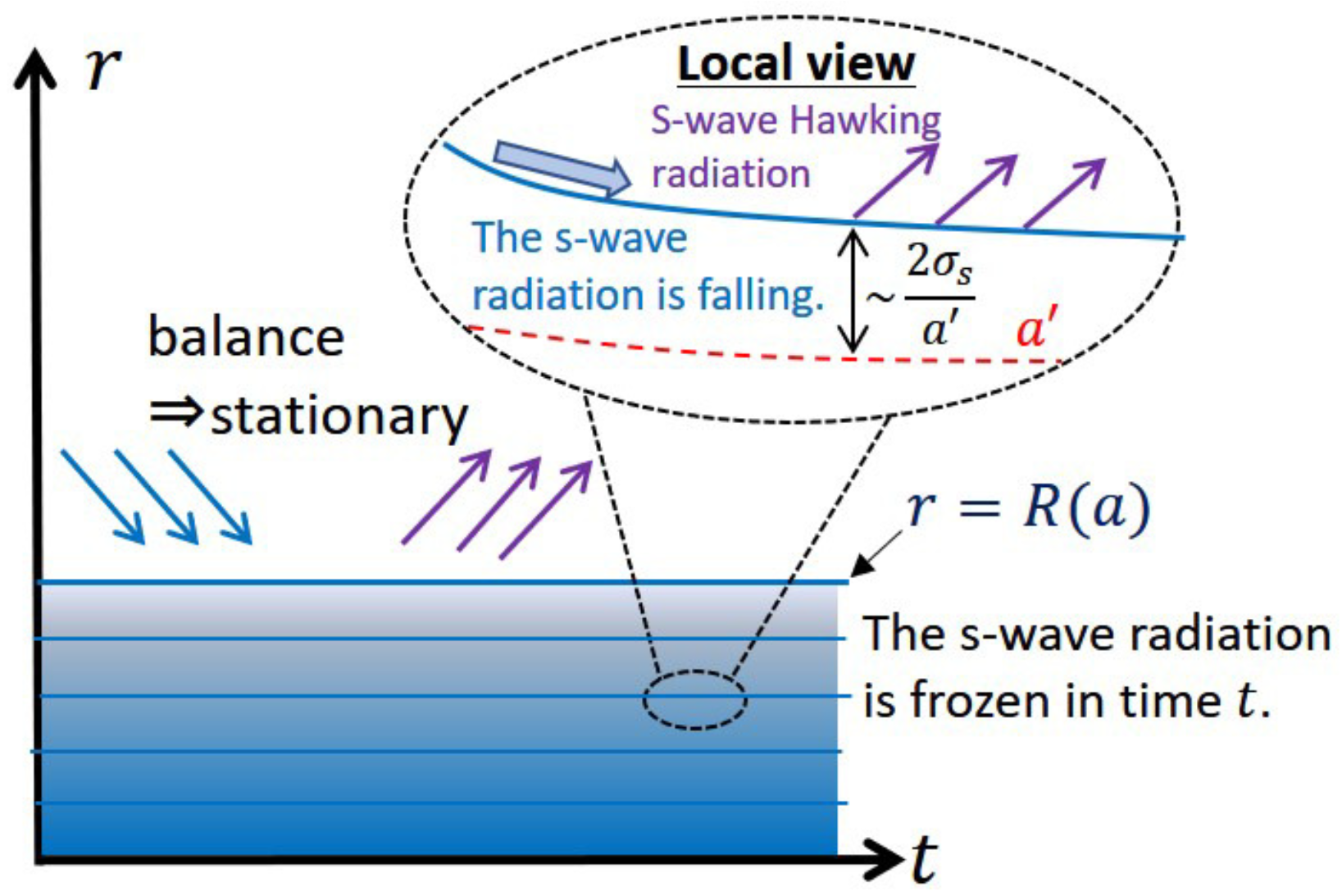
2.2. Step2: Pre-Hawking Radiation
2.2.1. Setup
2.2.2. Time Evolution of the Pre-Hawking Radiation
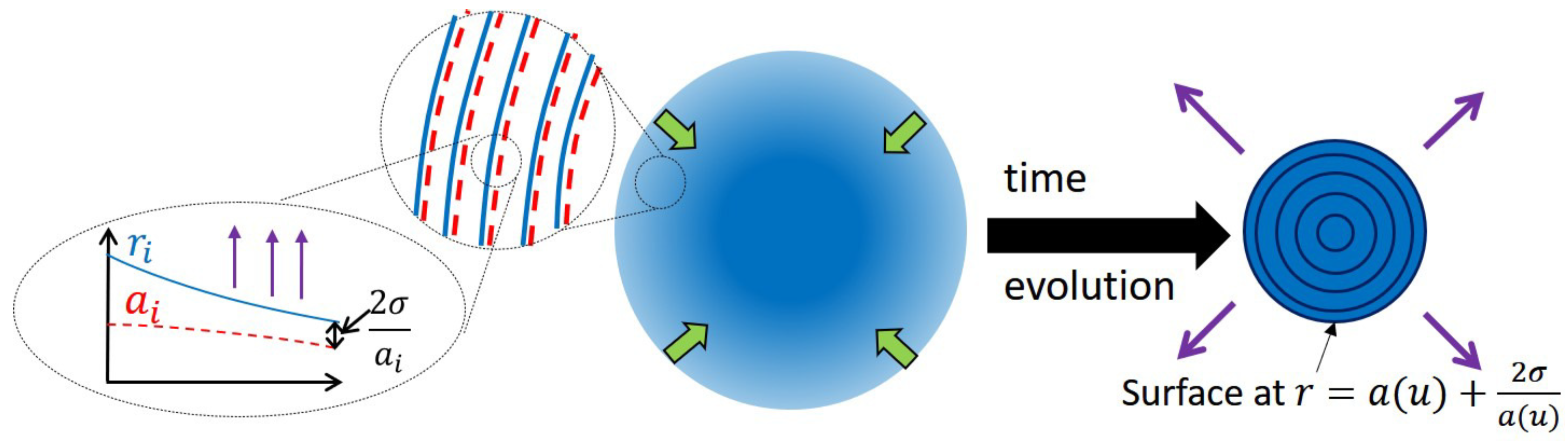
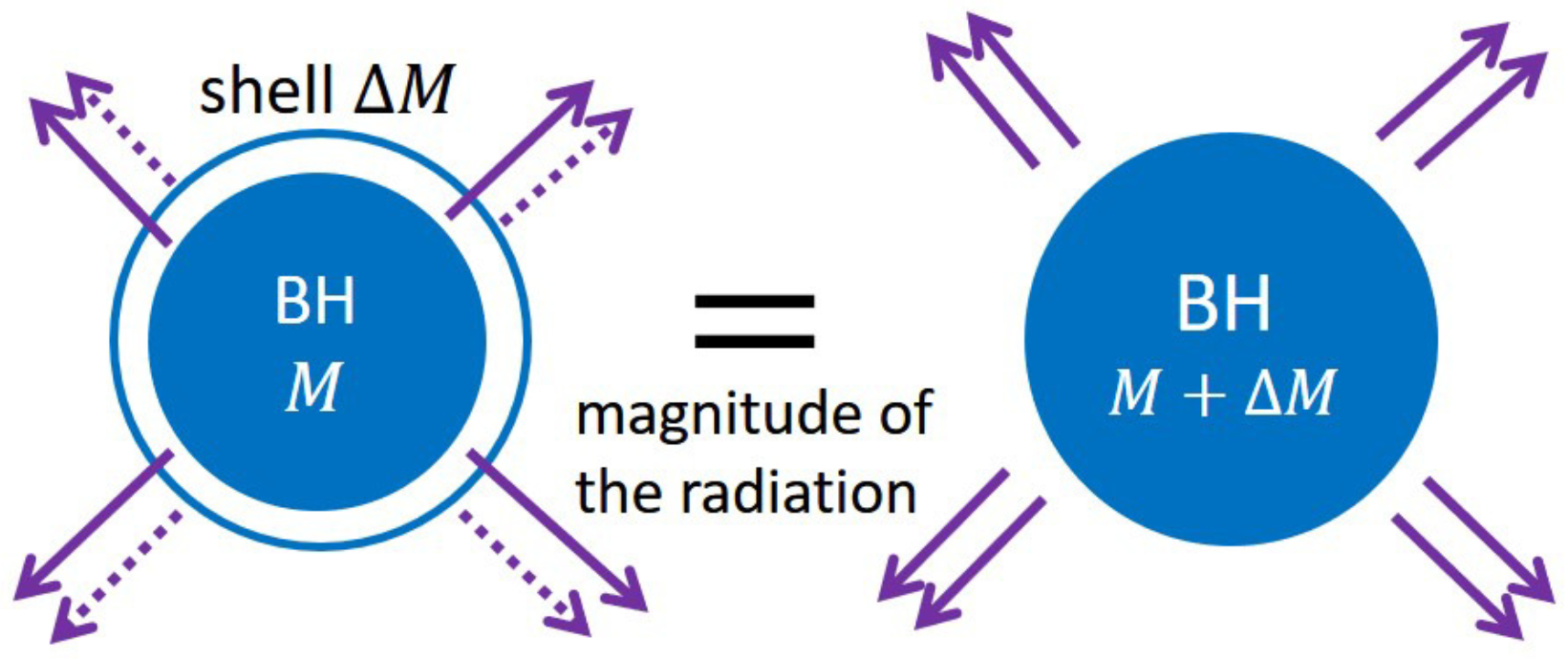
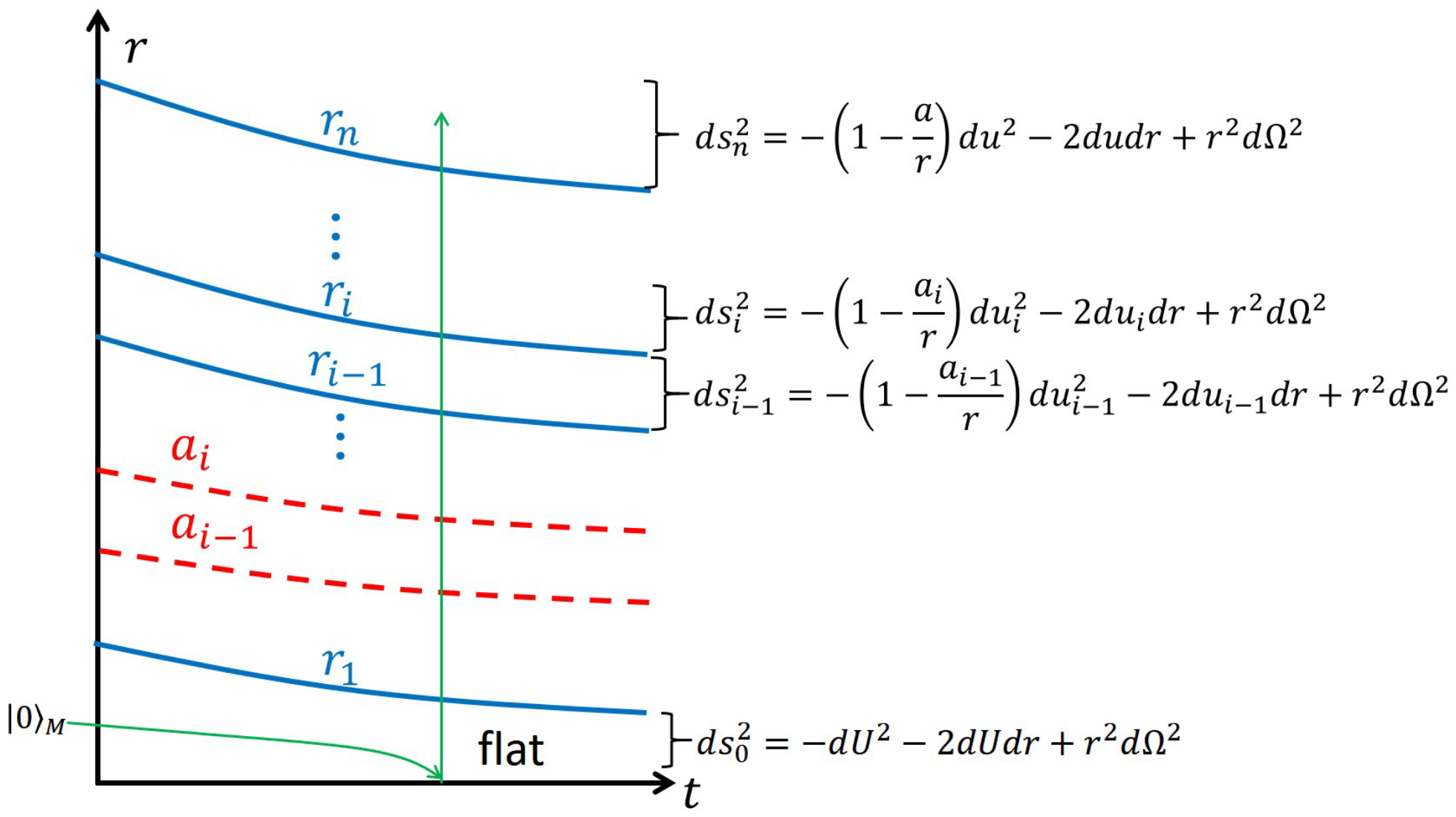
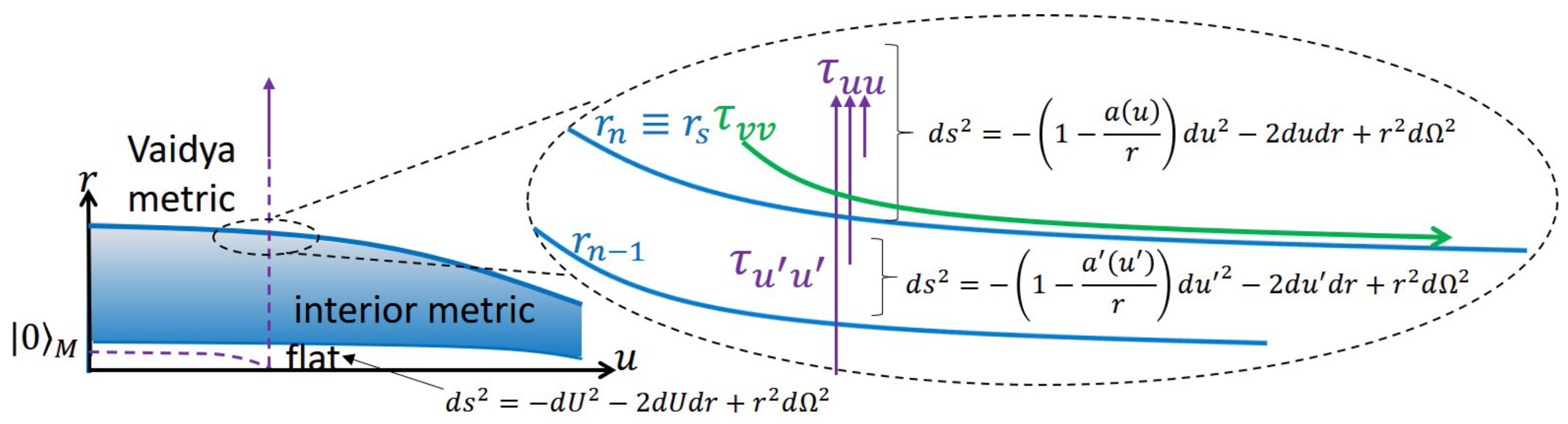
2.3. Step3: A Multi-Shell Model
2.3.1. Setup
2.3.2. Check of the Pre-Hawking Radiation
2.3.3. Surface Pressure Induced by the Pre-Hawking Radiation
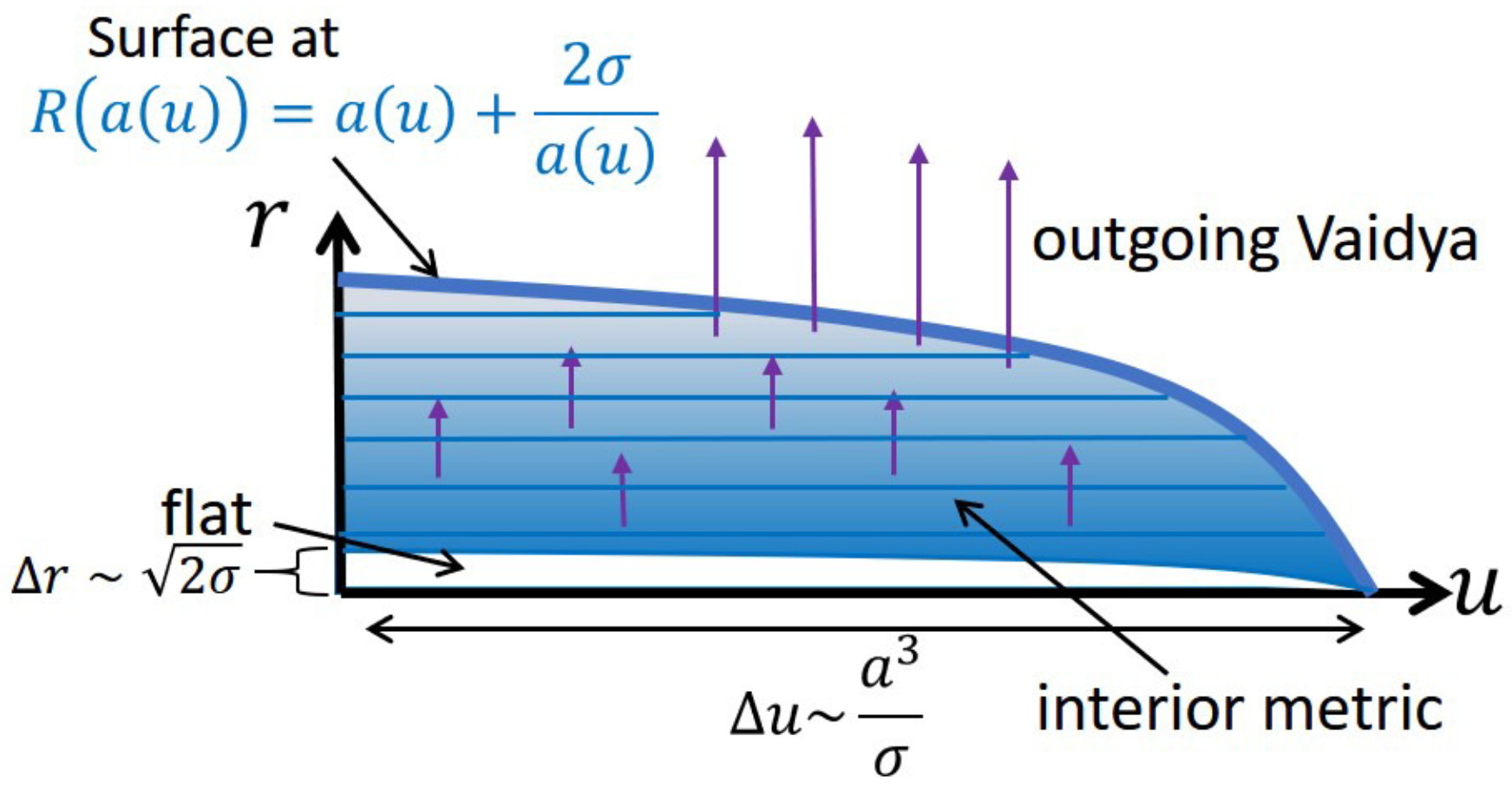
3. Construction of the Candidate Metric
3.1. The Interior Metric
3.2. Generalization of the Metric
3.2.1. Another Phenomenological Function
3.2.2. The Candidate Metric
4. Field Configurations
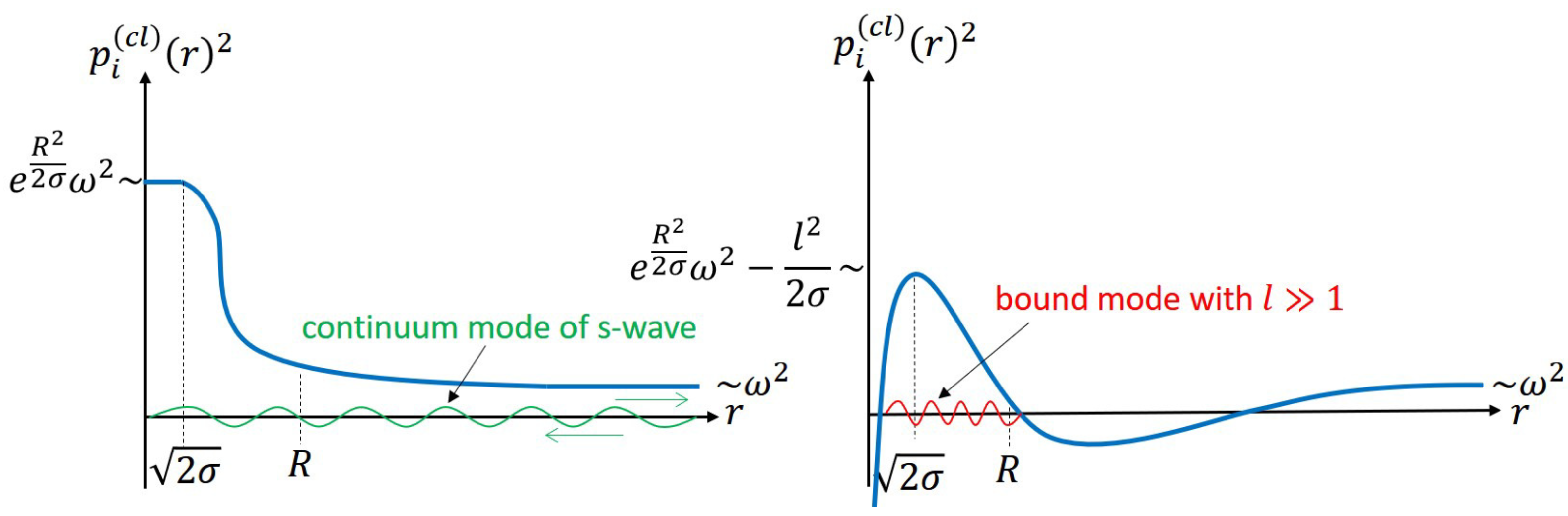
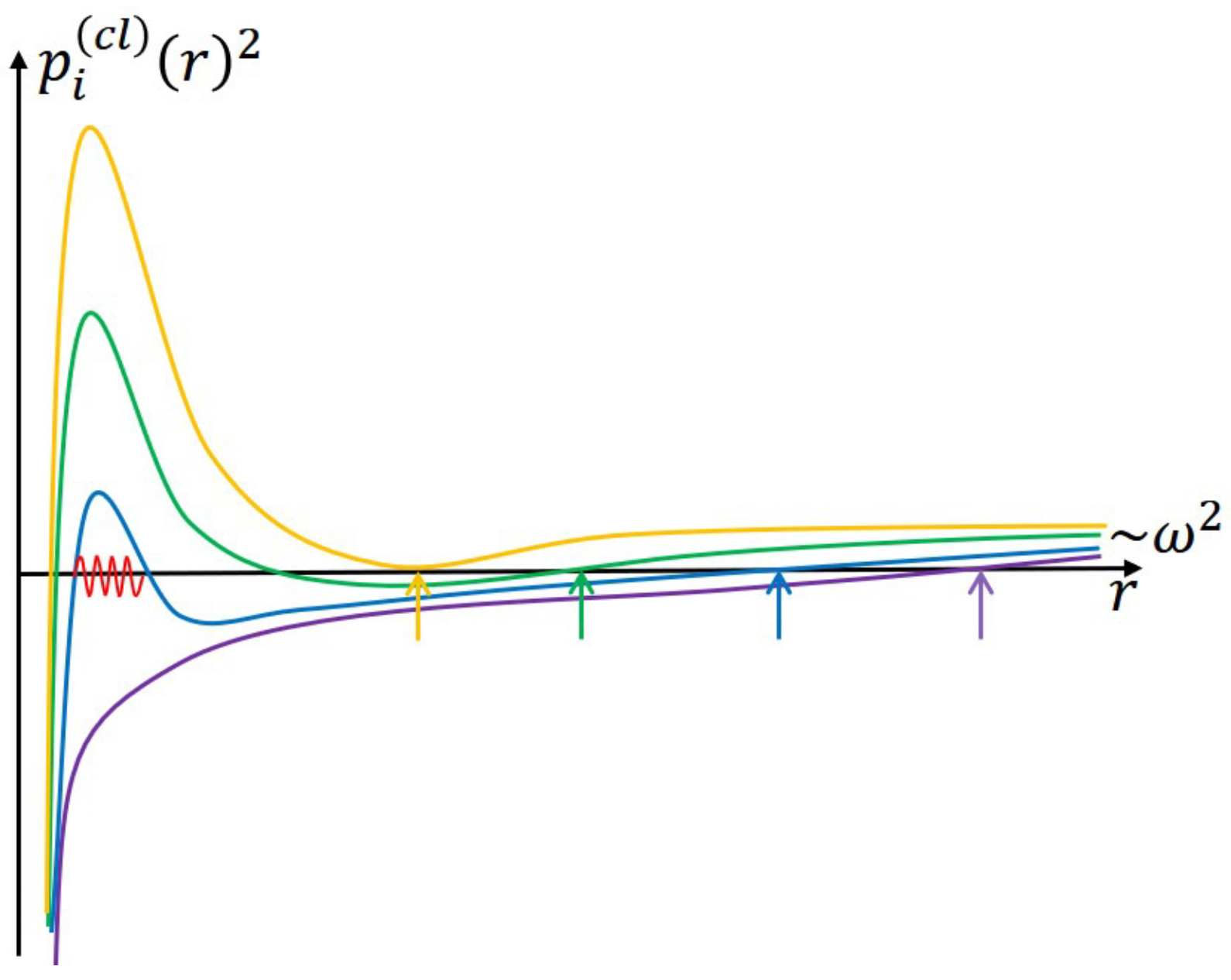
4.1. Classical Effective Potential and Bound Modes
4.2. WKB Approximation
4.3. A Candidate State
5. Energy-Momentum Tensor in the Ground State
5.1. Solutions of the Bound Modes
5.1.1. Breakdown of the WKB Approximation
5.1.2. A Perturbative Method and the Leading Exact Solution
5.2. Dimensional Regularization and Renormalization
5.3. Leading Terms of the Energy-Momentum Tensor
5.3.1. Fields in the Dimensional Regularization
5.3.2. Renormalized Energy-Momentum Tensor
5.4. Sub-Leading Terms of the Energy-Momentum Tensor
6. Contribution of S-Wave Excitations to the Energy-Momentum Tensor
6.1. Fluctuation of Mass of the Black Hole
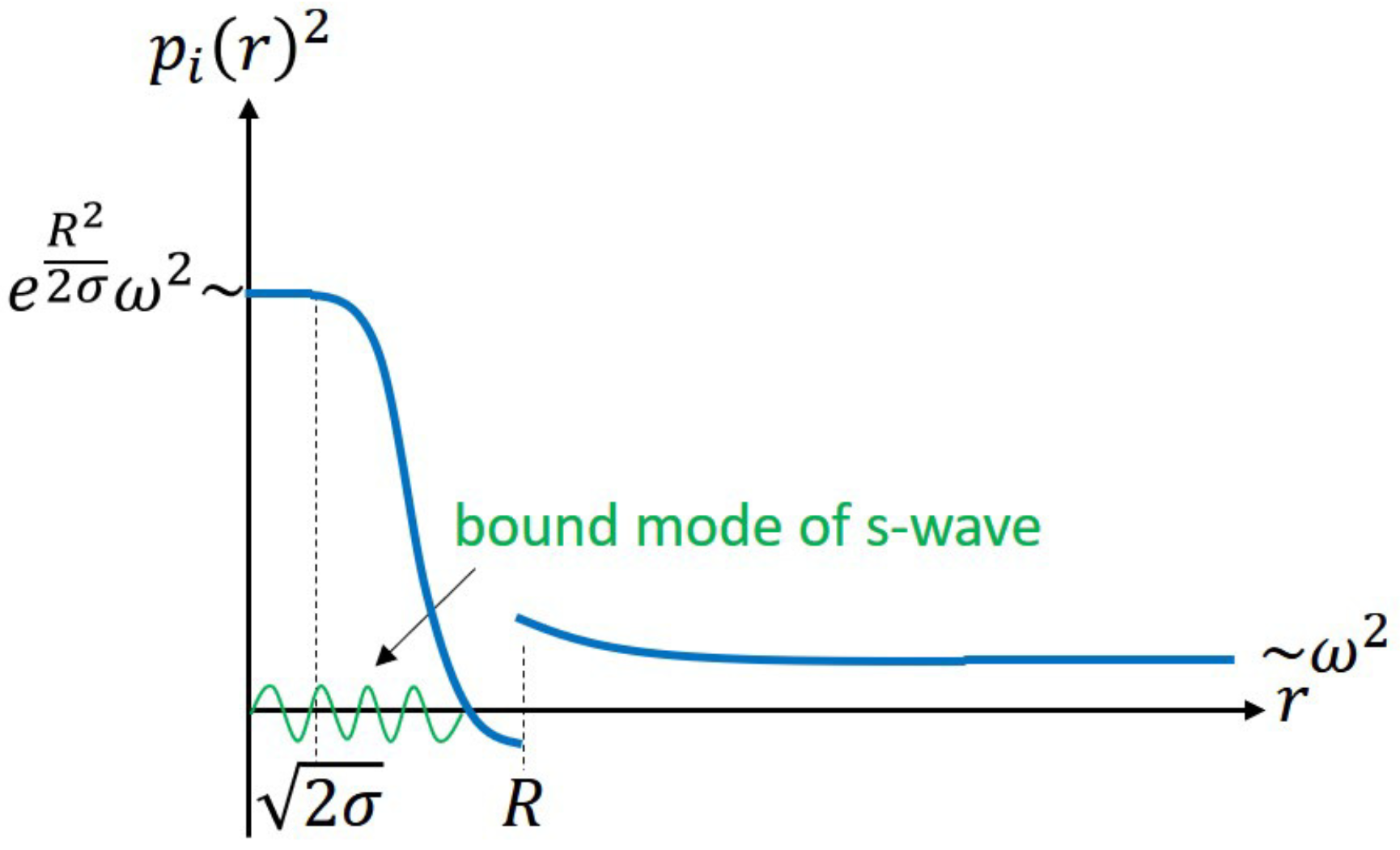
6.2. S-Wave Excitation inside the Black Hole and
6.3. The Form of
7. Self-Consistent Solution
7.1. Self-Consistent Values of for a Class of
7.2. Consistency Check
8. Black Hole Entropy
8.1. Adiabatic Formation in the Heat Bath
8.2. Micro-Counting of the S-Wave States
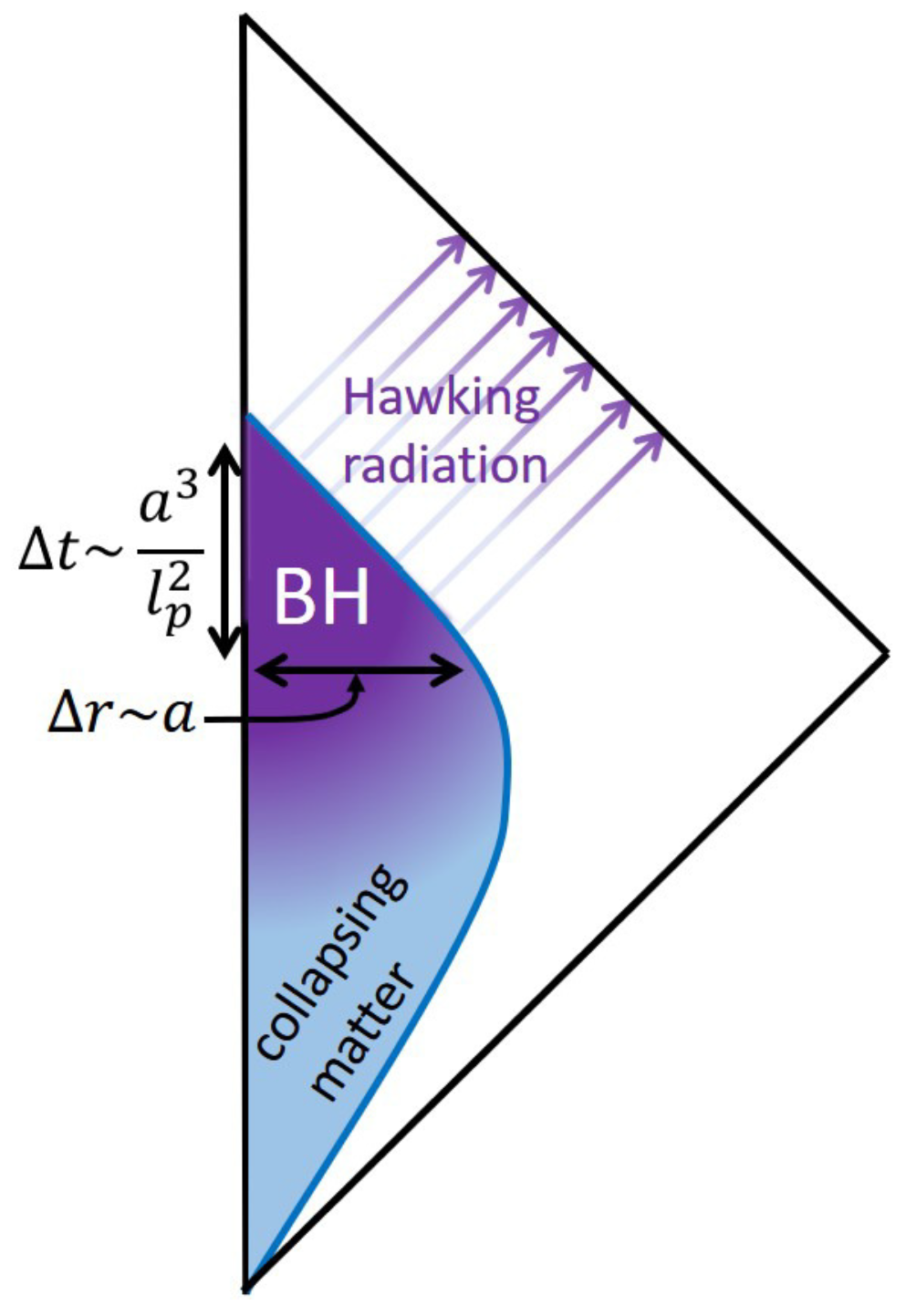
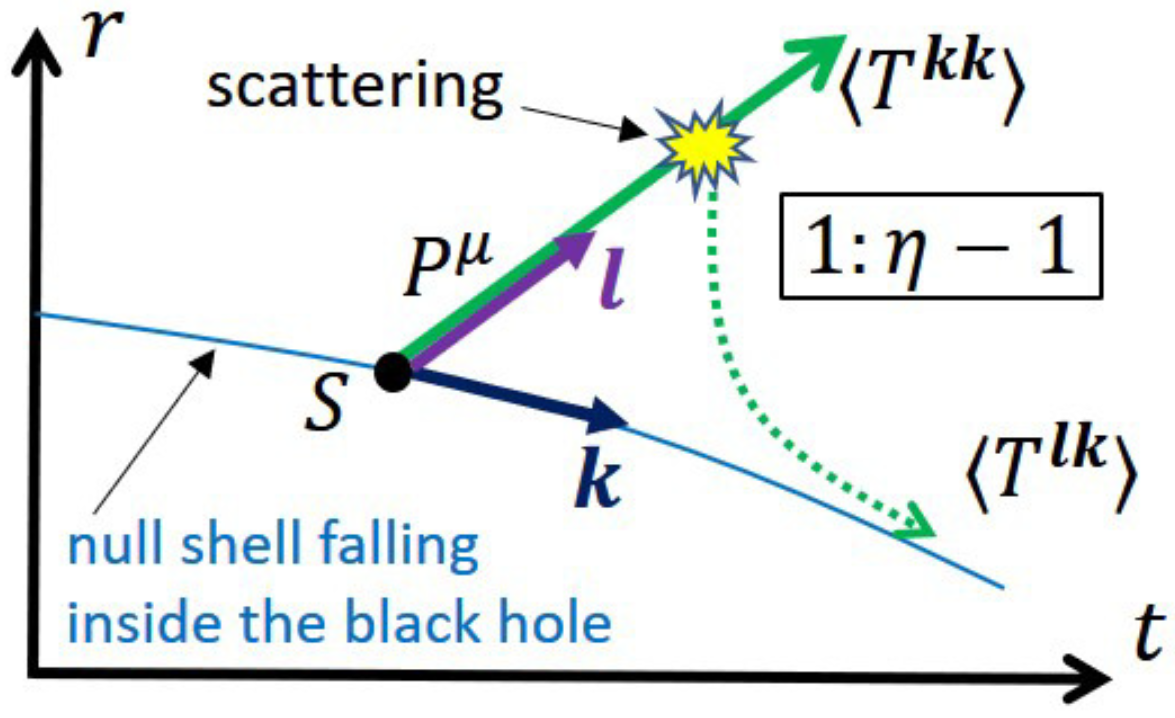
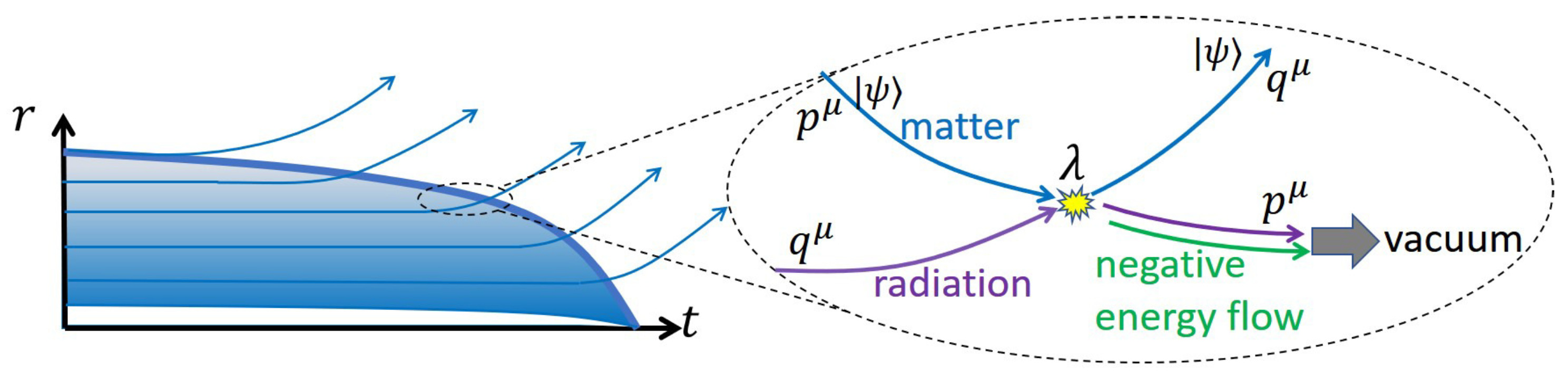
9. Mechanism of Energy Decrease of the Collapsing Matter
9.1. Setup
9.2. S-Wave Model of Quantum Fields
9.3. Hawking Radiation
9.4. Ingoing Negative Energy Flow Near the Surface
9.5. Configuration of S-Wave and
10. Conformal Matter Fields
10.1. Self-Consistent Values of for Conformal Matter Fields
10.2. A New Constraint to the Matter Content
11. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Motion of a Particle near the Evaporating Black Hole
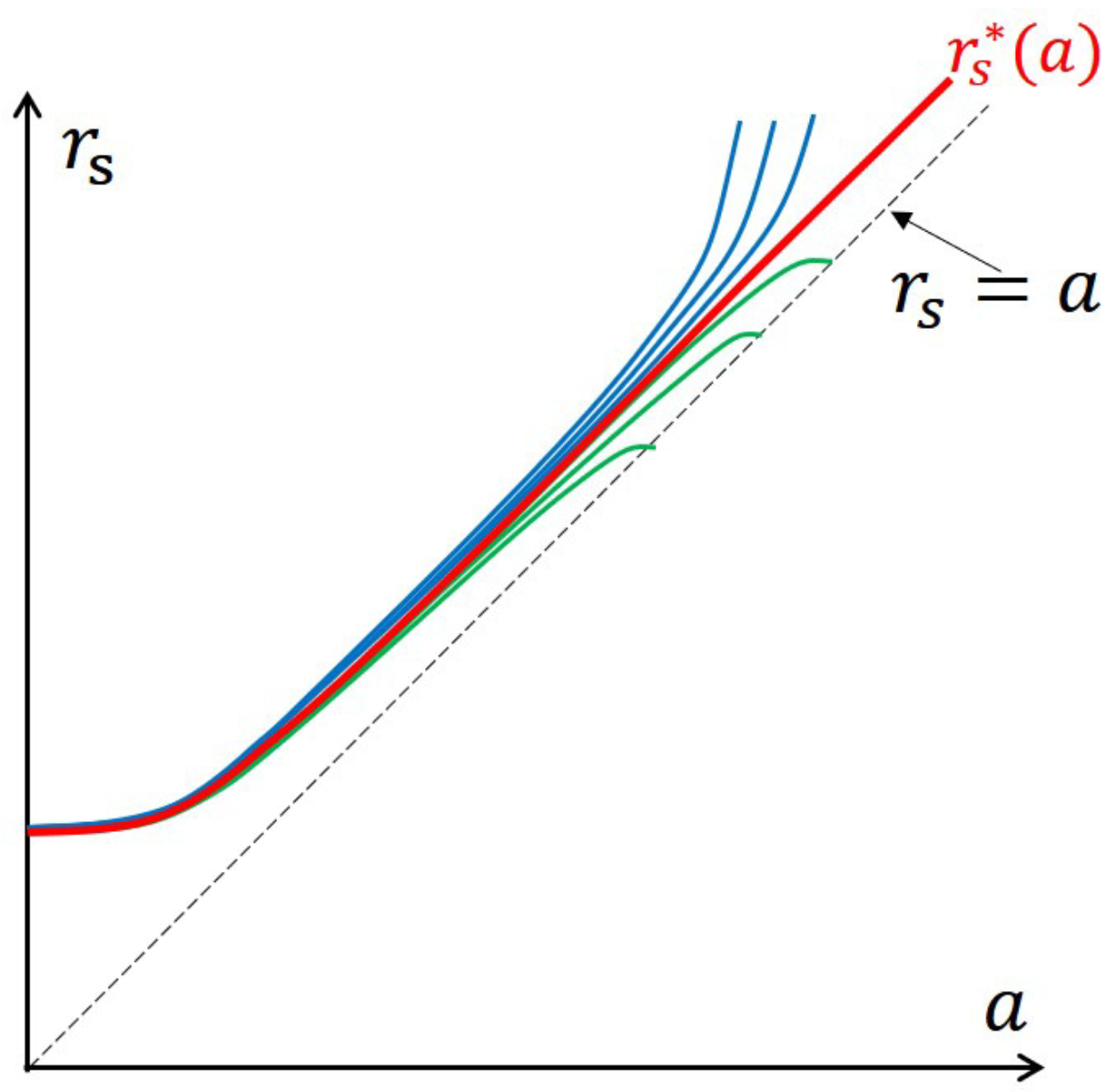
Appendix B. Behavior of rs in the Limit a→0
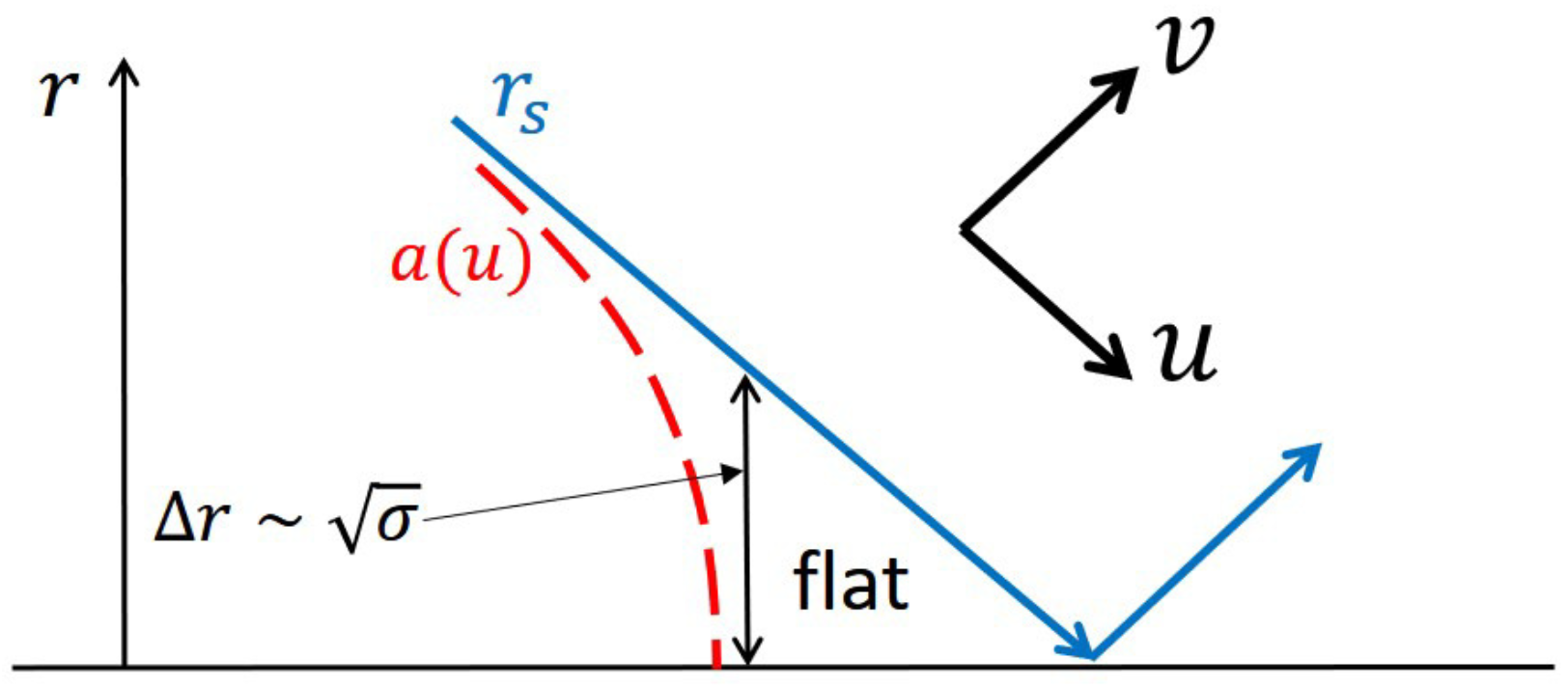
Appendix C. The Radiation in our Model and the Usual Hawking Radiation
Appendix D. Normalization Factor
Appendix E. Derivation of the Leading Solution φi(0) (ξ)
Appendix F. Evaluation of the Leading Values of the Regularized Energy-Momentum Tensor
Appendix F.1. Evaluation of
Appendix F.2. Evaluation of
Appendix F.3. Evaluation of
Appendix F.4. Evaluation of
Appendix F.5. Evaluation of
Appendix G. Derivation of τvv (u,vs)
Appendix H. Classical and Quantum Contributions to Energy Density
References
- Hawking, S.W. Particle Creation by Black Holes. Commun. Math. Phys. 1975, 43, 199. [Google Scholar] [CrossRef]
- Frolov, V.P.; Vilkovisky, G.A. Spherically Symmetric Collapse in Quantum Gravity. Phys. Lett. 1981, 106B, 307. [Google Scholar] [CrossRef]
- Hooft, G.T. The black hole interpretation of string theory. Nucl. Phys. B 1990, 335, 138. [Google Scholar] [CrossRef]
- Stephens, C.R.; Hooft, G.T.; Whiting, B.F. Black hole evaporation without information loss. Class. Quantum Gravity 1994, 11, 621. [Google Scholar] [CrossRef]
- Mathur, S.D. The Fuzzball proposal for black holes: An Elementary review. Fortsch. Phys. 2005, 53, 793. [Google Scholar] [CrossRef] [Green Version]
- Ashtekar, A.; Bojowald, M. Black hole evaporation: A Paradigm. Class. Quantum Gravity 2005, 22, 3349. [Google Scholar] [CrossRef]
- Hayward, S.A. Formation and evaporation of regular black holes. Phys. Rev. Lett. 2006, 96, 031103. [Google Scholar] [CrossRef] [Green Version]
- Hossenfelder, S.; Smolin, L. Conservative solutions to the black hole information problem. Phys. Rev. D 2010, 81, 064009. [Google Scholar] [CrossRef] [Green Version]
- Kawai, H.; Matsuo, Y.; Yokokura, Y. A Self-consistent Model of the Black Hole Evaporation. Int. J. Mod. Phys. A 2013, 28, 1350050. [Google Scholar] [CrossRef] [Green Version]
- Hawking, S.W. Information Preservation and Weather Forecasting for Black Holes. arXiv 2014, arXiv:1401.5761. [Google Scholar]
- Frolov, V.P. Information loss problem and a ’black hole‘ model with a closed apparent horizon. J. High Energy Phys. 2014, 1405, 049. [Google Scholar] [CrossRef] [Green Version]
- Pinol, M. A Model of Dustlike Spherically Symmetric Gravitational Collapse without Event Horizon Formation. Prog. Phys. 2015, 11, 331. [Google Scholar]
- Haggard, H.M.; Rovelli, C. Quantum-gravity effects outside the horizon spark black to white hole tunneling. Phys. Rev. D 2015, 92, 104020. [Google Scholar] [CrossRef] [Green Version]
- Kawai, H.; Yokokura, Y. Phenomenological description of the interior of the Schwarzschild black hole. Int. J. Mod. Phys. A 2015, 30, 1550091. [Google Scholar] [CrossRef] [Green Version]
- Ho, P.M. Comment on Self-Consistent Model of Black Hole Formation and Evaporation. J. High Energy Phys. 2015, 1508, 096. [Google Scholar] [CrossRef] [Green Version]
- Kawai, H.; Yokokura, Y. Interior of Black Holes and Information Recovery. Phys. Rev. D 2016, 93, 044011. [Google Scholar] [CrossRef] [Green Version]
- Barcelo, C.; Carballo-Rubio, R.; Garay, L.J. Where does the physics of extreme gravitational collapse reside? Universe 2016, 2, 7. [Google Scholar] [CrossRef] [Green Version]
- Ho, P.M. The Absence of Horizon in Black-Hole Formation. Nucl. Phys. B 2016, 909, 394. [Google Scholar] [CrossRef] [Green Version]
- De Lorenzo, T.; Perez, A. Improved Black Hole Fireworks: Asymmetric Black-Hole-to-White-Hole Tunneling Scenario. Phys. Rev. D 2016, 93, 124018. [Google Scholar] [CrossRef] [Green Version]
- Hawking, S.W.; Perry, M.J.; Strominger, A. Soft Hair on Black Holes. Phys. Rev. Lett. 2016, 116, 231301. [Google Scholar] [CrossRef] [Green Version]
- Ho, P.M. Asymptotic Black Holes. Class. Quantum Gravity 2017, 34, 085006. [Google Scholar] [CrossRef] [Green Version]
- Baccetti, V.; Mann, R.B.; Terno, D.R. Role of evaporation in gravitational collapse. Class. Quantum Gravity 2018, 35, 185005. [Google Scholar] [CrossRef] [Green Version]
- Baccetti, V.; Husain, V.; Terno, D.R. The information recovery problem. Entropy 2017, 19, 17. [Google Scholar] [CrossRef] [Green Version]
- Kawai, H.; Yokokura, Y. A Model of Black Hole Evaporation and 4D Weyl Anomaly. Universe 2017, 3, 51. [Google Scholar] [CrossRef] [Green Version]
- Bianchi, E.; Christodoulou, M.; D’Ambrosio, F.; Haggard, H.M.; Rovelli, C. White Holes as Remnants: A Surprising Scenario for the End of a Black Hole. Class. Quantum Gravity 2018, 35, 225003. [Google Scholar] [CrossRef] [Green Version]
- Ho, P.M.; Matsuo, Y. On the Near-Horizon Geometry of an Evaporating Black Hole. J. High Energy Phys. 2018, 1807, 047. [Google Scholar] [CrossRef] [Green Version]
- Ho, P.M.; Matsuo, Y.; Yang, S.J. Asymptotic States of Black Holes in KMY Model. Class. Quantum Gravity 2020, 37, 035002. [Google Scholar] [CrossRef] [Green Version]
- Cardoso, V.; Franzin, E.; Pani, P. Is the gravitational-wave ringdown a probe of the event horizon? Phys. Rev. Lett. 2016, 116, 171101. [Google Scholar] [CrossRef]
- Cardoso, V.; Hopper, S.; Macedo, C.F.B.; Palenzuela, C.; Pani, P. Gravitational-wave signatures of exotic compact objects and of quantum corrections at the horizon scale. Phys. Rev. D 2016, 94, 084031. [Google Scholar] [CrossRef] [Green Version]
- Abedi, J.; Dykaar, H.; Afshordi, N. Echoes from the Abyss: Tentative evidence for Planck-scale structure at black hole horizons. Phys. Rev. D 2017, 96, 082004. [Google Scholar] [CrossRef] [Green Version]
- Holdom, B.; Ren, J. Not quite a black hole. Phys. Rev. D 2017, 95, 084034. [Google Scholar] [CrossRef] [Green Version]
- Barcelo, C.; Carballo-Rubio, R.; Garay, L.J. Gravitational wave echoes from macroscopic quantum gravity effects. J. High Energy Phys. 2017, 1705, 054. [Google Scholar] [CrossRef] [Green Version]
- Conklin, R.S.; Holdom, B.; Ren, J. Gravitational wave echoes through new windows. Phys. Rev. D 2018, 98, 044021. [Google Scholar] [CrossRef] [Green Version]
- Oshita, N.; Afshordi, N. Probing microstructure of black hole spacetimes with gravitational wave echoes. Phys. Rev. D 2019, 99, 044002. [Google Scholar] [CrossRef] [Green Version]
- Carballo-Rubio, R.; Di Filippo, F.; Liberati, S.; Visser, M. Phenomenological aspects of black holes beyond general relativity. Phys. Rev. D 2018, 98, 124009. [Google Scholar] [CrossRef] [Green Version]
- Cardoso, V.; Pani, P. Testing the nature of dark compact objects: A status report. Living Rev. Rel. 2019, 22, 4. [Google Scholar] [CrossRef] [Green Version]
- Abedi, J.; Afshordi, N.; Oshita, N.; Wang, Q. Quantum Black Holes in the Sky. Universe 2020, 6, 43. [Google Scholar] [CrossRef] [Green Version]
- Oshita, N.; Tsuna, D.; Afshordi, N. Quantum Black Hole Seismology I: Echoes, Ergospheres, and Spectra. arXiv 2020, arXiv:2001.11642. [Google Scholar]
- Oshita, N.; Tsuna, D.; Afshordi, N. Quantum Black Hole Seismology II: Applications to Astrophysical Black Holes. arXiv 2020, arXiv:2004.06276. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields; Butterworth-Heinemann: Oxford, UK, 1980. [Google Scholar]
- Birrell, N.D.; Davies, P.C.W. Quantum Fields in Curved space; Cambridge Univ. Press: Cambridge, UK, 1982. [Google Scholar]
- Parker, L.; Toms, D. Quantum Field Theory in Curved Spacetime; Cambridge Univ. Press: Cambridge, UK, 2009. [Google Scholar]
- Barcelo, C.; Liberati, S.; Sonego, S.; Visser, M. Minimal conditions for the existence of a Hawking-like flux. Phys. Rev. D 2011, 83, 041501. [Google Scholar] [CrossRef] [Green Version]
- Barcelo, C.; Liberati, S.; Sonego, S.; Visser, M. Hawking-like radiation from evolving black holes and compact horizonless objects. J. High Energy Phys. 2011, 1102, 003. [Google Scholar] [CrossRef] [Green Version]
- Buchdahl, H.A. General Relativistic Fluid Spheres. Phys. Rev. 1959, 116, 1027. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Black holes and entropy. Phys. Rev. D 1973, 7, 2333. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Motl, L.; Nicolis, A.; Vafa, C. The String landscape, black holes and gravity as the weakest force. J. High Energy Phys. 2007, 0706, 060. [Google Scholar] [CrossRef]
- Palti, E. The Swampland: Introduction and Review. Fortsch. Phys. 2019, 67, 1900037. [Google Scholar] [CrossRef] [Green Version]
- Vaidya, P.C. The gravitational field of a radiating star. Proc. Indian Acad. Sci. A 1951, 33, 264. [Google Scholar] [CrossRef]
- Davies, P.C.W.; Fulling, S.A.; Unruh, W.G. Energy-momentum Tensor Near an Evaporating Black Hole. Phys. Rev. D 1976, 13, 2720. [Google Scholar] [CrossRef] [Green Version]
- Fabbri, A.; Navarro-Salas, J. Modeling Black Hole Evaporation; Imperial College Press: London, UK, 2005. [Google Scholar]
- Ho, P.M.; Matsuo, Y. Trapping Horizon and Negative Energy. J. High Energy Phys. 2019, 1906, 057. [Google Scholar] [CrossRef] [Green Version]
- Christensen, S.M.; Fulling, S.A. Trace Anomalies and the Hawking Effect. Phys. Rev. D 1977, 15, 2088. [Google Scholar] [CrossRef] [Green Version]
- Strominger, A. Les Houches lectures on black holes. arXiv 1995, arXiv:hep-th/9501071. [Google Scholar]
- Iso, S.; Morita, T.; Umetsu, H. Higher-spin Currents and Thermal Flux from Hawking Radiation. Phys. Rev. D 2007, 75, 124004. [Google Scholar] [CrossRef] [Green Version]
- Francesco, P.; Mathieu, P.; Senechal, D. Conformal Field Theory; Springer: New York, NY, USA, 1997. [Google Scholar]
- Poisson, E. A Relativistic Toolkit; Cambridge Univ. Press: Cambridge, UK, 2004. [Google Scholar]
- Barrabes, C.; Israel, W. Thin shells in general relativity and cosmology: The Lightlike limit. Phys. Rev. D 1991, 43, 1129. [Google Scholar] [CrossRef] [PubMed]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics; Butterworth-Heinemann: Oxford, UK, 1981. [Google Scholar]
- Hooft, G.T.; Veltman, M.J.G. Regularization and Renormalization of Gauge Fields. Nucl. Phys. B 1972, 44, 189. [Google Scholar] [CrossRef] [Green Version]
- Kawai, H.; Ninomiya, M. Renormalization Group and Quantum Gravity. Nucl. Phys. B 1990, 336, 115. [Google Scholar] [CrossRef]
- Duff, M.J. Twenty years of the Weyl anomaly. Class. Quantum Gravity 1994, 11, 1387. [Google Scholar] [CrossRef] [Green Version]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics; Butterworth-Heinemann: Oxford, UK, 1984. [Google Scholar]
- Park, I.Y. Quantum-corrected Geometry of Horizon Vicinity. Fortsch. Phys. 2017, 65, 1700038. [Google Scholar] [CrossRef] [Green Version]
- Nurmagambetov, A.J.; Park, I.Y. Quantum-induced trans-Planckian energy near horizon. J. High Energy Phys. 2018, 1805, 167. [Google Scholar] [CrossRef] [Green Version]
- Bolokhov, S.V.; Bronnikov, K.A.; Skvortsova, M.V. The Schwarzschild singularity: A semiclassical bounce? Gravitation Cosmol. 2018, 24, 315. [Google Scholar] [CrossRef] [Green Version]
- Hooft, G.T. On the Quantum Structure of a Black Hole. Nucl. Phys. B 1985, 256, 727. [Google Scholar] [CrossRef]
- Alexander, S.H.; Yagi, K.; Yunes, N. An Entropy-Area Law for Neutron Stars Near the Black Hole Threshold. Class. Quantum Gravity 2019, 36, 015010. [Google Scholar] [CrossRef] [Green Version]
- Ho, P.M.; Matsuo, Y. Static Black Holes With Back Reaction From Vacuum Energy. Class. Quantum Gravity 2018, 35, 065012. [Google Scholar] [CrossRef] [Green Version]
- Ho, P.M.; Matsuo, Y. Static Black Hole and Vacuum Energy: Thin Shell and Incompressible Fluid. J. High Energy Phys. 2018, 1803, 096. [Google Scholar] [CrossRef]
- Ho, P.M.; Matsuo, Y.; Yang, S.J. Vacuum Energy at Apparent Horizon in Conventional Model of Black Holes. arXiv 2019, arXiv:1904.01322. [Google Scholar]
- Ho, P.M.; Kawai, H.; Matsuo, Y.; Yokokura, Y. Back Reaction of 4D Conformal Fields on Static Geometry. J. High Energy Phys. 2018, 1811, 056. [Google Scholar] [CrossRef] [Green Version]
- Tsao, H.S. Conformal Anomalies in a General Background Metric. Phys. Lett. 1977, 68B, 79. [Google Scholar] [CrossRef]
- Gibbons, G.W.; Hawking, S.W.; Perry, M.J. Path Integrals and the Indefiniteness of the Gravitational Action. Nucl. Phys. B 1978, 138, 141. [Google Scholar] [CrossRef]
- Critchley, R. Trace Anomaly for Gravitons. Phys. Rev. D 1978, 18, 1849. [Google Scholar] [CrossRef]
- Ho, P.M.; Matsuo, Y.; Yokokura, Y. An Analytic Description of Semi-Classical Black-Hole Geometry. arXiv 2019, arXiv:1912.12855. [Google Scholar]
- Ho, P.M.; Matsuo, Y.; Yokokura, Y. Distance between collapsing matter and trapping horizon in evaporating black holes. arXiv 2019, arXiv:1912.12863. [Google Scholar]
- Gibbons, G.W.; Hawking, S.W. Action Integrals and Partition Functions in Quantum Gravity. Phys. Rev. D 1977, 15, 2752. [Google Scholar] [CrossRef]
- Ho, P.M.; Yokokura, Y. Firewall From Effective Field Theory. arXiv 2020, arXiv:2004.04956. [Google Scholar]
- Jacobson, T. Black hole evaporation and ultrashort distances. Phys. Rev. D 1991, 44, 1731. [Google Scholar] [CrossRef] [PubMed]
- Brout, R.; Massar, S.; Parentani, R.; Spindel, P. Hawking radiation without transPlanckian frequencies. Phys. Rev. D 1995, 52, 4559. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Helfer, A.D. Do black holes radiate? Rept. Prog. Phys. 2003, 66, 943. [Google Scholar] [CrossRef] [Green Version]
| 1. | |
| 2. | |
| 3. | A small black hole with should be described by some bound state in string theory and it may decay in a finite time. Therefore, we postulate that the remaining small part disappears in a finite time which is much smaller than . |
| 4. | Note that the mass may be different from the usual Bondi energy even if we neglect the matter outside the part and regard it as an isolated black hole. Outside the shell, there exists dilute radiation with energy density , where . Then, the outside region may have energy , which makes the difference. In the following, however, we use the name “Bondi energy" and “ADM energy" to represent the mass we are considering. |
| 5. | Later, we will give a more proper definition of the energy flux. See Equation (79). |
| 6. | One might think that the metric (4) is not proper to describe the region near the evaporating black hole because there is not an outgoing energy flow but an ingoing negative energy flow near the horizon in 2D models [41,50,51,52]. As shown in Section 9, such a negative energy flow has energy density . We will include this contribution into the interior of the black hole. Therefore, by using the metric (4), we describe the exterior of the black hole approximately in that we neglect a dilute radiation around it with . |
| 7. | See Appendix I in [16] for the precise derivation |
| 8. | If a were constant, the particle would keep approaching for an infinite amount of time , which means the coordinate singularity of u at . |
| 9. | For the general spherically-symmetric metric in the coordinate, the proper radial length is given by [40]. |
| 10. | Here, we consider the shell infinitely thin. |
| 11. | Here, we neglect the effect of scattering between the shell and Hawking radiation. This effect will be considered in Section 3.2.1 |
| 12. | Israel’s junction condition will be discussed in Section 2.3. |
| 13. | |
| 14. | Note that is much larger than , which is the difference between and . |
| 15. | A more general case is discussed in [21]. |
| 16. | If we want to emphasize or distinguish between the two, we explicitly say “pre-Hawking radiation”. |
| 17. | |
| 18. | We will discuss the stationary black hole more in Section 8. |
| 19. | . This point can be examined more by a phenomenological discussion [14]. |
| 20. | If the radiated particle is massive, is timelike, and we have . In this paper, however, we consider massless particles basically. |
| 21. | We can justify this expectation by a thermodynamical discussion [14]. |
| 22. | |
| 23. | We consider this metric as a first approximation metric in that we have neglected the effect of dilute radiation outside the surface (see footnote 6) and connected the interior and exterior metrics directly at . For a more proper description, we would need to consider such a small effect and construct an “interpolation” metric connecting the two metrics in a smooth manner. However, the most dominant effect of the back reaction of evaporation is incorporated into the interior of the metric (72). |
| 24. | Comparing in the both metrics, we put , from which we have . Then, we can obtain and see that holds if the condition (80) is satisfied. |
| 25. | In fact, the Ricci scalar (76) is approximately , which is negative and constant. |
| 26. | For simplicity, we write as in the following. |
| 27. | |
| 28. | In fact, is the same order as R inside the black hole. See Equation (76). |
| 29. | In particular, it is continuous at because the center region is flat, which means that for , as we have mentioned below the metric (72). |
| 30. | Note again that the field Equation (85) takes the same form as the Schrödinger equation with energy and the potential . Therefore, in order to solve the Equation (85), we can use the same technique as the WKB approximation in quantum mechanics. We just mean it by the term “WKB method (or approximation)”. |
| 31. | Note again that we are writing just by , and depends on the kind of fields. |
| 32. | ℏ does not appear in the l.h.s. of the condition (91) because is not momentum but wave number. |
| 33. | The function is like a Gaussian with width , and the integration has the dimension of the length. Therefore, we can have |
| 34. | In this sense, the spectrum of the black hole is quantized and gapped. |
| 35. | Here, we have dropped in , which will not affect the followings. |
| 36. | Note that in Section 4.3 we have used the WKB approximation only to evaluate the order of in the range where the approximation is good. |
| 37. | Note that , which is near the Planck scale, and the proper frequency should be smaller than it: . Therefore, . |
| 38. | Note that we don’t impose the Einstein Equation (131) here. |
| 39. | Because don’t have the poles , the finite renormalization terms in the definition (132) make and don’t contribute here. |
| 40. | The continuum modes of s-wave may contribute to this. |
| 41. | Equation (151) corresponds to the Tolman–Oppenheimer–Volkoff equation without . |
| 42. | One might wonder that bound modes of s-waves with also contribute to this excitation as discussed in Figure 13. As shown in Section 4.3, however, such modes cannot be excited inside the black hole, and only the continuum modes of s-wave are responsible for the energy density (165). |
| 43. | |
| 44. | See e.g., [66] for another semi-classical resolution of singularity. |
| 45. | Such terms may change each numerical coefficient up to , but they will not make a significant change to the basic picture. |
| 46. | |
| 47. | If we apply Tolman’s law to the interior metric (72) naively, the local temperature would be , which is exponentially large (for ) compared to the Planck scale. This is not allowed physically. |
| 48. | |
| 49. | |
| 50. | See [68] for another approach to the black-hole entropy from the interior region. |
| 51. | Even s-waves can have a tangential pressure, but the largest tangential pressure of in our picture comes from the bound modes with as we have seen in Section 7. Therefore, we can expect that the tangential pressure from s-waves does not make a significantly important effect. |
| 52. | Note that this vacuum is different from the ground state in the interior metric (96). |
| 53. | |
| 54. | |
| 55. | This exponential increase of the classical energy also appears in the interior metric. The excitation part of the energy density (105) takes the same form as the energy density of the outermost shell (225). This is natural because taking the continuum limit of the multi-shell model has led to the interior metric. |
| 56. | |
| 57. | |
| 58. | If a perturbation changes as , where b is a constant of , b would appear as terms of in Equation (229), and would contain b. This change corresponds to a shift , and it should be the leading perturbation for an expansion w.r.t . (Note that such a constant shift of could be removed by redefining a time coordinate). However, we can use a thermodynamical discussion to identify with the accuracy of [14]. Therefore, we can compare the both sides of Equation (229) properly to . |
| 59. | |
| 60. | If we relax the condition of more, at least must be non-negative: . If , the redshift would make no sense. |
| 61. | Here, we assume that the Standard Model is a kind of conformal field theory and study what happens to the formula (233). |
| 62. | See section 3D of [16] for a discussion on the non-conservation of baryon number in our picture. |
| 63. | Even if we consider the evaporating black hole as a closed trapped region, which is the conventional model, e.g., [7], the collapsing matter is below the timelike trapping horizon just by a proper Planckian distance [76,77]. This is similar to our picture in that the matter is above the would-be horizon by the Planckian distance (10). These imply that such a conventional model is eventually very close to ours. |
| 64. | The introduction of interaction is natural from a thermodynamic point of view: black holes are thermodynamical objects [78], and thermal equilibrium is reached by interaction [63]. In addition, higher-dimensional matter terms in effective action may induce scattering that occurs with a high probability inside the black hole [79]. |
| 65. | If there is no interaction, the earlier the matter parts start to go inward, the sooner they return. This is the reverse order of the case of Figure 16. |
| 66. | |
| 67. | The above analysis is based on the classical motion of particles. We can also show that this result is valid even if we treat them quantum mechanically. See section 2-B and Appendix A in [16]. |
| 68. | Note again that such a final stage of the evaporation is beyond the semi-classical approximation and should be investigated more properly, say, by string theory. |
| 69. | Note that this U is the same as that of the flat space before the collapse, and we can identify Equation (A11). |
| 70. | |
| 71. | This correction and the subleading solution contribute to the subleading value . |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kawai, H.; Yokokura, Y. Black Hole as a Quantum Field Configuration. Universe 2020, 6, 77. https://doi.org/10.3390/universe6060077
Kawai H, Yokokura Y. Black Hole as a Quantum Field Configuration. Universe. 2020; 6(6):77. https://doi.org/10.3390/universe6060077
Chicago/Turabian StyleKawai, Hikaru, and Yuki Yokokura. 2020. "Black Hole as a Quantum Field Configuration" Universe 6, no. 6: 77. https://doi.org/10.3390/universe6060077
APA StyleKawai, H., & Yokokura, Y. (2020). Black Hole as a Quantum Field Configuration. Universe, 6(6), 77. https://doi.org/10.3390/universe6060077



