Evidence of Time Evolution in Quantum Gravity
Abstract
1. Introduction
2. Classical Picture
3. Quantum Pictures with Time
3.1. The Schrödinger Equation with a Physical Hamiltonian (Method A)
3.2. Time Evolution from the WDW Equation (Method B)
3.3. An Evolution from the WDW Using the Grassmann Variables (Method C)
3.4. The quasi-Heisenberg Picture (Method D)
3.5. An Evolution Using the Unconstraint Schrödinger Equation in the Extended Space (Method E)
3.5.1. Canonical Gauge
3.5.2. Non-Canonical Gauge
4. Discussion and Possible Application of the Above Approaches to the General Case of Gravity Quantization
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Aidala, C.A.; Bass, S.D.; Hasch, D.; Mallot, G.K. The spin structure of the nucleon. Rev. Mod. Phys. 2013, 85, 655–691. [Google Scholar] [CrossRef]
- Kuchar, K.V. Time and interpretations of quantum gravity. Int. J. Mod. Phys. 2011, D20, 3–86. [Google Scholar] [CrossRef]
- Isham, C.J. Canonical Quantum Gravity and the Problem of Time. In Integrable Systems, Quantum Groups, and Quantum Field Theories; Ibort, L.A., Rodríguez, M.A., Eds.; Springer Netherlands: Dordrecht, The Netherlands, 1993; pp. 157–287. [Google Scholar] [CrossRef]
- Shestakova, T.P.; Simeone, C. The Problem of time and gauge invariance in the quantization of cosmological models. II. Recent developments in the path integral approach. Grav. Cosmol. 2004, 10, 257–268. [Google Scholar]
- Rovelli, C. “Forget time”. arXiv 2009, arXiv:0903.3832. [Google Scholar]
- Anderson, E. The Problem of Time in Quantum Gravity. arXiv 2010, arXiv:1009.2157. [Google Scholar] [CrossRef]
- DeWitt, B.S. Quantum Theory of Gravity. I. The Canonical Theory. Phys. Rev. 1967, 160, 1113–1148. [Google Scholar] [CrossRef]
- Kiefer, C. Conceptual Problems in Quantum Gravity and Quantum Cosmology. Isrn Math. Phys. 2013, 2013, 509316. [Google Scholar] [CrossRef]
- Shestakova, T.P. Is the Wheeler-DeWitt equation more fundamental than the Schrödinger equation? Int. J. Mod. Phys. D 2018, 27, 1841004. [Google Scholar] [CrossRef]
- Rovelli, C. Time in quantum Gravity: An hypothesis. Phys. Rev. D 1991, 43, 442–456. [Google Scholar] [CrossRef]
- Wallace, D. The Emergent Multiverse; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- O’Neill, W. Time and Eternity in Proclus. Phronesis 1962, 7, 163. [Google Scholar] [CrossRef]
- Bojowald, M. Quantum cosmology: A review. Rep. Prog. Phys. 2015, 78, 023901. [Google Scholar] [CrossRef] [PubMed]
- Kaku, M. Introduction to Superstrings; Springer: New York, NY, USA, 2012. [Google Scholar]
- Dirac, P.A.M. Generalized Hamiltonian Dynamics. Can. J. Math. 1950, 2, 129–148. [Google Scholar] [CrossRef]
- Dirac, P.A.M. Generalized Hamiltonian Dynamics. Proc. R. Soc. Lond. A 1958, 246, 326–332. [Google Scholar] [CrossRef]
- Gitman, D.; Tyutin, I.V. Quantization of Fields with Constraints; Springer: Berlin, Germany, 1990. [Google Scholar]
- Henneaux, M.; Teitelboim, C. Quantization of Gauge Systems; Princeton Univ. Press: Princeton, NJ, USA, 1992. [Google Scholar]
- Bojowald, M. Canonical Gravity and Applications; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Barvinsky, A.O.; Kamenshchik, A.Y. Selection rules for the Wheeler-DeWitt equation in quantum cosmology. Phys. Rev. D 2014, 89, 043526. [Google Scholar] [CrossRef]
- Kamenshchik, A.Y.; Tronconi, A.; Vardanyan, T.; Venturi, G. Time in quantum theory, the Wheeler–DeWitt equation and the Born–Oppenheimer approximation. Int. J. Mod. Phys. D 2019, 28, 1950073. [Google Scholar] [CrossRef]
- Supplementary Material Represents the Mathematica 12.0 Notebooks Containing the Calculations of and by the Methods A,B,C,D, and by the Method E. Available online: https://info.tuwien.ac.at/kalashnikov/supplemental.zip (accessed on 9 May 2020).
- Wheeler, J. Superspace and Nature of Quantum Geometrodynamics. In Battelle Rencontres; DeWitt, C., Wheeler, J., Eds.; Benjamin: New York, NY, USA, 1968; pp. 615–724. [Google Scholar]
- Wheeler, J.A. Superspace and the Nature of Quantum Geometrodynamics. Adv. Ser. Astrophys. Cosmol. 1987, 3, 27–92, [reprint of 1968 Edd.]. [Google Scholar]
- Ramírez, C.; Vázquez-Báez, V. Quantum supersymmetric FRW cosmology with a scalar field. Phys. Rev. D 2016, 93, 043505. [Google Scholar] [CrossRef]
- Mostafazadeh, A. Quantum mechanics of Klein-Gordon-type fields and quantum cosmology. Ann. Phys. (N.Y.) 2004, 309, 1–48. [Google Scholar] [CrossRef]
- Halliwell, J.J. Decoherent histories analysis of minisuperspace quantum cosmology. J. Phys. Conf. Ser. 2011, 306, 012023. [Google Scholar] [CrossRef]
- Ruffini, G. Quantization of simple parametrized systems. arXiv 2005, arXiv:gr-qc/0511088. [Google Scholar]
- Kimura, T. Explicit description of the Zassenhaus formula. Prog. Theor. Exp. Phys. 2017, 2017. [Google Scholar] [CrossRef]
- Cherkas, S.L.; Kalashnikov, V.L. Quantum evolution of the universe in the constrained quasi-Heisenberg picture: From quanta to classics? Grav. Cosmol. 2006, 12, 126–129. [Google Scholar]
- Cherkas, S.L.; Kalashnikov, V.L. An inhomogeneous toy model of the quantum gravity with the explicitly evolvable observables. Gen. Relativ. Gravit. 2012, 44, 3081–3102. [Google Scholar] [CrossRef][Green Version]
- Cherkas, S.L.; Kalashnikov, V.L. Quantization of the inhomogeneous Bianchi I model: quasi-Heisenberg picture. Nonlinear Phenom. Complex Syst. 2013, 18, 1–15. [Google Scholar]
- Cherkas, S.L.; Kalashnikov, V.L. Quantum Mechanics Allows Setting Initial Conditions at a Cosmological Singularity: Gowdy Model Example. Theor. Phys. 2017, 2, 124–135. [Google Scholar] [CrossRef]
- Savchenko, V.; Shestakova, T.; Vereshkov, G. Quantum geometrodynamics in extended phase space - I. Physical problems of interpretation and mathematical problems of gauge invariance. Grav. Cosmol. 2001, 7, 18–28. [Google Scholar]
- Vereshkov, G.; Marochnik, L. Quantum Gravity in Heisenberg Representation and Self-Consistent Theory of Gravitons in Macroscopic Spacetime. J. Mod. Phys. 2013, 04, 285–297. [Google Scholar] [CrossRef]
- Feynman, R.; Hibbs, A. Quantum Mechanics and Path Integrals; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Faddeev, L.; Slavnov, A. Gauge Fields. Introduction to Quantum Theory; Benjamin: London, UK, 1980. [Google Scholar]
- DeWitt, B.S. Dynamical Theory in Curved Spaces. I. A Review of the Classical and Quantum Action Principles. Rev. Mod. Phys. 1957, 29, 377–397. [Google Scholar] [CrossRef]
- Cianfrani, F.; Montani, G. Dirac prescription from BRST symmetry in FRW space-time. Phys. Rev. D 2013, 87. [Google Scholar] [CrossRef]
- Kocher, C.D.; McGuigan, M. Simulating 0+1 Dimensional Quantum Gravity on Quantum Computers: Mini-Superspace Quantum Cosmology and the World Line Approach in Quantum Field Theory. In Proceedings of the 2018 New York Scientific Data Summit (NYSDS), New York, NY, USA, 6–8 August 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Lloyd, S. A theory of quantum gravity based on quantum computation. arXiv 2005, arXiv:quant-ph/0501135. [Google Scholar]
- Ganguly, A.; Behera, B.K.; Panigrahi, P.K. Demonstration of Minisuperspace Quantum Cosmology Using Quantum Computational Algorithms on IBM Quantum Computer. arXiv 2019, arXiv:1912.00298. [Google Scholar]
- Cherkas, S.L.; Kalashnikov, V.L. Eicheons instead of Black holes. arXiv 2020, arXiv:2004.03947. [Google Scholar]
| 1 | The issue of compatibility of gauge invariance and the Schrödinger equation in connection with gravity quantization is discussed in [9]. |
| 2 | |
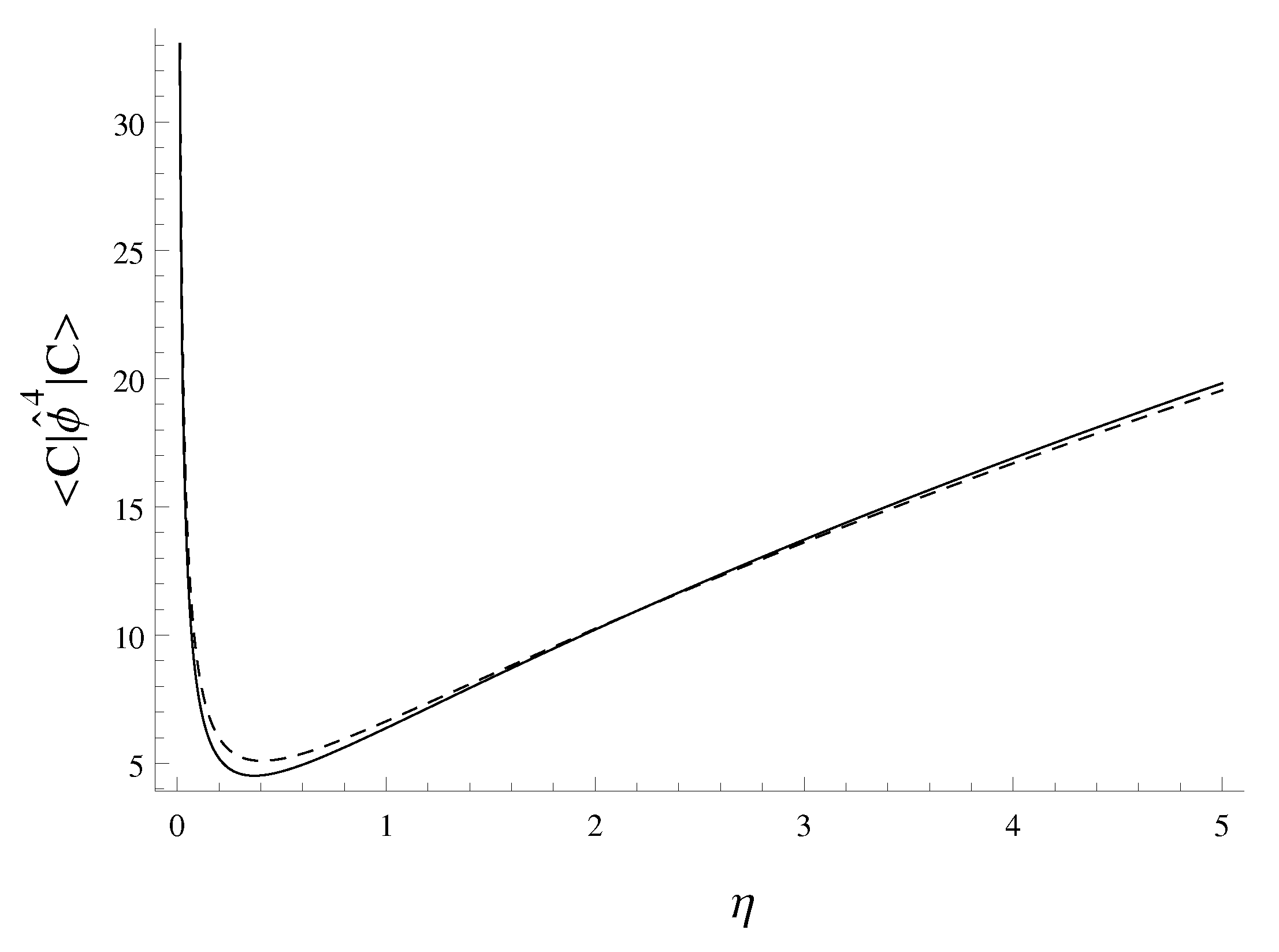
| 3 | One has to note that the methods considered are not the exclusive methods describing the quantum evolution of the universe. For instance, one could take a scale factor or a scalar field [25] as the “time variable.” |
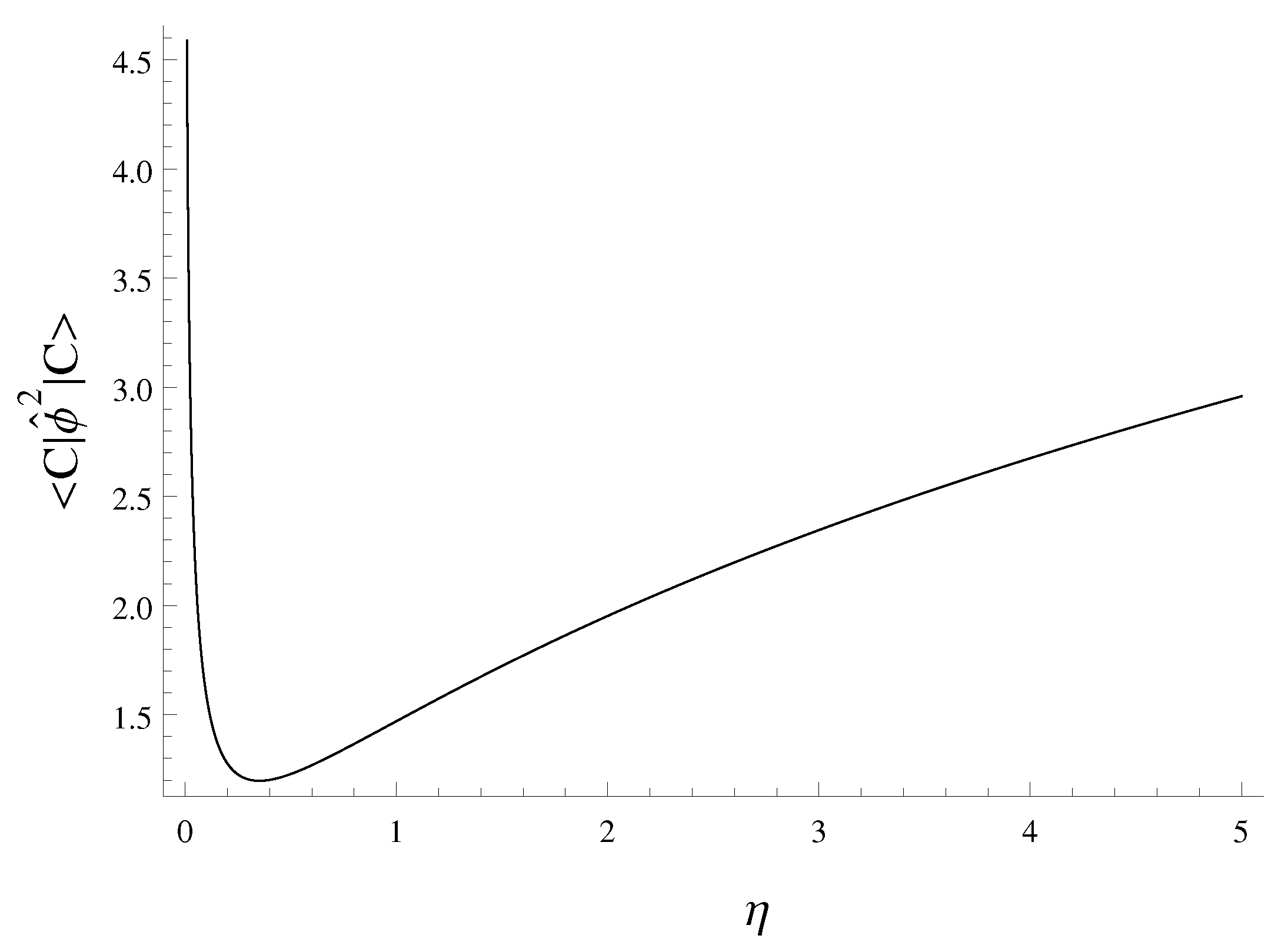
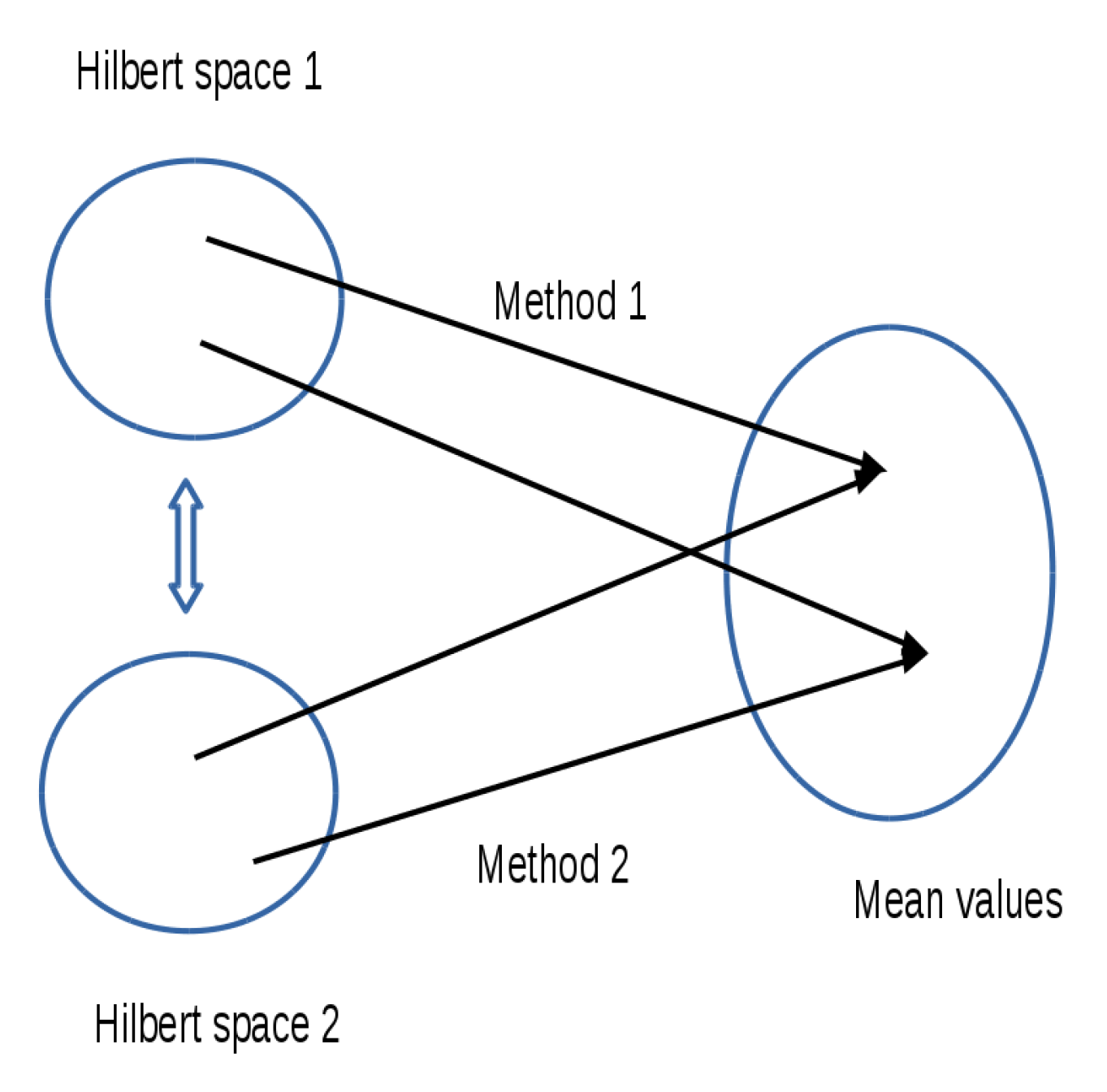
| Method | A | B | C | D | E |
|---|---|---|---|---|---|
| a | + | + | + | + | |
| + | + | + | + | + | |
| + | + | + | + | ||
| ⊕ | ⊗ | ⊗ | ⊕ | ||
| ⊕ | ⊕ | ||||
| ⊕ | ⊕ |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cherkas, S.; Kalashnikov, V. Evidence of Time Evolution in Quantum Gravity. Universe 2020, 6, 67. https://doi.org/10.3390/universe6050067
Cherkas S, Kalashnikov V. Evidence of Time Evolution in Quantum Gravity. Universe. 2020; 6(5):67. https://doi.org/10.3390/universe6050067
Chicago/Turabian StyleCherkas, Sergey, and Vladimir Kalashnikov. 2020. "Evidence of Time Evolution in Quantum Gravity" Universe 6, no. 5: 67. https://doi.org/10.3390/universe6050067
APA StyleCherkas, S., & Kalashnikov, V. (2020). Evidence of Time Evolution in Quantum Gravity. Universe, 6(5), 67. https://doi.org/10.3390/universe6050067






