A Table-Top Pilot Experiment for Narrow Mass Range Light Cold Dark Matter Particle Searches
Abstract
1. Introduction
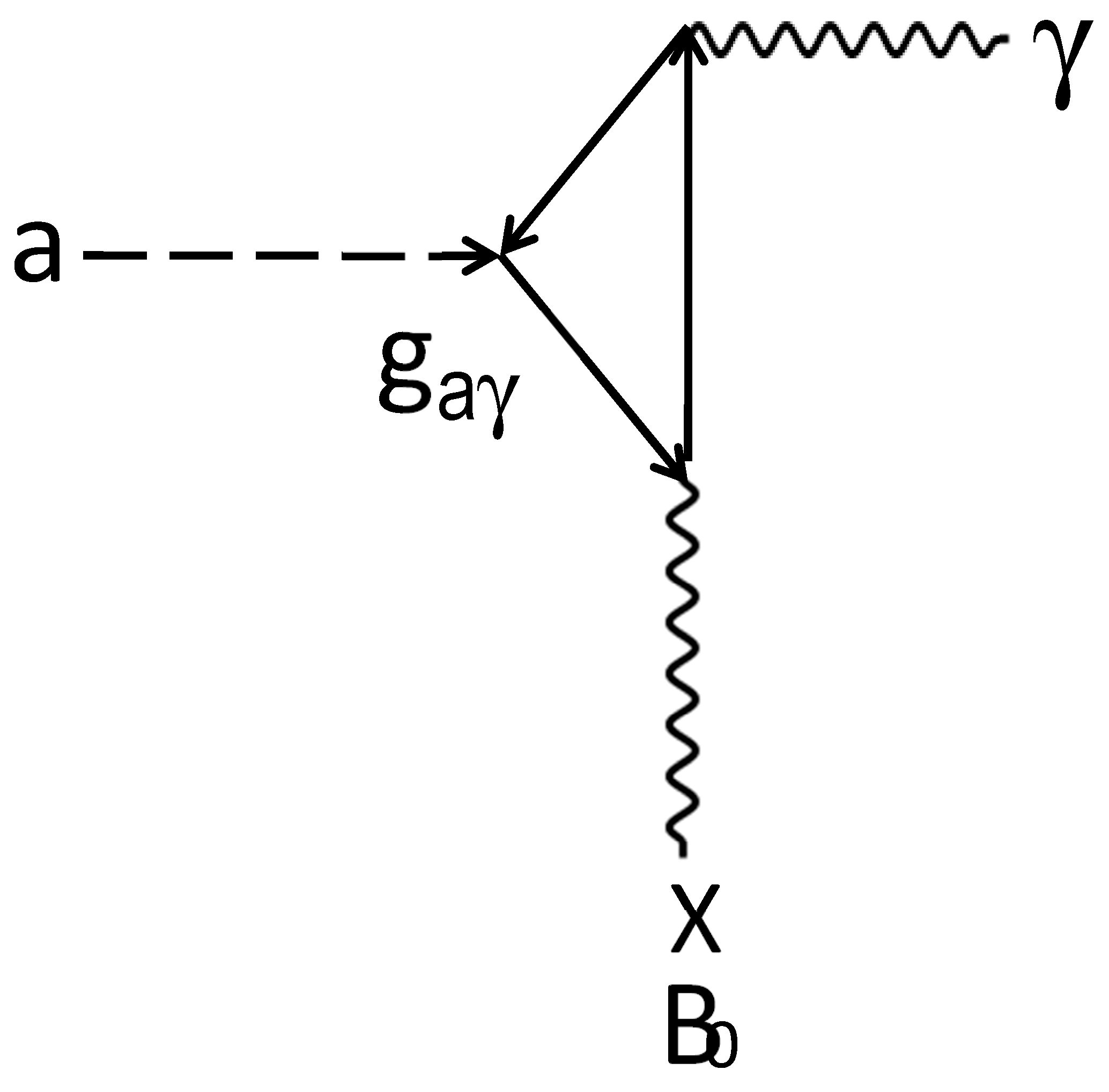
2. An Axion Model and Detection Framework
The Model
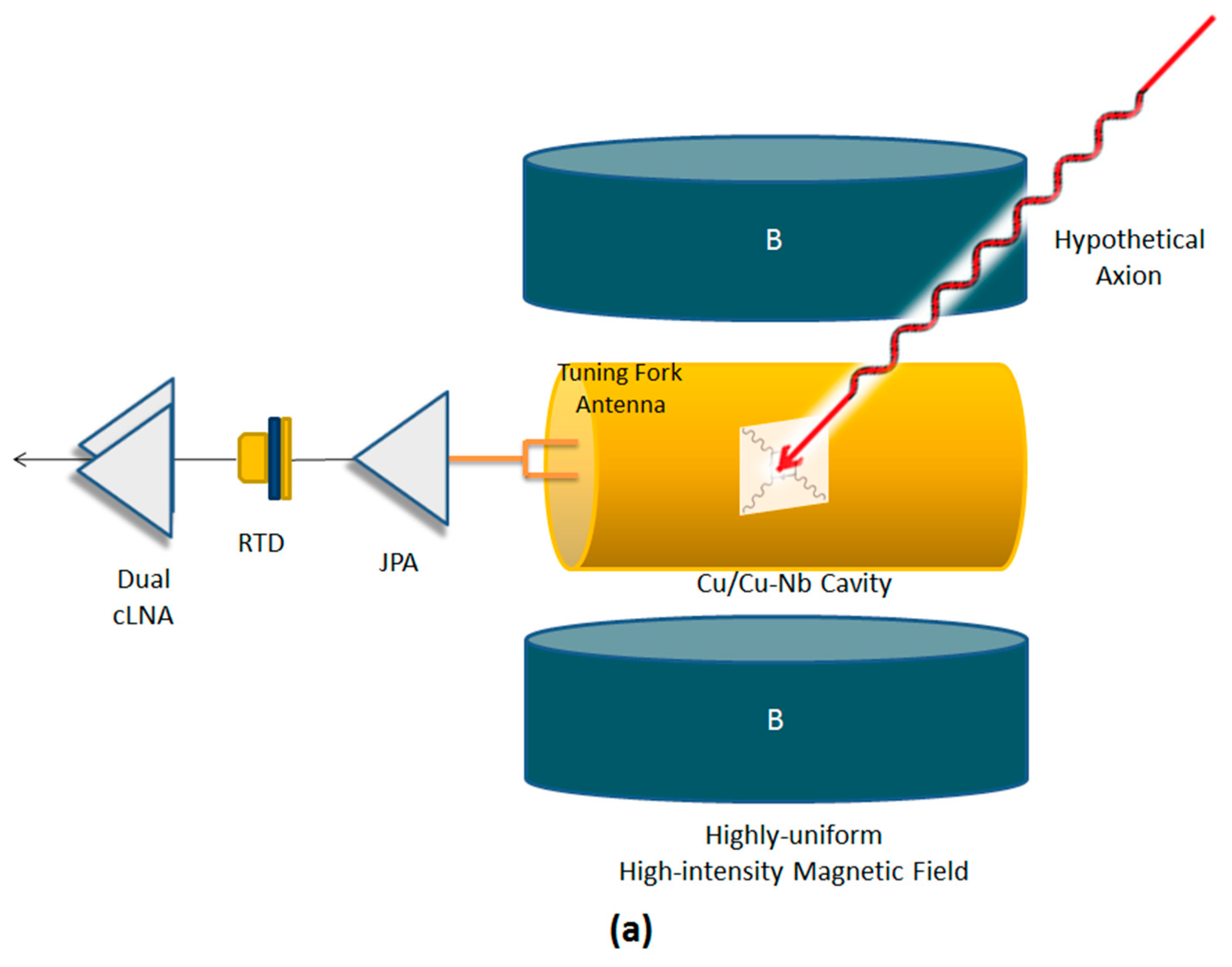
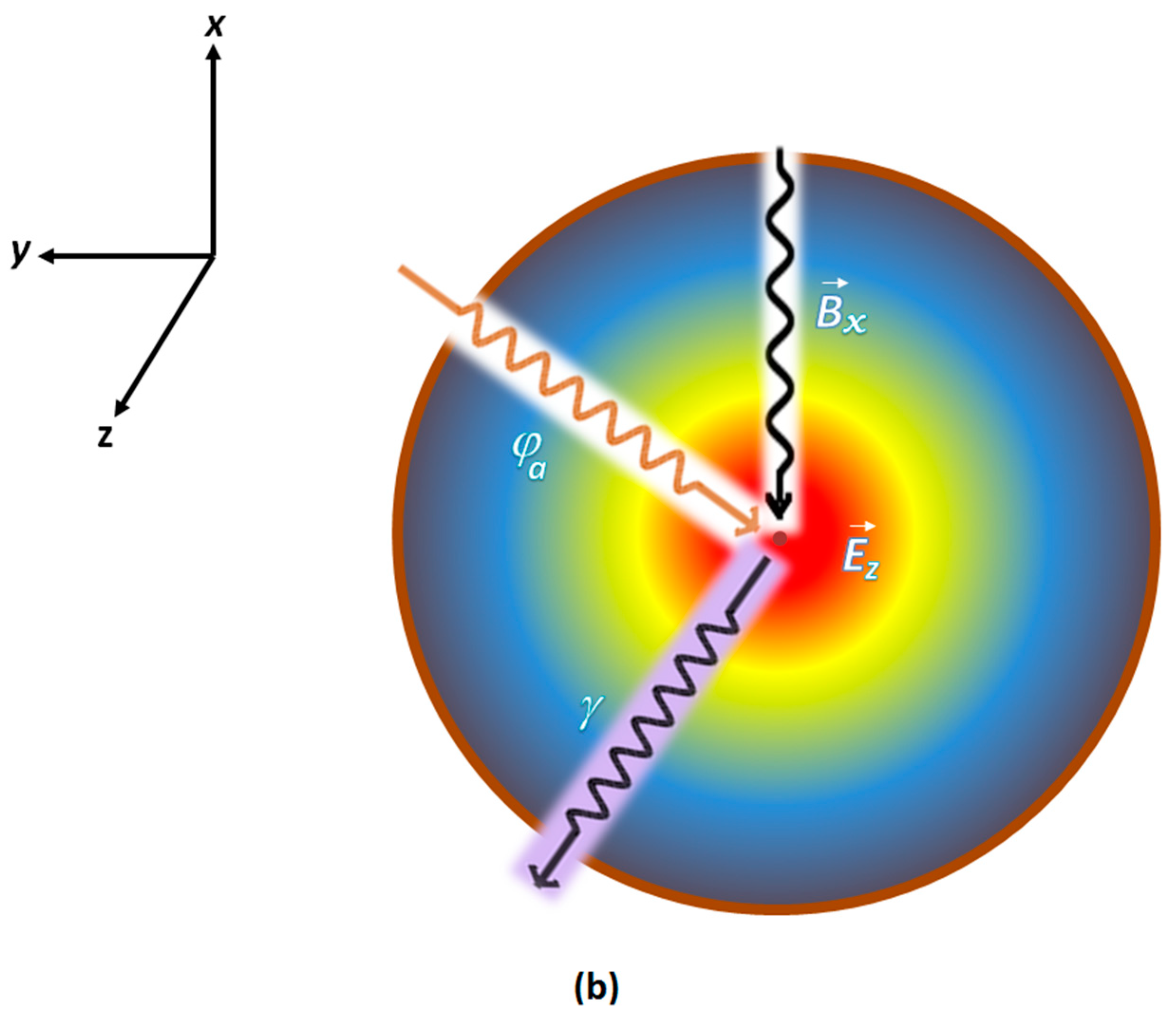
3. The Experiment
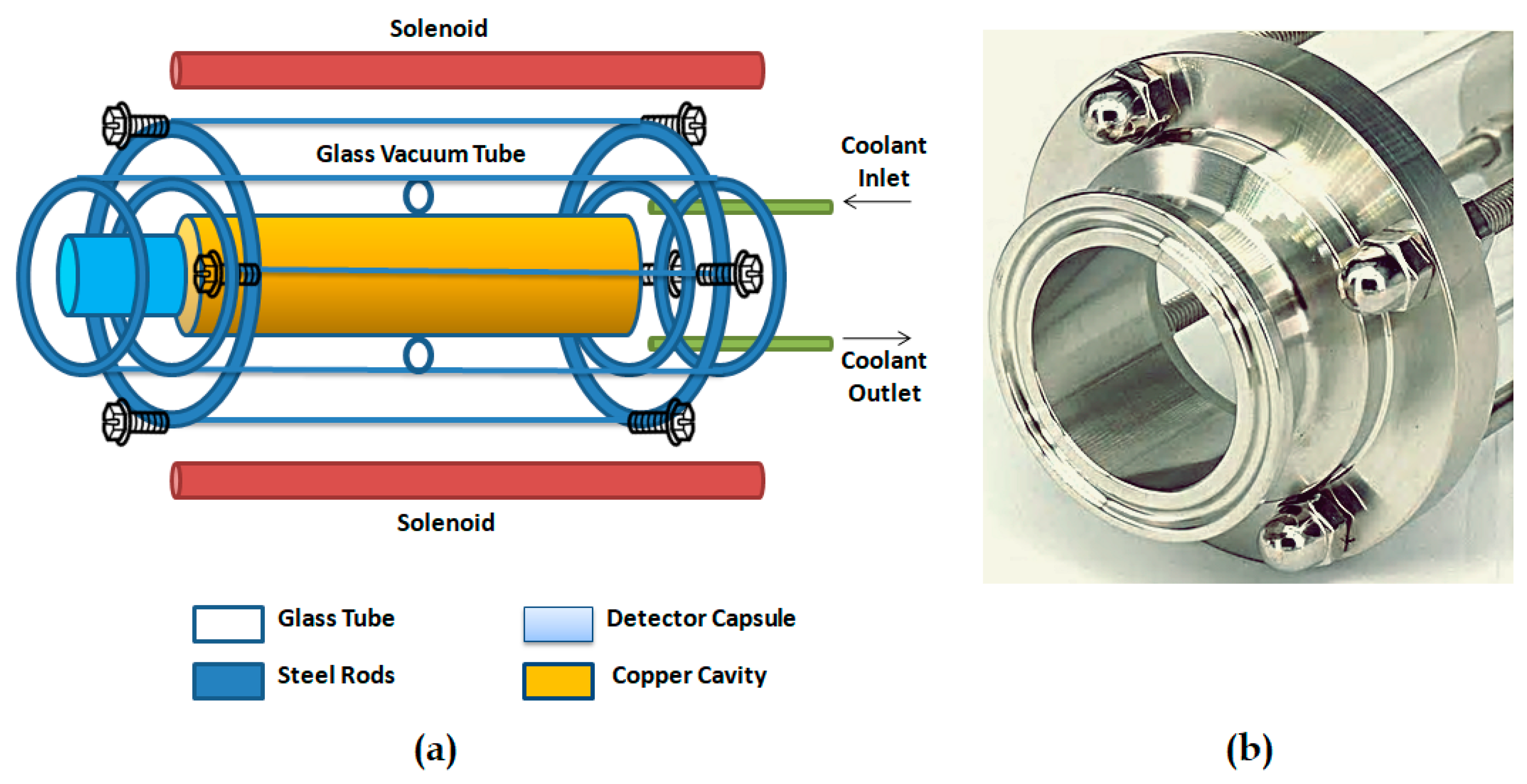
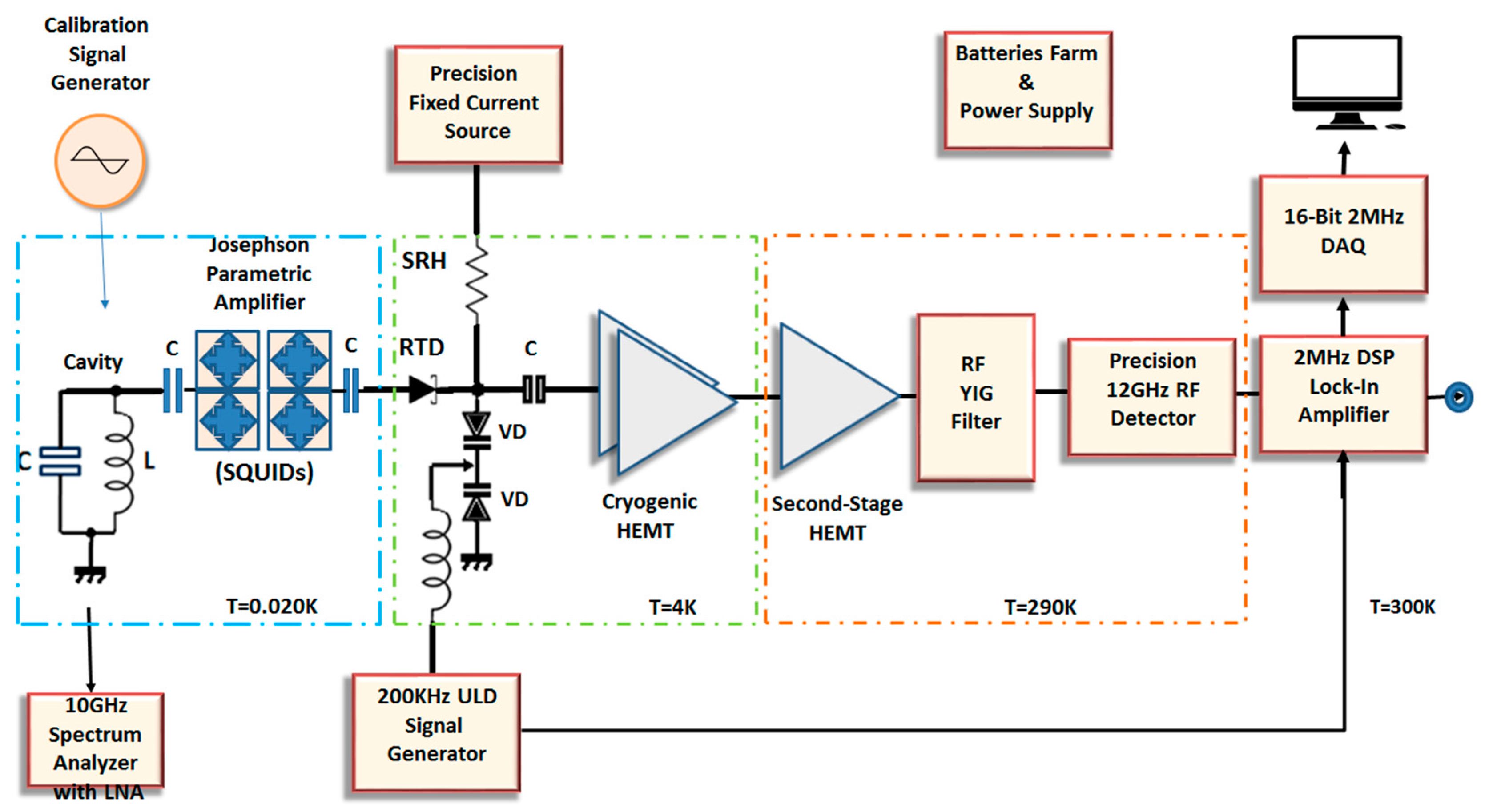
3.1. Detection Scheme
3.2. Noise Registry:
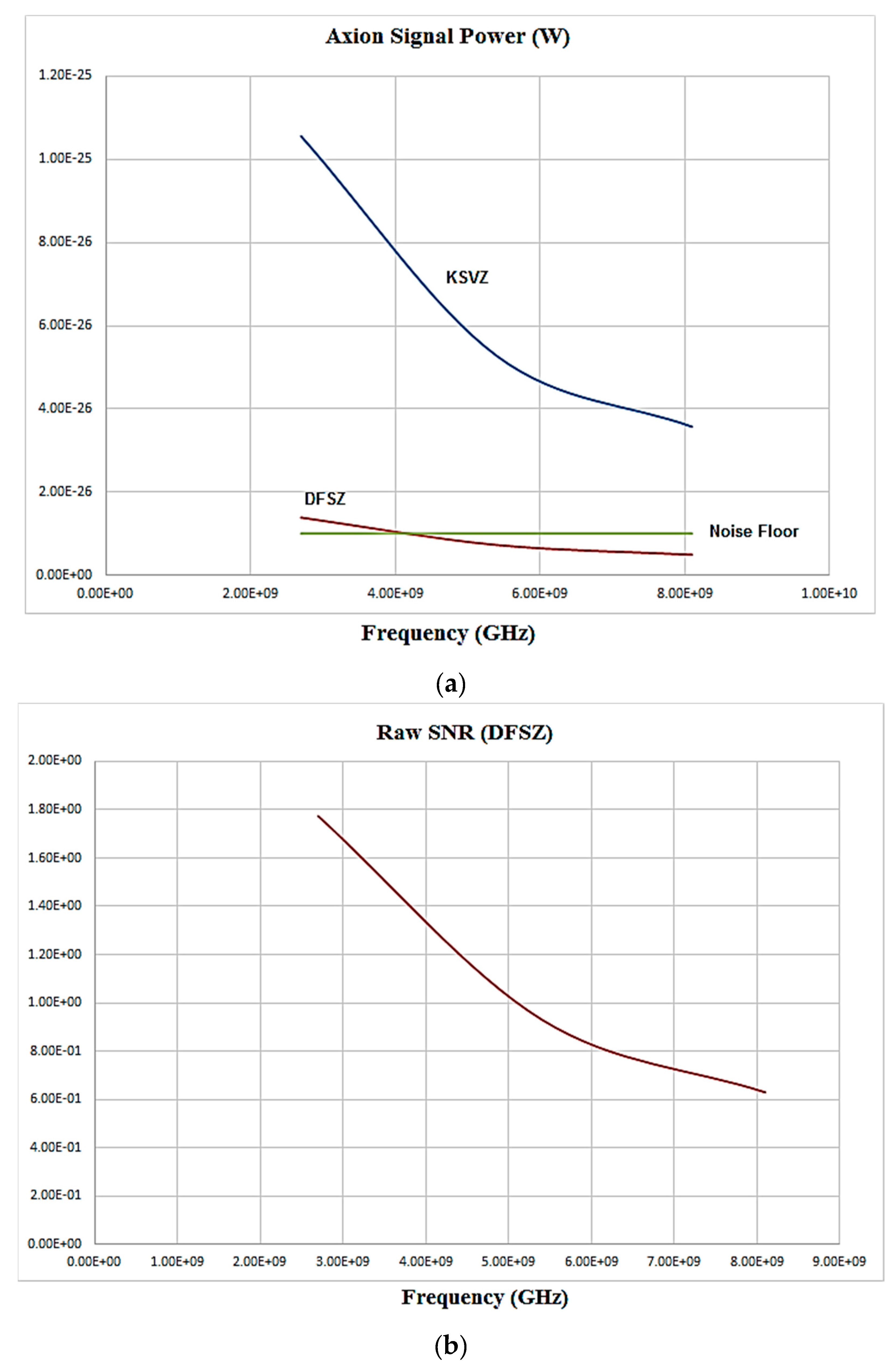
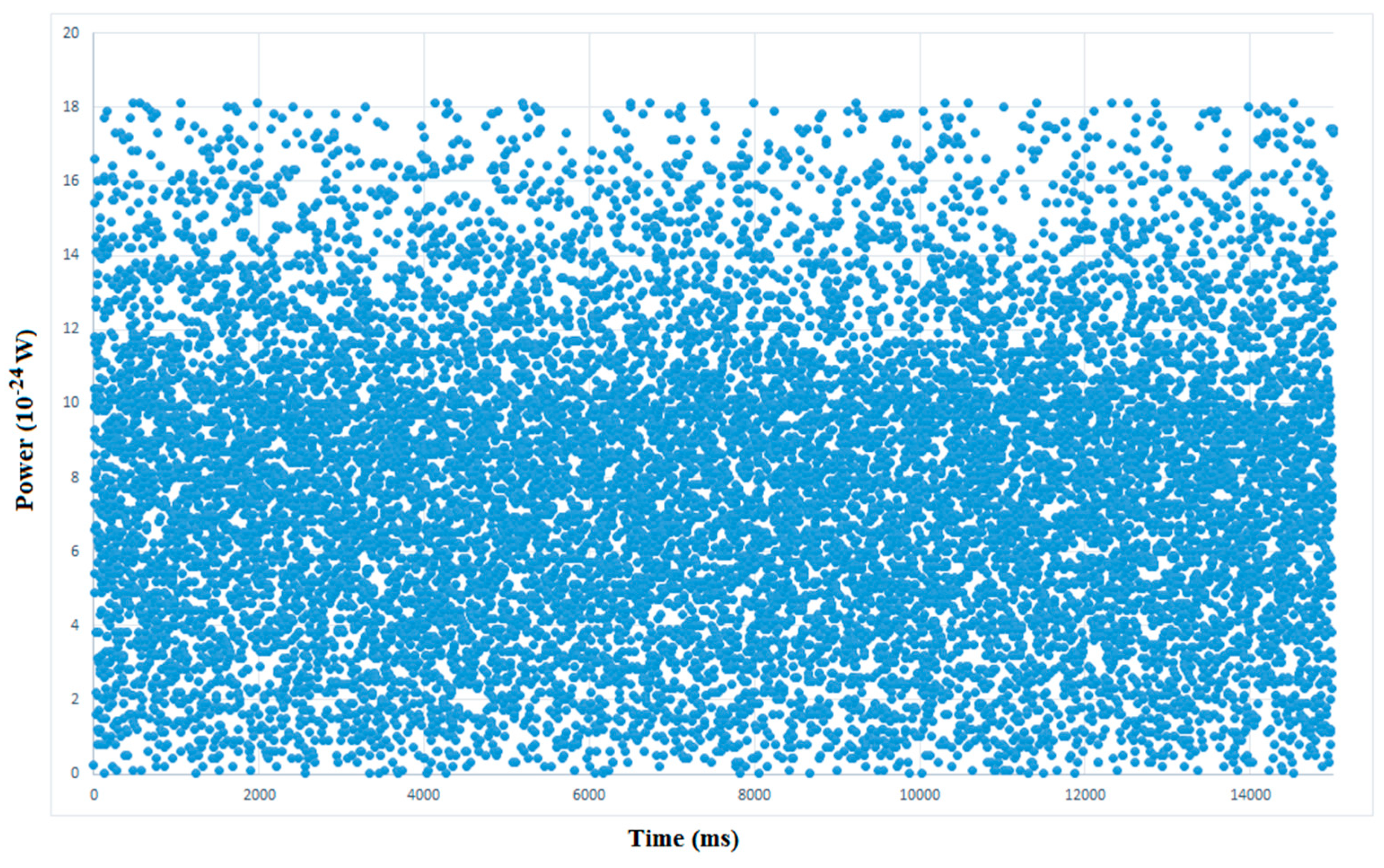
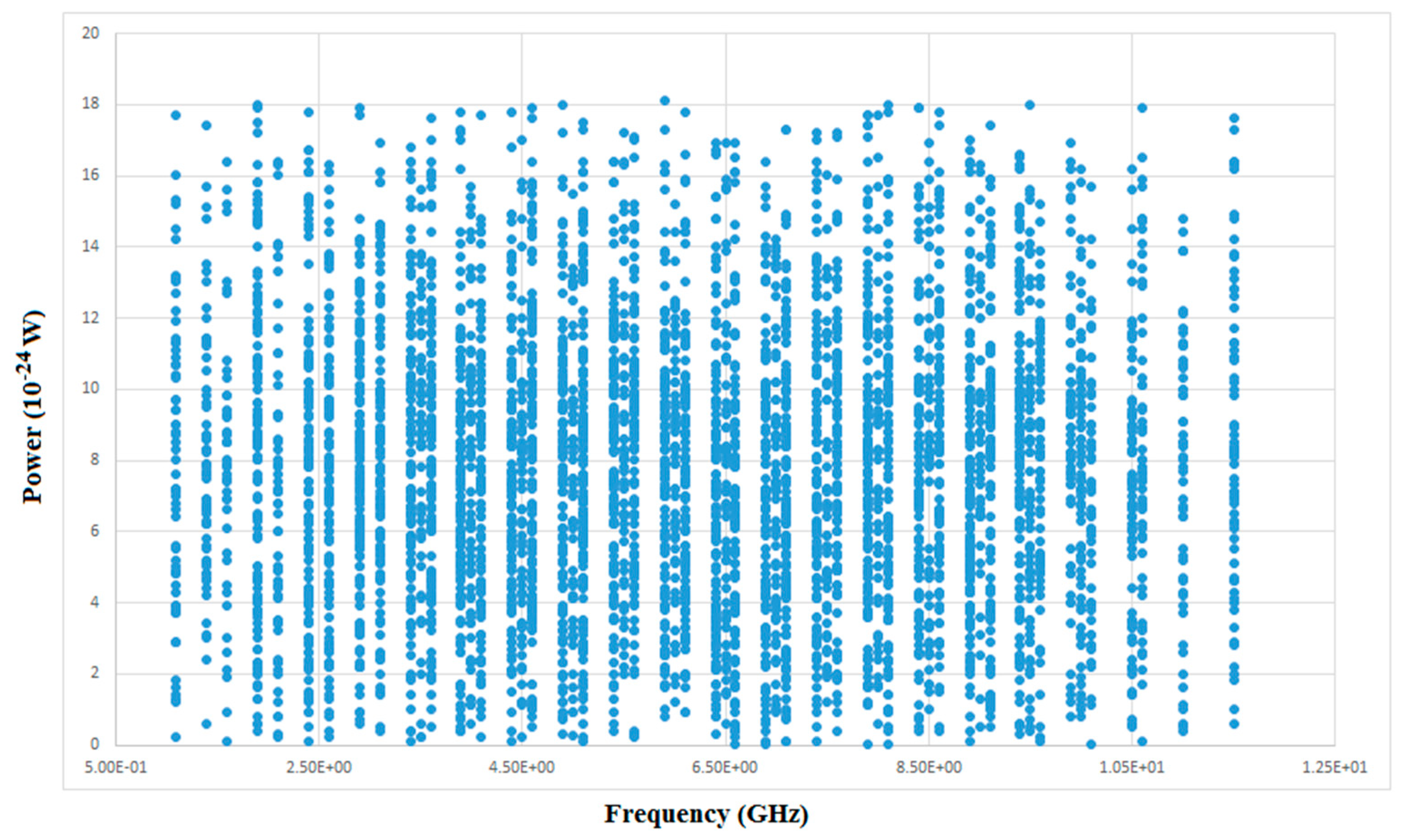
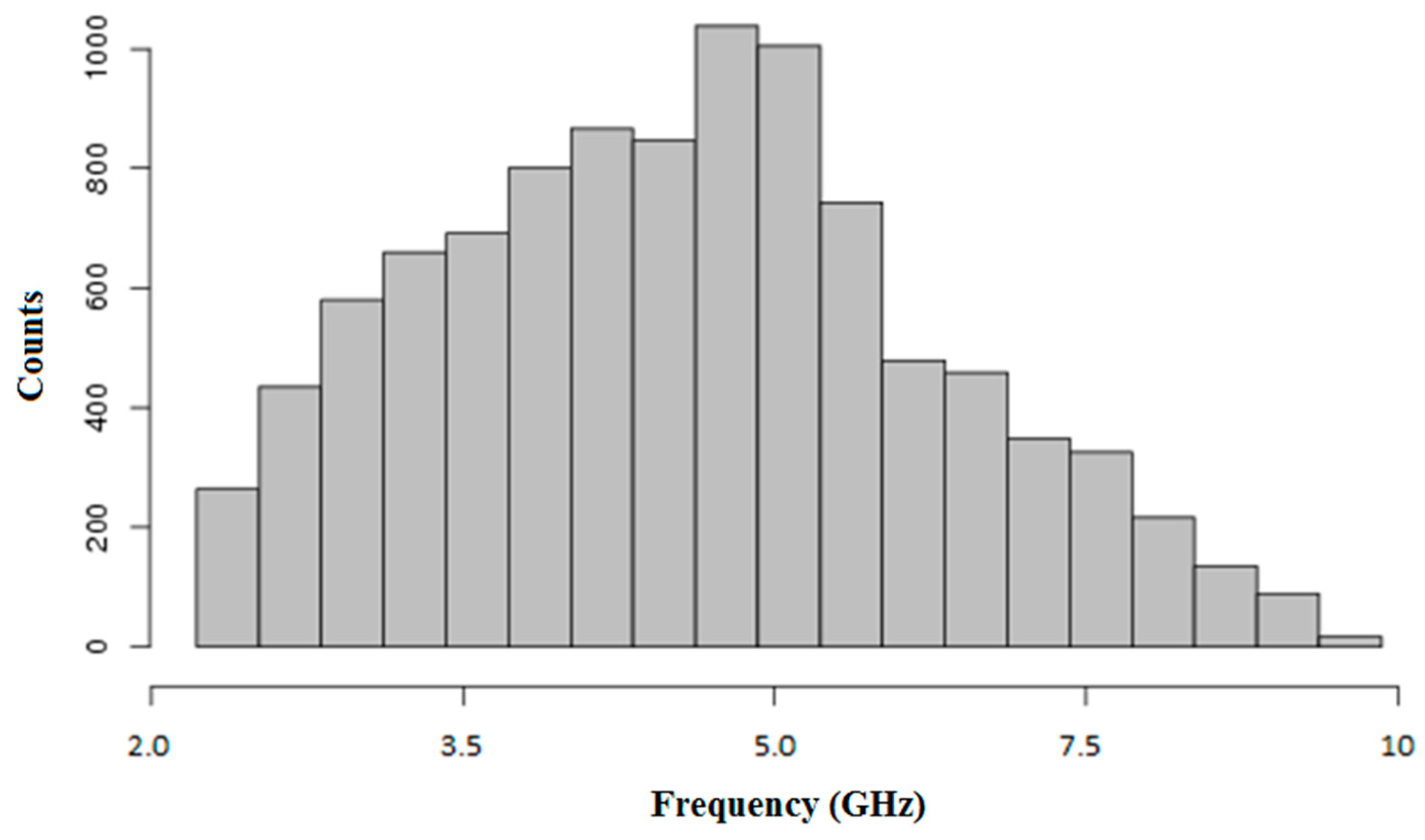
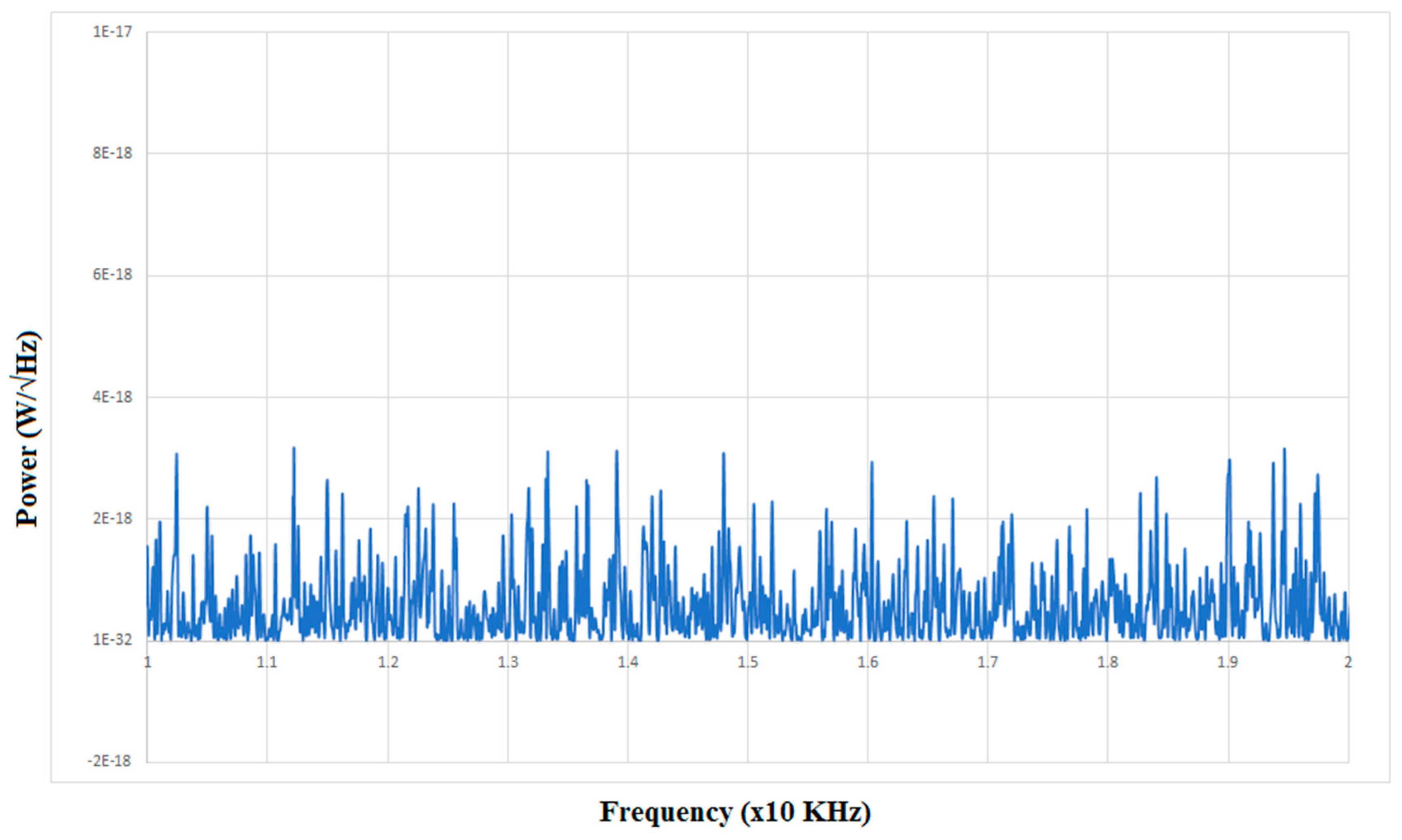
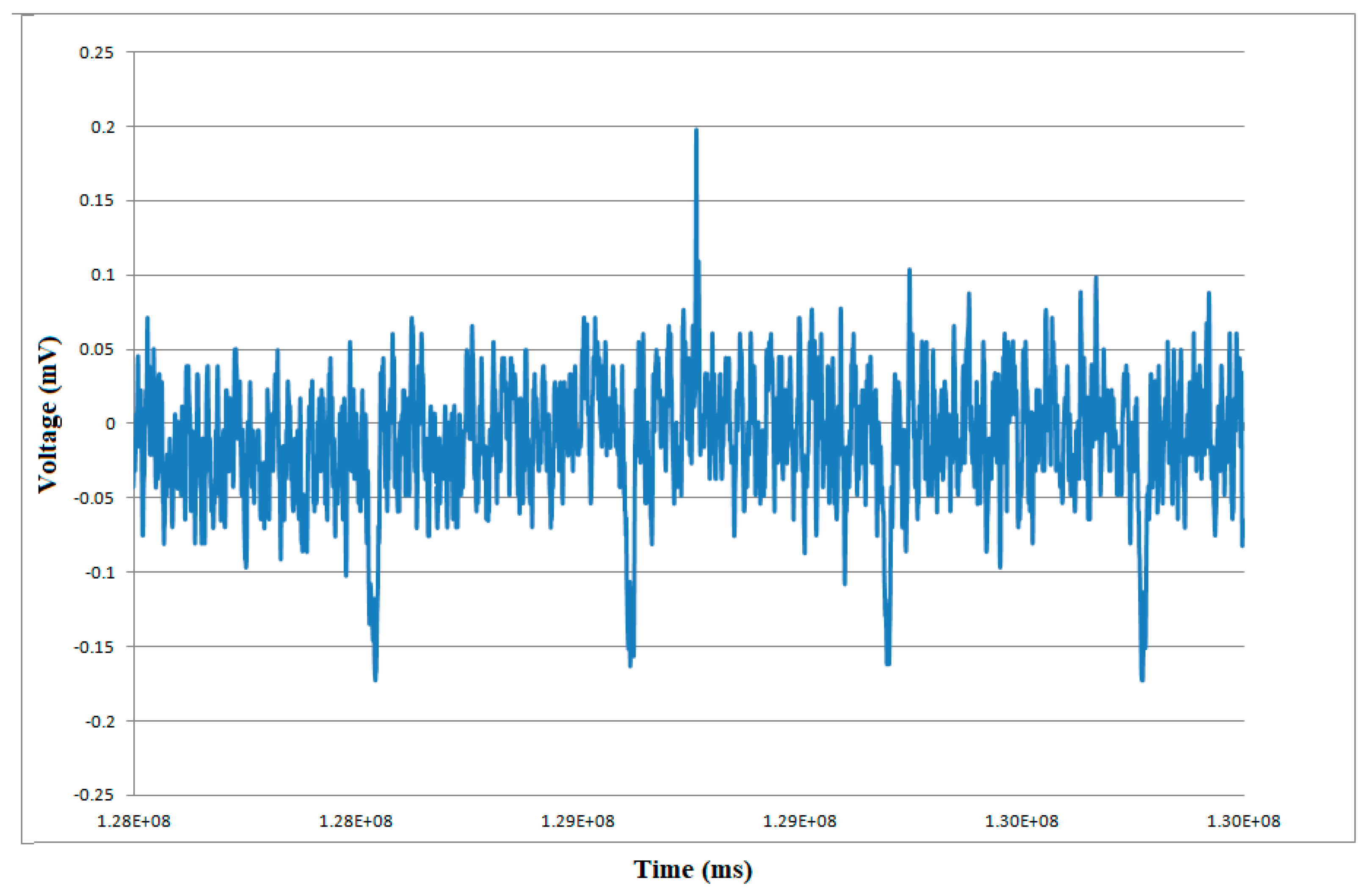
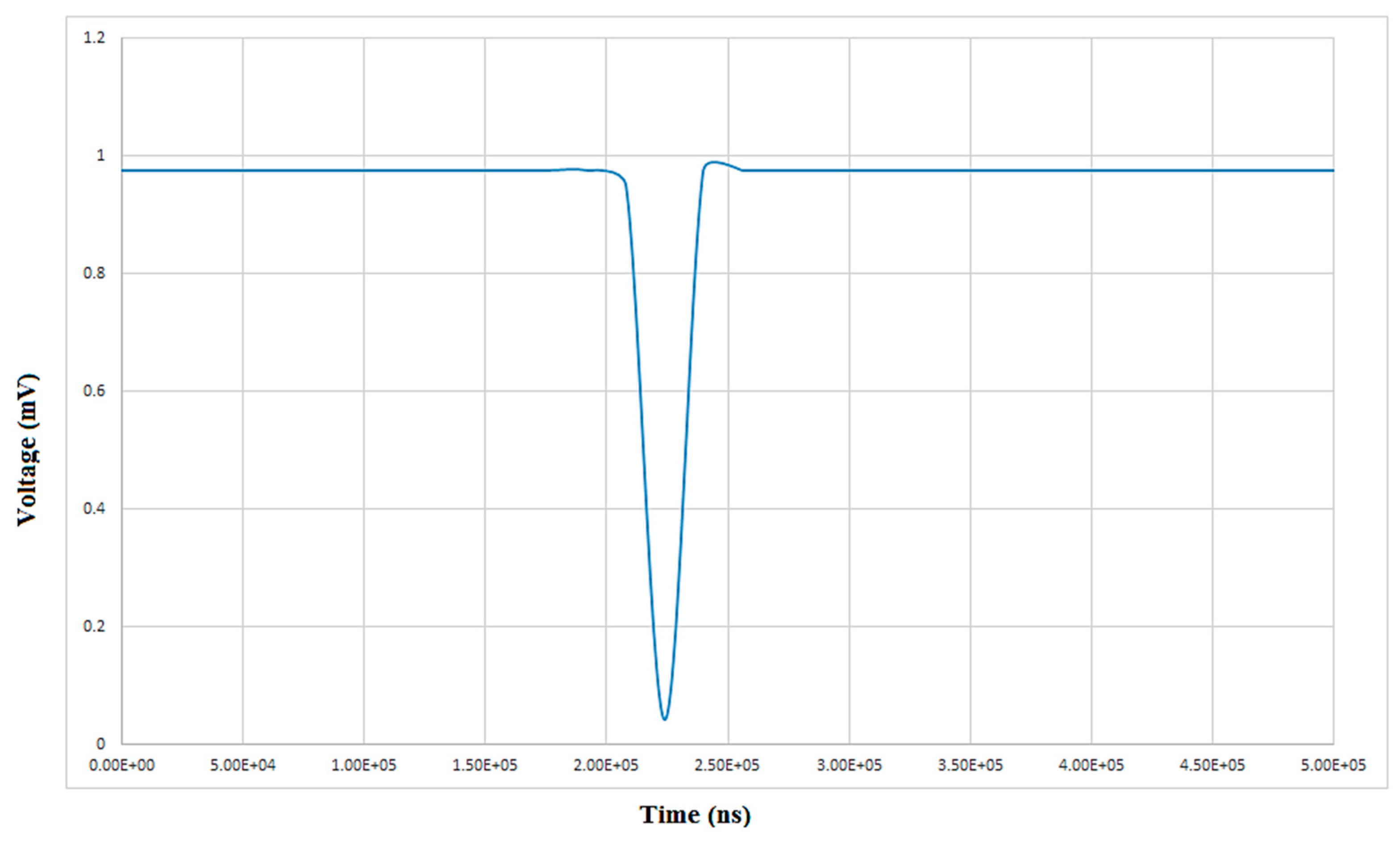
4. Preliminary Tests
5. Discussion and Conclusions
Supplementary Materials
Acknowledgments
Conflicts of Interest
References
- Seigar, M.S. The Dark Matter in the Universe. In Cold Dark Matter, Hot Dark Matter, and Their Alternatives; Morgan and Claypool: San Rafael, CA, USA, 2015. [Google Scholar]
- Marsh, D.J.E. Axion cosmology. Phys. Rept. 2016, 643, 1–79. [Google Scholar] [CrossRef]
- Visinelli, L.; Gondolo, P. Dark matter axions revisited. Phys. Rev. D 2009, 80, 035024. [Google Scholar] [CrossRef]
- Peccei, R.D.; Quinn, H.R. CP Conservation in the Presence of Instantons. Phys. Rev. Lett. 1977, 38, 1440. [Google Scholar] [CrossRef]
- Wilczek, F. Problem of Strong p and t Invariance in the Presence of Instantons. Phys. Rev. Lett. 1978, 40, 279. [Google Scholar] [CrossRef]
- Berezhiani, Z.G.; Khlopov, M.Y. Cosmology of spontaneously broken gauge family symmetry with axion solution of strong CP-problem. Z. Phys. C Part. Fields 1991, 49, 73. [Google Scholar] [CrossRef]
- Svrcek, P.; Witten, E. Axions in string theory. J. High Energ. Phys. 2016, 2016, 051. [Google Scholar] [CrossRef]
- Arvanitaki, A.; Dimopoulos, S.; Dubovsky, S.; Kaloper, N.; March-Russell, J. String axiverse. Phys. Rev. D 2010, 81, 123530. [Google Scholar] [CrossRef]
- Visinelli, L.; Vagnozzi, C. Cosmological window onto the string axiverse and the supersymmetry breaking scale. Phys. Rev. D 2019, 99, 063517. [Google Scholar] [CrossRef]
- Raffelt, G.G.; Rosenberg, L.J. Axions and other similar particles. Phys. Rev. D 2012, 86, 010001. [Google Scholar]
- Tanabashi, M.; Hagiwara, K.; Hikasa, K.; Nakamura, K.; Sumino, Y.; Takahashi, F.; Tanaka, J.; Agashe, K.; Aielli, G.; Amsler, C.; et al. Review of Particle Physics. Phys. Rev. D 2018, 98, 030001. [Google Scholar] [CrossRef]
- Cadamuro, D. Cosmological limits on axions and axion-like particles. arXiv 2012, arXiv:1210.3196. [Google Scholar]
- Kahn, Y.; Safdi, B.R.; Thaler, J. Broadband and resonant approaches to axion dark matter detection. Phys. Rev. Lett. 2016, 117, 141801. [Google Scholar] [CrossRef]
- Raffelt, G.; Stodolsky, L. Mixing of the photon with low-mass particles. Phys. Rev. D 1988, 37, 1237. [Google Scholar] [CrossRef]
- Sikivie, P.; Tanner, D.B.; van Bibber, K. Resonantly enhanced axion-photon regeneration. Phys. Rev. Lett. 2007, 98, 172002. [Google Scholar] [CrossRef]
- Sikivie, P. Axion Cosmology. Lect. Notes Phys. 2008, 741, 19–50. [Google Scholar]
- Gondolo, P.; Visinelli, L. Axion cold dark matter in view of BICEP2 results. Phys. Rev. Lett. 2014, 113, 011802. [Google Scholar] [CrossRef]
- Van Bibber, K.; Dagdeviren, N.R.; Koonin, S.E.; Kerman, A.K.; Nelson, H.N. Proposed experiment to produce and detect light pseudoscalars. Phys. Rev. Lett. 1987, 59, 759. [Google Scholar] [CrossRef]
- Asztalos, S.J.; Carosi, G.; Hagmann, C.; Kinion, D.; Van Bibber, K.; Hotz, M.; Rosenberg, L.J.; Rybka, G.; Hoskins, J.; Hwang, J.; et al. SQUID-based microwave cavity search for dark-matter axions. Phys. Rev. Lett. 2010, 104, 041301. [Google Scholar] [CrossRef]
- Majorovits, B. MADMAX: A new road to axion dark matter detection. J. Phys. Conf. Ser. 2017, 1342, 012098. [Google Scholar] [CrossRef]
- Redondo, J.; Ringwald, A. Light shining through walls. Contemp. Phys. 2011, 52, 211–236. [Google Scholar] [CrossRef]
- Ade, P.A.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. [Planck Collaboration] Planck 2015 results-xiii. cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar] [CrossRef]
- Bae, K.J.; Huh, J.H.; Kim, J.E. Update of axion CDM energy density. J. Cosmol. Astropart. Phys. 2008, 2008, 005. [Google Scholar] [CrossRef]
- Di Luzio, L.; Mescia, F.; Nardi, E. Window for preferred axion models. Phys. Rev. D 2017, 96, 075003. [Google Scholar] [CrossRef]
- Read, J.I. The local dark matter density. J. Phys. G: Nucl. Part. Phys. 2014, 41, 063101. [Google Scholar] [CrossRef]
- Dicke, R.H. The measurement of thermal radiation at microwave frequencies. In Classics in Radio Astronomy; Springer: Dordrecht, The Netherlands, 1946; pp. 106–113. [Google Scholar]
- McAllister, B.T.; Flower, G.; Ivanov, E.N.; Goryachev, M.; Bourhill, J.; Tobar, M.E. The ORGAN experiment: An axion haloscope above 15 GHz. Phys. Dark Universe 2017, 18, 67–72. [Google Scholar] [CrossRef]
- Bukhari, M.H.S.; Shah, Z.H. An Experiment and Detection Scheme for Cavity-Based Light Cold Dark Matter Particle Searches. Adv. High Energy Phys. 2017, 2017, 6432354. [Google Scholar] [CrossRef]
- Roy, A.; Devoret, M. Introduction to parametric amplification of quantum signals with Josephson circuits. C.R. Phys. 2016, 17, 740–755. [Google Scholar] [CrossRef]
- Beltran, M.A.C. Development of a Josephson Parametric Amplifier for the Preparation and Detection of Nonclassical States of Microwave Fields. Ph.D. Thesis, University of Colorado at Boulder, Boulder, CO, USA, 2010. [Google Scholar]
- Yurke, B.; Kaminsky, P.G.; Miller, R.E.; Whittaker, E.A.; Smith, A.D.; Silver, A.H.; Simon, R.W. Observation of 4.2-K equilibrium-noise squeezing via a Josephson-parametric amplifier. Phys. Rev. Lett. 1988, 60, 764–767. [Google Scholar] [CrossRef]
- Yurke, B.; Corruccini, L.R.; Kaminsky, P.G.; Rupp, L.W.; Smith, A.D.; Silver, A.H.; Simon, R.W.; Whittaker, E.A. Observation of parametric amplification and deamplification in a Josephson parametric amplifier. Phys. Rev. A 1989, 39, 2519. [Google Scholar] [CrossRef]
- Macklin, C.; O’Brien, K.; Hover, D.; Schwartz, M.E.; Bolkhovsky, V.; Zhang, X.; Oliver, W.D.; Siddiqi, I. A near-quantum-limited Josephson traveling-wave parametric amplifier. Science 2015, 350, 307–310. [Google Scholar] [CrossRef]
- Nag, B.R. Resonant Tunneling Diode. In Physics of Quantum Well Devices; Springer: Dordrecht, The Netherlands, 2002; pp. 188–201. [Google Scholar]
- Sollner, T.C.L.G.; Le, H.Q.; Brown, E.L. Microwave and Millimeter-Wave Resonant Tunneling Devices; Technical Report for Electronics and Electrical Engineering; NASA: Lexington, MA, USA, January 1988.
- Doychinov, V.; Steenson, D.P.; Patel, H. Resonant-Tunneling Diode Based Reflection Amplifier. In Proceedings of the 22nd European Workshop on Heterostructure Technology (HETECH), Glasgow, UK, 9–11 September 2013. [Google Scholar]
- Dubois, J.; Jullien, T.; Portier, F.; Roche, P.; Cavanna, A.; Jin, Y.; Glattli, D.C. Minimal-excitation states for electron quantum optics using levitons. Nature 2013, 502, 659–663. [Google Scholar] [CrossRef]
- Kasjoo, S.R. Novel Electronic Nanodevices Operating in the TeraHertz Region. Ph.D. Thesis, University of Manchester, Manchester, UK, 2012. [Google Scholar]
- Qi, H.; Guo, W.; Li, Y.; Zhang, X.; Li, X. InP-based RTD/HEMT monolithic integration. Trans. Tianjin Univ. 2010, 16, 267–269. [Google Scholar] [CrossRef]
- Reydellet, L.H.; Roche, P.; Glattli, D.C.; Etienne, B.; Jin, Y. Quantum partition noise of photon-created electron-hole pairs. Phys. Rev. Lett. 2003, 90, 176803. [Google Scholar] [CrossRef]
- O’Hare, C.A.J.; Green, A.M. Axion astronomy with microwave cavity experiments. Phys. Rev. D 2017, 95, 063017. [Google Scholar] [CrossRef]
- Caldwell, A.; Dvali, G.; Majorovits, B.; Millar, A.; Raffelt, G.; Redondo, J.; Reimann, O.; Simon, F.; Steffen, F.; MADMAX Working Group. Dielectric haloscopes: A new way to detect axion dark matter. Phys. Rev. Lett. 2017, 118, 091801. [Google Scholar] [CrossRef]
- Battaglieri, M.; Belloni, A.; Chou, A.; Cushman, P.; Echenard, B.; Essig, R.; Estrada, J.; Feng, J.L.; Flaugher, B.; Fox, P.J.; et al. US cosmic visions: New ideas in dark matter 2017: Community report. arXiv 2017, arXiv:1707.04591. [Google Scholar]
- Kawasaki, M.; Saikawa, K.I.; Sekiguchi, T. Axion dark matter from topological defects. Phys. Rev. D 2015, 91, 065014. [Google Scholar] [CrossRef]
- Shellard, E.P.S.; Battye, R.A. Spectrum of radiation from axionic strings. Nucl. Phys. B 1999, 72, 88. [Google Scholar]
- Ballesteros, G.; Redondo, J.; Ringwald, A.; Tamarit, C. Unifying inflation with the axion, dark matter, baryogenesis, and the seesaw mechanism. Phys. Rev. Lett. 2017, 118, 071802. [Google Scholar] [CrossRef]
- Ballesteros, G.; Redondo, J.; Ringwald, A.; Tamarit, C. Standard Model—axion—seesaw—Higgs portal inflation. Five problems of particle physics and cosmology solved in one stroke. J. Cosmol. Astropart. Phys. 2017, 08, 001. [Google Scholar] [CrossRef]
- Borsanyi, S.; Fodor, Z.; Kampert, K.H.; Katz, S.D.; Kawanai, T.; Kovacs, T.G.; Ringwald, A. Lattice QCD for cosmology. Nature 2016, 539, 69–71. [Google Scholar] [CrossRef]
- Khlopov, M.Y.; Sakharov, A.S.; Sokoloff, D.D. The nonlinear modulation of the density distribution in standard axionic CDM and its cosmological impact. Nucl. Phys. B 1999, 72, 105–109. [Google Scholar] [CrossRef]
- Gorghetto, M.; Hardy, E.; Villadoro, G. Axions from strings: The attractive solution. J. High Energy Phys. 2018, 7, 151. [Google Scholar] [CrossRef]
- Buschmann, M.; Foster, J.W.; Safdi, B.R. Early-Universe simulations of the cosmological axion. arXiv 2019, arXiv:1906.00967. [Google Scholar]
- Beck, C. Possible resonance effect of axionic dark matter in Josephson junctions. Phys. Rev. Lett. 2013, 111, 231801. [Google Scholar] [CrossRef]
- Freese, K.; Lisanti, M.; Savage, C. Annual modulation of dark matter: A review. arXiv 2012, arXiv:1209.3339. [Google Scholar]
- Everitt, C.F.; DeBra, D.B.; Parkinson, B.W.; Turneaure, J.P.; Conklin, J.W.; Heifetz, M.I.; Al-Meshari, M. Gravity probe B: Final results of a space experiment to test general relativity. Phys. Rev. Lett. 2011, 106, 221101. [Google Scholar] [CrossRef]
- Iorio, L.; Lichtenegger, H.I.; Ruggiero, M.L.; Corda, C. Phenomenology of the Lense-Thirring effect in the solar system. Astrophys. Space Sci. 2011, 331, 351–395. [Google Scholar] [CrossRef]
- Renzetti, G. History of the attempts to measure orbital frame-dragging with artificial satellites. Cent. Eur. J. Phys. 2013, 11, 531–544. [Google Scholar] [CrossRef]
- Lucchesi, D.M.; Anselmo, L.; Bassan, M.; Magnafico, C.; Pardini, C.; Peron, R.; Pucacco, G.; Visco, M. General Relativity Measurements in the Field of Earth with Laser-Ranged Satellites: State of the Art and Perspectives. Universe 2019, 5, 141. [Google Scholar] [CrossRef]
- Barbieri, R.; Braggio, C.; Carugno, G.; Gallo, C.S.; Lombardi, A.; Ortolan, A.; Pengo, R.; Ruoso, G.; Speake, C.C. Searching for galactic axions through magnetized media: The QUAX proposal. Phys. Dark Universe 2017, 15, 135–141. [Google Scholar] [CrossRef]
- Devoret, M.H.; Schoelkopf, R.J. Superconducting circuits for quantum information: An outlook. Science 2013, 339, 1169–1174. [Google Scholar] [CrossRef]
- Bergeal, N.; Schackert, F.; Metcalfe, M.; Vijay, R.; Manucharyan, V.E.; Frunzio, L.; Devoret, M.H. Phase-preserving amplification near the quantum limit with a Josephson ring modulator. Nature 2010, 465, 64–68. [Google Scholar] [CrossRef]
- Manucharyan, V.E.; Boaknin, E.; Metcalfe, M.; Vijay, R.; Siddiqi, I.; Devoret, M. Microwave bifurcation of a Josephson junction: Embedding-circuit requirements. Phys. Rev. B 2007, 76, 014524. [Google Scholar] [CrossRef]
- Hatridge, M.; Shankar, S.; Mirrahimi, M.; Schackert, F.; Geerlings, K.; Brecht, T.; Schoelkopf, R.J. Quantum back-action of an individual variable-strength measurement. Science 2013, 339, 178–181. [Google Scholar] [CrossRef]
- Crescini, N.; Braggio, C.; Carugno, G.; Falferi, P.; Ortolan, A.; Ruoso, G. Improved constraints on monopole–dipole interaction mediated by pseudo-scalar bosons. Phys. Lett. B 2017, 773, 677–680. [Google Scholar] [CrossRef]
- Opremcak, A.; Pechenezhskiy, I.V.; Howington, C.; Christensen, B.G.; Beck, M.A.; Leonard, E.; Thorbeck, T. Measurement of a superconducting qubit with a microwave photon counter. Science 2018, 361, 1239–1242. [Google Scholar] [CrossRef]
- Robertson, S. Optical Kerr effect in vacuum. Phys. Rev. A 2019, 100, 063831. [Google Scholar] [CrossRef]
- Braaten, E.; Zhang, H. Axion stars. arXiv 2018, arXiv:1810.11473. [Google Scholar]
- Ruffini, R.; Bonazzola, S. Systems of selfgravitating particles in general relativity and the concept of equation of state. Phys. Rev. 1969, 187, 1767–1783. [Google Scholar] [CrossRef]
- Colpi, M.; Shapiro, S.L.; Wasserman, I. Boson stars: Gravitational equilibria of self-interacting scalar fields. Phys. Rev. Lett. 1986, 57, 2485–2488. [Google Scholar] [CrossRef]
- Visinelli, L.; Baum, S.; Redondo, J.; Freese, K.; Wilczek, F. Dilute and dense axion stars. Phys. Lett. B 2018, 777, 64–72. [Google Scholar] [CrossRef]
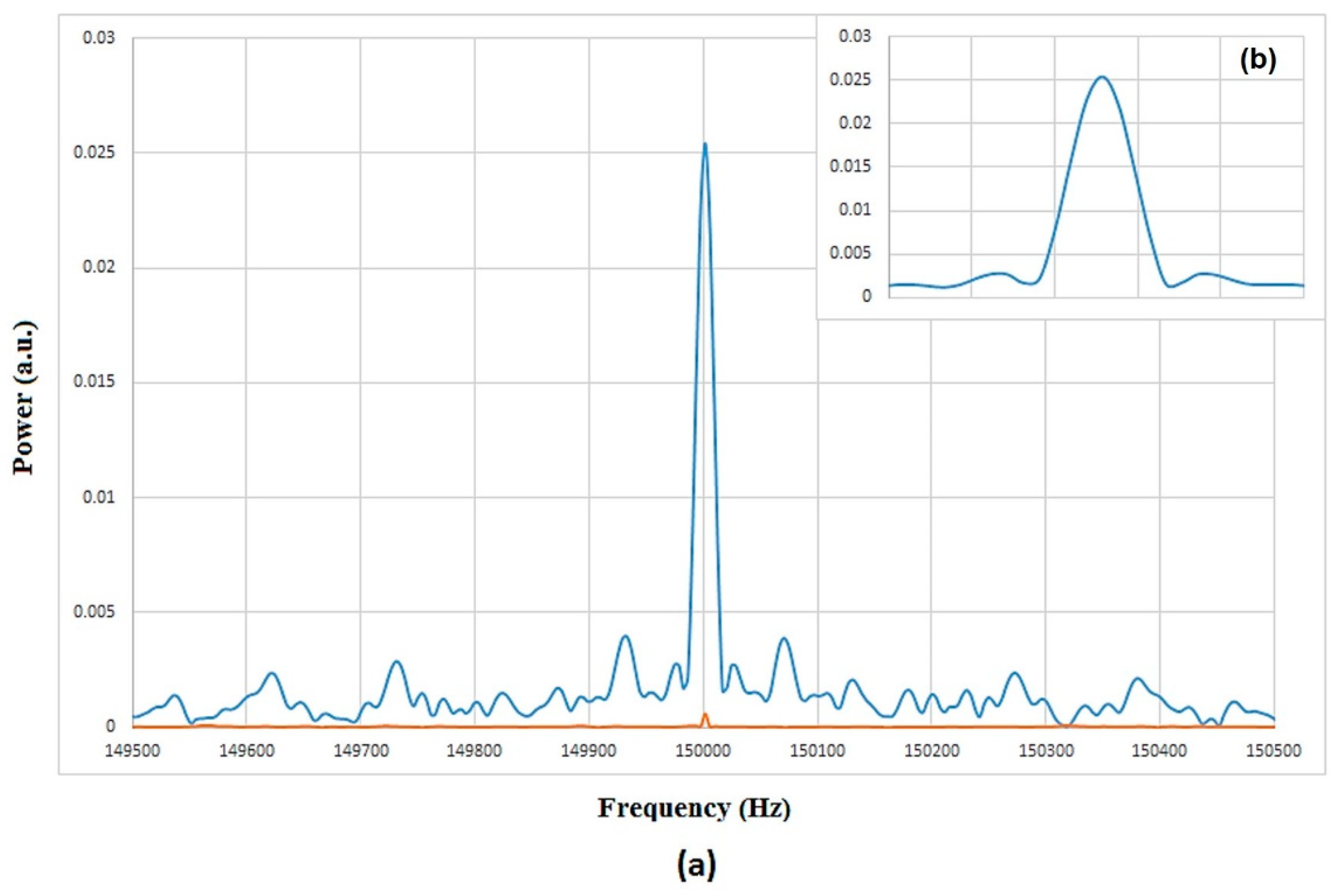
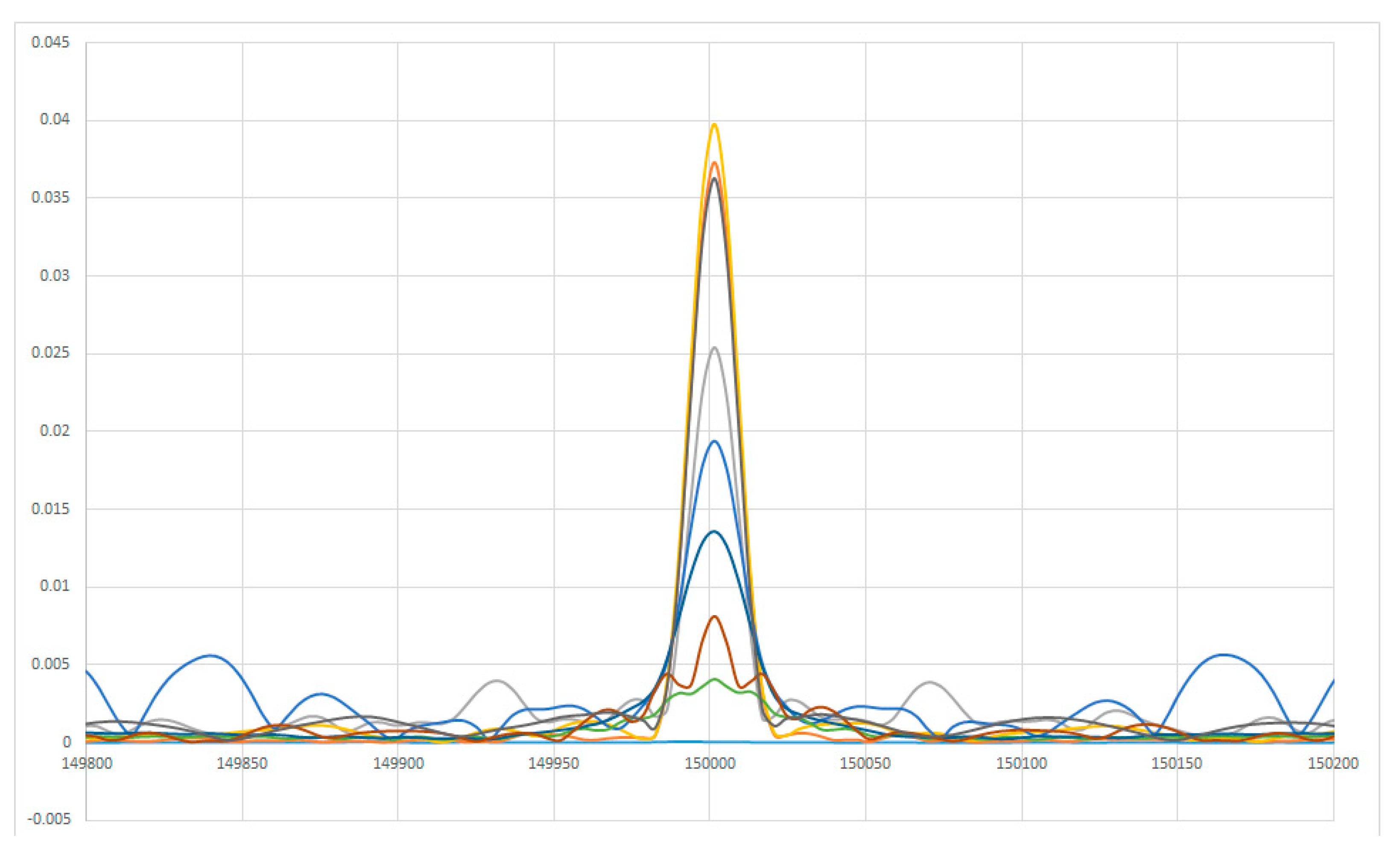
| Parameter | Value/Range |
|---|---|
| Mass (ma) | 22.5 ± 0.5 μeV to 112.5 ± 0.5 μeV |
| Corresponding Resonant Frequency (Axion Compton Frequency) (νres/νc) | 5.4 ± 0.12 GHz to 27.0 ± 0.12 GHz |
| Mean Axion Mass (〈m〉) | 101.25 + 0.5 μeV |
| Axion Coupling/Decay Constant (fa) | 1011 to 1010 GeV |
| Cosmological Axion Model | KSVZ/DFSZ |
| Axion-γγ Coupling (gaγγ) | 10−15 to 10−13 GeV−1 |
| Corresponding Compton Wavelength (λc) | 0.05 to 0.01 m |
| Galactic Axion Velocity (va) | 2.3 × 105 ms−1 |
| DM Density (Ωdm) | 0.3 0.1 GeV·cm3 |
| Axion Density (Ωa) | 0.323 ± 0.1 GeV·cm3 |
| Cavity Radius (r) | 2.1 cm to 4.2 mm |
| Cavity Length (l) | 24 cm |
| Cavity Mode (TMφρz) and Form Factor (Cφρz) | TM010~0.5 |
| Cavity Quality Factor (Q0) | 0.75–1.0 × 105 |
| Magnetic Field Intensity (B) | 8.0–10.0 T |
| Component | Tphys (K) | TnK (%) | Gain (dB) |
|---|---|---|---|
| Cavity | 0.020 | 0.020 (0.2) | 0 |
| JPA | 0.020 | 1.2 (4) | 15–25 |
| RTD | 2.0–4.0 | 1.0 (1) | 5–10 |
| cHEMT | 1.2–2.0 | 2 (5) | 28–38 |
| HEMT | 290 | 65 (80) | 40 |
| Cables | Various | 8 (10) | −10 |
| Total | ~78 (~100) | 78–100 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bukhari, M.H.S. A Table-Top Pilot Experiment for Narrow Mass Range Light Cold Dark Matter Particle Searches. Universe 2020, 6, 28. https://doi.org/10.3390/universe6020028
Bukhari MHS. A Table-Top Pilot Experiment for Narrow Mass Range Light Cold Dark Matter Particle Searches. Universe. 2020; 6(2):28. https://doi.org/10.3390/universe6020028
Chicago/Turabian StyleBukhari, Masroor H. S. 2020. "A Table-Top Pilot Experiment for Narrow Mass Range Light Cold Dark Matter Particle Searches" Universe 6, no. 2: 28. https://doi.org/10.3390/universe6020028
APA StyleBukhari, M. H. S. (2020). A Table-Top Pilot Experiment for Narrow Mass Range Light Cold Dark Matter Particle Searches. Universe, 6(2), 28. https://doi.org/10.3390/universe6020028





