Influence of Cosmic Repulsion and Magnetic Fields on Accretion Disks Rotating around Kerr Black Holes
Abstract
Contents
1. Introduction
2. Role of Cosmic Repulsion
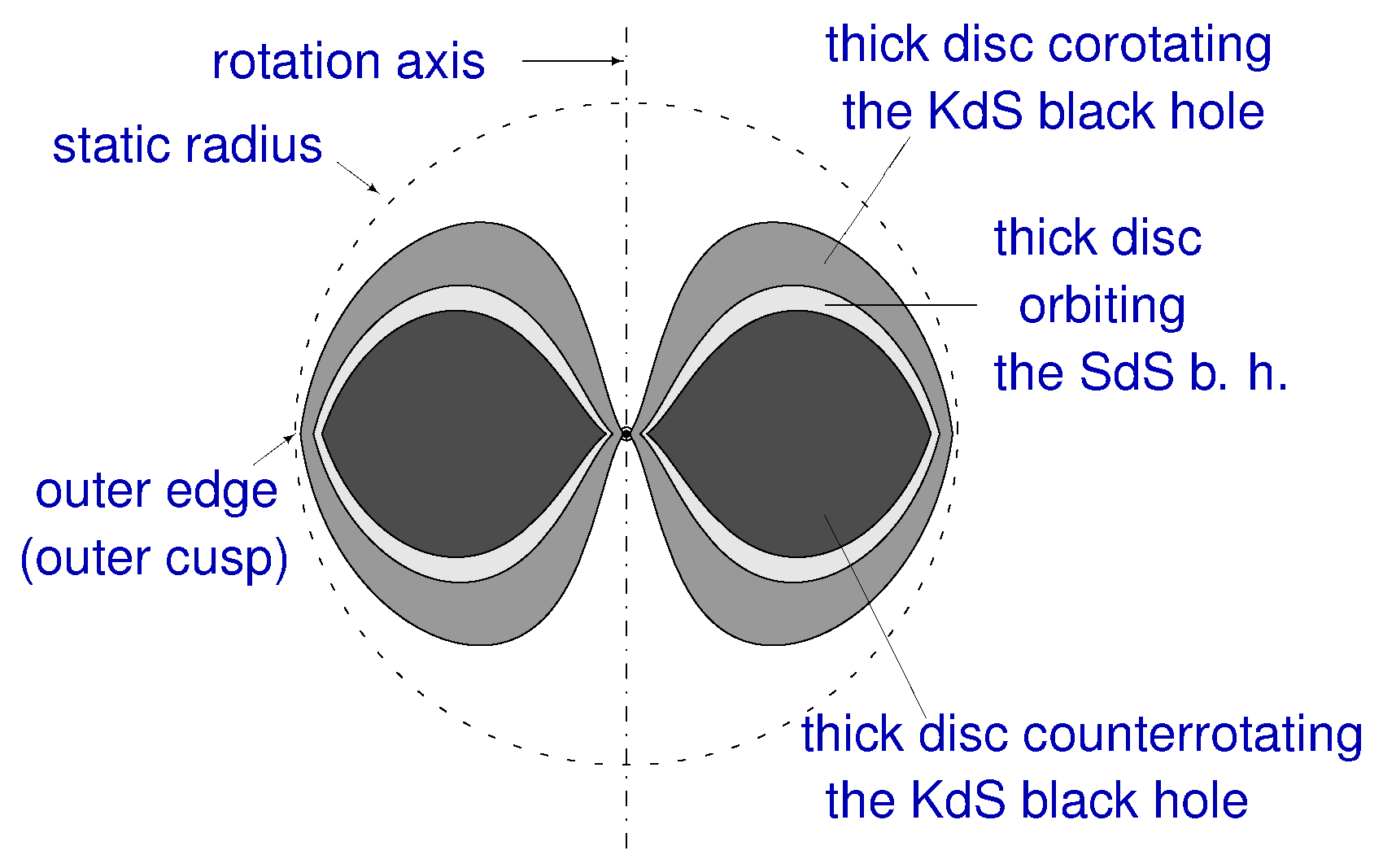
2.1. Kerr–de Sitter Black Holes and the Keplerian Disks
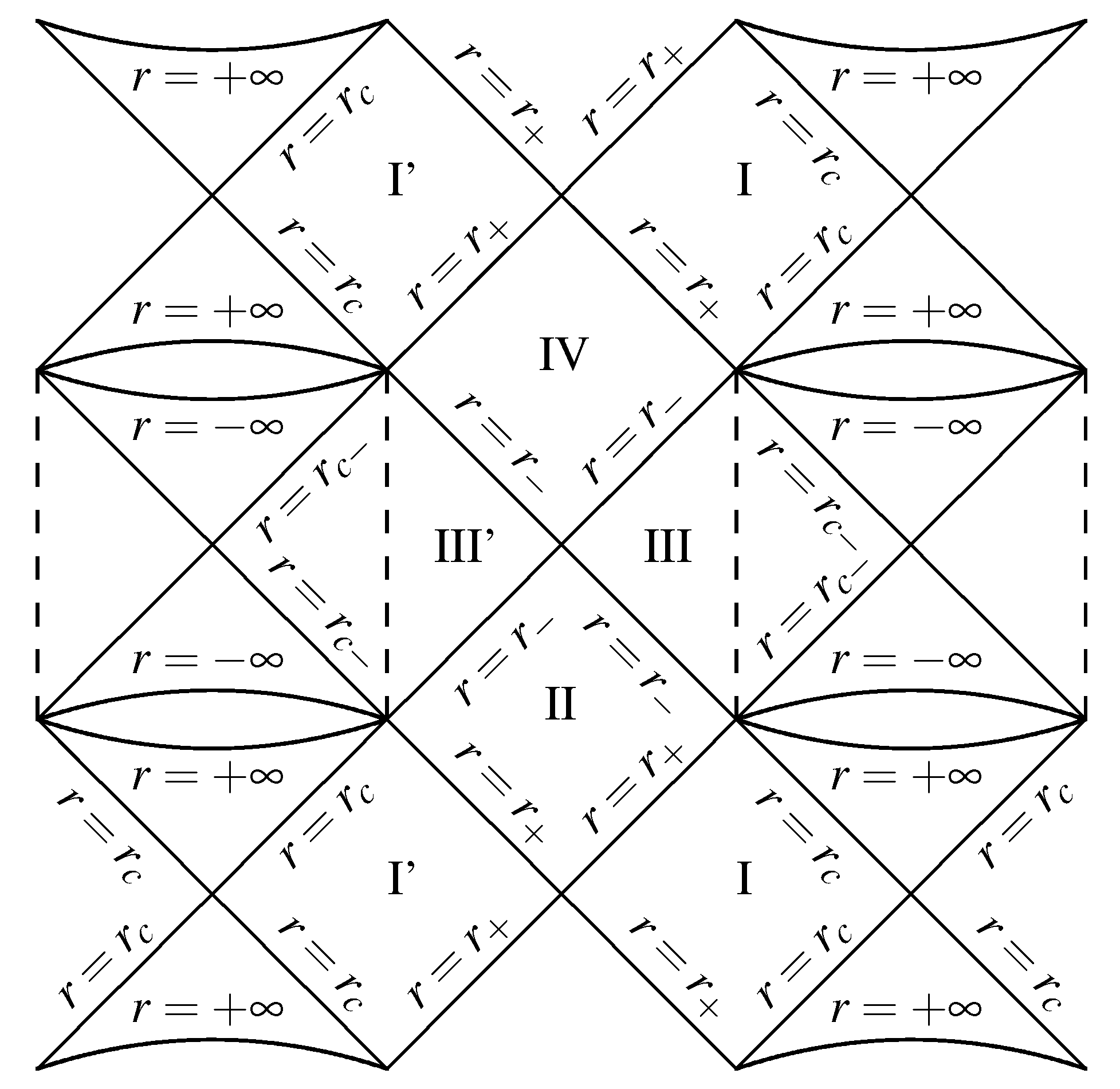
2.1.1. Kerr–de Sitter Spacetimes
2.1.2. Equatorial Motion in Kerr–de Sitter Spacetimes
2.1.2.1. Effective Potential
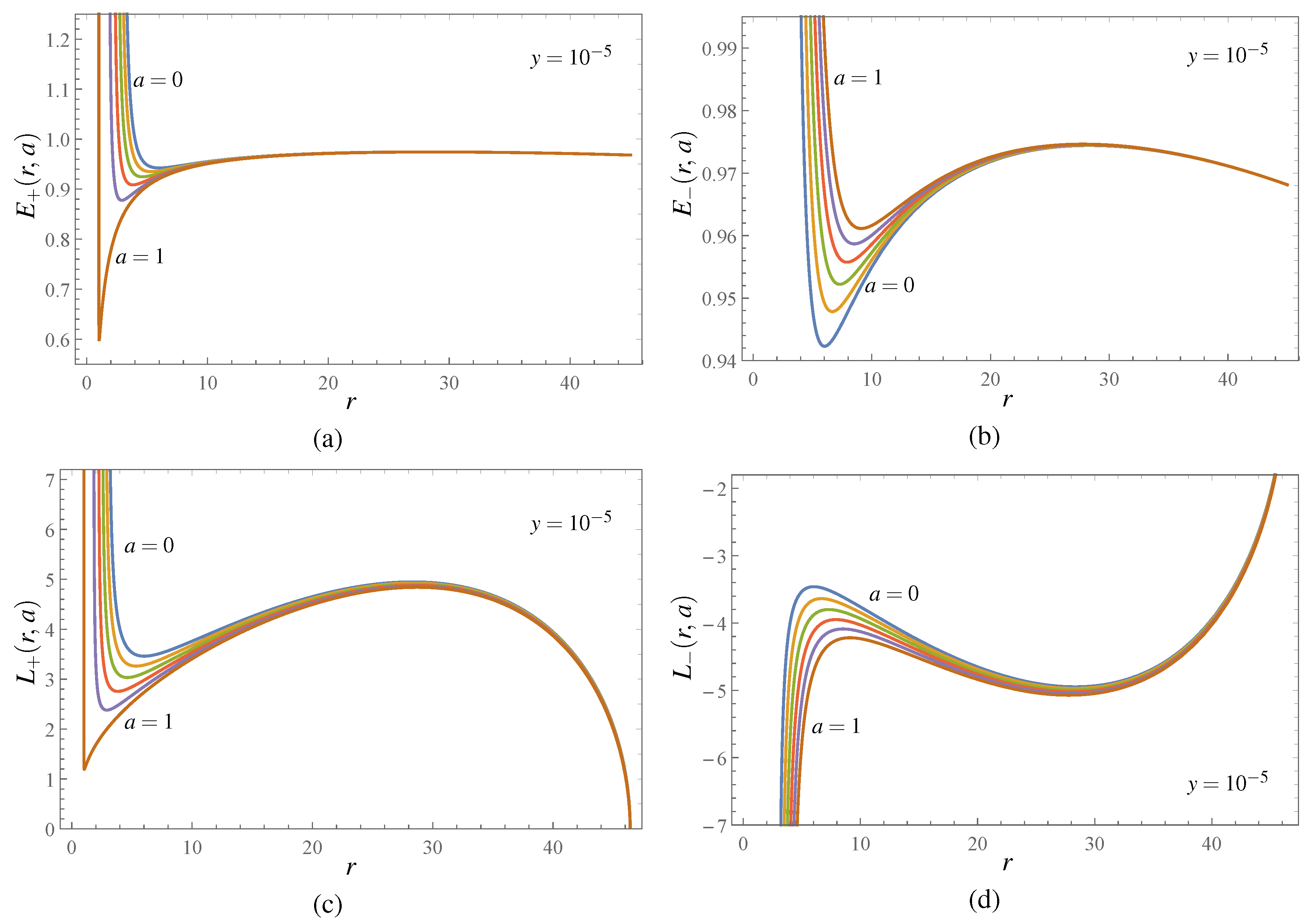
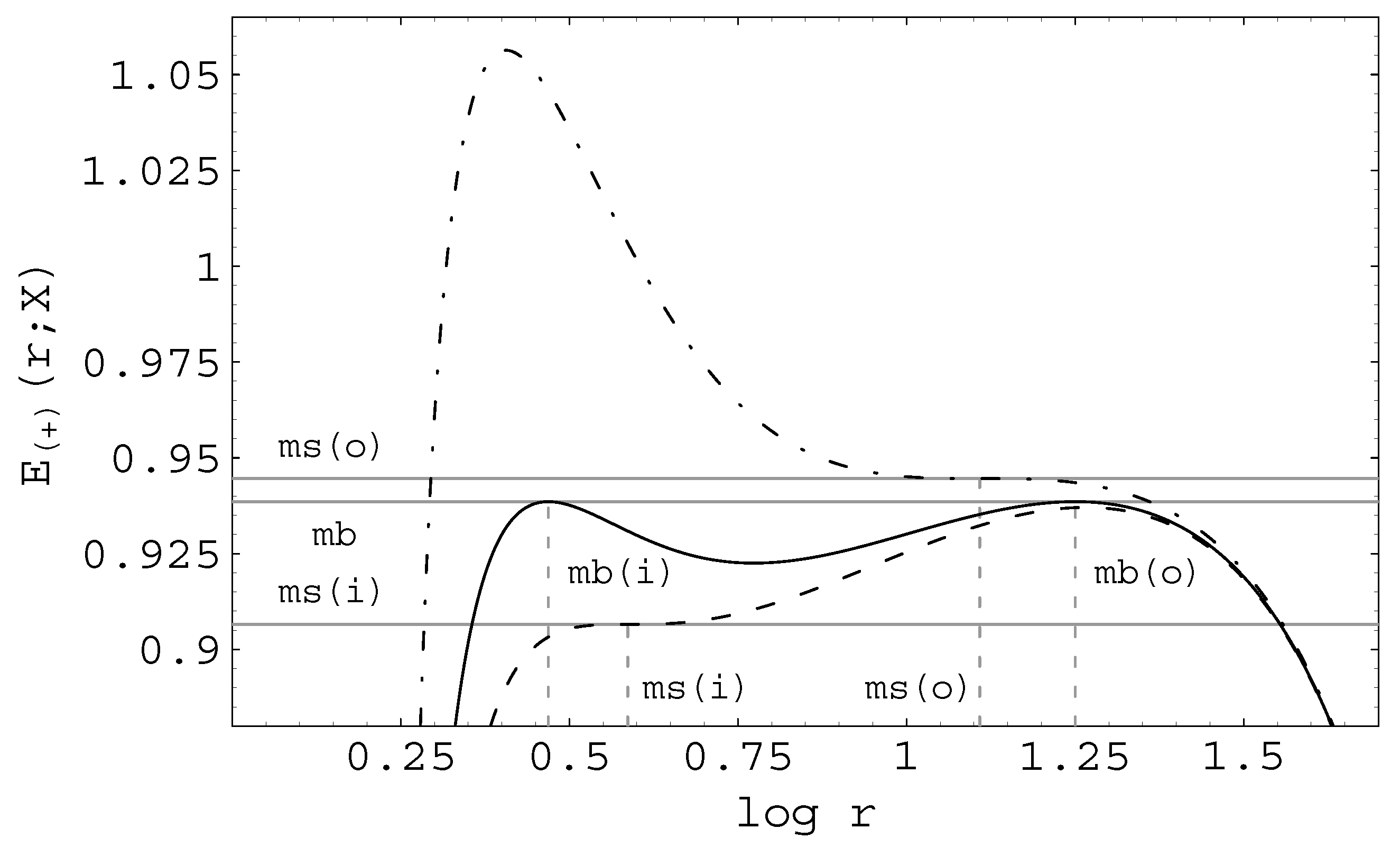
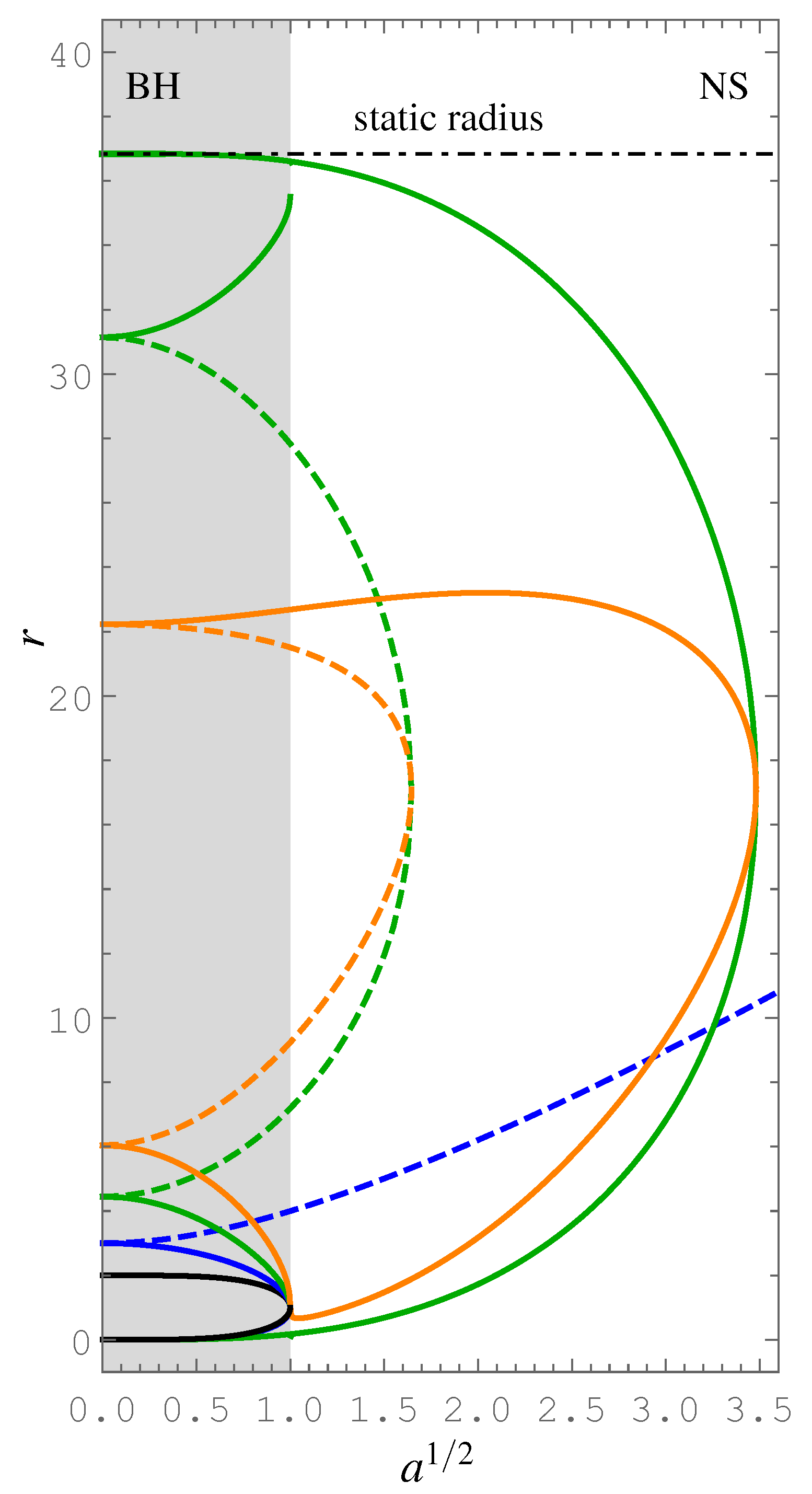
2.1.3. Equatorial Circular Orbits and Keplerian Disks
2.1.3.1. Orientation of the Circular Orbits
2.1.3.2. Stability of the Circular Geodesics
- . No stable circular orbits exist for any value of the spin parameter a.
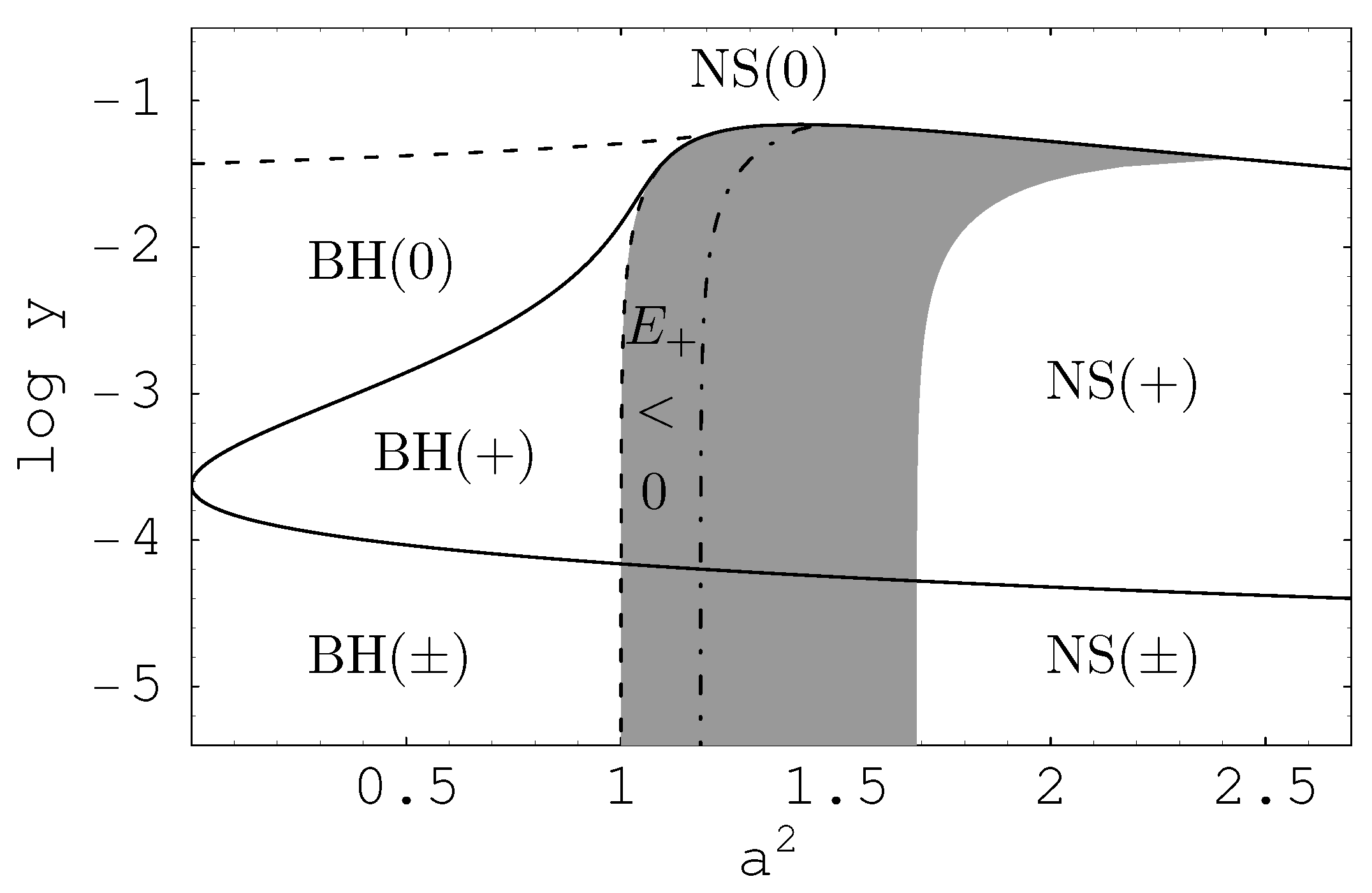
- . The function () has a local maximum (a local minimum ) at the same radius . For , determines two marginally stable plus-family circular geodesics (an inner, and an outer one). For and , no stable circular geodesics exist.
- . Two zero points of the function correspond to its local minima, its local maximum occurs at , where the maximum of the function is also located. For , no stable circular geodesics exist. For , two marginally stable plus-family circular geodesics exist. For , four marginally stable geodesics exist—the innermost and the outermost geodesics belong to the plus-family, the two orbits located in between belong to the minus-family; clearly, this last case corresponds to the black holes relevant in realistic astrophysical situations in the recent state of the Universe.
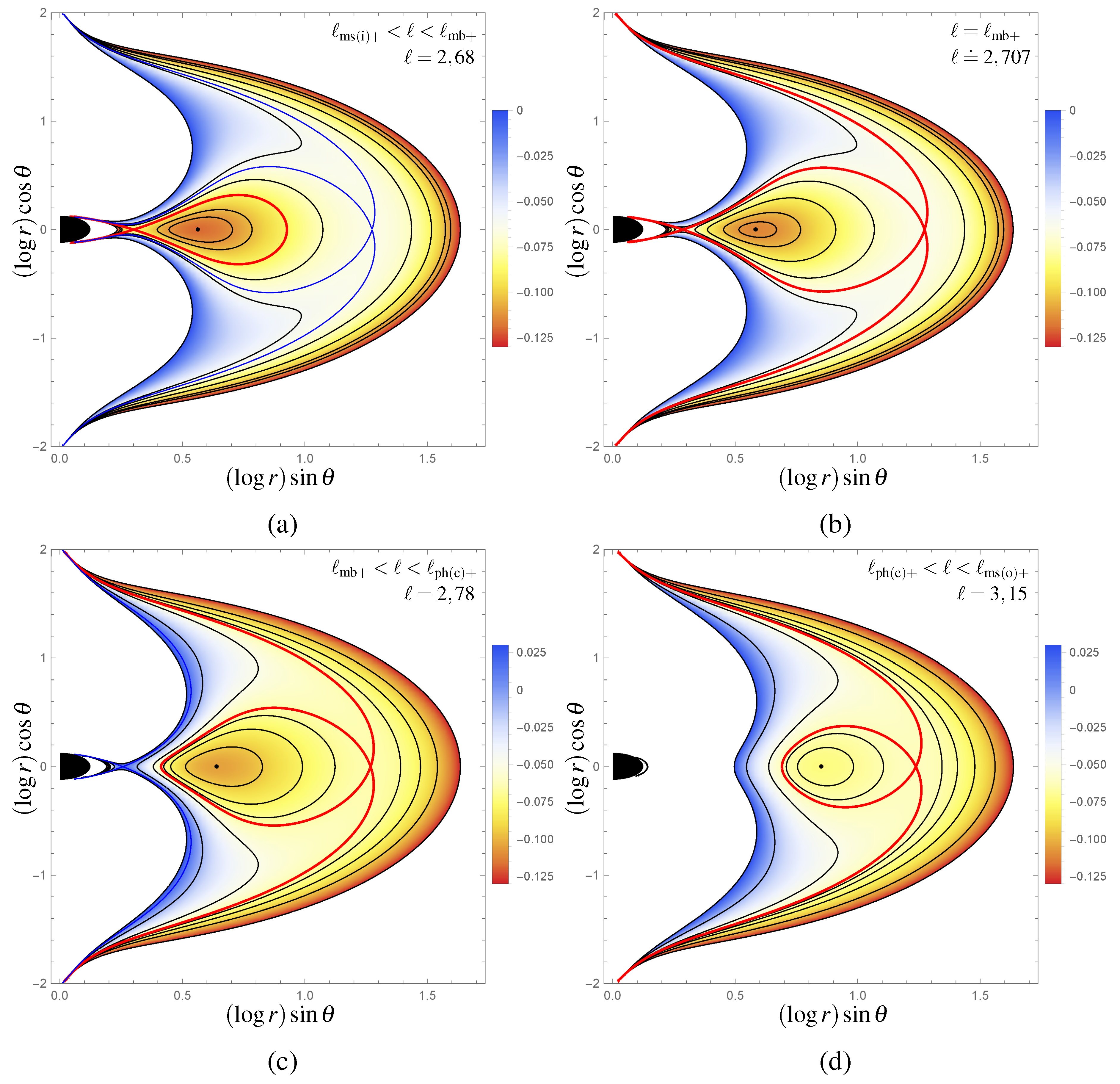
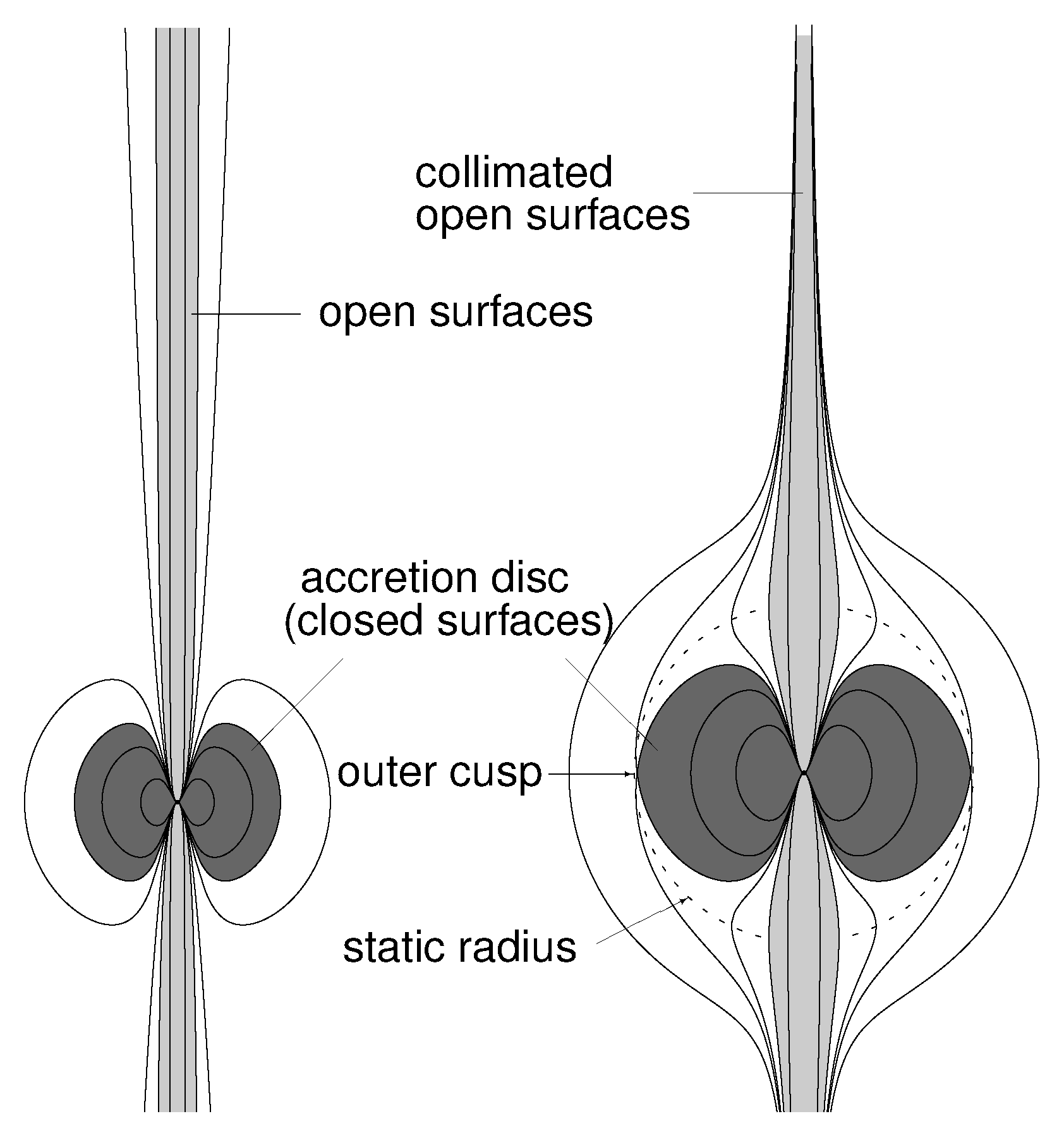
2.2. Toroidal Fluid Configurations and Collimation of Jets
2.2.1. Pressure Equations and Effective Potential Governing Orbiting Perfect Fluid
2.2.2. Limits on Extension of Toroidal Structures and Galaxy Extension
3. Role of Magnetic Fields
3.1. Magnetized Kerr Black Holes
3.2. Asymptotically Uniform Magnetic Field as Basic Approximation
3.3. Motion of Charged Test Particles
3.3.1. Hamiltonian Formalism and Effective Potential of the Motion
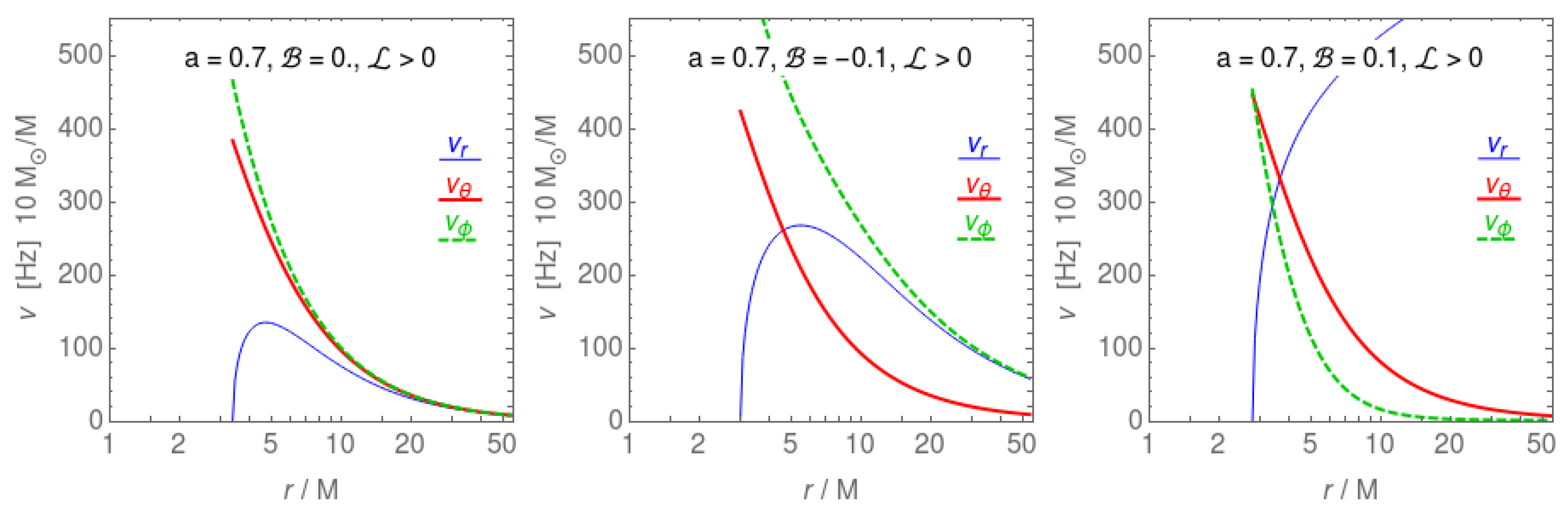
3.3.2. Circular Orbits of Charged Test Particles
3.4. Ionized Keplerian Discs around Magnetized Black Holes
3.4.1. Possible Fates of Ionized Keplerian Disks
3.4.2. Regular Epicyclic Motion and Explanation of HF QPOs in Microquasars by Magnetically Modified Geodesic Models
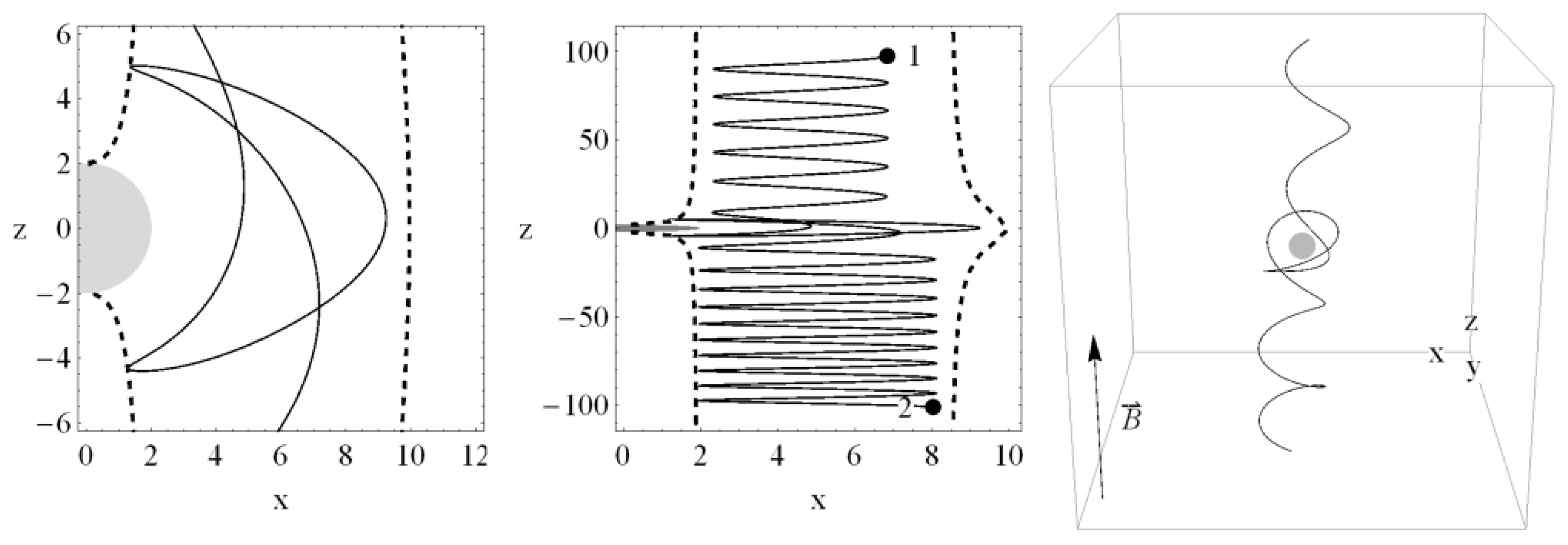
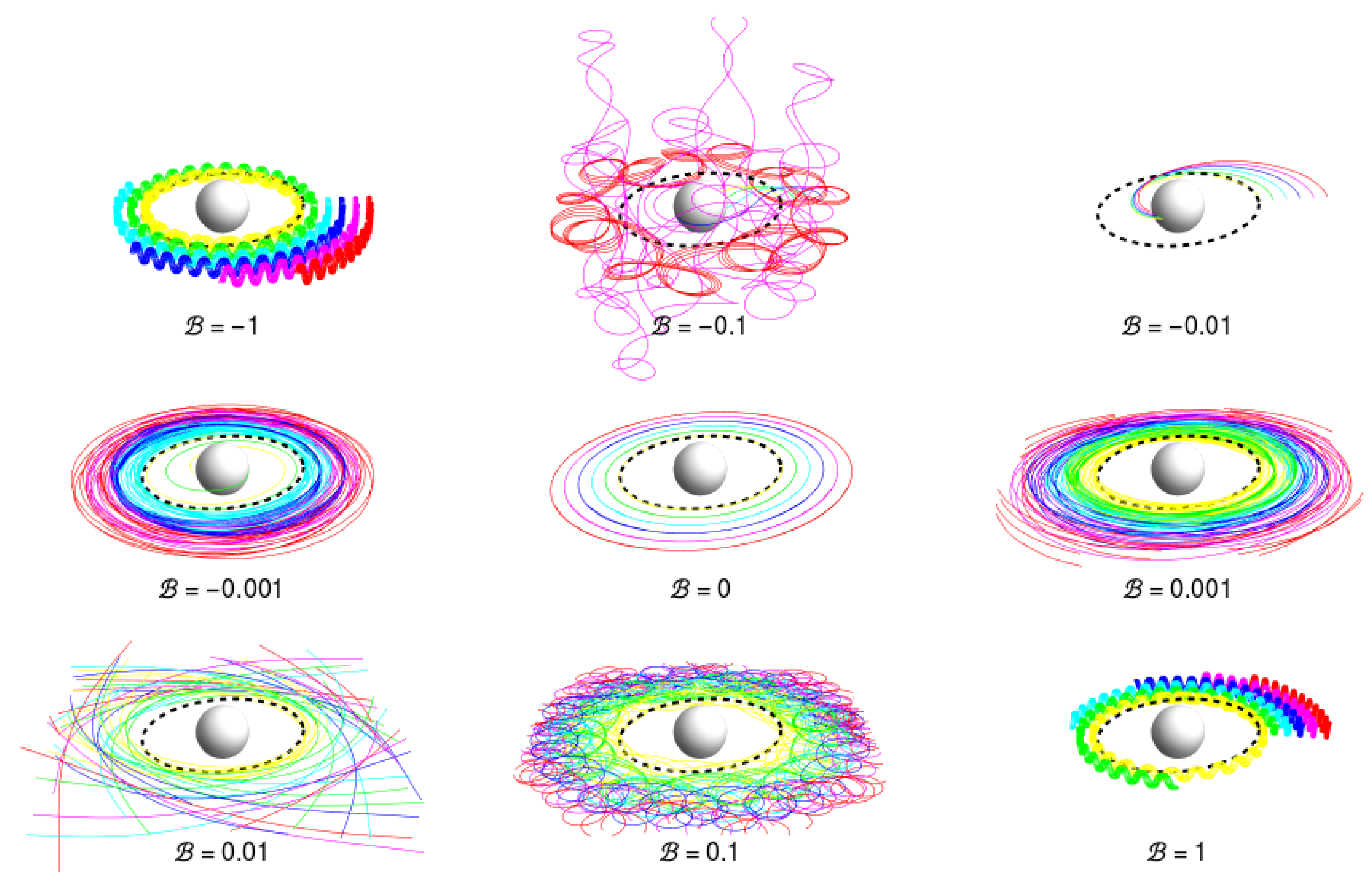
3.4.3. Chaotic Scattering
3.4.4. Modeling of Ionized Keplerian Disks around Magnetized Kerr Black Holes
3.5. Magnetic Penrose Process and Creation of Jets
3.5.1. Efficiency of the Magnetic Penrose Process and Its Three Regimes
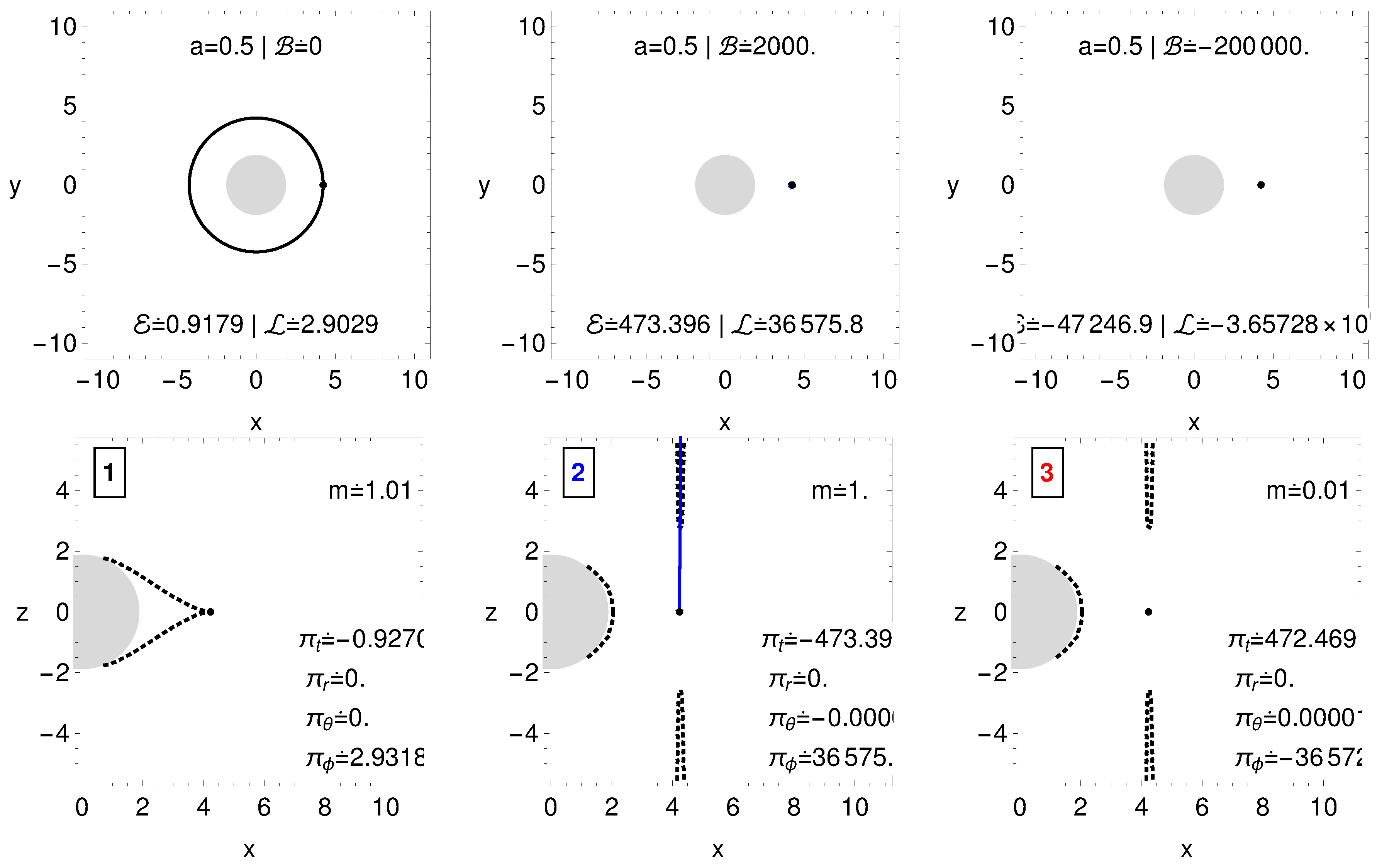
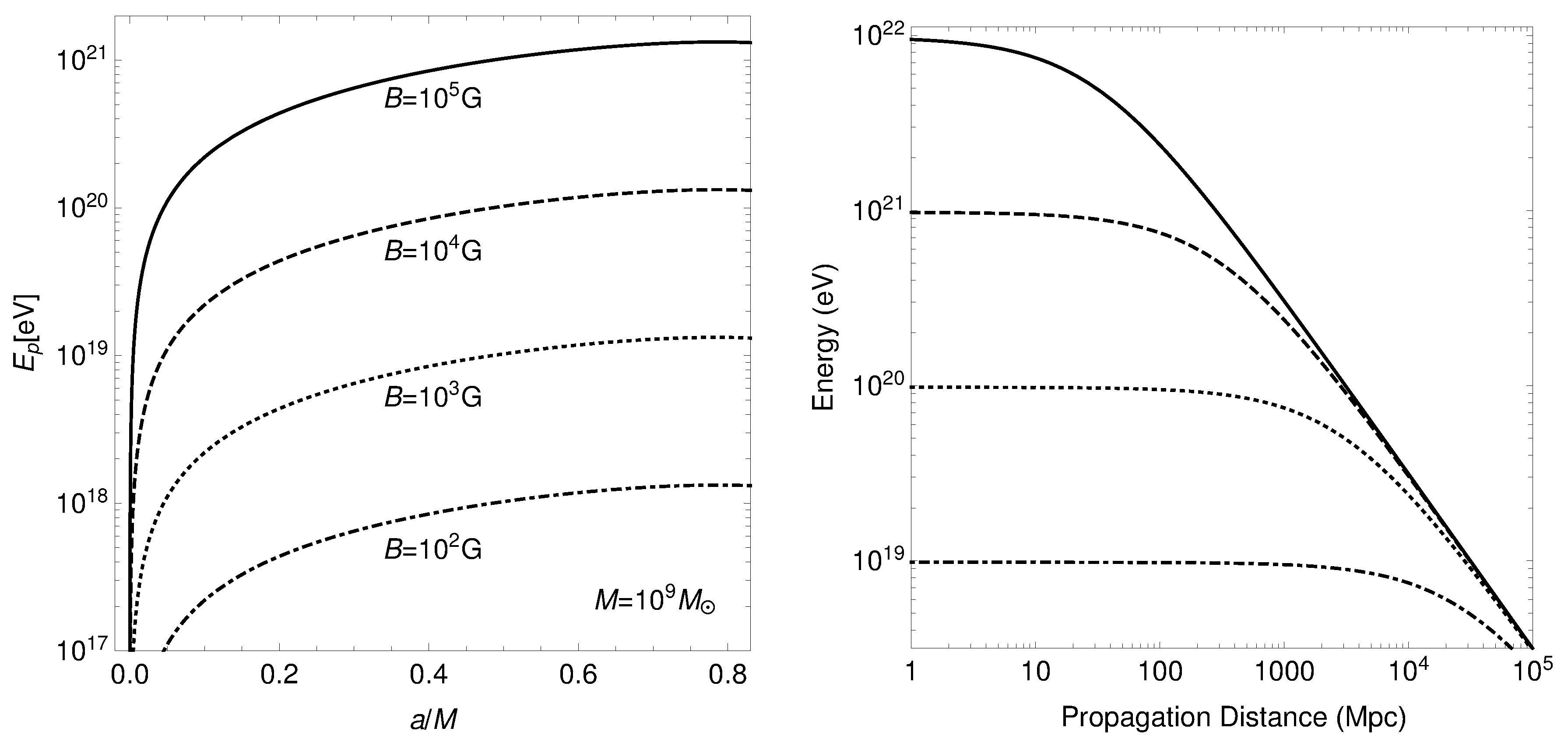
3.5.2. Ultra-High Energy Cosmic Rays as Products of MPP in the Extreme Regime
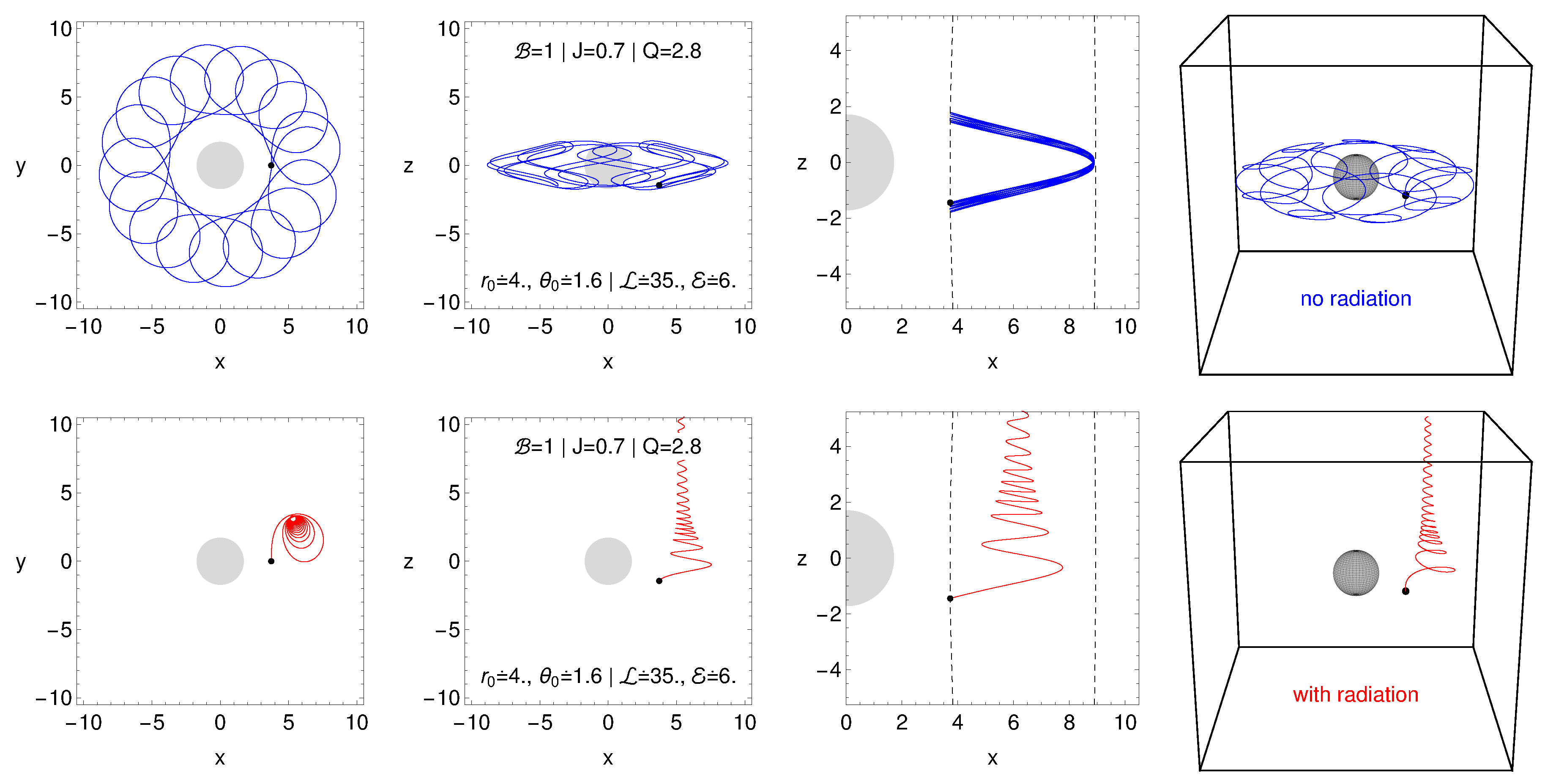
3.5.3. Synchrotron Radiation of Accelerated Charged Particles
3.5.4. Proton and Electron Energy after Leaving the Vicinity of Magnetized Black Holes
3.6. Charged Fluid Structures Circling around Magnetized Compact Objects
3.6.1. Model of Non-Conducting Charged Fluid Tori
3.6.2. Balance Equations of the Fluid
3.6.3. Rotation Regime and Charge Distribution
3.6.4. Integral Analytical Solution of the Pressure Balance Equations
3.6.5. Non-Conducting Charged Fluid Structures
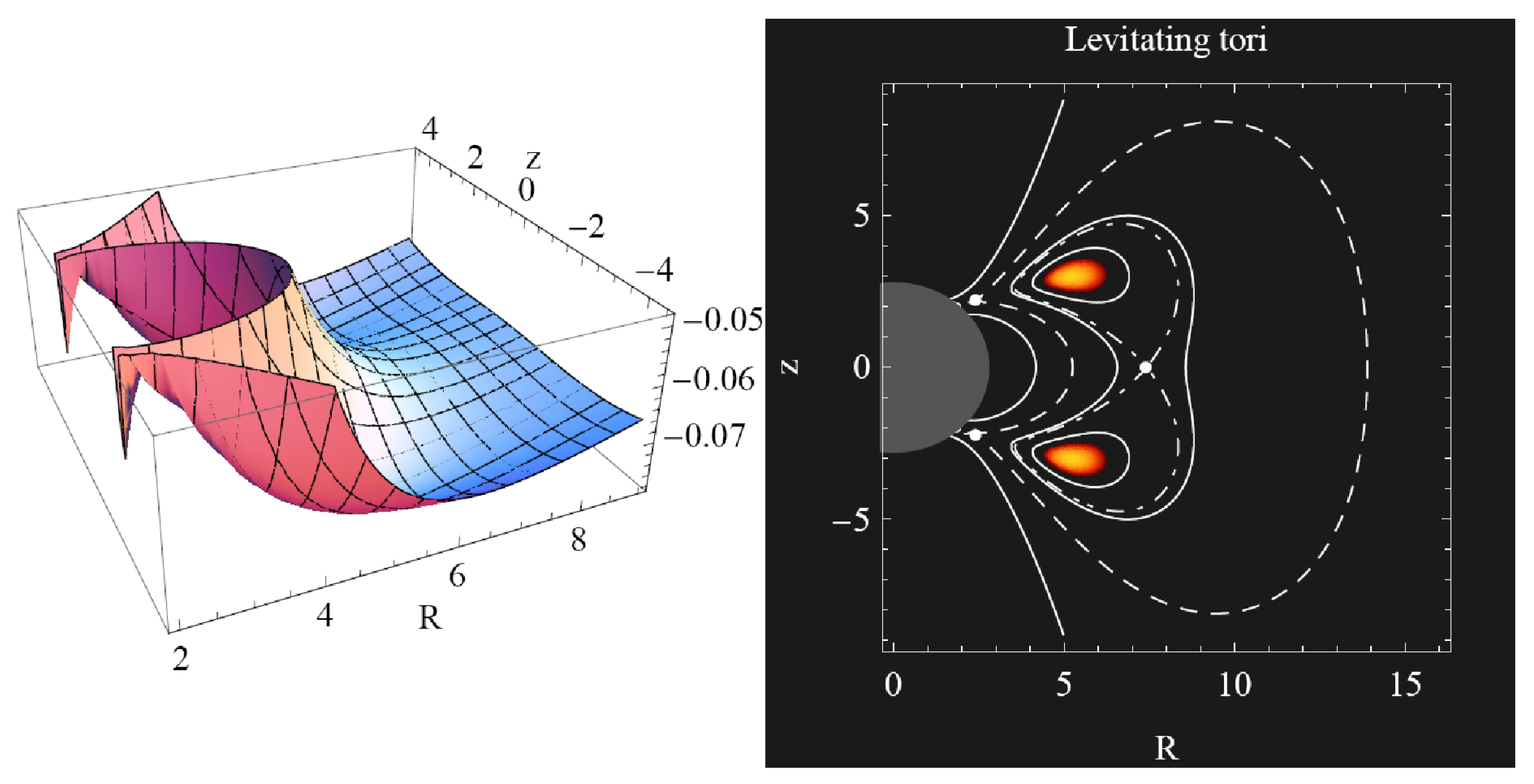
3.6.5.1. Double and Levitating Tori
- For and , we get the potential W embodying two minima and two saddle points in the equatorial plane (corresponding to the positions of two equatorial centers, cusp and pseudo-cusp), allowing construction of either one equatorial torus, two coupled equatorial tori, or the construction of two coupled equatorial tori joint throw the pseudo-cusp and accreting onto the central compact object through the cusp (see Figure 21).
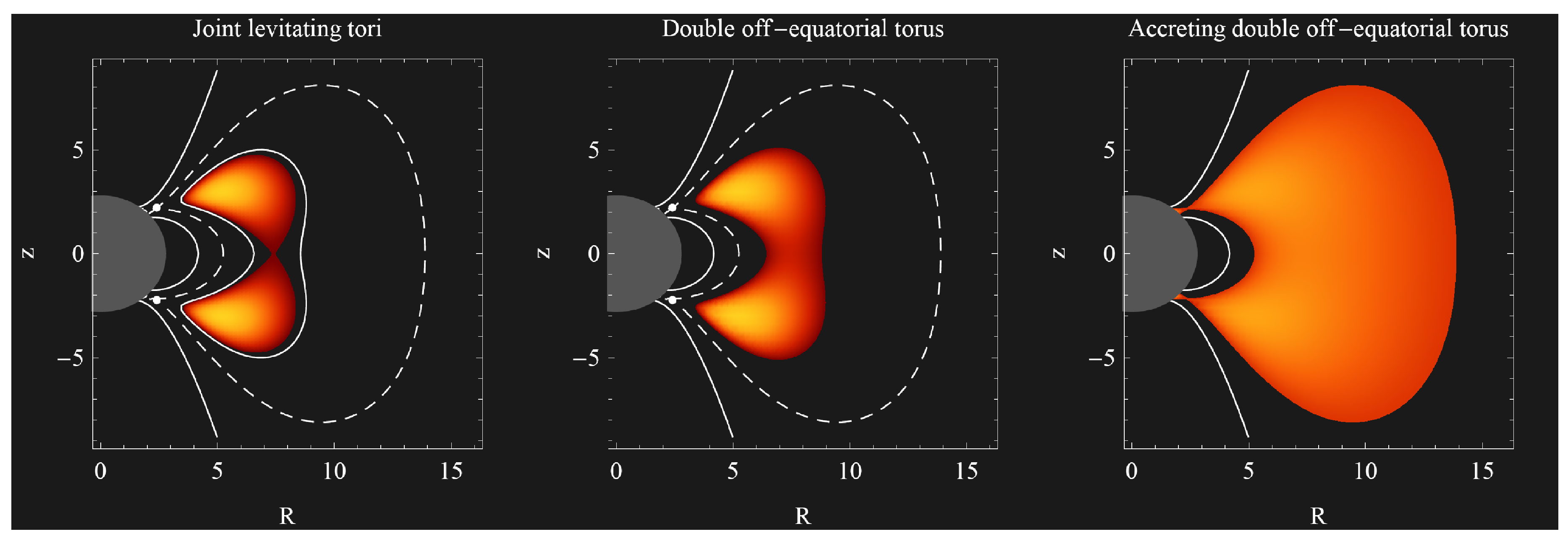
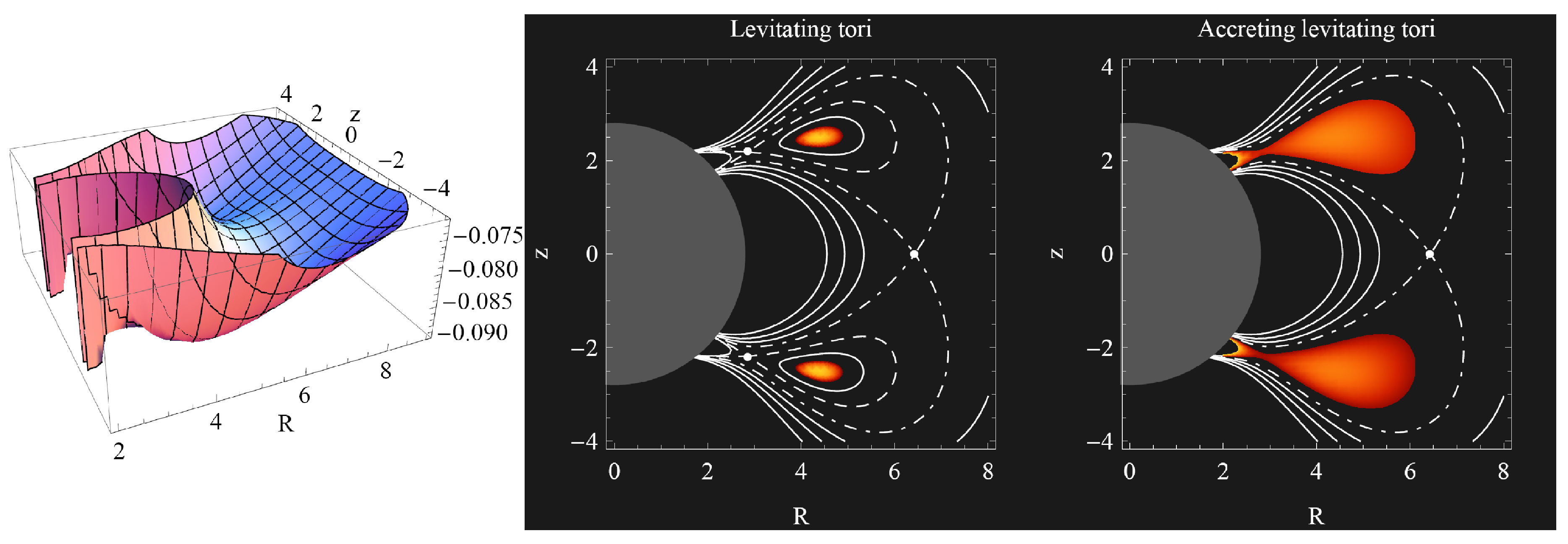
- For and , we get the potential W embodying two minima and saddle points out of the equatorial plane, and one saddle point in the equatorial plane (corresponding to the positions of two off-equatorial centers and cusp, and to the equatorial pseudo-cusp), allowing construction of either two off-equatorial tori—the levitating tori, two levitating tori joint throw the pseudo-cusp, one double off-equatorial torus, or one double off-equatorial torus accreting onto the central compact object through the off-equatorial cusps (see Figure 22 and Figure 23).
- For and , we get the potential W embodying two minima and saddle points out of the equatorial plane, and one saddle point in the equatorial plane (corresponding to the positions of two off-equatorial centers and cusp, and to equatorial pseudo-cusp), allowing construction of either two levitating tori, or two levitating tori accreting onto the central compact object through the off-equatorial cusps (see Figure 24).
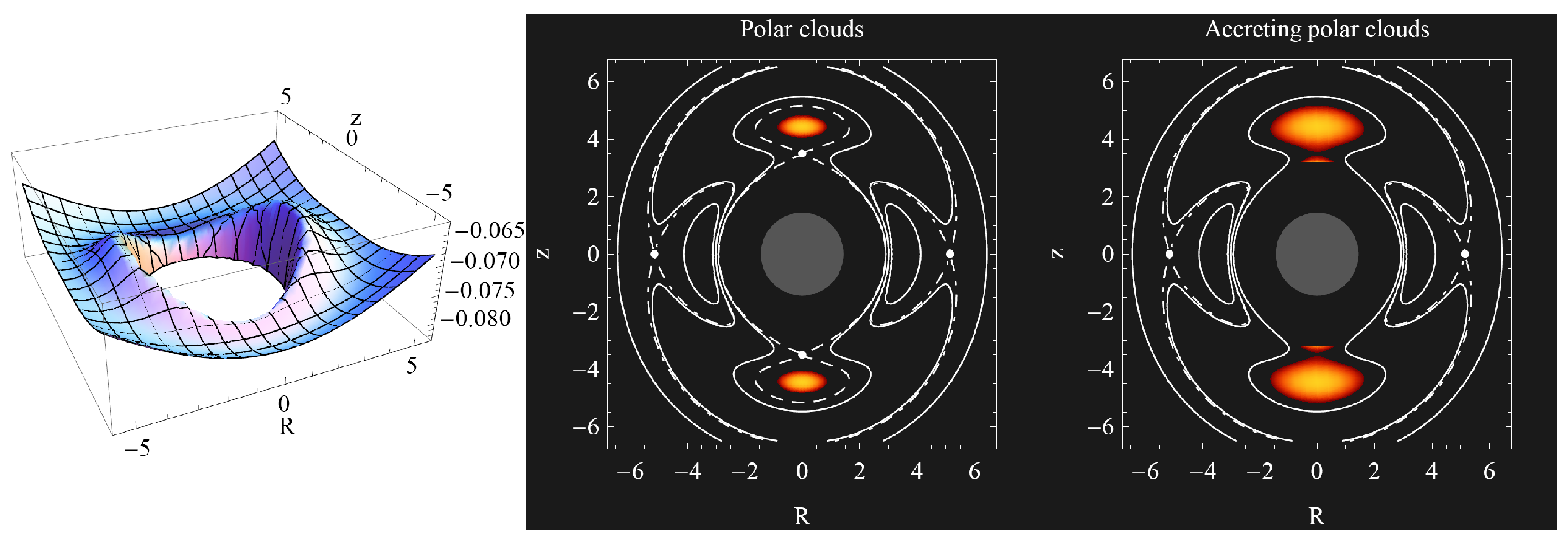
3.6.5.2. Polar Clouds
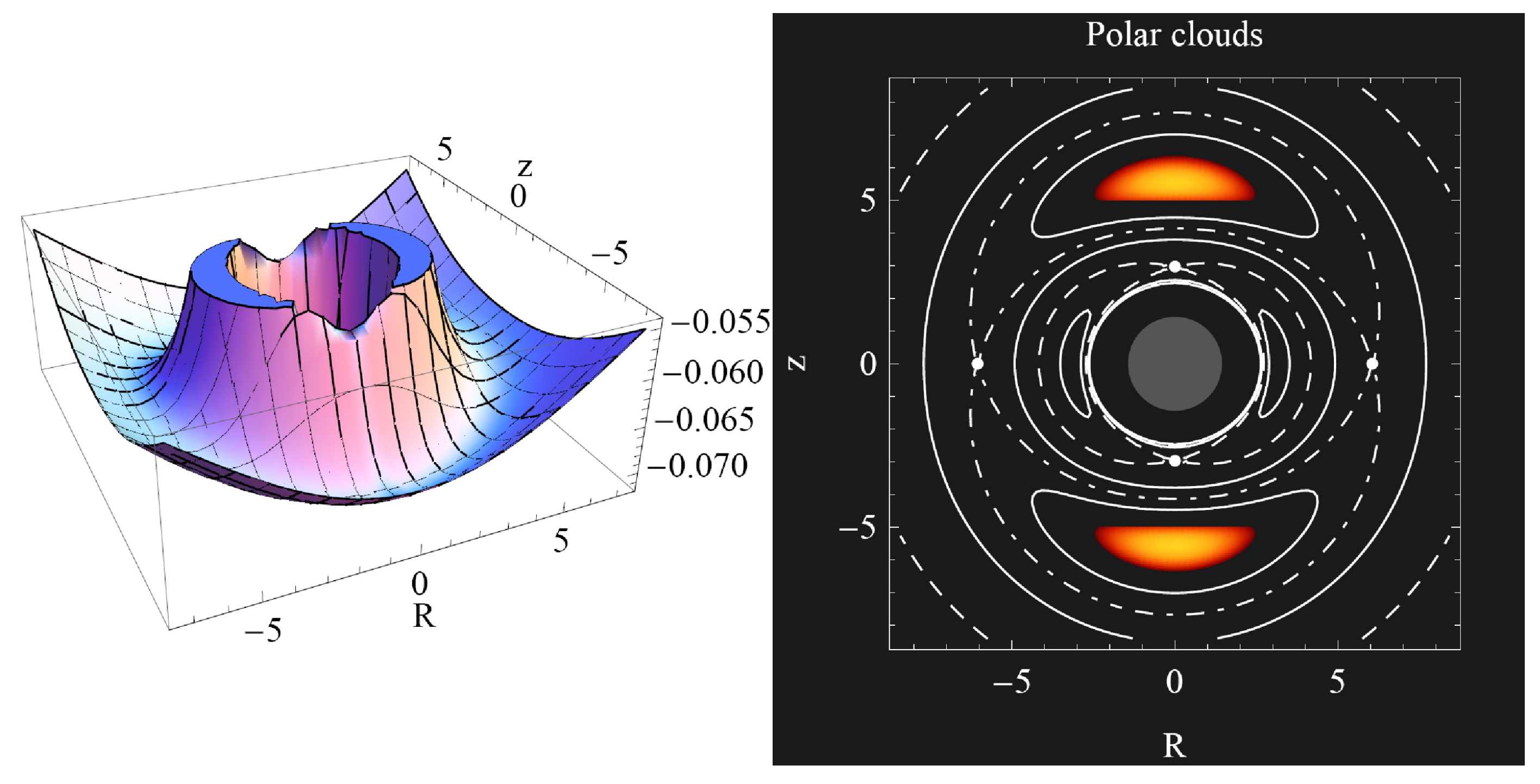
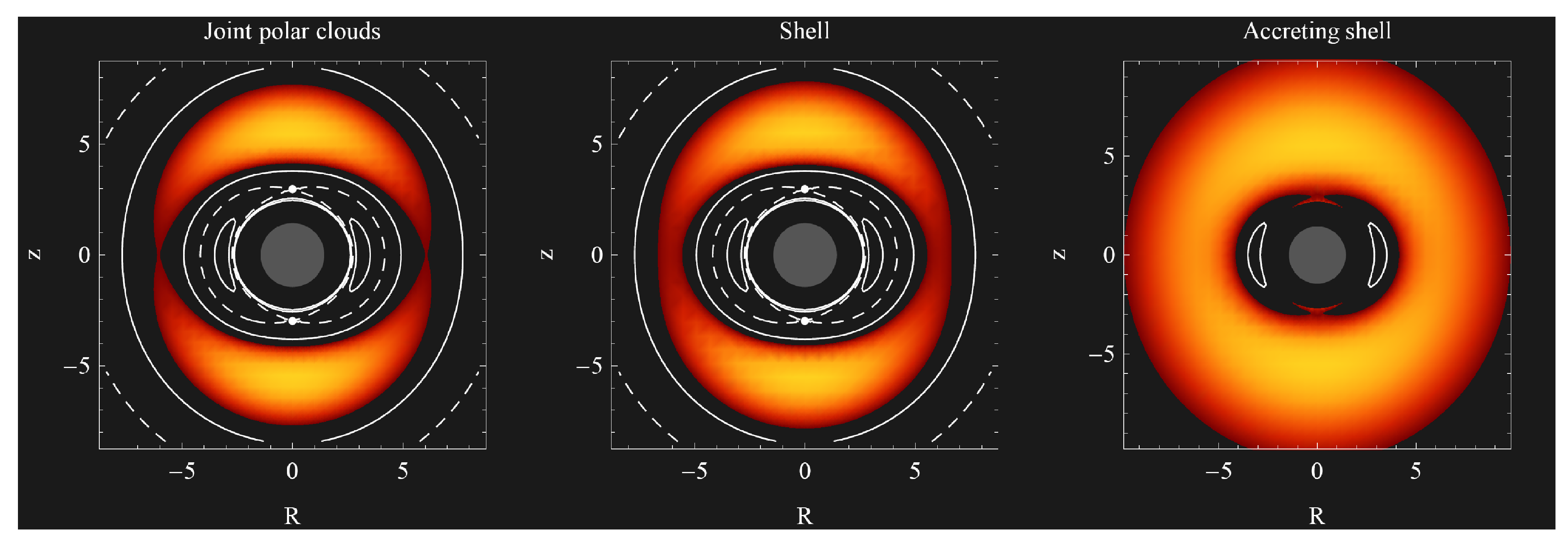
- For , we get the potential embodying two minima and saddle points on the polar axis, and two saddle points in the equatorial plane (corresponding to the positions of two polar centers and cusps, and equatorial pseudo-cusps), allowing construction of either two circling structures centered on the polar axis—the polar clouds, two polar clouds joint throw the pseudo-cusps, one closed encircling structure—the shell, or the accreting shell accreting onto the central black hole through the polar cusps (see Figure 25 and Figure 26). Note that the potential embodies also two equatorial maxima.
- For , we get the potential embodying two minima and saddle points out on the polar axis, and two saddle points in the equatorial plane (corresponding to the positions of two polar centers and cusps, and equatorial pseudo-cusps), allowing construction of either two polar clouds, or two polar clouds accreting onto the central black hole through the polar cusps (see Figure 27). Note that the potential embodies also two equatorial maxima.
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tchekhovskoy, A. Launching of Active Galactic Nuclei Jets. In The Formation and Disruption of Black Hole Jets; Contopoulos, I., Gabuzda, D., Kylafis, N., Eds.; Springer: Cham, Switzerland, 2015; Volume 414, pp. 45–82. [Google Scholar]
- Bardeen, J.M.; Petterson, J.A. The Lense-Thirring Effect and Accretion Disks around Kerr Black Holes. Astrophys. J. 1975, 195, L65. [Google Scholar] [CrossRef]
- Abramowicz, M.A.; Fragile, P.C. Foundations of Black Hole Accretion Disk Theory. Living Rev. Relat. 2013, 16, 1. [Google Scholar] [CrossRef]
- Novikov, I.D.; Thorne, K.S. Astrophysics of black holes. In Black Holes (Les Astres Occlus); Dewitt, C., Dewitt, B.S., Eds.; Gordon & Breach: New York, NY, USA, 1973; pp. 343–450. [Google Scholar]
- Kozlowski, M.; Jaroszynski, M.; Abramowicz, M.A. The analytic theory of fluid disks orbiting the Kerr black hole. Astron. Astrophys. 1978, 63, 209–220. [Google Scholar]
- Pugliese, D.; Stuchlík, Z. Ringed Accretion Disks: Equilibrium Configurations. Astrophys. J. Suppl. Ser. 2015, 221, 25. [Google Scholar] [CrossRef]
- Pugliese, D.; Stuchlík, Z. Ringed Accretion Disks: Instabilities. Astrophys. J. Suppl. Ser. 2016, 223, 27. [Google Scholar] [CrossRef]
- Pugliese, D.; Stuchlík, Z. Ringed Accretion Disks: Evolution of Double Toroidal Configurations. Astrophys. J. Suppl. Ser. 2017, 229, 40. [Google Scholar] [CrossRef]
- Stuchlík, Z. Influence of the RELICT Cosmological Constant on Accretion Discs. Mod. Phys. Lett. A 2005, 20, 561–575. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kološ, M.; Tursunov, A.A. Magnetized Black Holes: Ionized Keplerian Disks and Acceleration of Ultra-High Energy Particles. Proceedings 2019, 17, 13. [Google Scholar] [CrossRef]
- Stuchlik, Z. The Motion of Test Particles in Black-Hole Backgrounds with Non-Zero Cosmological Constant. Bull. Astron. Inst. Czechoslov. 1983, 34, 129–149. [Google Scholar]
- Stuchlík, Z.; Hledík, S. Some properties of the Schwarzschild-de Sitter and Schwarzschild-anti-de Sitter spacetimes. Phys. Rev. D 1999, 60, 044006. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Slaný, P. Equatorial circular orbits in the Kerr–de Sitter spacetimes. Phys. Rev. D 2004, 69, 064001. [Google Scholar] [CrossRef]
- Slaný, P.; Stuchlík, Z. Relativistic thick discs in the Kerr–de Sitter backgrounds. Class. Quantum Gravity 2005, 22, 3623–3651. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Hledík, S.; Novotný, J. General relativistic polytropes with a repulsive cosmological constant. Phys. Rev. D 2016, 94, 103513. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Slaný, P.; Hledík, S. Equilibrium configurations of perfect fluid orbiting Schwarzschild-de Sitter black holes. Astron. Astrophys. 2000, 363, 425–439. [Google Scholar]
- Kovář, J.; Kopáček, O.; Karas, V.; Stuchlík, Z. Off-equatorial orbits in strong gravitational fields near compact objects—II: Halo motion around magnetic compact stars and magnetized black holes. Class. Quantum Gravity 2010, 27, 135006. [Google Scholar] [CrossRef]
- Kovář, J.; Slaný, P.; Cremaschini, C.; Stuchlík, Z.; Karas, V.; Trova, A. Charged perfect fluid tori in strong central gravitational and dipolar magnetic fields. Phys. Rev. D 2016, 93, 124055. [Google Scholar] [CrossRef]
- Kovář, J.; Slaný, P.; Cremaschini, C.; Stuchlík, Z.; Karas, V.; Trova, A. Electrically charged matter in rigid rotation around magnetized black hole. Phys. Rev. D 2014, 90, 044029. [Google Scholar] [CrossRef]
- Frolov, V.P.; Shoom, A.A. Motion of charged particles near a weakly magnetized Schwarzschild black hole. Phys. Rev. D 2010, 82, 084034. [Google Scholar] [CrossRef]
- Kovář, J.; Stuchlík, Z.; Karas, V. Off-equatorial orbits in strong gravitational fields near compact objects. Class. Quantum Gravity 2008, 25, 095011. [Google Scholar] [CrossRef]
- Kološ, M.; Tursunov, A.; Stuchlík, Z. Possible signature of the magnetic fields related to quasi-periodic oscillations observed in microquasars. Eur. Phys. J. C 2017, 77, 860. [Google Scholar] [CrossRef]
- Wald, R.M. Black hole in a uniform magnetic field. Phys. Rev. D 1974, 10, 1680–1685. [Google Scholar] [CrossRef]
- Prasanna, A.R. General-relativistic analysis of charged-particle motion in electromagnetic fields surrounding black holes. Nuovo Cimento Rivista Serie 1980, 3, 1–53. [Google Scholar] [CrossRef]
- Aliev, A.N.; Galtsov, D.V. Radiation from relativistic particles in nongeodesic motion in a strong gravitational field. Gen. Relat. Gravit. 1981, 13, 899–912. [Google Scholar] [CrossRef]
- Kopáček, O.; Karas, V.; Kovář, J.; Stuchlík, Z. Transition from Regular to Chaotic Circulation in Magnetized Coronae near Compact Objects. Astrophys. J. 2010, 722, 1240–1259. [Google Scholar] [CrossRef]
- Abdujabbarov, A.A.; Ahmedov, B.J.; Jurayeva, N.B. Charged-particle motion around a rotating non-Kerr black hole immersed in a uniform magnetic field. Phys. Rev. D 2013, 87, 064042. [Google Scholar] [CrossRef]
- Al Zahrani, A.M.; Frolov, V.P.; Shoom, A.A. Critical escape velocity for a charged particle moving around a weakly magnetized Schwarzschild black hole. Phys. Rev. D 2013, 87, 084043. [Google Scholar] [CrossRef]
- Kopáček, O.; Karas, V. Inducing Chaos by Breaking Axial Symmetry in a Black Hole Magnetosphere. Astrophys. J. 2014, 787, 117. [Google Scholar] [CrossRef]
- Shiose, R.; Kimura, M.; Chiba, T. Motion of charged particles around a weakly magnetized rotating black hole. Phys. Rev. D 2014, 90, 124016. [Google Scholar] [CrossRef]
- Kološ, M.; Stuchlík, Z.; Tursunov, A. Quasi-harmonic oscillatory motion of charged particles around a Schwarzschild black hole immersed in a uniform magnetic field. Class. Quantum Gravity 2015, 32, 165009. [Google Scholar] [CrossRef]
- Tursunov, A.; Stuchlík, Z.; Kološ, M. Circular orbits and related quasi-harmonic oscillatory motion of charged particles around weakly magnetized rotating black holes. Phys. Rev. D 2016, 93, 084012. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kološ, M. Acceleration of the charged particles due to chaotic scattering in the combined black hole gravitational field and asymptotically uniform magnetic field. Eur. Phys. J. C 2016, 76, 32. [Google Scholar] [CrossRef]
- Kopáček, O.; Karas, V. Near-horizon Structure of Escape Zones of Electrically Charged Particles around Weakly Magnetized Rotating Black Hole. Astrophys. J. 2018, 853, 53. [Google Scholar] [CrossRef]
- Pánis, R.; Kološ, M.; Stuchlík, Z. Determination of chaotic behaviour in time series generated by charged particle motion around magnetized Schwarzschild black holes. arXiv 2019, arXiv:1905.01186. [Google Scholar] [CrossRef]
- Tursunov, A.; Kološ, M.; Stuchlík, Z.; Galtsov, D.V. Radiation Reaction of Charged Particles Orbiting a Magnetized Schwarzschild Black Hole. Astrophys. J. 2018, 861, 2. [Google Scholar] [CrossRef]
- Tursunov, A.A.; Kološ, M.; Stuchlík, Z. Orbital widening due to radiation reaction around a magnetized black hole. Astronomische Nachrichten 2018, 339, 341–346. [Google Scholar] [CrossRef]
- Dadhich, N.; Tursunov, A.; Ahmedov, B.; Stuchlík, Z. The distinguishing signature of magnetic Penrose process. Mon. Not. R. Astron. Soc. 2018, 478, L89–L94. [Google Scholar] [CrossRef]
- Tursunov, A.A.; Stuchlík, Z.; Kološ, M.; Dadhich, N.; Ahmedov, B. Supermassive Black Hole as a source of Ultra-High-Energy Cosmic Rays. arXiv 2019, arXiv:1811.11216v1. [Google Scholar]
- Abramowicz, M.; Jaroszynski, M.; Sikora, M. Relativistic, accreting disks. Astron. Astrophys. 1978, 63, 221–224. [Google Scholar]
- Komissarov, S.S. Magnetized tori around Kerr black holes: analytic solutions with a toroidal magnetic field. Mon. Not. R. Astron. Soc. 2006, 368, 993–1000. [Google Scholar] [CrossRef]
- Blandford, R.D.; Znajek, R.L. Electromagnetic extraction of energy from Kerr black holes. Mon. Not. R. Astron. Soc. 1977, 179, 433–456. [Google Scholar] [CrossRef]
- Kovář, J.; Slaný, P.; Stuchlík, Z.; Karas, V.; Cremaschini, C.; Miller, J.C. Role of electric charge in shaping equilibrium configurations of fluid tori encircling black holes. Phys. Rev. D 2011, 84, 084002. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astronom. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Wang, M.L.D.L.W. Dark energy: A brief review. Front. Phys. 2013, 8, 828–846. [Google Scholar]
- Bardeen, J.M.; Press, W.H.; Teukolsky, S.A. Rotating Black Holes: Locally Nonrotating Frames, Energy Extraction, and Scalar Synchrotron Radiation. Astrophys. J. 1972, 178, 347–370. [Google Scholar] [CrossRef]
- Stuchlík, Z. Equatorial circular orbits and the motion of the shell of dust in the field of a rotating naked singularity. Bull. Astron. Inst. Czechoslov. 1980, 31, 129–144. [Google Scholar]
- Stuchlík, Z.; Hledík, S.; Truparová, K. Evolution of Kerr superspinars due to accretion counterrotating thin discs. Class. Quantum Gravity 2011, 28, 155017. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kotrlová, A. Orbital resonances in discs around braneworld Kerr black holes. Gen. Relat. Gravit. 2009, 41, 1305–1343. [Google Scholar] [CrossRef]
- Blaschke, M.; Stuchlík, Z. Efficiency of the Keplerian accretion in braneworld Kerr-Newman spacetimes and mining instability of some naked singularity spacetimes. Phys. Rev. D 2016, 94, 086006. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Hledík, S. Equilibrium of a charged spinning test particle in Reissner-Nordström backgrounds with a nonzero cosmological constant. Phys. Rev. D 2001, 64, 104016. [Google Scholar] [CrossRef]
- Carter, B. Black hole equilibrium states. In Black Holes (Les Astres Occlus); Dewitt, C., Dewitt, B.S., Eds.; Gordon & Breach: New York, NY, USA, 1973; pp. 57–214. [Google Scholar]
- Gimon, E.G.; Hořava, P. Astrophysical violations of the Kerr bound as a possible signature of string theory. Phys. Lett. B 2009, 672, 299–302. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Schee, J. Appearance of Keplerian discs orbiting Kerr superspinars. Class. Quantum Gravity 2010, 27, 215017. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Schee, J. Observational phenomena related to primordial Kerr superspinars. Class. Quantum Gravity 2012, 29, 065002. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Schee, J. Ultra-high-energy collisions in the superspinning Kerr geometry. Class. Quantum Gravity 2013, 30, 075012. [Google Scholar] [CrossRef]
- Akcay, S.; Matzner, R.A. The Kerr-de Sitter universe. Class. Quantum Gravity 2011, 28, 085012. [Google Scholar] [CrossRef]
- Brill, D.; Hayward, S.A. Global structure of a black hole cosmos and its extremes. Class. Quantum Gravity 1994, 11, 359–370. [Google Scholar] [CrossRef]
- Hayward, S.A.; Shiromizu, T.; Nakao, K.-i. A cosmological constant limits the size of black holes. Phys. Rev. D 1994, 49, 5080–5085. [Google Scholar] [CrossRef]
- Bicak, J.; Stuchlik, Z. On the latitudinal and radial motion in the field of a rotating black hole. Bull. Astron. Inst. Czechoslov. 1976, 27, 129–133. [Google Scholar]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; W. H. Freeman: Princeton, NJ, USA, 1973. [Google Scholar]
- Balek, V.; Bicak, J.; Stuchlik, Z. The Motion of the Charged Particles in the Field of Rotating Charged Black Holes and Naked Singularities. II. The Motion in the Equatorial Plane. Bull. Astron. Inst. Czechoslov. 1989, 40, 133. [Google Scholar]
- Page, D.N.; Thorne, K.S. Disk-Accretion onto a Black Hole. Time-Averaged Structure of Accretion Disk. Astrophys. J. 1974, 191, 499–506. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The mathematical theory of black holes. In Proceedings of the General Relativity and Gravitation Conference, Padua, Italy, 4–9 July 1984; pp. 5–26. [Google Scholar]
- Stuchlík, Z.; Schee, J. Influence of the cosmological constant on the motion of Magellanic Clouds in the gravitational field of Milky Way. J. Cosmol. Astropart. Phys. 2011, 9, 18. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Schee, J.; Toshmatov, B.; Hladík, J.; Novotný, J. Gravitational instability of polytropic spheres containing region of trapped null geodesics: A possible explanation of central supermassive black holes in galactic halos. J. Cosmol. Astropart. Phys. 2017, 2017, 056. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Hledík, S. Equatorial photon motion in the Kerr-Newman spacetimes with a non-zero cosmological constant. Class. Quantum Gravity 2000, 17, 4541–4576. [Google Scholar] [CrossRef][Green Version]
- Charbulák, D.; Stuchlík, Z. Photon motion in Kerr-de Sitter spacetimes. Eur. Phys. J. C 2017, 77, 897. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Charbulák, D.; Schee, J. Light escape cones in local reference frames of Kerr-de Sitter black hole spacetimes and related black hole shadows. Eur. Phys. J. C 2018, 78, 180. [Google Scholar] [CrossRef]
- Boyer, R.H. Rotating fluid masses in general relativity. Proc. Camb. Philos. Soc. 1965, 61, 527. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Slaný, P.; Kovář, J. Pseudo-Newtonian and general relativistic barotropic tori in Schwarzschild-de Sitter spacetimes. Class. Quantum Gravity 2009, 26, 215013. [Google Scholar] [CrossRef]
- Seguin, F.H. The stability of nonuniform rotation in relativistic stars. Astrophys. J. 1975, 197, 745. [Google Scholar] [CrossRef]
- Abramowicz, M.A.; Calvani, M.; Nobili, L. Thick accretion disks with super-Eddington luminosities. Astrophys. J. 1980, 242, 772–788. [Google Scholar] [CrossRef]
- Spergel, D.N.; Verde, L.; Peiris, H.V.; Komatsu, E.; Nolta, M.R.; Bennett, C.L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; et al. First Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters. Astrophys. J. Suppl. 2003, 148, 175. [Google Scholar] [CrossRef]
- Ostlie, B.W.C.A. An Introduction to Modern Astrophysics; Addison-Wesley: Reading, MA, USA, 1996. [Google Scholar]
- Zanotti, L.R. Dynamics of thick discs around Schwarzschild-de Sitter black holes. Astron. Astrophys. 2003, 412, 603. [Google Scholar]
- Raine, J.F.K. Accretion Power in Astrophysics, 3rd ed.; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Ruffini, R. On the energetics of black holes. In Black Holes (Les Astres Occlus); Dewitt, C., Dewitt, B.S., Eds.; Gordon & Breach: New York, NY, USA, 1973; pp. 451–546. [Google Scholar]
- Balbus, S.A.; Hawley, J.F. A powerful local shear instability in weakly magnetized disks. I - Linear analysis. II—Nonlinear evolution. Astrophys. J. 1991, 376, 214–233. [Google Scholar] [CrossRef]
- Penrose, R. Gravitational Collapse:The Role of General Relativity. Nuovo Cimento Rivista Serie 1969, 1, 252. [Google Scholar]
- Tursunov, A.; Dadhich, N. Fifty Years of Energy Extraction from Rotating Black Hole: Revisiting Magnetic Penrose Process. Universe 2019, 5, 125. [Google Scholar] [CrossRef]
- Trova, A.; Schroven, K.; Hackmann, E.; Karas, V.; Kovář, J.; Slaný, P. Equilibrium configurations of charged fluid around Kerr black hole. Phys. Rev. D 2018, 97, 104019. [Google Scholar] [CrossRef]
- Slaný, P.; Kovář, J.; Stuchlík, Z.; Karas, V. Charged Tori in Spherical Gravitational and Dipolar Magnetic Fields. Astrophys. J. Suppl. 2013, 205, 3. [Google Scholar] [CrossRef]
- Dovčiak, M.; Muleri, F.; Goosmann, R.W.; Karas, V.; Matt, G. Polarization in lamp-post model of black-hole accretion discs. J. Phys. Conf. Ser. 2012, 372, 012056. [Google Scholar] [CrossRef]
- Petterson, J.A. Magnetic field of a current loop around a Schwarzschild black hole. Phys. Rev. D 1974, 10, 3166–3170. [Google Scholar] [CrossRef]
- Eatough, R.P.; Falcke, H.; Karuppusamy, R.; Lee, K.J.; Champion, D.J.; Keane, E.F.; Desvignes, G.; Schnitzeler, D.H.F.M.; Spitler, L.G.; Kramer, M.; et al. A strong magnetic field around the supermassive black hole at the centre of the Galaxy. Nature 2013, 501, 391–394. [Google Scholar] [CrossRef] [PubMed]
- Doeleman, S.S.; Fish, V.L.; Schenck, D.E.; Beaudoin, C.; Blundell, R.; Bower, G.C.; Broderick, A.E.; Chamberlin, R.; Freund, R.; Friberg, P.; et al. Jet-Launching Structure Resolved Near the Supermassive Black Hole in M87. Science 2012, 338, 355. [Google Scholar] [CrossRef]
- Daly, R.A. Black Hole Spin and Accretion Disk Magnetic Field Strength Estimates for More Than 750 Active Galactic Nuclei and Multiple Galactic Black Holes. Astrophys. J. 2019, 886, 37. [Google Scholar] [CrossRef]
- Gal’tsov, D.V.; Petukhov, V.I. Black hole in an external magnetic field. Sov. J. Exp. Theor. Phys. 1978, 47, 419. [Google Scholar]
- Bicak, J.; Stuchlik, Z. The fall of the shell of dust on to a rotating black hole. Mon. Not. R. Astron. Soc. 1976, 175, 381–393. [Google Scholar] [CrossRef]
- Bicak, J.; Janis, V. Magnetic fluxes across black holes. Mon. Not. R. Astron. Soc. 1985, 212, 899–915. [Google Scholar] [CrossRef]
- Zajaček, M.; Tursunov, A.; Eckart, A.; Britzen, S. On the charge of the Galactic centre black hole. Mon. Not. R. Astron. Soc. 2018, 480, 4408–4423. [Google Scholar] [CrossRef]
- Bičák, J.; Ledvinka, T. Electromagnetic fields around black holes and Meissner effect. Nuovo Cimento B Serie 2000, 115, 739. [Google Scholar]
- Komissarov, S.S. Blandford-Znajek Mechanism versus Penrose Process. J. Korean Phys. Soc. 2009, 54, 2503. [Google Scholar] [CrossRef]
- Punsly, B. Black Hole Gravitohydromagnetics; Springer: Heidelberg, Germany, 2001. [Google Scholar]
- Komissarov, S.S. Electrodynamics of black hole magnetospheres. Mon. Not. R. Astron. Soc. 2004, 350, 427–448. [Google Scholar] [CrossRef]
- Nakamura, M.; Asada, K.; Hada, K.; Pu, H.Y.; Noble, S.; Tseng, C.; Toma, K.; Kino, M.; Nagai, H.; Takahashi, K.; et al. Parabolic Jets from the Spinning Black Hole in M87. Astrophys. J. 2018, 868, 146. [Google Scholar] [CrossRef]
- Kopáček, O.; Karas, V.; Kovář, J.; Stuchlík, Z. Application of a symplectic integrator in a non-integrable relativistic system. In RAGtime 10-13: Workshops on Black Holes and Neutron Stars; Stuchlík, Z., Török, G., Pecháček, T., Eds.; Silesian University: Opava, Czech Republic, 2014; pp. 123–132. [Google Scholar]
- Bičák, J.; Stuchlík, Z.; Balek, V. The motion of charged particles in the field of rotating charged black holes and naked singularities. Bull. Astron. Inst. Czechoslov. 1989, 40, 65–92. [Google Scholar]
- Stuchlík, Z.; Kološ, M. String loops in the field of braneworld spherically symmetric black holes and naked singularities. J. Cosmol. Astropart. Phys. 2012, 10, 008. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kološ, M. String loops oscillating in the field of Kerr black holes as a possible explanation of twin high-frequency quasiperiodic oscillations observed in microquasars. Phys. Rev. D 2014, 89, 065007. [Google Scholar] [CrossRef]
- Remillard, R.A.; McClintock, J.E. X-Ray Properties of Black-Hole Binaries. Annu. Rev. Astron. Astrophys. 2006, 44, 49–92. [Google Scholar] [CrossRef]
- Carpano, S.; Jin, C. Discovery of a 23.8 h QPO in the Swift light curve of XMMU J134736.6+173403. Mon. Not. R. Astron. Soc. 2018, 477, 3178–3184. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kotrlová, A.; Török, G. Multi-resonance orbital model of high-frequency quasi-periodic oscillations: possible high-precision determination of black hole and neutron star spin. Astron. Astrophys. 2013, 552, A10. [Google Scholar] [CrossRef]
- Török, G.; Stuchlík, Z. Radial and vertical epicyclic frequencies of Keplerian motion in the field of Kerr naked singularities. Comparison with the black hole case and possible instability of naked-singularity accretion discs. Astron. Astrophys. 2005, 437, 775–788. [Google Scholar] [CrossRef]
- Cremaschini, C.; Stuchlík, Z. Magnetic loop generation by collisionless gravitationally bound plasmas in axisymmetric tori. Phys. Rev. E 2013, 87, 043113. [Google Scholar] [CrossRef]
- Belloni, T.M.; Sanna, A.; Méndez, M. High-frequency quasi-periodic oscillations in black hole binaries. Mon. Not. R. Astron. Soc. 2012, 426, 1701–1709. [Google Scholar] [CrossRef]
- Abramowicz, M.A.; Kluźniak, W. A precise determination of black hole spin in GRO J1655-40. Astron. Astrophys. 2001, 374, L19–L20. [Google Scholar] [CrossRef]
- Török, G.; Abramowicz, M.A.; Kluźniak, W.; Stuchlík, Z. The orbital resonance model for twin peak kHz quasi periodic oscillations in microquasars. Astron. Astrophys. 2005, 436, 1–8. [Google Scholar] [CrossRef]
- Goluchová, K.; Török, G.; Šrámková, E.; Abramowicz, M.A.; Stuchlík, Z.; Horák, J. Mass of the active galactic nucleus black hole XMMUJ134736.6+173403. Astron. Astrophys. 2019, 622, L8. [Google Scholar] [CrossRef]
- Török, G.; Kotrlová, A.; Šrámková, E.; Stuchlík, Z. Confronting the models of 3:2 quasiperiodic oscillations with the rapid spin of the microquasar GRS 1915+105. Astron. Astrophys. 2011, 531, A59. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kološ, M. Models of quasi-periodic oscillations related to mass and spin of the GRO J1655-40 black hole. Astron. Astrophys. 2016, 586, A130. [Google Scholar] [CrossRef]
- McClintock, J.E.; Narayan, R.; Davis, S.W.; Gou, L.; Kulkarni, A.; Orosz, J.A.; Penna, R.F.; Remillard, R.A.; Steiner, J.F. Measuring the spins of accreting black holes. Class. Quantum Gravity 2011, 28, 114009. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kološ, M. Mass of intermediate black hole in the source M82 X-1 restricted by models of twin high-frequency quasi-periodic oscillations. Mon. Not. R. Astron. Soc. 2015, 451, 2575–2588. [Google Scholar] [CrossRef]
- Stella, L.; Vietri, M. Lense-Thirring Precession and Quasi-periodic Oscillations in Low-Mass X-Ray Binaries. Astrophys. J. Lett. 1998, 492, L59. [Google Scholar] [CrossRef]
- Parthasarathy, S.; Wagh, S.M.; Dhurandhar, S.V.; Dadhich, N. High efficiency of the Penrose process of energy extraction from rotating black holes immersed in electromagnetic fields. Astrophys. J. 1986, 307, 38–46. [Google Scholar] [CrossRef]
- Shakura, N.I. Geodesics in a Kerr Metric. Sov. Astron. Lett. 1987, 13, 99. [Google Scholar]
- de Felice, F.; Calvani, M. Orbital and vortical motion in the Kerr metric. Nuovo Cimento B Serie 1972, 10, 447–458. [Google Scholar]
- Dhurandhar, S.V.; Dadhich, N. Energy-extraction processes from a Kerr black hole immersed in a magnetic field. II. The formalism. Phys. Rev. D 1984, 30, 1625–1631. [Google Scholar] [CrossRef]
- Bardeen, J.M. Timelike and null geodesics in the Kerr metric. In Black Holes (Les Astres Occlus); Gordon & Breach: New York, NY, USA, 1973; pp. 215–239. [Google Scholar]
- Blandford, R.D.; Payne, D.G. Hydromagnetic flows from accretion disks and the production of radio jets. Mon. Not. R. Astron. Soc. 1982, 199, 883–903. [Google Scholar] [CrossRef]
- Greisen, K. End to the Cosmic-Ray Spectrum? Phys. Rev. Lett. 1966, 16, 748–750. [Google Scholar] [CrossRef]
- Parsa, M.; Eckart, A.; Shahzamanian, B.; Karas, V.; Zajaček, M.; Zensus, J.A.; Straubmeier, C. Investigating the Relativistic Motion of the Stars Near the Supermassive Black Hole in the Galactic Center. Astrophys. J. 2017, 845, 22. [Google Scholar] [CrossRef]
- Eckart, A.; Schödel, R.; Meyer, L.; Trippe, S.; Ott, T.; Genzel, R. Polarimetry of near-infrared flares from Sagittarius A*. Astron. Astrophys. 2006, 455, 1–10. [Google Scholar] [CrossRef]
- Eckart, A.; Hüttemann, A.; Kiefer, C.; Britzen, S.; Zajaček, M.; Lämmerzahl, C.; Stöckler, M.; Valencia-S, M.; Karas, V.; García-Marín, M. The Milky Way’s Supermassive Black Hole: How Good a Case Is It? Found. Phys. 2017, 47, 553–624. [Google Scholar] [CrossRef]
- Bonazzola, S.; Gourgoulhon, E.; Marck, J.A. Numerical approach for high precision 3D relativistic star models. Phys. Rev. D 1998, 58, 104020. [Google Scholar] [CrossRef]
- Gourgoulhon, E.; Grandclément, P.; Marck, J.A.; Novak, J.; Taniguchi, K. LORENE: Spectral methods differential equations solver. arXiv 2016, arXiv:1608.018. [Google Scholar]
- Hartle, J.B.; Thorne, K.S. Slowly Rotating Relativistic Stars. II. Models for Neutron Stars and Supermassive Stars. Astrophys. J. 1968, 153, 807. [Google Scholar] [CrossRef]
- Török, G.; Bakala, P.; Šrámková, E.; Stuchlík, Z.; Urbanec, M. On Mass Constraints Implied by the Relativistic Precession Model of Twin-peak Quasi-periodic Oscillations in Circinus X-1. Astrophys. J. 2010, 714, 748–757. [Google Scholar] [CrossRef]
- Urbanec, M.; Miller, J.C.; Stuchlík, Z. Quadrupole moments of rotating neutron stars and strange stars. Mon. Not. R. Astron. Soc. 2013, 433, 1903–1909. [Google Scholar] [CrossRef]
- Urbancová, G.; Urbanec, M.; Török, G.; Stuchlík, Z.; Blaschke, M.; Miller, J.C. Epicyclic Oscillations in the Hartle-Thorne External Geometry. Astrophys. J. 2019, 877, 66. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kološ, M. Test of the string loop oscillation model using kHz quasiperiodic oscillations in a neutron star binary. Gen. Relat. Gravit. 2015, 47, 27. [Google Scholar] [CrossRef][Green Version]
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields; Pergamon Press: Oxford, UK, 1976. [Google Scholar]
- Poisson, E. The Motion of Point Particles in Curved Spacetime. Living Rev. Relat. 2004, 7, 6. [Google Scholar] [CrossRef]
- DeWitt, B.S.; Brehme, R.W. Radiation damping in a gravitational field. Ann. Phys. 1960, 9, 220–259. [Google Scholar] [CrossRef]
- Hobbs, J. A vierbein formalism of radiation damping. Ann. Phys. 1968, 47, 141–165. [Google Scholar] [CrossRef]
- Dewitt, B.S.; Dewitt, C.M. Falling charges. Phys. N. Y. 1964, 1, 3–20. [Google Scholar] [CrossRef]
- Smith, A.G.; Will, C.M. Force on a static charge outside a Schwarzschild black hole. Phys. Rev. D 1980, 22, 1276–1284. [Google Scholar] [CrossRef]
- Chrzanowski, P.L.; Misner, C.W. Geodesic synchrotron radiation in the Kerr geometry by the method of asymptotically factorized Green’s functions. Phys. Rev. D 1974, 10, 1701–1721. [Google Scholar] [CrossRef]
- Gal’tsov, D.V. Radiation reaction in the Kerr gravitational field. J. Phys. A Math. Gen. 1982, 15, 3737–3749. [Google Scholar] [CrossRef]
- Sokolov, A.A.; Ternov, I.M.; Aliev, A.N.; Gal’tsov, D.V. Synchrotron radiation in curved space-time. Sov. Phys. J. 1983, 26, 36–40. [Google Scholar] [CrossRef]
- Sokolov, A.A.; Gal’tsov, D.V.; Petukhov, V.I. Radiation emitted by relativistic particles moving in the vicinity of the Schwarzschild black hole, immersed in an external magnetic field. Phys. Lett. A 1978, 68, 1–2. [Google Scholar] [CrossRef]
- Shoom, A.A. Synchrotron radiation from a weakly magnetized Schwarzschild black hole. Phys. Rev. D 2015, 92, 124066. [Google Scholar] [CrossRef]
- Piotrovich, M.Y.; Silant’ev, N.A.; Gnedin, Y.N.; Natsvlishvili, T.M. Magnetic fields and quasi-periodic oscillations of black hole radiation. Astrophys. Bull. 2011, 66, 320–324. [Google Scholar] [CrossRef]
- Baczko, A.K.; Schulz, R.; Kadler, M.; Ros, E.; Perucho, M.; Krichbaum, T.P.; Böck, M.; Bremer, M.; Grossberger, C.; Lindqvist, M.; et al. A highly magnetized twin-jet base pinpoints a supermassive black hole. Astron. Astrophys. 2016, 593, A47. [Google Scholar] [CrossRef]
- Johnson, M.D.; Fish, V.L.; Doeleman, S.S.; Marrone, D.P.; Plambeck, R.L.; Wardle, J.F.C.; Akiyama, K.; Asada, K.; Beaudoin, C.; Blackburn, L.; et al. Resolved magnetic-field structure and variability near the event horizon of Sagittarius A*. Science 2015, 350, 1242–1245. [Google Scholar] [CrossRef] [PubMed]
- Kovář, J. Spiral motion formation in astrophysics. Eur. Phys. J. Plus 2013, 128, 142. [Google Scholar] [CrossRef]
- Kovář, J.; Kopáček, O.; Karas, V.; Kojima, Y. Regular and chaotic orbits near a massive magnetic dipole. Class. Quantum Gravity 2013, 30, 025010. [Google Scholar] [CrossRef]
- Pugliese, D.; Stuchlík, Z. Relating Kerr SMBHs in active galactic nuclei to RADs configurations. Class. Quantum Gravity 2018, 35, 185008. [Google Scholar] [CrossRef]
- Pugliese, D.; Stuchlík, Z. RADs energetics and constraints on emerging tori collisions around super-massive Kerr black holes. Eur. Phys. J. C 2019, 79, 288. [Google Scholar] [CrossRef]
- Cremaschini, C.; Kovář, J.; Slaný, P.; Stuchlík, Z.; Karas, V. Kinetic Theory of Equilibrium Axisymmetric Collisionless Plasmas in Off-equatorial Tori around Compact Objects. Astrophys. J. Suppl. 2013, 209, 15. [Google Scholar] [CrossRef]
- Bao, G.; Stuchlik, Z. Accretion Disk Self-Eclipse: X-Ray Light Curve and Emission Line. Astrophys. J. 1992, 400, 163. [Google Scholar] [CrossRef]
- Prasanna, A.R.; Sengupta, S. Charged particle trajectories in the presence of a toroidal magnetic field on a Schwarzschild background. Phys. Lett. A 1994, 193, 25. [Google Scholar] [CrossRef]
- Bakala, P.; Šrámková, E.; Stuchlík, Z.; Török, G. On magnetic-field-induced non-geodesic corrections to relativistic orbital and epicyclic frequencies. Class. Quantum Gravity 2010, 27, 045001. [Google Scholar] [CrossRef]
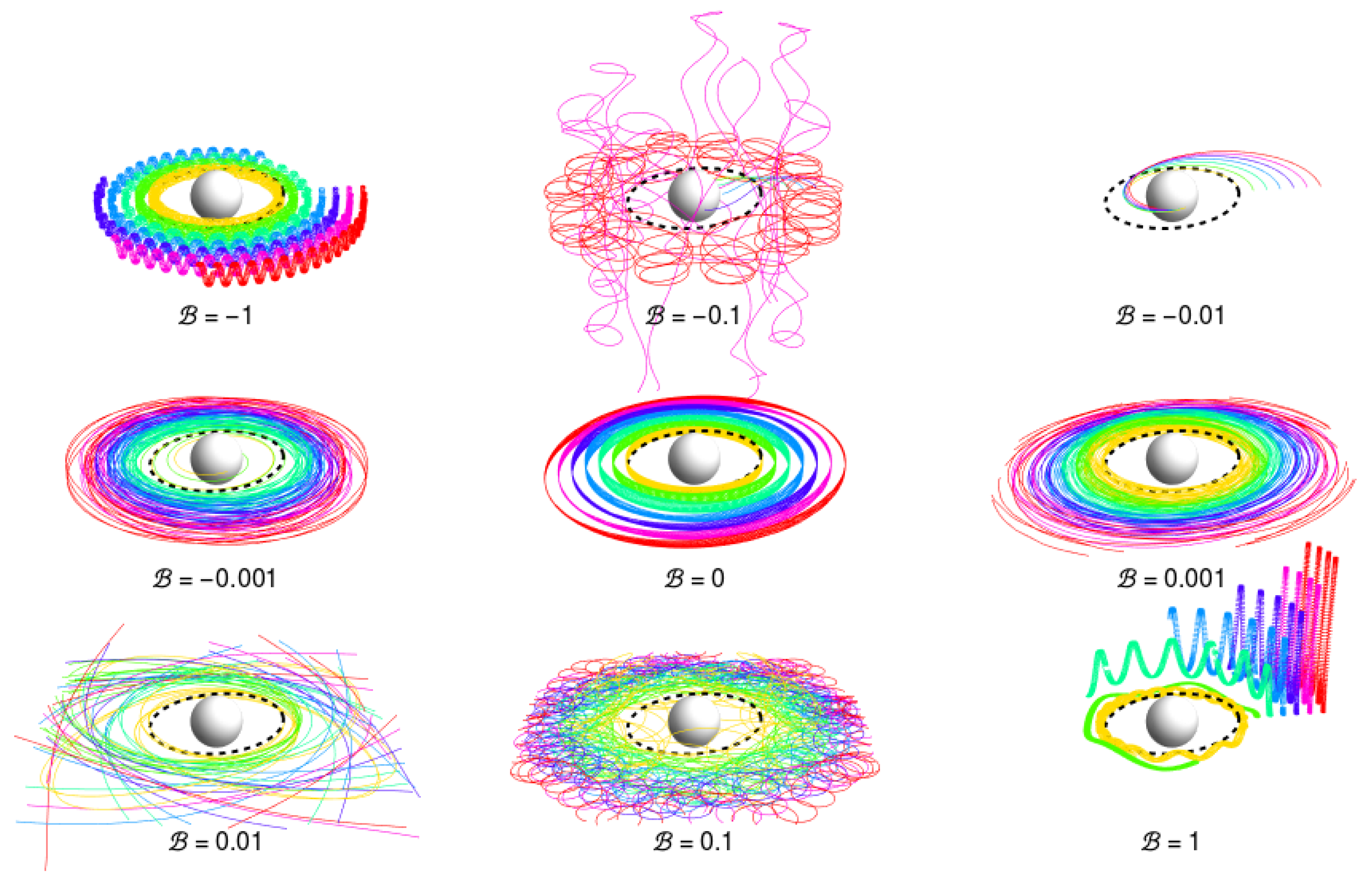
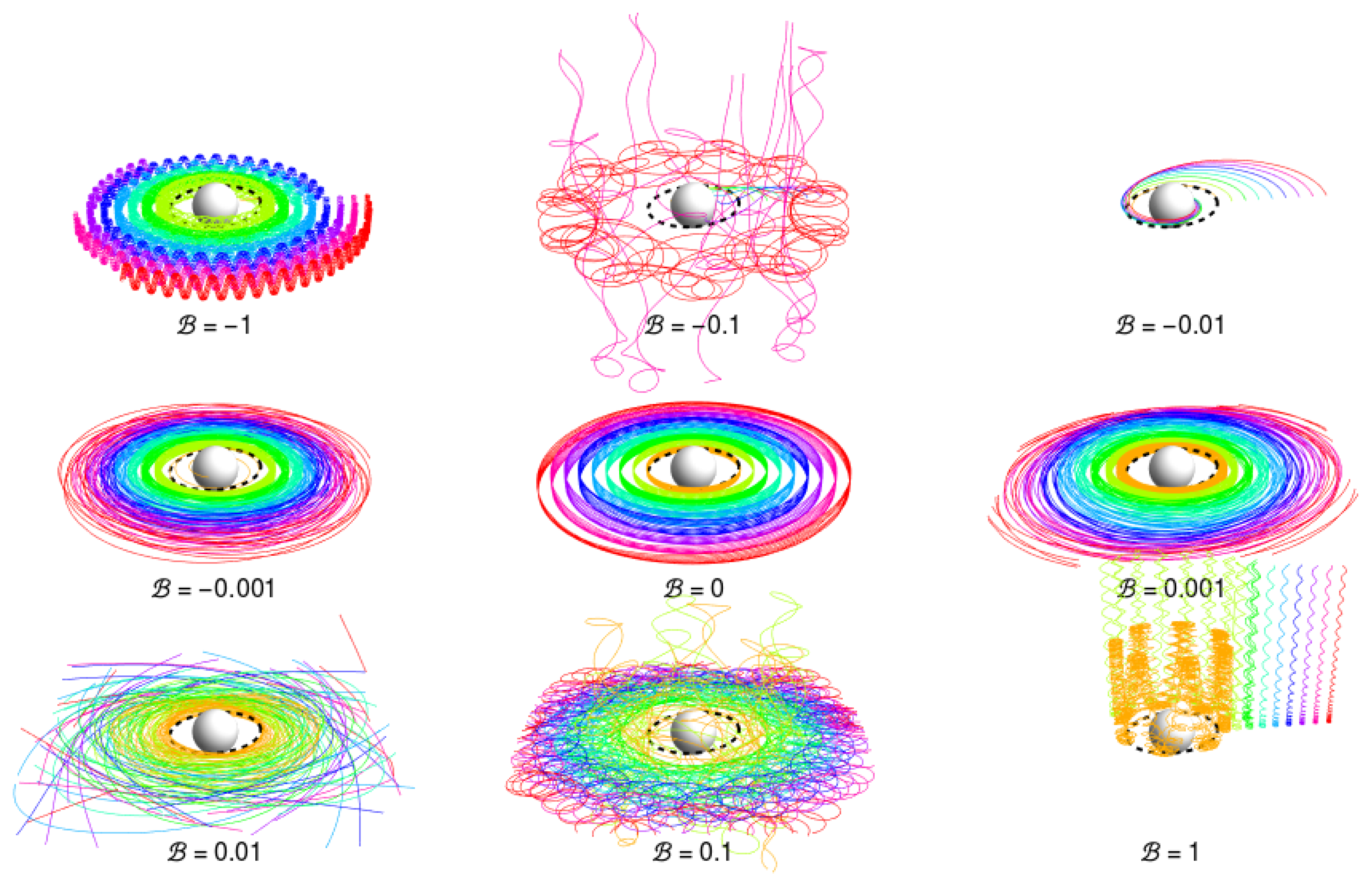
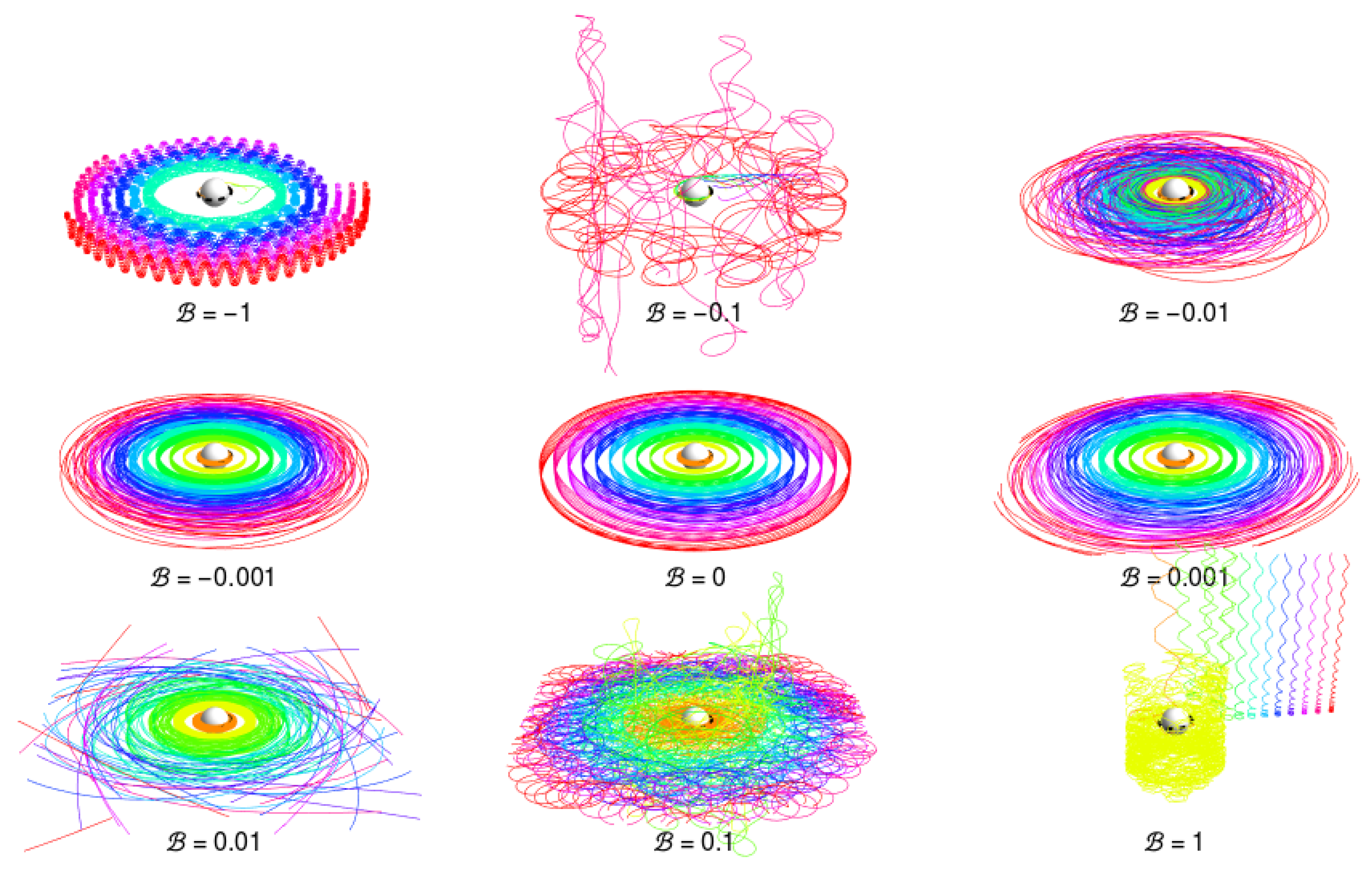
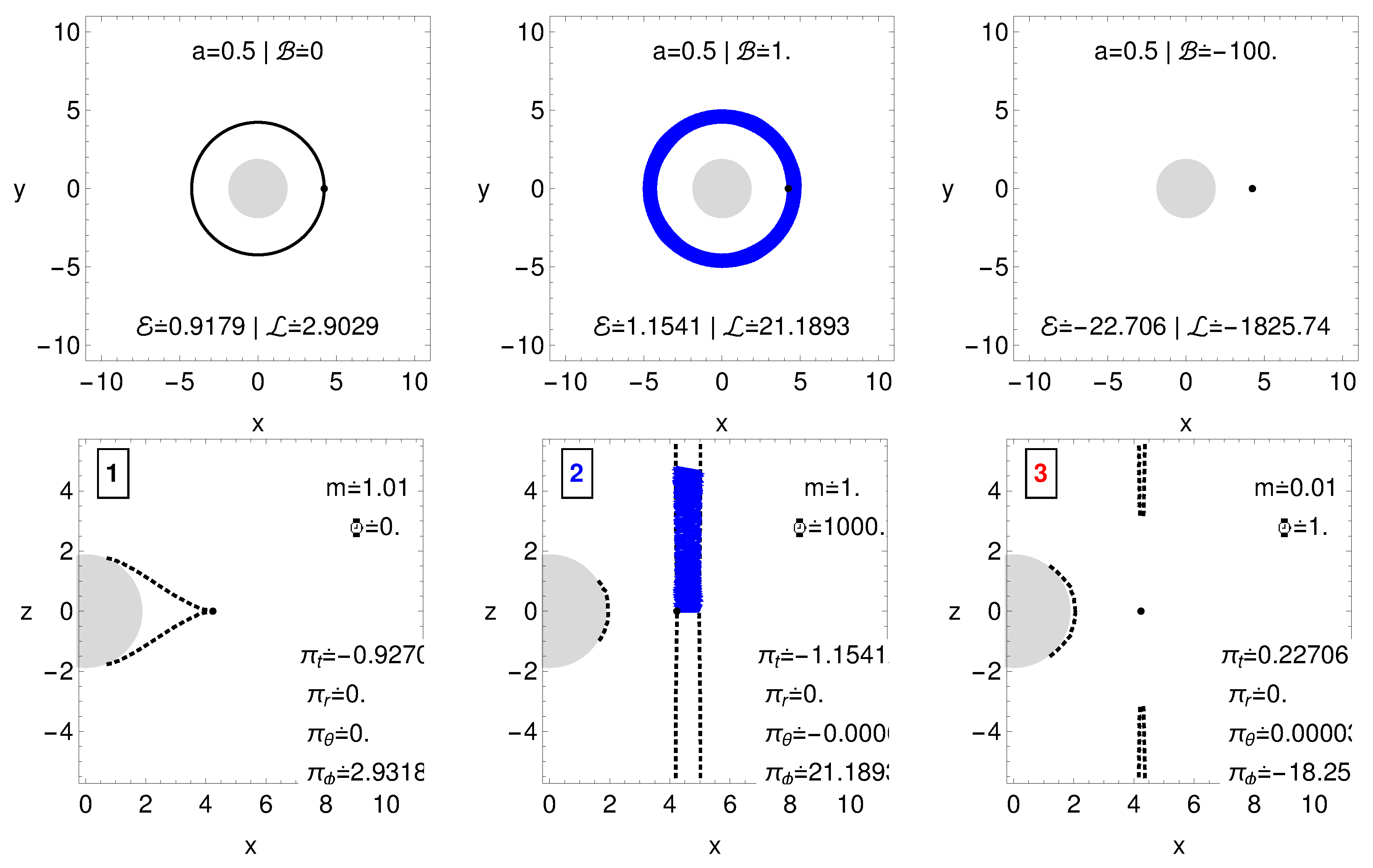
| 1. | The character of the geodesic motion in the complete Kerr–de Sitter spacetime and the relevance of the effective potential , governing particles in the negative-root states at the stationary region between the black-hole and cosmological horizons, is qualitatively the same as discussed in [62]. |
| 2. | For analogical estimates for primordial black holes and an effective cosmological constant related to vacuum energy density connected with the electroweak symmetry breaking or the quark confinement, see [16]. |
| 3. | Location of the “static radius” out of the equatorial plane is roughly given by its location in the SdS spacetime having the same cosmological parameter (relation (18)), as far away from the rotating black hole these two backgrounds almost coincide for y. |
| 4. | |
| 5. | For the case of inclined magnetic field see [91]. |
| 6. | |
| 7. | For detailed information on the so-called geodesic models of HF QPOs that could be related to binary systems containing both black holes or neutron stars, see [104]. |
| 8. | For exceptions related to Kerr naked singularities, see [105]. |
| 9. | |
| 10. | We can consider the MPP as a general process relevant in any magnetic field around a rotating black hole, but, for the Blanford–Znajek process, a threshold magnetic field of high magnitude is necessary [38]. |
| 11. | |
| 12. | Note that the double or multi-toroidal structures can be constructed also in the model of uncharged hydrodynamical tori, in the framework of the so-called ringed accretion disks mixing relatively counter-rotating tori that could be created during evolution of accretion structures in active galactic nuclei [6,7,8,149,150]. |
| 13. | Of course, it would be instructive to consider both the terms in the right hand side of the Ohm law and combine the both limiting approaches. We plan such studies in future research. |
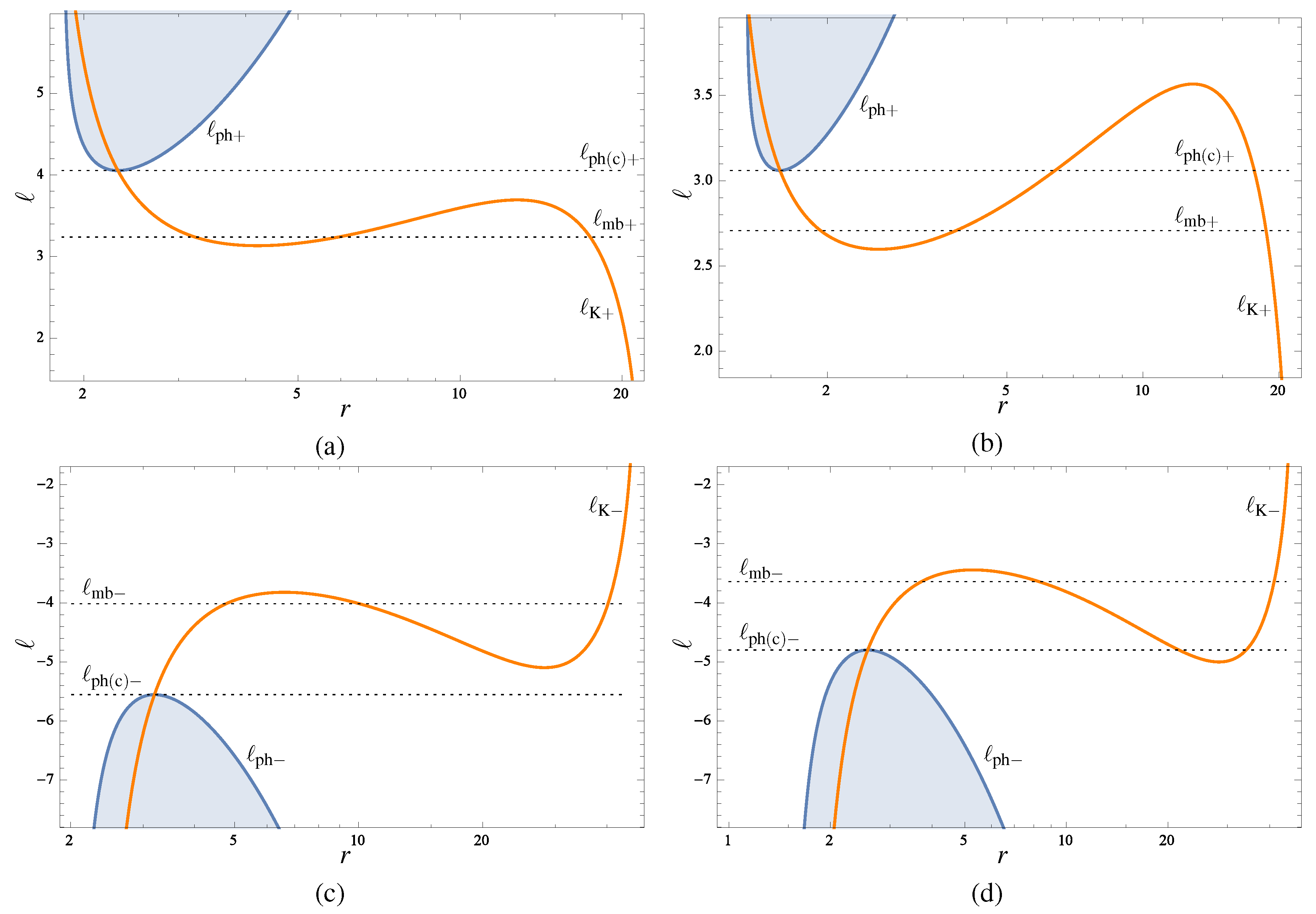


| y | M | |||
|---|---|---|---|---|
| [] | [kpc] | [kpc] | [kpc] | |
| 10 | 0.23 | 0.15 | 0.23 | |
| 1.1 | 0.67 | 1.1 | ||
| 11 | 6.7 | 11 | ||
| 67 | ||||
| / | Electron | Proton | Fe+ | Charged Dust |
|---|---|---|---|---|
| Source | [Hz] | [Hz] | [Hz] | M [] | a |
|---|---|---|---|---|---|
| GRO 1655-40 | 18 | 300 | 450 | 6.03–6.57 | 0.65–0.75 |
| XTE 1550-564 | 13 | 184 | 276 | 8.5–9.7 | 0.29–0.52 |
| GRS 1915+105 | 10 | 113 | 168 | 10.6–14.4 |
| GRO 1655-40 | XTE 1550-564 | GRS 1915+105 | |
|---|---|---|---|
| ER model | |||
| PALO | 11.5–23.0 | 8.2–16.3 | 0–14.5 |
| RLO | noexist | 21.8–∞ | 9.6–∞ |
| PLO | 0–61.4 | 10.9–43.6 | 0– 28.9 |
| RALO | 23.1–26.9 | 13.6–16.3 | 7.2–19.3 |
| B (Gauss) | (s) | (s) |
|---|---|---|
| 1 | ||
| 1 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stuchlík, Z.; Kološ, M.; Kovář, J.; Slaný, P.; Tursunov, A. Influence of Cosmic Repulsion and Magnetic Fields on Accretion Disks Rotating around Kerr Black Holes. Universe 2020, 6, 26. https://doi.org/10.3390/universe6020026
Stuchlík Z, Kološ M, Kovář J, Slaný P, Tursunov A. Influence of Cosmic Repulsion and Magnetic Fields on Accretion Disks Rotating around Kerr Black Holes. Universe. 2020; 6(2):26. https://doi.org/10.3390/universe6020026
Chicago/Turabian StyleStuchlík, Zdeněk, Martin Kološ, Jiří Kovář, Petr Slaný, and Arman Tursunov. 2020. "Influence of Cosmic Repulsion and Magnetic Fields on Accretion Disks Rotating around Kerr Black Holes" Universe 6, no. 2: 26. https://doi.org/10.3390/universe6020026
APA StyleStuchlík, Z., Kološ, M., Kovář, J., Slaný, P., & Tursunov, A. (2020). Influence of Cosmic Repulsion and Magnetic Fields on Accretion Disks Rotating around Kerr Black Holes. Universe, 6(2), 26. https://doi.org/10.3390/universe6020026






