Discerning the Nature of Neutrinos: Decoherence and Geometric Phases
Abstract
1. Introduction
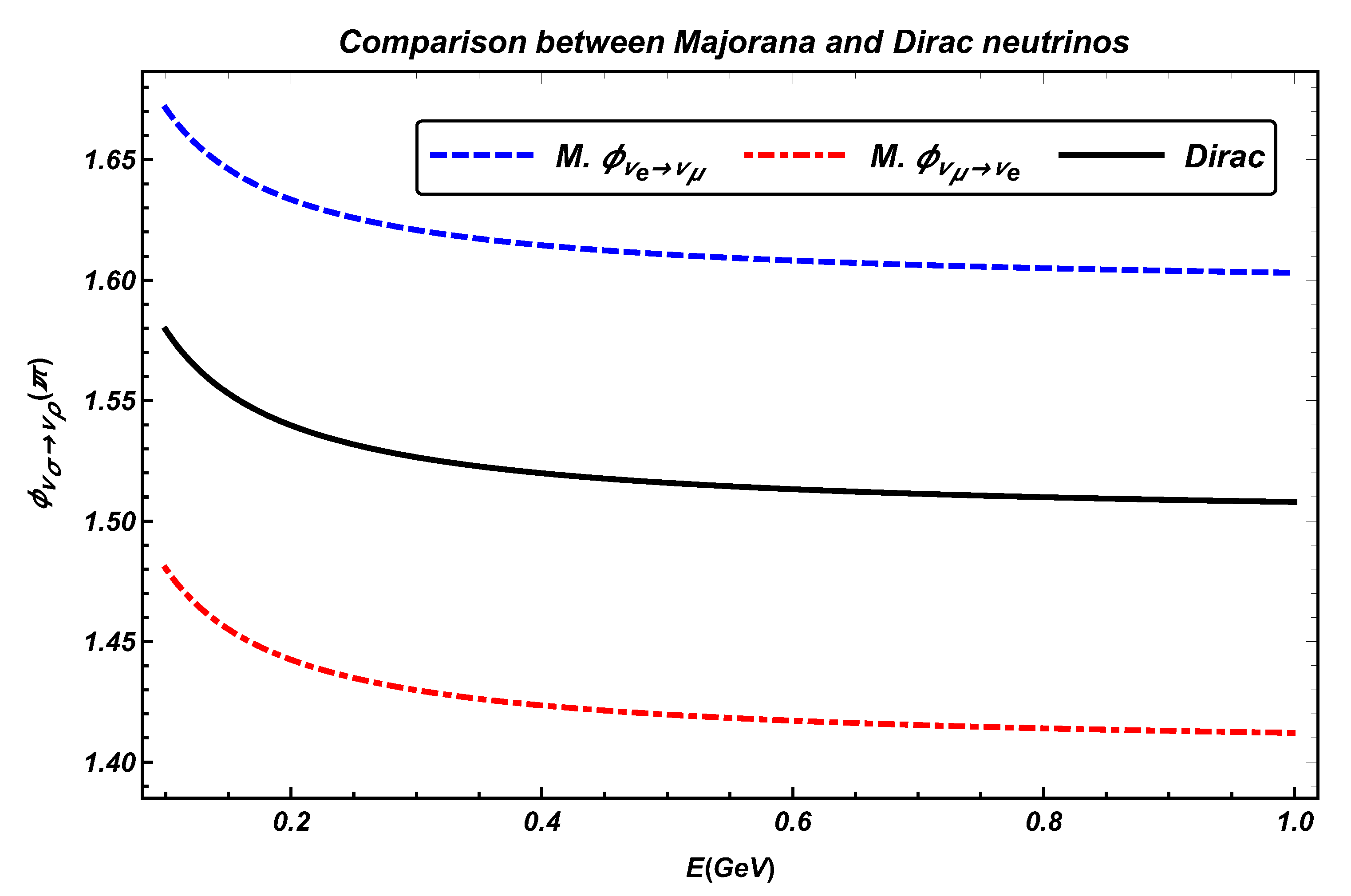
2. Majorana and Dirac Neutrino
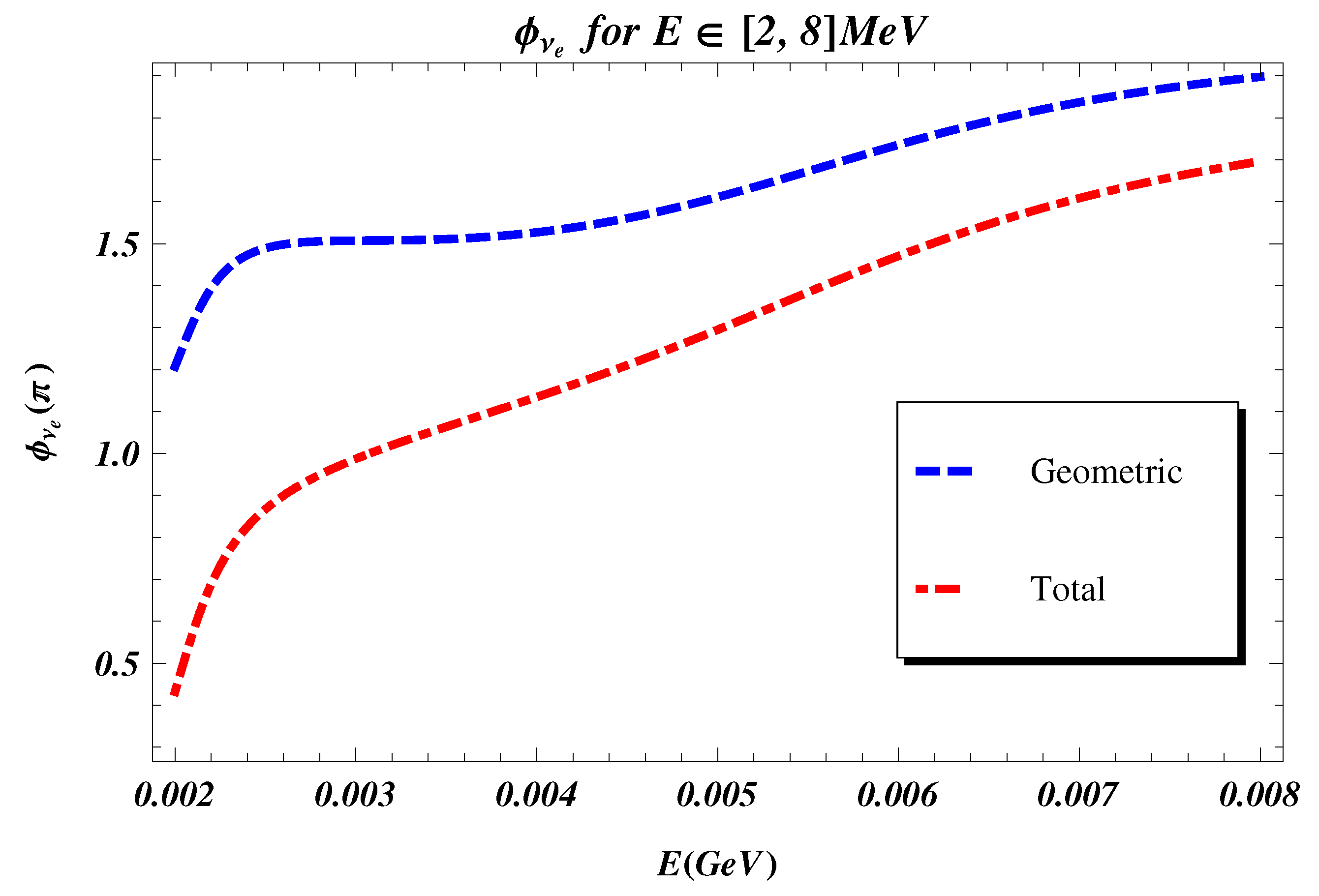
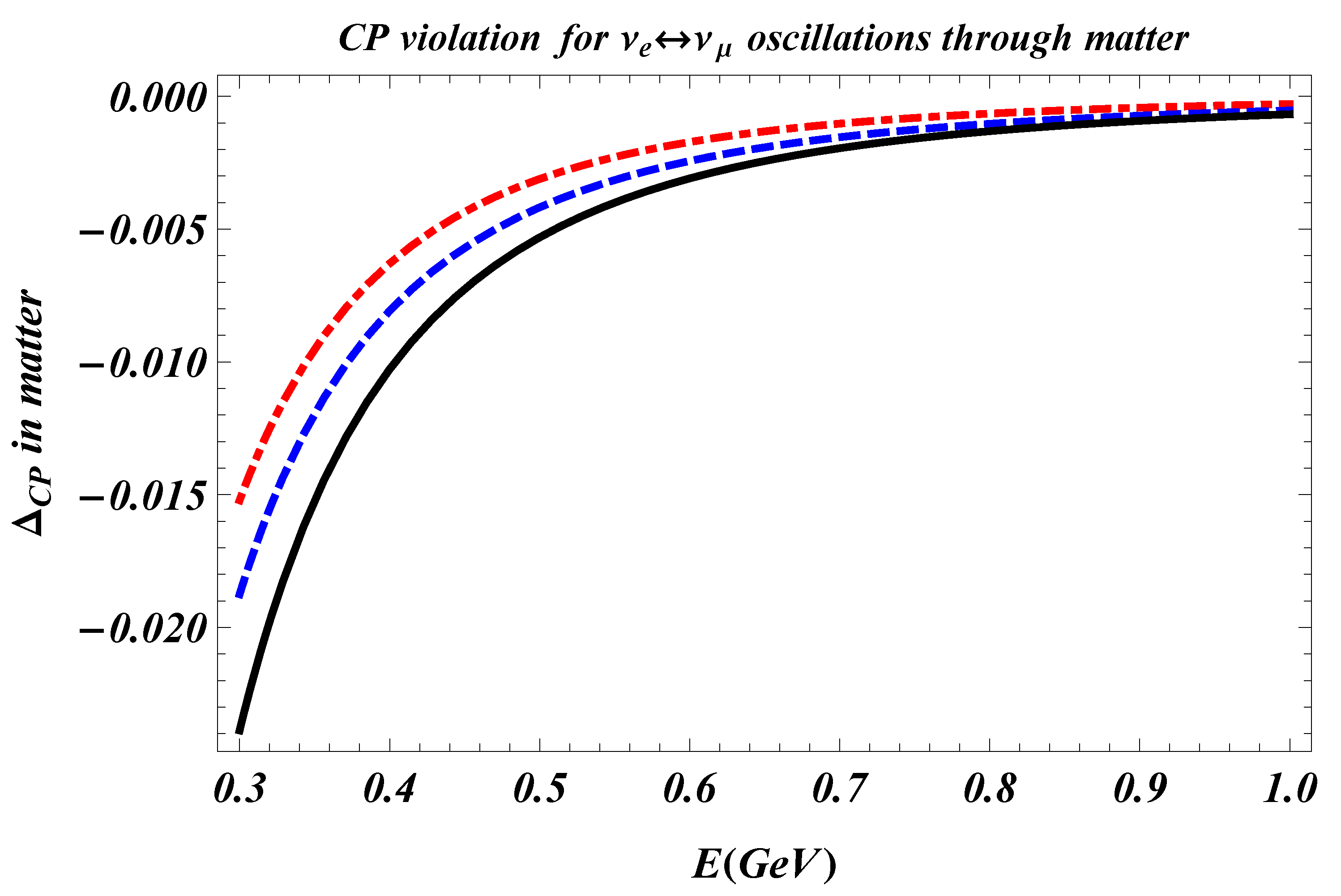
3. Total and Geometric Phases for Neutrinos in Matter
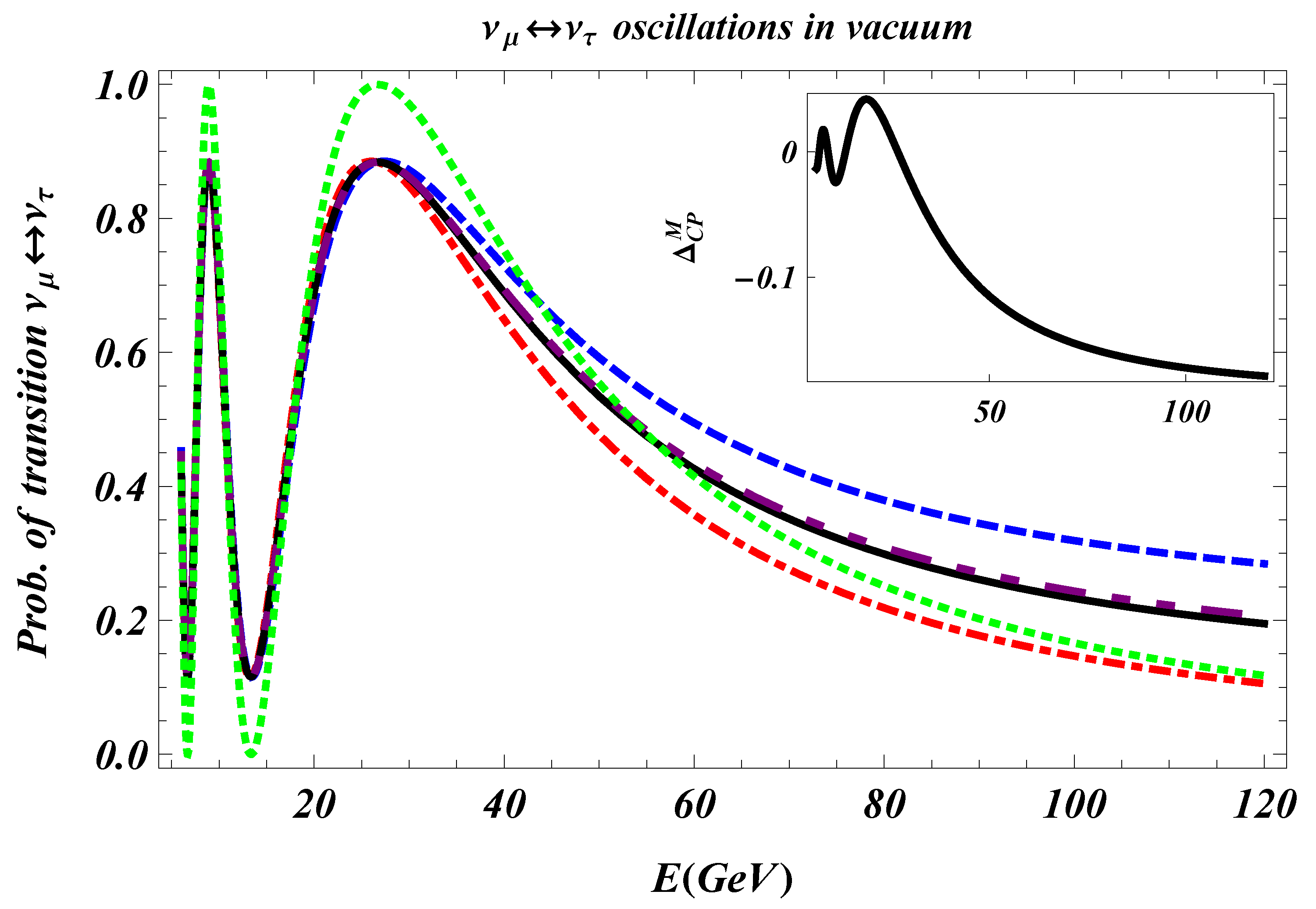
4. Neutrino Oscillations with Decoherence
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pontecorvo, B. Mesonium and anti-mesonium. Zh. Eksp. Teor. Fiz. 1957, 33, 549–551. [Google Scholar]
- Bilenky, S.M.; Pontecorvo, B. Lepton mixing and neutrino oscillations. Phys. Rep. 1978, 41, 225–261. [Google Scholar] [CrossRef]
- Bilenky, S.M.; Petcov, S.T. Massive Neutrinos And Neutrino Oscillations. Rev. Mod. Phys. 1987, 59, 671. [Google Scholar] [CrossRef]
- An, F.P.; Bai, J.Z.; Balantekin, A.B.; Band, H.R.; Beavis, D.; Beriguete, W.; Cai, B. Observation of electron-antineutrino disappearance at Daya Bay. Phys. Rev. Lett. 2012, 108, 171803. [Google Scholar] [CrossRef] [PubMed]
- Ahn, J.K.; Chebotaryov, S.; Choi, J.H.; Choi, S.; Choi, W.; Choi, Y.; Jang, H.I.; Jang, J.S.; Leon, E.J.; Jeong, I.S.; et al. Observation of Reactor Electron Antineutrino Disappearance in the RENO experiment. Phys. Rev. Lett. 2012, 108, 191802. [Google Scholar] [CrossRef]
- Abe, Y.; Aberle, C.; Akiri, T.; dos Anjos, J.C.; Ardellier, F.; Barbosa, A.F.; Baxter, A.; Bergevin, M.; Bernstein, A.; Bezerra, T.J.C.; et al. (Double Chooz Collaboration). Indication of Reactor ῡe Disappearance in the Double Chooz Experiment. Phys. Rev. Lett. 2012, 108, 131801. [Google Scholar] [CrossRef]
- Abe, K.; N. Abgrall; Y. Ajima; H. Aihara; J.B. Albert; C. Andreopoulos; B. Andrieu; S. Aoki; O. Araoka; J. Argyriades et al. (T2K Collaboration). Indication of Electron Neutrino Appearance from an Accelerator-produced Off-axis Muon Neutrino Beam. Phys. Rev. Lett. 2011, 107, 041801. [Google Scholar] [CrossRef]
- Adamson, P.; Auty, D.J.; Ayres, D.S.; Backhouse, C.; Barr, G.; Betancourt, M.; Bishai, M.; Blake, A.; Bock, G.J.; Boehnlein, D.J.; et al. Improved search for muon-neutrino to electron-neutrino oscillations in MINOS. Phys. Rev. Lett. 2011, 107, 181802. [Google Scholar] [CrossRef]
- Nakamura, K.; Petcov, S.T. Neutrino mass, mixing, and oscillations. Phys. Rev. D 2013, 86, 010001. [Google Scholar]
- Giunti, C. No effect of Majorana phases in neutrino oscillations. Phys. Lett. B 2010, 686, 41. [Google Scholar] [CrossRef]
- Giuliani, A.; Poves, A. Neutrinoless Double-Beta Decay. Adv. High Energy Phys. 2012, 2012, 1. [Google Scholar] [CrossRef]
- Richter, M.; Dziewit, B.; Dajka, J. Leggett-Garg K3 quantity discriminates between Dirac and Majorana neutrinos. Phys. Rev. D 2017, 96, 076008. [Google Scholar] [CrossRef]
- Benatti, F.; Floreanini, R. Open system approach to neutrino oscillations. JHEP 2000, 2, 32. [Google Scholar] [CrossRef]
- Benatti, F.; Floreanini, R. Massless neutrino oscillations. Phys. Rev. D 2001, 64, 085015. [Google Scholar] [CrossRef]
- Capolupo, A.; Giampaolo, S.M.; Hiesmayr, B.C.; Vitiello, G. Geometric phase of neutrinos: Differences between Dirac and Majorana neutrinos. Phys. Lett. B 2018, 780, 216. [Google Scholar] [CrossRef]
- Capolupo, A.; Giampaolo, S.M.; Lambiase, G. Decoherence in neutrino oscillations, neutrino nature and CPT violation. Phys. Lett. B 2019, 792, 298–303. [Google Scholar] [CrossRef]
- Berry, M.V. Quantal phase factors accompanying adiabatic changes. Proc. Roy. Soc. Lond. A 1984, 392, 45–57. [Google Scholar]
- Berry, M.V. Classical adiabatic angles and quantal adiabatic phase. J. Phys. A 1985, 18, 15–27. [Google Scholar] [CrossRef]
- Hinterbichler, K. Theoretical aspects of massive gravity. Rev. Mod. Phys. 2012, 84, 671. [Google Scholar] [CrossRef]
- Aharonov, Y.; Anandan, J. Phase Change During A Cyclic Quantum Evolution, Phys. Rev. Lett. 1987, 58, 1593. [Google Scholar] [CrossRef]
- Samuel, J.; Bhandari, R. General Setting for Berry’s Phase. Phys. Rev. Lett. 1988, 60, 2339. [Google Scholar] [CrossRef] [PubMed]
- Pancharatnam, S. Generalized theory of interference, and its applications. Proc. Indian Acad. Sci. A 1956, 44, 1225. [Google Scholar]
- Shapere, A.; Wilczek, F. Geometric Phases in Physics; World Scientific: Singapore, 1989. [Google Scholar]
- Garrison, J.C.; Wright, E.M. Complex geometrical phases for dissipative systems. Phys. Lett. A 1988, 128, 177. [Google Scholar] [CrossRef]
- Pati, A.K. Gauge-invariant reference section and geometric phase. J. Phys. A 1995, 28, 2087. [Google Scholar] [CrossRef]
- Pati, A.K. Geometric aspects of noncyclic quantum evolutions. Phys. Rev. A 1995, 52, 2576. [Google Scholar] [CrossRef] [PubMed]
- Mukunda, N.; Simon, R. Quantum Kinematic Approach to the Geometric Phase. I. General formalism. Ann. Phys. (N. Y.) 1993, 228, 205. [Google Scholar] [CrossRef]
- Mostafazadeh, A. Noncyclic geometric phase and its non-Abelian generalization. J. Phys. A 1999, 32, 8157. [Google Scholar] [CrossRef][Green Version]
- Anandan, J. Non-adiabatic non-Abelian geomtric phase. Phys. Lett. A 1988, 133, 171. [Google Scholar] [CrossRef]
- Tomita, A.; Chiao, R.Y. Observation of Berry’s Topological Phase by Use of an Optical Fiber. Phys. Rev. Lett. 1986, 57, 937. [Google Scholar] [CrossRef]
- Jones, J.A.; Vedral, V.; Ekert, A.; Castagnoli, G. Geometric quantum computation using nuclear magnetic resonance. Nature 2000, 403, 869. [Google Scholar] [CrossRef]
- Leek, P.J.; Fink, J.M.; Blais, A.; Bianchetti, R.; Goppl, M.; Gambetta, J.M.; Schuster, D.I.; Frunzio, L.; Schoelkopf, R.J.; Wallraff, A. Observation of Berry’s Phase in a Solid-State Qubit. Science 2007, 318, 1889. [Google Scholar] [CrossRef] [PubMed]
- Neeley, M.; Ansmann, M.; Bialczak, R.C.; Hofheinz, M.; Lucero, E.; O’Connell, A.D.; Sank, D.; Wang, H.; Wenner, J.; Cleland, A.N.; et al. Emulation of a Quantum Spin with a Superconducting Phase Qudit. Science 2009, 325, 722–725. [Google Scholar] [CrossRef]
- Pechal, M.; Berger, S.; Abdumalikov, A.A., Jr.; Fink, J.M.; Mlynek, J.A.; Steffen, L.; Wallraff, A.; Filipp, S. Geometric Phase and Nonadiabatic Effects in an Electronic Harmonic Oscillator. Phys. Rev. Lett. 2012, 108, 170401. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Tan, Y.-W.; Stormer, H.L.; Kim, P. Experimental observation of the quantum Hall effect and Berry’s phase in graphene. Nature 2005, 438, 201–204. [Google Scholar] [CrossRef] [PubMed]
- Falci, G.; Fazio, R.; Palma, G.M.; Siewert, J.; Vedral, V. Detection of geometric phases in superconducting nanocircuits. Nature 2000, 407, 355–358. [Google Scholar] [CrossRef]
- Mottonen, M.; Vartiainen, J.J.; Pekola, J.P. Experimental determination of the Berry phase in a superconducting charge pump. Phys. Rev. Lett. 2008, 100, 177201. [Google Scholar] [CrossRef]
- Murakawa, H.; Bahramy, M.S.; Tokunaga, M.; Kohama, Y.; Bell, C.; Kaneko, Y.; Nagaosa, N.; Hwang, H.Y.; Tokura, Y. Detection of Berry’s Phase in a Bulk Rashba Semiconductor. Science 2013, 342, 1490–1493. [Google Scholar] [CrossRef]
- Capolupo, A.; Vitiello, G. Spontaneous supersymmetry breaking probed by geometric invariants. Adv. High Energy Phys. 2013, 2013, 850395. [Google Scholar] [CrossRef]
- Capolupo, A.; Vitiello, G. Probing Hawking and Unruh effects and quantum field theory in curved space by geometric invariants. Phys. Rev. D 2013, 88, 024027. [Google Scholar] [CrossRef]
- Capolupo, A.; Vitiello, G. Vacuum Condensate, Geometric Phase, Unruh Effect and Temperature Measurement. Adv. High Energy Phys. 2015, 2015, 878043. [Google Scholar] [CrossRef]
- Xiao, D.; Chang, M.-C.; Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 2010, 82, 1959. [Google Scholar] [CrossRef]
- Bruno, A.; Capolupo, A.; Kak, S.; Raimondo, G.; Vitiello, G. Gauge theory and two level systems. Mod. Phys. Lett. B 2011, 25, 1661. [Google Scholar] [CrossRef]
- Hu, J.; Yu, H. Geometric phase for accelerated two-level atom and the Unruh effect. Phys. Rev. A 2012, 85, 032105. [Google Scholar] [CrossRef]
- Nakagawa, N. Geometrical phase factors and higher-order adiabatic approximations. Ann. Phys. 1987, 1987 179, 145. [Google Scholar] [CrossRef]
- Capolupo, A. Probing CPT violation in meson mixing by non-cyclic phase. Phys. Rev. D 2011, 84, 116002. [Google Scholar] [CrossRef]
- Naumov, V.A. Berry phases for three-neutrino oscillations in matter. Phys. Lett. B 1994, 323, 351. [Google Scholar] [CrossRef]
- Syska, J.; Dajka, J.; Luczka, J. Interference phenomenon and geometric phase for Dirac neutrino in π+ decay. Phys. Rev. D 2013, 87, 117302. [Google Scholar] [CrossRef]
- Blasone, M.; Capolupo, A.; Celeghini, E.; Vitiello, G. Non-cyclic phases for neutrino oscillations in quantum field theory. Phys. Lett. B 2009, 674, 73. [Google Scholar] [CrossRef][Green Version]
- Johns, L.; Fuller, G.M. Geometric phases in neutrino oscillations with nonlinear refraction. Phys. Rev. D 2017, 95, 043003. [Google Scholar] [CrossRef]
- Joshi, S.; Jain, S.R. Geometric phase for neutrino propagation in magnetic field. Phys. Lett. B 2016, 754, 135. [Google Scholar] [CrossRef][Green Version]
- Capolupo, A.; Lambiase, G.; Vitiello, G. Probing mixing of photons and axion-like particles by geometric phase. Adv. High Energy Phys. 2015, 2015, 826051. [Google Scholar] [CrossRef]
- He, X.-G.; Li, X.-Q.; McKellar, B.; Zhang, Y. Berry phase in neutrino oscillations. Phys. Rev. D 2005, 72, 053012. [Google Scholar] [CrossRef]
- Dixit, K.; Alok, A.K.; Banerjee, S.; Kumar, D. Geometric phase and neutrino mass hierarchy problem. J. Phys. G Nucl. Part. Phys. 2018, 45, 085002. [Google Scholar] [CrossRef]
- Wang, Z.; Pan, H. Exploration of CPT violation via time-dependent geometric quantities embedded in neutrino oscillation through fluctuating matter. Nucl. Phys. B 2017, 915, 414–430. [Google Scholar] [CrossRef]
- Syska, J.; Dajka, J.; Luczka, J. Geometric phase of neutrino propagating through dissipative matter. J. Phys. Rev. D 2011, 83, 097302. [Google Scholar]
- Bandyopadhyay, P. Solar-neutrino problem and the Berry phase. Il Nuovo Cimento C 1994, 17, 191–198. [Google Scholar] [CrossRef]
- Mehta, P. Topological phase in two flavor neutrino oscillations. Phys. Rev. D 2009, 79, 096013. [Google Scholar] [CrossRef]
- Mehta, P. Topological phase in two flavor neutrino oscillations and imprint of the CP phase. Nucl. Phys. B Proc. Suppl. 2012, 229–232, 467. [Google Scholar] [CrossRef]
- Naumov, V.A. Three-neutrino oscillations in matter, CP-violation and topological phases. Int. J. Mod. Phys. D 1992, 1, 379–399. [Google Scholar] [CrossRef]
- Wolfenstein, L. Neutrino oscillations in matter. Phys. Rev. D 1978, 17, 2369. [Google Scholar] [CrossRef]
- Mikheev, S.P.; Yu, A. Smirnov. Resonance enhancement of oscillations in matter and solar neutrino spectroscopy. Sov. J. Nucl. Phys. 1985, 42, 913–917. [Google Scholar]
- Rovelli, C. Quantum Gravity; Cambridge University Press: New York, NY, USA, 2004; ISBN 0-521-71596-2. [Google Scholar]
- Amelino-Camelia, G. Quantum-Spacetime Phenomenology. Liv. Rev. Rel. 2013, 16, 5. [Google Scholar] [CrossRef] [PubMed]
- Giampaolo, S.M.; Macri’, T. Entanglement, holonomic constraints, and the quantization of fundamental interactions. arXiv 2018, arXiv:1806.08383. [Google Scholar] [CrossRef] [PubMed]
- Kostelecky, V.A. Gravity, Lorentz violation and the standard model. Phys. Rev. D 2004, 69, 105009. [Google Scholar] [CrossRef]
- Amelino-Camelia, G. Doubly-Special Relativity: Facts, Myths and Some Key Open Issues. Symmetry 2010, 2, 230. [Google Scholar] [CrossRef]
- Bernabéu, J.; Botell, F.J.; Mavromatos, N.E.; Nebot, M. The signal of ill-defined CPT weakening entanglement in the Bd system. Eur. Phys. J. C 2017, 77, 865. [Google Scholar] [CrossRef]
- Capolupo, A.; Giampaolo, S.M.; Quaranta, A. Neutrinos in a dense medium, CP and CPT violations: Beyond the MSW effect. arXiv 2020, arXiv:2008.08119v1. [Google Scholar]
- Simonov, K.; Capolupo, A.; Giampaolo, S.M. Gravity, entanglement and CPT-symmetry violation in particle mixing, Eur. Phys. J. C 2019, 79, 902. [Google Scholar] [CrossRef]
- Fogli, G.L.; Lisi, E.; Marrone, A.; Montanino, D.; Palazzo, A. Probing nonstandard decoherence effects with solar and KamLAND neutrinos. Phys. Rev. D 2007, 76, 033006. [Google Scholar] [CrossRef]
- Gago, A.M.; Santos, E.M.; Teves, W.J.C.; Zukanovich Funchal, R. Quantum dissipative effects and neutrinos: Current constraints and future perspectives. Phys. Rev. D 2001, 63, 073001. [Google Scholar] [CrossRef]
- Lisi, E.; Marrone, A.; Montanino, D. Probing Possible Decoherence Effects in Atmospheric Neutrino Oscillations. Phys. Rev. Lett. 2000, 85, 1166. [Google Scholar] [CrossRef] [PubMed]
- Morgan, D.; Winstanley, E.; Brunner, J.; Thompson, L.F. Probing quantum decoherence in atmospheric neutrino oscillations with a neutrino telescope. Astropart. Phys. 2006, 25, 311. [Google Scholar] [CrossRef]
- Farzan, Y.; Schwetz, T.; Smirnov, A.Y. Reconciling results of LSND, MiniBooNE and other experiments with soft decoherence. JHEP 2008, 0807, 067. [Google Scholar] [CrossRef]
- Oliveira, R.L.N.; Guzzo, M.M. Quantum dissipation in vacuum neutrino oscillation. Eur. Phys. J. C 2010, 69, 493. [Google Scholar] [CrossRef]
- Balieiro Gomes, G.; Guzzo, M.M.; de Holanda, P.C.; Oliveira, R.L.N. Parameter limits for neutrino oscillation with decoherence in KamLAND. Phys. Rev. D 2016, 95, 113005. [Google Scholar] [CrossRef]
- Bakhti, P.; Farzan, Y.; Schwetz, T. Revisiting the quantum decoherence scenario as an explanation for the LSND anomaly. JHEP 2015, 05, 007. [Google Scholar] [CrossRef]
- Oliveira, R.L.N. Dissipative effect in long baseline neutrino experiments. Eur. Phys. J. C 2016, 76, 417. [Google Scholar] [CrossRef]
- Guzzo, M.M.; de Holanda, P.C.; Oliveira, R.L.N. Quantum dissipation in a neutrino system propagating in vacuum and in matter. Nucl. Phys. B 2016, 908, 408–422. [Google Scholar] [CrossRef]
- Lindblad, G. On the generators of quantum dynamical semigroups. Commun. Math. Phys. 1976, 48, 119–130. [Google Scholar] [CrossRef]
- Gorini, V.; Kossakowski, A. Completely positive dynamical semigroups of N level systems. J. Math. Phys. 1976, 17, 821. [Google Scholar] [CrossRef]
- Aartsen, M.G.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Al Samarai, I.; Altmann, D.; Andeen, K.; Anderson, T.; et al. Measurement of Atmospheric Neutrino Oscillations at 6–56 GeV with IceCube DeepCore, Phys. Rev. Lett. 2018, 120, 071801. [Google Scholar] [CrossRef] [PubMed]
- Coloma, P.; Lopez-Pavon, J.; Martinez-Soler, I.; Nunokawa, H. Decoherence in neutrino propagation through matter, and bounds from IceCube/DeepCore. Eur. Phys. J. C 2018, 78, 614. [Google Scholar] [CrossRef]
- Gomes, G.B.; Forero, D.V.; Guzzo, M.M.; de Holanda, P.C.; Oliveira, R.L.N. Quantum Decoherence Effects in Neutrino Oscillations at DUNE. Phys. Rev. D 2019, 100, 055023. [Google Scholar] [CrossRef]
- Carpio, J.A.; Massoni, E.; Gago, A.M. Revisiting quantum decoherence in the matter neutrino oscillation framework. Phys. Rev. D 2018, 97, 115017. [Google Scholar] [CrossRef]
- Alfinito, E.; Blasone, M.; Iorio, A.; Vitiello, G. Squeezed neutrino oscillations in quantum field theory. Phys. Lett. B 1995, 362, 91. [Google Scholar] [CrossRef]
- Cardall, C.Y. Coherence of neutrino flavor mixing in quantum field theory. Phys. Rev. D 2000, 61, 073006. [Google Scholar] [CrossRef]
- Blasone, M.; Capolupo, A.; Vitiello, G. Quantum field theory of three flavor neutrino mixing and oscillations with CP violation. Phys. Rev. D 2002, 66, 025033. [Google Scholar] [CrossRef]
- Hannabuss, K.C.; Latimer, D.C. Fermion mixing in quasifree states. J. Phys. A 2003, 36, L69. [Google Scholar] [CrossRef]
- Beuthe, M. Oscillations of neutrinos and mesons in quantum field theory. Phys. Rep. 2003, 375, 105. [Google Scholar] [CrossRef]
- Blasone, M.; Capolupo, A.; Romei, O.; Vitiello, G. Quantum field theory of boson mixing, Phys. Rev. D 2001, 63, 125015. [Google Scholar] [CrossRef]
- Ji, C.R.; Mishchenko, Y. Nonperturbative vacuum effect in the quantum field theory of meson mixing. Phys. Rev. D 2001, 64, 076004. [Google Scholar] [CrossRef]
- Beuthe, M. Towards a unique formula for neutrino oscillations in vacuum. Phys. Rev. D 2002, 66, 013003. [Google Scholar] [CrossRef]
- Capolupo, A.; Ji, C.R.; Mishchenko, Y.; Vitiello, G. Phenomenology of flavor oscillations with non-perturbative effects from quantum field theory. Phys. Lett. B 2004, 594, 135. [Google Scholar] [CrossRef]
- Fujii, K.; Habe, C.; Yabuki, T. Remarks on flavor-neutrino propagators and oscillation formulas. Phys. Rev. D 2001, 64, 013011. [Google Scholar] [CrossRef]
- Blasone, M.; Capolupo, A.; Terranova, F.; Vitiello, G. Lepton charge and neutrino mixing in pion decay processes. Phys. Rev. D 2005, 72, 013003. [Google Scholar] [CrossRef]
- Nishi, C.C. First quantized approaches to neutrino oscillations and second quantization. Phys. Rev. D 2006, 73, 053013. [Google Scholar] [CrossRef]
- Akhmedov, E.K.; Wilhelm, A. Quantum field theoretic approach to neutrino oscillations in matter. J. High Energy Phys. 2013, 165. [Google Scholar] [CrossRef]
- Kobach, A.; Manohar, A.V.; McGreevy, J. Neutrino oscillation measurements computed in quantum field theory. Phys. Lett. B 2018, 783, 59–75. [Google Scholar] [CrossRef]
- Naumov, D.V.; Naumov, V.A. Quantum Field Theory of Neutrino Oscillations. Phys. Part. Nuclei 2020, 51, 1–106. [Google Scholar] [CrossRef]
- Capolupo, A. Dark matter and dark energy induced by condensates, Adv. High Energy Phys. 2016, 2016, 8089142. [Google Scholar]
- Capolupo, A. Quantum Vacuum, Dark Matter, Dark Energy and Spontaneous Supersymmetry Breaking. Adv. High Energy Phys. 2018, 2018, 9840351. [Google Scholar] [CrossRef]
- Capolupo, A.; Capozziello, S.; Vitiello, G. Dark energy and particle mixing, Phys. Lett. A 2009, 373, 601. [Google Scholar] [CrossRef]
- Capolupo, A.; Capozziello, S.; Vitiello, G. Neutrino mixing as a source of dark energy. Phys. Lett. A 2007, 363, 53–56. [Google Scholar] [CrossRef]
- Capolupo, A.; Capozziello, S.; Vitiello, G. Dark Energy, Cosmological Constant and Neutrino Mixing. Int. J. Mod. Phys. A 2008, 23, 4979. [Google Scholar] [CrossRef]
- Blasone, M.; Capolupo, A.; Capozziello, S.; Carloni, S.; Vitiello, G. Neutrino mixing contribution to the cosmological constant. Phys. Lett. A 2004, 323, 182. [Google Scholar] [CrossRef]
- Capolupo, A.; Mauro, M.D.; Iorio, A. Mixing-induced Spontaneous Supersymmetry Breaking. Phys. Lett. A 2011, 375, 3415. [Google Scholar] [CrossRef]
- Capolupo, A.; Lambiase, G.; Quaranta, A.; Giampaolo, S.M. Probing dark matter and quantum field theory effects with Rydberg atoms. Eur. Phys. J. C 2020, 80, 423. [Google Scholar] [CrossRef]
- Capolupo, A.; Martino, I.D.; Lambiase, G.; Stabile, A. Axion-photon mixing in quantum field theory and vacuum energy. Phys. Lett. B 2019, 790, 427. [Google Scholar] [CrossRef]
- Capolupo, A.; Lambiase, G.; Quaranta, A. Neutrinos in curved space-time: Particle mixing and flavor oscillations. Phys. Rev. D 2020, 101, 095022. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Capolupo, A.; Giampaolo, S.M.; Lambiase, G.; Quaranta, A. Discerning the Nature of Neutrinos: Decoherence and Geometric Phases. Universe 2020, 6, 207. https://doi.org/10.3390/universe6110207
Capolupo A, Giampaolo SM, Lambiase G, Quaranta A. Discerning the Nature of Neutrinos: Decoherence and Geometric Phases. Universe. 2020; 6(11):207. https://doi.org/10.3390/universe6110207
Chicago/Turabian StyleCapolupo, Antonio, Salvatore Marco Giampaolo, Gaetano Lambiase, and Aniello Quaranta. 2020. "Discerning the Nature of Neutrinos: Decoherence and Geometric Phases" Universe 6, no. 11: 207. https://doi.org/10.3390/universe6110207
APA StyleCapolupo, A., Giampaolo, S. M., Lambiase, G., & Quaranta, A. (2020). Discerning the Nature of Neutrinos: Decoherence and Geometric Phases. Universe, 6(11), 207. https://doi.org/10.3390/universe6110207






