Abstract
We present new approaches to distinguish between Dirac and Majorana neutrinos. The first is based on the analysis of the geometric phases associated to neutrinos in matter, the second on the effects of decoherence on neutrino oscillations. In the former we compute the total and geometric phase for neutrinos, and find that they depend on the Majorana phase and on the parametrization of the mixing matrix. In the latter, we show that Majorana neutrinos might violate symmetry, whereas Dirac neutrinos preserve . A phenomenological analysis is also reported showing the possibility to highlight the distinctions between Dirac and Majorana neutrinos.
1. Introduction
Neutrino oscillations, first theorized by Pontecorvo [1,2,3], and later confirmed by several experiments [4,5,6,7,8,9], hint at physics beyond the Standard Model of particles. The experimental demonstration of neutrino mixing has shown that neutrinos are massive particles. In our current knowledge, they come in three flavors , yet the existence of other species, possibly sterile (non–weakly interacting), is still a matter of debate. Beside that, many issues of neutrino physics, including their absolute masses, their exact mass generation mechanism and their fundamental nature, remain open. Indeed, since neutrinos are electrically neutral, they can be either Dirac or Majorana particles.
Perhaps the most striking difference between Dirac and Majorana neutrinos is that, while the Lagrangian for Dirac neutrinos is characterized by the invariance under global transformations, implying the conservation of the associated charges (electric,leptonic, etc.), the Majorana Lagrangian breaks the symmetry, allowing for lepton number violation. As a consequence, Majorana neutrinos allow for processes in which total lepton number is not preserved, like neutrino–less double beta decay, whereas the same processes cannot take place if the neutrinos are Dirac in nature. This, of course, has consequences on the phenomenon of neutrino mixing as well. Indeed, the Pontecorvo-Maki-Nakagawa-Sakata (PMNS) mixing matrix for n flavors contains or physical, i.e., unremovable, phases, according to the Dirac or Majorana nature of neutrinos. One can express the mixing matrix for Majorana neutrinos in terms of the mixing matrix for Dirac neutrinos by means of the equation
where , with are known as the Majorana phases. By rephasing the charged lepton fields appearing in the charged current interaction Lagrangian [10] one obtains all the possible representations of and . As an example, in the case of two flavors, both the following matrices can be used to diagonalize the Majorana mixing Hamiltonian
or
where is the mixing angle and is the (unique) Majorana phase. can be eliminated for Dirac neutrinos. In the standard treatment of neutrino oscillations, the Majorana phase has no effect on the transition probabilities. However, as we will show, this is no longer the case when the effects of decoherence are taken into account. Moreover, the total and geometric phases associated to neutrino oscillations are affected by the Majorana phase.
As Majorana neutrinos allow for the violation of lepton number, experiments based on the detection of the (lepton–number violating) phenomenon of neutrino–less double beta decay have been proposed [11] to discriminate between the two. Alternative proposals rely on the analysis of the Leggett-Garg quantity [12]. A further distinction might be induced in presence of decoherence, in which case the neutrino oscillation formulae have been shown to depend on the Majorana phase [13,14].
In this work we present two approaches to discriminate between Dirac and Majorana neutrinos. The first approach is based on the analysis of the phases for neutrinos [15], both total and geometric. We prove that these are sensitive to the nature of neutrinos, so that interferometric experiments might distinguish between Dirac and Majorana neutrinos. In the second [16] we take into account the effect of quantum decoherence on neutrino oscillations, showing that Majorana neutrinos may violate symmetry when decoherence is taken into account whereas Dirac neutrinos preserve it. The results obtained also depend on the representation of the mixing matrix. The nature of neutrinos could then be revealed in long baseline experiments.
2. Majorana and Dirac Neutrino
In this section we briefly recap the main differences between Majorana and Dirac fields.
Majorana fields: The fields satisfy the Dirac equation, and coincide with their own charge conjugated field: , where the matrix C has the following properties: In the free Majorana Lagrangian , only the left-handed component of the field and the right-handed component of the antiparticle field appear, where , and , with , are the Dirac matrices. Then one can write , and the free mass Lagrangian is , (being ). This means that has the structure , which breaks all the -charges of two units under the transformations.
For the mixing of two Majorana neutrinos, the lepton–number violating interaction Hamiltonian can be written as
with , , having the dimensions of energy. This Hamiltonian can be diagonalized by one of the mixing matrices in Equations (2) and (3), where the phase cannot be removed.
Dirac fields: At odds with Majorana fields, Dirac fields are distinct from their charge conjugate . Then both the left-handed and the right-handed components enter the mass Lagrangian, which is , (the and terms are zero). In this occurrence, and L are invariant under the transformations and , implying conservation of the related charges (electric, leptonic, etc.).
For Dirac neutrinos, the interaction Hamiltonian preserving the lepton number is
where , with are the antineutrino fields. In this case, the phase is not needed to diagonalize the Hamiltonian.
In the following we will analyze the effect of the Majorana phase on the geometric phase and on the oscillation formulae of neutrinos.
3. Total and Geometric Phases for Neutrinos in Matter
Geometric phases [17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34] arise in many physical systems [35,36,37,38,39,40,41,42,43,44]. They emerge in the evolution of any quantum state , and depend only on the geometric properties of its trajectory within the system’s Hilbert space; namely, they are both reparametrization and gauge invariant. Berry phases, associated to cyclical and adiabatic evolutions on a parameter space, and Berry-like phases, defined in more general frameworks, contain a precious amount of information about the system. Their relevance and their ties to the properties of the quantum system to which are related, have been established experimentally. In some cases, geometric phases turn out to be physical observables themselves [31,32,33,34,35,36].
Geometric phases and, more generally, geometric invariants, have also been studied in connection with the particle mixing phenomena [45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60]. Here we focus on the geometric phases associated to the propagation of neutrinos and show that they can be a valuable tool to tell Dirac and Majorana neutrinos apart.
The formalism is identical for neutrinos propagating in vacuum and in matter, except that in the latter case the mixing angle and are to be replaced with and . These parameters take into account the interaction with matter, and are defined by the relations , . The quantities describe the Mikhaev-Smirnow-Wolfenstein (MSW) effect [61,62] and are defined as , where the sign + is reserved for antineutrino oscillations, while the − for neutrino oscillations. In particular, the mixing matrix (3) becomes ( in the Dirac case)
and similar for (2). It is accepted that the Majorana phase does not change in presence of matter, since its origin can be traced back to the (non-)invariance of the Majorana Lagrangian under transformations of the fields. Indeed for Dirac fields the considered invariance implies that the Majorana phase can be removed independently on the presence of matter. On the contrary, for Majorana fields the phase cannot be removed and is not affected by the presence of matter as it is well-known (see for instance [10]).
Assuming the mixing matrix (4), the flavor neutrino states at distance z in the ultrarelativistic approximation , are explicitly given by
In order to calculate the geometric and the total phases associated to the states (5), we employ the Mukunda-Simon [27] definition, which is a kinematical generalization of the Berry phase to evolutions that are not necessarily cyclic nor adiabatic. For a quantum system that traces out a trajectory in its Hilbert space , and istantaneous state vector , where is the curve parameter, one writes the Mukunda–Simon phase as the difference between total and dynamical phase:
Here the dot is used to denote the derivative with respect to s. In Equation (6), is the total phase, and is the dynamical phase.
Specializing the definition (6) to the propagation of an electron neutrino, with initial state , we obtain
and, for the case at hand
Likewise, the geometric phase for the muon neutrino, for the initial state , is . One has . Equation (8) does not depend on the Majorana phase , and therefore holds for both Dirac and Majorana neutrinos.
However, considering that neutrinos oscillate between different flavors, along with the phases and , we must also consider the phases
By employing the states in Equation (5) for Majorana neutrinos, recalling that one cannot eliminate , we get
Similarly one has
As , the geometric phase is asymmetrical with respect to the transitions and because of the Majorana phase .
The case is different for Dirac neutrinos, for which the phase can be freely be set to zero. Indeed, setting , Equations (9) and (10) (or equivalently Equations (11) and (12)) become identical, yielding
The asymmetry that we have pointed out for Majorana neutrinos, disappears for Dirac neutrinos.
We stress that the result of Equation (8) is independent on the choice of the mixing matrix. Indeed one obtains the same result considering the mixing matrix , obtained from (2) by the replacement . On the other hand, the phases defined in Equation (9) depend on which mixing matrix is chosen. In fact, if one picks the mixing matrix , the phase for Majorana neutrinos is identical with Equation (13). We deduce that the phases and , besides discriminating between Dirac and Majorana neutrinos, are also sensitive to the parametrization of the mixing matrix.
We point out that different parametrizations do not correspond to different mass matrices, nor to different transition probabilities in absence of decoherence. Anyway, the transition amplitudes between different flavors are actually dependent on the parametrization of the mixing matrix. The amplitudes do in general depend on the Majorana phase, see for instance Equation (22) of ref. [10]. Upon taking the squared modulus, the dependence on the phase disappears, implying that the oscillation formulae are independent on the Majorana phase (in absence of decoherence). On the other hand the total and geometric phases depend on the transition amplitude and thus they can depend on the Majorana phase and then on the choice of the mixing matrix. This is clear from the definition (6). In fact, amplitudes involving neutrino states in general depend on the choice of the mixing matrix, and are thus different for Equations (2) and (3).
Geometric phases, however, are physical quantities in their own right (see for instance [31,32,33,34]). In our case, one cannot dismiss geometric phases as unphysical on the grounds of their dependence on the parametrization of the mixing matrix. Rather, they can serve as a tool to determine which of the parametrizations (2), (3) is the physical, correct one.
While it is still unclear how the geometric phase can be measured, in the case of neutrino oscillations, there is no doubt on its physical relevance. Indeed, a vast literature devoted to the theoretical analysis of the geometric phase for neutrinos has been produced [45,60].
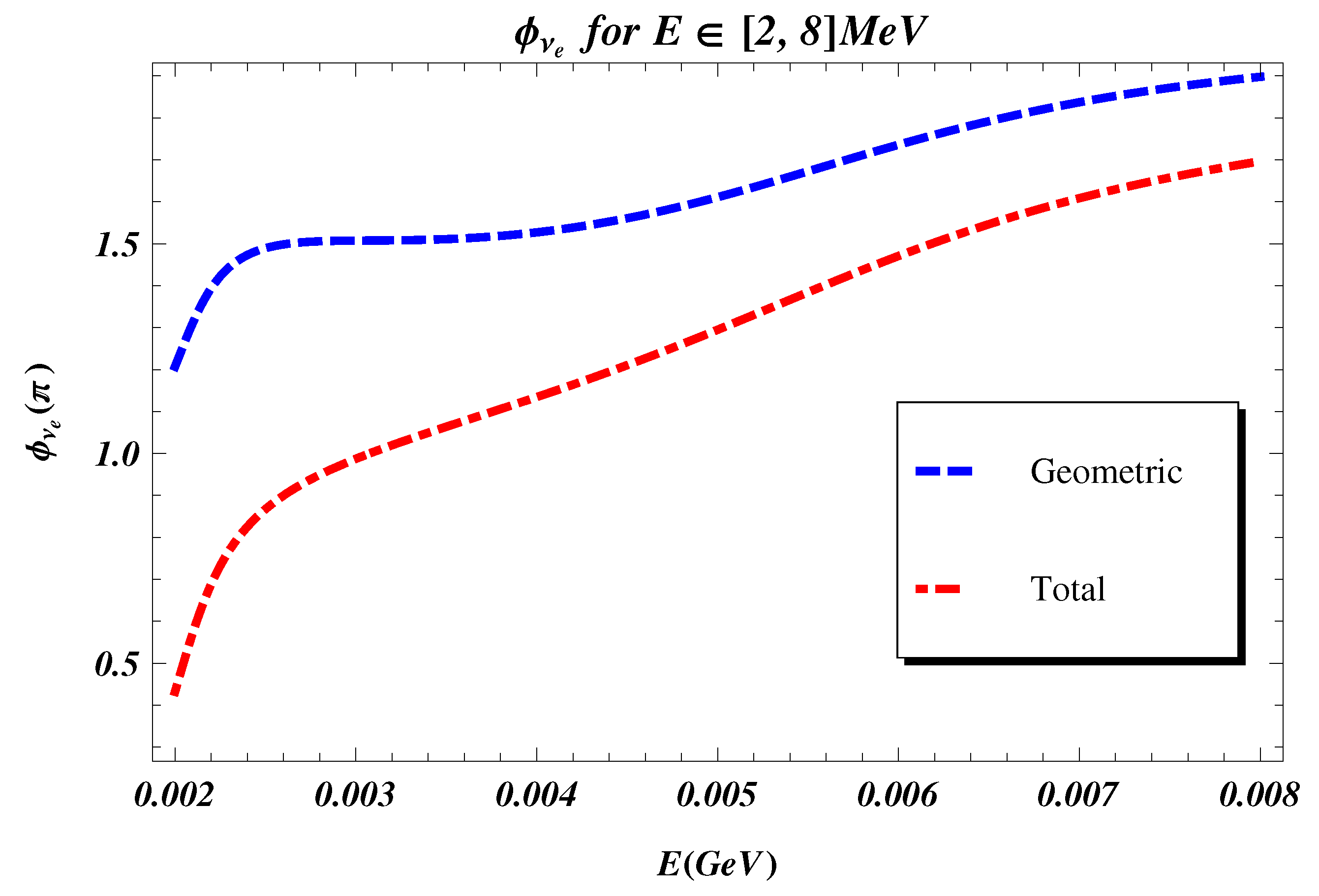
In the figures we show the behaviour of the total and the geometric phases for regimes compatible with RENO and T2K experiments. In Figure 1, for the total and geometric phases associated with the evolution of , we consider the energy of neutrinos produced in nuclear reactors MeV, the earth electron density cm−3, eV2 and a distance km. The results reported in Figure 1 could be, in principle, detected in experiments like RENO [5]. In Figure 2 we show the geometric phases associated to the flavor oscillations (Equations (9) and (10)). There we consider energies GeV and a distance z = 300 km, which are typical of long baseline experiments, like . We use the values , cm−3 and eV2.
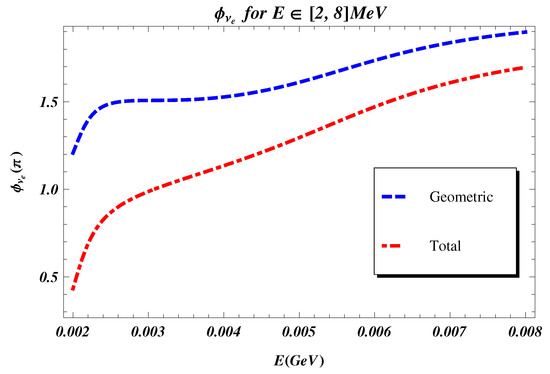
Figure 1.
(Color online) Plots of the total and the geometric phases for , as a function of the neutrino energy E, for a distance length z = 100 km. - The red dot dashed line is the total phase; - the blue dashed line is the geometric phase.
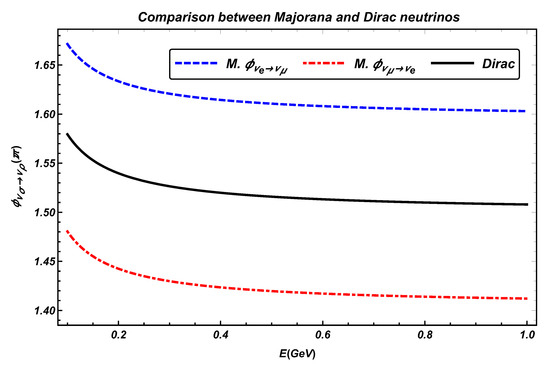
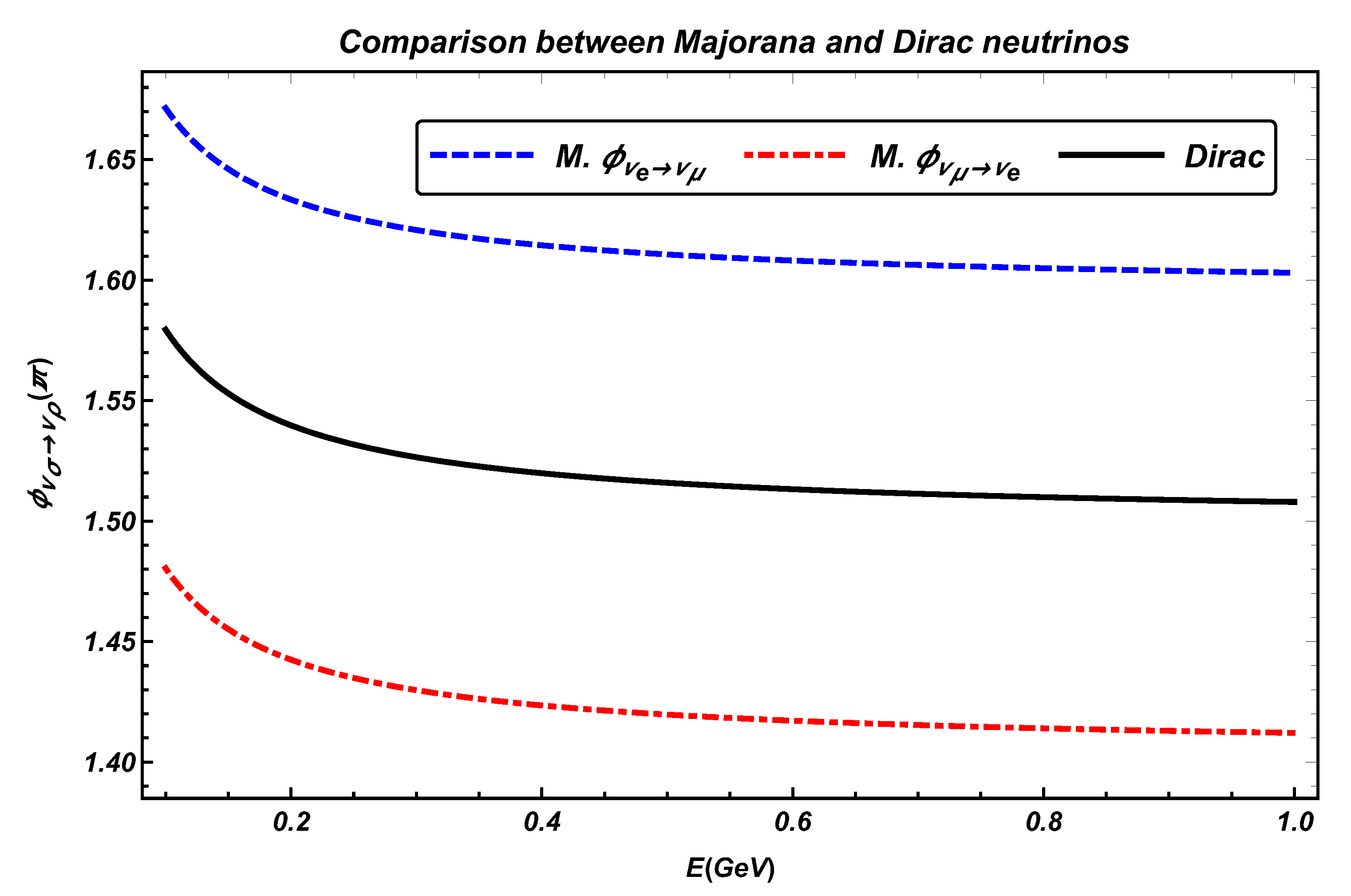
Figure 2.
(Color online) Plot of the geometric phases (the blue dashed line) and (the red dot dashed line) for Majorana neutrinos as a function of the neutrino energy E, for a distance length z = 300 km. The geometric phases for Dirac neutrinos is represented by the black solid line.
4. Neutrino Oscillations with Decoherence
The phenomena of dissipation and decoherence characterize any quantum system, and result from interactions with the environment. In the case of neutrinos, decoherence might be induced by quantum gravity effects, strings and branes [63,64,65,66,67,68], or the neutrino oscillation in dense matter [69]. The effects of dissipation and decoherence on neutrino oscillations have been studied in [13,70,71,72,73,74,75,76,77,78,79,80], where it has been shown that they can modify the oscillation frequencies and the oscillation formulae. In particular, it was pointed out that dissipation can produce oscillation formulae that differ between Dirac and Majorana neutrinos [13]. Here we analyze the issue in depth, providing additional theoretical results, and revealing, in particular, the possibility of violation for Majorana neutrinos. This is excluded for Dirac neutrinos, producing yet another distinction between the two kinds.
We introduce the decoherence effects by regarding the neutrino as an open system in contact with a bath. The neutrino state is described by a density matrix , whose evolution is dictated by the Lidbland–Kossakowski master equation [81,82]
Here, is the effective hamiltonian, and is the dissipator defined as
The coefficients of the Kossakowski matrix are phenomenological, and must be deduced from the properties of the environment [13]. The , with , are a set of traceless operators, satisfying . In the three flavor neutrino mixing, are the Gell-Mann matrices . In the two flavor case, which we consider, are just the Pauli matrices .
Expanding Equations (14) and (15) in the basis, we have
where , with and is a decoherence matrix (also known as dissipator). Probability conservation entails , so that
The parameters in Equation (17) are real, and the diagonal elements have to be positive in order for the density matrix to fulfill the requirement at any istant t. To evaluate the effects of decoherence matrix which is non–diagonal, we consider a simplified form:
This form is obtained from Equation (17), by setting, and . Since the density matrix has to be completely positive , the inequality must hold.
By setting , and recalling Equation (18), one has , which in the two flavor case implies . The resulting master Equation (16) is
We employ the mixing matrix of Equation (3) to obtain the density matrix for the flavored neutrinos, obtaining, at time ,
and an analogous result is found for muon neutrinos. Then at time t we have
with and
where and .
The transition probabilities , with and neutrino flavors, can be computed as . These are
In a similar fashion, we get
for antineutrino transitions. Equations (23) and (24) show an asymmetry between the transitions and , i.e., . Notice that the asymmetry disappears, as soon as one sets , i.e., for Dirac neutrinos one has
The asymmetry is in fact due to Majorana phase , and also affects the survival probabilities of electron, muon and tau neutrinos. Indeed, for . The asymmetry, which is a result of the oscillation Formulae (23) and (24), is explicitly given by
As for the energy dependence of the asymmetry in Equation (26), one would expect, from the practical confusion theorem, that the differences between Dirac and Majorana neutrinos are the more negligible the higher energies are considered. These consideration, however, applies only in absence of decoherence. Our results, in particular Equations (23) and (24), show that for Majorana neutrinos the difference of transition probabilities for particles and antiparticles at a fixed time are depending on the function , where . Then, as , , and . As , is increased up to the maximum value , implying that the difference between Dirac and majorana neutrinos increases with the energy (up to the maximum value in correspondence with ).
On the other hand, the decoherence induces by itself a violation of the T symmetry. Here we are concerned with the T asymmetry owing to neutrino oscillations. For neutrino oscillations, the T asymmetry has two equivalent definitions
In our case, because of decoherence, the first definition is unviable. Indeed, employing the first definition, we get
Because of the hyperbolic functions, the definition (28) produces, for large enough times t, a value of not physically acceptable, since it is not included in the interval [16]. Nevertheless, the second definition, , is well–behaved at any time t and we get that there is no T asymmetry for two flavor neutrino oscillation when decoherence is taken into account
This holds both for Dirac and Majorana neutrinos.
By comparing Equations (26) and (29), it is clear that , which implies a asymmetry for Majorana neutrinos . Notice that, even employing the definition of the T asymmetry as , the equality , which implies the symmetry, does not hold. Then, also in this case, symmetry is broken. For Dirac neutrinos, as noted above, , implying no asymmetry for such a kind of neutrinos.
The asymmetry obtained for Majorana neutrinos, results from the combined effect of neutrino oscillations and decoherence, for which the quantum mechanical operator might be ill–defined. The presence of a dissipation term in the quantum mechanical evolution of the system (14) undermines the Lorentz invariance (and the T reversal symmetry) of the theory, so that the theorem does not hold. The interplay between decoherence and neutrino oscillations is such that the asymmetry is manifest in the transition probabilities only if the neutrinos are Majorana. We remark that the symmetry breaking presented here is distinct from the explicit breaking that would occur at the Hamiltonian level, in virtue of a non–vanishing commutator .
Moreover, we point out that the dissipator has to be non–diagonal to produce these effects. This can be seen by repeating the same analysis presented above for a diagonal form of the dissipator, i.e., by setting in (18), . In this case the oscillation formulae for Majorana neutrinos do not depend on , and are the same as those for Dirac neutrinos,
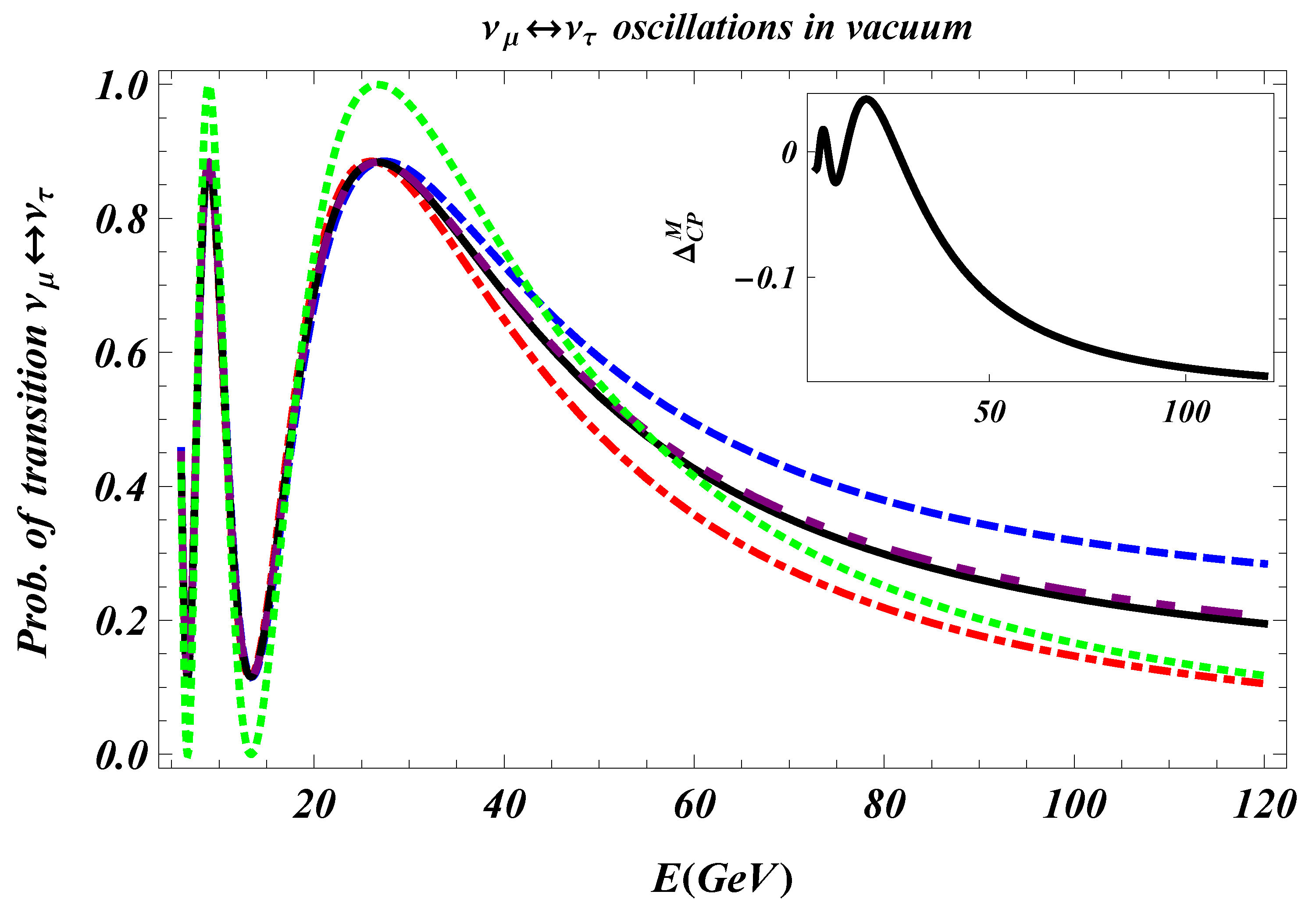
In the figures we report a numerical analysis of Equations (23)–(25), where the distinction between Dirac and Majorana neutrinos is evident, and of Equation (26) in order to analyze the and violations for Majorana neutrinos. The parameters we consider are those characteristic of the IceCube DeepCore experiment [83] for the oscillations, and those characteristic of the DUNE experiment for the oscillations. In Figure 3, we plot the oscillation formulas in vacuum and , as a function of the neutrino energy E. The plots refer to Majorana neutrinos and to Dirac neutrinos, (cfr. Equations (23)–(25), respectively). The comparison with the oscillation formula for a diagonal dissapator, (cfr. Equation (30)) and the Pontecorvo-Bilenky oscillation formula is also presented [1,2,3]. The plots are derived assuming . We used a distance () equal to the Earth diameter km, considered the energy interval GeV and the following values of the parameters: , eV2, GeV, GeV, GeV [84].
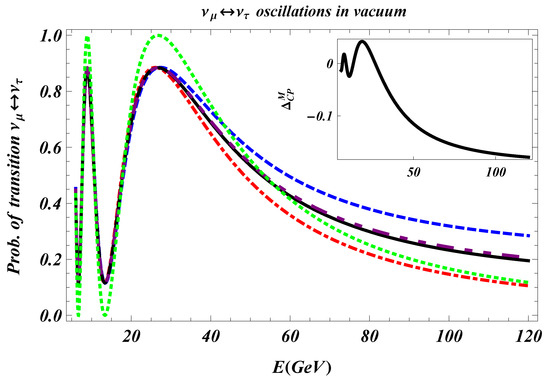
Figure 3.
(Color online) Plots of the oscillation formulas (the red dot dashed line) and (the blue dashed line) for Majorana neutrinos and for Dirac neutrinos (, the black line), as a function of the energy E, in vacuum. The purple, dashed line is obtained for . In this case and one has the same formula for Majorana and for Dirac neutrinos. The Pontecorvo formula is represented by the green dotted line. We consider the following values of the parameters: , km, , eV2, GeV, GeV, GeV. Picture in the inset: plot of for the same values of the parameters used in the main plots.
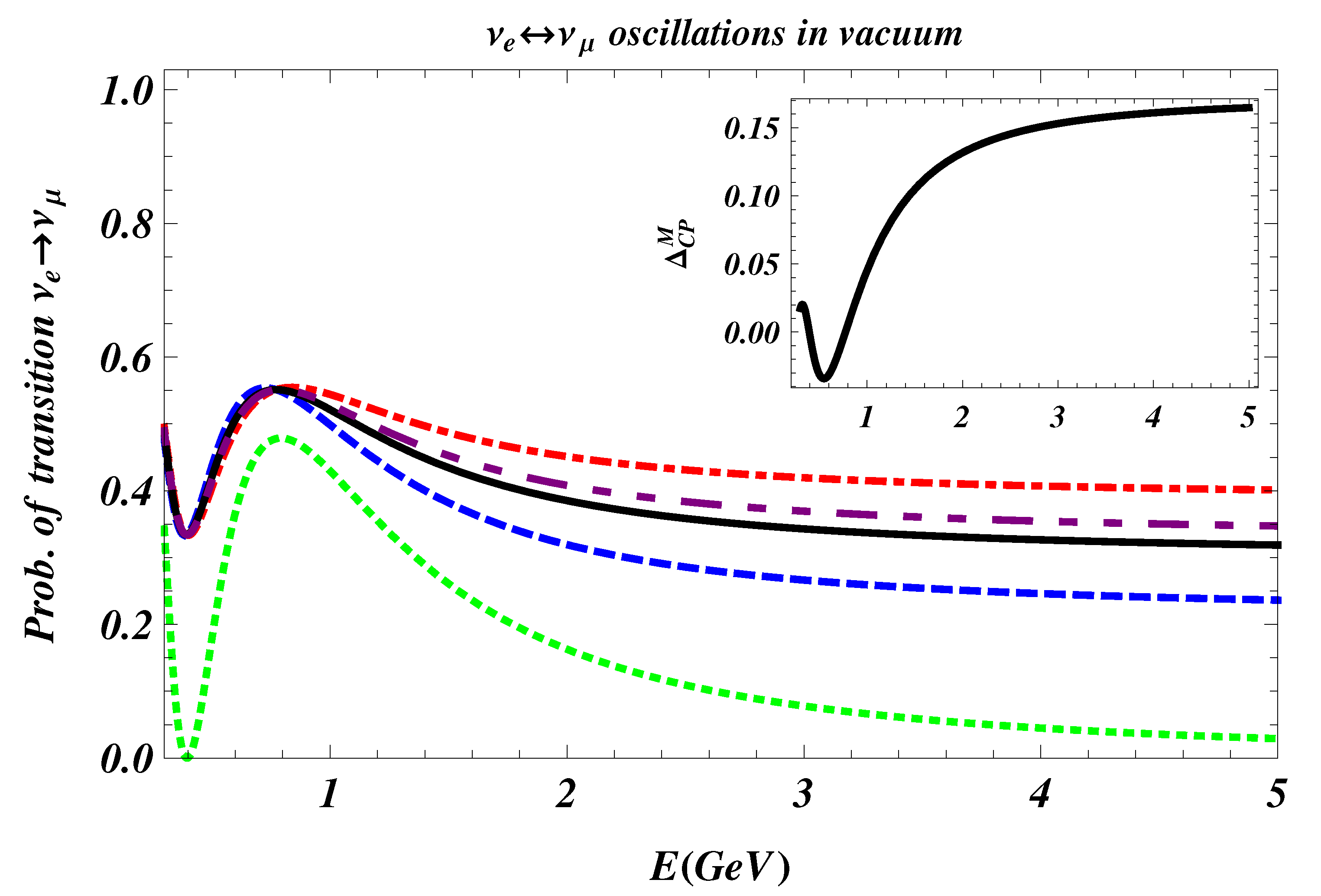
In Figure 4, we plot the oscillation formulae in vacuum, and and in the inset the asymmetry . We use the same values of and z considered in Figure 1, moreover we use , eV2, GeV, GeV, GeV [85].
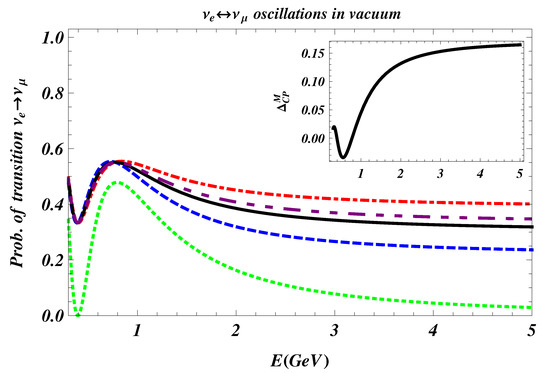
Figure 4.
(Color online) Plots of (red dot dashed line) and (blue dashed line) for Majorana neutrinos and for Dirac neutrinos (, black line), as a function of E, in vacuum. The purple, dashed line is obtained by setting . In this case . The Pontecorvo formula is represented by the green dotted line. We use the same values of and z of Figure 1, and consider: , eV2, GeV, GeV, GeV. Picture in the inset: plot of .
The results we presented hold for neutrino oscillations in vacuum. The matter effects can be also considered by using the procedure introduced in Ref. [86]. In this case, since matter affects neutrinos and antineutrinos in a asymmetric fashion, the oscillations break the and symmetry even in absence of decoherence. Therefore, the analysis of these symmetries is better conducted by studying the oscillations in vacuum. In any case, for completeness, we also show how to deal with decoherence in matter, following the procedure of Ref. [86].
Analyzing the plots in Figure 3 and Figure 4, we see that the differences between Majorana and Dirac neutrinos, the and violations are, at least in principle, detectable.
Even in absence of decoherence, neutrinos and antineutrinos behave differently in matter, because only electrons, protons and neutrons are present, while the corresponding antiparticles are not. It is well known, indeed, that the parameters characterizing the MSW effect, namely R and , depend on wheter one is considering neutrinos or antineutrinos propagating in the medium. This in turn implies that the and oscillations in matter already break the and symmetries in absence of decoherence.
Following [86], the decoherence matrix in the basis of the mass eigenstates in matter is given by (compare with Equation (18))
where , , and , with and . Equation (31) can be used to compute the violation in matter along the same lines for the calculation of the violation in vacuum.
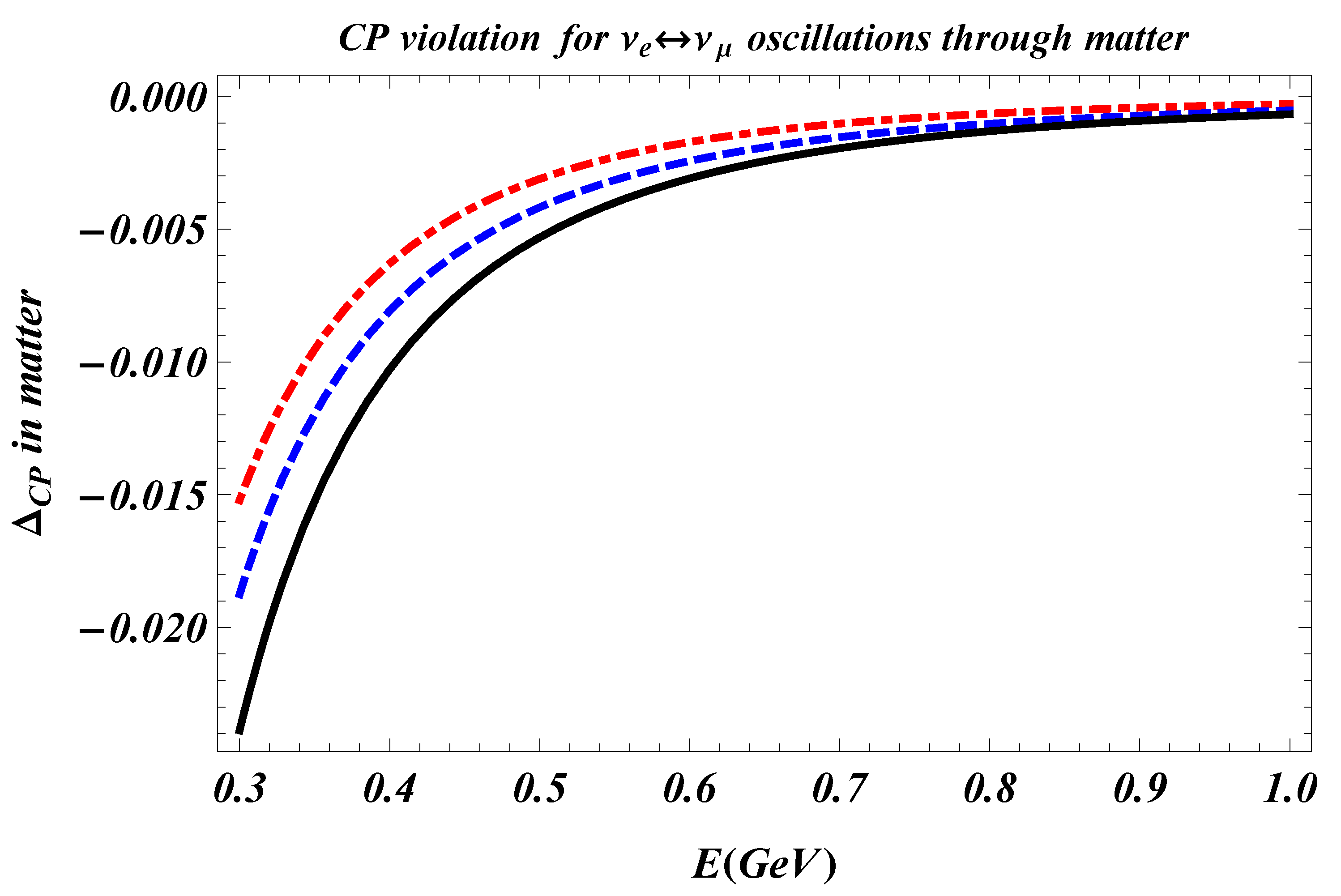
In Figure 5 we show the asymmetry , for Majorana and for Dirac neutrinos in presence of decoherence and including the matter effects. We used the electron number density of the Earth mantle cm−3 and the energy range [0.3–1] GeV, compatible with the DUNE baseline parameters. It is evident from the plots that is different for Majorana and Dirac neutrinos in presence of decoherence, and it is also clear that the asymmetries are distinct from the case in which there is no decoherence but the matter effects are included. We note that in the energy range considered, there are negligible differences between the results obtained by employing the full procedure of Ref. [86], and those obtained by symply replacing and with their counterparts in matter and .
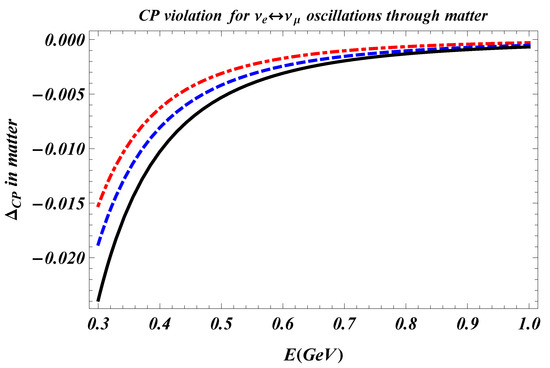
Figure 5.
(Color online) Plots of , for Majorana neutrinos (the red dot dashed line) and Dirac neutrinos (the blue dashed line), in matter and in presence of decoherence with off-diagonal term, and for neutrinos in matter in absence of decoherence (the black dotted line). In the plots, we consider the same parameters of Figure 4 and the energy range (0.3–1) GeV.
5. Conclusions
We have reported recent results obtained by analyzing the geometric phase and the phenomenon of decoherence for neutrino oscillations.
Geometric phase: We have studied the phases associated to the propagation of neutrinos, and we have shown that those associated to the flavor oscillations, and , depend explicitly on the Majorana phase and on the parametrization of the mixing matrix. These phases are in principle detectable, and long baseline neutrino experiments like [7], or short baseline experiments like RENO [5], could in principle reveal, by means of an interferometric analysis, both the correct mixing matrix for Majorana neutrinos and the fundamental nature of neutrinos.
Decoherence in neutrino oscillations: We have also analyzed several aspects of the phenomenon of decoherence in neutrino oscillations. We have shown that Majorana neutrinos might violate symmetry. This violation is excluded for Dirac neutrinos, and thus constitutes another difference between the two kinds. The transition probabilities, in presence of decoherence, turn out to depend explicitly on the Majorana phase. We have compared oscillations for Majorana and Dirac neutrinos adopting realistic phenomenological parameters, characteristic of some of the current experiments (IceCube DeepCore and DUNE), and taking into account the constraints on decoherence parameters [84,85]. The numerical analysis shows that the differences in the oscillation formulae for the two kinds of neutrinos, and the and asymmetry, are, at least in principle, detectable. Both geometric phases and the oscillation formulae in presence of decoherence provide valuable tools to discriminate between Dirac and Majorana neutrinos. Notice that, the effects revealed by analyzing particle mixing and oscillations in quantum field theory framework [87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110] and the effects induced by the space-time curvature on neutrino oscillations [111] are negligible. These effects can represent components of dark energy and dark matter of the universe.
Moreover, the origin of quantum-decoherence in neutrino evolution can be the result of interactions with matter [69] and it depends on the neutrino nature. This kind of decoherence is mostly relevant in high density environments, such as astrophysical objects and the primordial universe. Hence, the neutrino nature and its behavior in presence of decoherence can affect the evolution of the universe and possibly its accelerating expansion.
Author Contributions
All the authors contributed equally to conceptualization, methodology and writing–original draft preparation. All authors have read and agreed to the published version of the manuscript.
Funding
A.C., G.L. and A.Q. thank partial financial support from MIUR and INFN. A.C. and G.L. also thanks the COST Action CA1511 Cosmology and Astrophysics Network for Theoretical Advances and Training Actions (CANTATA). S.M.G. acknowledges support from the European Regional Development Fund the Competitiveness and Cohesion Operational Programme (KK.01.1.1.06–RBI TWIN SIN) and the Croatian Science Fund Project No. IP-2016–6–3347 and IP-2019-4-3321. S.M.G. also acknowledges the QuantiXLie Center of Excellence, co–financed by the Croatian Government and European Union (Grant KK.01.1.1.01.0004).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pontecorvo, B. Mesonium and anti-mesonium. Zh. Eksp. Teor. Fiz. 1957, 33, 549–551. [Google Scholar]
- Bilenky, S.M.; Pontecorvo, B. Lepton mixing and neutrino oscillations. Phys. Rep. 1978, 41, 225–261. [Google Scholar] [CrossRef]
- Bilenky, S.M.; Petcov, S.T. Massive Neutrinos And Neutrino Oscillations. Rev. Mod. Phys. 1987, 59, 671. [Google Scholar] [CrossRef]
- An, F.P.; Bai, J.Z.; Balantekin, A.B.; Band, H.R.; Beavis, D.; Beriguete, W.; Cai, B. Observation of electron-antineutrino disappearance at Daya Bay. Phys. Rev. Lett. 2012, 108, 171803. [Google Scholar] [CrossRef] [PubMed]
- Ahn, J.K.; Chebotaryov, S.; Choi, J.H.; Choi, S.; Choi, W.; Choi, Y.; Jang, H.I.; Jang, J.S.; Leon, E.J.; Jeong, I.S.; et al. Observation of Reactor Electron Antineutrino Disappearance in the RENO experiment. Phys. Rev. Lett. 2012, 108, 191802. [Google Scholar] [CrossRef]
- Abe, Y.; Aberle, C.; Akiri, T.; dos Anjos, J.C.; Ardellier, F.; Barbosa, A.F.; Baxter, A.; Bergevin, M.; Bernstein, A.; Bezerra, T.J.C.; et al. (Double Chooz Collaboration). Indication of Reactor ῡe Disappearance in the Double Chooz Experiment. Phys. Rev. Lett. 2012, 108, 131801. [Google Scholar] [CrossRef]
- Abe, K.; N. Abgrall; Y. Ajima; H. Aihara; J.B. Albert; C. Andreopoulos; B. Andrieu; S. Aoki; O. Araoka; J. Argyriades et al. (T2K Collaboration). Indication of Electron Neutrino Appearance from an Accelerator-produced Off-axis Muon Neutrino Beam. Phys. Rev. Lett. 2011, 107, 041801. [Google Scholar] [CrossRef]
- Adamson, P.; Auty, D.J.; Ayres, D.S.; Backhouse, C.; Barr, G.; Betancourt, M.; Bishai, M.; Blake, A.; Bock, G.J.; Boehnlein, D.J.; et al. Improved search for muon-neutrino to electron-neutrino oscillations in MINOS. Phys. Rev. Lett. 2011, 107, 181802. [Google Scholar] [CrossRef]
- Nakamura, K.; Petcov, S.T. Neutrino mass, mixing, and oscillations. Phys. Rev. D 2013, 86, 010001. [Google Scholar]
- Giunti, C. No effect of Majorana phases in neutrino oscillations. Phys. Lett. B 2010, 686, 41. [Google Scholar] [CrossRef]
- Giuliani, A.; Poves, A. Neutrinoless Double-Beta Decay. Adv. High Energy Phys. 2012, 2012, 1. [Google Scholar] [CrossRef]
- Richter, M.; Dziewit, B.; Dajka, J. Leggett-Garg K3 quantity discriminates between Dirac and Majorana neutrinos. Phys. Rev. D 2017, 96, 076008. [Google Scholar] [CrossRef]
- Benatti, F.; Floreanini, R. Open system approach to neutrino oscillations. JHEP 2000, 2, 32. [Google Scholar] [CrossRef]
- Benatti, F.; Floreanini, R. Massless neutrino oscillations. Phys. Rev. D 2001, 64, 085015. [Google Scholar] [CrossRef]
- Capolupo, A.; Giampaolo, S.M.; Hiesmayr, B.C.; Vitiello, G. Geometric phase of neutrinos: Differences between Dirac and Majorana neutrinos. Phys. Lett. B 2018, 780, 216. [Google Scholar] [CrossRef]
- Capolupo, A.; Giampaolo, S.M.; Lambiase, G. Decoherence in neutrino oscillations, neutrino nature and CPT violation. Phys. Lett. B 2019, 792, 298–303. [Google Scholar] [CrossRef]
- Berry, M.V. Quantal phase factors accompanying adiabatic changes. Proc. Roy. Soc. Lond. A 1984, 392, 45–57. [Google Scholar]
- Berry, M.V. Classical adiabatic angles and quantal adiabatic phase. J. Phys. A 1985, 18, 15–27. [Google Scholar] [CrossRef]
- Hinterbichler, K. Theoretical aspects of massive gravity. Rev. Mod. Phys. 2012, 84, 671. [Google Scholar] [CrossRef]
- Aharonov, Y.; Anandan, J. Phase Change During A Cyclic Quantum Evolution, Phys. Rev. Lett. 1987, 58, 1593. [Google Scholar] [CrossRef]
- Samuel, J.; Bhandari, R. General Setting for Berry’s Phase. Phys. Rev. Lett. 1988, 60, 2339. [Google Scholar] [CrossRef] [PubMed]
- Pancharatnam, S. Generalized theory of interference, and its applications. Proc. Indian Acad. Sci. A 1956, 44, 1225. [Google Scholar]
- Shapere, A.; Wilczek, F. Geometric Phases in Physics; World Scientific: Singapore, 1989. [Google Scholar]
- Garrison, J.C.; Wright, E.M. Complex geometrical phases for dissipative systems. Phys. Lett. A 1988, 128, 177. [Google Scholar] [CrossRef]
- Pati, A.K. Gauge-invariant reference section and geometric phase. J. Phys. A 1995, 28, 2087. [Google Scholar] [CrossRef]
- Pati, A.K. Geometric aspects of noncyclic quantum evolutions. Phys. Rev. A 1995, 52, 2576. [Google Scholar] [CrossRef] [PubMed]
- Mukunda, N.; Simon, R. Quantum Kinematic Approach to the Geometric Phase. I. General formalism. Ann. Phys. (N. Y.) 1993, 228, 205. [Google Scholar] [CrossRef]
- Mostafazadeh, A. Noncyclic geometric phase and its non-Abelian generalization. J. Phys. A 1999, 32, 8157. [Google Scholar] [CrossRef][Green Version]
- Anandan, J. Non-adiabatic non-Abelian geomtric phase. Phys. Lett. A 1988, 133, 171. [Google Scholar] [CrossRef]
- Tomita, A.; Chiao, R.Y. Observation of Berry’s Topological Phase by Use of an Optical Fiber. Phys. Rev. Lett. 1986, 57, 937. [Google Scholar] [CrossRef]
- Jones, J.A.; Vedral, V.; Ekert, A.; Castagnoli, G. Geometric quantum computation using nuclear magnetic resonance. Nature 2000, 403, 869. [Google Scholar] [CrossRef]
- Leek, P.J.; Fink, J.M.; Blais, A.; Bianchetti, R.; Goppl, M.; Gambetta, J.M.; Schuster, D.I.; Frunzio, L.; Schoelkopf, R.J.; Wallraff, A. Observation of Berry’s Phase in a Solid-State Qubit. Science 2007, 318, 1889. [Google Scholar] [CrossRef] [PubMed]
- Neeley, M.; Ansmann, M.; Bialczak, R.C.; Hofheinz, M.; Lucero, E.; O’Connell, A.D.; Sank, D.; Wang, H.; Wenner, J.; Cleland, A.N.; et al. Emulation of a Quantum Spin with a Superconducting Phase Qudit. Science 2009, 325, 722–725. [Google Scholar] [CrossRef]
- Pechal, M.; Berger, S.; Abdumalikov, A.A., Jr.; Fink, J.M.; Mlynek, J.A.; Steffen, L.; Wallraff, A.; Filipp, S. Geometric Phase and Nonadiabatic Effects in an Electronic Harmonic Oscillator. Phys. Rev. Lett. 2012, 108, 170401. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Tan, Y.-W.; Stormer, H.L.; Kim, P. Experimental observation of the quantum Hall effect and Berry’s phase in graphene. Nature 2005, 438, 201–204. [Google Scholar] [CrossRef] [PubMed]
- Falci, G.; Fazio, R.; Palma, G.M.; Siewert, J.; Vedral, V. Detection of geometric phases in superconducting nanocircuits. Nature 2000, 407, 355–358. [Google Scholar] [CrossRef]
- Mottonen, M.; Vartiainen, J.J.; Pekola, J.P. Experimental determination of the Berry phase in a superconducting charge pump. Phys. Rev. Lett. 2008, 100, 177201. [Google Scholar] [CrossRef]
- Murakawa, H.; Bahramy, M.S.; Tokunaga, M.; Kohama, Y.; Bell, C.; Kaneko, Y.; Nagaosa, N.; Hwang, H.Y.; Tokura, Y. Detection of Berry’s Phase in a Bulk Rashba Semiconductor. Science 2013, 342, 1490–1493. [Google Scholar] [CrossRef]
- Capolupo, A.; Vitiello, G. Spontaneous supersymmetry breaking probed by geometric invariants. Adv. High Energy Phys. 2013, 2013, 850395. [Google Scholar] [CrossRef]
- Capolupo, A.; Vitiello, G. Probing Hawking and Unruh effects and quantum field theory in curved space by geometric invariants. Phys. Rev. D 2013, 88, 024027. [Google Scholar] [CrossRef]
- Capolupo, A.; Vitiello, G. Vacuum Condensate, Geometric Phase, Unruh Effect and Temperature Measurement. Adv. High Energy Phys. 2015, 2015, 878043. [Google Scholar] [CrossRef]
- Xiao, D.; Chang, M.-C.; Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 2010, 82, 1959. [Google Scholar] [CrossRef]
- Bruno, A.; Capolupo, A.; Kak, S.; Raimondo, G.; Vitiello, G. Gauge theory and two level systems. Mod. Phys. Lett. B 2011, 25, 1661. [Google Scholar] [CrossRef]
- Hu, J.; Yu, H. Geometric phase for accelerated two-level atom and the Unruh effect. Phys. Rev. A 2012, 85, 032105. [Google Scholar] [CrossRef]
- Nakagawa, N. Geometrical phase factors and higher-order adiabatic approximations. Ann. Phys. 1987, 1987 179, 145. [Google Scholar] [CrossRef]
- Capolupo, A. Probing CPT violation in meson mixing by non-cyclic phase. Phys. Rev. D 2011, 84, 116002. [Google Scholar] [CrossRef]
- Naumov, V.A. Berry phases for three-neutrino oscillations in matter. Phys. Lett. B 1994, 323, 351. [Google Scholar] [CrossRef]
- Syska, J.; Dajka, J.; Luczka, J. Interference phenomenon and geometric phase for Dirac neutrino in π+ decay. Phys. Rev. D 2013, 87, 117302. [Google Scholar] [CrossRef]
- Blasone, M.; Capolupo, A.; Celeghini, E.; Vitiello, G. Non-cyclic phases for neutrino oscillations in quantum field theory. Phys. Lett. B 2009, 674, 73. [Google Scholar] [CrossRef][Green Version]
- Johns, L.; Fuller, G.M. Geometric phases in neutrino oscillations with nonlinear refraction. Phys. Rev. D 2017, 95, 043003. [Google Scholar] [CrossRef]
- Joshi, S.; Jain, S.R. Geometric phase for neutrino propagation in magnetic field. Phys. Lett. B 2016, 754, 135. [Google Scholar] [CrossRef][Green Version]
- Capolupo, A.; Lambiase, G.; Vitiello, G. Probing mixing of photons and axion-like particles by geometric phase. Adv. High Energy Phys. 2015, 2015, 826051. [Google Scholar] [CrossRef]
- He, X.-G.; Li, X.-Q.; McKellar, B.; Zhang, Y. Berry phase in neutrino oscillations. Phys. Rev. D 2005, 72, 053012. [Google Scholar] [CrossRef]
- Dixit, K.; Alok, A.K.; Banerjee, S.; Kumar, D. Geometric phase and neutrino mass hierarchy problem. J. Phys. G Nucl. Part. Phys. 2018, 45, 085002. [Google Scholar] [CrossRef]
- Wang, Z.; Pan, H. Exploration of CPT violation via time-dependent geometric quantities embedded in neutrino oscillation through fluctuating matter. Nucl. Phys. B 2017, 915, 414–430. [Google Scholar] [CrossRef]
- Syska, J.; Dajka, J.; Luczka, J. Geometric phase of neutrino propagating through dissipative matter. J. Phys. Rev. D 2011, 83, 097302. [Google Scholar]
- Bandyopadhyay, P. Solar-neutrino problem and the Berry phase. Il Nuovo Cimento C 1994, 17, 191–198. [Google Scholar] [CrossRef]
- Mehta, P. Topological phase in two flavor neutrino oscillations. Phys. Rev. D 2009, 79, 096013. [Google Scholar] [CrossRef]
- Mehta, P. Topological phase in two flavor neutrino oscillations and imprint of the CP phase. Nucl. Phys. B Proc. Suppl. 2012, 229–232, 467. [Google Scholar] [CrossRef]
- Naumov, V.A. Three-neutrino oscillations in matter, CP-violation and topological phases. Int. J. Mod. Phys. D 1992, 1, 379–399. [Google Scholar] [CrossRef]
- Wolfenstein, L. Neutrino oscillations in matter. Phys. Rev. D 1978, 17, 2369. [Google Scholar] [CrossRef]
- Mikheev, S.P.; Yu, A. Smirnov. Resonance enhancement of oscillations in matter and solar neutrino spectroscopy. Sov. J. Nucl. Phys. 1985, 42, 913–917. [Google Scholar]
- Rovelli, C. Quantum Gravity; Cambridge University Press: New York, NY, USA, 2004; ISBN 0-521-71596-2. [Google Scholar]
- Amelino-Camelia, G. Quantum-Spacetime Phenomenology. Liv. Rev. Rel. 2013, 16, 5. [Google Scholar] [CrossRef] [PubMed]
- Giampaolo, S.M.; Macri’, T. Entanglement, holonomic constraints, and the quantization of fundamental interactions. arXiv 2018, arXiv:1806.08383. [Google Scholar] [CrossRef] [PubMed]
- Kostelecky, V.A. Gravity, Lorentz violation and the standard model. Phys. Rev. D 2004, 69, 105009. [Google Scholar] [CrossRef]
- Amelino-Camelia, G. Doubly-Special Relativity: Facts, Myths and Some Key Open Issues. Symmetry 2010, 2, 230. [Google Scholar] [CrossRef]
- Bernabéu, J.; Botell, F.J.; Mavromatos, N.E.; Nebot, M. The signal of ill-defined CPT weakening entanglement in the Bd system. Eur. Phys. J. C 2017, 77, 865. [Google Scholar] [CrossRef]
- Capolupo, A.; Giampaolo, S.M.; Quaranta, A. Neutrinos in a dense medium, CP and CPT violations: Beyond the MSW effect. arXiv 2020, arXiv:2008.08119v1. [Google Scholar]
- Simonov, K.; Capolupo, A.; Giampaolo, S.M. Gravity, entanglement and CPT-symmetry violation in particle mixing, Eur. Phys. J. C 2019, 79, 902. [Google Scholar] [CrossRef]
- Fogli, G.L.; Lisi, E.; Marrone, A.; Montanino, D.; Palazzo, A. Probing nonstandard decoherence effects with solar and KamLAND neutrinos. Phys. Rev. D 2007, 76, 033006. [Google Scholar] [CrossRef]
- Gago, A.M.; Santos, E.M.; Teves, W.J.C.; Zukanovich Funchal, R. Quantum dissipative effects and neutrinos: Current constraints and future perspectives. Phys. Rev. D 2001, 63, 073001. [Google Scholar] [CrossRef]
- Lisi, E.; Marrone, A.; Montanino, D. Probing Possible Decoherence Effects in Atmospheric Neutrino Oscillations. Phys. Rev. Lett. 2000, 85, 1166. [Google Scholar] [CrossRef] [PubMed]
- Morgan, D.; Winstanley, E.; Brunner, J.; Thompson, L.F. Probing quantum decoherence in atmospheric neutrino oscillations with a neutrino telescope. Astropart. Phys. 2006, 25, 311. [Google Scholar] [CrossRef]
- Farzan, Y.; Schwetz, T.; Smirnov, A.Y. Reconciling results of LSND, MiniBooNE and other experiments with soft decoherence. JHEP 2008, 0807, 067. [Google Scholar] [CrossRef]
- Oliveira, R.L.N.; Guzzo, M.M. Quantum dissipation in vacuum neutrino oscillation. Eur. Phys. J. C 2010, 69, 493. [Google Scholar] [CrossRef]
- Balieiro Gomes, G.; Guzzo, M.M.; de Holanda, P.C.; Oliveira, R.L.N. Parameter limits for neutrino oscillation with decoherence in KamLAND. Phys. Rev. D 2016, 95, 113005. [Google Scholar] [CrossRef]
- Bakhti, P.; Farzan, Y.; Schwetz, T. Revisiting the quantum decoherence scenario as an explanation for the LSND anomaly. JHEP 2015, 05, 007. [Google Scholar] [CrossRef]
- Oliveira, R.L.N. Dissipative effect in long baseline neutrino experiments. Eur. Phys. J. C 2016, 76, 417. [Google Scholar] [CrossRef]
- Guzzo, M.M.; de Holanda, P.C.; Oliveira, R.L.N. Quantum dissipation in a neutrino system propagating in vacuum and in matter. Nucl. Phys. B 2016, 908, 408–422. [Google Scholar] [CrossRef]
- Lindblad, G. On the generators of quantum dynamical semigroups. Commun. Math. Phys. 1976, 48, 119–130. [Google Scholar] [CrossRef]
- Gorini, V.; Kossakowski, A. Completely positive dynamical semigroups of N level systems. J. Math. Phys. 1976, 17, 821. [Google Scholar] [CrossRef]
- Aartsen, M.G.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Al Samarai, I.; Altmann, D.; Andeen, K.; Anderson, T.; et al. Measurement of Atmospheric Neutrino Oscillations at 6–56 GeV with IceCube DeepCore, Phys. Rev. Lett. 2018, 120, 071801. [Google Scholar] [CrossRef] [PubMed]
- Coloma, P.; Lopez-Pavon, J.; Martinez-Soler, I.; Nunokawa, H. Decoherence in neutrino propagation through matter, and bounds from IceCube/DeepCore. Eur. Phys. J. C 2018, 78, 614. [Google Scholar] [CrossRef]
- Gomes, G.B.; Forero, D.V.; Guzzo, M.M.; de Holanda, P.C.; Oliveira, R.L.N. Quantum Decoherence Effects in Neutrino Oscillations at DUNE. Phys. Rev. D 2019, 100, 055023. [Google Scholar] [CrossRef]
- Carpio, J.A.; Massoni, E.; Gago, A.M. Revisiting quantum decoherence in the matter neutrino oscillation framework. Phys. Rev. D 2018, 97, 115017. [Google Scholar] [CrossRef]
- Alfinito, E.; Blasone, M.; Iorio, A.; Vitiello, G. Squeezed neutrino oscillations in quantum field theory. Phys. Lett. B 1995, 362, 91. [Google Scholar] [CrossRef]
- Cardall, C.Y. Coherence of neutrino flavor mixing in quantum field theory. Phys. Rev. D 2000, 61, 073006. [Google Scholar] [CrossRef]
- Blasone, M.; Capolupo, A.; Vitiello, G. Quantum field theory of three flavor neutrino mixing and oscillations with CP violation. Phys. Rev. D 2002, 66, 025033. [Google Scholar] [CrossRef]
- Hannabuss, K.C.; Latimer, D.C. Fermion mixing in quasifree states. J. Phys. A 2003, 36, L69. [Google Scholar] [CrossRef]
- Beuthe, M. Oscillations of neutrinos and mesons in quantum field theory. Phys. Rep. 2003, 375, 105. [Google Scholar] [CrossRef]
- Blasone, M.; Capolupo, A.; Romei, O.; Vitiello, G. Quantum field theory of boson mixing, Phys. Rev. D 2001, 63, 125015. [Google Scholar] [CrossRef]
- Ji, C.R.; Mishchenko, Y. Nonperturbative vacuum effect in the quantum field theory of meson mixing. Phys. Rev. D 2001, 64, 076004. [Google Scholar] [CrossRef]
- Beuthe, M. Towards a unique formula for neutrino oscillations in vacuum. Phys. Rev. D 2002, 66, 013003. [Google Scholar] [CrossRef]
- Capolupo, A.; Ji, C.R.; Mishchenko, Y.; Vitiello, G. Phenomenology of flavor oscillations with non-perturbative effects from quantum field theory. Phys. Lett. B 2004, 594, 135. [Google Scholar] [CrossRef]
- Fujii, K.; Habe, C.; Yabuki, T. Remarks on flavor-neutrino propagators and oscillation formulas. Phys. Rev. D 2001, 64, 013011. [Google Scholar] [CrossRef]
- Blasone, M.; Capolupo, A.; Terranova, F.; Vitiello, G. Lepton charge and neutrino mixing in pion decay processes. Phys. Rev. D 2005, 72, 013003. [Google Scholar] [CrossRef]
- Nishi, C.C. First quantized approaches to neutrino oscillations and second quantization. Phys. Rev. D 2006, 73, 053013. [Google Scholar] [CrossRef]
- Akhmedov, E.K.; Wilhelm, A. Quantum field theoretic approach to neutrino oscillations in matter. J. High Energy Phys. 2013, 165. [Google Scholar] [CrossRef]
- Kobach, A.; Manohar, A.V.; McGreevy, J. Neutrino oscillation measurements computed in quantum field theory. Phys. Lett. B 2018, 783, 59–75. [Google Scholar] [CrossRef]
- Naumov, D.V.; Naumov, V.A. Quantum Field Theory of Neutrino Oscillations. Phys. Part. Nuclei 2020, 51, 1–106. [Google Scholar] [CrossRef]
- Capolupo, A. Dark matter and dark energy induced by condensates, Adv. High Energy Phys. 2016, 2016, 8089142. [Google Scholar]
- Capolupo, A. Quantum Vacuum, Dark Matter, Dark Energy and Spontaneous Supersymmetry Breaking. Adv. High Energy Phys. 2018, 2018, 9840351. [Google Scholar] [CrossRef]
- Capolupo, A.; Capozziello, S.; Vitiello, G. Dark energy and particle mixing, Phys. Lett. A 2009, 373, 601. [Google Scholar] [CrossRef]
- Capolupo, A.; Capozziello, S.; Vitiello, G. Neutrino mixing as a source of dark energy. Phys. Lett. A 2007, 363, 53–56. [Google Scholar] [CrossRef]
- Capolupo, A.; Capozziello, S.; Vitiello, G. Dark Energy, Cosmological Constant and Neutrino Mixing. Int. J. Mod. Phys. A 2008, 23, 4979. [Google Scholar] [CrossRef]
- Blasone, M.; Capolupo, A.; Capozziello, S.; Carloni, S.; Vitiello, G. Neutrino mixing contribution to the cosmological constant. Phys. Lett. A 2004, 323, 182. [Google Scholar] [CrossRef]
- Capolupo, A.; Mauro, M.D.; Iorio, A. Mixing-induced Spontaneous Supersymmetry Breaking. Phys. Lett. A 2011, 375, 3415. [Google Scholar] [CrossRef]
- Capolupo, A.; Lambiase, G.; Quaranta, A.; Giampaolo, S.M. Probing dark matter and quantum field theory effects with Rydberg atoms. Eur. Phys. J. C 2020, 80, 423. [Google Scholar] [CrossRef]
- Capolupo, A.; Martino, I.D.; Lambiase, G.; Stabile, A. Axion-photon mixing in quantum field theory and vacuum energy. Phys. Lett. B 2019, 790, 427. [Google Scholar] [CrossRef]
- Capolupo, A.; Lambiase, G.; Quaranta, A. Neutrinos in curved space-time: Particle mixing and flavor oscillations. Phys. Rev. D 2020, 101, 095022. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).