A Test of Gravitational Theories Including Torsion with the BepiColombo Radio Science Experiment
Abstract
1. Introduction
2. MORE Relativity Experiment
- the parameters defining the model of Mercury’s rotation (“rotation experiment”, all of the details can be found in [17]);
- the “relativity” parameters, which are the PPN parameters , , , and the Nordtvedt parameter , which characterize the expansion of the spacetime metric in the limit of slow motion and weak field (see, e.g., [8,18])1, together with some related parameters, such as the oblateness of the Sun , the solar gravitational mass (where G is the gravitational constant and the mass of the Sun), possibly its time derivative , and the solar angular momentum which appears in the Lense–Thirring effect on the orbit of Mercury (see, e.g., [19,20,21] for a general discussion; moreover, the topic has been addressed by the authors in the case of MORE in [22]).
2.1. The Heliocentric Dynamics of Mercury and the EMB
2.2. Mathematical Methods
2.3. The ORBIT14 Software
- the data simulator: awaiting for real data, it generates the simulated observables and the nominal value for the orbital elements of the Mercury-centric orbit of the spacecraft and the heliocentric orbits of Mercury and the EMB; and,
- the differential corrector: it is the core of the code, solving for the parameters of interest by means of a global non-linear LS fit, within a constrained multi-arc strategy [29].
3. Dynamical Model with Torsion
3.1. Spacetime with Torsion in a PPN Framework
3.2. Implementation of Torsion in ORBIT14
4. Numerical Analysis
4.1. Simulation Scenario and Assumptions
4.2. Simulation Results
4.3. Analysis of the Correlations
4.4. Possible Benefits from an Extended Mission
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hehl, F.; von der Heyde, P.; Kerlick, G.; Nester, J. General relativity with spin and torsion: Foundations and prospects. Rev. Mod. Phys. 1976, 48, 393–416. [Google Scholar] [CrossRef]
- Hehl, F.; Obukhov, Y. Elie Cartan’s torsion in geometry and in field theory, an essay. arXiv 2007, arXiv:0711.1535. [Google Scholar]
- Cartan, E. Sur un generalisation de la notion de courbure de Riemann et les espaces a torsion. Comptes Rendus de l’Academie des Sciences 1922, 174, 593–595. [Google Scholar]
- Hammond, R.T. Torsion gravity. Rep. Prog. Phys. 2002, 65, 599–649. [Google Scholar] [CrossRef]
- Ciufolini, I.; Wheeler, J. Gravitation and Inertia; Princeton University Press: Princeton, NJ, USA, 1995. [Google Scholar]
- Mao, Y.; Tegmark, M.; Guth, A.H.; Cabi, S. Constraining torsion with Gravity Probe B. Phys. Rev. D 2007, 76, 104029. [Google Scholar] [CrossRef]
- March, R.; Bellettini, G.; Tauraso, R.; Dell’Agnello, S. Constraining spacetime torsion with the Moon and Mercury. Phys. Rev. D 2011, 83, 104008. [Google Scholar] [CrossRef]
- Will, C.M. Theory and Experiment in Gravitational Physics, 2nd ed.; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Benkhoff, J.; Casterena, J.V.; Hayakawa, H.; Fujimoto, M.; Laakso, H.; Novaraa, M.; Ferri, P.; Middletond, H.R.; Ziethea, R. BepiColombo-comprehensive exploration of Mercury: Mission overview and science goals. Planet. Space Sci. 2013, 58, 2–20. [Google Scholar] [CrossRef]
- Milani, A.; Rossi, A.; Vokrouhlicky, D.; Villani, D.; Bonanno, C. Gravity field and rotation state of Mercury from the BepiColombo Radio Science Experiments. Planet. Space Sci. 2001, 49, 1579–1596. [Google Scholar] [CrossRef]
- Milani, A.; Vokrouhlicky, D.; Villani, D.; Bonanno, C.; Rossi, A. Testing general relativity with the BepiColombo radio science experiment. Phys. Rev. D 2002, 66, 082001. [Google Scholar] [CrossRef]
- Iess, L.; Asmar, S.; Tortora, P. MORE: An advanced tracking experiment for the exploration of Mercury with the mission BepiColombo. Acta Astronaut. 2009, 65, 666–675. [Google Scholar] [CrossRef]
- Bender, P.L.; Ashby, N.; Vincent, M.A.; Wahr, J.M. Conceptual Design for a Mercury Relativity Satellite. Adv. Space Res. 1989, 9, 113–116. [Google Scholar] [CrossRef]
- Iess, L.; Boscagli, G. Advanced radio science instrumentation for the mission BepiColombo to Mercury. Planet. Space Sci. 2001, 49, 1597–1608. [Google Scholar] [CrossRef]
- Milani, A.; Gronchi, G.F. Theory of Orbit Determination; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Kozai, Y. Effects of the Tidal Deformation of the Earth on the Motion of Close Earth Satellites. Publ. Astron. Soc. Jpn. 1965, 17, 395. [Google Scholar]
- Cicaló, S.; Milani, A. Determination of the rotation of Mercury from satellite gravimetry. MNRAS 2012, 427, 468–482. [Google Scholar] [CrossRef]
- Will, C.M. The Confrontation between General Relativity and Experiment. Living Rev. Relativ. 2014, 17, 4. [Google Scholar] [CrossRef] [PubMed]
- Iorio, L. Gravitomagnetism and the Earth-Mercury range. Adv. Space Res. 2011, 48, 1403–1410. [Google Scholar] [CrossRef]
- Iorio, L.; Lichtenegger, H.I.; Ruggiero, M.L.; Corda, C. Phenomenology of the Lense-Thirring effect in the solar system. Astrophys. Space Sci. 2011, 331, 351–395. [Google Scholar] [CrossRef]
- Iorio, L. Analytically calculated post-Keplerian range and range-rate perturbations: The solar Lense-Thirring effect and BepiColombo. Mon. Notices R. Astron. Soc. 2018, 476, 1811–1825. [Google Scholar] [CrossRef]
- Schettino, G.; Serra, D.; Tommei, G.; Milani, A. Addressing some critical aspects of the BepiColombo MORE relativity experiment. Celest. Mech. Dyn. Astron. 2018, 130, 72. [Google Scholar] [CrossRef]
- Asmar, S.; Armstrong, J.; Iess, L.; Tortora, P. Spacecraft Doppler tracking: Noise budget and accuracy achievable in precision radio science observations. Radio Sci. 2005, 40, 1–9. [Google Scholar] [CrossRef]
- Schettino, G.; Tommei, G. Testing General Relativity with the Radio Science Experiment of the BepiColombo mission to Mercury. Universe 2016, 2, 21. [Google Scholar] [CrossRef]
- Cicalò, S.; Schettino, G.; Di Ruzza, S.; Alessi, E.M.; Tommei, G.; Milani, A. The BepiColombo MORE gravimetry and rotation experiments with the ORBIT14 software. Mon. Not. R. Astron. Soc. 2016, 457, 1507–1521. [Google Scholar] [CrossRef]
- Tommei, G.; Milani, A.; Vokrouhlicky, D. Light time computations for the BepiColombo Radioscience experiment. Celest. Mech. Dyn. Astron. 2010, 107, 285–298. [Google Scholar] [CrossRef]
- Tommei, G.; Dimare, L.; Serra, D.; Milani, A. On the Juno Radio Science Experiment: Models, algorithms and sensitivity analysis. Mon. Notices R. Astron. Soc. 2015, 446, 3089–3099. [Google Scholar] [CrossRef]
- Serra, D.; Dimare, L.; Tommei, G.; Milani, A. Gravimetry, rotation and angular momentum of Jupiter from the Juno Radio Science experiment. Planet. Space Sci. 2016, 134, 100–111. [Google Scholar] [CrossRef]
- Alessi, E.M.; Cicalò, S.; Milani, A.; Tommei, G. Desaturation manoeuvres and precise orbit determination for the BepiColombo mission. MNRAS 2012, 423, 2270–2278. [Google Scholar] [CrossRef][Green Version]
- Serra, D.; Lari, G.; Tommei, G.; Durante, D.; Gomez Casajus, L.; Notaro, V.; Zannoni, M.; Iess, L.; Tortora, P.; Bolton, S.J. A solution of Jupiter’s gravitational field from Juno data with the ORBIT14 software. MNRAS 2019, 490, 766–772. [Google Scholar] [CrossRef]
- De Marchi, F.; Cascioli, G. Testing General Relativity in the solar system: Present and future perspectives. Class. Quantum Gravity 2020, 37, 095007. [Google Scholar] [CrossRef]
- Schettino, G.; Imperi, L.; Iess, L.; Tommei, G. Sensitivity study of systematic errors in the BepiColombo relativity experiment. In Proceedings of the IEEE Metrology for Aerospace (MetroAeroSpace), Florence, Italy, 22–23 June 2016. [Google Scholar]
- Serra, D.; Di Pierri, V.; Schettino, G.; Tommei, G. Test of general relativity during the BepiColombo interplanetary cruise to Mercury. Phys. Rev. D 2019, 98, 064059. [Google Scholar] [CrossRef]
- Nordtvedt, K.J. Post-Newtonian metric for a general class of scalar-tensor gravitational theories and observational consequences. Astrophys. J. 1960, 161, 1059–1067. [Google Scholar] [CrossRef]
- Fienga, A.; Laskar, J.; Exertier, P.; Manche, H.; Gastineau, M. Numerical estimation of the sensitivity of INPOP planetary ephemerides to general relativity parameters. Celest. Mech. Dyn. Astron. 2015, 123, 325–349. [Google Scholar] [CrossRef]
- Williams, J.G.; Turyshev, S.G.; Boggs, D.H. Lunar Laser Ranging Tests of the Equivalence Principle with the Earth and Moon. Int. J. Mod. Phys. D 2009, 18, 1129–1175. [Google Scholar] [CrossRef]
- Pitjeva, E.V.; Pitjev, N.P. Relativistic effects and dark matter in the Solar System from observations of planets and spacecraft. MNRAS 2013, 432, 3431–3437. [Google Scholar] [CrossRef]
- Iorio, L. Constraining the Preferred-Frame α1, α2 Parameters from Solar System Planetary Precessions. Int. J. Mod. Phys. D 2014, 23, 1450006. [Google Scholar] [CrossRef]
- Park, R.S.; Folkner, W.M.; Konopliv, A.S.; Williams, J.G.; Smith, D.E.; Zuber, M.T. Precession of Mercury’s Perihelion from Ranging to the MESSENGER Spacecraft. Astrophys. J. 2017, 153, 121. [Google Scholar]
- Nordtvedt, K. Probing Gravity to the Second Post-Newtonian Order and to One Part in 10-7 Using the Spin Axis of the Sun. Astrophys. J. 1987, 320, 871. [Google Scholar] [CrossRef]
- De Marchi, F.; Tommei, G.; Milani, A.; Schettino, G. Constraining the Nordtvedt parameter with the BepiColombo Radioscience experiment. Phys. Rev. D 2016, 93, 123014. [Google Scholar] [CrossRef]
- Konopliv, A.S.; Park, R.S.; Ermakov, A.I. The Mercury gravity field, orientation, love number, and ephemeris from the MESSENGER radiometric tracking data. Icarus 2020, 335, 113386. [Google Scholar] [CrossRef]
| 1. | We point out that the parameter is not independent from the other PPN parameters (see, e.g., [18]): this issue will be addressed in Section 4.1. |
| 2. | This is the case of the Nordtvedt equation introduced in Section 4.1 |
| 3. | |
| 4. | For a discussion on this assumption see [7]—Section 6 for details. |
| 5. | We rearranged Equation (6.6) in [7], making explicit the dependence of the coefficients by . |
| 6. | We omitted the multiplicative factor , while we restored the G factor. |
| 7. | The first solar superior conjunction of BepiColombo is expected on March 2021. |
| 8. | This follows from the fact that, since is highly constrained by the SCE apriori and and can be neglected, the Nordtvedt equation forces a linear dependency of from . |
| 9. | Value from latest JPL ephemerides publicly available at: http://ssd.jpl.nasa.gov/?constants. Accessed 23 June 2020. |
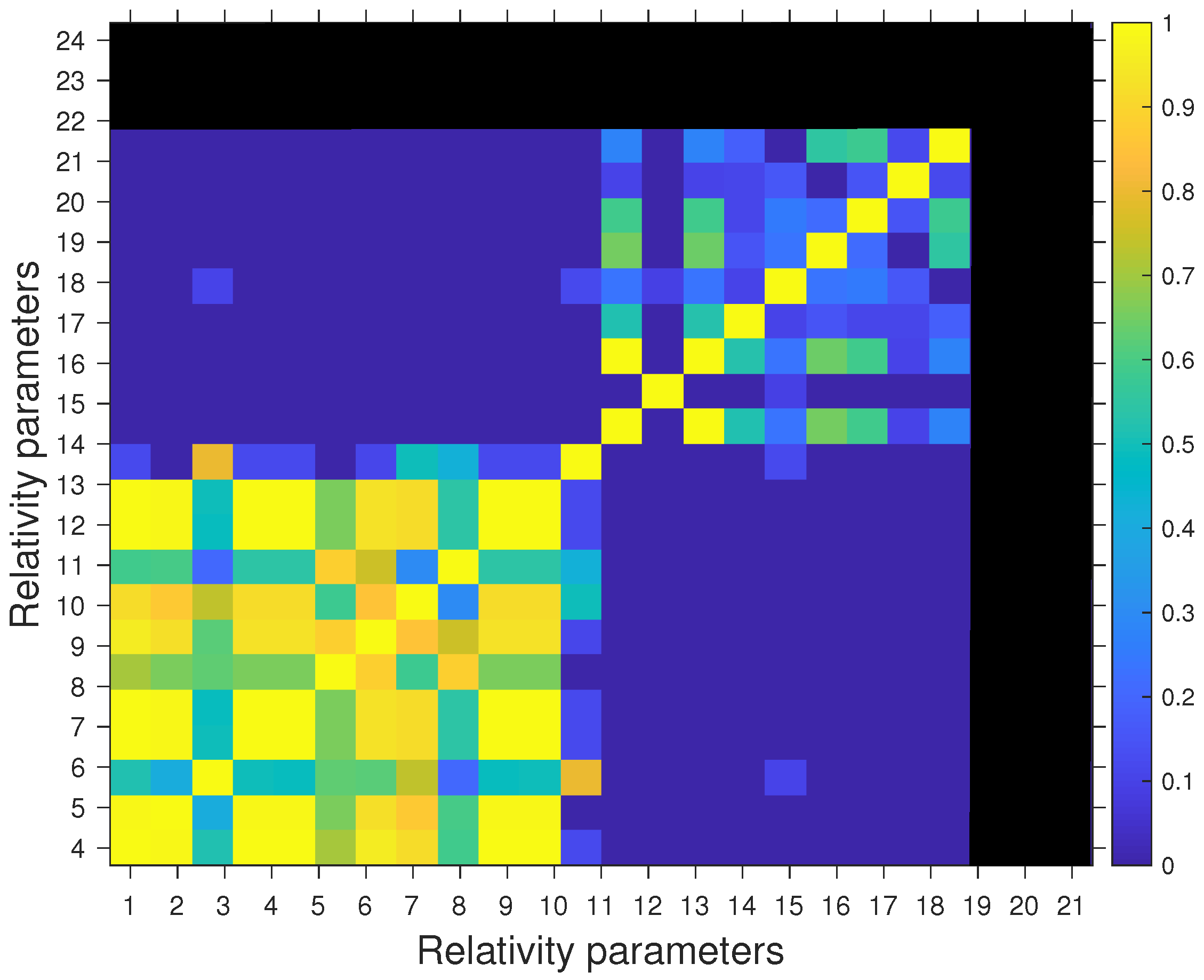
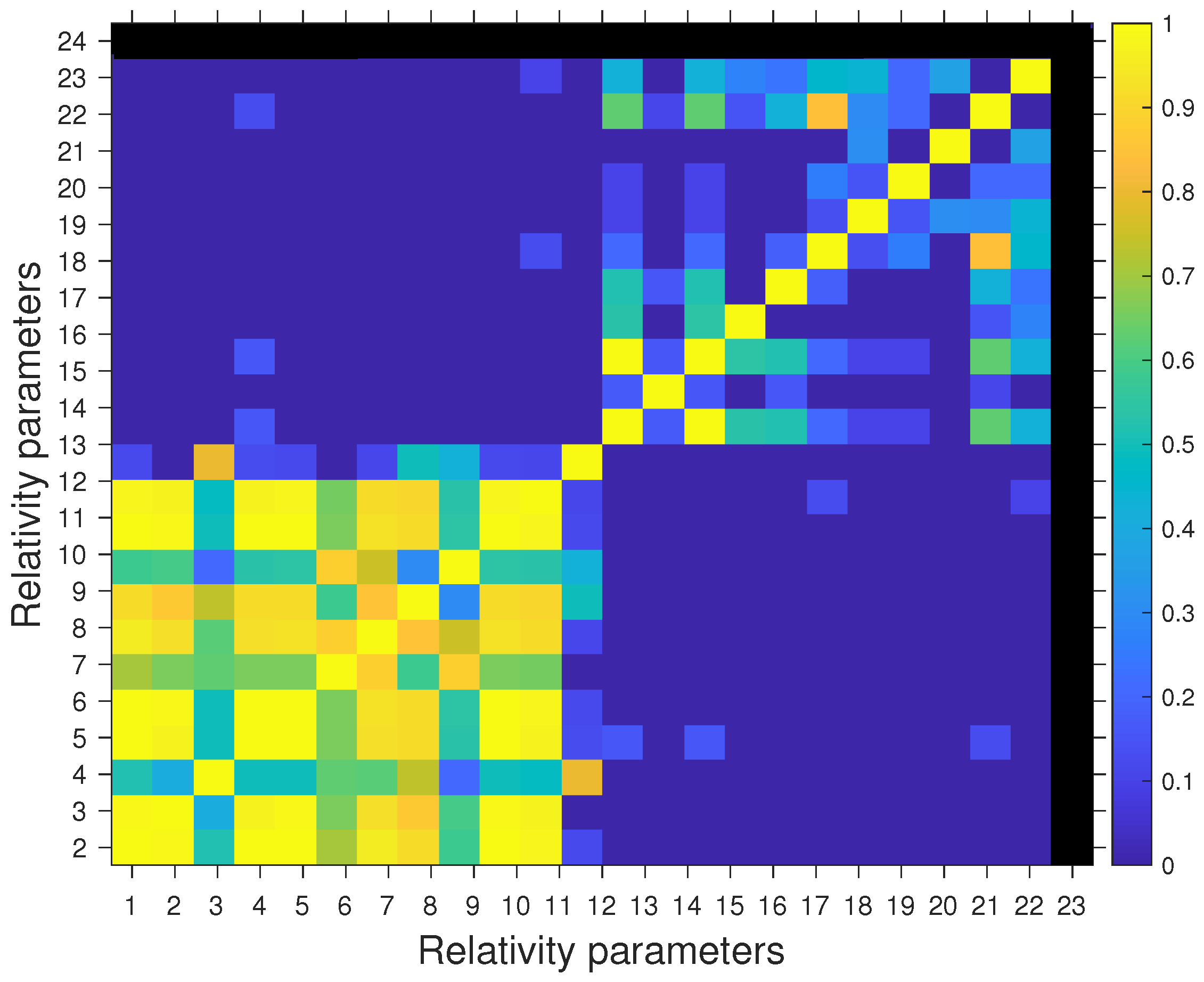
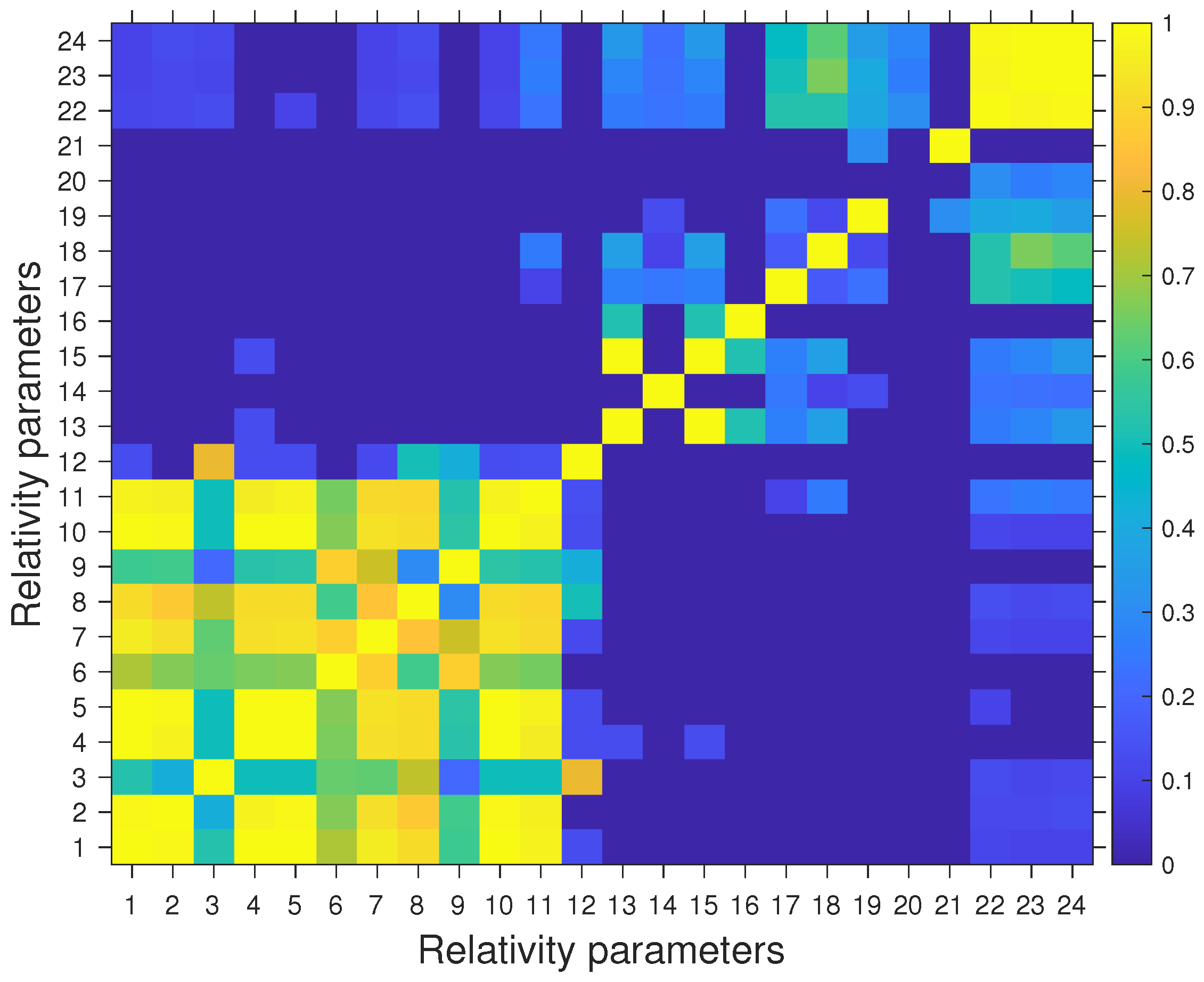
| Parameter | Accuracy | Parameter | Accuracy |
|---|---|---|---|
| [35] | [35] | ||
| [33] | 9 | ||
| [36] | [37] | ||
| [38] | [39] | ||
| [38] |
| Scenario | Solved Parameters |
|---|---|
| Reference | state vectors of Mercury and EMB; relativity parameters |
| Simulation (a) | state vectors of Mercury and EMB; relativity parameters; , |
| Simulation (b) | state vectors of Mercury and EMB; relativity parameters; , , |
| Parameter | Reference | Simulation (a) | Simulation (b) | N |
|---|---|---|---|---|
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 | ||||
| 7 | ||||
| 8 | ||||
| 9 | ||||
| 10 | ||||
| 11 | ||||
| 12 |
| Parameter | Reference | Simulation (a) | Simulation (b) | N |
|---|---|---|---|---|
| 13 | ||||
| 14 | ||||
| 15 | ||||
| 16 | ||||
| 17 | ||||
| 18 | ||||
| 19 | ||||
| 20 | ||||
| 21 | ||||
| – | 22 | |||
| – | 23 | |||
| – | – | 24 |
| Parameter | Reference | Simulation (a) | Simulation (b) | |||
|---|---|---|---|---|---|---|
| 4.7 | 4.1 | 4.1 | ||||
| 1.4 | 1.4 | 1.4 | ||||
| 4.7 | 4.3 | 4.0 | ||||
| 5.4 | 5.2 | 4.8 | ||||
| 2.2 | 2.2 | 2.6 | ||||
| 3.0 | 2.1 | 2.2 | ||||
| 1.7 | 2.1 | 2.2 | ||||
| 3.0 | 3.1 | 3.1 | ||||
| 1.8 | 1.4 | 1.4 | ||||
| – | – | 2.0 | 3.3 | |||
| – | – | 2.0 | 3.2 | |||
| – | – | – | – | 2.6 |
| Parameter | Simulation (b) | Case I | Case II |
|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schettino, G.; Serra, D.; Tommei, G.; Di Pierri, V. A Test of Gravitational Theories Including Torsion with the BepiColombo Radio Science Experiment. Universe 2020, 6, 175. https://doi.org/10.3390/universe6100175
Schettino G, Serra D, Tommei G, Di Pierri V. A Test of Gravitational Theories Including Torsion with the BepiColombo Radio Science Experiment. Universe. 2020; 6(10):175. https://doi.org/10.3390/universe6100175
Chicago/Turabian StyleSchettino, Giulia, Daniele Serra, Giacomo Tommei, and Vincenzo Di Pierri. 2020. "A Test of Gravitational Theories Including Torsion with the BepiColombo Radio Science Experiment" Universe 6, no. 10: 175. https://doi.org/10.3390/universe6100175
APA StyleSchettino, G., Serra, D., Tommei, G., & Di Pierri, V. (2020). A Test of Gravitational Theories Including Torsion with the BepiColombo Radio Science Experiment. Universe, 6(10), 175. https://doi.org/10.3390/universe6100175






