Gravity-Induced Geometric Phases and Entanglement in Spinors and Neutrinos: Gravitational Zeeman Effect
Abstract
1. Introduction
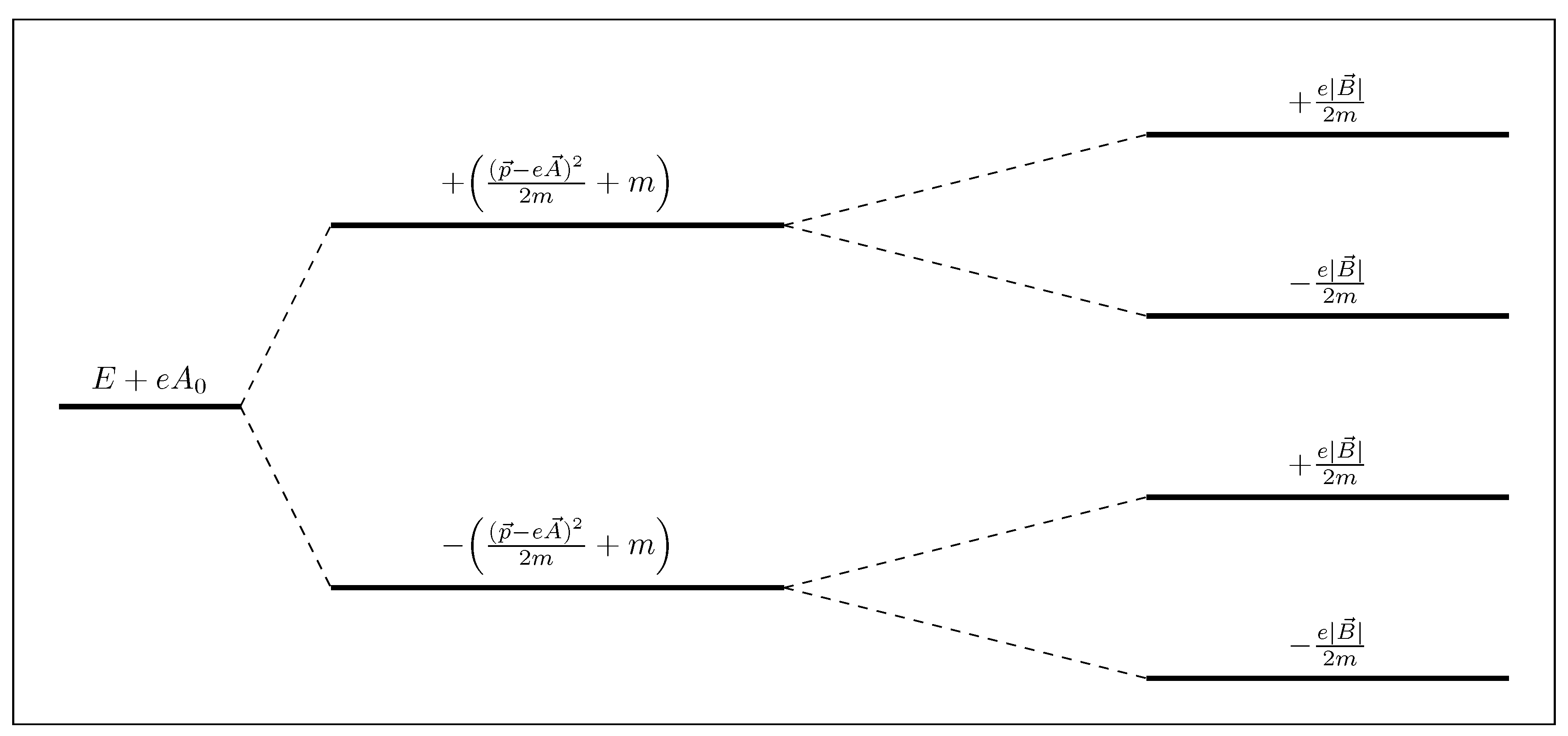
2. Geometric Phases in the Presence of Electromagnetic and Gravitational Fields
2.1. In Electromagnetic Field
2.2. In Gravitational Field
3. Neutrino States in the Presence of Gravitational Field
3.1. Neutrino–Antineutrino Mixing
3.2. Mixing of Mass Eigenstates
3.3. Flavor Mixing
4. Dynamic and Geometric Phases
4.1. Neutrino-Antineutrino Mixing
4.2. Mixing of Mass Eigenstates
4.3. Flavor Mixing
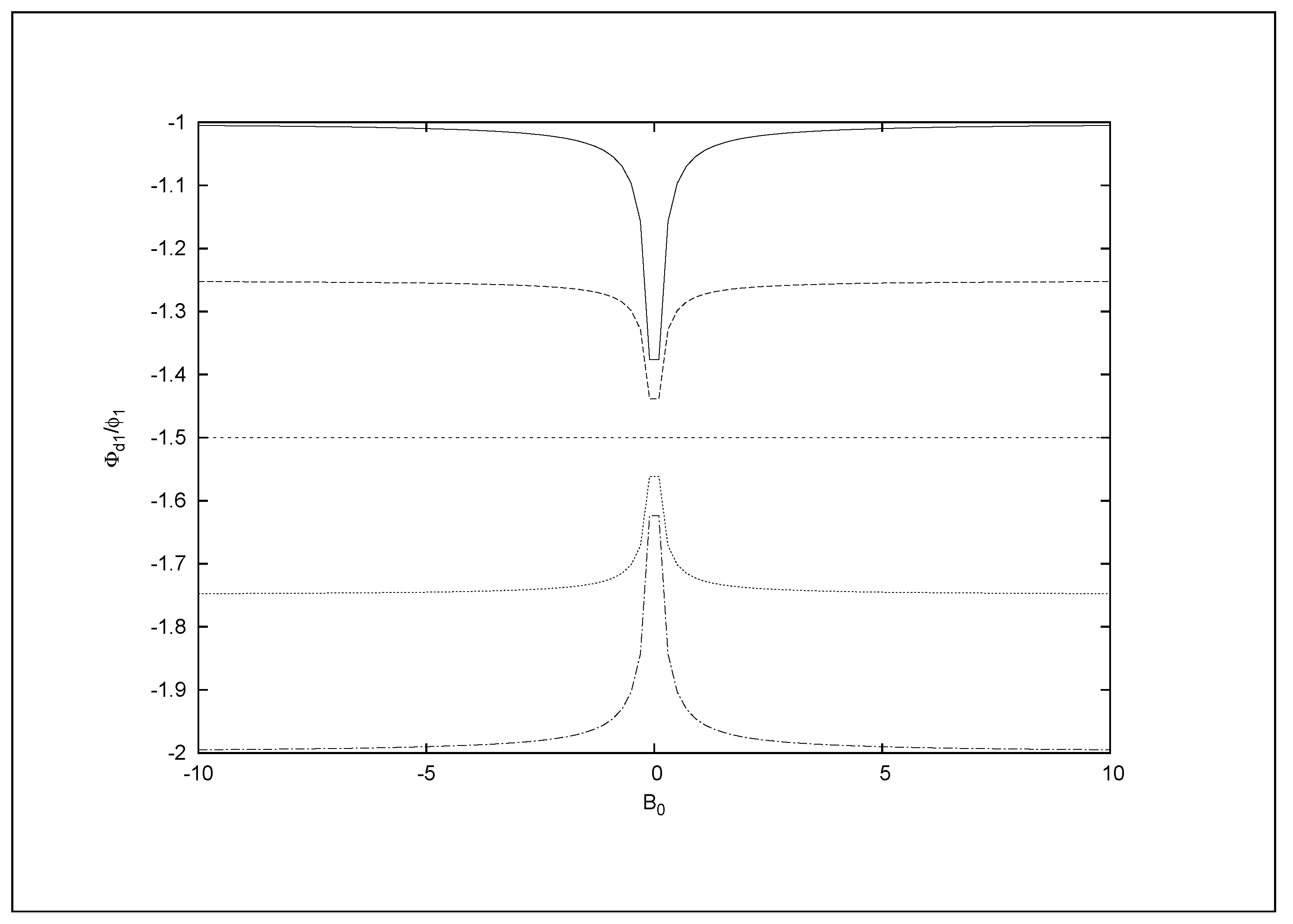
5. Entanglement of Neutrino States and Corresponding Geometric Phases
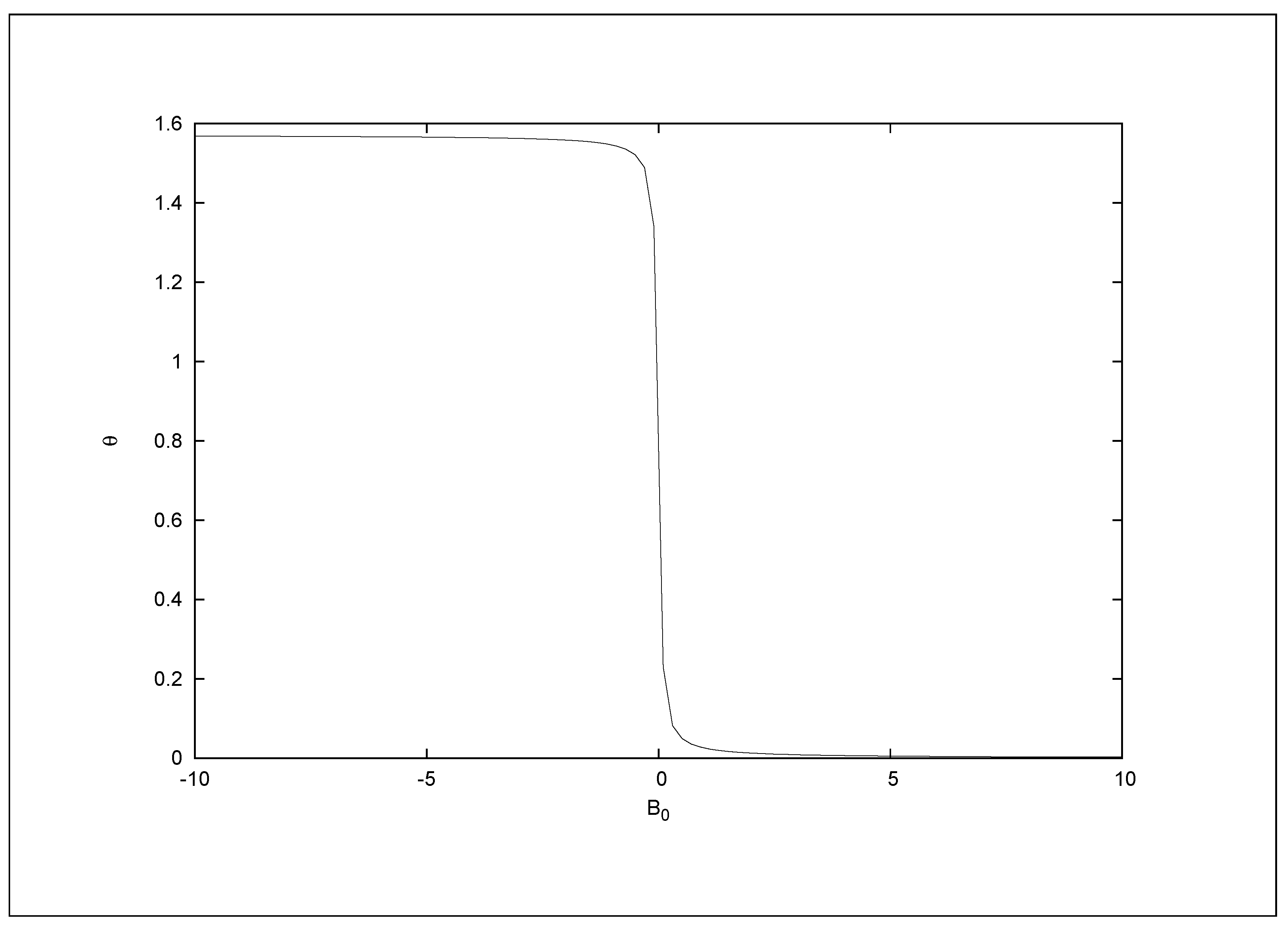
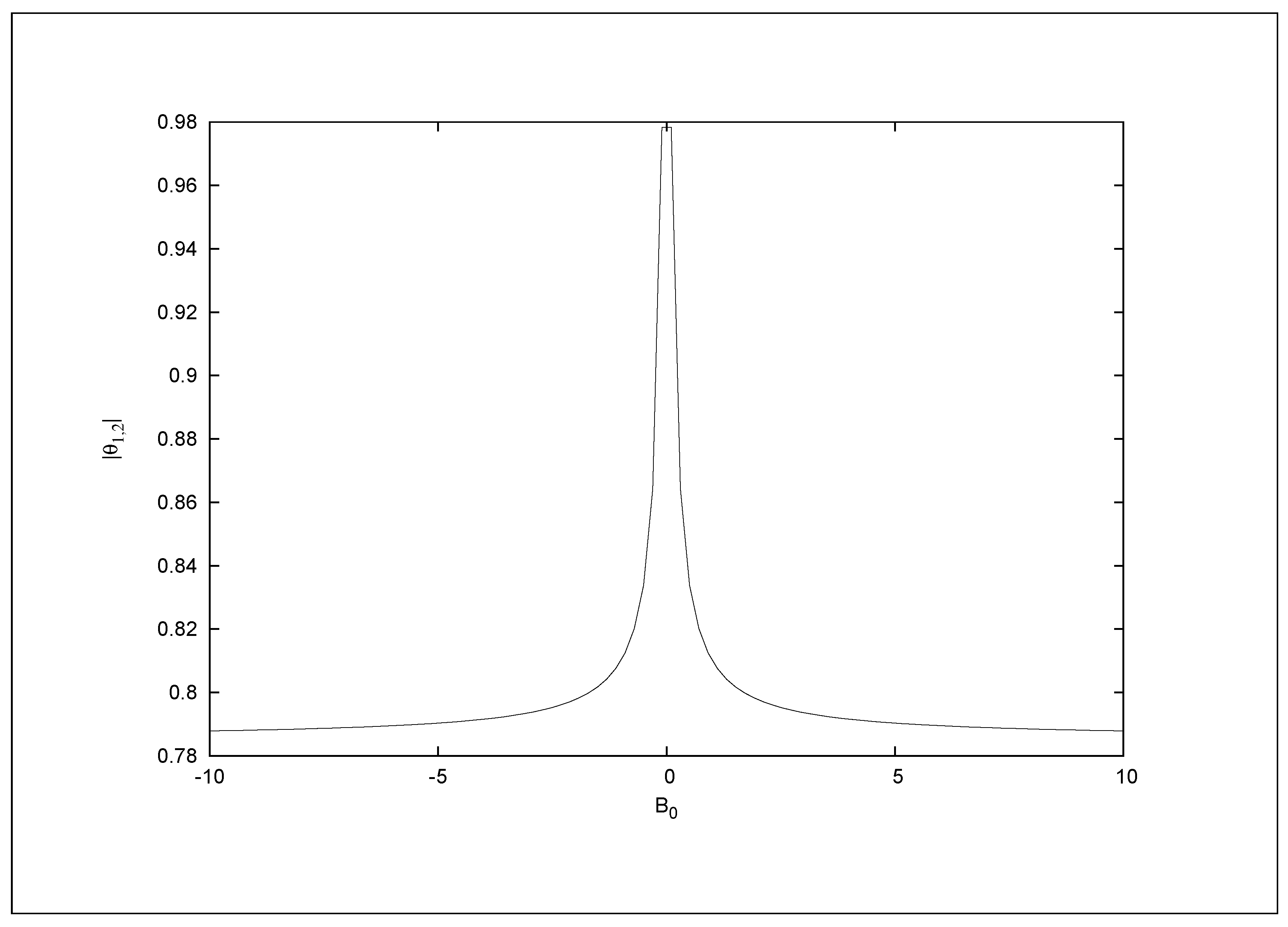
6. Variation of Mixing Angles with Gravitational Field
7. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Berry, M.V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. A 1984, 392, 45. [Google Scholar]
- Aharonov, Y.; Anandan, J. Phase change during a cyclic quantum evolution. Phys. Rev. Lett. 1987, 58, 1593. [Google Scholar] [CrossRef] [PubMed]
- Samuel, J.; Bhandari, R. General setting for Berry’s phase. Phys. Rev. Lett. 1988, 60, 2339. [Google Scholar] [CrossRef] [PubMed]
- Mukunda, N.; Simon, R. Quantum kinematic approach to the geometric phase. I. General formalism. Ann. Phys. (N. Y.) 1993, 228, 205. [Google Scholar] [CrossRef]
- Nakagawa, N. Geometrical phase factors and higher-order adiabatic approximations. Ann. Phys. (N. Y.) 1987, 179, 145. [Google Scholar] [CrossRef]
- Vidal, J.; Wudka, J. Non-dynamical contributions to left-right transitions in the solar neutrino problem. Phys. Lett. B 1990, 249, 473. [Google Scholar] [CrossRef]
- Aneziris, C.; Schechter, J. Three Majorana neutrinos in a twisting magnetic field. Phys. Rev. D 1992, 45, 1053. [Google Scholar] [CrossRef]
- Smirnov, A.Y. The geometrical phase in neutrino spin precession and the solar neutrino problem. Phys. Lett. B 1991, 260, 161. [Google Scholar] [CrossRef]
- Guzzo, M.M.; Bellandi, J. On the question of neutrino spin precession in a magnetic field. Phys. Lett. B 1992, 294, 243. [Google Scholar] [CrossRef][Green Version]
- He, X.-G.; Li, X.-Q.; McKellar, B.H.J.; Zhang, Y. Berry phase in neutrino oscillations. Phys. Rev. D 2005, 72, 053012. [Google Scholar] [CrossRef]
- Blasone, M.; Henning, P.A.; Vitiello, G. Berry phase for oscillating neutrinos. Phys. Lett. B 1999, 466, 262. [Google Scholar] [CrossRef]
- Wang, X.-B.; Kwek, L.C.; Liu, Y.; Oh, C.H. Noncyclic phase for neutrino oscillation. Phys. Rev. D 2001, 63, 053003. [Google Scholar] [CrossRef]
- Joshi, S.; Jain, S. Geometric phase for neutrino propagation in magnetic field. Phys. Lett. B 2016, 754, 135. [Google Scholar] [CrossRef][Green Version]
- Ramaseshan, S.; Nityananda, R. The interference of polarized light as an early example of Berry’s phase. Curr. Sci. 1986, 55, 1225. [Google Scholar]
- Pancharatnam, S. Generalized theory of interference, and its applications. Proc. Indian Acad. Sci. A 1956, 44, 247. [Google Scholar] [CrossRef]
- Mehta, P. Topological phase in two flavor neutrino oscillations. Phys. Rev. D 2009, 79, 096013. [Google Scholar] [CrossRef]
- Dajka, J.; Syska, J.; Łuczka, J. Geometric phase of neutrino propagating through dissipative matter. Phys. Rev. D 2011, 83, 097302. [Google Scholar] [CrossRef]
- Syska, J.; Dajka, J.; Łuczka, J. Interference phenomenon and geometric phase for Dirac neutrino in π+ decay. Phys. Rev. D 2013, 87, 117302. [Google Scholar] [CrossRef]
- Joshi, S.; Jain, S.R. Noncyclic geometric phases and helicity transitions for neutrino oscillations in a magnetic field. Phys. Rev. D 2017, 96, 096004. [Google Scholar] [CrossRef]
- Johns, L.; Fuller, G.M. Geometric phases in neutrino oscillations with nonlinear refraction. Phys. Rev. D 2017, 95, 043003. [Google Scholar] [CrossRef]
- Wang, Z.; Pan, H. Exploration of CPT violation via time-dependent geometric quantities embedded in neutrino oscillation through fluctuating matter. Nuc. Phys. B 2017, 915, 414. [Google Scholar] [CrossRef]
- Dixit, K.; Alok, A.K.; Banerjee, S.; Kumar, D. Geometric phase and neutrino mass hierarchy problem. J. Phys. G 2018, 45, 085002. [Google Scholar] [CrossRef]
- Capolupo, A.; Giampaolo, S.M.; Hiesmayr, B.C.; Vitiello, G. Geometric phase of neutrinos: Differences between Dirac and Majorana neutrinos. Phys. Lett. B 2018, 780, 216. [Google Scholar] [CrossRef]
- Simonov, K.; Capolupo, A.; Giampaolo, S.M. Gravity, entanglement and CPT-symmetry violation in particle mixing. Eur. Phys. J. C 2019, 79, 902. [Google Scholar] [CrossRef]
- Mukhopadhyay, B. Gravity-induced neutrino-antineutrino oscillation: CPT and lepton number non-conservation under gravity. Class. Quantum Gravity 2007, 24, 1433. [Google Scholar] [CrossRef][Green Version]
- Sinha, M.; Mukhopadhyay, B. CPT and lepton number violation in the neutrino sector: Modified mass matrix and oscillation due to gravity. Phys. Rev. D 2008, 77, 025003. [Google Scholar] [CrossRef]
- Singh, P.; Mukhopadhyay, B. Gravitationally induced neutrino asymmetry. Mod. Phys. Lett. A 2003, 18, 779. [Google Scholar] [CrossRef]
- Mukhopadhyay, B. Neutrino asymmetry around black holes: Neutrinos interact with gravity. Mod. Phys. Lett. A 2005, 20, 2145. [Google Scholar] [CrossRef]
- Debnath, U.; Mukhopadhyay, B.; Dadhich, N. Spacetime Curvature Coupling of Spinors in Early Universe:. Neutrino Asymmetry and a Possible Source of Baryogenesis. Mod. Phys. Lett. A 2006, 21, 399. [Google Scholar] [CrossRef]
- Kim, C.W.; Sze, W.K.; Nussinov, S. Neutrino oscillations and the Landau-Zener formula. Phys. Rev. D 1987, 35, 4014. [Google Scholar] [CrossRef]
- Stodolsky, L. Treatment of neutrino oscillations in a thermal environment. Phys. Rev. D 1987, 36, 2273. [Google Scholar] [CrossRef] [PubMed]
- Píriz, D.; Roy, M.; Wudka, J. Neutrino oscillations in strong gravitational fields. Phys. Rev. D 1996, 54, 1587. [Google Scholar] [CrossRef] [PubMed]
- Mohanty, S.; Mukhopadhyay, B.; Prasanna, A.R. Experimental tests of curvature couplings of fermions in general relativity. Phys. Rev. D 2002, 65, 122001. [Google Scholar] [CrossRef]
- Dixit, K.; Naikoo, J.; Mukhopadhyay, B.; Banerjee, S. Quantum correlations in neutrino oscillations in curved spacetime. Phys. Rev. D 2019, 100, 055021. [Google Scholar] [CrossRef]
- Birrell, N.D.; Davies, P. Quantum Fields in Curved Space; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Kaku, M. Quantum Field Theory; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Schwinger, J. Particles, Sources, and Fields III; Addison-Wesley: Redwood City, CA, USA, 1989. [Google Scholar]
- Obukhov, Y.N. Spin, Gravity, and Inertia. Phys. Rev. Lett. 2001, 86, 192. [Google Scholar] [CrossRef]
- Huang, X.; Parker, L. Hermiticity of the Dirac Hamiltonian in curved spacetime. Phys. Rev. D 2009, 79, 024020. [Google Scholar] [CrossRef]
- Mukhopadhyay, B. Exploring the Universe: From Near Space to Extra-Galactic. In Astrophysics and Space Science Proceedings; Mukhopadhyay, B., Sasmal, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; Volume 53, p. 3. [Google Scholar]
- Colladay, D.; Kostelecký, V.A. CPT violation and the standard model. Phys. Rev. D 1997, 55, 6760. [Google Scholar] [CrossRef]
- Ellis, J.; Mavromatos, N.E. Role of space-time foam in breaking supersymmetry via the Barbero-Immirzi parameter. Phys. Rev. D 2011, 84, 085016. [Google Scholar] [CrossRef]
- Mavromatos, N.E.; Sarkar, S. CPT-violating leptogenesis induced by gravitational defects. Eur. Phys. J. C 2013, 73, 2359. [Google Scholar] [CrossRef]
- Mosquera Cuesta, H.J. Neutrino astrophysics in slowly rotating spacetimes permeated by nonlinear electrodynamics fields. Astrophys. J. 2017, 835, 215. [Google Scholar] [CrossRef]
- Diaz, J.S.; Katori, T.; Spitz, J.; Conrad, J.M. Search for neutrino-antineutrino oscillations with a reactor experiment. Phys. Lett. B 2013, 727, 412. [Google Scholar] [CrossRef]
- Shapiro, S.L.; Teukolsky, S.A. Black Holes, White Dwarfs, and Neutron Stars: The Physics of Compact Objects; John Wiley & Sons: New York, NY, USA, 1983. [Google Scholar]
- Sjöqvist, E. Geometric phase for entangled spin pairs. Phys. Rev. A 2000, 62, 022109. [Google Scholar] [CrossRef]
| 1. | Note that the corresponding temperature GeV [46]. |

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mukhopadhyay, B.; Ganguly, S.K. Gravity-Induced Geometric Phases and Entanglement in Spinors and Neutrinos: Gravitational Zeeman Effect. Universe 2020, 6, 160. https://doi.org/10.3390/universe6100160
Mukhopadhyay B, Ganguly SK. Gravity-Induced Geometric Phases and Entanglement in Spinors and Neutrinos: Gravitational Zeeman Effect. Universe. 2020; 6(10):160. https://doi.org/10.3390/universe6100160
Chicago/Turabian StyleMukhopadhyay, Banibrata, and Soumya Kanti Ganguly. 2020. "Gravity-Induced Geometric Phases and Entanglement in Spinors and Neutrinos: Gravitational Zeeman Effect" Universe 6, no. 10: 160. https://doi.org/10.3390/universe6100160
APA StyleMukhopadhyay, B., & Ganguly, S. K. (2020). Gravity-Induced Geometric Phases and Entanglement in Spinors and Neutrinos: Gravitational Zeeman Effect. Universe, 6(10), 160. https://doi.org/10.3390/universe6100160





