Formation and Clustering of Primordial Black Holes in Brans-Dicke Theory
Abstract
1. Introduction
2. Primordial Black Holes in the Brans-Dicke Theory
2.1. Basic Equations
2.2. Zero Approximation
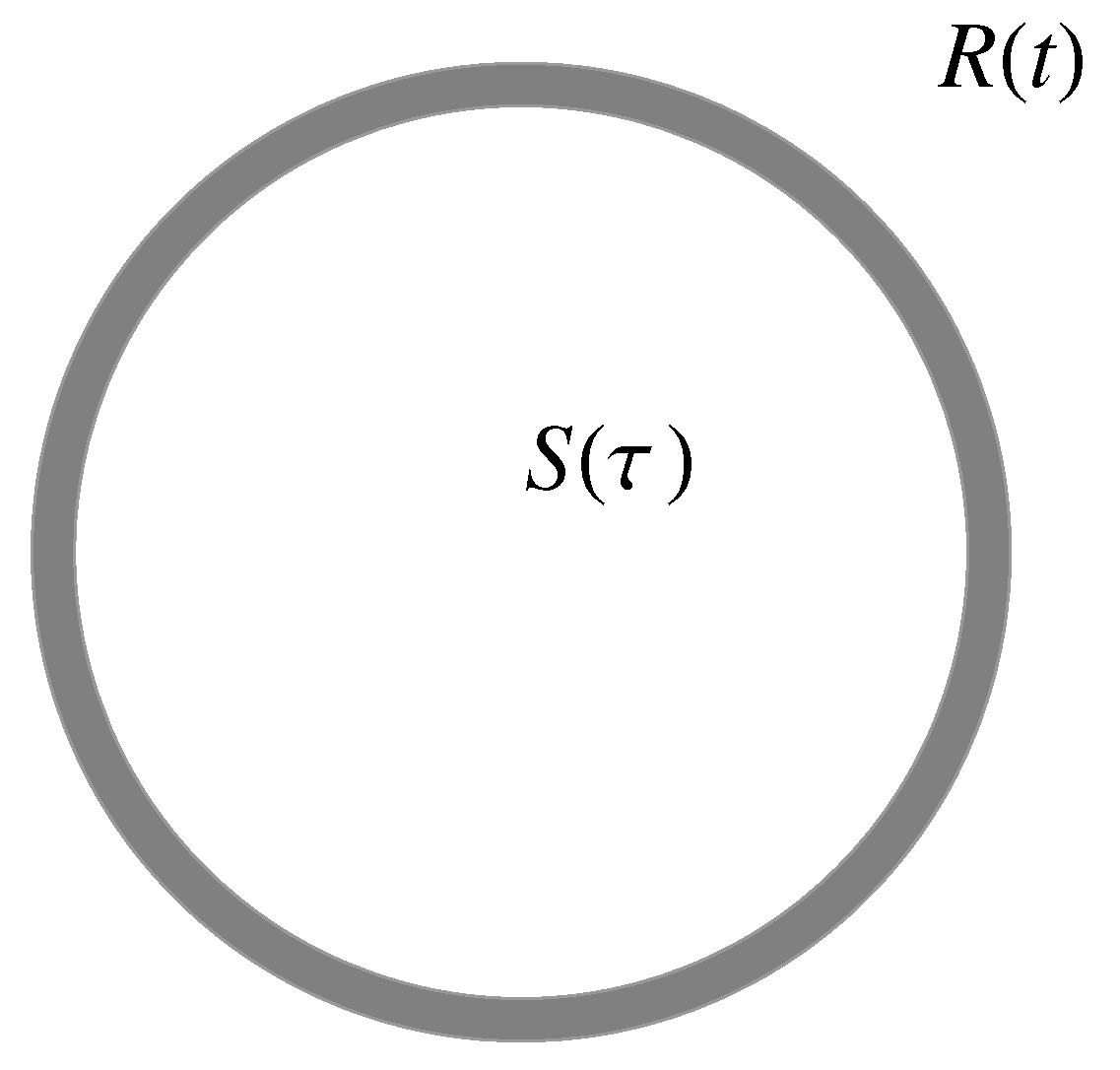
2.3. Corrections to the Black Hole’s Formation Threshold
3. Clustering of Black Holes
3.1. Perturbations in the PBH Number Density
3.2. Influence of Inhomogeneities on the Rate of Gravitational Bursts
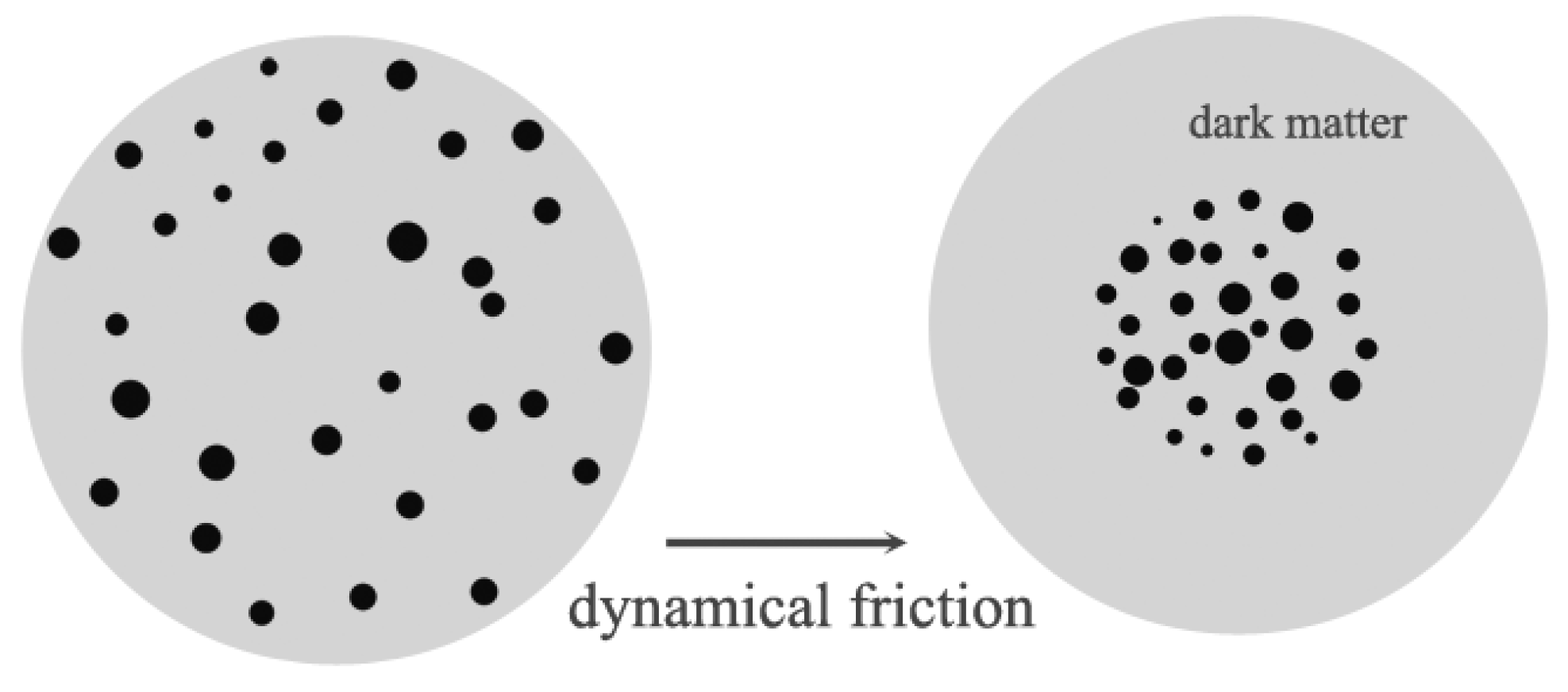
3.3. Clusters of Primordial Black Holes
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviation
| PBH | primordial black hole |
References
- Zeldovich, Y.B.; Novikov, I.D. The Hypothesis of Cores Retarded during Expansion and the Hot Cosmological Model. Sov. Astron. 1967, 10, 602. [Google Scholar]
- Hawking, S. Gravitationally collapsed objects of very low mass. Mon. Not. R. Astron. Soc. 1971, 152, 75–78. [Google Scholar] [CrossRef]
- Carr, B.J.; Hawking, S.W. Black holes in the early Universe. Mon. Not. R. Astron. Soc. 1974, 168, 399–415. [Google Scholar] [CrossRef]
- Carr, B.J. The primordial black hole mass spectrum. Astrophys. J. 1975, 201, 1–19. [Google Scholar] [CrossRef]
- Khlopov, M.Y.; Polnarev, A.G. Primordial black holes as a cosmological test of grand unification. Phys. Lett. B 1980, 97, 383–387. [Google Scholar] [CrossRef]
- Zabotin, N.A.; Naselskii, P.D.; Polnarev, A.G. High-Amplitude Peaks of Density Disturbances and the Formation of Primordial Black-Holes in the Dust like Universe. Sov. Astron. 1987, 64, 673–685. [Google Scholar]
- Berezin, V.A.; Kuzmin, V.A.; Tkachev, I.I. Thin-wall vacuum domain evolution. Phys. Lett. B 1983, 120, 91–96. [Google Scholar] [CrossRef]
- Khlopov, M.Y.; Konoplich, R.V.; Rubin, S.G.; Sakharov, A.S. Formation of Black Holes in First Order Phase Transitions. Preprint 1203 I Roma University. arXiv 1998, arXiv:hep-ph/9807343. [Google Scholar]
- Khlopov, M.Y.; Rubin, S.G.; Sakharov, A.S. Primordial Structure of Massive Black Hole Clusters. Astropart. Phys. 2005, 23, 265–277. [Google Scholar] [CrossRef]
- Dolgov, A.; Silk, J. Baryon isocurvature fluctuations at small scales and baryonic dark matter. Phys. Rev. D 1993, 47, 4244. [Google Scholar] [CrossRef]
- Dolgov, A.D. Massive and supermassive black holes in the contemporary and early Universe and problems in cosmology and astrophysics. Physics-Uspekhi 2018, 61, 115–132. [Google Scholar] [CrossRef]
- Dolgov, A.; Postnov, K. Why the mean mass of primordial black hole distribution is close to 10M⊙. arXiv 2004, arXiv:2004.11669. [Google Scholar]
- Nakamura, T.; Sasaki, M.; Tanaka, T.; Thorne, K.S. Gravitational Waves from Coalescing Black Hole MACHO Binaries. Astrophys. J. 1997, 487, L139–L142. [Google Scholar] [CrossRef]
- Ioka, K.; Chiba, T.; Tanaka, T.; Nakamura, T. Black hole binary formation in the expanding universe: Three body problem approximation. Phys. Rev. D 1998, 58, 063003. [Google Scholar] [CrossRef]
- Sasaki, M.; Suyama, T.; Tanaka, T.; Yokoyama, S. Primordial Black Hole Scenario for the Gravitational-Wave Event GW150914. Phys. Rev. Lett. 2016, 117, 061101. [Google Scholar] [CrossRef] [PubMed]
- Blinnikov, S.; Dolgov, A.; Porayko, N.K.; Postnov, K. Solving puzzles of GW150914 by primordial black holes. J. Cosmol. Astropart. Phys. 2016, 11, 036. [Google Scholar] [CrossRef]
- Dolgov, A.D.; Kuranov, A.G.; Mitichkin, N.A.; Porey, S.; Postnov, K.A.; Sazhina, O.S.; Simkin, I.V. On mass distribution of coalescing black holes. arXiv 2020, arXiv:2005.00892. [Google Scholar]
- Starobinskii, A.A. Spectrum of adiabatic perturbations in the universe when there are singularities in the inflaton potential. J. Exp. Theor. Phys. Lett. 1992, 55, 489–494. [Google Scholar]
- Ivanov, P.; Naselsky, P.; Novikov, I. Inflation and primordial black holes as dark matter. Phys. Rev. D. 1994, 50, 7173–7178. [Google Scholar] [CrossRef]
- Yokoyama, J. Formation of MACHO-Primordial Black Holes in Inflationary Cosmology. Astron. Astrophys. 1997, 318, 673–679. [Google Scholar]
- Barrow, J.D.; Carr, B.J. Formation and evaporation of primordial black holes in scalar-tensor gravity theories. Phys. Rev. D 1996, 54, 3920–3931. [Google Scholar] [CrossRef] [PubMed]
- Nayak, B.; Majumdar, A.S.; Singh, L.P. Astrophysical constraints on primordial black holes in Brans-Dicke theory. J. Cosmol. Astropart. Phys. 2010, 1008, 039. [Google Scholar] [CrossRef]
- Aliferis, G.; Zarikas, V. Electroweak baryogenesis by primordial black holes in Brans-Dicke modified gravity. arXiv 2020, arXiv:2006.13621. [Google Scholar]
- Escriva, A.; Germani, C.; Sheth, R.K. Analytical thresholds for black hole formation in general cosmological backgrounds. arXiv 2020, arXiv:2007.05564. [Google Scholar]
- Chen, C.-Y. Threshold of primordial black hole formation in modified theories of gravity. arXiv 2019, arXiv:1912.10690. [Google Scholar]
- Kaiser, N. On the spatial correlations of Abell clusters. Astrophys. J. 1984, 284, L9–L12. [Google Scholar] [CrossRef]
- Meszaros, P. The behaviour of point masses in an expanding cosmological substratum. Astron. Astrophys. 1974, 37, 225–228. [Google Scholar]
- Meszaros, P. Primeval black holes and galaxy formation. Astron. Astrophys. 1975, 38, 5–13. [Google Scholar]
- Carr, B.J. The statistical clustering of primordial black holes. Astron. Astrophys. 1977, 56, 377–383. [Google Scholar]
- Chisholm, J.R. Clustering of primordial black holes: Basic results. Phys. Rev. D 2006, 73, 083504. [Google Scholar] [CrossRef]
- Desjacques, V.; Riotto, A. The Spatial Clustering of Primordial Black Holes. Phys. Rev. D 2018, 98, 123533. [Google Scholar] [CrossRef]
- Suyama, T.; Yokoyama, S. Clustering of primordial black holes with non-Gaussian initial fluctuations. Prog. Theor. Exp. Phys. 2019, 2019, 103E02. [Google Scholar] [CrossRef]
- Byrnes, C.T.; Copeland, E.J.; Green, A.M. Primordial black holes as a tool for constraining non-Gaussianity. Phys. Rev. D 2012, 86, 043512. [Google Scholar] [CrossRef]
- Tada, Y.; Yokoyama, S. Primordial black holes as biased tracers. Phys. Rev. D 2015, 91, 123534. [Google Scholar] [CrossRef]
- Young, S.; Byrnes, C.T. Signatures of non-gaussianity in the isocurvature modes of primordial black hole dark matter. J. Cosmol. Astropart. Phys. 2015, 1504, 034. [Google Scholar] [CrossRef]
- Belotsky, K.M.; Dokuchaev, V.I.; Eroshenko, Y.N.; Esipova, E.A.; Khlopov, M.Y.; Khromykh, L.A.; Kirillov, A.A.; Nikulin, V.V.; Rubin, S.G.; Svadkovsky, I.V. Clusters of primordial black holes. Eur. Phys. J. C 2019, 79, 246. [Google Scholar] [CrossRef]
- Atal, V.; Sanglas, A.; Triantafyllou, N. LIGO black holes and dark matter: The effect of spatial clustering. arXiv 2007, arXiv:2007.07212. [Google Scholar]
- Brans, C.H.; Dicke, R.H. Mach’s Principle and a Relativistic Theory of Gravitation. Phys. Rev. 1961, 124, 925. [Google Scholar] [CrossRef]
- Starobinsky, A.A.; Yokoyama, J. Density fluctuations in Brans-Dicke inflation. arXiv 1995, arXiv:gr-qc/9502002. [Google Scholar]
- Tahmasebzadeh, B.; Rezazadeh, K.; Karami, K. Brans-Dicke inflation in light of the Planck 2015 data. J. Cosmol. Astropart. Phys. 2016, 07, 006. [Google Scholar] [CrossRef]
- Weinberg, S. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity; Wiley: New York, NY, USA, 1972; p. 623. [Google Scholar]
- Harrison, E.R. Fluctuations at the Threshold of Classical Cosmology. Phys. Rev. D 1970, 1, 2726–2730. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields; Pergamon: Oxford, UK, 1975. [Google Scholar]
- Kopp, M.; Hofmann, S.; Weller, J. Separate universes do not constrain primordial black hole formation. Phys. Rev. D 2011, 83, 124025. [Google Scholar] [CrossRef]
- Carr, B.J.; Harada, T. Separate universe problem: 40 years on. Phys. Rev. D 2015, 91, 084048. [Google Scholar] [CrossRef]
- Harada, T.; Yoo, C.-M.; Kohri, K. Threshold of primordial black hole formation. Phys. Rev. D 2013, 88, 084051, Erratum in 2014, 89, 029903. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the newtonian dynamics: Implications for galaxy systems. Astrophys. J. 1983, 270, 384–389. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. Astrophys. J. 1983, 270, 365–370. [Google Scholar] [CrossRef]
- Arraut, I. Can a nonlocal model of gravity reproduce Dark Matter effects in agreement with MOND? Int. J. Mod. Phys. D 2014, 23, 1450008. [Google Scholar] [CrossRef]
- Lee, J.; Shandarin, S.F. Large-Scale Biasing and the Primordial Gravitational Potential. Astrophys. J. Lett. 1998, 505, L75. [Google Scholar] [CrossRef]
- Quinlan, G.D.; Shapiro, S.L. The Collapse of Dense Star Clusters to Supermassive Black Holes: Binaries and Gravitational Radiation. Astrophys. J. 1987, 321, 199–210. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berezin, V.; Dokuchaev, V.; Eroshenko, Y.; Smirnov, A. Formation and Clustering of Primordial Black Holes in Brans-Dicke Theory. Universe 2020, 6, 158. https://doi.org/10.3390/universe6100158
Berezin V, Dokuchaev V, Eroshenko Y, Smirnov A. Formation and Clustering of Primordial Black Holes in Brans-Dicke Theory. Universe. 2020; 6(10):158. https://doi.org/10.3390/universe6100158
Chicago/Turabian StyleBerezin, Victor, Vyacheslav Dokuchaev, Yury Eroshenko, and Alexey Smirnov. 2020. "Formation and Clustering of Primordial Black Holes in Brans-Dicke Theory" Universe 6, no. 10: 158. https://doi.org/10.3390/universe6100158
APA StyleBerezin, V., Dokuchaev, V., Eroshenko, Y., & Smirnov, A. (2020). Formation and Clustering of Primordial Black Holes in Brans-Dicke Theory. Universe, 6(10), 158. https://doi.org/10.3390/universe6100158






