Open-Charm Hadron Measurements in Au+Au Collisions at √sNN = 200 GeV by the STAR Experiment †
Abstract
1. Introduction
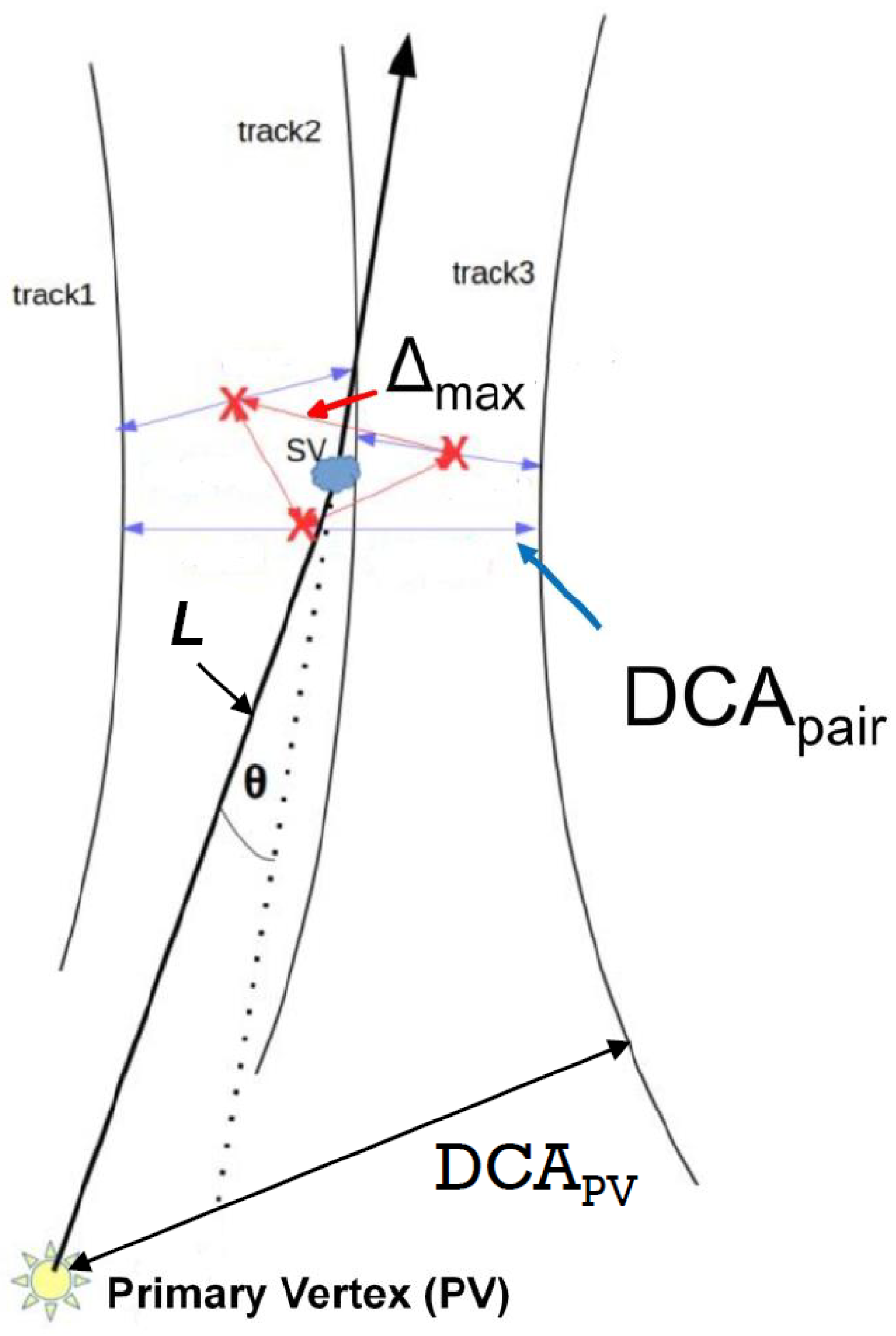
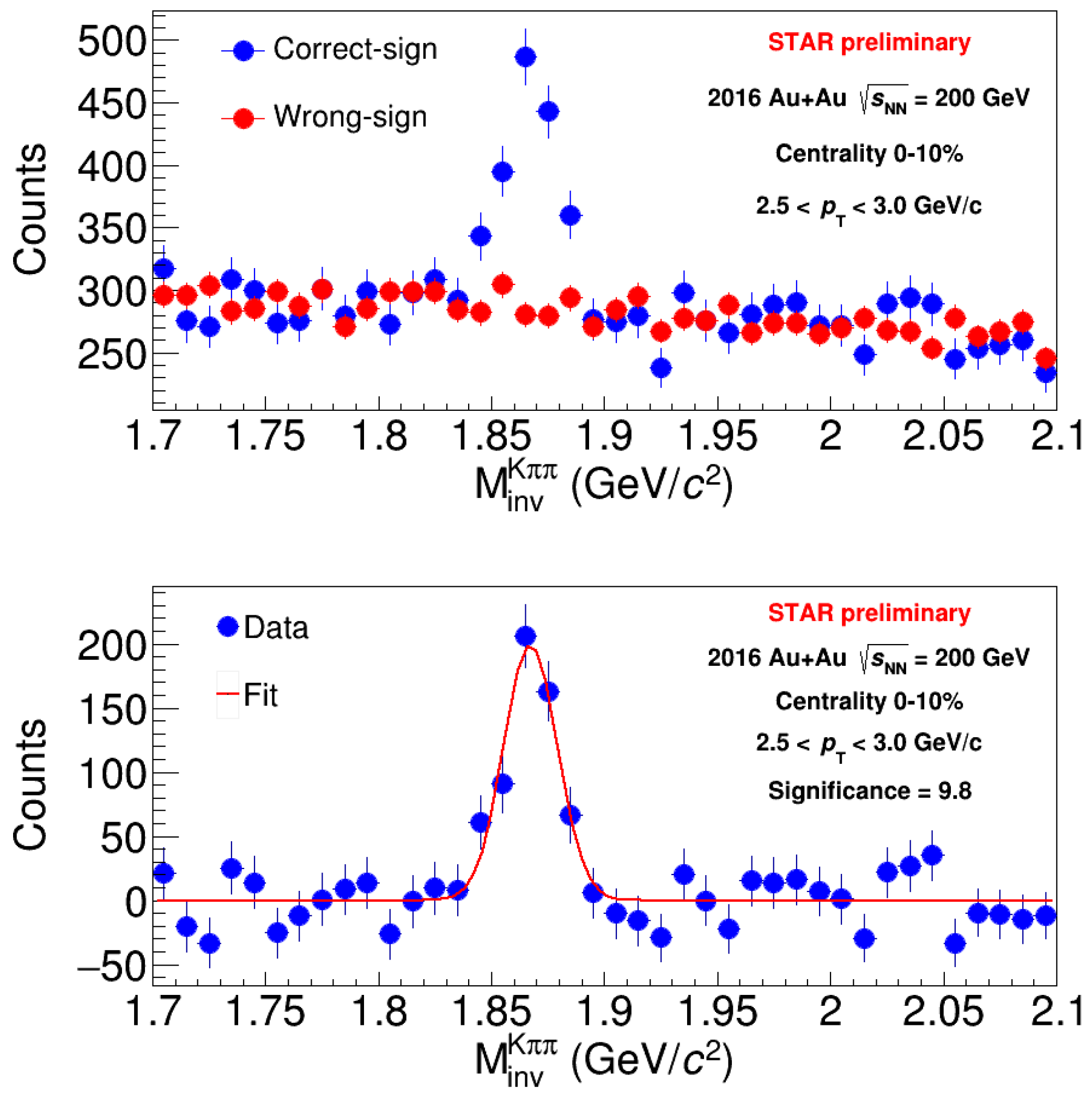
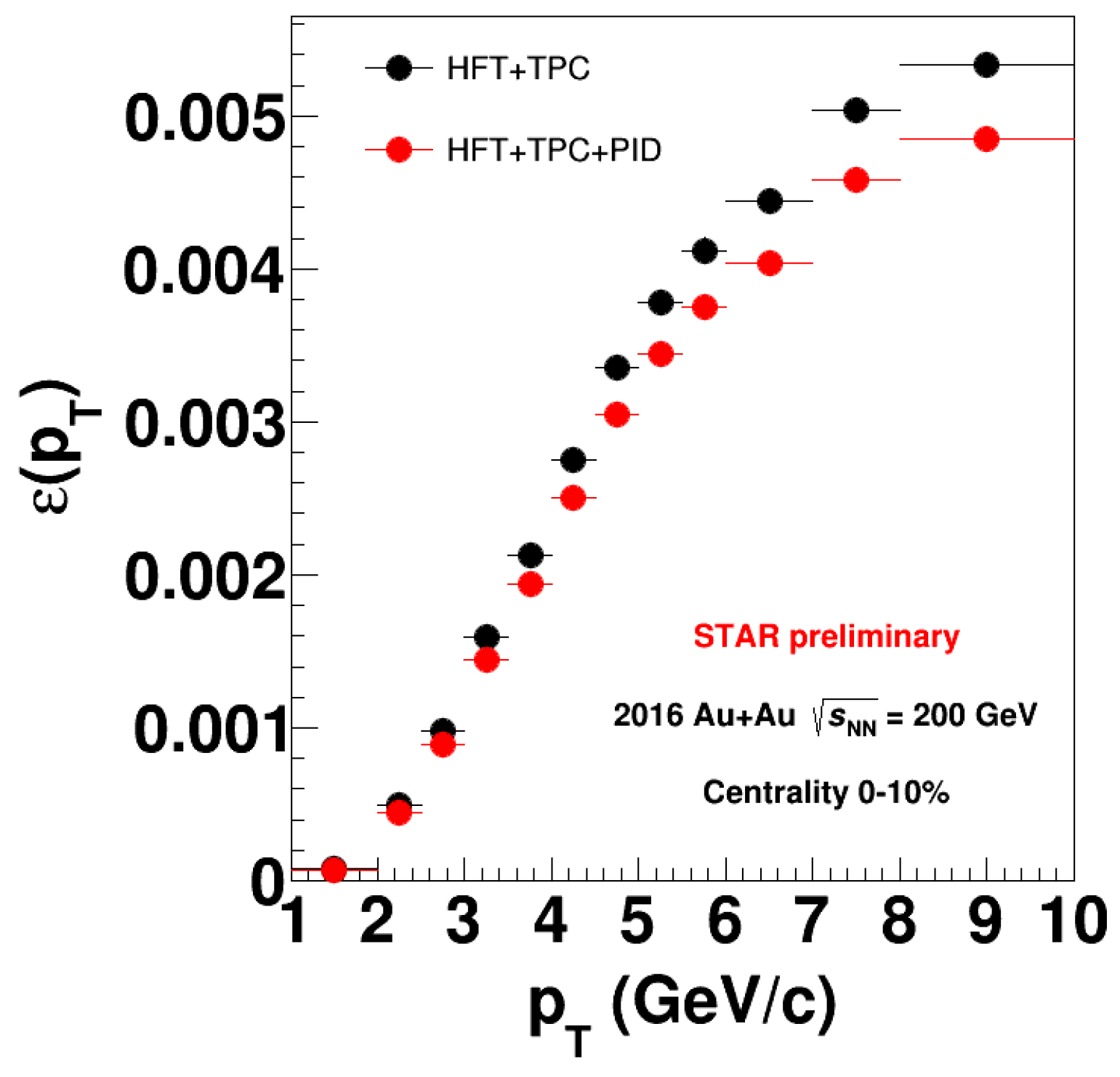
2. Open-Charm Measurements with the HFT
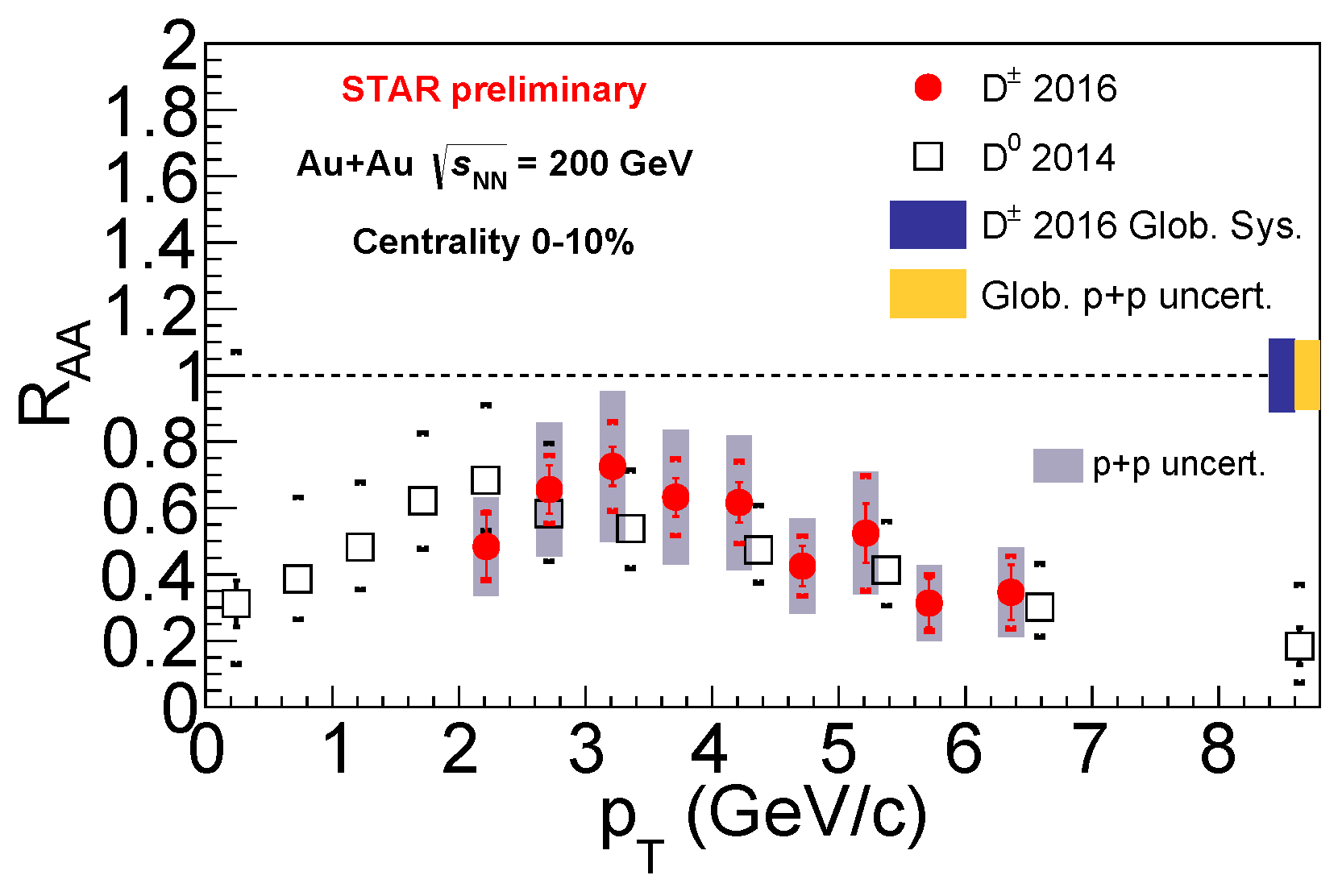
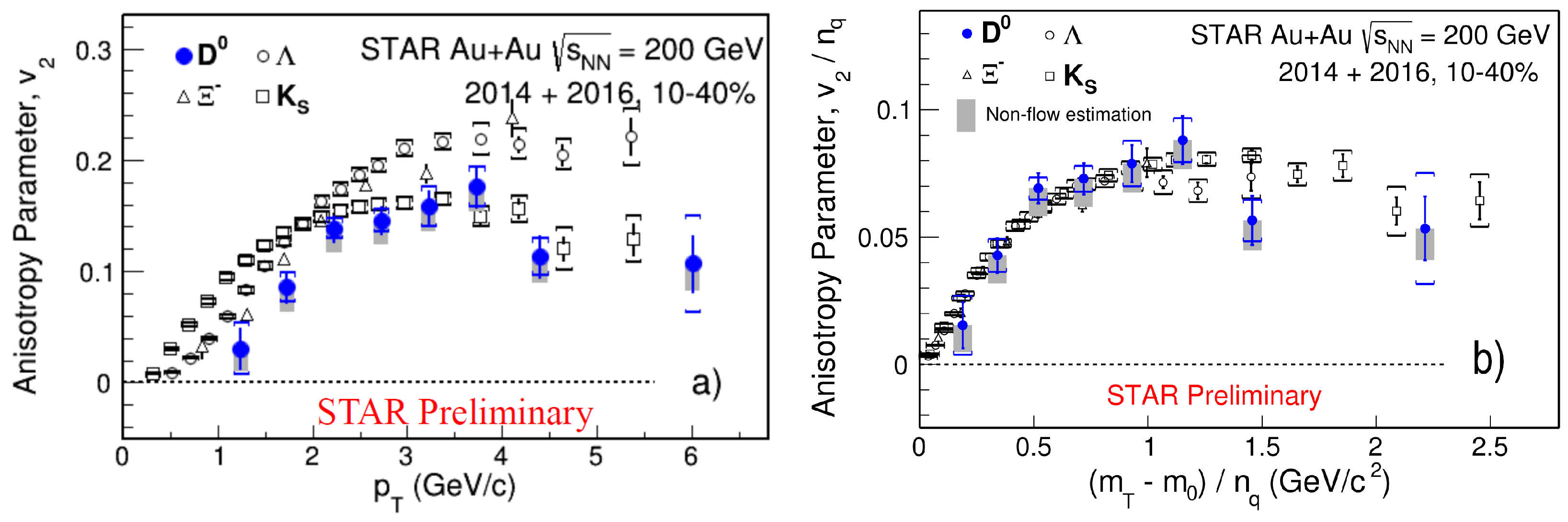
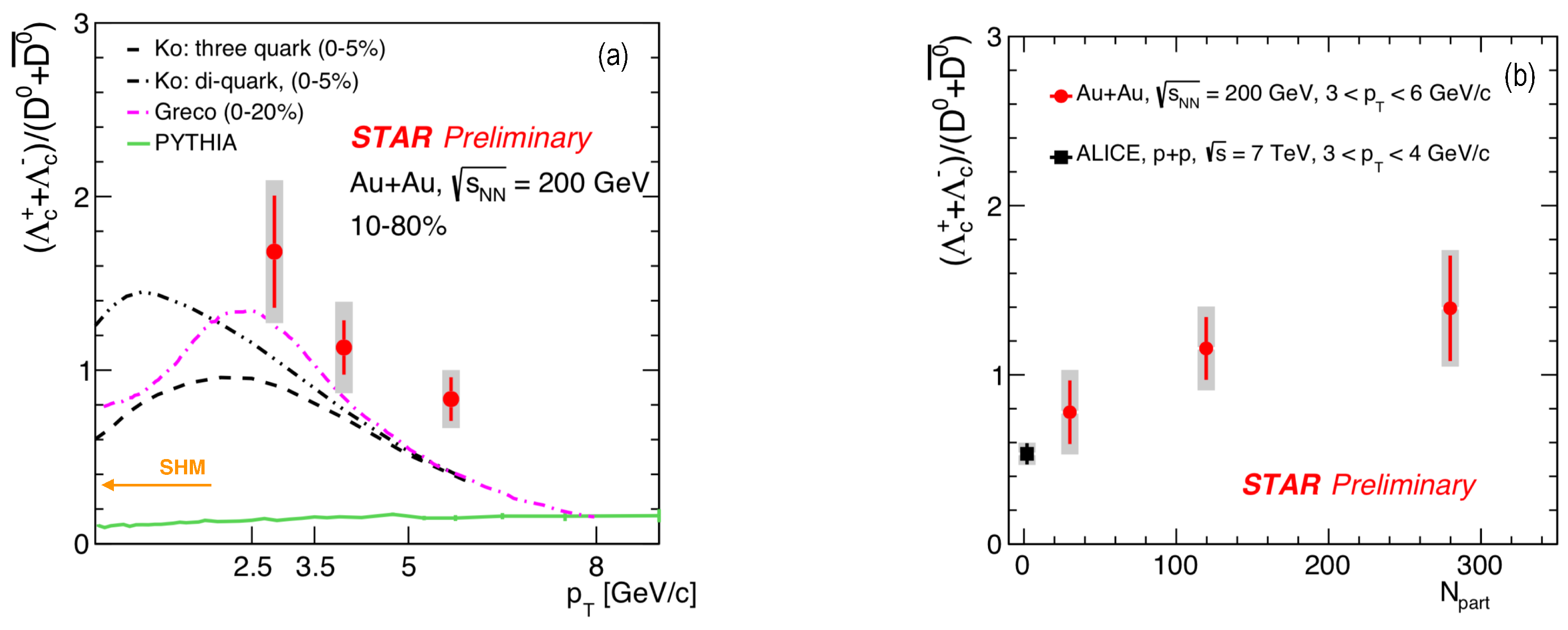
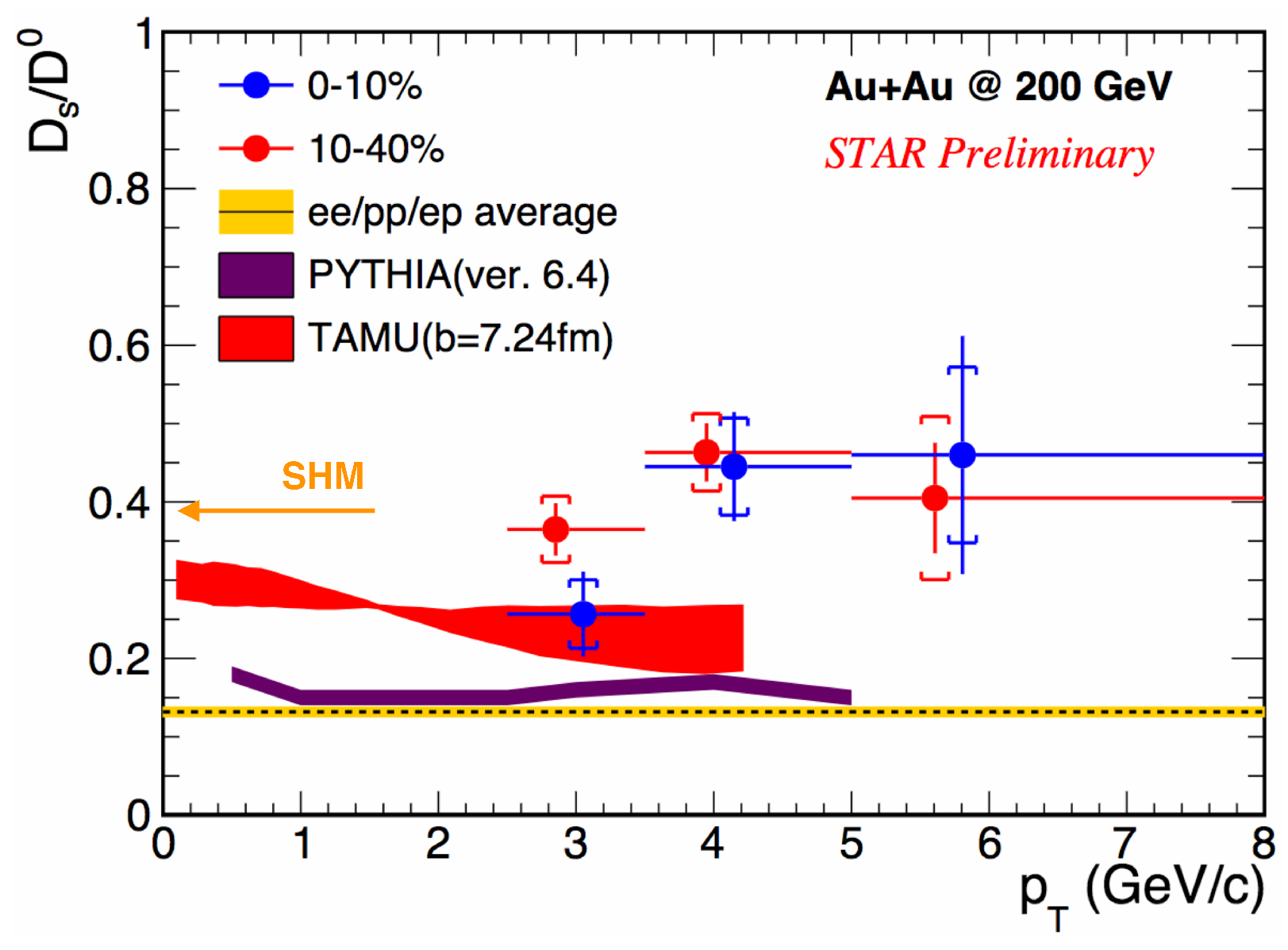
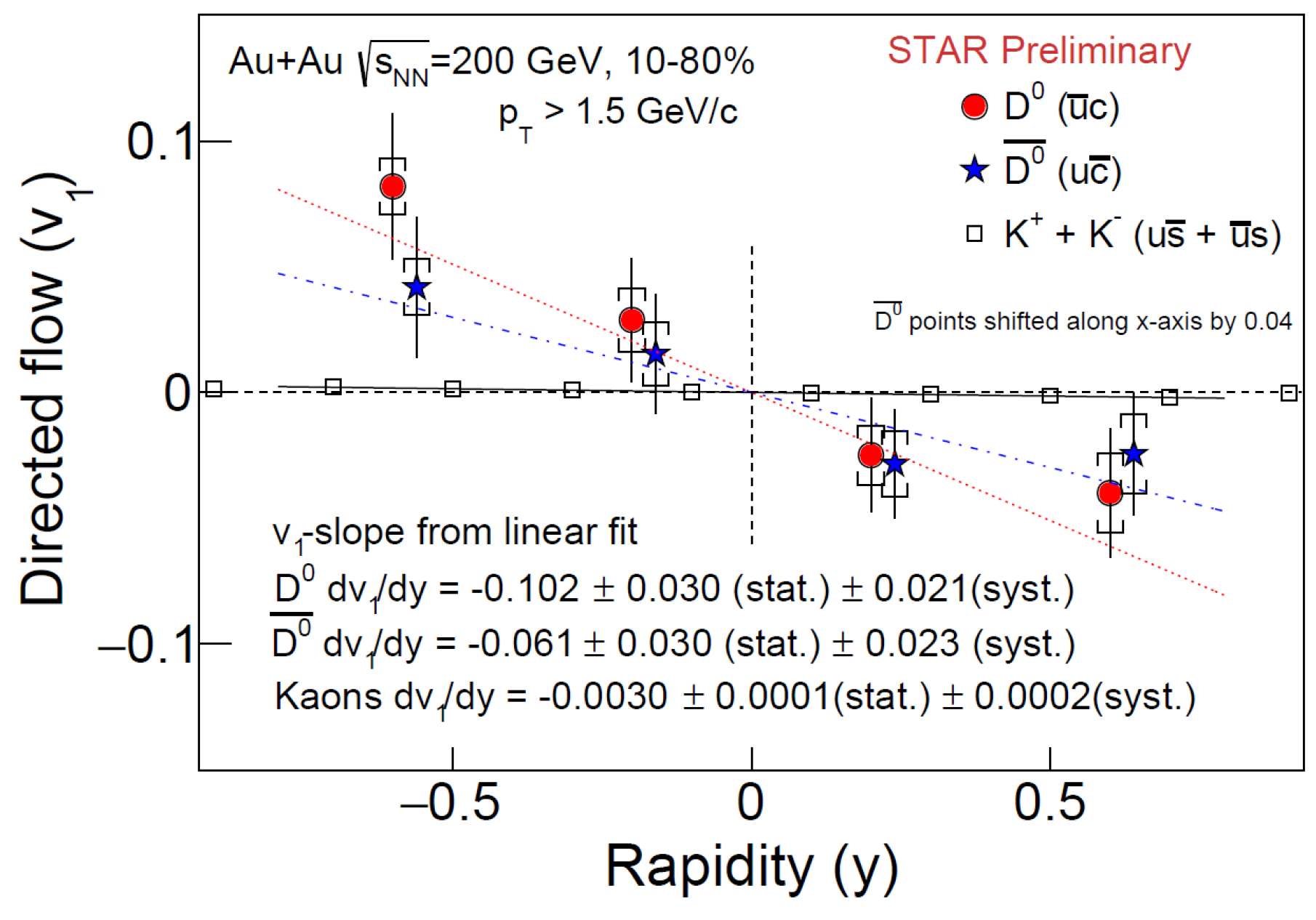
3. Results
4. Summary
Funding
Acknowledgments
Conflicts of Interest
References
- Miller, M.L.; Reygers, K.; Sanders, S.J.; Steinberg, P. Glauber modeling in high energy nuclear collisions. Ann. Rev. Nucl. Part. Sci. 2007, 57, 205–243. [Google Scholar] [CrossRef]
- Cao, S.; Luo, T.; Qin, G.Y.; Wang, X.N. Linearized Boltzmann transport model for jet propagation in the quark-gluon plasma: Heavy quark evolution. Phys. Rev. C 2016, 94, 014909. [Google Scholar] [CrossRef]
- Xu, Y.; Bernhard, J.E.; Bass, S.A.; Nahrgang, M.; Cao, S. Data-driven analysis for the temperature and momentum dependence of the heavy-quark diffusion coefficient in relativistic heavy-ion collisions. Phys. Rev. C 2018, 97, 014907. [Google Scholar] [CrossRef]
- Oh, Y.; Ko, C.M.; Lee, S.H.; Yasui, S. Ratios of heavy baryons to heavy mesons in relativistic nucleus-nucleus collisions. Phys. Rev. C 2009, 79, 044905. [Google Scholar] [CrossRef]
- Plumari, S.; Minissale, V.; Das, S.K.; Coci, G.; Greco, V. Charmed hadrons from coalescence plus fragmentation in relativistic nucleus-nucleus collisions at RHIC and LHC. Eur. Phys. J. C 2018, 78, 348. [Google Scholar] [CrossRef]
- Chatterjee, S.; Bożek, P. Large directed flow of open-charm mesons probes the three-dimensional distribution of datter in heavy-ion collisions. Phys. Rev. Lett. 2018, 120, 192301. [Google Scholar] [CrossRef]
- Das, S.K.; Plumari, S.; Chatterjee, S.; Alam, J.; Scardina, F.; Greco, V. Directed flow of charm quarks as a witness of the initial strong magnetic field in ultra-relativistic heavy ion collisions. Phys. Lett. B 2017, 768, 260. [Google Scholar] [CrossRef]
- Beavis, D.; Debbe, R.; Lee, J.H.; LeVine, M.J.; Scheetz, R.A.; Videbaek, F.; Xu, Z.; Bielcik, J.; Krus, M.; Dunkelberger, L.E.; et al. The STAR Heavy-Flavor Tracker, Technical Design Report. 2011. Available online: https://drupal.star.bnl.gov/STAR/starnotes/public/sn0600 (accessed on 6 September 2019).
- Tanabashi, M.; et al. [Particle Data Group] Review of particle physics. Phys. Rev. Lett. 2018, 98, 030001. [Google Scholar]
- Anderson, M.; Berkovitz, J.; Betts, W.; Bossingham, R.; Bieser, F.; Brown, R.; Burks, M.; Calderón de la Barca Sánchez, M.; Cebra, D.; Cherney, M.; et al. The STAR Time Projection Chamber: A unique tool for studying high multiplicity events at RHIC. Nucl. Instrum. Meth. A 2003, 499, 659–678. [Google Scholar] [CrossRef]
- Llope, W.J.; Zhou, J.; Nussbaum, T.; Hoffmann, G.W.; Asselta, K.; Brandenburg, J.D.; Butterworth, J.; Camarda, T.; Christie, W.; Crawford, H.J.; et al. The STAR Vertex Position Detector. Nucl. Instrum. Meth. A 2014, 759, 23–28. [Google Scholar] [CrossRef]
- STAR TOF Collaboration. Proposal for a Large Area Time of Flight System for STAR. 2004. Available online: https://drupal.star.bnl.gov/STAR/starnotes/public/sn0621 (accessed on 6 September 2019).
- Shao, M.; Barannikova, O.; Dong, X.; Fisyak, Y.; Ruan, L.; Sorensen, P.; Xu, Z. Extensive particle identification with TPC and TOF at the STAR experiment. Nucl. Instrum. Meth. A 2006, 558, 419–429. [Google Scholar] [CrossRef]
- TMVA Official. Available online: http://tmva.sourceforge.net (accessed on 23 July 2019).
- Adam, J.; et al. [STAR Collaboration] Centrality and transverse momentum dependence of D0-meson production at mid-rapidity in Au+Au collisions at . Phys. Rev. C 2019, 99, 034908. [Google Scholar] [CrossRef]
- Adamczyk, L.; et al. [STAR Collaboration] Measuremets of D0 and D★ production in p+p collisions at . Phys. Rev. D 2012, 86, 072013. [Google Scholar] [CrossRef]
- Adamczyk, L.; et al. [STAR Collaboration] Measurement of D0 azimuthal anizothropy at midrapidity in Au+Au collisions at . Phys. Rev. Lett. 2017, 118, 212301. [Google Scholar] [CrossRef] [PubMed]
- Abelev, B.I.; et al. [STAR Collaboration] Centrality dependence of charged hadron and strange hadron elliptic flow from Au+Au collisions. Phys. Rev. C 2008, 77, 054901. [Google Scholar] [CrossRef]
- Andronic, A.; Braun-Munzinger, P.; Redlich, K.; Stachel, J. Statistical hadronization of charm in heavy-ion collisions at SPS, RHIC and LHC. Phys. Lett. B 2003, 571, 36–44. [Google Scholar] [CrossRef]
- Acharya, S.; et al. [The ALICE Collaboration] production in pp collisions at and in p-Pb collisions at . J. High Energ. Phys. 2018, 2018, 108. [Google Scholar] [CrossRef]
- Lisovyi, M.; Verbytskyi, A.; Zenaiev, O. Combined analysis of charm-quark fragmentation-function measurements. Eur. Phys. J. C 2017, 76, 397. [Google Scholar] [CrossRef]
- He, M.; Fries, R.J.; Rapp, R. Ds Meson as a quantitative probe of diffusion and hadronization in nuclear collisions. Phys. Rev. Lett. 2013, 110, 112301. [Google Scholar] [CrossRef]
- Chatterjee, S.; Bozek, P. Interplay of drag by hot matter and electromagnetic force on the directed flow of heavy quarks. arXiv 2018, arXiv:1804.04893. [Google Scholar]
- Adamczyk, L.; et al. [STAR Collaboration] Beam-energy dependence of directed flow of , , , , and ϕ in Au+Au collisions. Phys. Rev. Lett. 2018, 120, 062301. [Google Scholar] [CrossRef] [PubMed]
| 1 | The HFT consists of total of four layers of silicon detectors. The two innermost layers are Monolithic Active Pixel Sensors (MAPS), PXL1 and PXL2. The outer layers are strip detectors, the Intermediate Silicon Tracker (IST) and the Silicon Strip Detector (SSD). |
| 2 | This method is sufficient for D analysis. In case of e.g., D or , the correlated background needs to be addressed separately as it is more significant for those analyses. |
| 3 | For combinatorial reasons, there are approximately three times as many wrong-sign charge combinations as the correct-sign ones in this case. The wrong-sign spectrum is therefore scaled so that it matches the correct-sign one in order to estimate the combinatorial background. The scale factor is determined from ratio of integrals of the correct and wrong-sign spectrum outside the D mass peak region which is set . |
| Decay Channel | [%] | |
|---|---|---|
| D K | ||
| D K | ||
| D K K | ||
| Kp |
| Event selection | |||
| Track selection | |||
| HFT tracks = PXL1 + PXL2 + (IST or SSD) | |||
| Particle identification | TPC | ||
| TOF | |||
| Decay topology | |||
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vanek, J. Open-Charm Hadron Measurements in Au+Au Collisions at √sNN = 200 GeV by the STAR Experiment. Universe 2019, 5, 196. https://doi.org/10.3390/universe5090196
Vanek J. Open-Charm Hadron Measurements in Au+Au Collisions at √sNN = 200 GeV by the STAR Experiment. Universe. 2019; 5(9):196. https://doi.org/10.3390/universe5090196
Chicago/Turabian StyleVanek, Jan. 2019. "Open-Charm Hadron Measurements in Au+Au Collisions at √sNN = 200 GeV by the STAR Experiment" Universe 5, no. 9: 196. https://doi.org/10.3390/universe5090196
APA StyleVanek, J. (2019). Open-Charm Hadron Measurements in Au+Au Collisions at √sNN = 200 GeV by the STAR Experiment. Universe, 5(9), 196. https://doi.org/10.3390/universe5090196




