1. Introduction
Primordial quantum fluctuations occurring in the preinflationary epoch have left indelible imprints which we measure today in the form of tiny temperature anisotropies,
∼
, in the Cosmic Microwave Background (CMB) radiation. The inflationary mechanism furnishes a simple explanation for the presence of these anisotropies [
1] and it has become a paradigm in the description of the primordial evolution of the universe within the standard cosmological model.
The spectrum of the CMB reproduces an almost perfect black-body radiation at an average temperature
∼
K. The distribution of temperature fluctuations in the CMB is described by the power spectra of scalar and tensorial perturbations. These spectra are essentially characterized by two parameters: The spectral index
, giving information on the scale dependence of the power spectrum of scalar fluctuations; and the tensor-to-scalar ratio
r, measuring the suppression of tensorial perturbations against the scalar ones. The values of the spectral index
, and tensor-to-scalar ratio
r, can be obtained from the observational data. In particular, the most recent observations to date [
2] constrain the spectral index to be
at
CF, and limit the tensor-to-scalar ratio to values
. Note that, although the scalar power spectrum is almost scale-invariant, perfect scale invariance, corresponding to
, seems to be excluded.
The extraordinary predictive power of the inflationary scenario, combined with the current limits on the determination of
r, makes it difficult to distinguish between different models of cosmic inflation [
3]. The simplest inflationary model capable of explaining the current observational data is the Starobinsky model [
4]. In the Einstein frame, the only free parameter of the model is the inflaton mass, and this mass is fixed by the normalization of the amplitude of the scalar power spectrum [
2]. In addition, the Starobinsky Lagrangian is conformally equivalent to Einstein gravity coupled to the Standard-Model Higgs boson by means of the nonminimal interaction term
[
5,
6], making this model particularly interesting.
Although Starobinsky inflation and other models characterized by an inflationary potential with a plateau are favored by observations [
2], it has been argued that they might reintroduce the fine-tuning problems that inflation is supposed to solve, resulting in the so-called “unlikeness problem” [
7]. In fact, the upper bound on the tensor-to-scalar ratio arising from the CMB data lowers the scale of inflation down to ∼
, and a proper resolution of the flatness and horizon problems requires an inflationary potential with
∼
[
7]. A more fundamental understanding of inflation and its role in the cosmological evolution of the universe thus requires these inflationary models to be understood and embedded in a more general framework, explaining the origin of the plateau based on first principles, e.g., on short-distance modifications of General Relativity due to quantum gravity.
Adopting the Wilsonian point of view, a quantum field theory is well-defined and predictive if its renormalization group flow is equipped with an ultraviolet fixed point, endowed with a finite-dimensional basin of attraction. This fixed point, ensuring the renormalizability of the theory [
8], can be Gaussian (GFP), corresponding to a free theory; or non-Gaussian (NGFP). In the latter case, the fundamental theory is interacting and termed “asymptotically safe”. As shown by numerous computations [
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23,
24,
25,
26,
27] employing functional renormalization group (FRG) techniques [
28,
29], the gravitational RG flow could attain a NGFP in the ultraviolet limit. The asymptotic-safety mechanism would hence allow to quantize gravity in the well-established framework of quantum field theory.
In these proceedings, we exploit the consequences of the existence of a gravitational fixed point in cosmological contexts. To this end, we will use the toy model constructed in [
30], where an effective action for inflation was derived from the renormalization group improvement of the Einstein–Hilbert action (see also [
31,
32,
33,
34,
35,
36,
37]). Using the equivalence of the description in the Jordan and Einstein frames, it will be shown explicitly that a period of slow-roll inflation can be generated by the departure of the RG flow from the scale-invariant regime associated with the cosmological “fixed-point era” [
31,
38]. We will show that this scenario has two important consequences. First of all, the generation of a nearly-scale-invariant power spectrum of scalar perturbations in the CMB can be seen as a relict of the nearly-scale-invariant behavior of the gravitational RG flow in the vicinity of its ultraviolet attractor. In this scenario, the inflationary potential is characterized by a plateau region—however, due to the running of the gravitational couplings, the bound on the tensor-to-scalar ratio might not necessarily reintroduce the fine-tuning problems discussed in [
7]. Secondly, the inflationary potential depends on universality properties of the gravitational interaction and therefore, compatibility with observations can constrain the way the RG trajectories depart from the fixed point and put bounds on the corresponding critical exponents [
30].
This paper is organized as follows. In
Section 2, we review key features of Asymptotically Safe Gravity and introduce a variant of the RG-improved model constructed in [
30].
Section 3 discusses the conformal representation of RG-improved theories and their relation to observations. Assuming that the dynamics and output of cosmic inflation are determined solely by the quantum fluctuations of the spacetime, in
Section 4, we provide a simplified but explicit explanation of how a period of slow-roll inflation can be triggered by the departure of the RG flow from the scale-invariant regime defined by the interacting fixed point. Finally,
Section 5 summarizes our conclusions.
2. Running Couplings and Effective Actions
In the
-theory-space, the beta functions for the dimensionless Newton coupling
and cosmological constant
are determined by the projection of the functional renormalization group equation (FRGE) [
29,
39,
40] on the Einstein–Hilbert subspace. The renormalization group equations for
and
can generally be written as:
where
is the anomalous dimension of the Newton coupling. A nontrivial fixed point
exists if
vanishes and at the same time the anomalous dimension
flows to
. The existence of a non-Gaussian fixed point (NGFP) thus entails an effective dimensional reduction from
to
spacetime dimensions [
41,
42]. This property seems to be a common prediction of several approaches to quantum gravity [
43,
44,
45,
46]. A key consequence of this dimensional reduction is a modification of the graviton propagator at short distances. Under certain approximations, it scales as
∼
for
[
41] and gives rise to a scale-invariant scalar power spectrum [
38,
41,
47,
48]. It is thereby possible that the nearly-scale-invariant power spectrum of temperature fluctuations in the CMB arises from the nearly-scale-invariant regime following the NGFP epoch. In order to understand if and under which conditions this mechanism is realized, it is important to study the departure of the renormalization group (RG) flow from its ultraviolet fixed point.
The universality properties of the RG flow about the nontrivial fixed point
are determined by the stability matrix
. Denoting by
its eigenvectors; and by
the corresponding eigenvalues, the running of the dimensionless gravitational couplings about
can be written as:
where
∼
is the reduced Planck mass.
The NGFP typically found in the functional renormalization group (FRG) computations in the Einstein–Hilbert truncation is characterized by
and
. The positivity of the real part of the universal critical exponents
indicates that, in the aforementioned truncation, the fixed point
is endowed with two relevant directions. FRG computations in higher-order truncations show that there might be one more relevant direction, associated with 4th-order derivative operators. These relevant directions identify the UV critical surface. The NGFP can thus act as an ultraviolet “sink” for the RG trajectories belonging to its basin of attraction. The constants
are integration constants, corresponding to different initial conditions of the flow. Every pair
identifies a particular RG trajectory. These free parameters should be fixed by equating the infrared values of the dimensionful running couplings
and
with the values of the Newton and cosmological constants at observational scales, namely
∼
and
∼
. This comparison allows selection of the particular RG trajectory realized by nature [
49].
Starting from a classical action of the form:
the introduction of quantum effects typically results in the emergence of higher-derivative terms. The renormalization effects thus modify the interactions of the theory and, as a consequence, the coupling constants appearing in the bare Lagrangian turn into running functions of the energy (or length) scale. Reversing the argument, replacing the coupling constants in the classical action with running functions and promoting the corresponding energy-scale to a proper coordinate-dependent quantity
should provide an effective action which mimics, at least qualitatively, the effects of quantum loops [
28,
50]. Neglecting the running of the matter couplings, the scale-dependent version of the action
is:
and the corresponding field equations read [
50]:
Here,
is the Einstein tensor,
, and
is an effective energy-momentum tensor generated by the running of the Newton coupling [
50].
Assuming that there is no energy-momentum flow between the gravitational and matter components of the theory, i.e., that the energy-momentum tensor
is separately conserved, the momentum-scale
is determined by a set of of consistency conditions dictated by the Bianchi identities [
50,
51,
52,
53,
54]. In particular, diffeomorphism invariance requires [
51,
53,
54]:
In the fixed-point regime, the scaling of the dimensionful Newton: coupling and cosmological constant read:
Combining Equation (7) with the constraint (6) yields [
53,
54]:
A similar relation should also hold when additional operators of the form
are added to the bare Lagrangian, at least in the fixed-point regime [
53].
The replacement
in the scale-dependent action
generates an effective
action, whose analytical expression is determined by the running of the gravitational couplings [
34,
53,
55]. In particular, in the vicinity of the NGFP, the running
leads to the following effective action [
30]:
where the fixed-point action is given by [
53]:
and the coefficients
read [
30]:
In what follows, the critical exponents
will be assumed to be real numbers, as indicated by computations of the gravitational RG flow in the presence of matter fields [
25,
56].
The combination of the scaling relation (
8) with the scale-dependent Einstein–Hilbert action (
4) correctly reproduces the fixed-point Lagrangian
∼
found in the study of the renormalization group flow of
-gravity theories [
20,
57,
58]. Notably, in cosmological contexts, the action
∼
gives rise to a perfectly scale-invariant power spectrum,
(flat inflationary potential). By lowering the energy-scale
∼
R towards the infrared, the gravitational RG flow departs from the fixed-point regime and generates additional operators in the Lagrangian,
. As is clear from Equation
, the form of the deviation
depends crucially on the running of the gravitational couplings. Therefore, the study of the inflationary scenario arising from the RG-improvement of the Einstein–Hilbert action might actually put constraints on microscopic details of the theory—for instance, its critical exponents [
30,
37]. Moreover, the nearly-scale-invariant power spectrum of temperature anisotropies in the CMB might be related to the deviation of the Lagrangian
from the scale-invariant regime described by
. This will be shown explicitly in the following sections.
3. Conformal Representation of RG-Improved f(R) Theories
Replacing the running couplings in the scale-dependent action
yields an effective gravitational action of the form:
Provided that
, and introducing the field
, this action can be re-expressed as:
where the function
is given by:
It is now convenient to perform a conformal transformation, mapping the metric
in the Jordan frame to the metric
in the Einstein frame. Rescaling the metric
by the conformal factor
maps the purely gravitational theory
to General Relativity (i.e., Einstein–Hilbert action) minimally coupled to the scalar field
:
The scalar degree of freedom, introduced by the function in the Jordan frame, can thus be seen as a scalar field subject to the potential in the Einstein frame.
Due to the coupling to gravity, and depending on the form of the potential
, the time evolution of the scalar field
might lead to a period of inflation. In fact, specializing the metric
to that of a Friedmann–Lemaıtre–Robertson–Walker (FLRW) universe, the time evolution of the scalar field
and the growth of the scale factor
are related to each other and are described: by the following Friedmann and Klein–Gordon equations:
In the slow-roll approximation, the kinetic energy of the inflation field is negligible—
and
. Note that the reliability of the slow-roll approximation is corroborated by the recent Planck data which, so far, have not found hints for inflationary dynamics beyond slow roll [
2].
The first and second variations of the potential define the slow-roll parameters:
The slow-roll conditions
and
are satisfied when the evolution of the scalar field
along its potential
is slow in comparison to the rate of exponential expansion of the universe. The violation of the slow-roll conditions, encoded in the equation
, defines the value of the field at the end of inflation,
. Fixing the number of e-folds before the end of inflation:
to
[
1], provides the initial condition
. The spectral index and tensor-to-scalar ratio:
are determined by the values of the slow-roll parameters at the beginning of the period of exponential growth of the universe, i.e., at
. Therefore, under the slow-roll approximation, the theoretical values
can be determined and compared to the values provided by the analysis of the observational data on the anisotropies of the CMB.
Finally, for a single-field inflationary model with inflationary potential
, the amplitude of the primordial scalar power spectrum takes the form [
2]:
Every inflationary model has to be normalized in order to fit this value (see [
3] for details), and this normalization puts constraints on the scale of inflation.
For instance, for inflationary potentials with a plateau, inflation is assumed to start from the plateau region, so that
—
m being the “inflaton mass” defined via
. In these cases, the normalization (
21) constrains the order of magnitude of the inflaton mass to
[
3].
4. The Inflationary Mechanism in Asymptotically Safe Gravity
The RG-improved
-type action
and the corresponding scalar potential
in the Einstein frame, depend on the critical exponents
. Here, we assume that the density fluctuations at the last scattering surface are generated by the amplification of quantum-gravity fluctuations in the preinflationary era. Hence, requiring the compatibility of the inflationary dynamics generated by the effective action
with the Planck data constrains the universality properties of the theory in the vicinity of the NGFP. Moreover, since the gravitational critical exponents
are influenced by the presence of matter [
25,
56,
59], the conditions on the critical exponents imposed by compatibility with observations could be used, at least in principle, to identify the primordial matter content of universe [
30]. We remark however, that the current systematic uncertainties on the computation of the critical exponents are still too large to put strong constraints on the matter content of the early universe based on the aforementioned conditions on the critical exponents.
The fixed-point regime is described by the action
. Following the procedure described in the previous section, it is not difficult to see that the fixed-point action
is conformally equivalent to a scalar-tensor theory (4), where the scalar field
is minimally coupled to gravity and subject to the constant potential:
The fixed-point potential
should give rise to a perfectly scale-invariant scalar power spectrum. However, as the RG flow moves away from the NGFP, additional operators are generated and the potential
is dynamically modified by this running:
The deviation
of the scalar potential from its fixed-point value
is determined by the function
and, in accordance with the simple RG-improved model introduced above, depends on the critical exponents
. Its analytical form can be determined by performing a conformal transformation of the original
theory, as detailed in
Section 3. As already mentioned, we assume the critical exponents to be real numbers. The results are displayed in
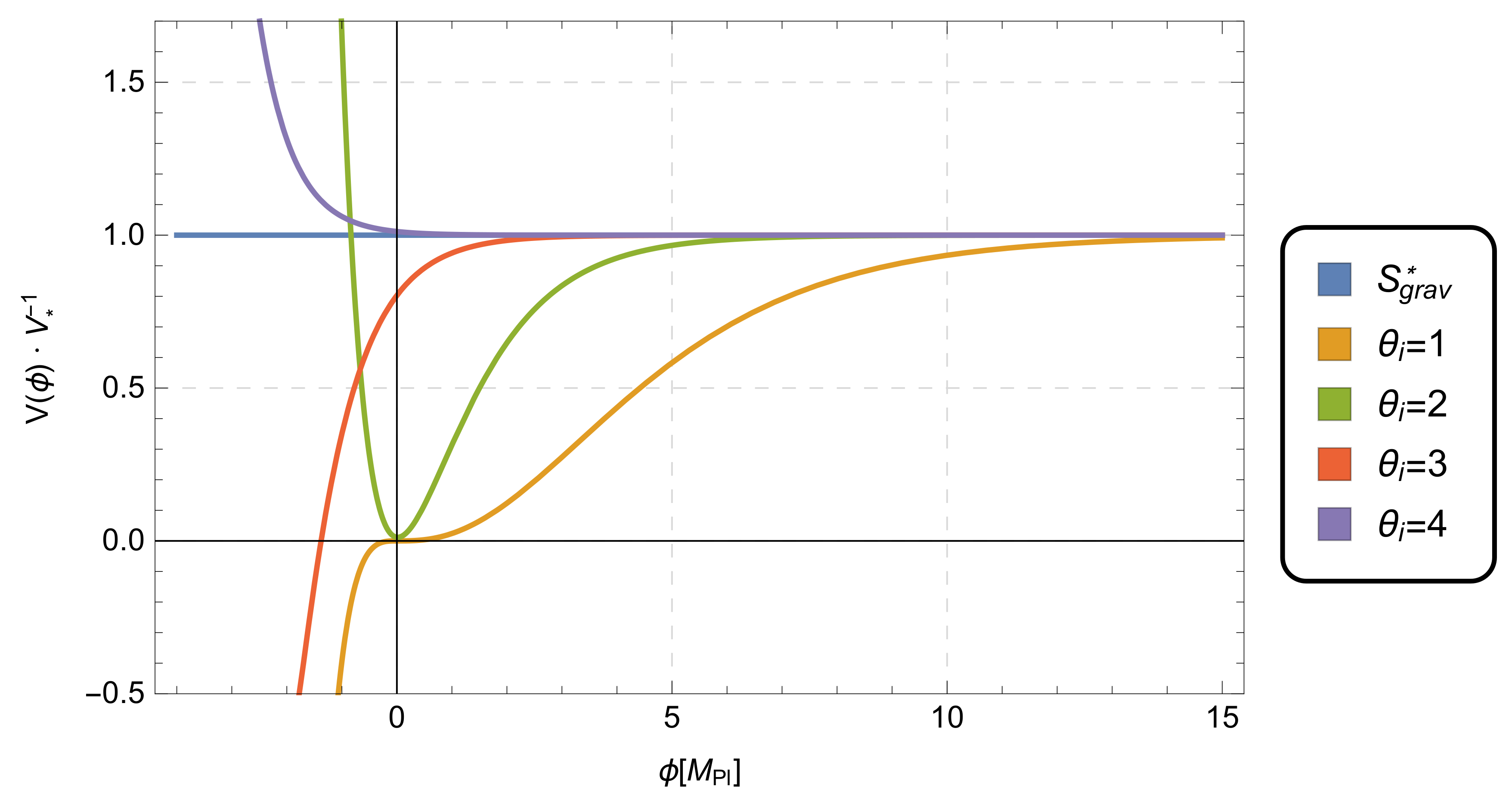
Figure 1 for the special case
, and for
taking values
. These bounds are justified as follows:
Note that, due to the structure of the function
and provided that
, the
term in the action (4) does not gain any additional contribution from the operators in
(at least in the regime where the couplings scale as in Equation (
2)). Therefore, its coefficient inherits the universality properties of the fixed-point action
and defines a mass scale:
determined by the universal product
[
60], which is typically
. It is interesting to notice that when higher derivative operators:
are included in the ansatz for the bare action,
being dimensionless couplings, the RG-improvement generated by the consistency Equation (
8) preserves the structure of the fixed-point effective action. Specifically,
will maintain its pure
-form, while the mass scale
m will be corrected by the presence of other fixed-point quantities. Assuming that a UV-attractive NGFP persists in arbitrary large truncations, the new fixed-point potential
yields the mass scale:
The general form of the RG-improved action (
9) is preserved as well, but a contribution from the critical exponent
due to the additional relevant operator
should appear: The normalization of the scalar CMB power spectrum dictated by Equation (
21) implies a nontrivial constraint on the fixed-point values of the dimensionless couplings
,
As functional RG computations indicate that
[
60], the sum in the denominator would be required to be very large in order to fit observations. On the other hand, going beyond the fixed-point approximation introduced in
Section 2 modifies the scaling relations (
2). If the integration of fast-fluctuating modes generates additional contributions to the
-operator (or, equivalently, if the coupling to the
operator runs), the “plateau scale” (
26) will be dynamically modified by the departure of the flow from the fixed-point regime. In this case, the initial conditions for inflation would be defined by the fixed-point mass scale (
26), which can even be Planckian, while the amplitude of the scalar fluctuations at the horizon exit, Equation (
21), would be fixed by the “renormalized” plateau scale. If this dynamical-plateau mechanism is realized, it could provide a solution to the “unlikeness problem” raised in [
7]. As addressing this question goes far beyond the purpose of these proceedings, in what follows, we will restrict ourselves to the fixed-point approximation introduced in
Section 2.
The departure from the fixed-point regime causes an instability of
and results in a scalar potential
whose first derivative is nonzero at
∼
. As a consequence, even if
in the NGFP era, the inflaton field acquires a nonzero kinetic energy,
∼
, which provides an initial boost towards the subsequent time evolution of the universe. In particular, depending on the shape of the potential, this mechanism can potentially trigger a period of slow-roll inflation, the growth of the scale factor
being controlled by the function
according to Equation
. Particularly interesting is the case
, which realizes a Starobinsky-like potential (see
Figure 1):
in the presence of an effective cosmological constant
. As it is well known, this model leads to cosmic parameters:
in good agreement with the Planck data. The case
is a limiting case, where the function
reduces to a constant term
plus an additional
operator. Operators of the form
, with
, are suppressed at curvature scales
and hence do not contribute to the inflationary dynamics [
30]. Overall, neglecting the
contribution to the action
, the inflationary potential can be approximated by:
This potential has no local minima and, depending on the sign of
, diverges to
as
. As a consequence, no reheating phase by standard parametric-oscillations of the inflaton field is possible, and a new mechanism to reheating the universe after inflation would be required. The spectral index and tensor-to-scalar ratio generated by the class of potentials
read:
Assuming
, these numbers are compatible with observations if
is sufficiently small and negative. Note that, in principle, the presence of a negative
at inflationary scales is not necessarily incompatible with the current phase of accelerated expansion of the universe. In fact, for
, the approximation (2) breaks down and additional operators start contributing to the scale-dependent action (4). In particular, operators of the form
start playing a role at cosmological scales and could overcome the effects of a negative cosmological constant—and drive the late-time evolution of the universe towards the current phase of accelerated expansion [
61]. The case of a positive effective cosmological constant, with
, would instead lead to a spectral index
and not allow for a “natural” exit from the inflationary phase by violation of the slow-roll conditions. In this case, compatibility with the Planck data would rather constrain the ultraviolet value of the cosmological constant to be negative,
(see also [
25,
30,
62,
63]). Within the present fixed-point approximation, where the inflaton mass is defined by Equation (
24), a negative ultraviolet cosmological constant would entail the presence of a tachionic inflaton field. This result seems in contradiction with [
30], where the
avoidance of a tachionic inflaton field required
. This mismatch is caused by a different ratio
—in [
30], the infrared cutoff
k was related to the Ricci scalar by means of an unspecified positive constant
,
. The inflaton mass is thus given by
, and is positive for arbitrary values of
only when
. However, if
sets the scale of Quantum Gravity according to Equation
, then
is no longer an arbitrary constant, and our result
is recovered.
5. Conclusions
According to the Asymptotic Safety conjecture, in the deep ultraviolet, the gravitational interaction reaches a scale-invariant regime due to the existence of a nontrivial fixed point of the renormalization group (RG) flow. In these proceedings we have reviewed some key consequences of the existence of a fixed-point epoch in the “RG-improved” cosmological evolution of the universe.
Assuming that the running of the gravitational couplings can be incorporated into the classical spacetime dynamics by means of a scale-dependent infrared cutoff
, a period of slow-roll inflation can be associated with the displacement of the RG flow from the regime where the theory is scale invariant. Following [
51,
53,
54], the invariance of the theory under diffeomorphisms requires the scale-dependent cutoff
to vary at the same rate as the scalar curvature
R. Starting from a scale-dependent Einstein–Hilbert action, the replacement
generates an effective
-Lagrangian of the form
, where
∼
is realized at the fixed point, in accordance with several FRG computations [
20,
57,
58], and
introduces additional operators, mimicking the effect of a Wilsonian RG flow—although, starting from a simple bare theory at the fixed point, at lower energy scales the effective degrees of freedom interact through more complicated interactions, generated by the integration of high-frequency fluctuating modes in the functional integral. This mechanism could provide a simple explanation for the origin and distribution of the temperature fluctuations of the Cosmic Microwave Background (CMB). The fixed-point action
, in fact describes a scale-invariant gravitational theory and, in the Einstein frame, corresponds to Einstein gravity coupled to a scalar degree of freedom whose interaction potential is constant,
. This potential defines the universal mass scale
∼
. The departure from the fixed-point regime destabilizes the fixed-point potential
, the correction
corresponding to the variation
of the gravitational Lagrangian caused by the Wilsonian RG flow. Specifically, for
, the scalar potential develops a minimum or diverges. The region
remains instead unaffected: The renormalized scalar potential
is characterized by a plateau region, where
∼
, relict of the fixed-point epoch. The nearly-scale-invariant scalar power spectrum is thus understood as the result of the nearly-scale-invariant behavior of gravity in the vicinity of the ultraviolet fixed point.
In the RG-improved model introduced in [
30] and revisited here, the RG running of the couplings is approximated by their scaling about the nontrivial fixed point. Due to this approximation, the variation
does not yield additional
operators, and leaves the mass scale
∼
unaffected. In a more complete description, accounting for the full running of the couplings and possibly including higher-derivatives operators in the action, we expect the coupling of the quadratic term
to run and to redefine the plateau scale [
36]. The scale of inflation is then determined by the renormalized plateau. This dynamical-plateau scenario would allow to setup the initial conditions for inflation at Planckian energies, where the scalar potential is constant and
, while being able to reproduce the correct amplitude of scalar perturbations at the horizon exit. This mechanism could provide a solution to the “unlikeness problem” raised in [
7]. However, this behavior is not captured by the simple RG-improved model reviewed here, and addressing this problem requires going beyond the fixed-point approximation employed in the present proceedings.
The departure of the RG flow from the fixed-point regime induces a scalar potential
characterized by a plateau, and can potentially trigger a period of slow-roll inflation. The specific form of the potential
depends on universality properties of the gravitational RG flow and, as a consequence, a comparison with the observational data can put constraints on the gravitational critical exponents [
30]. Specifically, since the power spectrum of primordial scalar perturbations is almost scale-invariant but not exactly scale-invariant, at least one of the critical exponents must be
. Among the class of inflationary models derived from the action (4), the case
reproduces the well-known Starobinsky model and is thereby compatible with observations.
It would be interesting to understand if similar conclusions can be drawn by using a self-consistent RG-improvement [
64] of the classical cosmological solutions. In a first approximation, it has been shown that the anti-screening character of the Newton coupling could replace the classical initial singularity with a regular bounce or with an emergent universe scenario [
62], both characterized by a nonvanishing minimum value of the scale factor and a period of inflation following the bounce. Finding the class of actions giving rise to this type of regular cosmologies is the first step towards understanding the relation between the results obtained in [
30,
37] and the results summarized in these proceedings, and the inflationary scenario following a cosmological bounce [
62]. We reserve to discuss these problems in future works.