Nucleosynthesis and Kilonovae from Strange Star Mergers
Abstract
1. Introduction
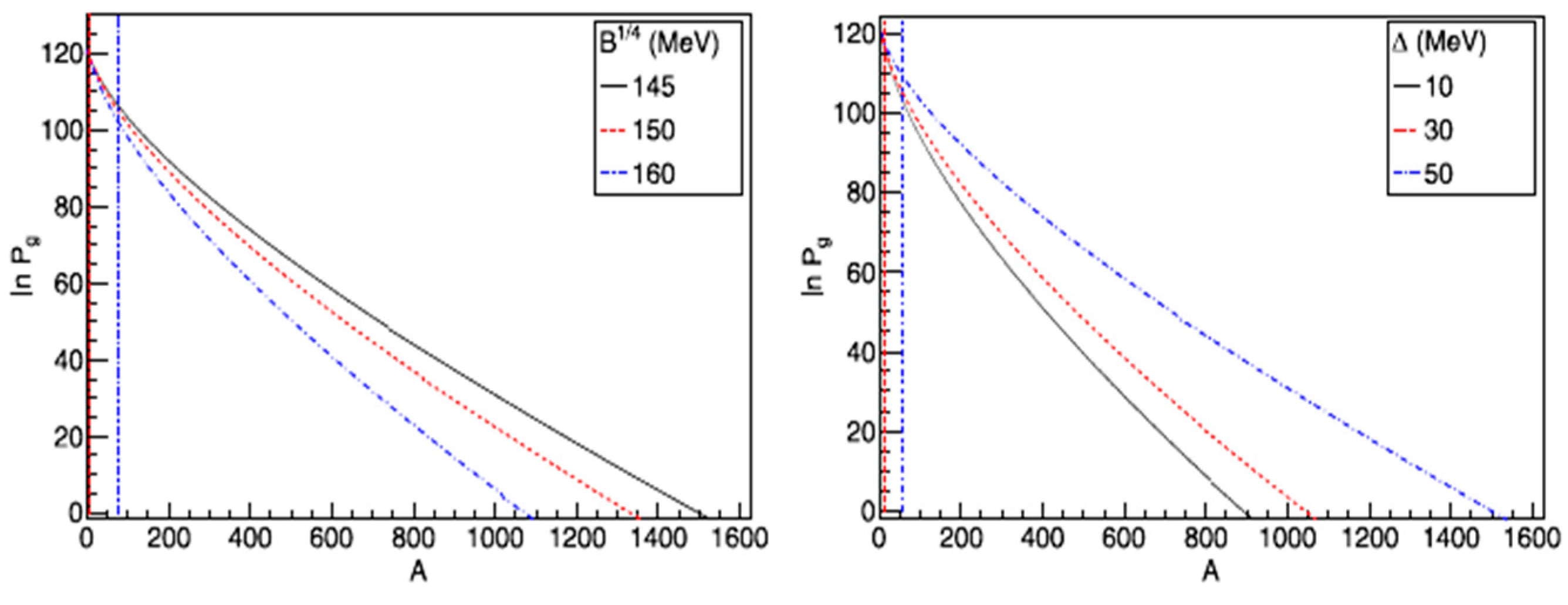
2. Was GW170817 a Merger of Two “Strange Stars”?
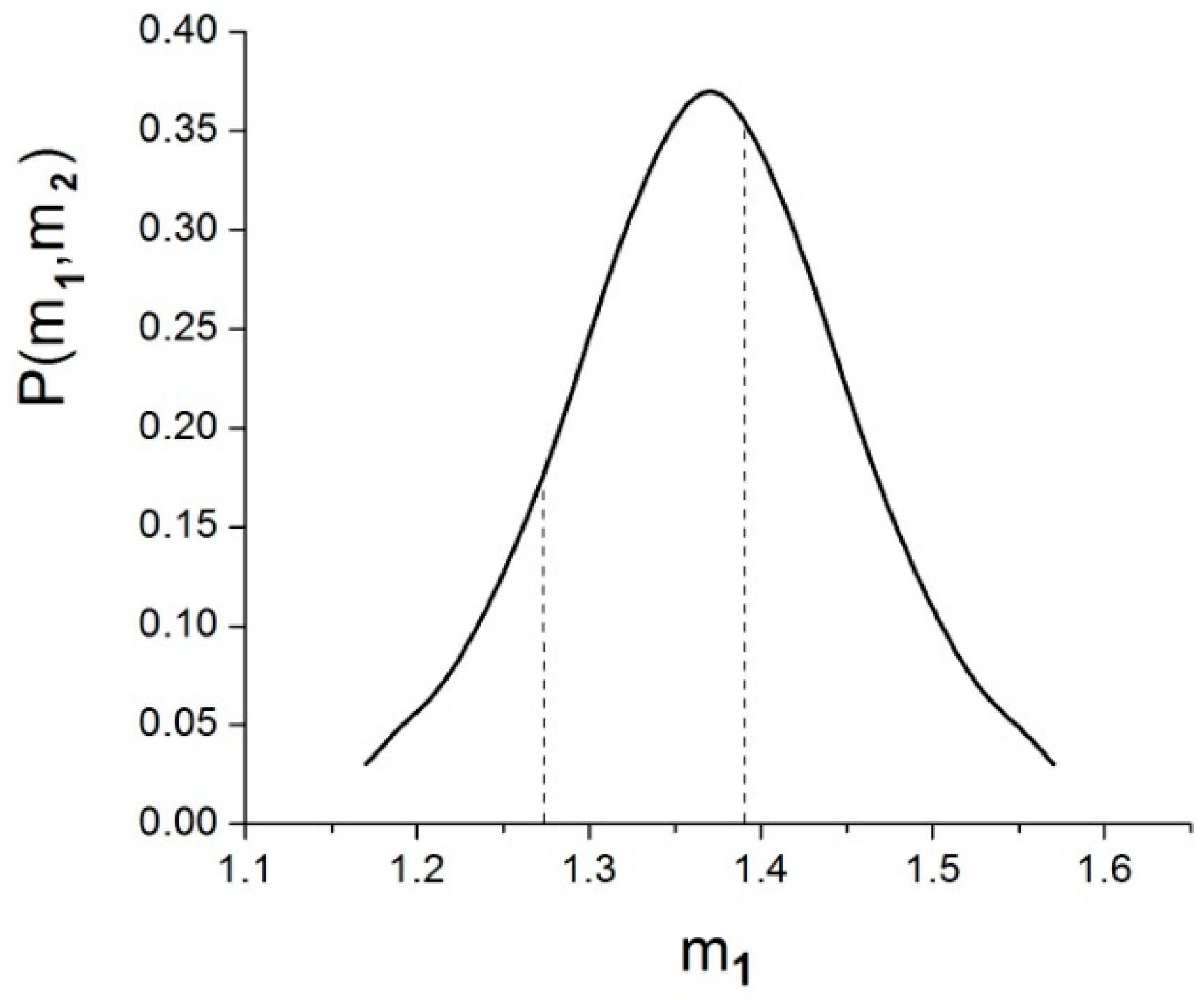
3. Was GW170817 Caused by an Asymmetric Binary System?
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tanvir, N.R.; LeVan, A.J.; Fruchter, A.S.; Hjorth, J.; Hounsell, R.A.; Wiersema, K.; Tunnicliffe, R. A "kilonova" associated with short-duration gamma-ray burst 130603B. Nature 2013, 500, 547–549. [Google Scholar] [CrossRef]
- Abbott, B.P. [LIGO Scientific Collaboration and Virgo Collaboration] GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Science Site. Available online: http://www.sciencemag.org/news/2017/10/merging-neutron-stars-generate-gravitational-waves-and-celestial-light-show (accessed on 26 March 2019).
- Cowan, J.J.; Sneden, C.; Lawler, J.E.; Aprahamian, A.; Wiescher, M.; Langanke, K.; Martínez-Pinedo, G.; Thielemann, F.-K. Making the Heaviest Elements in the Universe: A Review of the Rapid Neutron Capture Process. arXiv 2019, arXiv:1901.01410. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Gravitational Waves and Gamma-Rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. Astrophys. J. 2017, 848, L13. [Google Scholar] [CrossRef]
- Goldstein, A.; Veres, P.; Burns, E.; Briggs, M.S.; Hamburg, R.; Kocevski, D.; Wilson-Hodge, C.A.; Preece, R.D.; Poolakkil, S.; Roberts, O.J.; et al. An Ordinary Short Gamma-Ray Burst with Extraordinary Implications: Fermi -GBM Detection of GRB 170817A. Astrophys. J. 2017, 848, L14. [Google Scholar] [CrossRef]
- Piran, T. Mergers and GRBs: Past, present and future. In Proceedings of the 8th International Workshop on Astronomy and Relativistic Astrophysics (IWARA 2018), Ollantaytambo, Peru, 8–15 September 2018. [Google Scholar]
- Bodmer, A.R. Collapsed Nuclei. Phys. Rev. D 1971, 4, 1601. [Google Scholar] [CrossRef]
- Terazawa, H. Super-hypernuclei in the quark shell model. J. Phys. Soc. Jpn. 1989, 58, 3555. [Google Scholar] [CrossRef]
- Witten, E. Cosmic separation of phases. Phys. Rev. D 1984, 30, 272. [Google Scholar] [CrossRef]
- Itoh, N. Hydrostatic Equilibrium of Hypothetical Quark Stars. Prog. Theor. Phys. 1970, 44, 291–292. [Google Scholar]
- Ivanenko, D.; Kurdgelaidze, D.F. Remarks on quark stars. Lett. Nuovo Cimento 1969, 2, 13–14. [Google Scholar] [CrossRef]
- Stenjer, M.; Madsen, J. Gaps below strange star crusts. Phys. Rev. D 2005, 72, 123005. [Google Scholar]
- Paulucci, L.; Horvath, J. Strange quark matter fragmentation in astrophysical events. Phys. Lett. B 2014, 733, 164–168. [Google Scholar] [CrossRef]
- Paulucci, L.; Horvath, J.E.; Benvenuto, O.G. Nucleosynthesis in strange star mergers. Int. Jour. Mod. Phys. Conf. Series 2017, 45, 1760042. [Google Scholar] [CrossRef]
- Observed Neutron Star Masses. Available online: https://stellarcollapse.org/nsmasses (accessed on 26 March 2019).
- Zhang, C.-M.; Wang, J.; Zhao, Y.H.; Yin, H.X.; Song, L.M.; Menezes, D.P.; Wickramasinghe, D.T.; Ferrario, L.; Chardonnet, P. Study of measured pulsar masses and their possible conclusions. Astron. Astrophys. 2011, 527, A83–A91. [Google Scholar] [CrossRef]
- Kiziltan, B.; Kottas, A.; De Yoreo, M.; Thorsett, S.E. The Neutron Star Mass Distribution. Astrophys. J. 2013, 778, A66. [Google Scholar] [CrossRef]
- Özel, F.; Psaltis, D.; Narayan, R.; Santos Villareal, A. On the Mass Distribution and Birth Masses of Neutron Stars. Astrophys. J. 2012, 757, 55. [Google Scholar] [CrossRef]
- Özel, F.; Freire, P. Masses, Radii, and the Equation of State of Neutron Stars. Annu. Rev. Astron. Astrophys. 2016, 54, 401–440. [Google Scholar] [CrossRef]
- Valentim, R.; (UFABC, Brazil). Personal communication, 2018.
- Valentim, R.; Rangel, E.; Horvath, J.E. On the mass distribution of neutron stars. Mon. Not. R. Astron. Soc. 2011, 414, 1427–1431. [Google Scholar] [CrossRef]
- Schwab, J.; Podsiadlowski, P.; Rappaport, S. Further Evidence for the Bimodal Distribution of Neutron-Star Masses. Astrophys. J. 2010, 719, 722–727. [Google Scholar] [CrossRef]
- Ertl, T.; Janka, H.-T.; Woosley, S.E.; Sukhbold, T.; Ugliano, M. A Two-parameter Criterion for Classifying the Explodability of Massive Stars by the Neutrino-driven Mechanism. Astrophys. J. 2016, 818, 124. [Google Scholar] [CrossRef]
- Raithel, C.A.; Sukhbold, T.; Özel, F. Confronting Models of Massive Star Evolution and Explosions with Remnant Mass Measurements. Astrophys. J. 2018, 856, 35. [Google Scholar] [CrossRef]
- Martínez, J.G.; Stovall, K.; Freire, P.C.C.C.; Deneva, J.S.; Jenet, F.A.; McLaughlin, M.A.; Bagchi, M.; Bates, S.D.; Ridolfi, A. Pulsar J0453+1559: A Double Neutron Star System with a Large Mass Asymmetry. Astrophys. J. 2015, 812, 143. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Properties of the Binary Neutron Star Merger GW170817. Phys. Rev. X 2019, 9, 011001. [Google Scholar] [CrossRef]
- Pankow, C. On GW170817 and the Galactic Binary Neutron Star Population. Astrophys. J. 2018, 866, 60–68. [Google Scholar] [CrossRef]
- De, K.; Kasliwal, M.M.; Ofek, E.O.; Moriya, T.J.; Burke, J.; Cao, Y.; Cenko, S.B.; Doran, G.B.; Duggan, G.E.; Fender, R.P.; et al. A hot and fast ultra-stripped supernova that likely formed a compact neutron star binary. Science 2018, 362, 201–206. [Google Scholar] [CrossRef]
| Amplitude | ||
|---|---|---|
| 1.25 | 0.07 | 0.14 |
| 1.4 | 0.08 | 0.50 |
| 1.8 | 0.28 | 0.36 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Horvath, J.E.; Benvenuto, O.G.; Bauer, E.; Paulucci, L.; Bernardo, A.; Viturro, H.R. Nucleosynthesis and Kilonovae from Strange Star Mergers. Universe 2019, 5, 144. https://doi.org/10.3390/universe5060144
Horvath JE, Benvenuto OG, Bauer E, Paulucci L, Bernardo A, Viturro HR. Nucleosynthesis and Kilonovae from Strange Star Mergers. Universe. 2019; 5(6):144. https://doi.org/10.3390/universe5060144
Chicago/Turabian StyleHorvath, J. E., O. G. Benvenuto, E. Bauer, L. Paulucci, A. Bernardo, and H. R. Viturro. 2019. "Nucleosynthesis and Kilonovae from Strange Star Mergers" Universe 5, no. 6: 144. https://doi.org/10.3390/universe5060144
APA StyleHorvath, J. E., Benvenuto, O. G., Bauer, E., Paulucci, L., Bernardo, A., & Viturro, H. R. (2019). Nucleosynthesis and Kilonovae from Strange Star Mergers. Universe, 5(6), 144. https://doi.org/10.3390/universe5060144





