1. Introduction
There are several papers claiming that the quaternion or the octonion can be used to describe the laws of classical electromagnetism in a simpler way [
1,
2,
3,
4,
5,
6]. However, they are mainly limited to describing Maxwell equations. Furthermore, the meaning of quaternion and the reasons electromagnetic laws can be concisely described by them have not been well discussed up to now. Here, we list more diverse quaternion representations of the relations in electromagnetism than previously known and we introduce a new simpler notation to express quaternions. The proposed notation makes the quaternion representation of electromagnetic relations look similar to the differential-form representation of them. Moreover, the classical electromagnetic mass density and the complex Lagrangian can be newly defined and used to represent electromagnetic relations as quaternions.
It has been already well known that the quaternion can describe the Lorentz transformations of four vectors [
7]. We here rederive the quaternion representation of the Lorentz boost and the rotation, by using isomorphism between the basis of quaternion and the set of sigma matrices. Hence, we find that not only four vector quantities but also electromagnetic fields can be transformed simply in the quaternion representation. Starting from the
matrix representation of quaternion, we define a new complex electromagnetic field tensor. By using it, a complex energy–momentum stress tensor of electromagnetic fields and a complex Lagrangian can be nicely expressed. Interestingly, the eigenvalues of the complex energy–momentum stress tensor are the classical electromagnetic mass density up to sign. To define complex tensors, we introduce a new spacetime index called “tilde-spacetime index”. Imaginary number
i is usually linked to time so that it can be regarded as imaginary time, but we insist that it is more natural for
i to be linked to space. In our representation, we also find that the complex conjugate of a quaternion is equal to the quaternion consisting of the physical quantities with parity inversion.
The two-spinor formalism is known to be a spinor approach, which is useful to deal with the general relativity [
8,
9]. In the formalism, all world-tensors can be changed to even-indexed spinors and there we derive spinor descriptions of electromagnetism [
10]. We here prove that the quaternion representations including Maxwell’s equations are equivalent to the spinor representations of electromagnetism. We also explain how spinors in two-spinor formalism are generally linked to the quaternion. Finally, we explore the meaning of quaternion and more extended algebras such as octonion as n-fold rotation.
2. Complex Quaternion
Let us denote quaternions by characters with a lower dot such as
. Quaternions are generally represented in the form
where
are real numbers and
are the units of quaternions which satisfy
Equation (
1) consists of two parts, namely a “scalar” part
s and a “quaternion vector” part
. If we denote the quaternion vector part by
, Equation (
1) is written as
All quaternion vectors, denoted by an over-arrow symbol , can be interpreted as coordinate vectors in . We do not distinguish between vectors and quaternion vectors in this paper.
If
and
are two quaternions, the multiplication of the quaternions can be described as
by applying Equation (
2), where
is the dot product and
is the cross product. The dot product and the cross product, which are operations for three-dimensional vectors are used in quaternion vectors.
The components of quaternions can be extended to complex numbers. We call such a quaternion “complex quaternion”. The general form of complex quaternion is
where
and components of
are real numbers, and
i is a complex number
, which differs from the quaternion unit
.
We denote the operation of complex conjugation by a bar
, and the complex conjugate of
is
For a quaternion vector
, the exponential of
is defined by
since
[
11].
3. Laws of Electromagnetism in the Complex Quaternion Representation
3.1. Electromagnetic Quantities
We use the unit system which satisfies where is vacuum permittivity, is vacuum permeability and c is speed of light. The sign conventions for the Minkowski metric is .
In the classical electromagnetism, the density of electromagnetic field momentum
and the density of electromagnetic field energy
are defined by
where
is an electric field and
is a magnetic field [
12,
13]. In our unit system, the electromagnetic momentum
(in SI units) is the same as the Poynting vector
(in SI units).
We define a complex Lagrangian
and an electromagnetic mass density
by
The electromagnetic mass density
is defined from the energy–momentum relation
where
is four-momentum of a particle of mass
m. The meaning of
should be investigated more in detail; however, it is not discussed here. Comparing
and
, we can see that
3.2. Complex Quaternion Representations of Electromagnetic Relations
Let us define a few physical quantities in the form of complex quaternion,
where
is
for the velocity
v,
V is the electric potential,
is the vector potential,
is the electric field,
is the magnetic field,
is the charge density, and
is the electric current density.
is just a quaternion vector and the terms in
are defined in Equation (
8).
is equal to
where
is the proper charge density, which is the density in the rest system of the charge. The scalar part of
is the rate of work done by electric field on the charge and the vector part is the Lorentz force.
We define a quaternion differential operator by
where
t is the time and
is the vector differential operator in the three-dimensional Cartesian coordinate system.
The relations in electromagnetism can be described in the complex quaternion form simply as follows:
where
.
We can check all quaternion relations by expanding multiplications of quaternions using Equation (
4). Some expansions are proven in
Appendix A. Relations (1), (3) and (4) are already well known in quaternion forms, but the others are not well mentioned thus far. Each quaternion equation in Equation (13) contains several relations, which are known in classical electromagnetism.
Let us discuss in more detail each relation in Equation (13).
- (1)
is the d’Alembert operator.
- (2)
describes the gauge transformation of gauge fields.
- (3)
contains three relations. One is Lorentz gauge condition and the others are the relations between fields strength and gauge fields, as shown in Equation (
A1),
- (4)
contains all four Maxwell’s equations in Equation (A2),
It can be the wave equations of gauge fields with sources in the Lorentz gauge,
- (5)
contains the charge conservation relation and the wave equations of
and
fields in Equation (A3),
Those can be derived from taking ḍ operation on the both side of Relation (4) in Equation (13).
- (6)
includes the Lorentz force term and the work done by electromagnetic fields term . However, the meaning of is not yet well known.
- (7)
We have found that
is equal to
where
is the quaternion differential operator. The proof of this is given in
Appendix A.2.
- (8)
is the quaternion representation of electromagnetic energy and momentum. It can be easily verified, by expanding the left side, that
- (9)
It can be guessed that
from the analogy with the force-momentum relation
, where
is the four-force,
D is the covariant derivative,
is the proper time,
q is the electric charge,
is the four-velocity, and
is the electromagnetic tensor, which is the relation of the four-force acting to a charged particle situated in electromagnetic fields.
is expanded as
Substituting Equation (
22) into Equation (
23), we get
where
for vector fields
and
.
Equation (
24) is the work–energy relation in electromagnetism. Equation (25) can be rearranged as
where
is the Maxwell stress tensor and
Equation (26) is not a well-known relation. The proof of the expansion is given in
Appendix B. By looking at Equations (
24)–(26), we can observe that it is difficult to find a simple quaternion formula such as
. The exact formula of
is obtained as
- (10)
is the relation between the complex Lagrangian and electromagnetic fields. The complex Lagrangian
is defined as
. This is, in fact, the Euclidean Lagrangian including topological term [
14,
15]. The real part
is the Lagrangian of electromagnetic fields
, where
for
gauge field
. The variation of this part gives the first two Maxwell’s equations in Equation (
17). The complex part
is
, which is the topological term of gauge fields where
is Hodge dual of
. Its variation gives the other two Maxwell’s equations in Equation (18).
- (11)
is a Lorentz invariant and a gauge invariant quantity.
4. Lorentz Transformation in the Complex Quaternion Representation
For a quaternion basis
, the algebra of
is isomorphic to the algebra of sigma matrices
, where
is
identity matrix and
are Pauli matrices,
It means that complex quaternions that have the form are isomorphic to where and .
We can get the quaternion representation of Lorentz transformation by using isomorphism given above and the spinor representation of the Lorentz group. Let us denote by the spinor representation of the Lorentz group, which acts on Dirac spinor . Then, Dirac spinor transforms as under a Lorentz transformation .
In the chiral representation of the Clifford algebra, the spinor representation of rotations
and boosts
are
where
,
,
is the rotation angle,
is the unit vector of rotation axis,
is the boost velocity, and
is the unit vector of boost velocity.
Since it is known [
16] that
the following relation also holds:
for any four-vector
.
The components of Equation (
34) are
where
. This represents the quaternion Lorentz transformation for the form
, since
.
Let us define Lorentz transformation factor
by
where
,
. Since
is the quaternion velocity
of a boosted frame with a boost velocity
, Equation (
37) can be rewritten as
where
. The inverse of
and its complex conjugate are defined as
From Equations (
35) and (
36), the Lorentz transformations of a quaternion that has the form
is written as
Therefore, the Lorentz transformations of a quaternion gauge field
Ạ and a quaternion strength field
are
As an example, if we boost a frame with a speed
v along
x axis, then
which is a very efficient representation in computing rotations and boosts.
5. The Role of Complex Number “” in Complex Quaternions
5.1. Complex Space and Real Time
In this section, we explain that it is more natural to attach imaginary number
i to the spatial coordinates rather than to the time coordinate. The infinitesimal version of the Lorentz transformation in one dimension is
This can be manipulated to
where
is a boost velocity,
is an infinitesimal displacement of the moving frame and
is an infinitesimal time it takes for the frame to move along the displacement.
If we put imaginary number “
i” to the spatial coordinate as Equations (46) and (47), the Lorentz transformation can be seen as a kind of rotation,
for pure imaginary angles
,
and
.
In contrast, if we put
i to the time coordinate rather than to the spatial coordinate, then
which means that Equations (46) and (47) cannot be regarded as a kind of rotation.
5.2. Parity Inversion and Conjugate of i
All physical quantities that are located in the real part of quaternions, such as
, etc., do not change signs under parity inversion; and all physical quantities that are located in the imaginary part of quaternions, such as
, etc., change signs under parity inversion. This means that the operation of complex conjugation on a quaternion corresponds to the parity inversion of the physical quantities in the quaternion representation. The reason is related to tilde-spacetime indices, which are defined in
Section 6.1 and
Section 7.2.
All quantities in the imaginary part may be regarded as “imaginary quantities’, not just as “real quantities placed in the imaginary part”, i.e. imaginary space, imaginary momentum, imaginary electric field, etc. It is the same as replacing length units, such as “”, with imaginary length unit such as “”.
6. Complex Electromagnetic Tensor Related to Quaternion and Electromagnetic Laws
6.1. Electromagnetic Tensor with Tilde-Spacetime Index
For a vector
, let us define “vector matrix of
” as
and the vector matrix by # notation as
where
are the Levi–Civita symbols.
Then, the electromagnetic tensor
can be represented as
where
,
are vector matrix of
,
and superscript
means the transpose of a matrix
. The dual tensor can be represented as
where
is the rank-4 Levi–Civita symbol with the sign convention
.
Now, we define tensor indices with tilde such as “
”, called “tilde-spacetime indices”.
and
for any
and
are defined as
Then, the components of and become equal, since in Minkowski metric. As an example, is . Since this is isomorphic to the quaternion basis , we can rewrite as a quaternion basis so that .
Generally speaking, the way to convert a quantity with multiple spacetime indices to the quantity with multiple tilde-spacetime indices is multiplying with or dividing by imaginary number i when each spacetime index has the value 1, 2 or 3. As an example, the Minkowski metric with tilde indices is , since .
Applying this rule to electromagnetic tensors, we get
6.2. The 4 × 4 Representation of Complex Quaternions
The basis elements of quaternion,
, can be represented as
matrices
A quaternion such as
can be represented in the tensor representation
where
T means the tensor representation. When
,
has a simple form
.
For a quaternion field strength
, the tensor form of
is
where
which is a vector matrix of the vector
. This is eventually identical to
[
17,
18,
19].
6.3. Complex Electromagnetic Tensor and Electromagnetic Laws
Let us define
and its conjugate
as
A few complex tensors can also be defined as follows,
where
is the vector matrix of
,
is the vector matrix of
,
∇ is the vector matrix of
∇, and
is the vector matrix of
.
Then, the following tensor relations hold:
where
is unit matrix.
and
are the complex Lagrangian and the electromagnetic mass density (Equation (
9)). All relations can be easily verified by simple calculations. Actually, the components of
,
and
are equal to the components of
,
and
, where
is the four-gradient,
is the electric current density and
is the electromagnetic stress–energy tensor defined as
Those listed relations of complex tensors can be verified by using several known tensor relations in electromagnetism and tilde-spacetime indices, instead of the direct calculation. For example, Equation (65), which represents Maxwell’s equations, can be easily verified from and .
The complex electromagnetic stress–energy tensor
contains the information about electromagnetic energy density
, momentum density
and stress
, as shown by Equations (
8) and (
28). It is interesting that
is linked to the electromagnetic mass density, as shown in Equations (68) and (69). Especially, Equation (69) cannot be simply derived from known relations of electromagnetism.
By differentiating both sides of the relation in Equation (
64), we get
since
. Substituting Equation (65) into Equation (
71) and comparing it with Equation (66), we further get the following relations:
7. Relations between Quaternions and Two-Spinor Formalism
7.1. The Correspondence of Two-Spinor Representations and Quaternion Representations in Electromagnetism
Let us start with some basic contents of two-spinor formalism [
8,
9,
10]. Mathematically, any null-like spacetime four-vector
can be described as a composition of two spinors,
where
are sigma matrices
, the components of
are
for proper complex numbers
and
, and
. It can be rewritten as
by using the relation
and
, where
,
,
, and
are the
-spinors whose components are
as follows in [
10].
We now define a spinor
as
which is equivalent to
. The factor, which connects a four-vector to a corresponding spinor, is called “Infeld–van der Waerden symbol” [
20], such as
in Equation (
76). It can be generally written as
. We can extend this notation not only to a null-like four-vector but also to any tensors by multiplying more than one Infeld–van der Waerden symbols: any tensor such as
with spacetime indices
can be written as a spinor
with spinor indices
, by multiplying
with
,
.., such as
. This can be simply written as
Any antisymmetric tensor
can be divided into two parts
where
and
(unprimed spinor indices and primed spinor indices can be rearranged back and forth). If
is real, then
and
Since an electromagnetic field tensor
(Equation (
52)) is antisymmetric, it can be written as
with an appropriate field
. There we find closely related electromagnetic relations [
10]:
where
(in Minkowski spacetime) is the four-gradient,
is the electromagnetic potential and
is the charge-current vector. The former is the relation of electromagnetic potentials and strength fields, and the latter is equivalent to the two Maxwell’s equations.
Since
corresponds to
,
corresponds to
,
corresponds to
, and
corresponds to
, Equations (
81) and (82) are exactly corresponding to quaternion relations in Equation (13) as follows:
Our proof starts from manipulating
as
Since
becomes
where
are the three-dimensional vector indices, which have the value 1, 2 or 3, and
is
for the Levi–Civita symbol
. Einstein summation convention is understood for three-dimensional vector indices
and
k. Similar to Equations (
90) and (
91),
Finally, for an electromagnetic tensor
, Equations (
83) and (84) hold. Equations (
91) and (
93) also show the link between Equation (
64) and the spinor form of the electromagnetic energy–stress tensor
.
7.2. General Relations of Quaternion and Two-Spinor Formalism and the Equivalence between Quaternion Basis and Minkowski Tetrads
Generally speaking, all spinors with spinor indices in two-spinor formalism are directly linked to quaternion. Since is isomorphic to quaternion basis , are also isomorphic to . For any spinors with two spinor indices in the form , it can be rewritten as . It means that we can think of all spinors of the form to be obtained by multiplying the four-vector with .
Any spinor
can be represented with spin basis
such as
where
is normalized so that
. It is well known that Minkowski tetrads
, which is a basis of four-vectors, can be constructed from spin basis
[
21],
Therefore,
where a bold index, which represents a “component”, is distinguished from a normal index. Any spacetime tensor can be divided into components and basis such as
The component matrix of Minkowski tetrads with respect to the spin basis is
We can replace
by the tilde-tetrads
. The component matrix of tilde-tetrads
with respect to the spin basis is
which is isomorphic to
. From this isomorphism, we can set
, which is equivalent to
Then, any four-vector with tilde-spacetime index can be written as
where
.
8. Discussion on Meaning of the Quaternion and The Extended Algebra
8.1. The Role of Sigma Matrices and Quaternion Basis as Operators
Let us multiply one of sigma matrices with a tilde-spacetime index by
as an operator: Multiplying
by
, we then get
This is the operation of changing the spin basis as
Since
is isomorphic to
,
can be written as
. Multiplying
by
, we can see
This corresponds to changing the spin basis as
and can be written as
. Multiplying
by
gives
This corresponds to changing the spin basis as
and can be written as
.
Since the component of
is equal to
and
we can interpret that raising or lowering indices means changing spacetime basis.
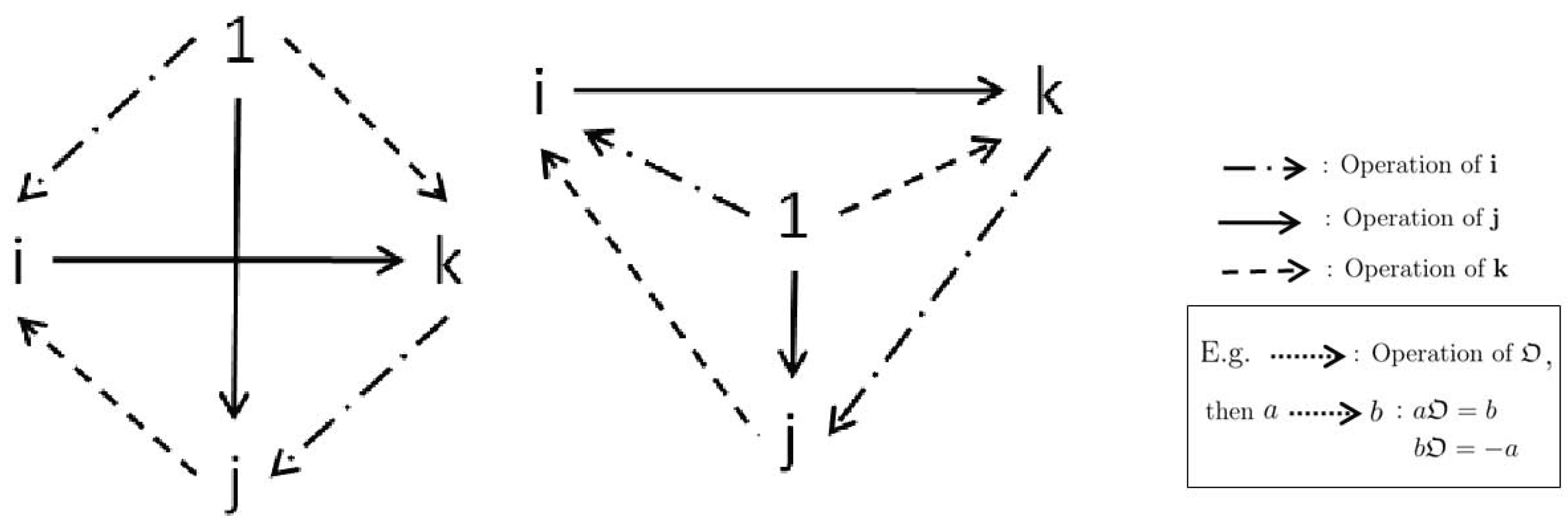
In summary, the quaternion basis roles as a basis of spacetime itself as well as works as an operator of changing spacetime and spin bases. Similar to the fact that quantities in classical physics act as operators in quantum mechanics, they allow us to think that spacetime might be formed from fundamental operators. The operation on each element of quaternion basis is graphically shown in
Figure 1. In the figure, the three types of arrows indicate the operations of
,
, and
, respectively. As shown in the lower right box, if the arrow corresponds to the operation
from
a to
b, then
and
. As an example, the solid line indicates the operation of
, then
and
.
8.2. General Discussion on Extended Complex Algebra, and Appropriate Meaning
Quaternion algebra
is isomorphic to
with non-commutative multiplication rule, and the elements of
can be represented with the secondary complex number
j [
22]. The set of elements of the form
where
is isomorphic to the set of quaternions
. In a similar way, we can construct a larger algebraic system of quaternions, which is called “Octonion”
by introducing tertiary complex number
l, such as
. “Sedenion”
, which is an even larger algebraic system than octonion, can also be derived by performing analogous procedure. This procedure is called Cayley–Dickson construction.
It is still questionable how octonions and sedenions can be used in physics. Since octonions have the similar structure of complex quaternions, they can be used to describe electromagnetism. Furthermore, it is known that a specific octonion is useful to describe SU(3) group, which is the symmetry group of strong interaction [
23]. Sedenion is an algebra which have 16 basis elements. We suggest that its basis can be written in the form
, where
is a quaternion basis
. We also speculate that this may be related to SU(4) group, which has 15 generators, or even to the theory of gravity. Since electromagnetic strength field tensor
can be expressed in quaternion representation, Weyl tensor
may be expressed by using sedenion. The representation of the basis and possible uses of each algebraic system are listed in
Table 1.
We can think of physical meaning of the algebras made through Cayley–Dickson construction. Multiplying complex numbers by a field implies a change in scale and phase of the field. In this point of view, the spatial rotation can be interpreted as a kind of two-fold rotation because quaternions can describe three-dimensional spatial rotation and they consist of two independent imaginary units i and j. Moreover, it might be that the space itself is constructed from a kind of two-fold rotation. Similarly, since the basis of octonion can be represented with three complex numbers (one quaternion and one complex number), the rotation between gluon color charges can be considered as a three-fold rotation. Likewise, if sedenion has useful relation with the gravity, the metric of spacetime can be deemed as a four-fold rotation.
9. Conclusions
We have seen that quaternions can describe electromagnetism very concisely and beautifully. They can also represent Lorentz boost and spatial rotation in a simpler way. The complex conjugation of complex quaternion corresponds to parity inversion of the physical quantities belonging to the quaternion. We can also take a hint from the matrix representation of quaternion and apply it to define the complex tensor, which in turn provides a new representation of electromagnetism. We have verified that the quaternion representation is directly linked to spinor representation in two-spinor formalism, and then investigated meaning of quaternions; not only as a basis but also as an operator.
The use of quaternion could be extended not only for actual calculations, but also to obtain deep insights and new interpretations of physics. Any null-like vectors can be described by two-spinors, and, furthermore, Minkowski tetrads can also be constructed within the two-spinor formalism. This formalism has the implication that the spacetime may come from two-spinor fields. The beautiful conciseness of quaternion representation of electromagnetism and the link between quaternion and two-spinor formalism may imply that spinors are the fundamental ingredients of all fields and the spacetime also consists of two-spinor fields. Conversely, if those conjectures are true, then it is natural to explain why the algebras formed by the Cayley–Dickson procedure, such as quaternion, is useful in the description of nature.
Author Contributions
Conceptualization, I.K.H. and C.S.K.; investigation, I.K.H.; writing–original draft preparation, I.K.H.; writing–review and editing, C.S.K. supervision, C.S.K.; funding acquisition, C.S.K.
Funding
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIP) (NRF-2018R1A4A1025334).
Acknowledgments
We would like to thank Gorazd Cvetic for helpful discussions.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Expansions of a few Quaternion Products in Equation (13)
Appendix A.1. Expansions of Products in (3), (4) and (5) of Equation (13)
Using the multiplication expression shown in Equation (
4), the left sides of the relations (3), (4) and (5) in Equation (13) are expanded as follows.
Appendix A.2. The proof of (7) in Equation (13)
Here we show that
is equal to
where
is the quaternion differential operator.
where we have used the following relations:
Appendix B. The Proof of Equation (26)
where
for vector fields
and
. Substituting this into Equation (
A9), we get Equation (26).
Appendix C. The Proof of Equation (30)
As we mentioned on Equation (4), is isomorphic to where , and .
Let us introduce some quantities that are isomorphic to some quaternions
where
,
,
.
We have used the relations
[
24] for spinor indices
and
.
References
- Majernik, V. Quaternionic formulation of the classical fields. Adv. Appl. Clifford Algebras 1999, 9, 119. [Google Scholar] [CrossRef]
- Rawat, A.; Negi, O. Quaternion gravi-electromagnetism. Int. J. Theor. Phys. 2012, 51, 738–745. [Google Scholar] [CrossRef][Green Version]
- Weng, Z.H. Field equations in the complex quaternion spaces. Adv. Math. Phys. 2014, 2014. [Google Scholar] [CrossRef]
- Gamba, A. Maxwell’s equations in octonion form. Nuovo Cimento A 1998, 111, 293–299. [Google Scholar]
- Mironov, V.L.; Mironov, S.V. Octonic representation of electromagnetic field equations. J. Math. Phys. 2009, 50, 012901. [Google Scholar] [CrossRef]
- Honig, W. Quaternionic electromagnetic wave equation and a dual charge-filled space. Lettere Al Nuovo Cimento (1971–1985) 1977, 19, 137–140. [Google Scholar] [CrossRef]
- De Leo, S. Quaternions and special relativity. J. Math. Phys. 1996, 37, 2955–2968. [Google Scholar] [CrossRef]
- Penrose, R. A spinor approach to general relativity. Ann. Phys. 1960, 10, 171–201. [Google Scholar] [CrossRef]
- Bain, J. The coordinate-independent 2-component spinor formalism and the conventionality of simultaneity. Stud. Hist. Philos. Sci. Part B Stud. Hist. Philos. Mod. Phys. 2000, 31, 201–226. [Google Scholar] [CrossRef]
- Penrose, R.; Rindler, W. Spinors and Space-Time: Volume 1, Two-Spinor Calculus and Relativistic Fields; Cambridge University Press: Cambridge, UK, 1984. [Google Scholar]
- Liu, Q.; Prakash, E.C. The parameterization of joint rotation with the unit quaternion. In Proceedings tth Digital Image Computing: Techniques and Applications, Sydney, NSW, Australia, 10–12 December 2003; Sun, C., Talbot, H., Ourselin, S., Adriaansen, T., Eds.; CSIRO Publishing: Clayton, Australia, 2003. [Google Scholar]
- Griffiths, D.J. Introduction to Electrodynamics; Pearson: Glenview, IL, USA, 2005. [Google Scholar]
- Boyer, T.H. Classical model of the electron and the definition of electromagnetic field momentum. Phys. Rev. D 1982, 25, 3246. [Google Scholar] [CrossRef]
- Polyakov, A.M. Gauge Fields and Strings. Contemp. Concepts Phys. 1987, 3, 85–110. [Google Scholar]
- Preskill, J. Magnetic monopoles. Annu. Rev. Nucl. Part. Sci. 1984, 34, 461–530. [Google Scholar] [CrossRef]
- Tong, D. Quantum Field Theory; Lecture Notes; University of Cambridge: Cambridge, UK, 2007. [Google Scholar]
- Girard, P.R. Quaternions, Clifford Algebras and Relativistic Physics; Springer Science & Business Media: Berlin, Germany, 2007. [Google Scholar]
- Sbitnev, V.I. Hydrodynamics of superfluid quantum space: Particle of spin-1/2 in a magnetic field. Quantum Stud. Math. Found. 2018, 5, 297–314. [Google Scholar] [CrossRef]
- Sbitnev, V.I. Quaternion algebra on 4D superfluid quantum space-time: Gravitomagnetism. Found. Phys. 2019, 49, 107–143. [Google Scholar] [CrossRef]
- Infeld, L.; Van der Waerden, B.L. Die Wellengleichung des Elektrons in der allgemeinen Relativitätstheorie; Verlag d. Akad. d. Wissenschaften: Vienna, Austria, 1933. [Google Scholar]
- O’donnell Peter, J. Introduction to Two-Spinors in General Relativity; World Scientific: Singapore, 2003. [Google Scholar]
- Cowles, J.; Gamboa, R. The Cayley-Dickson Construction in ACL2. arXiv 2017, arXiv:1705.06822. [Google Scholar] [CrossRef]
- Chanyal, B.; Bisht, P.; Li, T.; Negi, O. Octonion quantum chromodynamics. Int. J. Theor. Phys. 2012, 51, 3410–3422. [Google Scholar] [CrossRef]
- Wess, J.; Bagger, J. Supersymmetry and Supergravity; Princeton University Press: Princeton, NJ, USA, 1992. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).