Multiplicity Dependence in the Non-Extensive Hadronization Model Calculated by the HIJING++ Framework
Abstract
1. Introduction
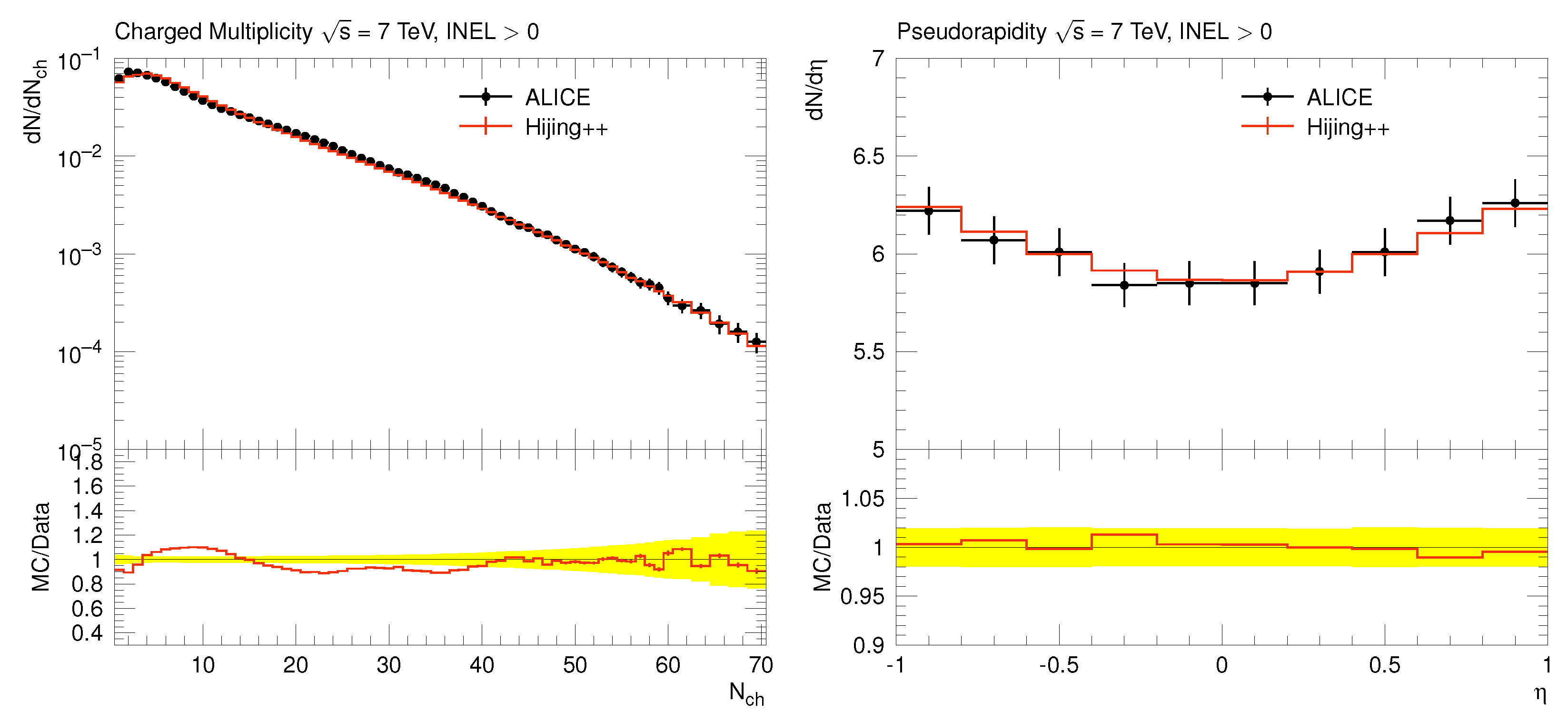
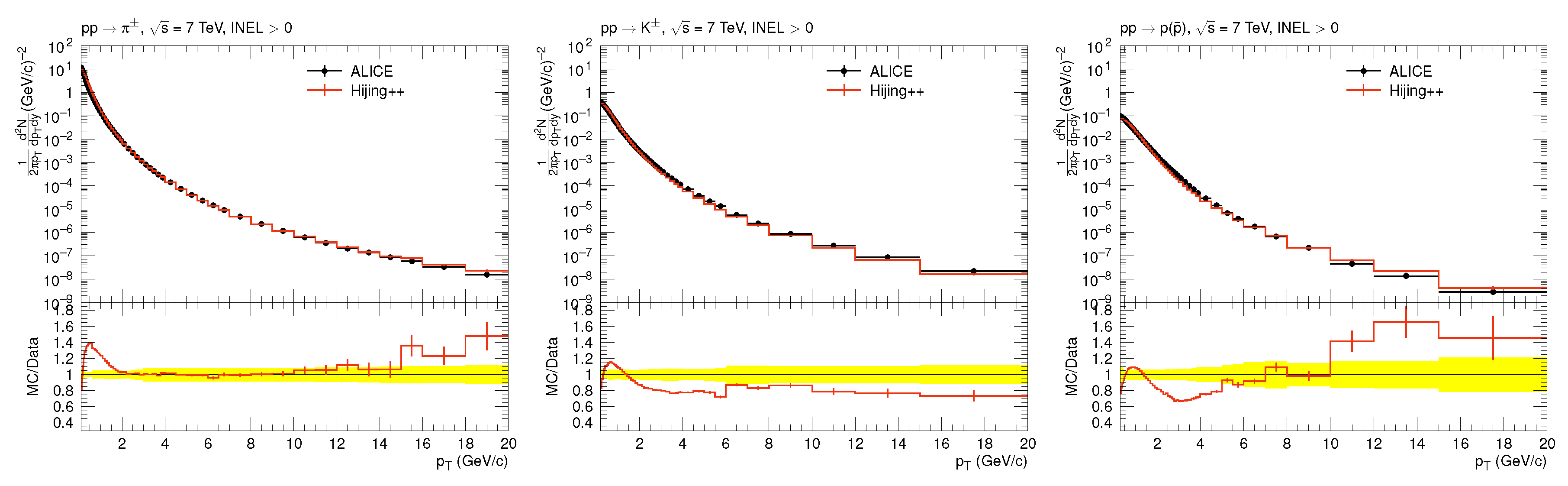
2. Tuning of HIJING++ Parameters
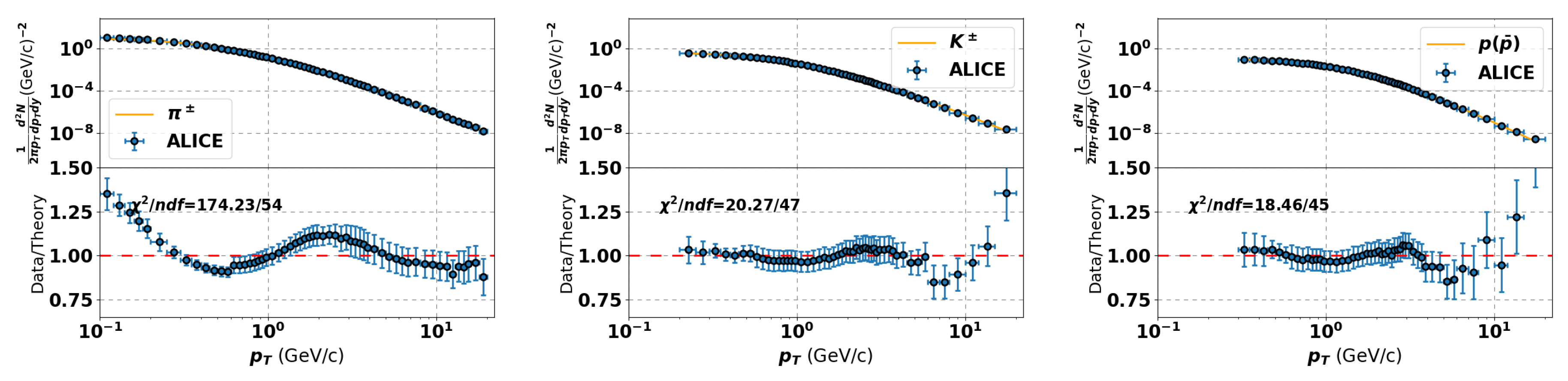
3. The Non-Extensive Hadronization Model
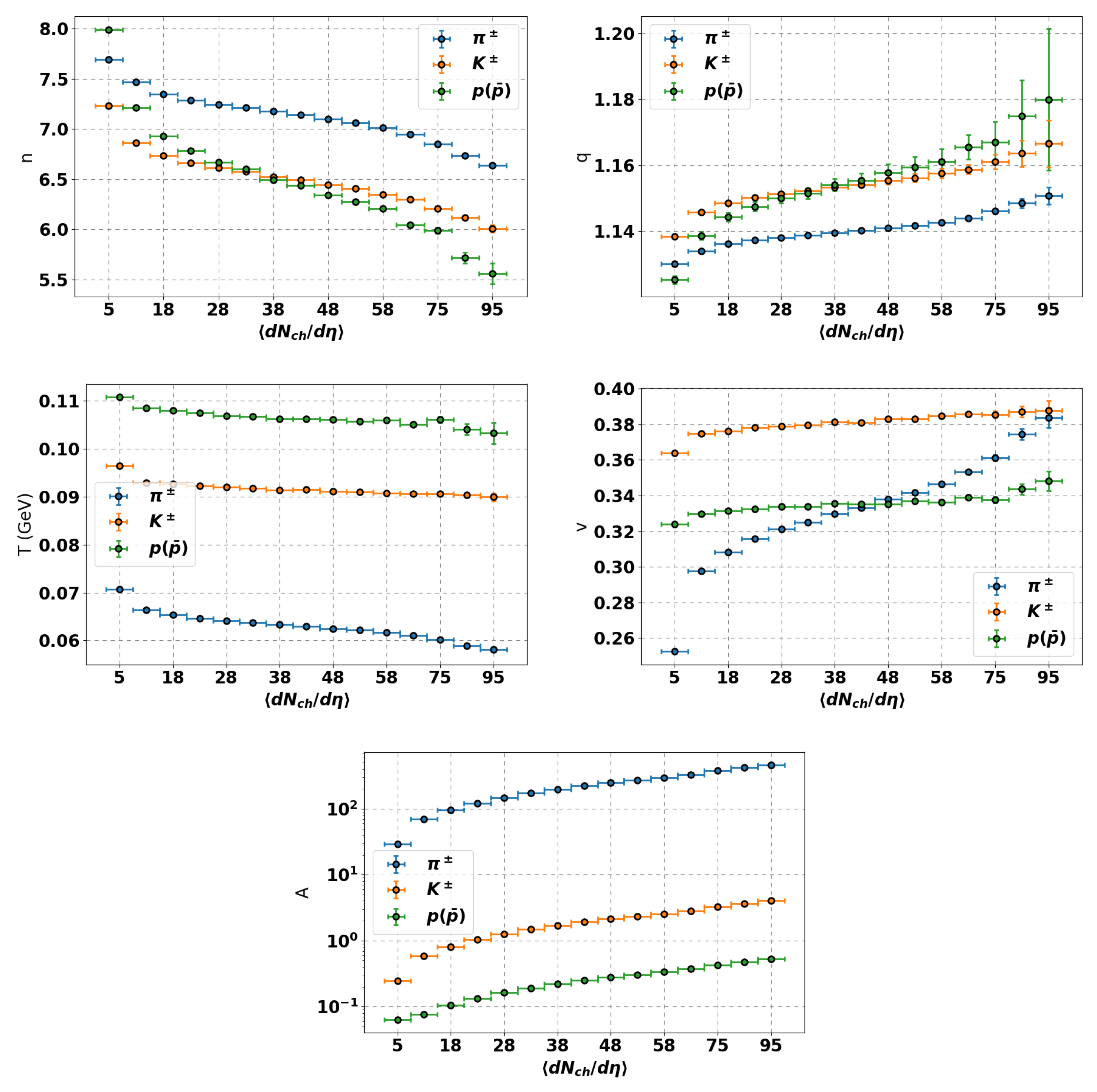
4. The Multiplicity Dependence of the Non-Extensive Model
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bíró, G.; Barnaföldi, G.G.; Biró, T.S.; Ürmössy, K.; Takács, Á. Systematic Analysis of the Non-extensive Statistical Approach in High Energy Particle Collisions—Experiment vs. Theory. Entropy 2017, 19, 88. [Google Scholar] [CrossRef]
- Grigoryan, S. Using the Tsallis distribution for hadron spectra in pp collisions: Pions and quarkonia at = 5–13000 GeV. Phys. Rev. D 2017, 9, 056021. [Google Scholar] [CrossRef]
- Zheng, H.; Zhu, L.; Bonasera, A. Systematic analysis of hadron spectra in p+p collisions using Tsallis distributions. Phys. Rev. D 2015, 92, 074009. [Google Scholar] [CrossRef]
- Wong, C.Y.; Wilk, G.; Cirto, L.J.L.; Tsallis, C. Possible Implication of a Single Nonextensive pT Distribution for Hadron Production in High-Energy pp Collisions. Eur. Phys. J. Web Conf. 2015, 90, 04002. [Google Scholar] [CrossRef]
- Tripathy, S.; Bhattacharyya, T.; Garg, P.; Kumar, P.; Sahoo, R.; Cleymans, J. Nuclear Modification Factor Using Tsallis Non-extensive Statistics. Eur. Phys. J. A 2016, 52, 289. [Google Scholar] [CrossRef]
- Bhattacharyya, T.; Cleymans, J.; Marques, L.; Mogliacci, S.; Paradza, M.W. On the precise determination of the Tsallis parameters in proton–proton collisions at LHC energies. J. Phys. G Nucl. Part. Phys. 2018, 45, 055001. [Google Scholar] [CrossRef]
- Shen, K.; Barnaföldi, G.G.; Biró, T.S. Hadronization within Non-Extensive Approach and the Evolution of the Parameters. arXiv 2019, arXiv:1905.05736. [Google Scholar]
- Bíró, G.; Barnaföldi, G.G.; Biró, T.S.; Shen, K. Mass hierarchy and energy scaling of the Tsallis–Pareto parameters in hadron productions at RHIC and LHC energies. Eur. Phys. J. Web Conf. 2018, 171, 14008. [Google Scholar] [CrossRef]
- Bíró, G.; Barnaföldi, G.G.; Biró, T.S.; Ürmössy, K. Application of the Non-extensive Statistical Approach to High Energy Particle Collisions. AIP Conf. Proc. 2017, 1853, 080001. [Google Scholar] [CrossRef]
- Barnaföldi, G.G.; Ürmössy, K.; Bíró, G. A ’soft+hard’ model for Pion, Kaon, and Proton Spectra and v2 measured in PbPb Collisions at = 2.76ATeV. J. Phys. Conf. Ser. 2015, 612, 012048. [Google Scholar] [CrossRef]
- Takacs, A.; Barnaföldi, G.G. Non-extensive Motivated Parton Fragmentation Functions. Proceedings 2019, 10, 12. [Google Scholar] [CrossRef]
- Khuntia, A.; Sharma, H.; Kumar Tiwari, S.; Sahoo, R.; Cleymans, J. Radial flow and differential freeze-out in proton–proton collisions at = 7 TeV at the LHC. Eur. Phys. J. A 2019, 55, 3. [Google Scholar] [CrossRef]
- Wilk, G.; Włodarczyk, Z. Some intriguing aspects of multiparticle production processes. Int. J. Mod. Phys. A 2018, 33, 1830008. [Google Scholar] [CrossRef]
- Urmossy, K.; Biro, T.S. Cooper-Frye Formula and Non-extensive Coalescence at RHIC Energy. Phys. Lett. B 2010, 689, 14. [Google Scholar] [CrossRef]
- Van, P.; Barnafoldi, G.G.; Biro, T.S.; Urmossy, K. Nonadditive thermostatistics and thermodynamics. J. Phys. Conf. Ser. 2012, 394, 012002. [Google Scholar] [CrossRef]
- Shen, K.; Biro, T.S.; Wang, E. Different Non-extensive Models for heavy-ion collisions. Physica A 2018, 492, 2353–2360. [Google Scholar] [CrossRef]
- Wang, X.N.; Gyulassy, M. HIJING: A Monte Carlo model for multiple jet production in pp, pA, and AA collisions. Phys. Rev. D 1991, 44, 3501–3516. [Google Scholar] [CrossRef]
- Deng, W.T.; Wang, X.N.; Xu, R. Hadron production in p+p, p+Pb, and Pb+Pb collisions with the HIJING 2.0 model at energies available at the CERN Large Hadron Collider. Phys. Rev. C 2011, 83, 014915. [Google Scholar] [CrossRef]
- Barnaföldi, G.G.; Bíró, G.; Gyulassy, M.; Haranozó, S.M.; Lévai, P.; Ma, G.; Papp, G.; Wang, X.N.; Zhang, B.W. First Results with HIJING++ in High-Energy Heavy-Ion Collisions. Nucl. Part. Phys. Proc. 2017, 289–290, 373. [Google Scholar] [CrossRef][Green Version]
- Papp, G.; Barnaföldi, G.G.; Bíró, G.; Gyulassy, M.; Harangozó, S.M.; Ma, G.; Lévai, P.; Wang, X.N.; Zhang, B.W. First Results with HIJING++ on High-energy Heavy Ion Collisions. arXiv 2018, arXiv:1805.02635. [Google Scholar]
- Albacete, J.L.; Arleo, F.; Barnaföldi, G.G.; Bíró, G.; d’Enterria, D.; Ducloué, B.; Eskola, K.J.; Ferreiro, E.G.; Gyulassy, M.; Harangozó, S.M.; et al. Predictions for Cold Nuclear Matter Effects in p+Pb Collisions at = 8.16 TeV. Nucl. Phys. A 2018, 972, 18–85. [Google Scholar] [CrossRef]
- Bíró, G.; Papp, G.; Barnaföldi, G.G.; Nagy, D.; Gyulassy, M.; Lévai, P.; Wang, X.N.; Zhang, B.W. HIJING++, a Heavy Ion Jet INteraction Generator for the High-luminosity Era of the LHC and Beyond. Proceedings 2019, 10, 4. [Google Scholar] [CrossRef]
- Sjöstrand, T.; Ask, S.; Christiansen, J.R.; Corke, R.; Desai, N.; Ilten, P.; Mrenna, S.; Prestel, S.; Rasmussen, C.O.; Skands, P.Z. An Introduction to PYTHIA 8.2. Comput. Phys. Commun. 2015, 191, 159–177. [Google Scholar] [CrossRef]
- Buckley, A.; Ferrando, J.; Lloyd, S.; Nordström, K.; Page, B.; Rüfenacht, M.; Schönherr, M.; Watt, G. LHAPDF6: Parton density access in the LHC precision era. Eur. Phys. J. C 2015, 75, 132. [Google Scholar] [CrossRef]
- Galassi, M.; Davies, J.; Theiler, J.; Gough, B.; Jungman, G.; Alken, P.; Booth, M.; Rossi, F.; Ulerich, R. GNU Scientific Library Reference Manual, 3rd ed.; Network Theory Limited: London, UK, 2009; ISBN 0954612078. [Google Scholar]
- Lepage, G.P. A new algorithm for adaptive multidimensional integration. J. Comp. Phys. 1978, 27, 192–203. [Google Scholar] [CrossRef]
- ROOT Data Analysis Framework. Available online: https://root.cern.ch/ (accessed on 30 April 2019).
- Dulat, S.; Hou, T.J.; Gao, J.; Guzzi, M.; Huston, J.; Nadolsky, P.; Pumplin, J.; Schmidt, C.; Stump, D.; Yuan, C.P. New parton distribution functions from a global analysis of quantum chromodynamics. Phys. Rev. D 2016, 93, 033006. [Google Scholar] [CrossRef]
- Eskola, K.J.; Paakkinen, P.; Paukkunen, H.; Salgado, C.A. EPPS16: Nuclear parton distributions with LHC data. Eur. Phys. J. C 2017, 77, 163. [Google Scholar] [CrossRef] [PubMed]
- Buckley, A.; Hoeth, H.; Lacker, H.; Schulz, H.; von Seggern, J.E. Systematic event generator tuning for the LHC. Eur. Phys. J. C 2010, 65, 331. [Google Scholar] [CrossRef]
- Tange, O. GNU Parallel: The Command-Line Power Tool. Available online: https://www.usenix.org/system/files/login/articles/105438-Tange.pdf (accessed on 26 May 2019).
- Adam, J.; Adamová, D.; Aggarwal, M.M.; Rinella, G.A.; Agnello, M.; Agrawal, N.; Ahammed, Z.; Ahmad, S.; Ahn, S.U.; Aiola, S.; et al. Multiplicity dependence of charged pion, kaon, and (anti)proton production at large transverse momentum in p-Pb collisions at = 5.02 TeV. Phys. Lett. B 2016, 760, 720–735. [Google Scholar] [CrossRef]
- Aamodt, K.; Abel, N.; Abeysekara, U.; Quintana, A.A.; Abramyan, A.; Adamova, D.; Aggarwal, M.M.; Rinella, G.A.; Agocs, A.G.; Salazar, S.A.; et al. Charged-particle multiplicity measurement in proton–proton collisions at = 7 TeV with ALICE at LHC. Eur. Phys. J. C 2010, 68, 345. [Google Scholar] [CrossRef]
- Acharya, S.; Adamová, D.; Adolfsson, J.; Aggarwal, M.M.; AglieriRinella, G.; Agnello, M.; Agrawal, N.; Ahammed, Z.; Ahmad, N.; Ahn, S.U.; et al. Charged-particle multiplicity distributions over a wide pseudorapidity range in proton–proton collisions at = 0.9, 7, and 8 TeV. Eur. Phys. J. C 2017, 77, 852. [Google Scholar] [CrossRef]
- Wilk, G.; Wlodarczyk, Z. Tsallis Distribution Decorated With Log-Periodic Oscillation. Entropy 2015, 17, 384. [Google Scholar] [CrossRef]
- Rybczyński, M.; Wilk, G.; Włodarczyk, Z. System size dependence of the log-periodic oscillations of transverse momentum spectra. Eur. Phys. J. Web Conf. 2015, 90, 01002. [Google Scholar] [CrossRef]

| Parameter | Description |
|---|---|
| soft-hard separation scale: minimum transfer of hard or semihard scatterings | |
| the inclusive cross section for soft interactions | |
| the cross section that characterizes the geometrical size of a nucleon | |
| the parameter in the scaled eikonal function of nucleon used to calculate total cross-section | |
| K | K-factor for the differential jet cross sections in the lowest order pQCD calculation |
| cut for classifying the connected-independent type strings at fragmentation | |
| invariant mass cut-off for the dipole radiation of a string system below which soft gluon radiations are terminated | |
| minimum value for the invariant mass of the excited string system in a hadron–hadron interaction | |
| the parameter that regularizes the singularity at in the distribution of the soft kick | |
| the parameter that gives the scale beyond which the kick distribution will be similar to | |
| F | the scale in the form factor to suppress the transfer to diquarks in hard scatterings |
| phenomenological parameters () of the soft parton distribution function that yield an x distribution of the valence quarks in a soft interaction | |
| phenomenological parameters () of the soft parton distribution function that yield an x distribution of the sea quarks in a soft interaction | |
| StringPT:temperature | the temperature parameter in the Lund fragmentation model as described in [23] |
| StringPT:tempPreFactor | the temperature prefactor for strange quarks and diquarks in the Lund fragmentation model as described in [23] |
| StringZ:aExtraSQuark | parameters in the Lund symmetric fragmentation function as described in [23] |
| StringZ:aExtraDiuark |
| Hadron | n | q | T (GeV) | A | v | |
|---|---|---|---|---|---|---|
| 7.415 ± 0.033 | 1.135 ± 0.005 | 0.089 ± 0.010 | 73.188 ± 9.700 | 0.000 ± 0.119 | 174.225/54 | |
| 7.539 ± 0.086 | 1.133 ± 0.013 | 0.155 ± 0.010 | 0.915 ± 0.095 | 0.000 ± 0.066 | 20.274/47 | |
| 8.805 ± 0.184 | 1.114 ± 0.023 | 0.191 ± 0.012 | 0.124 ± 0.013 | 0.000 ± 0.054 | 18.462/45 |
| Class | I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII | XIII | XIV | XV |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 70 | 80 | 90 | |
| 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 70 | 80 | 90 | 100 |
| Hadron | (GeV) |
|---|---|
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bíró, G.; Barnaföldi, G.G.; Papp, G.; Biró, T.S. Multiplicity Dependence in the Non-Extensive Hadronization Model Calculated by the HIJING++ Framework. Universe 2019, 5, 134. https://doi.org/10.3390/universe5060134
Bíró G, Barnaföldi GG, Papp G, Biró TS. Multiplicity Dependence in the Non-Extensive Hadronization Model Calculated by the HIJING++ Framework. Universe. 2019; 5(6):134. https://doi.org/10.3390/universe5060134
Chicago/Turabian StyleBíró, Gábor, Gergely Gábor Barnaföldi, Gábor Papp, and Tamás Sándor Biró. 2019. "Multiplicity Dependence in the Non-Extensive Hadronization Model Calculated by the HIJING++ Framework" Universe 5, no. 6: 134. https://doi.org/10.3390/universe5060134
APA StyleBíró, G., Barnaföldi, G. G., Papp, G., & Biró, T. S. (2019). Multiplicity Dependence in the Non-Extensive Hadronization Model Calculated by the HIJING++ Framework. Universe, 5(6), 134. https://doi.org/10.3390/universe5060134





