Study of Angular Correlations in Monte Carlo Simulations in Pb-Pb Collisions
Abstract
:1. Introduction
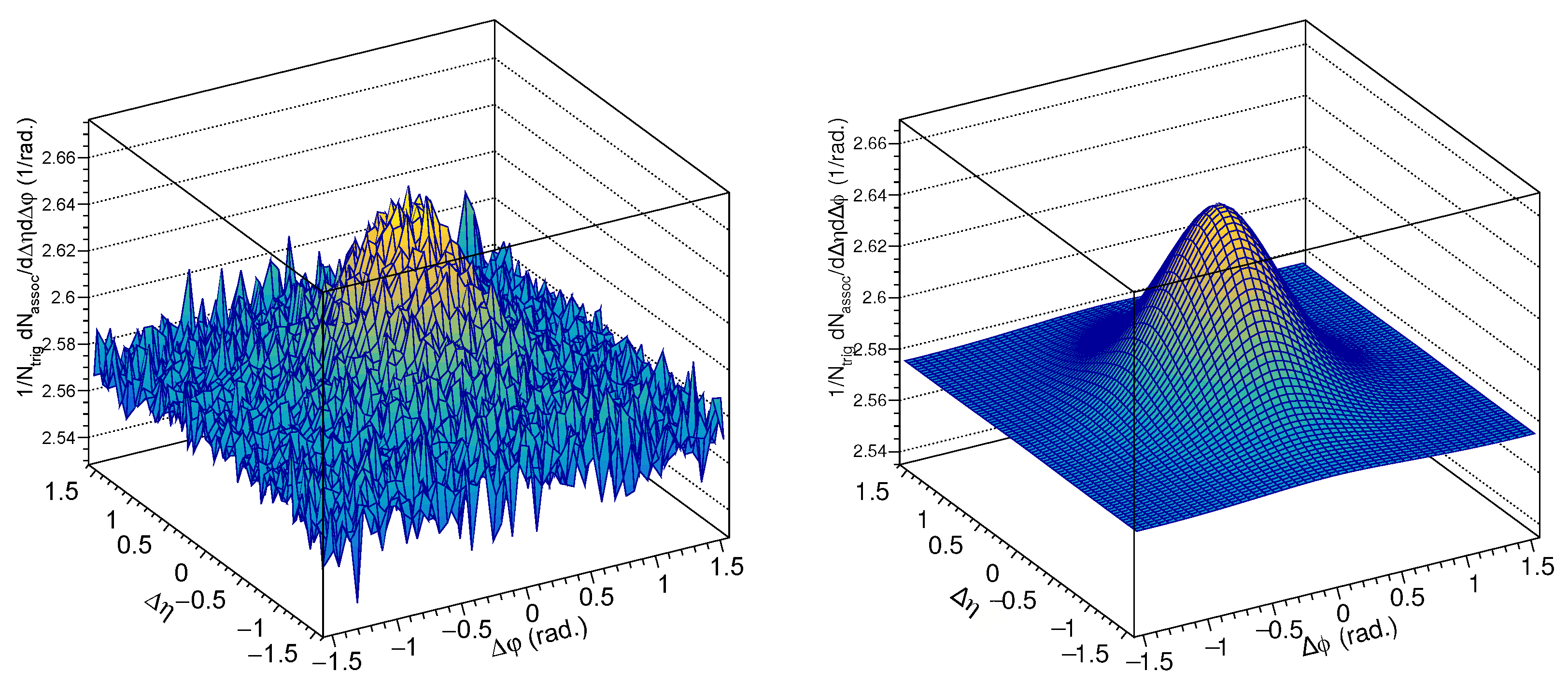
2. Analysis Method
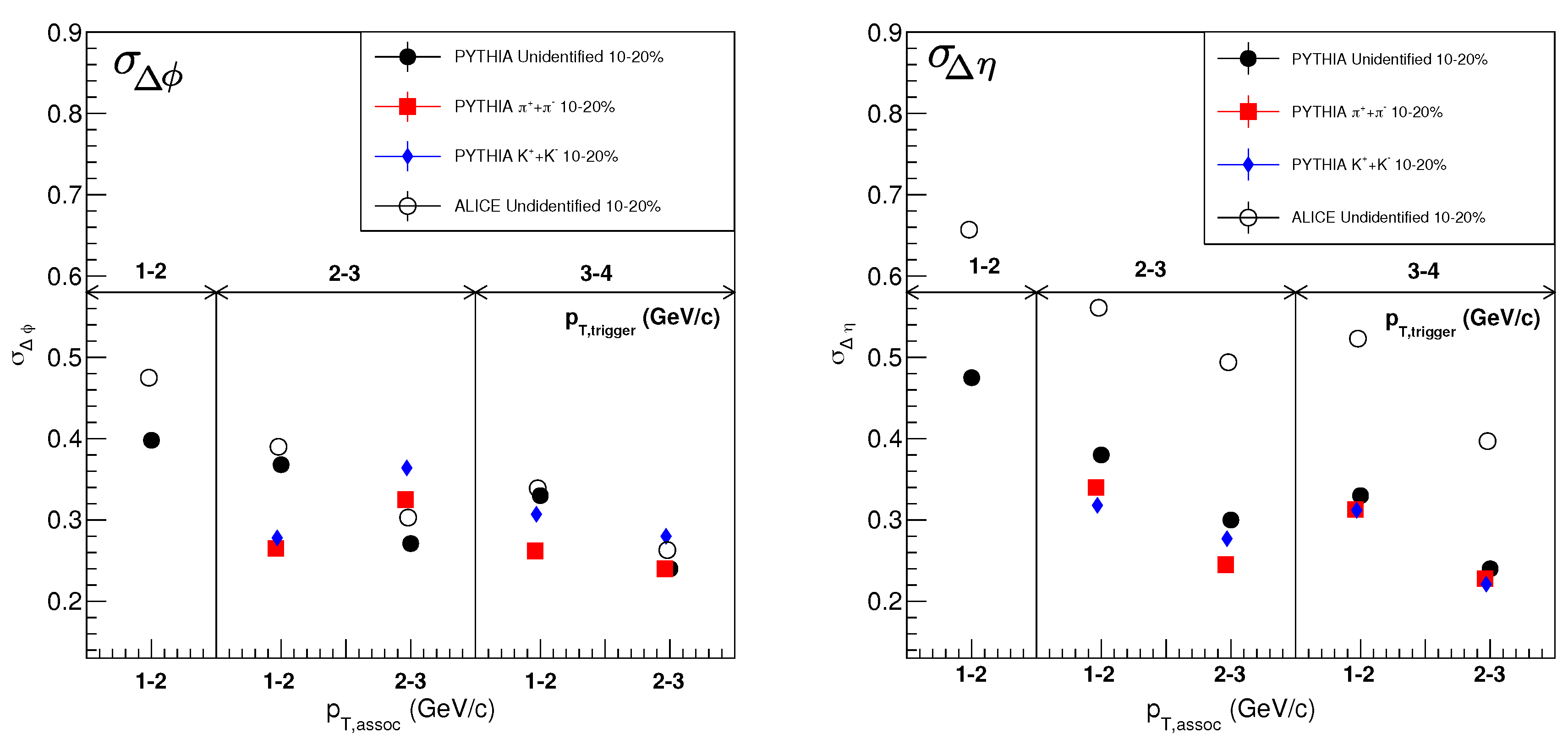
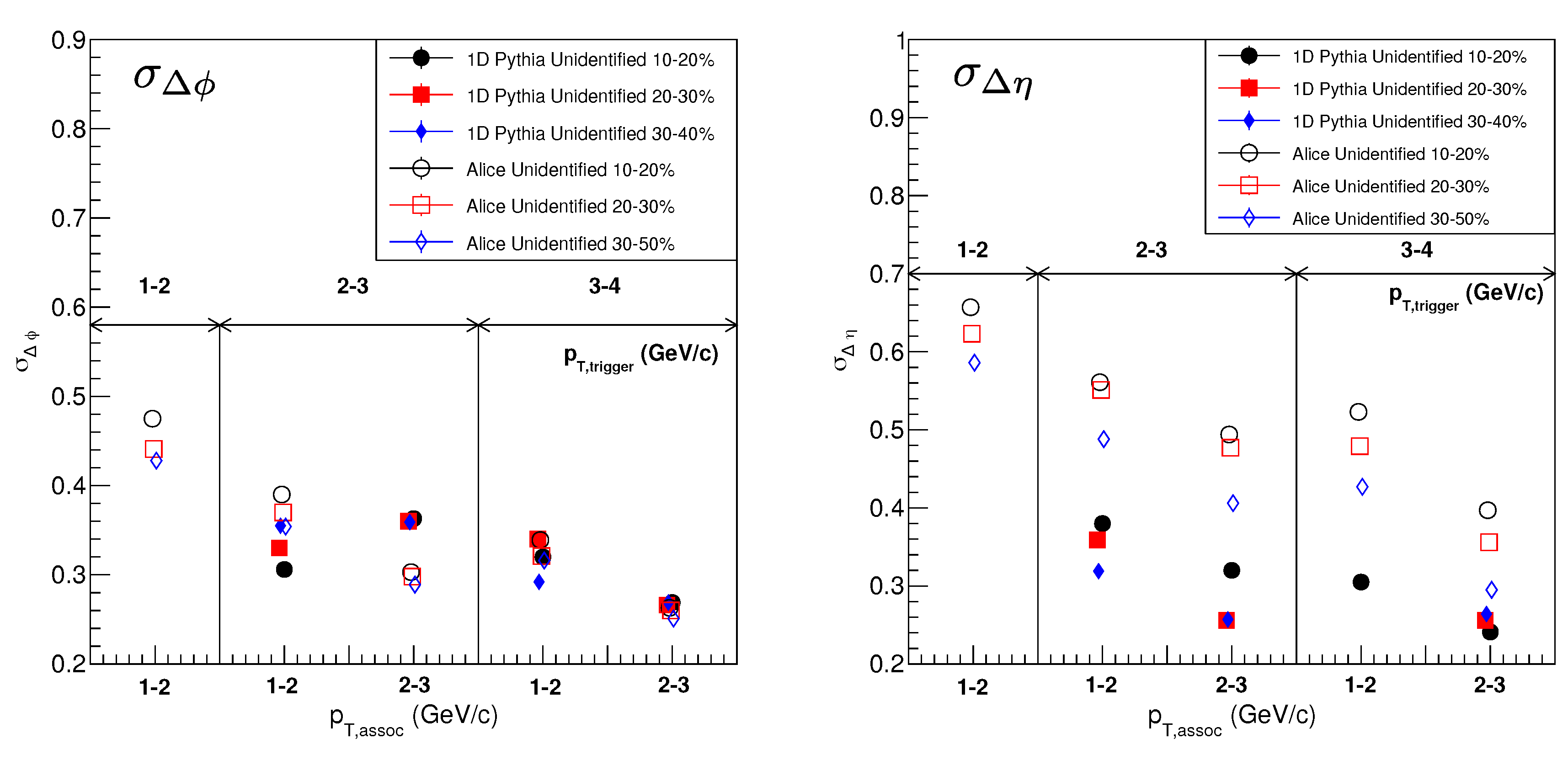
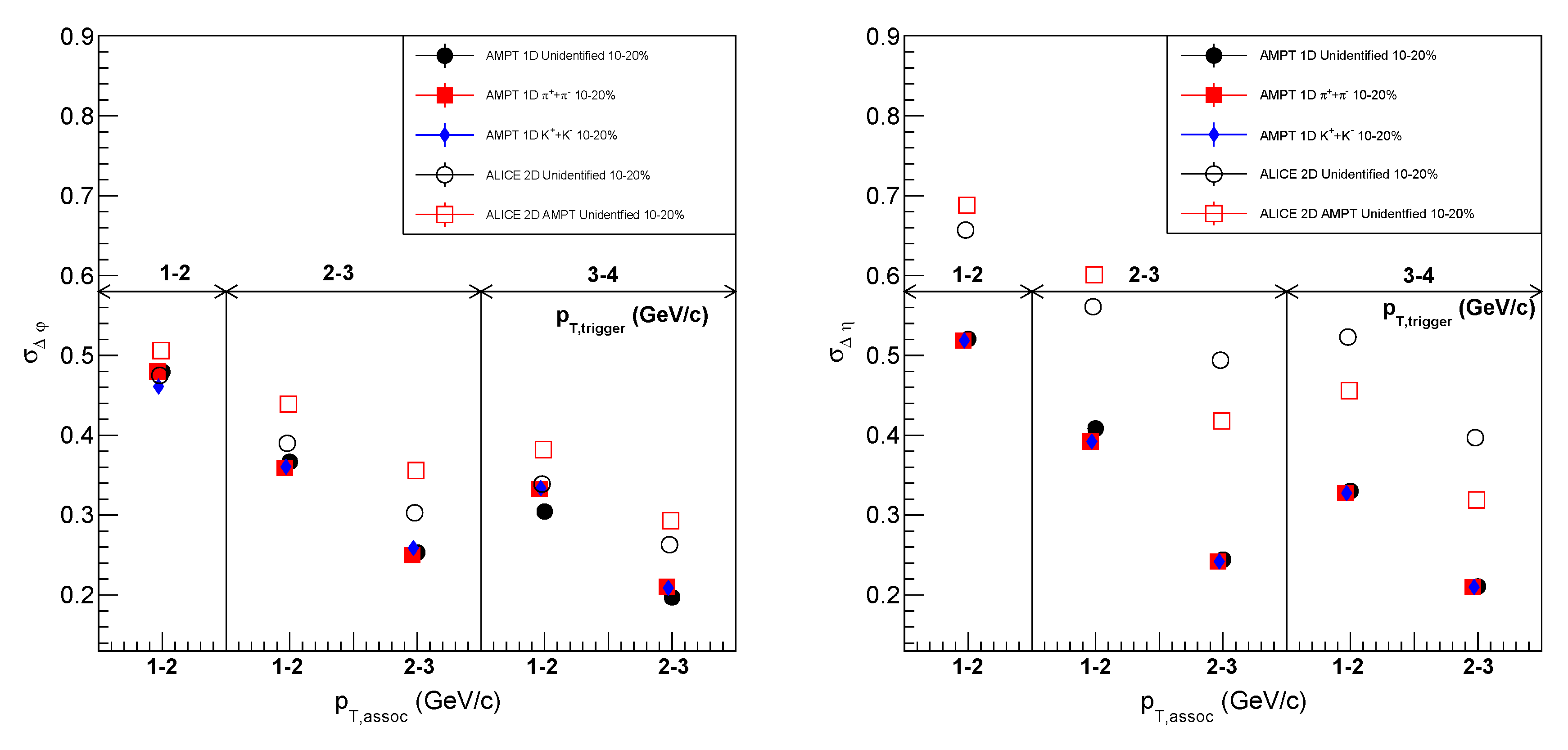
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ALICE | A Large Ion Collider Experiment |
| QCD | Quantum chromodynamics |
| AMPT | A Multi-Phase Transport Model |
| MPI | Multi-Parton Interaction |
| CR | Color Reconnection |
References
- Gross, D.; Wilczek, F. Ultraviolet Behavior of Non-abelian Gauge Theories. Phys. Rev. Lett. 1973, 30, 1343. [Google Scholar] [CrossRef]
- Cao, S.; Luo, T.; Qin, G.; Wang, X. Heavy and light flavor jet quenching at RHIC and LHC energies. Phys. Lett. B 2018, 777, 255–259. [Google Scholar] [CrossRef]
- The ALICE Collaboration. Performance of the ALICE Experiment at the CERN LHC. Int. J. Mod. Phys. A 2014, 2014 29, 1430044. [Google Scholar]
- The ALICE Collaboration. Evolution of the longitudinal and azimuthal structure of the near-side jet peak in Pb-Pb collisions at sNN=2.76 TeV. Phys. Rev. C 2017, 96, 034904. [Google Scholar] [CrossRef]
- The ALICE Collaboration. Anomalous evolution of the near-side jet peak shape in Pb-Pb collisions at sNN=2.76 TeV. Phys. Rev. Lett. 2017, 119, 102301. [Google Scholar] [CrossRef] [PubMed]
- Sjöstrand, T.; Ask, S.; Christiansen, J.R.; Corke, R.; Desai, N.; Ilten, P.; Mrenna, S.; Prestel, S.; Rasmussen, C.O.; Skands, P.Z. An Introduction to PYTHIA 8.2. Comput. Phys. Commun. 2015, 191, 159–177. [Google Scholar] [CrossRef]
- Bierlich, C.; Gustafson, G.; Lönnblad, L.; Shah, H. The Angantyr model for Heavy-Ion Collisions in PYTHIA8. J. High Energy Phys. 2018, 134. [Google Scholar] [CrossRef]
- Lin, Z.W.; Ko, C.M.; Li, B.A.; Zhang, B.; Pal, S. A Multi-Phase Transport Model for Relativistic Heavy Ion Collisions. Phys. Rev. C 2005, 72, 064901. [Google Scholar] [CrossRef]
- Andersson, B.; Gustafson, G.; Pi, H. The FRITIOF model for very high energy hadronic collisions. Z. Phys. C Part. Fields 1993, 57, 485–494. [Google Scholar] [CrossRef]
| 1 | String melting: on, Hadronic rescattering: off, Lund String fragmentation parameters: 0.30 GeV/, 0.15 GeV/, The cutoff for minijets: 2.0 GeV/c, Quenching flag: off, Shadowing flag: on, Parton screening mass: 2.265 fm. |
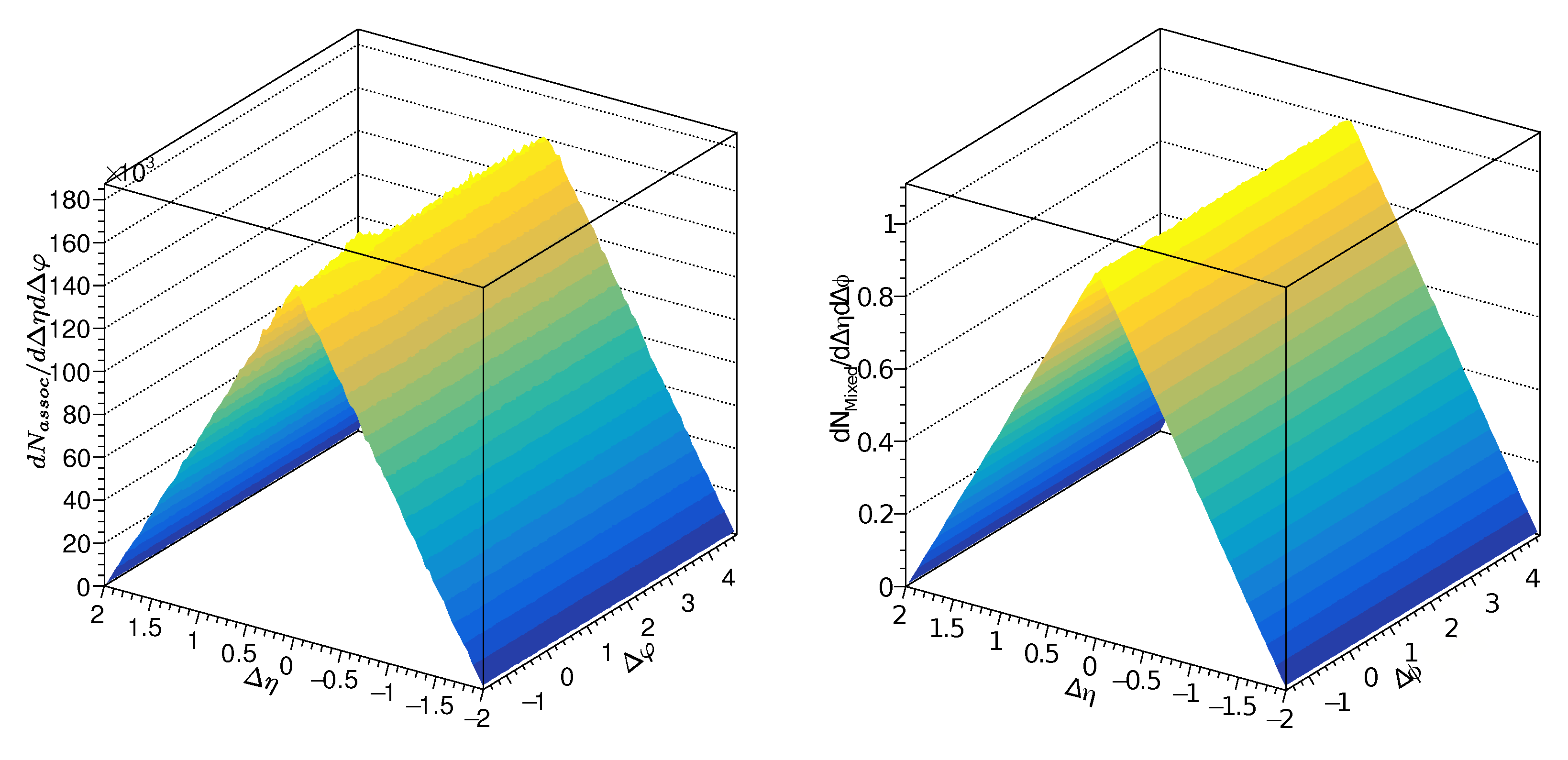
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szigeti, B.E.; Varga-Kofarago, M. Study of Angular Correlations in Monte Carlo Simulations in Pb-Pb Collisions. Universe 2019, 5, 97. https://doi.org/10.3390/universe5050097
Szigeti BE, Varga-Kofarago M. Study of Angular Correlations in Monte Carlo Simulations in Pb-Pb Collisions. Universe. 2019; 5(5):97. https://doi.org/10.3390/universe5050097
Chicago/Turabian StyleSzigeti, Balázs Endre, and Monika Varga-Kofarago. 2019. "Study of Angular Correlations in Monte Carlo Simulations in Pb-Pb Collisions" Universe 5, no. 5: 97. https://doi.org/10.3390/universe5050097




