Quarkonium Phenomenology from a Generalised Gauss Law
Abstract
1. Introduction
2. The Gauss Law Potential Model
2.1. A Novel Formulation
2.2. Vetting with Lattice QCD Data
3. Phenomenology
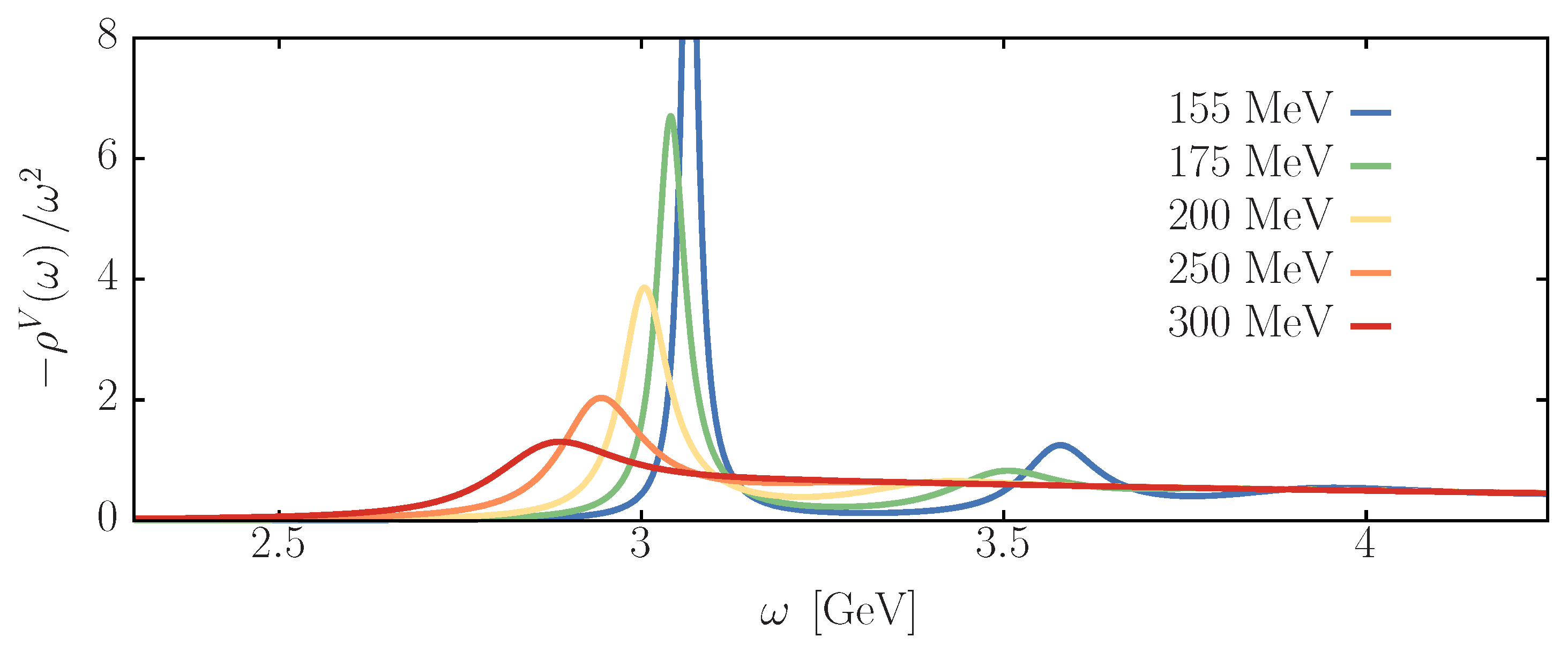
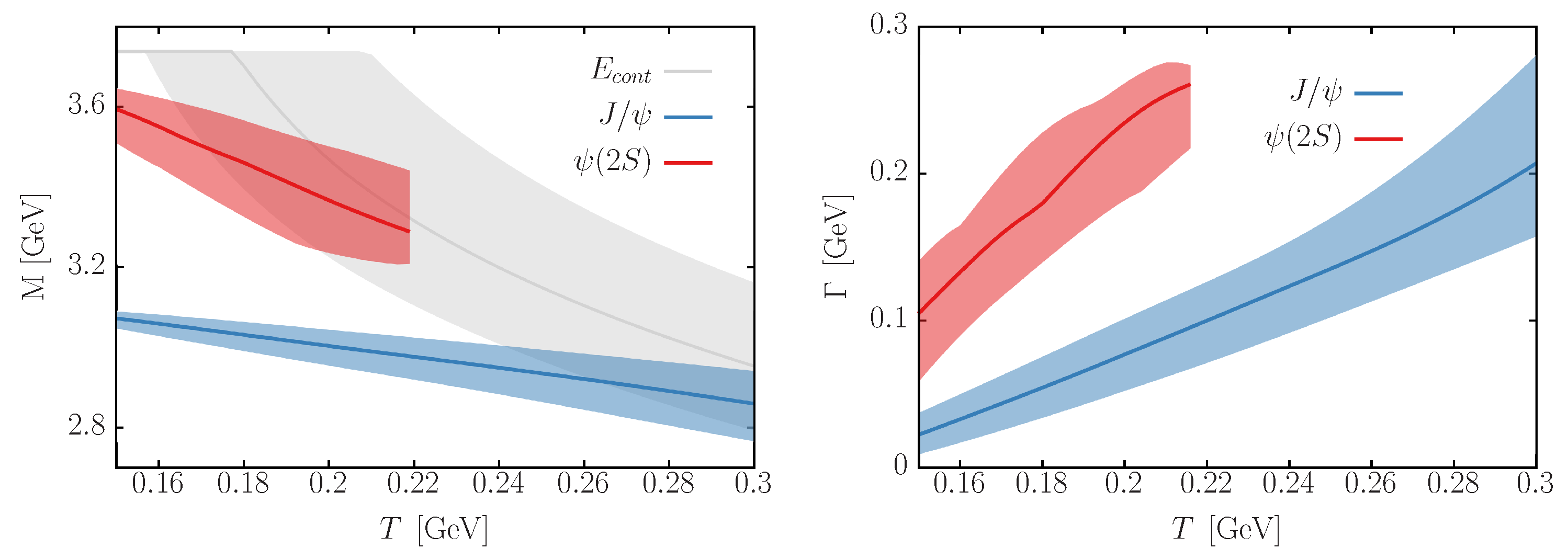
3.1. Spectral Functions at Finite Temperature
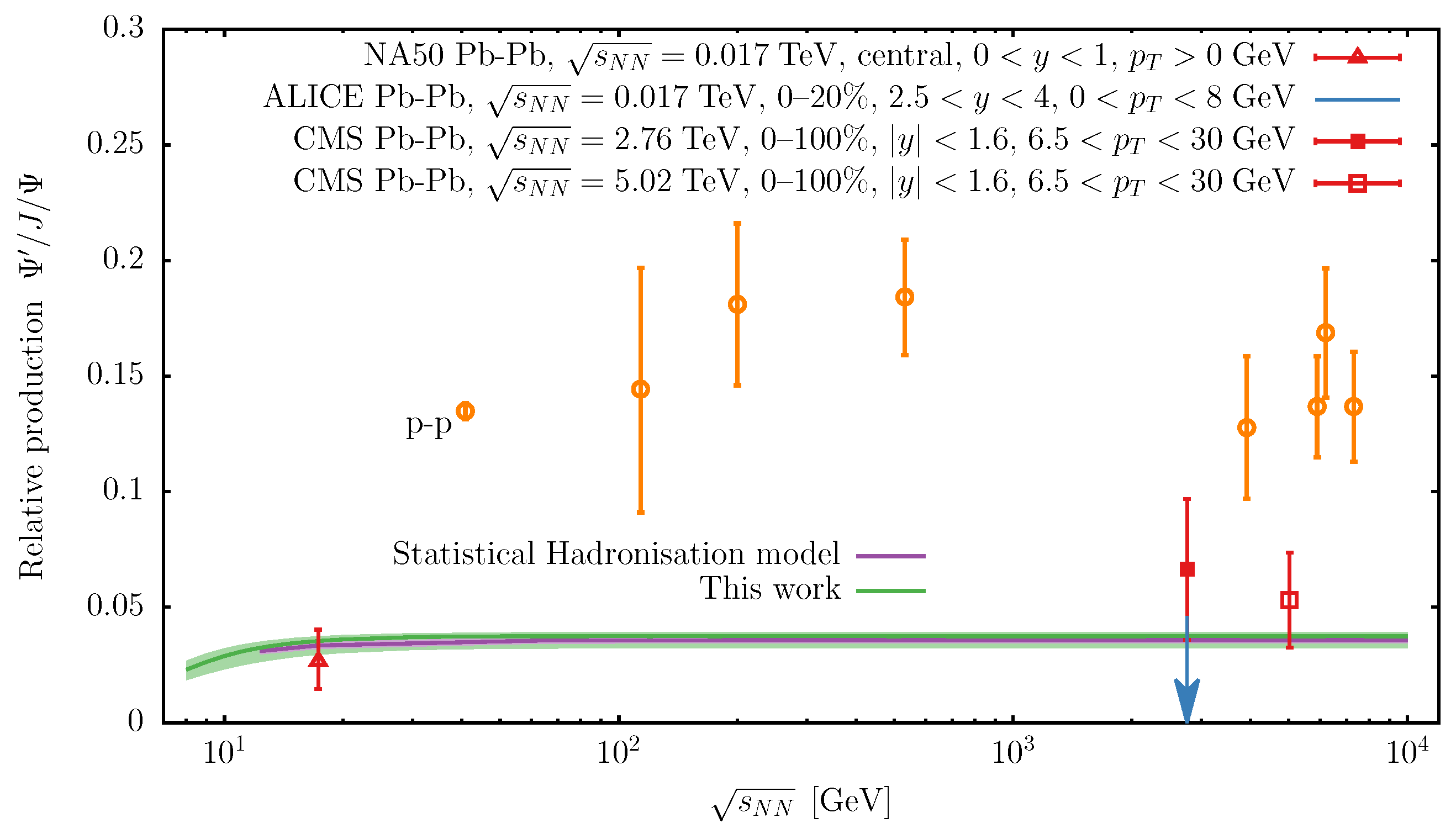
3.2. Applications to Heavy Ion Collisions
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Andronic, A.; Arleo, F.; Arnaldi, R.; Beraudo, A.; Bruna, E.; Caffarri, D.; Conesa del Valle, Z.; Contreras, J.G.; Dahms, T.; Dainese, A.; et al. Heavy-flavour and quarkonium production in the LHC era: From proton–proton to heavy-ion collisions. Eur. Phys. J. 2016, 76, 107. [Google Scholar] [CrossRef] [PubMed]
- Brambilla, N.; Pineda, A.; Soto, J.; Vairo, A. Effective-field theories for heavy quarkonium. Rev. Mod. Phys. 2005, 77, 1423. [Google Scholar] [CrossRef]
- Burnier, Y.; Rothkopf, A. Disentangling the timescales behind the nonperturbative heavy quark potential. Phys. Rev. D 2012, 86, 051503. [Google Scholar] [CrossRef]
- Laine, M.; Philipsen, O.; Tassler, M.; Romatschke, P. Real-time static potential in hot QCD. J. High Energy Phys. 2007, 3, 054. [Google Scholar] [CrossRef]
- Brambilla, N.; Ghiglieri, J.; Vairo, A.; Petreczky, P. Static quark-antiquark pairs at finite temperature. Phys. Rev. D 2008, 78, 014017. [Google Scholar] [CrossRef]
- Kajimotoa, S.; Akamatsua, Y.; Asakawaa, M.; Rothkopf, A. Quantum dynamical dissociation of quarkonia by wave function decoherence in quark-gluon plasma. Nucl. Phys. A 2019, 982, 711–714. [Google Scholar] [CrossRef]
- Petreczky, P.; Rothkopf, A.; Weber, J. Realistic in-medium heavy-quark potential from high statistics lattice QCD simulations. Nucl. Phys. A 2019, 982, 735–738. [Google Scholar] [CrossRef]
- Burnier, Y.; Rothkopf, A. A gauge invariant Debye mass and the complex heavy-quark potential. Phys. Lett. B 2016, 753, 232–236. [Google Scholar] [CrossRef]
- Kapusta, J.I.; Gale, C. Finite-Temperature Field Theory. Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Thakur, L.; Kakade, U.; Patra, B.K. Dissociation of quarkonium in a complex potential. Phys. Rev. D 2014, 89, 094020. [Google Scholar] [CrossRef]
- Burnier, Y.; Kaczmarek, O.; Rothkopf, A. Static Quark-Antiquark Potential in the Quark-Gluon Plasma from Lattice QCD. Phys. Rev. Lett. 2015, 114, 082001. [Google Scholar] [CrossRef]
- Bazavov, A.; Bhattacharya, T.; Cheng, M.; DeTar, C.; Ding, H.-T.; Gottlieb, S.; Gupta, R.; Hegde, P.; Heller, U.M.; Karsch, F.; et al. The chiral and deconfinement aspects of the QCD transition. Phys. Rev. D 2012, 85, 054503. [Google Scholar] [CrossRef]
- Burnier, Y.; Kaczmarek, O.; Rothkopf, A. Quarkonium at finite temperature: towards realistic phenomenology from first principles. J. High Energy Phys. 2015, 12, 1–34. [Google Scholar] [CrossRef]
- Burnier, Y.; Laine, M.; Vepsalainen, M. Heavy quarkonium in any channel in resummed hot QCD. J. High Energy Phys. 2008, 1, 43. [Google Scholar] [CrossRef]
- Andronic, A.; Braun-Munzinger, P.; Redlich, K.; Stachel, J. Decoding the phase structure of QCD via particle production at high energy. Nature 2018, 561, 321–330. [Google Scholar] [CrossRef]
- Laine, M.; Vuorinen, A. Basics of Thermal Field Theory. Lect. Notes Phys. 2016, 925, 1–281. [Google Scholar]
- Bodwin, G.T.; Braaten, E.; Lepage, G.P. Rigorous QCD analysis of inclusive annihilation and production of heavy quarkonium. Phys. Rev. D 1995, 51, 1125–1171. [Google Scholar] [CrossRef]
- Alessandro, B.; et al.; [NA50 Collaboration] Ψ′ production in Pb–Pb collisions at 158 GeV/nucleon. Eur. Phys. J. C 2007, 49, 559–567. [Google Scholar] [CrossRef]
- Adam, J.; et al.; [ALICE Collaboration] Differential studies of inclusive J/Ψ and Ψ(2S) production at forward rapidity in Pb-Pb collisions at = 2.76 TeV. J. High Energy Phys. 2016, 5, 179. [Google Scholar] [CrossRef]
- Khachatryan, V.; et al.; [CMS Collaboration] Measurement of Prompt ψ(2S) to J/ψ Yield Ratios in Pb-Pb and p-p Collisions at = 2.76 TeV. Phys. Rev. Lett. 2014, 113, 262301. [Google Scholar] [CrossRef]
- Sirunyan, A.M.; et al.; [CMS Collaboration] Relative Modification of Prompt ψ(2S) and J/ψ Yields from pp to PbPb Collisions at = 5.02 TeV. Phys. Rev. Lett. 2017, 118, 162301. [Google Scholar] [CrossRef]
- Adare, A.; et al.; [PHENIX Collaboration] Relative Yields and Nuclear Modification of Ψ′ to J/Ψ mesons in p+p, p(3He)+A Collisions at = 200 GeV, measured in PHENIX. Nucl. Part. Phys. Proc. 2017, 289–290, 417–420. [Google Scholar]
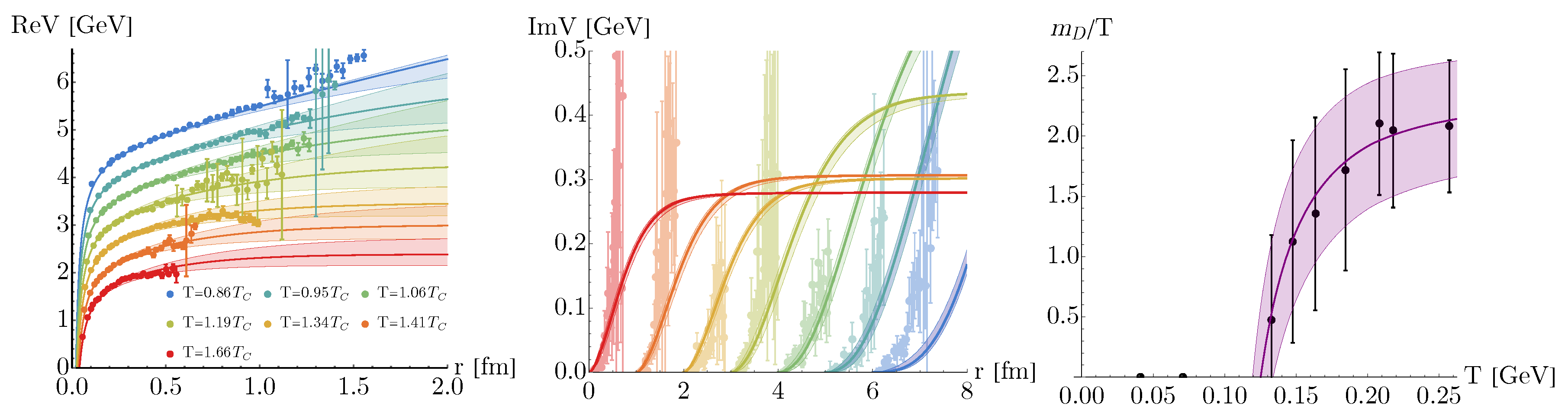
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lafferty, D.; Rothkopf, A. Quarkonium Phenomenology from a Generalised Gauss Law. Universe 2019, 5, 119. https://doi.org/10.3390/universe5050119
Lafferty D, Rothkopf A. Quarkonium Phenomenology from a Generalised Gauss Law. Universe. 2019; 5(5):119. https://doi.org/10.3390/universe5050119
Chicago/Turabian StyleLafferty, David, and Alexander Rothkopf. 2019. "Quarkonium Phenomenology from a Generalised Gauss Law" Universe 5, no. 5: 119. https://doi.org/10.3390/universe5050119
APA StyleLafferty, D., & Rothkopf, A. (2019). Quarkonium Phenomenology from a Generalised Gauss Law. Universe, 5(5), 119. https://doi.org/10.3390/universe5050119




