Highlight Talk from Super-Kamiokande †
Abstract
1. Introduction
2. Super-Kamiokande Detector
3. Atmospheric Neutrino
3.1. Introduction
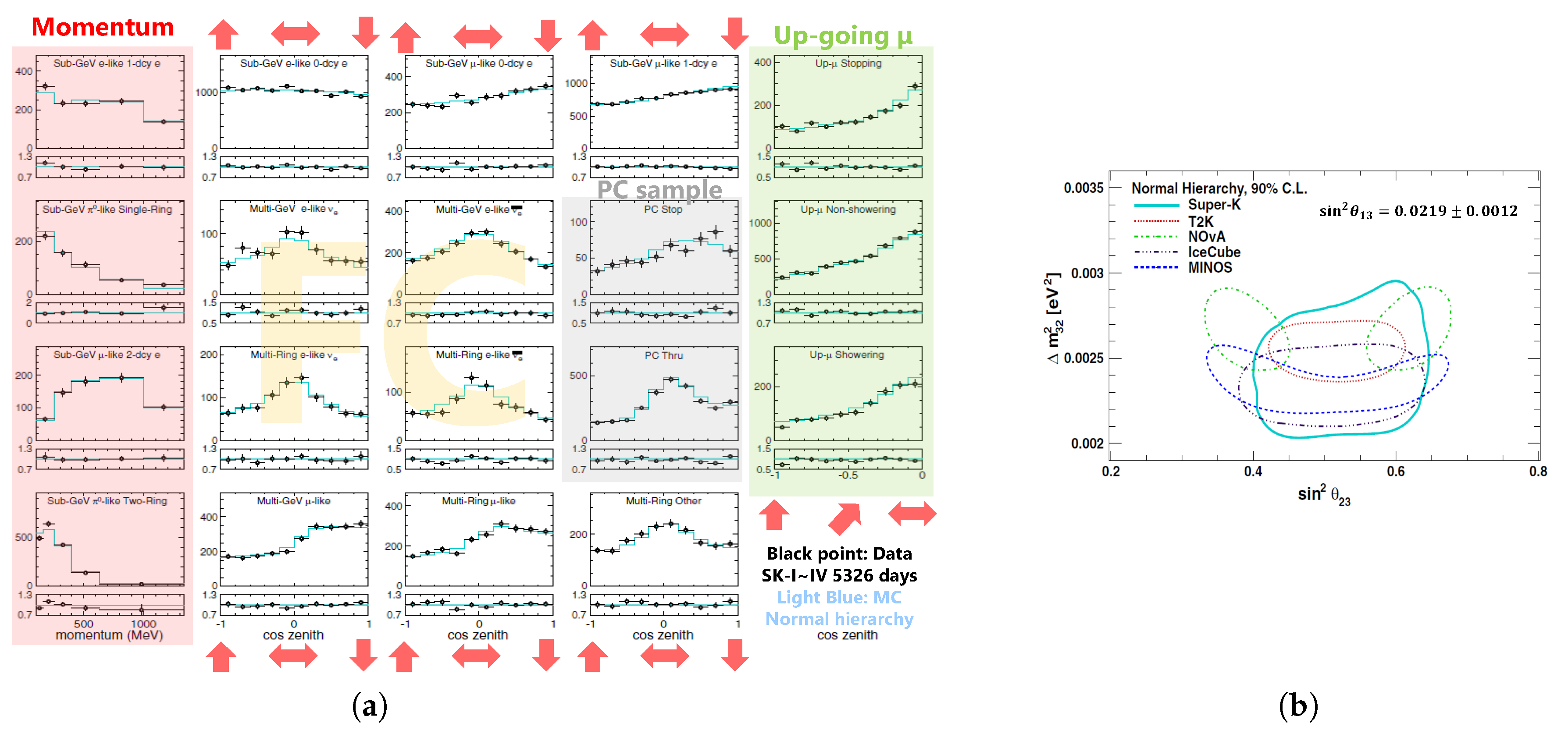
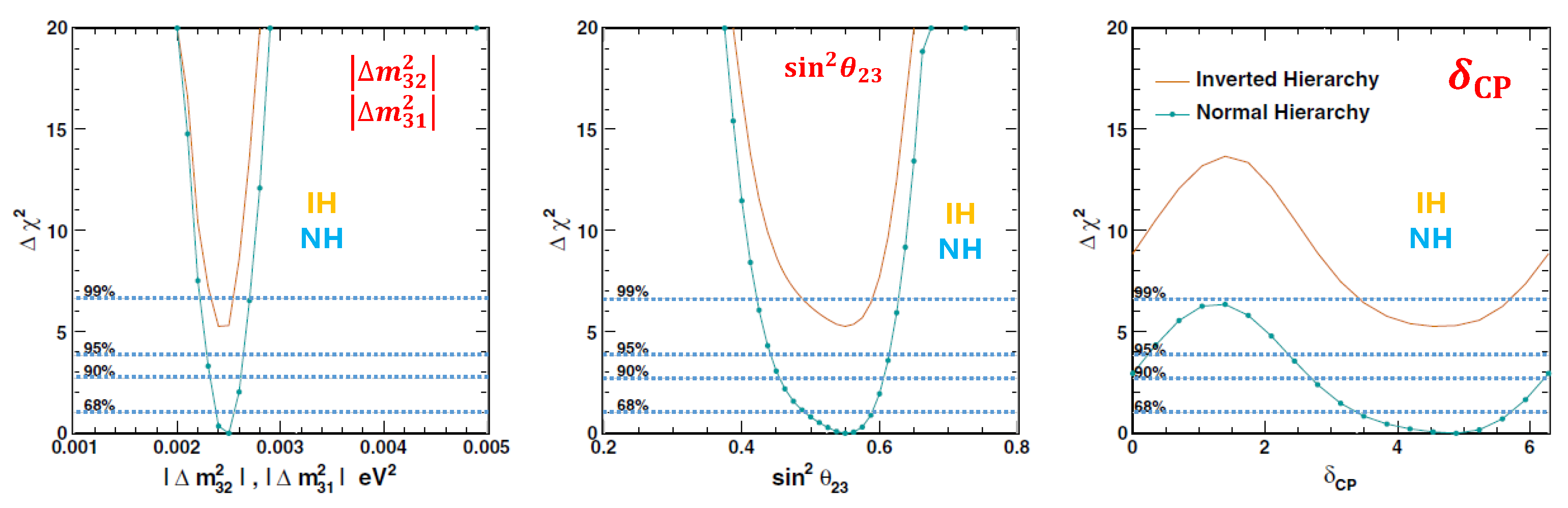
3.2. Three-Flavor Oscillation Analysis
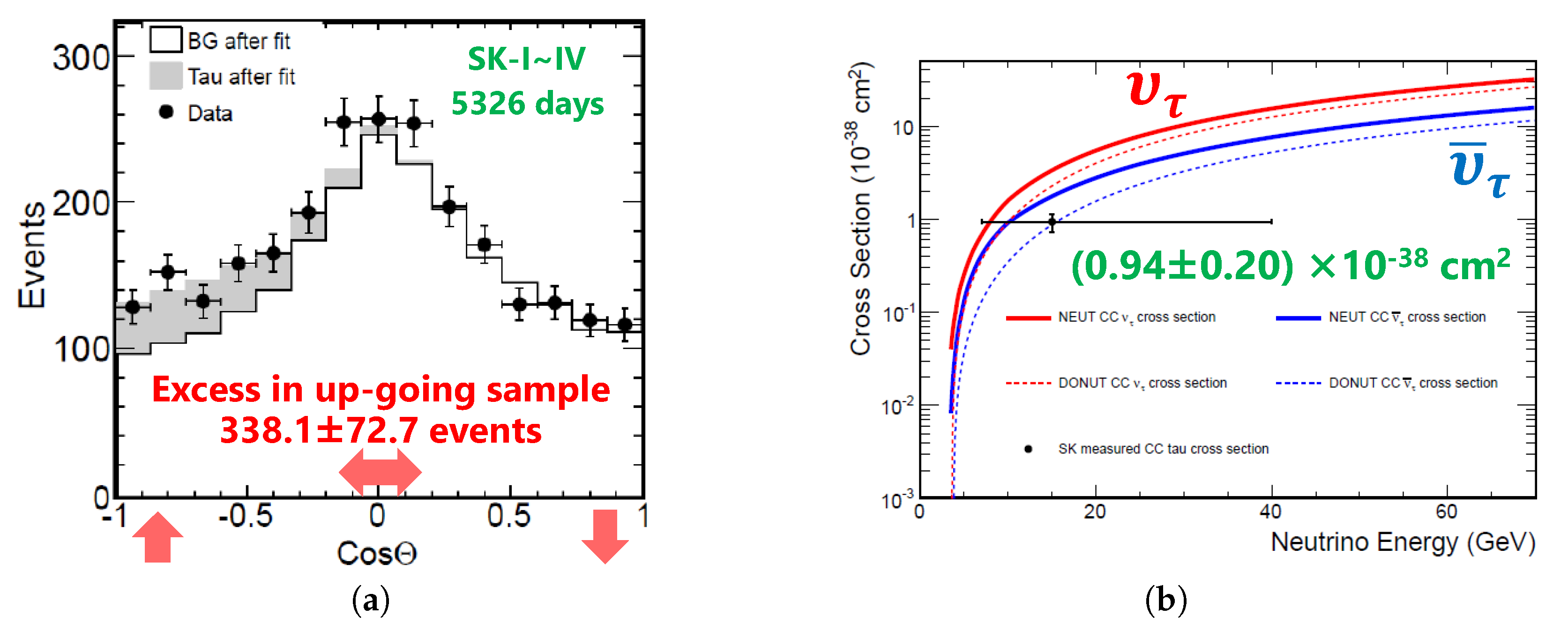
3.3. Tau Neutrino Appearance
4. Solar Neutrino
4.1. Introduction
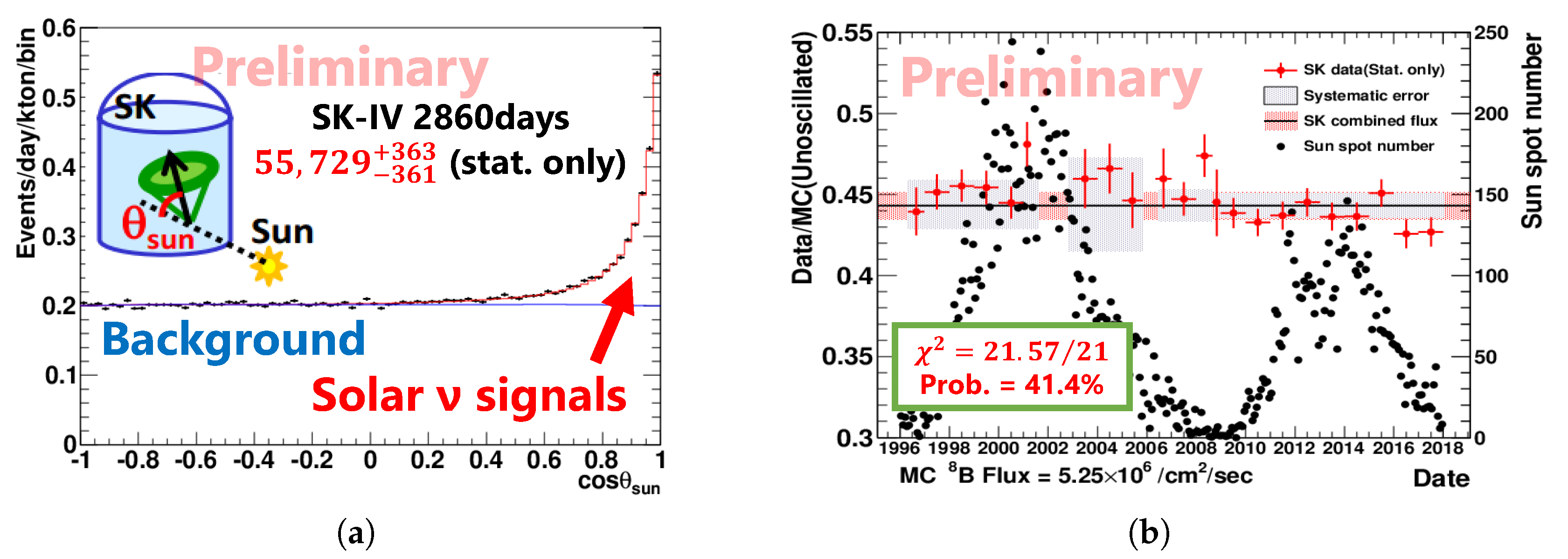
4.2. Flux Measurement
4.3. Energy Spectrum Analysis
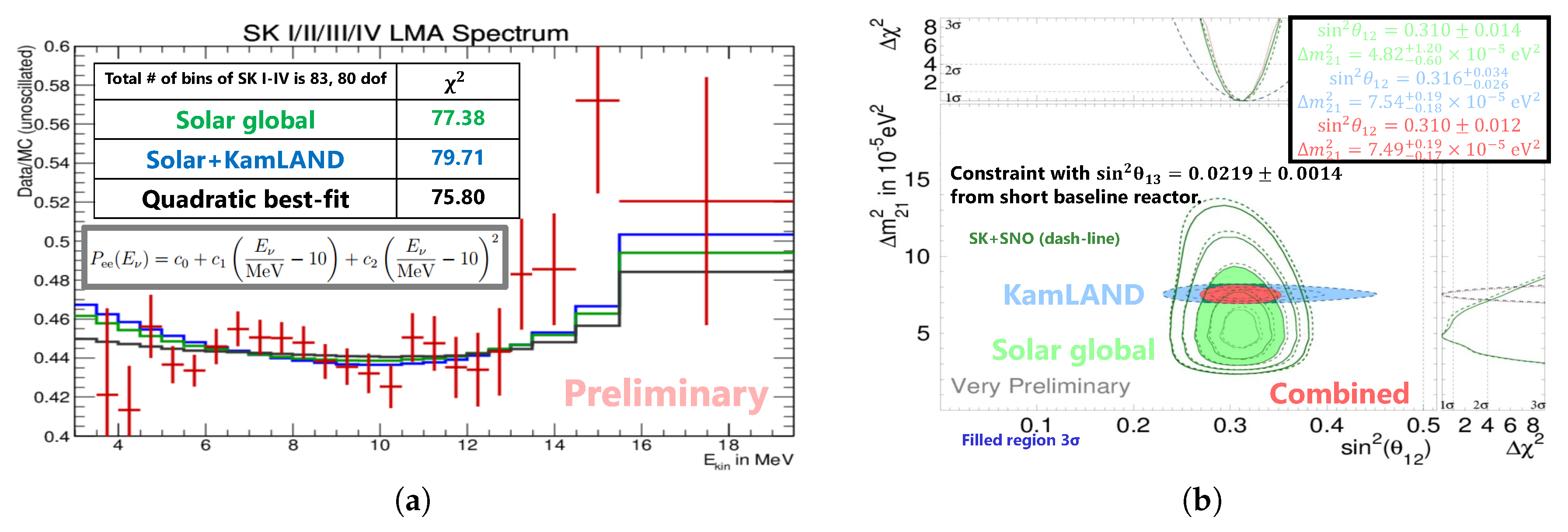
4.4. Neutrino Oscillation Analysis
5. Future Prospect (SK-Gd)
5.1. Physics Motivation
5.2. Tank Refurbish Work and Future Plan
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ziro, M.; Masami, N.; Sakata, S. Remarks on the Unified Model of Elementary Particles. Prog. Theor. Phys. 1962, 28, 870–880. [Google Scholar]
- Pontecorvo, B. Neutrino experiments and the problem of conservation of leptonic. Sov. Phys. JETP 1968, 26, 984–988. [Google Scholar]
- Fukuda, Y.; et al. [Super-Kamiokande Collaboration] Evidence for Oscillation of Atmospheric Neutrinos. Phys. Rev. Lett. 1998, 81, 1562. [Google Scholar] [CrossRef]
- Mikheyev, S.P.; Smirnov, A.Y. Resonance Amplification of Oscillations in Matter and Spectroscopy of Solar Neutrinos. Sov. J. Nucl. Phys. 1985, 42, 913–917. [Google Scholar]
- Wolfenstein, L. Neutrino oscillations in matter. Phys. Rev. D 1978, 17, 2369. [Google Scholar] [CrossRef]
- Fukuda, S.; et al. [Super-Kamiokande Collaboration] The Super-Kamiokande detector. Nucl. Instrum. Methods A 2003, 501, 418–462. [Google Scholar] [CrossRef]
- Abe, K.; et al. [Super-Kamiokande Collaboration] Calibration of the Super-Kamiokande detector. Nucl. Instrum. Methods A 2014, 737, 253–272. [Google Scholar] [CrossRef]
- Kume, H.; Sawaki, S.; Ito, M.; Arisaka, K.; Suzuki, A. 20 inch diameter photomultiplier. Nucl. Instrum. Methods A 1983, 205, 443–449. [Google Scholar] [CrossRef]
- Tanimori, T.; Ikeda, H.; Mori, M.; Kihara, K.; Kitagawa, H.; Haren, Y. Design and performance of semi-custom analog IC including two TACs and two current integrators for ‘Super-Kamiokande’. IEEE Trans. Nucl. Sci. 1989, 36, 497–501. [Google Scholar] [CrossRef]
- Ikeda, H.; Ikeda, M.; Inaba, S.; Takasaki, F. Monolithic shaper amplifier for multianode PMT readout. Nucl. Instrum. Methods A 1990, 292, 439–444. [Google Scholar] [CrossRef]
- Nishino, H.; Awai, K.; Hayato, Y.; Nakayama, S.; Okumura, K.; Shiozawa, M.; Takeda, A.; Ishikawa, K.; Minegishi, A.; Arai, Y. High-speed charge-to-time converter ASIC for the Super-Kamiokande detector. Nucl. Instrum. Methods A 2009, 610, 710–717. [Google Scholar] [CrossRef]
- Yamada, S.; Awai, K.; Hayato, Y.; Kaneyuki, K.; Kouzuma, Y.; Nakayama, S.; Nishino, H.; Okumura, K.; Obayashi, Y.; Shimizu, Y.; et al. Commissioning of the New Electronics and Online System for the Super-Kamiokande Experiment. IEEE Trans. Nucl. Sci. 2010, 57, 428–432. [Google Scholar] [CrossRef]
- Richard, E.; et al. [Super-Kamiokande Collaboration] Measurements of the atmospheric neutrino flux by Super-Kamiokande: Energy spectra, geomagnetic effects, and solar modulation. Phys. Rev. D 2016, 94, 052001. [Google Scholar] [CrossRef]
- Abe, K.; et al. [Super-Kamiokande Collaboration] Atmospheric neutrino oscillation analysis with external constraints in Super-Kamiokande I–IV. Phys. Rev. D 2018, 97, 072001. [Google Scholar] [CrossRef]
- Li, Z.; et al. [Super-Kamiokande Collaboration] Measurement of the tau neutrino cross section in atmospheric neutrino oscillations with Super-Kamiokande. Phys. Rev. D 2018, 98, 052006. [Google Scholar] [CrossRef]
- Renshaw, A.; et al. [Super-Kamiokande Collaboration] First Indication of Terrestrial Matter Effects on Solar Neutrino Oscillation. Phys. Rev. Lett. 2014, 112, 091805. [Google Scholar] [CrossRef] [PubMed]
- Abe, K.; et al. [Super-Kamiokande Collaboration] Solar neutrino measurements in Super-Kamiokande-IV. Phys. Rev. D 2016, 94, 052010. [Google Scholar] [CrossRef]
- Zhang H.; et al. [Super-Kamiokande Collaboration] Supernova Relic Neutrino search with neutron tagging at Super-Kamiokande-IV. Astropart. Phys. 2015, 60, 41–46. [Google Scholar] [CrossRef]
- Abe, K.; et al. [Super-Kamiokande Collaboration] Search for proton decay via p → e+ π0 and p → μ+ π0 in 0.31 megaton·years exposure of the Super-Kamiokande water Cherenkov detector. Phys. Rev. D 2017, 95, 012004. [Google Scholar] [CrossRef]
- Abe, K.; et al. [Super-Kamiokande Collaboration] Search for nucleon decay into charged antilepton plus meson in 0.316 megaton·years exposure of the Super-Kamiokande water Cherenkov detector. Phys. Rev. D 2017, 96, 012003. [Google Scholar] [CrossRef]
- Press, W.H.; Spergel, D.N. Capture by the sun of a galactic population of weakly interacting, massive particles. Astrophys. J. 1985, 296, 679–684. [Google Scholar] [CrossRef]
- Joseph, S.; Keith, O.; Mark, S. The photino, the sun, and high-energy neutrinos. Phys. Rev. Lett. 1985, 55, 257. [Google Scholar]
- Gaisser, T.K.; Steigman, G.; Tilav, S. Limits on cold-dark-matter candidates from deep underground detectors. Phys. Rev. D 1986, 34, 2206. [Google Scholar] [CrossRef]
- Andrew, G. Resonant enhancements in weakly interacting massive particle capture by the earth. Astrophys. J. 1987, 321, 571–585. [Google Scholar]
- John, E.; Enqvist, K.; Nanopoulous, D.V.; Tamvakis, K. Gaugino masses and grand unification. Phys. Lett. B 1985, 155, 381–386. [Google Scholar]
- Bottino, A.; Fornengo, N.; Scopel, S. Light relic neutralinos. Phys. Rev. D. 2003, 67, 063519. [Google Scholar] [CrossRef]
- Niro, V.; Bottino, A.; Fornengo, N.; Scopel, S. Investigating light neutralinos at neutrino telescopes. Phys. Rev. D 2009, 80, 095019. [Google Scholar] [CrossRef]
- Kaustubh, A.; Yanou, C.; Lina, N.; Jesse, T. (In)direct detection of boosted dark matter. Cosmol. Astropart. Phys. 2014, 10, 62. [Google Scholar]
- Huang, J.; Zhao, Y. Dark matter induced nucleon decay: Model and signatures. J. High Energy Phys. 2014, 2014, 77. [Google Scholar] [CrossRef]
- Cherry, J.F.; Frandsen, M.T.; Shoemaker, I.M. Direct Detection Phenomenology in Models Where the Products of Dark Matter Annihilation Interact with Nuclei. Phys. Rev. Lett. 2015, 114, 231303. [Google Scholar] [CrossRef]
- Kachulis, C.; et al. [Super-Kamiokande Collaboration] Search for Boosted Dark Matter Interacting with Electrons in Super-Kamiokande. Phys. Rev. Lett. 2018, 120, 0221301. [Google Scholar] [CrossRef] [PubMed]
- Choi, K.; et al. [Super-Kamiokande Collaboration] Search for Neutrinos from Annihilation of Captured Low-Mass Dark Matter Particles in the Sun by Super-Kamiokande. Phys. Rev. Lett. 2014, 114, 141301. [Google Scholar]
- Abe, K.; et al. [Super-Kamiokande Collaboration] Limits on sterile neutrino mixing using atmospheric neutrinos in Super-Kamiokande. Phys. Rev. D 2015, 91, 052019. [Google Scholar] [CrossRef]
- Abe, K.; et al. [Super-Kamiokande Collaboration] Test of Lorentz invariance with atmospheric neutrinos. Phys. Rev. D 2015, 91, 052003. [Google Scholar] [CrossRef]
- Super-Kamiokande Web Page. Available online: http://www-sk.icrr.u-tokyo.ac.jp/sk/publications/index-e.html (accessed on 9 January 2019).
- Sanuki, T.; Honda, M.; Kajita, T.; Kasahara, K.; Midorikawa, S. Study of cosmic ray interaction model based on atmospheric muons for the neutrino flux calculation. Phys. Rev. D 2007, 75, 043005. [Google Scholar] [CrossRef]
- Honda, M.; Kajita, T.; Kasahara, K.; Midorikawa, S.; Sanuki, T. Calculation of atmospheric neutrino flux using the interaction model calibrated with atmospheric muon data. Phys. Rev. D 2007, 75, 043006. [Google Scholar] [CrossRef]
- Honda, M.; Kajita, T.; Kasahara, K.; Midorikawa, S. Improvement of low energy atmospheric neutrino flux calculation using the JAM nuclear interaction model. Phys. Rev. D 2011, 83, 123001. [Google Scholar] [CrossRef]
- Honda, M.; Sajjad, A.M.; Kajita, T.; Kasahara, K.; Midorikawa, S. Atmospheric neutrino flux calculation using the NRLMSISE-00 atmospheric model. Phys. Rev. D 2015, 92, 023004. [Google Scholar] [CrossRef]
- Bernabeu, J.; Palomares-Ruiz, S.; Petcov, S.T. Atmospheric neutrino oscillations, θ13 and neutrino mass hierarchy. Nucl. Phys. B 2003, 669, 255–276. [Google Scholar] [CrossRef]
- Chizhov, M.; Maris, M.; Petcov, S.T. On the Oscillation Length Resonance in the Transitions of Solar and Atmospheric Neutrinos Crossing the Earth Core. arXiv, 1998; arXiv:hep-ph/9810501. [Google Scholar]
- Akhmedov, E.K.; Dighe, A.; Lipari, P.; Smirnov, A.Y. Atmospheric neutrinos at super-Kamiokande and parametric resonance in neutrino oscillations. Nucl. Phys. B 1999, 542, 3–30. [Google Scholar] [CrossRef]
- Peres, O.L.G.; Smirnov, A.Y. Atmospheric neutrinos: LMA oscillations, Ue3 induced interference and CP-violation. Nucl. Phys. B 2004, 680, 479–509. [Google Scholar] [CrossRef]
- Olive, K.A.; et al. [Particle Data Group] Review of Particle Physics. Chin. Phys. C 2014, 38, 090001. [Google Scholar] [CrossRef]
- Abe, K.; et al. [T2K Collaboration] Combined Analysis of Neutrino and Antineutrino Oscillations at T2K. Phys. Rev. Lett. 2017, 118, 0151801. [Google Scholar] [CrossRef] [PubMed]
- Abe, K.; et al. [T2K Collaboration] Measurements of neutrino oscillation in appearance and disappearance channels by the T2K experiment with 6.6 × 1020 protons on target. Phys. Rev. D 2015, 118, 072010. [Google Scholar]
- Adamson, P.; et al. [NOvA Collaboration] Measurement of the Neutrino Mixing Angle θ23 in NOvA. Phys. Rev. Lett. 2017, 118, 151802. [Google Scholar] [CrossRef] [PubMed]
- Aartsen, M.G.; Abraham, K.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Altmann, D.; Anderson, T.; Ansseau, I.; Archinger, M.; et al. Neutrino oscillation studies with IceCube-DeepCore. Nucl. Phys. B 2016, 908, 161–177. [Google Scholar] [CrossRef]
- Adamson, P.; et al. [MINOS Collaboration] Combined Analysis of νμ Disappearance and νμ → νe Appearance in MINOS Using Accelerator and Atmospheric Neutrinos. Phys. Rev. Lett. 2014, 112, 191801. [Google Scholar] [CrossRef]
- Martin, A.D.; Ryskin, M.G.; Stasto, A.M. Prompt neutrinos from atmospheric c-cbar and b-bbar production and the gluon at very small x. Acta Phys. Pol. B 2003, 34, 3273–3304. [Google Scholar]
- Abe, K.; et al. [Super-Kamiokande Collaboration] Evidence for the Appearance of Atmospheric Tau Neutrinos in Super-Kamiokande. Phys. Rev. Lett. 2013, 110, 181803. [Google Scholar]
- Kodama, K.; et al. [DONuT Collaboration] Final tau-neutrino results from the DONuT experiment. Phys. Rev. D 2008, 78, 052002. [Google Scholar] [CrossRef]
- Agafonova, N.; et al. [OPERA Collaboration] Final Results of the OPERA Experiment on ντ Appearance in the CNGS Neutrino Beam. Phys. Rev. Lett. 2018, 120, 211801. [Google Scholar] [CrossRef] [PubMed]
- Philipp, E.; Feifei, H.; Michael, L. Measurement of Atmospheric Tau Neutrino Appearance with IceCube/DeepCore. In Proceedings of theNEUTRINO2018– XXVIII International Conference on Neutrino Physics and Astrophysics, Heidelberg, Germany, 4–10 June 2018. [Google Scholar]
- Bahcall John, N.; Ulrich Roger, K. Solar models, neutrino experiments, and helioseismology. Rev. Mod. Phys. 1988, 60, 297. [Google Scholar] [CrossRef]
- Cleveland, B.T.; Daily, T.; Davis, R., Jr.; Distel, J.R.; Lande, K.; Lee, C.K.; Wildenhain, P.S.; Ullman, J. Measurement of the Solar Electron Neutrino Flux with the Homestake Chlorine Detector. Astrophys. J. 1998, 496, 505–526. [Google Scholar] [CrossRef]
- Abdurashitov, J.N.; et al. [SAGE Collaboration] Measurement of the solar neutrino capture rate with gallium metal. III. Results for the 2002–2007 data-taking period. Phys. Rev. C 2009, 80, 015807. [Google Scholar] [CrossRef]
- Fukuda, Y.; et al. [Kamiokande Collaboration] Solar Neutrino Data Covering Solar Cycle 22. Phys. Rev. Lett. 1996, 77, 1683. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, Q.R.; et al. [SNO Collaboration] Direct Evidence for Neutrino Flavor Transformation from Neutral-Current Interactions in the Sudbury Neutrino Observatory. Phys. Rev. Lett. 2002, 89, 011301. [Google Scholar] [CrossRef]
- Bellini, G.; et al. [Borexino Collaboration] Final results of Borexino Phase-I on low-energy solar neutrino spectroscopy. Phys. Rev. D 2014, 89, 112007. [Google Scholar] [CrossRef]
- Gando, A.; et al. [KamLAND Collaboration 7Be solar neutrino measurement with KamLAND. Phys. Rev. C 2015, 92, 055808. [Google Scholar] [CrossRef]
- Fkuda, S.; et al. [Super-Kamiokande Collaboration] Solar 8B and hep Neutrino Measurements from 1258 Days of Super-Kamiokande Data. Phys. Rev. Lett. 2001, 86, 5651. [Google Scholar] [CrossRef]
- Ahmad, Q.R.; et al. [SNO Collaboration] Measurement of the Rate of νe + d → p + p + e− Interactions Produced by 8B Solar Neutrinos at the Sudbury Neutrino Observatory. Phys. Rev. Lett. 2001, 87, 071301. [Google Scholar] [CrossRef]
- Smirnov, A.Y. Solar neutrinos: Oscillations or No-oscillations? arXiv, 2016; arXiv:1609:02386. [Google Scholar]
- De Holanda, P.C.; Smirnov, A.Y. Homestake result, sterile neutrinos, and low energy solar neutrino experiments. Phys. Rev. D 2004, 69, 113002. [Google Scholar] [CrossRef]
- De Holanda, P.C.; Smirnov, A.Y. Solar neutrino spectrum, sterile neutrinos, and additional radiation in the Universe. Phys. Rev. D 2011, 83, 113011. [Google Scholar] [CrossRef]
- Barger, V.; Patrick, H.; Danny, M. Solar Mass-Varying Neutrino Oscillations. Phys. Rev. Lett. 2005, 95, 211802. [Google Scholar] [CrossRef] [PubMed]
- Friedland, A.; Lunardini, C.; Pena-Garay, C. Solar neutrinos as probes of neutrino–matter interactions. Phys. Lett. B 2004, 594, 347–354. [Google Scholar] [CrossRef]
- Miranda, O.G.; Tórtola, M.A.; Valle, J.W. Are solar neutrino oscillations robust? J. High Energy Phys. 2006, 10, 008. [Google Scholar] [CrossRef]
- Nakahata, M.; et al. [Super-Kamiokande Collaboration] Calibration of Super-Kamiokande using an electron LINAC. Nucl. Instrum. Methods A 1999, 421, 113–129. [Google Scholar] [CrossRef]
- Blaufuss, E.; et al. [Super-Kamiokande Collaboration] 16N as a calibration source for Super-Kamiokande. Nucl. Instrum. Methods A 2001, 458, 638–649. [Google Scholar] [CrossRef]
- Hosaka, J.; et al. [Super-Kamiokande Collaboration] Solar neutrino measurements in Super-Kamiokande-I. Phys. Rev. D 2006, 73, 112001. [Google Scholar] [CrossRef]
- Cravens, J.P.; et al. [Super-Kamiokande Collaboration] Solar neutrino measurements in Super-Kamiokande-II. Phys. Rev. D 2008, 78, 032002. [Google Scholar] [CrossRef]
- Abe K.; et al. [Super-Kamiokande Collaboration] Solar neutrino results in Super-Kamiokande-III. Phys. Rev. D 2011, 83, 052010. [Google Scholar] [CrossRef]
- Aharmim, B.; et al. [SNO Collaboration] Combined analysis of all three phases of solar neutrino data from the Sudbury Neutrino Observatory. Phys. Rev. C 2013, 88, 025501. [Google Scholar] [CrossRef]
- Source: WDC-SILSO, Royal Observatory of Belgium, Brussels. Available online: http://www.sidc.be/silso/datafiles (accessed on 9 January 2019).
- Nakano, Y.; Sekiya, H.; Tasaka, S.; Takeuchi, Y.; Wendell, R.A.; Matsubara, M.; Nakahata, M. Measurement of radon concentration in Super-Kamiokande’s buffer gas. Nucl. Instrum. Methods A 2017, 867, 108–114. [Google Scholar] [CrossRef]
- Nakano, Y. Radon background study in Super-Kamiokande. J. Phys. Conf. Ser. 2017, 888, 012191. [Google Scholar] [CrossRef]
- Nakano, Y. 8B Solar Neutrino Spectrum Measurement Using Super-Kamiokande IV. Ph.D. Thesis, The University of Tokyo, Tokyo, Japan, 2016. Available online: http://www-sk.icrr.u-tokyo.ac.jp/sk/_pdf/articles/2016/doc_thesis_naknao.pdf (accessed on 9 January 2019).
- Agostini, M.; et al. [Borexino Collaboration] First Simultaneous Precision Spectroscopy of pp, 7Be, and pep Solar Neutrinos with Borexino Phase-II. arXiv, 2017; arXiv:1707:09279. [Google Scholar]
- Gando, A.; et al. [KamLAND Collaboration] Reactor on-off antineutrino measurement with KamLAND. Phys. Rev. D 2013, 88, 033001. [Google Scholar] [CrossRef]
- An, F.P.; et al. [Daya Bay Collaboration] Improved measurement of electron antineutrino disappearance at Daya Bay. Chin. Phys. C 2013, 37, 011001. [Google Scholar] [CrossRef]
- Ahn, J.K.; et al. [RENO Collaboration] Observation of Reactor Electron Antineutrinos Disappearance in the RENO Experiment. Phys. Rev. Lett. 2012, 108, 191802. [Google Scholar] [CrossRef]
- Abe, Y.; et al. [Double Chooz Collaboration] Reactor disappearance in the Double Chooz experiment. Phys. Rev. D 2012, 86, 052008. [Google Scholar] [CrossRef]
- Ken’ichiro, N.; Eri, M.; Yuu, N.; Hideyuki, S. Spectrum of the supernova relic neutrino background and metallicity evolution of galaxies. Astrophys. J. 2015, 804, 75. [Google Scholar]
- Horiuchi, S.; Beacom, J.F.; Dwek, E. Diffuse supernova neutrino background is detectable in Super-Kamiokande. Phys. Rev. D 2009, 79, 083013. [Google Scholar] [CrossRef]
- Bays K.; et al. [Super-Kamiokande Collaboration] Supernova relic neutrino search at Super-Kamiokande. Phys. Rev. D 2012, 85, 052007. [Google Scholar] [CrossRef]
- Watanabe, H.; et al. [Super-Kamiokande Collaboration] First study of neutron tagging with a water Cherenkov detector. Astropart. Phys. 2009, 31, 320–328. [Google Scholar] [CrossRef]
- Beacom John, F.; Vargins Mark, R. Antineutrino Spectroscopy with Large Water Čerenkov Detectors. Phys. Rev. Lett. 2004, 93, 171101. [Google Scholar] [CrossRef] [PubMed]
| Phase | SK-I | SK-II | SK-III | SK-IV |
|---|---|---|---|---|
| Period | April 1996–July 2001 | October 2002–October 2005 | July 2006–August 2008 | September 2008–May 2018 |
| ID PMTs [8] | 11,149 | 5182 | 11,129 | 11,129 |
| OD PMTs | 1885 | 791 | 1885 | 1885 |
| Photo coverage | ||||
| Energy threshold | 4.5 MeV | 6.5 MeV | 4.0 MeV | 3.5 MeV |
| Electronics | ATM [9,10] | ATM | ATM | Qbee [11,12] |
| Mass Hierarchy | ||||
|---|---|---|---|---|
| Normal hierarchy | ||||
| Inverted hierarchy |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nakano, Y.; On behalf of the Super-Kamiokande Collaboration. Highlight Talk from Super-Kamiokande. Universe 2019, 5, 20. https://doi.org/10.3390/universe5010020
Nakano Y, On behalf of the Super-Kamiokande Collaboration. Highlight Talk from Super-Kamiokande. Universe. 2019; 5(1):20. https://doi.org/10.3390/universe5010020
Chicago/Turabian StyleNakano, Yuuki, and On behalf of the Super-Kamiokande Collaboration. 2019. "Highlight Talk from Super-Kamiokande" Universe 5, no. 1: 20. https://doi.org/10.3390/universe5010020
APA StyleNakano, Y., & On behalf of the Super-Kamiokande Collaboration. (2019). Highlight Talk from Super-Kamiokande. Universe, 5(1), 20. https://doi.org/10.3390/universe5010020





