Prospects for Heavy-Ion Physics with the MPD Detector at NICA

Abstract

The construction of the NICA accelerator facility is underway at Joint Institute for Nuclear Research (JINR) (Dubna, Russia). The main goal of the MPD experiment at NICA will be the experimental exploration of the Quantum Chromodynamics (QCD) phase structure at high baryon density. In this article, the current status of the NICA/MPD project is presented.

1. Introduction

Using relativistic heavy-ion collisions in the laboratory, one can create nuclear matter under extreme conditions of density and temperature. According to lattice QCD calculations, a crossover phase transition from the hadronic phase to the phase of deconfined quarks and gluons—Quark–Gluon Plasma (QGP)—is suggested at a vanishing baryon chemical potential ${\mu }_B$ [1]. The order of the phase transformation is expected to change with the net baryon density: arguments based on several approaches of QCD [2,3] predict both a first order phase transition at large ${\mu }_B$ values and the existence of a critical endpoint (CEP). At present, despite many experimental data obtained at high and ultra-high collision energies at the Super Proton Synchrotron (SPS), Relativistic Heavy Ion Collider (RHIC), and Large Hadron collider (LHC) [4], there is scarce knowledge about the structure of QCD phase diagram in the region of finite net-baryon density. A new experimental program at the NICA accelerator complex at JINR (Dubna) is aimed to close this gap by performing a comprehensive study of nuclear matter in the range of collision energies where the net-baryon density increases substantially [5].

2. NICA Physics Topics

The NICA scientific program will cover a broad range of physics phenomena in dense nuclear matter, including hadroproduction, in-medium modification of hadron properties, features of hyperon–nucleon interaction at high baryon density, and critical behavior of the QCD matter [6]. In particular, during the first period of the project realization, a detailed energy and system size scan will be performed in the energy range $4<\sqrt{s_{NN}}<11$ GeV with the emphasis on studying the excitation function of event-by-event fluctuations and correlations, and production of multistrange hyperons, dileptons, and hypernuclei. Measurements of elementary reactions are foreseen as well to provide a reference for heavy-ion studies.

Production of strangeness is of particular interest because enhanced production of strange hadrons in A + A collisions (relative to the yields from elementary pp reactions) was predicted as a signal for the QGP formation [7]. This enhancement is more pronounced for hyperons with larger strangeness content (cascades and Omega). At present, a complete theoretical description of the multi-strangeness production mechanism at collision energies (in the center of mass) of several GeV has not yet been achieved. To better understand the dynamics of hot and dense hadronic matter, new precise experimental data on the total yields, rapidity, transverse momentum, and azimuthal angle distributions of hyperons and antihyperons are needed in this energy range. Moreover, because of the large orbital angular momentum in non-central collisions of two heavy nuclei at relativistic energies, the experimental values of the vorticity field in the deconfined matter can be very large. It has been argued that, due to their spin–orbit interactions, quarks and antiquarks can be polarized along the direction of the orbital angular momentum by this vorticity field causing the production of polarized (anti)hyperons. The degree of hyperon polarization is growing towards NICA energies [8].

Dense nuclear mater favors formation of composite objects with strangeness (hypernuclei), which are a unique tool to probe new nuclear structures or unknown properties of the hyperon–baryon interactions. Since the energy range of the NICA covers the region of high net-baryon density, the production rates of nuclear clusters with strangeness are predicted to be enhanced considerably [9].

If the QCD critical point exists, it is expected that abnormal event-by-event fluctuations of conserved quantities can be observed near this point (net-baryon, net-strangeness, and net-charge numbers). It is believed that the higher order moments of the multiplicity distributions of the conserved charges are able to give signatures for such critical phenomena. As experimental data indicate, the curtosis of the net-proton multiplicity distribution shows an interesting non-monotonic behavior at low energies deviating from the Poisson baseline: it drops below unity around 19.6–27 GeV and increases above unity below 11 GeV [10]. To relate these observations to a possible signal for the critical point [11,12], one has to unveil the details of the energy dependence of the net-proton higher moments at energies below 11 GeV, where the uncertainties in the measurements are too high. Moreover, the moments of net-protons are changing dramatically if the apparatus has geometrical constraints (i.e., not full acceptance), thus future high statistics measurements for the moments of the conserved charges over a large phase-space are highly desirable.

In non-central heavy-ion collisions, the initial spatial asymmetry results in the asymmetry of the particle emission pattern in momentum space. The magnitude of the anisotropic flow coefficients relative to the reaction plane is sensitive to the nuclear matter equation-of-state (EOS) and transport coefficients. For example, the minimum in the proton’s direct flow coefficient $v_1$ is predicted near the EOS softest point, consistent with the first order phase transition and formation of a mixed phase [13]. The excitation function of collective flow coefficients will be studied at NICA in great detail to search for abnormal matter states and phase transitions.

Currently, the future beam energy scan programs at finite net-baryon density include the phase II at RHIC, the upcoming SIS100 facility at FAIR, and the NICA program at JINR in Dubna. The maximal energy of the SIS100 accelerator is limited to 10 GeV per nucleon in the fixed target mode (equivalent to about 4 GeV in the center-of-mass), while at RHIC due to luminosity limitations at low energies the rate of useful physics events is very low below the center-of-mass energy of 10 GeV. The NICA facility will be able to achieve a high level of luminosity for heavy ions (two orders of magnitude higher than at RHIC) in the energy range not accessible at FAIR.

3. The NICA Accelerator Complex

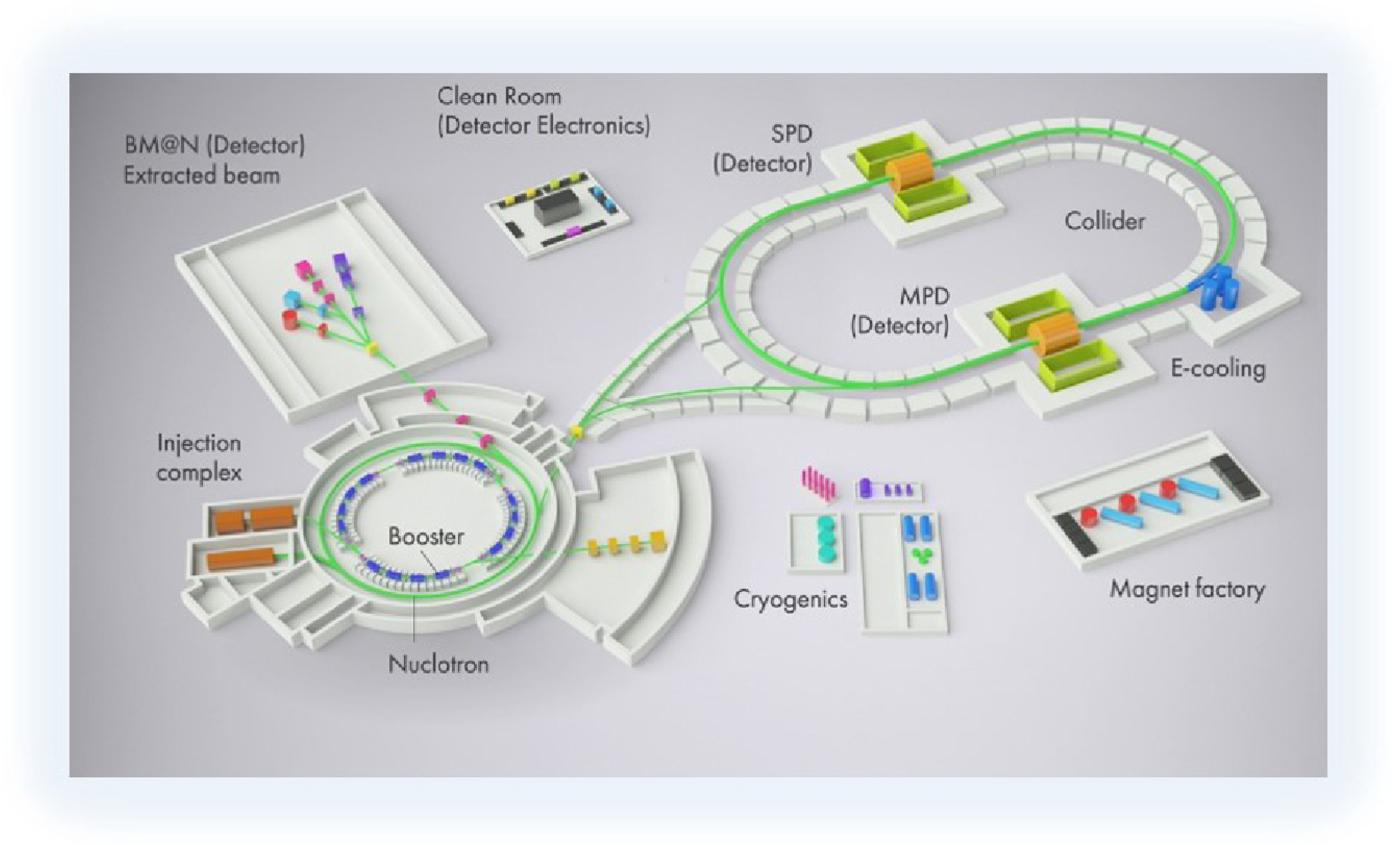
The main components of the NICA accelerator facility (see Figure 1) are the following:

• Injector complex
• Booster-synchrotron
• Nuclotron
• Collider

The Injector complex consists of an ion source of the Electron String Ion Source (ESIS) type, a high current heavy-ion linear accelerator (HILAC), and transfer channels. The Booster takes partially stripped ions from the HILAC and transports them to the Nuclotron accelerator. Before entering the Nuclotron, the ions are further stripped and accelerated up to 600 MeV per nucleon. The Nuclotron raises the kinetic energy of fully stripped ions in the range of 1–4.5 GeV/u. Then, the ions, grouped into 22 bunches of $10\times {10}^9$ particles each, are transported to two storage rings of the NICA Collider. The rings of a 503 m circumference and the maximum magnetic rigidity of 45 Tm are placed one above the other inside an underground tunnel. The Collider uses both the stochastic and electron cooling techniques for improving beam quality and increasing the luminosity lifetime. A set of service systems will provide cryogenics, electric power, and cooling water to feed the accelerator complex and detectors. NICA parameters allow reaching the luminosity of ${10}^{27}$ s${}^{-1}$cm${}^{-2}$ at the ion kinetic energy above 3 GeV/u. The beams are only allowed to collide at two interaction points where detectors for heavy-ion collisions (MPD) and spin physics studies (SPD) are present.

Serial fabrication of the magnets for the NICA facility is in progress, and for now all the dipoles for the Booster have being constructed and tested. The commissioning of the Booster accelerator is scheduled for 2019. The construction of the NICA collider tunnel, detector buildings, transfer lines, and service systems is progressing according to plan (see Figure 2). The first heavy-ion collision at the NICA collider is expected in 2021 and during the initial data taking period the peak luminosity will be decreased to $5\times {10}^{25}$ s${}^{-1}$cm${}^{-2}$. After the completion of machine commissioning and beam studies, the data taking will be continued in 2023 with the collider luminosity increased to its nominal value.

4. The MPD Detector

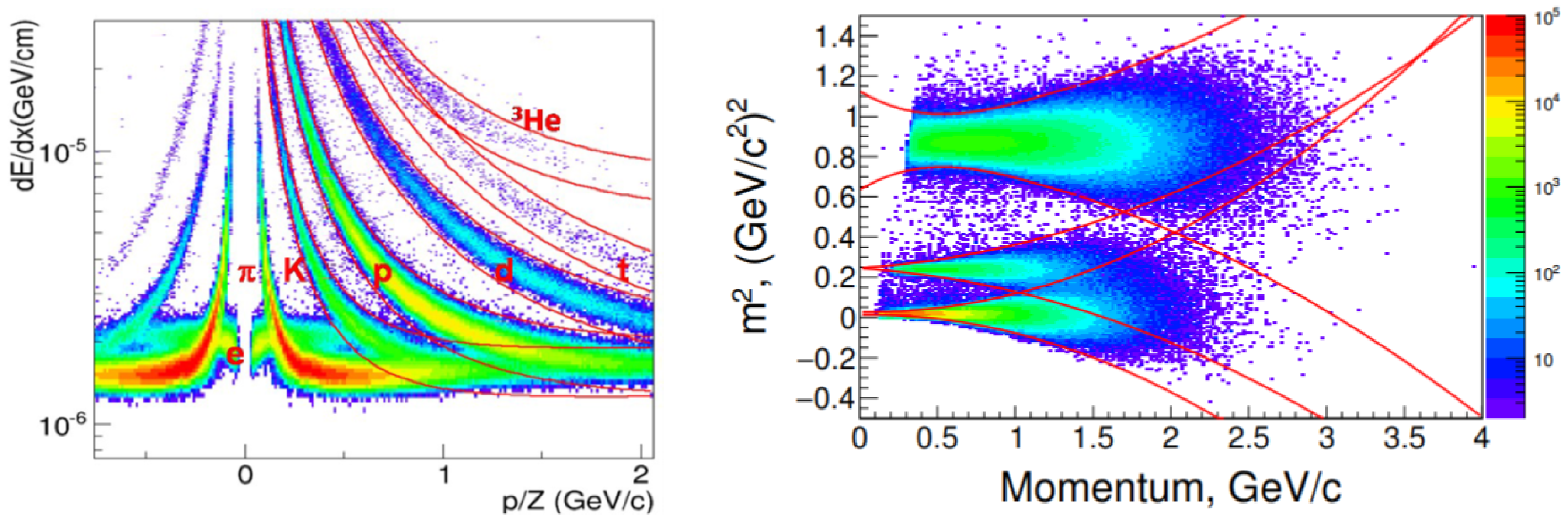
The MultiPurpose Detector (MPD), one of the two detectors situated around the NICA collider, has been designed to provide large acceptance measurements of particle production in heavy-ion collisions. The main subsystems of the experimental setup, shown in Figure 3, are the tracking system, the particle identification (PID) system (for hadrons, electrons and gammas), and the event characterization system. The tracking and PID systems sit inside a superconducting solenoid magnet delivering a very homogeneous magnetic field of 0.6 T. The MPD tracking system consists of a cylindrical Time-Projection Chamber (TPC), a straw-tube End Cap Tracker (ECT), and an Inner Tracker (IT) as a vertex detector. MPD TPC with a 2.8 m diameter and 3.4 m length is required to have a high efficiency and momentum resolution over the pseudorapidity range $\left|\eta \right|<2$. It will provide measurement of the ionization energy loss of up to 53 samples along charged track trajectories enabling particle identification via $dE/dx$ information with a precision better than 8% (see Figure 4, left). Track reconstruction within the midrapidity region will be supplemented by the ECT tracker located just after the TPC end plates. The Inner Tracker (IT) system is composed of several layers of double-sided silicon microstrip detector serving mainly for a very precise determination of the position of secondary decay vertices.

The MPD Time-of-Flight (TOF) system, which can discriminate between charged particle species in the intermediate momentum region, is based on the multigap resistive plate chamber (MRPC) technology. The barrel part of the TOF detector covers a pseudorapidity interval $\left|\eta \right|<1.4$ over the full azimuth. It is segmented into 14 azimuthal sectors and 20 modules along the beam direction. The TOF readout consist of 6720 strips of 10 × 650 mm${}^2$ each. The overall time resolution of 80 ps will provide $\pi$/K separation at the 3$\sigma$ level up to 1.3 GeV/c and K/p separation up to 2 GeV/c (see Figure 4, right).

Just behind the TOF detector is a high segmented Electromagnetic Calorimeter (ECAL) whose primary purpose is to measure the spatial position and energy of electrons and photons. The ECAL barrel comprises about 43,000 modules of the “shashlyk” lead-scintillator type. Each module with a front size of 4 × 4 cm${}^2$ contains 250 alternating tiles of lead and plastic scintillator of 0.275 mm and 1.5 mm thickness, respectively. The cells of each module are optically combined by nine longitudinally penetrating wavelength shifting fibers for light collection. The collected light is read out by avalanche photodiode (MAPD) units. A high MPD ECAL energy resolution and good timing performance allow many physics channels to be explored.

The MPD Forward Detector (FD) consists of two arrays of quartz counters capable of registering high energy photons and relativistic charged particles with the 40 ps time resolution. Each FFD module is made of 1.5 cm thick quartz Cherenkov radiator optically coupled to a multi-anode micro-channel phototube. The main goal of this system, arranged around the beam pipe at ≈75 cm on both sides of the MPD center, is to provide fast timing and triggering signals to the experiment.

Two arms of hadron calorimeters (FHCAL), made of 44 modules of lead-scintillator sampling calorimeters and covering the pseudorapidity range $2.8<\left|\eta \right|<4.5$, will measure the forward going energy distribution. The information from FHCAL about the energy deposit will be used for the offline centrality estimate and event plane analysis.

A more detailed description of the MPD detector elements can be found in [14].

During the first data taking period (2021–2023), the MPD setup will include only TPC, the barrel part of the PID system (TOF and ECAL), and the event characterizations system (FHCAL and FD). From 2023 on, the MPD detector will be upgraded to include the vertex detector IT, the endcap tracker followed by the endcap PID (TOF and ECAL) system.

Currently, industrial production of MPD detector elements is in process. For example, Vitkovice Heavy Mashinery (VHM) from Czech Republic has completed manufacture of the yoke for the unique MPD magnet (see Figure 5). In Figure 6, fabrication of a single MRPC TOF module by members of the TOF team is shown.

5. MPD Feasibility Study

All the feasibility study tasks for the MPD experiment have been performed within a dedicated ROOT-based software framework—MPDRoot [15]. It comprises multiple interfaces to heavy-ion event generators, propagation of particles through the detector material based on the GEANT package, as well as detector response simulation and reconstruction algorithms for all the MPD subsystems. In the following, several selected results of multiple Monte Carlo studies is outlined.

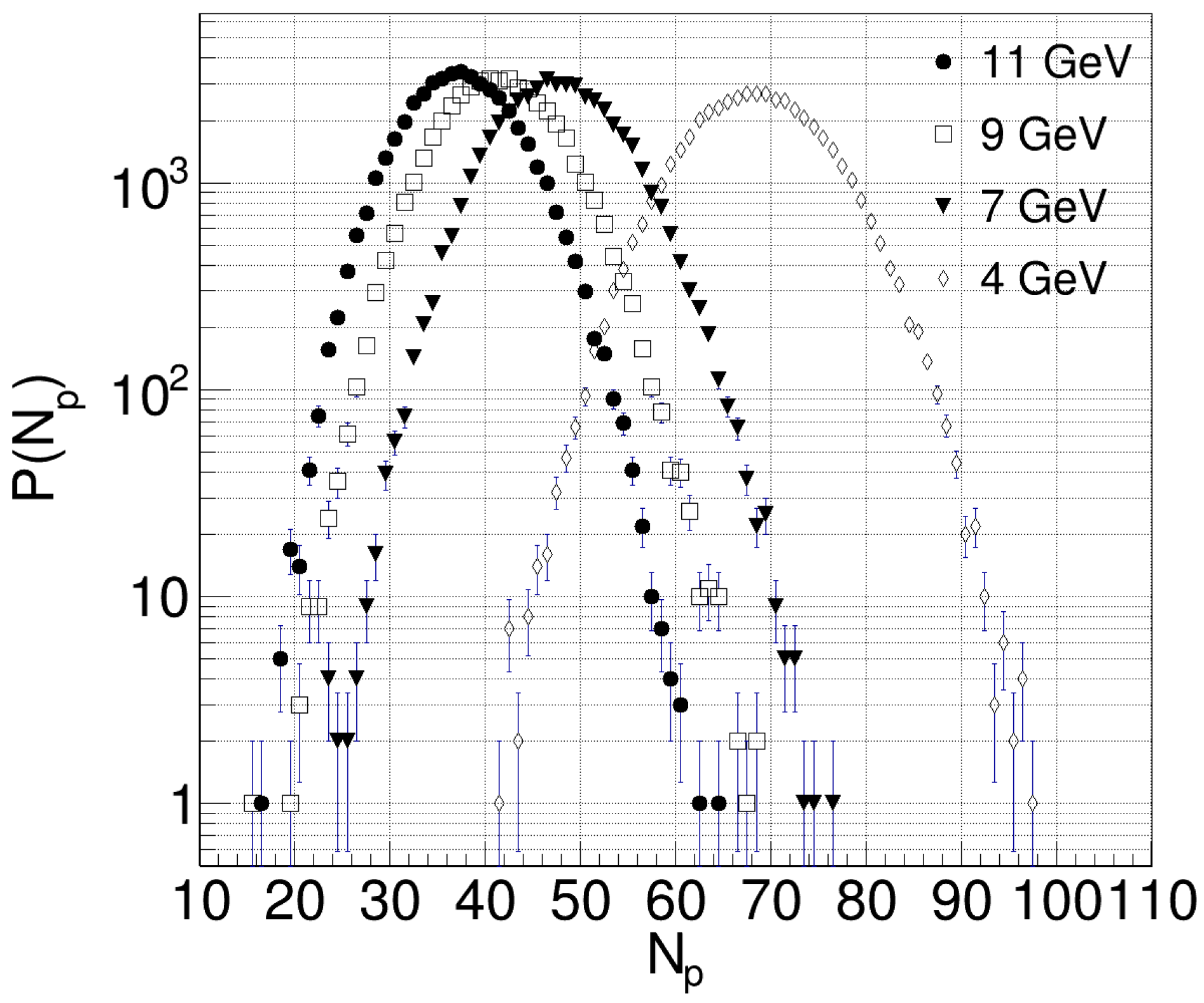
A large fraction (up to ≈80%) of the charged particles produced in an event can be detected with the MPD setup. This allows some properties of the collision system to be studied on an event-by-event basis. As an example, in Figure 7 are shown the multiplicity of net-protons (protons minus antiprotons) registered in the MPD detector in a single central Au + Au collision. As can be seen in this figure (the results are for 0–1% central Au + Au from the UrQMD model), we are able to detect roughly 35 and 70 net-protons at 11 and 4 GeV, respectively.

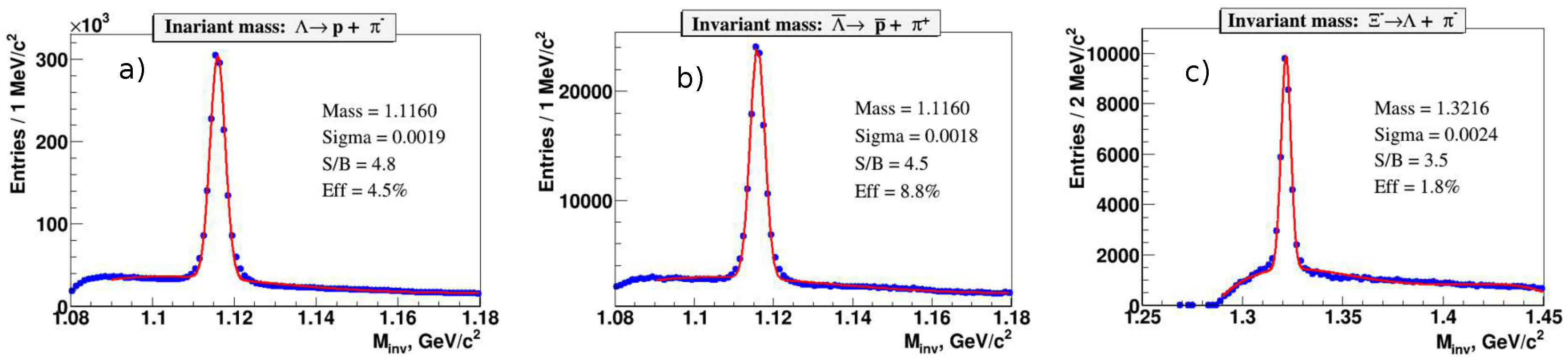
The MPD performance for hyperon and hypernuclei measurements was studied for the combination of TPC and TOF detectors within the midrapidity region ($\left|\eta \right|<1.2$). A sample of $2\times {10}^6$ minimum bias Au + Au collisions at $\sqrt{s_{NN}}$ = 9 GeV was used as an input for this study. Hyperons and hypernuclei were reconstructed using the secondary vertex finding technique with an optimized set of topological and track quality cuts as described in [16]. This allowed invariant mass spectra of hyperons in the whole $p_t$-range to be plotted as in Figure 8. The estimated efficiencies and signal-to-background (S/B) ratios are also indicated for three hyperon species.

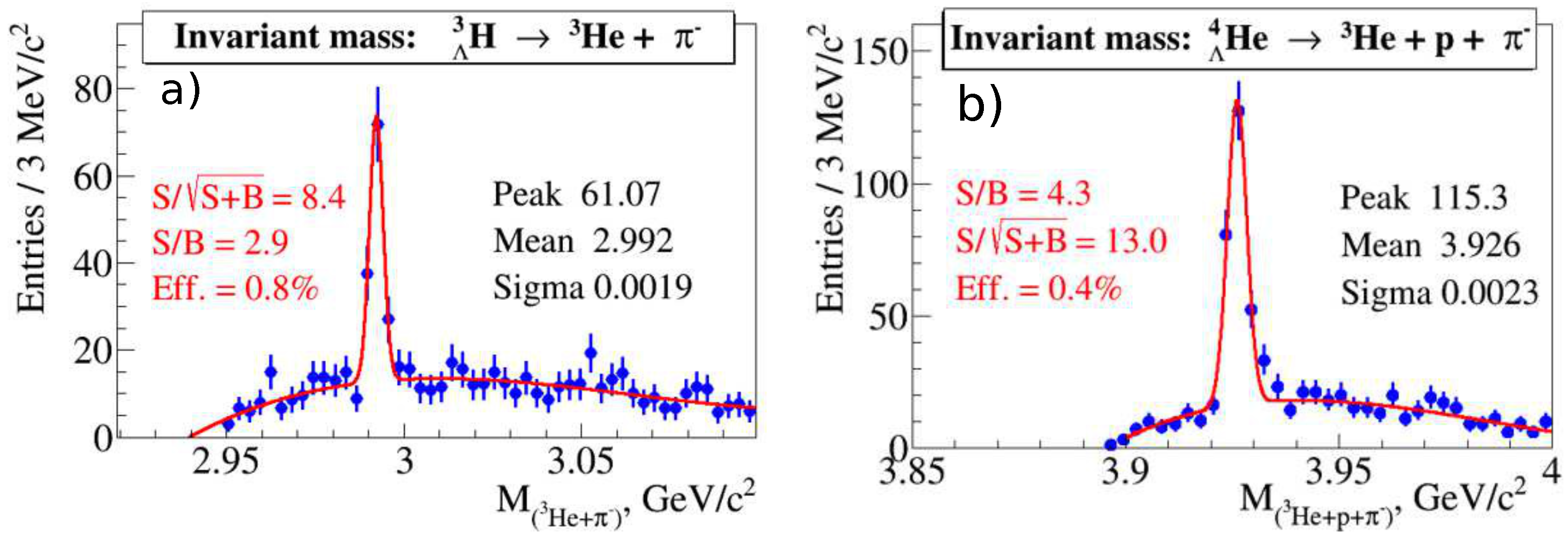
Figure 9a shows the invariant mass distribution of (${}^3$He, ${\pi }^{-}$) pairs after subtraction of the combinatorial background, while the signal for hyperhelium-4 is plotted in Figure 9b. These positive feasibility study results indicate that the MPD setup has a good efficiency for hypernuclei. With a typical event rate of 7 kHz for the design NICA luminosity, we are able to register about ${10}^5$ hypertritons in a week of data taking.

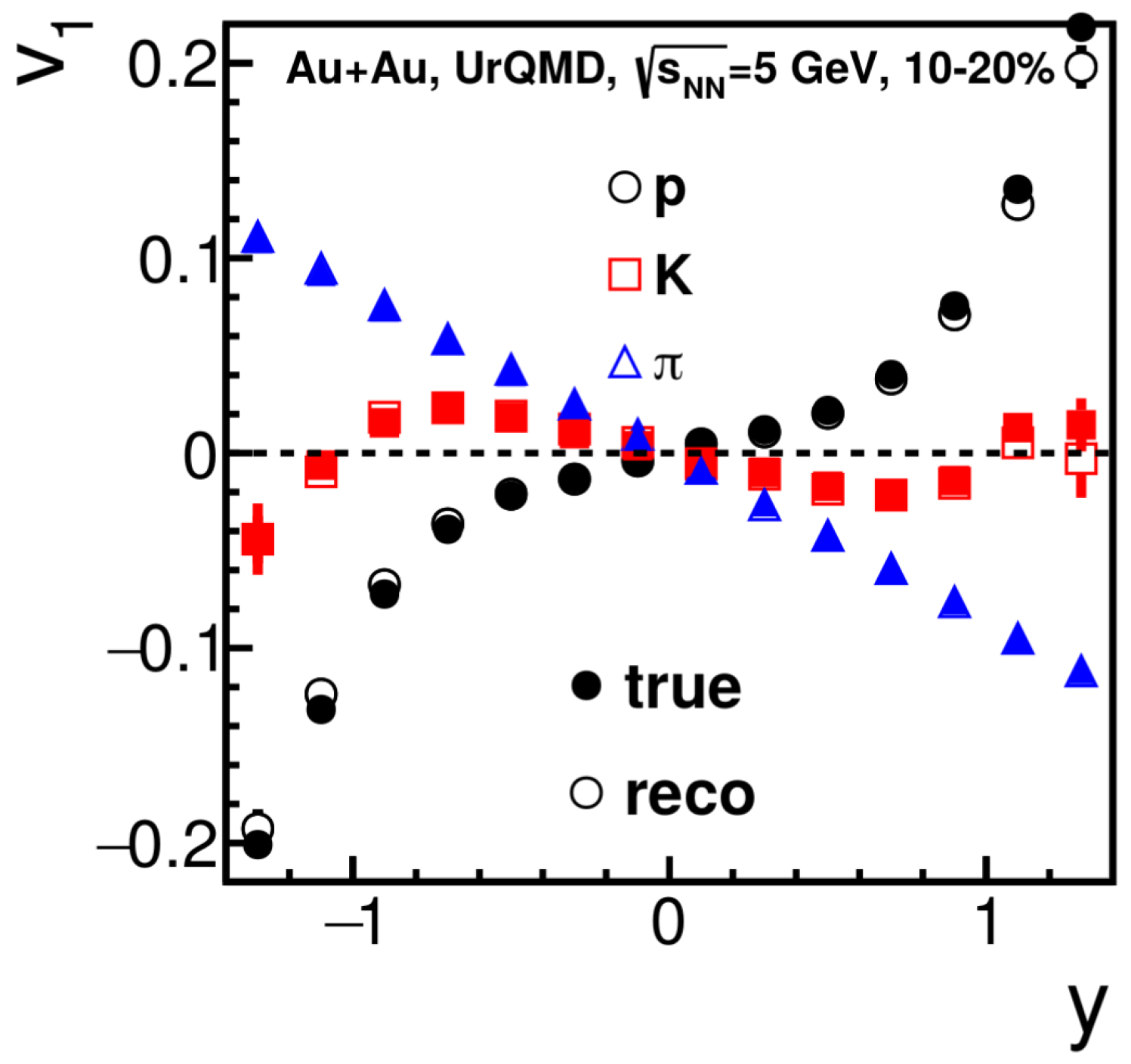
In the study of the MPD detector performance in the measurements of direct flow, a set of Au + Au collisions from the UrQMD event generators was used. Event centrality was defined using the TPC charged track multiplicity with the resolution better than 10%. Particle ID was achieved by means of the combined ionization energy loss (TPC) and time-of-flight (TOF) information. The event plane angle was calculated using the energy deposition in the FHCAL calorimeter. In Figure 10 are shown the calculated values of the direct flow coefficient $v_1$ for protons, $K^{+}$, and ${\pi }^{+}$ in several rapidity bins. As one can see, the results for the reconstructed values (reco) and those from the model (true) agree within the errors.

6. Conclusions

In this report, an overview of the current status of the NICA project realization is given. The realization plan foresees putting the startup configuration of the NICA collider into operation in 2021. The MPD detector parameters allow precise measurements of the hadroproduction per-event basis as well as reconstruction of hyperons and hypernuclei.