Light Propagation through Nanophotonics Wormholes
Abstract
1. Introduction
2. Traversable Wormhole Spacetimes
3. Embedding Wormhole Surfaces
4. Surfaces of Revolution in the Laboratory
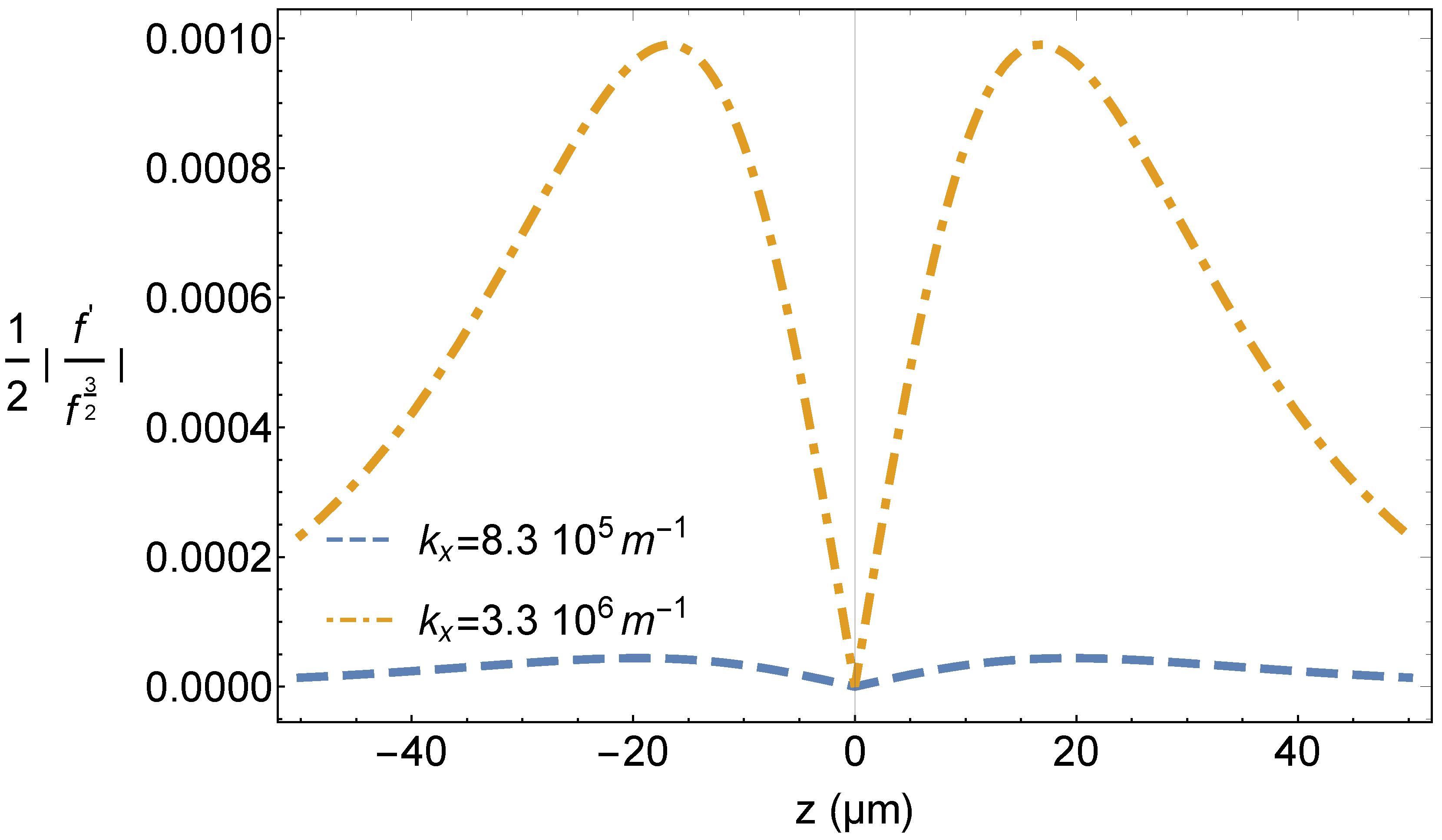
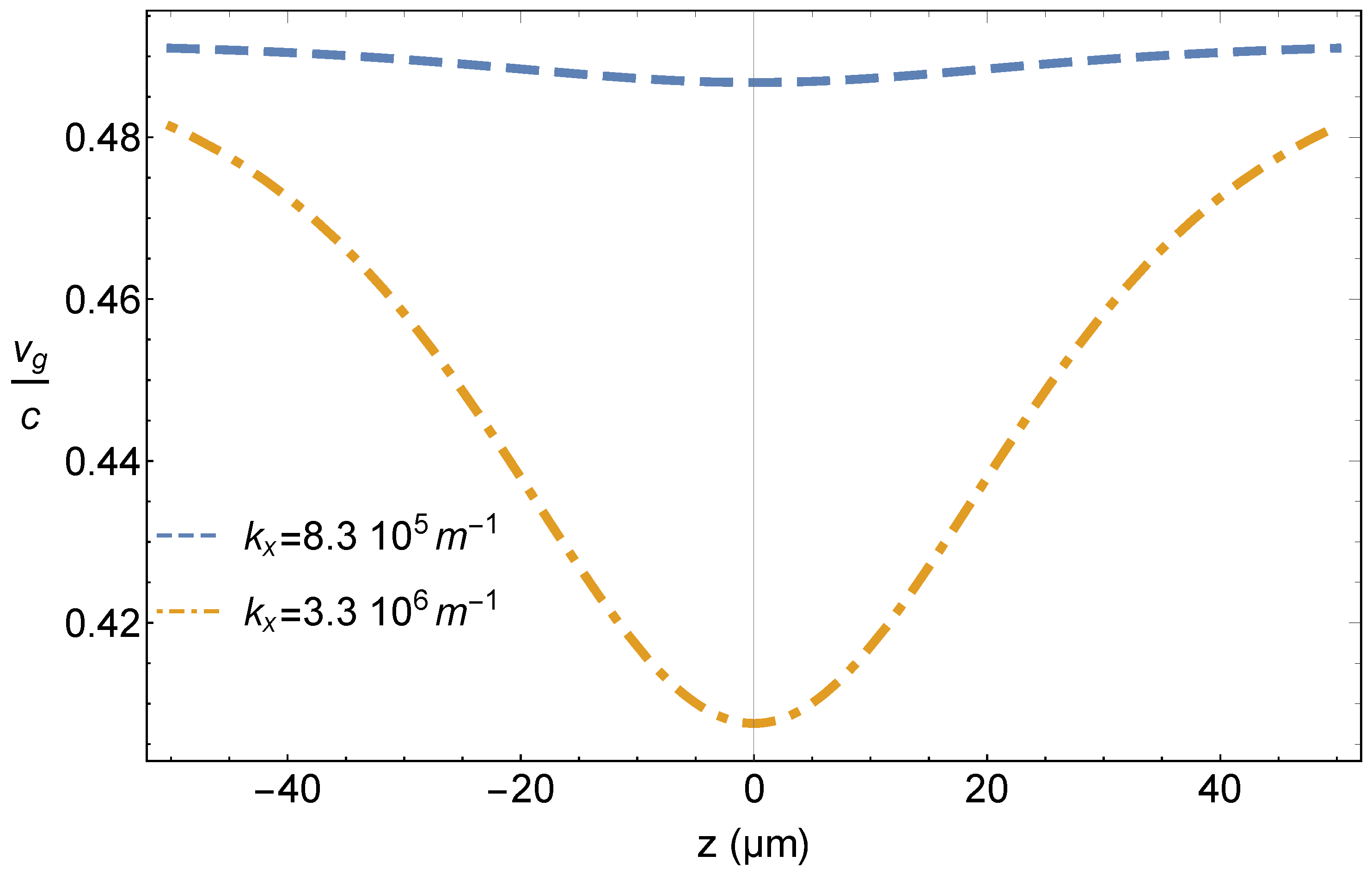
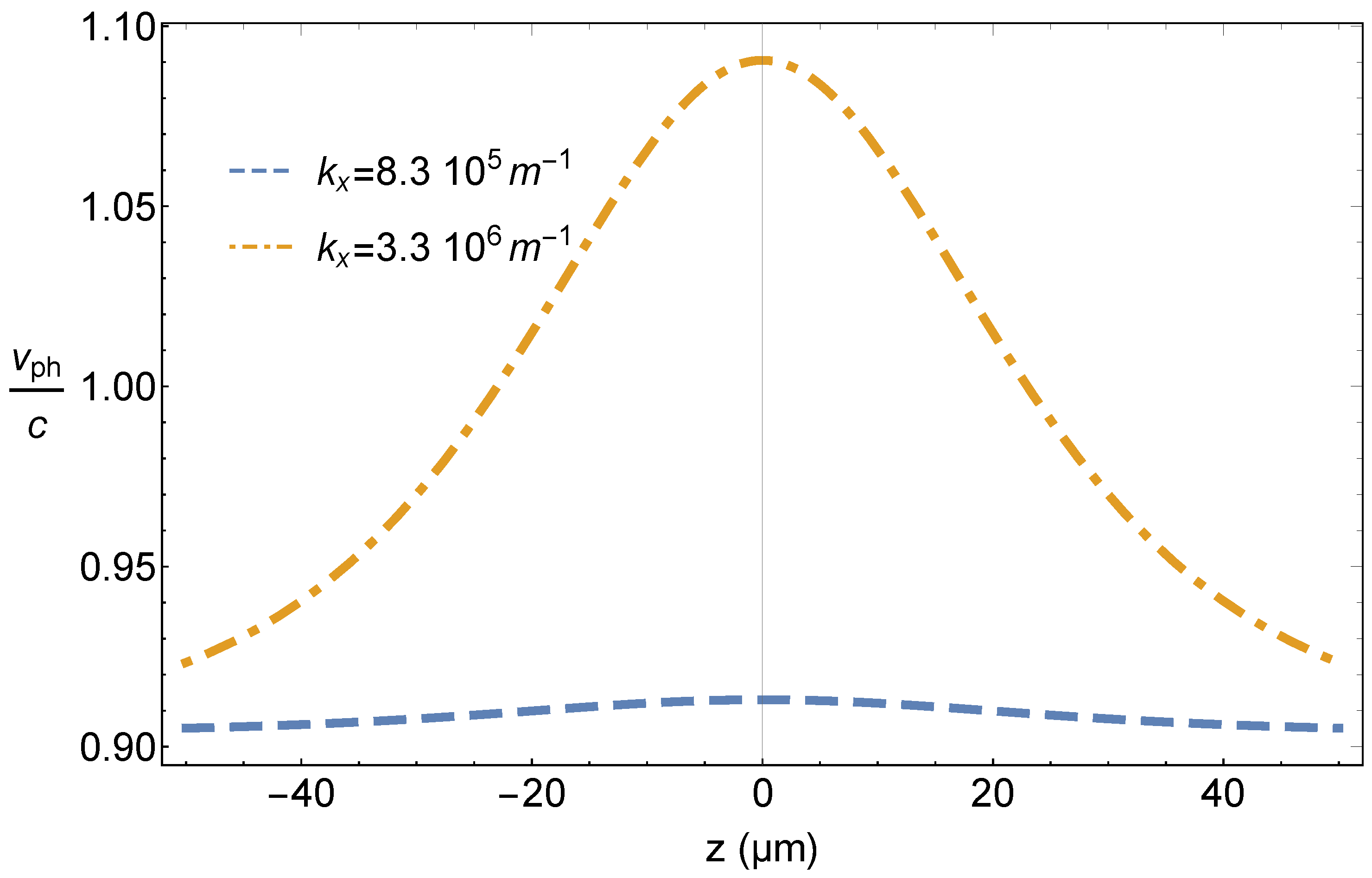
5. Wave Equations
6. Results
7. Conclusions
Acknowledgments
Conflicts of Interest
References
- Shoresh, T.; Katanov, N.; Malka, N. 1 × 4 MMI visible light wavelength demultiplexer based on a GaN slot-waveguide structure. Photonics Nanostruct. Fundam. Appl. 2018, 30, 45–49. [Google Scholar] [CrossRef]
- Nikolaevsky, L.; Shchori, T.; Malka, D. Modeling a 1 × 8 MMI green light power splitter based on Gallium-Nitride slot waveguide structure. IEEE Photonics Technol. Lett. 2018, 30, 720–723. [Google Scholar] [CrossRef]
- Malka, D.; Danan, Y.; Ramon, Y.; Zalevsky, Z.A. Photonic 1 × 4 Power Splitter Based on Multimode Interference in Silicon-Gallium-Nitride Slot Waveguide Structures. Materials 2016, 9, 516. [Google Scholar] [CrossRef]
- Leonhardt, U.; Philbin, T.G. General relativity in electrical engineering. New J. Phys. 2006, 8, 247. [Google Scholar] [CrossRef]
- Schultheiss, V.H.; Batz, S.; Szameit, A.; Dreisow, F.; Nolte, S.; Tünnermann, A.; Peschel, U. Optics in curved space. Phys. Rev. Lett. 2010, 105, 149301. [Google Scholar] [CrossRef]
- Bekenstein, R.; Nemirowsky, J.; Kaminer, I.; Segev, M. Shape-preserving accelerating electromagnetic wave-packets in curved space. Phys. Rev. X 2014, 4, 011038. [Google Scholar] [CrossRef]
- Bekenstein, R.; Kabessa, Y.; Sharabi, Y.; Tal, O.; Engheta, N.; Eisenstein, G.; Segev, M. Control of light by curved space in nanophotonic structures. Nat. Photonics 2017, 11, 664. [Google Scholar] [CrossRef]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; W. H. Freeman: San Francisco, CA, USA, 1973. [Google Scholar]
- Ellis, H.G. Ether Flow Through a Drainhole: A Particle Model in General Relativity. J. Math. Phys. 1973, 14, 104–118. [Google Scholar] [CrossRef]
- Morris, M.S.; Thorne, K.S.; Yurtsever, U. Wormholes, Time Machines, and the Weak Energy Condition. Phys. Rev. Lett. 1988, 61, 1446. [Google Scholar] [CrossRef]
- Takahashi, R.; Asada, H. Observational upper bound on the cosmic abundances of negative-mass compact objects and Ellis wormholes from the Sloan digital sky survey quasar lens search. Astrophys. J. Lett. 2013, 768, L16. [Google Scholar] [CrossRef]
- Morris, M.S.; Thorne, K.S. Wormholes in spacetime and their use for interstellar travel: A tool for teaching general relativity. Am. J. Phys. 1988, 56, 395–412. [Google Scholar] [CrossRef]
- Hawking, S.W. Chronology protection conjecture. Phys. Rev. D 1992, 46, 603. [Google Scholar] [CrossRef]
- Deutsch, D. Quantum mechanics near closed timelike lines. Phys. Rev. D 1991, 44, 3197. [Google Scholar] [CrossRef]
- Ford, L.H.; Roman, T.A. Averaged energy conditions and quantum inequalities. Phys. Rev. D 1995, 51, 4277. [Google Scholar] [CrossRef]
- Li, Z.; Bambi, C. Distinguishing black holes and wormholes with orbiting hot spots. Phys. Rev. D 2014, 90, 024071. [Google Scholar] [CrossRef]
- Cardoso, V.; Franzin, E.; Pani, P. Is the Gravitational-Wave Ringdown a Probe of the Event Horizon? Phys. Rev. Lett. 2016, 116, 171101. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zhidenko, A. Wormholes versus black holes: Quasinormal ringing at early and late times. J. Cosmol. Astropart. Phys. 2016, 12, 043. [Google Scholar] [CrossRef]
- Yuan, X.; Assad, S.M.; Thompson, J.; Haw, J.-Y.; Vedral, V.; Ralph, T.C.; Gu, M. Replicating the benefits of Deutschian closed timelike curves without breaking causality. NPJ Quant. Inf. 2015, 1, 15007. [Google Scholar] [CrossRef]
- Maldacena, J.; Susskind, L. Cool horizons for entangled black holes. Fortschritte del Physik 2013, 61, 781–811. [Google Scholar] [CrossRef]
- Müller, T. Exact geometric optics in a Morris-Thorne wormhole spacetime. Phys. Rev. D 2008, 77, 044043. [Google Scholar] [CrossRef]
- Taylor, P. Propagation of test particles and scalar fields on a class of wormhole space-times. Phys. Rev. D 2014, 90, 024057. [Google Scholar] [CrossRef]
- Sabín, C. Mapping curved spacetimes into Dirac spinors. Sci. Rep. 2017, 7, 40346. [Google Scholar] [CrossRef]
- Abe, F. Gravitational Microlensing by the Ellis Wormhole. Astrophys. J. 2010, 725, 787. [Google Scholar] [CrossRef]
- Nakajima, K.; Asada, H. Deflection angle of light in an Ellis wormhole geometry. Phys. Rev. D 2012, 85, 107501. [Google Scholar] [CrossRef]
- Ohgami, T.; Sakai, N. Wormhole shadows. Phys. Rev. D 2015, 91, 124020. [Google Scholar] [CrossRef]
- Sabín, C. Quantum detection of wormholes. Sci. Rep. 2017, 7, 716. [Google Scholar] [CrossRef]
- Peloquin, C.; Euvé, L.-P.; Philbin, T.; Rousseaux, G. Analogue wormholes and black hole LASER effect in hidrodynamics. Phys. Rev. D 2016, 93, 084032. [Google Scholar] [CrossRef]
- Euvé, L.-P.; Rousseaux, G. Classical analogue of an interstellar travel through a hidrodynamic wormhole. Phys. Rev. D 2017, 96, 064042. [Google Scholar] [CrossRef]
- Prat-Camps, J.; Navau, C.; Sanchez, A. A magnetic wormhole. Sci. Rep. 2015, 5, 12488. [Google Scholar] [CrossRef]
- Sabín, C. Quantum simulation of traversable wormhole spacetimes in a dc-SQUID array. Phys. Rev. D 2016, 94, 081501. [Google Scholar] [CrossRef]
- Mateos, J.; Sabín, C. Quantum simulation of traversable wormhole spacetimes in a Bose-Einstein condensate. Phys. Rev. D 2018, 97, 044045. [Google Scholar] [CrossRef]
- Sabín, C. One-dimensional sections of exotic spacetimes with superconducting circuits. New J. Phys. 2018, 20, 053028. [Google Scholar] [CrossRef]

© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sabín, C. Light Propagation through Nanophotonics Wormholes. Universe 2018, 4, 137. https://doi.org/10.3390/universe4120137
Sabín C. Light Propagation through Nanophotonics Wormholes. Universe. 2018; 4(12):137. https://doi.org/10.3390/universe4120137
Chicago/Turabian StyleSabín, Carlos. 2018. "Light Propagation through Nanophotonics Wormholes" Universe 4, no. 12: 137. https://doi.org/10.3390/universe4120137
APA StyleSabín, C. (2018). Light Propagation through Nanophotonics Wormholes. Universe, 4(12), 137. https://doi.org/10.3390/universe4120137