Hamiltonian Dynamics of Doubly-Foliable Space-Times

Abstract

The 2 + 1 + 1 decomposition of space-time is useful in monitoring the temporal evolution of gravitational perturbations/waves in space-times with a spatial direction singled-out by symmetries. Such an approach based on a perpendicular double foliation has been employed in the framework of dark matter and dark energy-motivated scalar-tensor gravitational theories for the discussion of the odd sector perturbations of spherically-symmetric gravity. For the even sector, however, the perpendicularity has to be suppressed in order to allow for suitable gauge freedom, recovering the 10th metric variable. The 2 + 1 + 1 decomposition of the Einstein–Hilbert action leads to the identification of the canonical pairs, the Hamiltonian and momentum constraints. Hamiltonian dynamics is then derived via Poisson brackets.

1. Introduction

In the curved space-time of general relativity, gravitational waves propagate with the speed of light (the velocity limit), correcting the Newtonian description of gravity. Whenever a reference system is chosen, time needs to be singled out. In the 3 + 1 decomposition of space-time, known as the Arnowitt–Deser–Misner (ADM) formalism of gravity [1], the constant time three-surfaces form a foliation. While the time parameter is constant on each hypersurface, it changes monotonically from one hypersurface to the other. The role of the four-dimensional metric ${\tilde{g}}_{ab}$ (with $10$ independent components) is taken by the metric induced on the three-dimensional hypersurfaces (six variables) and their extrinsic curvature (six variables), which generate canonical pairs. Einstein equations are replaced by the Hamiltonian evolution of these canonical pairs. Beside these, there are constraint equations to be fulfilled in each instant (on each hypersurface). These are the Hamiltonian and diffeomorphism constraints. In the generic case of the 3 + 1 decompositions, there is no preferred time; the formalism has to be valid for any possible temporal choices (“many-fingered time” formalism [2,3,4]). Preferred choices arise by either imposing coordinate conditions [5,6] or by filling space-time with an adequate reference fluid [7,8]. Although the 3 + 1 decomposition breaks space-time covariance, a manifestly covariant canonical formalism based on the hyperspace (defined by all space-like hypersurfaces) has been also proposed [9,10,11,12]. The ADM decomposition has been generalized for some of the modified gravity theories, as well, e.g., for the $f\left(R\right)$ gravitational theories [13].

If in addition, a spatial direction plays a special role, the 2 + 1 + 1 decomposition of space-time may prove useful. This special role can be provided by a Killing-symmetry, for example the radial directions in either spherical or cylindrical symmetric space-times are such singled-out directions. We do not explore however simplifications arising from the imposition of symmetries, as for example applying mini-superspace or midi-superspace approaches [14,15]. The scenario we have in mind is to discuss generic perturbations of a background with certain symmetry. In the most generic case, both singled-out directions have expansion, shear and vorticity [16]. The corresponding optical scalars were explored in the discussion of perturbations of spherically-symmetric space-times [17], also for the discussion of gravitational waves in anisotropic Kantowski–Sachs space-times [18].

In another, much simpler 2 + 1 + 1 decomposition formalism, the decomposition is made along a perpendicular double foliation [19,20]. This formalism has been employed in the framework of dark matter and dark energy-motivated scalar-tensor gravitational theories in the discussion of the odd sector perturbations of spherically-symmetric gravity in the effective field theory approach [21]. The requirement of perpendicularity however consumes one gauge degree of freedom by fixing a metric function to vanish. This has posed no problem in the discussion of the odd sector; however for the even sector, it generates an arbitrary function in the solution, hampering the physical interpretation of perturbations. Therefore, a modified 2 + 1 + 1 decomposition formalism would be desirable, which keeps the relative simplicity of the formalism of [19,20] (as compared to the formalism exploring optical scalars [16]), but employs 10 metric functions instead of nine, hence becoming suitable for the discussion of the even sector. Such a formalism could be worked out at the price of relaxing the perpendicularity requirement [22].

In this conference report, we summarize the main feature of this new formalism and sketch the derivation of the Hamiltonian formalism, without insisting on the involved computational details and related proofs of the statements, which are given in [22] together with additional details.

Latin indices denote four-dimensional space-time indices. Boldface lower-case (as $\mathbf{i}$) or uppercase (as $\mathbf{A}$) Latin letters count two-dimensional or four-dimensional basis vectors.

2. The Nonorthogonal Double Foliation

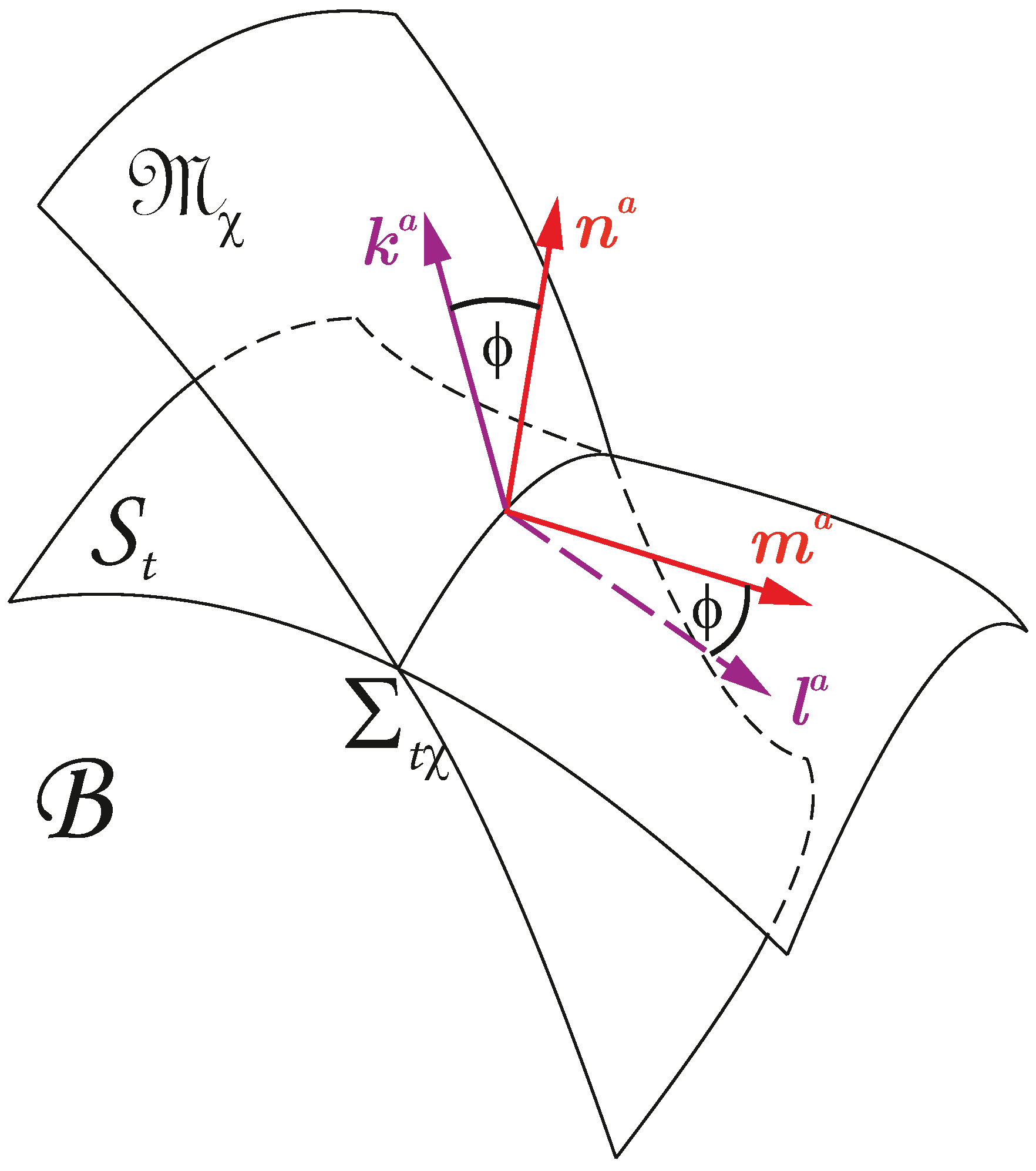
We generalize the orthogonal 2 + 1 + 1 decomposition of [19,20] such that the hypersurfaces ${\mathcal{S}}_t$ of constant t and ${\mathfrak{M}}_{\chi }$ of constant $\chi$ with normal vectors $n^a$ and $l^a$, respectively, are nonorthogonal, as presented in Figure 1.

Their intersection is the surface ${\mathsf{\Sigma }}_{t\chi }$, with an adapted vector basis $\left\{F_{\mathbf{i}}\right\}$. We introduce two orthonormal bases adapted to the two foliations, as follows: $f_{\mathbf{A}}=\left\{n,m,F_{\mathbf{i}}\right\}$ and $g_{\mathbf{A}}=\left\{k,l,F_{\mathbf{i}}\right\}$. The four-dimensional metric can then be decomposed in both:

$$\begin{array}{ccc}\hfill {\tilde{g}}_{ab}& =& -n_a{n}_b+m_a{m}_b+g_{ab},\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill {\tilde{g}}_{ab}& =& -k_a{k}_b+l_a{l}_b+g_{ab}.\hfill \end{array}$$

(2)

Here, $g_{ab}$ is the metric induced on ${\mathsf{\Sigma }}_{t\chi }$.

The temporal and selected spatial evolution vectors in the $f_{\mathbf{A}}$ basis are:

$$\begin{array}{ccc}\hfill {\left(\frac{\partial }{\partial t}\right)}^a& =& N{n}^a+N^a+\mathcal{N}{m}^a,\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill {\left(\frac{\partial }{\partial \chi }\right)}^a& =& M{m}^a+M^a+\mathcal{M}{n}^a.\hfill \end{array}$$

(4)

They define a coordinate-basis, the duality relations of which imply [22]:

$$\mathcal{M}=0,$$

(5)

making manifest that $\partial /\partial \chi$ is tangent to ${\mathcal{S}}_t$. The shift component $\mathcal{N}$ arises due to the non-orthogonality of the foliations and generates all new terms arising as compared to the formalism presented in References [19,20], where $\mathcal{N}=0$ was imposed. With the introduction of a nonvanishing $\mathcal{N}$, full gauge freedom is re-established, with 10 metric components in the formalism (three for $g_{ab}$, two for $M^a$ and $N^a$ each, one for each of the lapses N, M and shift component $\mathcal{N}$). At times, it will be convenient to parametrize this 10th metric function as $\mathcal{N}=Ntanh\varphi$ and also employ the notations $\mathfrak{s}=sinh\varphi$, $\mathfrak{c}=cosh\varphi$. This is especially convenient in proving [22] that the two bases are related by a Lorentz rotation:

$$\left(\begin{array}{c}{k}^a\\ l^a\end{array}\right)=\left(\begin{array}{cc}\mathfrak{c}& \mathfrak{s}\\ \mathfrak{s}& \mathfrak{c}\end{array}\right)\left(\begin{array}{c}{n}^a\\ m^a\end{array}\right)$$

(6)

also to derive the decomposition of the evolution vectors in the basis $g_{\mathbf{A}}$:

$$\begin{array}{ccc}\hfill {\left(\frac{\partial }{\partial t}\right)}^a& =& \frac{N}{\mathfrak{c}}{k}^a+N^a,\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill {\left(\frac{\partial }{\partial \chi }\right)}^a& =& M\left(-\mathfrak{s}{k}^a+\mathfrak{c}{l}^a\right)+M^a.\hfill \end{array}$$

(8)

Note that $\partial /\partial t$ is manifestly tangent to the hypersurface ${\mathfrak{M}}_{\chi }$.

Finally, in the basis $f_{\mathbf{A}}$, it is straightforward to check:

$${\left[m,F_{\mathbf{j}}\right]}^a{n}_a=0,$$

(9)

reassuring (due to the Frobenius theorem) that $n^a$ is hypersurface-orthogonal and:

$${\left[n,F_{\mathbf{j}}\right]}^a{m}_a=\frac{M}{N}{\partial }_{\mathbf{j}}\left(\frac{\mathcal{N}}{M}\right),$$

(10)

implying that the vector $m^a$ has vorticity. Similarly, in the basis $g_{\mathbf{A}}$, we find that $l^a$ is hypersurface-orthogonal and $k^a$ has vorticity:

$$\begin{array}{ccc}\hfill {\left[k,F_{\mathbf{j}}\right]}^a{l}_a& =& 0,\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill {\left[l,F_{\mathbf{j}}\right]}^a{k}_a& =& \frac{N}{{\mathfrak{c}}^{2}M}{\partial }_{\mathbf{j}}\left(\frac{\mathfrak{sc}M}{N}\right).\hfill \end{array}$$

(12)

Hence the 10th metric function $\mathcal{N}$ bears a double interpretation: (1) it gives the angle of the Lorentz rotation between the two bases and, (2) generates the vorticity of the complementary basis vectors $m^a$ and $k^a$. More details of these interpretations are presented in [22].

3. The 2 + 1 + 1 Decomposition of Covariant Derivatives

The projected covariant derivative of any tensor $T_{b_1\dots b_r}^{a_1\dots a_r}$ defined on ${\mathsf{\Sigma }}_{t\chi }$ arises by projecting in all indices with $g_a^b$:

$$D_a{T}_{b_1\dots b_q}^{a_1\dots a_r}\equiv g_a^c{g}_{c_1}^{a_1}\dots g_{c_r}^{a_r}{g}_{b_1}^{d_1}\dots g_{b_q}^{d_q}{\tilde{\nabla }}_c{T}_{d_1\dots d_q}^{c_1\dots c_r}.$$

(13)

The D-derivative obtained in this way is related to the connection compatible with the two-metric due to the property:

$$D_a{g}_{bc}=0.$$

(14)

It will be of particular importance to 2 + 1 + 1 decompose the covariant derivatives of the basis vectors. We found:

$${\tilde{\nabla }}_a{n}_b=K_{ab}+2m_{(a}{\mathcal{K}}_{b)}+m_a{m}_b\mathcal{K}-n_a\left({\mathfrak{a}}_b-m_b{\mathcal{L}}^{*}\right),$$

(15)

$${\tilde{\nabla }}_a{m}_b=L_{ab}^{*}+n_a{\mathcal{L}}_b^{*}+n_b{\mathcal{K}}_a+n_a{n}_b{\mathcal{L}}^{*}+m_a\left({\mathfrak{b}}_b^{*}+n_b\mathcal{K}\right),$$

(16)

$${\tilde{\nabla }}_a{k}_b=K_{ab}^{*}+l_a{\mathcal{K}}_b^{*}+l_b{\mathcal{L}}_a+l_a{l}_b{\mathcal{K}}^{*}-k_a\left({\mathfrak{a}}_b^{*}-l_b\mathcal{L}\right),$$

(17)

$${\tilde{\nabla }}_a{l}_b=L_{ab}+2k_{(a}{\mathcal{L}}_{b)}+k_a{k}_b\mathcal{L}+l_a\left({\mathfrak{b}}_b+k_b{\mathcal{K}}^{*}\right),$$

(18)

where $K_{ab}=g_a^c{g}_b^d{\tilde{\nabla }}_c{n}_d$, $L_{ab}^{*}=g_a^c{g}_b^d{\tilde{\nabla }}_c{m}_d$, $K_{ab}^{*}=g_a^c{g}_b^d{\tilde{\nabla }}_c{k}_d$ and $L_{ab}=g_a^c{g}_b^d{\tilde{\nabla }}_c{l}_d$ are extrinsic curvatures of the surface ${\mathsf{\Sigma }}_{t\chi }$; ${\mathcal{K}}_a=g_a^c{m}^d{\tilde{\nabla }}_c{n}_d$ and ${\mathcal{L}}_a=-g_a^c{k}^d{\tilde{\nabla }}_c{l}_d$ are normal fundamental forms; $\mathcal{K}=m^d{m}^c{\tilde{\nabla }}_c{n}_d$, ${\mathcal{L}}^{*}=n^c{n}^d{\tilde{\nabla }}_c{m}_d$, ${\mathcal{K}}^{*}=l^d{l}^c{\tilde{\nabla }}_c{k}_d$ and $\mathcal{L}=k^d{k}^c{\tilde{\nabla }}_c{l}_d$ are normal fundamental scalars [23]. The quantities ${\mathcal{L}}_a^{*}=-g_a^d{n}^c{\tilde{\nabla }}_c{m}_d$ and ${\mathcal{K}}_a^{*}=g_a^d{l}^c{\tilde{\nabla }}_c{k}_d$ are defined similarly to the normal fundamental forms, but they also contain the contributions of the vorticities of the corresponding vectors. Finally ${\mathfrak{a}}_a=g_a^d{n}^c{\tilde{\nabla }}_c{n}_d$, ${\mathfrak{b}}_a^{*}=g_a^i{m}^b{\tilde{\nabla }}_b{m}_i$, ${\mathfrak{a}}_a^{*}=g_a^i{k}^b{\tilde{\nabla }}_b{k}_i$ and ${\mathfrak{b}}_a=g_a^d{l}^c{\tilde{\nabla }}_c{l}_d$ are the projections onto ${\mathsf{\Sigma }}_{t\chi }$ of the nongravitational accelerations of the respective observers (among which those moving along $n^a$ and $k^a$ are physical).

The set of above quantities is not independent. As shown in detail in [22], it is enough to select the sets $\left(K_{ab},{\mathcal{K}}^a,\mathcal{K}\right)$, $\left(L_{ab}^{*},{\mathcal{L}}^{*}\right)$, $\left({\mathfrak{a}}_a,{\mathfrak{b}}_a^{*}\right)$ and $\mathcal{N}$ in order to express all the others. In particular, for orthogonal foliations, all starry quantities reduce to non-starred ones. Beside, the set $\left(K_{ab},{\mathcal{K}}^a,\mathcal{K}\right)$ is related to time derivatives of the metric variables:

$$\begin{array}{ccc}\hfill K_{ab}& =& \frac{1}{N}\left[\frac{1}{2}{\partial }_t{g}_{ab}-D_{(a}{N}_{b)}\right]-\frac{\mathfrak{s}}{M\mathfrak{c}}\left[\frac{1}{2}{\partial }_{\chi }{g}_{ab}-D_{(a}{M}_{b)}\right],\hfill \end{array}$$

(19)

$$\begin{array}{ccc}\hfill {\mathcal{K}}^a& =& \frac{1}{2MN}\left({\partial }_t{M}^a-{\partial }_{\chi }{N}^a-N^b{D}_b{M}^a+M^b{D}_b{N}^a\right)\hfill \\ & & -\frac{M}{2N}{D}^a\left(\frac{\mathcal{N}}{M}\right),\hfill \end{array}$$

(20)

$$\begin{array}{ccc}\hfill \mathcal{K}& =& \frac{1}{MN}\left[{\partial }_{t}M-{\partial }_{\chi }\mathcal{N}-N^a{D}_{a}M+M^a{D}_a\mathcal{N}\right],\hfill \end{array}$$

(21)

while the set $\left(L_{ab}^{*},{\mathcal{L}}^{*}\right)$ is connected to their $\chi$-derivatives only:

$$\begin{array}{ccc}\hfill L_{ab}^{*}& =& \frac{1}{M}\left[\frac{1}{2}{\partial }_{\chi }{g}_{ab}-D_{(a}{M}_{b)}\right],\hfill \end{array}$$

(22)

$$\begin{array}{ccc}\hfill {\mathcal{L}}^{*}& =& -\frac{1}{M}\left[{\partial }_{\chi }\left(lnN\right)-M^a{D}_a\left(lnN\right)\right].\hfill \end{array}$$

(23)

Moreover, the accelerations can be expressed as D-derivatives of the lapses:

$$\begin{array}{ccc}\hfill {\mathfrak{a}}_b& =& D_b\left(lnN\right),\hfill \end{array}$$

(24)

$$\begin{array}{ccc}\hfill {\mathfrak{b}}_b^{*}& =& -D_b\left(lnM\right)\hfill \end{array}$$

(25)

4. Hamiltonian Dynamics

The Einstein–Hilbert action:

$$S_{EH}=\int d^{4}x\sqrt{-\tilde{g}}\tilde{R}$$

(26)

can be rewritten by employing the twice contracted Gauss identity [22] and the decomposition $\sqrt{-\tilde{g}}=NM\sqrt{g}$ as:

$$\begin{array}{ccc}{S}_{EH}\hfill & =\hfill & S_{EH}\left[\left\{g_{ab},M^a,M\right\};\left\{K_{ab},{\mathcal{K}}^a,\mathcal{K}\right\};\left\{L_{ab}^{*},{\mathcal{L}}^{*}\right\};\left\{N,N^a,\mathcal{N}\right\}\right]\hfill \\ & =\hfill & \int dt\int d\chi {\int }_{{\mathsf{\Sigma }}_{t\chi }}{d}^{2}xNM\sqrt{g}\left\{R+K_{ab}{K}^{ab}-K^2-2K\mathcal{K}+2{\mathcal{K}}^a{\mathcal{K}}_a\right.\hfill \\ & & -L_{ab}^{*}{L}^{*ab}+L^{*2}-2{\mathcal{L}}^{*}{L}^{*}+2{\left(NM\right)}^{-1}{D}^{a}M{D}_{a}N\hfill \\ & & \left.-2{\tilde{\nabla }}_a\left[{\alpha }^a-{\beta }^{*a}-n^{a}K+m^a{L}^{*}\right]\right\},\hfill \end{array}$$

(27)

which besides scalars contains only tensors and vectors defined on ${\mathsf{\Sigma }}_{t\chi }$. The total covariant divergence is not yet decomposed; however upon decomposition, it will generate only boundary terms. The set of variables $\left(g_{ab},M^a,M\right)$ comprises the generalized coordinates, $\left(K_{ab},{\mathcal{K}}^a,\mathcal{K}\right)$ the generalized velocities, while $\left(L_{ab}^{*},{\mathcal{L}}^{*}\right)$ can be perceived as shorthand notations for the $\chi$-derivatives of the generalized coordinates. Similarly to the 3 + 1 decomposition, time derivatives of $\left(N,N^a,\mathcal{N}\right)$ do not emerge in the action. The generalized momenta arise as derivatives with respect to the time derivatives of the generalized coordinates as:

$$\begin{array}{ccc}\hfill {\pi }^{ab}& =& \sqrt{g}M\left[K^{ab}-g^{ab}\left(K+\mathcal{K}\right)\right],\hfill \end{array}$$

(28)

$$\begin{array}{ccc}\hfill p_a& =& 2\sqrt{g}{\mathcal{K}}_a,\hfill \end{array}$$

(29)

$$\begin{array}{ccc}\hfill p& =& -2\sqrt{g}K.\hfill \end{array}$$

(30)

Then, the action can be rewritten in an already Hamiltonian form as [22]:

$$\begin{array}{ccc}{S}_{EH}\hfill & =\hfill & \int dt\int d\chi {\int }_{{\mathsf{\Sigma }}_{t\chi }}{d}^{2}x\left[{\pi }^{ab}{\dot{g}}_{ab}+p_a{\dot{M}}^a+p\dot{M}\right.\hfill \\ & & \left.-N{\mathcal{H}}_{\perp }^G-N^a{\mathcal{H}}_a^G-{\mathcal{NH}}_{\mathcal{N}}^G+Q\right]\hfill \end{array}$$

(31)

where Q is a sum of boundary terms, given explicitly in [22], while:

$$\begin{array}{ccc}{\mathcal{H}}_{\perp }^G\hfill & =\hfill & \sqrt{g}\left[-M\left(R+3L^{*ab}{L}_{ab}^{*}-L^{*2}\right)+2g^{ab}{\partial }_{\chi }{L}_{ab}^{*}\right.\hfill \\ & & -2\left(M^c{D}_c{L}^{*}+2L_{ab}^{*}{D}^a{M}^b\right)+2D^a{D}_{a}M\hfill \\ & & +\frac{M}{\sqrt{g}}\left[\frac{1}{M^2}\left({\pi }_{ab}{\pi }^{ab}-\frac{{\pi }^2}{2}\right)+\frac{1}{2}{p}_a{p}^a+\frac{1}{8}{p}^2-\frac{\pi p}{2M}\right]\hfill \end{array}$$

(32)

is the Hamiltonian constraint,

$${\mathcal{H}}_a^G=-2D_b{\pi }_a^b+p{D}_{a}M-{\partial }_{\chi }{p}_a+p_a{D}_b{M}^b+M^b{D}_b{p}_a+p_b{D}_a{M}^b,$$

(33)

and:

$${\mathcal{H}}_{\mathcal{N}}^G=2L_{ab}^{*}{\pi }^{ab}-2p^a{D}_{a}M-M{D}_a{p}^a-{\partial }_{\chi }p+D_a\left(p{M}^a\right)$$

(34)

are the diffeomorphism constraints. Note that as expected, $\left(N,N^a,\mathcal{N}\right)$ only appear as Lagrange-multipliers.

The evolution equations for the generalized coordinates and momenta then emerge as the Hamiltonian equations written for the gravitational Hamiltonian density:

$${\mathcal{H}}^G=N{\mathcal{H}}_{\perp }^G+N^a{\mathcal{H}}_a^G+{\mathcal{NH}}_{\mathcal{N}}^G.$$

(35)

They are explicitly worked out in [22].

5. Conclusions

We generalized the formalism of [19,20] by allowing for nonorthogonal foliations. As the main benefit, this led to the reestablishment of the full gauge freedom, allowing a generic discussion of perturbations. We gave a two-fold geometrical interpretation the 10th metric variable as the angle of the Lorentz rotation of the basis vectors and the measure of the vorticity of the basis vectors.

In the ADM formalism, the induced metric and extrinsic curvature of the hypersurface play the role of Hamiltonian coordinates and momenta. In the new formalism, we identified those geometrical quantities characterizing the embedding, which bear a dynamical role (they contain time derivatives). Non-dynamical geometrical quantities appear only in the basis $f_{\mathbf{A}}$; hence, we employed that for the 2 + 1 + 1 decomposition of the Einstein–Hilbert action. From among the geometric variables, we identified those that combine into canonical pairs and proceeded with performing the Hamiltonian analysis. We identified the 2 + 1 + 1 decomposed gravitational Hamiltonian, as well as the Hamiltonian and momentum constraints in terms of canonical coordinates and momenta.

We intend to apply this formalism both for the discussion of the even sector of perturbations of spherically-symmetric gravity in the effective field theories of gravity and for the Hamiltonian treatment of canonically-quantizable cylindrical gravitational waves. The first of these has the potential to address the stability of dark matter halo models in scalar-tensor gravity. Furthermore, for the discussion of gravitational waves in space-times with particular symmetries, the 2 + 1 + 1 decomposition of the Weyl-tensor would be an asset.