Modified Gravity with Vector Distortion and Cosmological Applications
Abstract
:1. Introduction
2. Geometry with Vector Distortion
3. Gravitational Lagrangians with Vector Distortion
3.1. Theories
3.2. Quadratic Actions
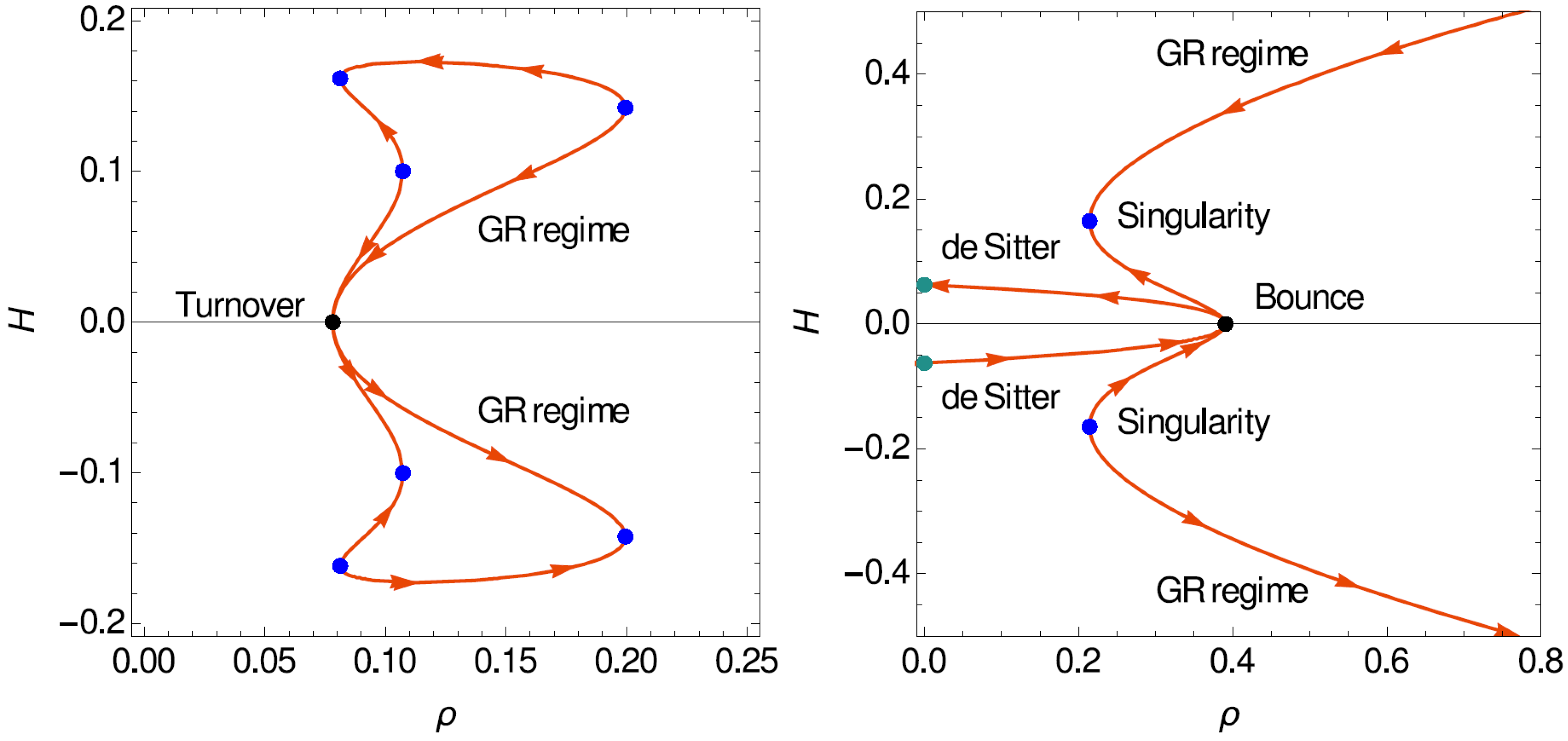
3.3. Cubic Theories
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Olmo, G.J. Palatini Approach to Modified Gravity: f(R) Theories and Beyond. Int. J. Mod. Phys. D 2011, 20, 413–462. [Google Scholar] [CrossRef]
- Capozziello, S.; Harko, T.; Koivisto, T.S.; Lobo, F.S.N.; Olmo, G.J. Hybrid metric-Palatini gravity. Universe 2015, 1, 199–238. [Google Scholar] [CrossRef]
- Hammond, R.T. Torsion gravity. Rep. Prog. Phys. 2002, 65, 599–649. [Google Scholar] [CrossRef]
- Krasnov, K. Non-Metric Gravity. I. Field Equations. Class. Quant. Gravity 2008, 25, 025001. [Google Scholar] [CrossRef]
- Sobreiro, R.F.; Vasquez Otoya, V.J. Aspects of nonmetricity in gravity theories. Braz. J. Phys. 2010, 40, 370–374. [Google Scholar] [CrossRef]
- Vitagliano, V. The role of nonmetricity in metric-affine theories of gravity. Class. Quant. Gravity 2014, 31, 045006. [Google Scholar] [CrossRef]
- Beltran Jimenez, J.; Golovnev, A.; Karciauskas, M.; Koivisto, T.S. The Bimetric variational principle for General Relativity. Phys. Rev. D 2012, 86, 084024. [Google Scholar] [CrossRef]
- Scholz, E. The unexpected resurgence of Weyl geometry in late 20-th century physics. arXiv, 2017; arXiv:1703.03187. [Google Scholar]
- Tanhayi, M.R.; Dengiz, S.; Tekin, B. Weyl-Invariant Higher Curvature Gravity Theories in n Dimensions. Phys. Rev. D 2012, 85, 064016. [Google Scholar] [CrossRef]
- Haghani, Z.; Khosravi, N.; Shahidi, S. The Weyl-Cartan Gauss-Bonnet gravity. Class. Quant. Gravity 2015, 32, 215016. [Google Scholar] [CrossRef]
- Beltran Jimenez, J.; Koivisto, T.S. Extended Gauss-Bonnet gravities in Weyl geometry. Class. Quant. Gravity 2014, 31, 135002. [Google Scholar] [CrossRef]
- Beltran Jimenez, J.; Koivisto, T.S. Spacetimes with vector distortion: Inflation from generalised Weyl geometry. Phys. Lett. B 2016, 756, 400–404. [Google Scholar] [CrossRef]
- Hehl, F.W.; Macias, A. Metric affine gauge theory of gravity. 2. Exact solutions. Int. J. Mod. Phys. D 1999, 8, 399–416. [Google Scholar] [CrossRef]
- Kallosh, R.; Linde, A.; Roest, D. Superconformal Inflationary α-Attractors. J. High Energy Phys. 2013, 2013, 198. [Google Scholar] [CrossRef]
- Ozkan, M.; Pang, Y.; Tsujikawa, S. Planck constraints on inflation in auxiliary vector modified f(R) theories. Phys. Rev. D 2015, 92, 023530. [Google Scholar] [CrossRef]
- Ozkan, M.; Roest, D. Universality Classes of Scale Invariant Inflation. arXiv, 2015; arXiv:1507.03603. [Google Scholar]
- Akarsu, O.; Boran, S.; Kahya, E.O.; Ozdemir, N.; Ozkan, M. Broken Scale Invariance, Alpha-Attractors and Vector Impurity. arXiv, 2016; arXiv:1606.05308. [Google Scholar]
- Beltran Jimenez, J.; Heisenberg, L.; Koivisto, T.S. Cosmology for quadratic gravity in generalized Weyl geometry. J. Cosmol. Astropart. Phys. 2016, 2016, 046. [Google Scholar] [CrossRef]
- Cembranos, J.A.R.; Hallabrin, C.; Maroto, A.L.; Jareno, S.J.N. Isotropy theorem for cosmological vector fields. Phys. Rev. D 2012, 86, 021301. [Google Scholar] [CrossRef]
- Cembranos, J.A.R.; Maroto, A.L.; Jareno, S.J.N. Isotropy theorem for cosmological Yang-Mills theories. Phys. Rev. D 2013, 87, 043523. [Google Scholar] [CrossRef]
- Cembranos, J.A.R.; Maroto, A.L.; Jareno, S.J.N. Isotropy theorem for arbitrary-spin cosmological fields. J. Cosmol. Astropart. Phys. 2014, 2014, 042. [Google Scholar] [CrossRef]
- Tasinato, G. Cosmic Acceleration from Abelian Symmetry Breaking. J. High Energy Phys. 2014, 2014, 067. [Google Scholar] [CrossRef]
- Heisenberg, L. Generalization of the Proca Action. J. Cosmol. Astropart. Phys 2014, 2014, 015. [Google Scholar] [CrossRef]
- Allys, E.; Peter, P.; Rodriguez, Y. Generalized Proca action for an Abelian vector field. J. Cosmol. Astropart. Phys. 2016, 2016, 004. [Google Scholar] [CrossRef]
- Beltran Jimenez, J.; Heisenberg, L. Derivative self-interactions for a massive vector field. Phys. Lett. B 2016, 757, 405–411. [Google Scholar] [CrossRef]
- Beltran Jimenez, J.; Maroto, A.L. Dark energy, non-minimal couplings and the origin of cosmic magnetic fields. J. Cosmol. Astropart. Phys. 2010, 2010, 025. [Google Scholar] [CrossRef]
- Beltran Jimenez, J.; Piazza, F.; Velten, H. Evading the Vainshtein Mechanism with Anomalous Gravitational Wave Speed: Constraints on Modified Gravity from Binary Pulsars. Phys. Rev. Lett. 2016, 116, 061101. [Google Scholar] [CrossRef] [PubMed]
- Horndeski, G.W. Conservation of Charge and the Einstein-Maxwell Field Equations. J. Math. Phys. 1976, 17, 1980–1987. [Google Scholar] [CrossRef]
- Barrow, J.D.; Thorsrud, M.; Yamamoto, K. Cosmologies in Horndeski’s second-order vector-tensor theory. J. High Energy Phys. 2013, 2013, 146. [Google Scholar] [CrossRef]
- Beltran Jimenez, J.; Durrer, R.; Heisenberg, L.; Thorsrud, M. Stability of Horndeski vector-tensor interactions. J. Cosmol. Astropart. Phys. 2013, 2013, 064. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beltrán Jiménez, J.; Koivisto, T.S. Modified Gravity with Vector Distortion and Cosmological Applications. Universe 2017, 3, 47. https://doi.org/10.3390/universe3020047
Beltrán Jiménez J, Koivisto TS. Modified Gravity with Vector Distortion and Cosmological Applications. Universe. 2017; 3(2):47. https://doi.org/10.3390/universe3020047
Chicago/Turabian StyleBeltrán Jiménez, Jose, and Tomi S. Koivisto. 2017. "Modified Gravity with Vector Distortion and Cosmological Applications" Universe 3, no. 2: 47. https://doi.org/10.3390/universe3020047
APA StyleBeltrán Jiménez, J., & Koivisto, T. S. (2017). Modified Gravity with Vector Distortion and Cosmological Applications. Universe, 3(2), 47. https://doi.org/10.3390/universe3020047






