Bouncing Cosmologies with Dark Matter and Dark Energy
Abstract
:1. Introduction
2. The ΛCDM Bounce Scenario
2.1. Background Space-Time
2.2. Perturbations
3. Interacting Dark Matter and Dark Energy
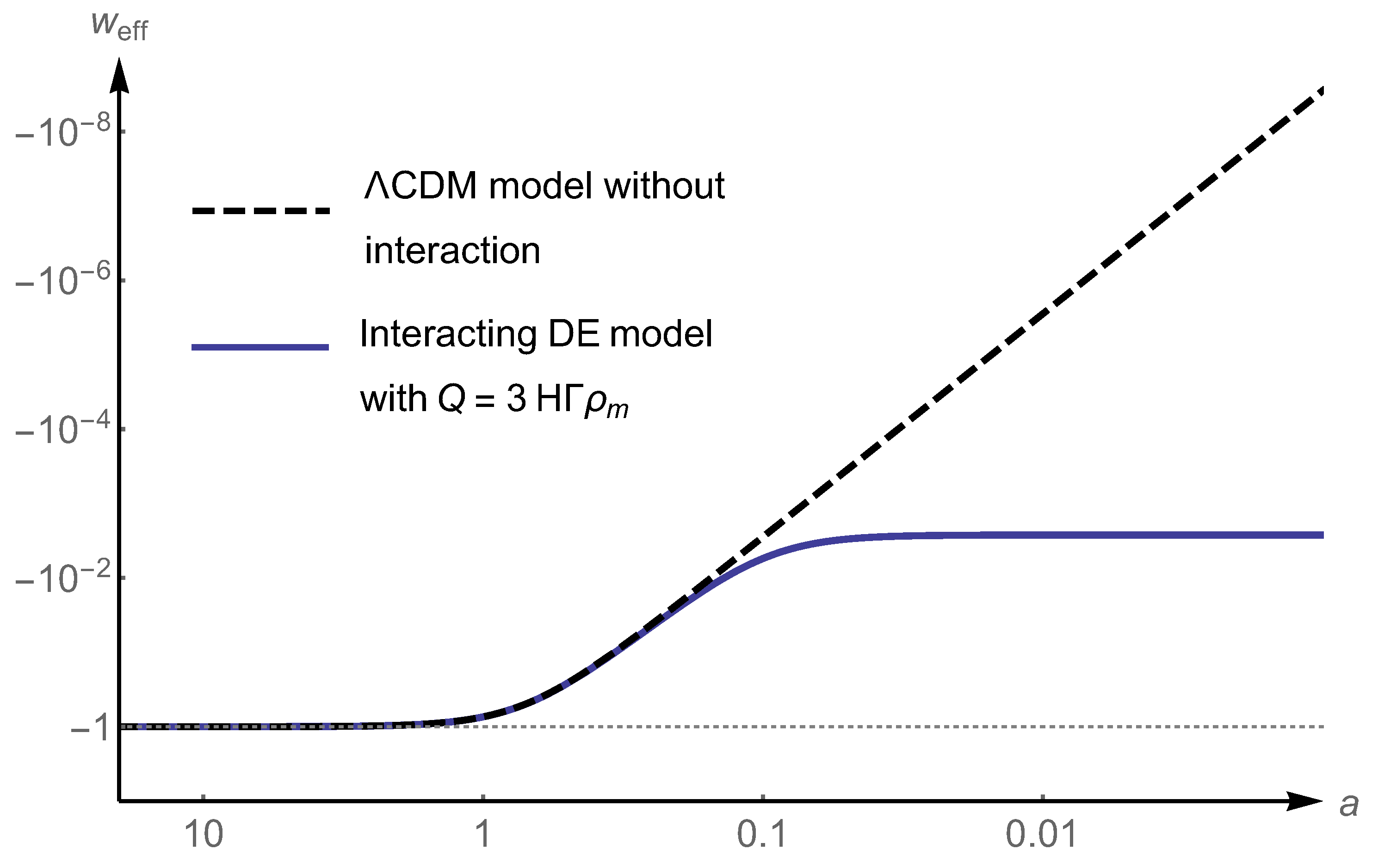
3.1. Background Space-Time
3.2. Perturbations
4. Observational Signatures
4.1. Positive Running Index
4.2. Tilt of the Tensor Spectrum
4.3. Primordial Non-Gaussianity
4.4. Other Cosmological Constraints
5. Bounce Mechanisms
5.1. Loop Quantum Cosmology
5.2. String Cosmology
5.3. f(R) Gravity
5.4. Bounce within an Effective Field Theory
5.5. Fermi Bounce
6. Discussion and Conclusion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Brandenberger, R.H. The Matter Bounce Alternative to Inflationary Cosmology. arXiv 2012. [Google Scholar]
- Cai, Y.-F.; McDonough, E.; Duplessis, F.; Brandenberger, R.H. Two Field Matter Bounce Cosmology. J. Cosmol. Astropart. Phys. 2013, 2013, 024. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Battaner, E. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar]
- Ade, P.A.; Aghanim, N.; Ahmed, Z.; Aikin, R.W.; Alexander, K.D.; Arnaud, M.; Barreiro, R.B. Joint Analysis of BICEP2/KeckArray and Planck Data. Phys. Rev. Lett. 2015, 114, 101301. [Google Scholar] [CrossRef] [PubMed]
- Quintin, J.; Sherkatghanad, Z.; Cai, Y.-F.; Brandenberger, R.H. Evolution of cosmological perturbations and the production of non-Gaussianities through a nonsingular bounce: Indications for a no-go theorem in single field matter bounce cosmologies. Phys. Rev. D 2015, 92, 063532. [Google Scholar] [CrossRef]
- Wilson-Ewing, E. The Matter Bounce Scenario in Loop Quantum Cosmology. J. Cosmol. Astropart. Phys. 2013, 2013, 026. [Google Scholar] [CrossRef]
- Cai, Y.-F.; Wilson-Ewing, E. A ΛCDM bounce scenario. J. Cosmol. Astropart. Phys. 2015, 2015, 006. [Google Scholar] [CrossRef] [PubMed]
- Cai, Y.-F.; Duplessis, F.; Easson, D.A.; Wang, D.-G. Searching for a matter bounce cosmology with low redshift observations. Phys. Rev. D 2016, 93, 043546. [Google Scholar] [CrossRef]
- Cai, Y.-F.; Brandenberger, R.; Zhang, X. The Matter Bounce Curvaton Scenario. J. Cosmol. Astropart. Phys. 2011, 2011, 003. [Google Scholar] [CrossRef] [PubMed]
- Fertig, A.; Lehners, J.-L.; Mallwitz, E.; Wilson-Ewing, E. Converting entropy to curvature perturbations after a cosmic bounce. J. Cosmol. Astropart. Phys. 2016, 10, 005. [Google Scholar] [CrossRef] [PubMed]
- Wilson-Ewing, E. Separate universes in loop quantum cosmology: Framework and applications. Int. J. Mod. Phys. D 2016, 25, 1642002. [Google Scholar] [CrossRef]
- Balbi, A.; Bruni, M.; Quercellini, C. Lambda-alpha DM: Observational constraints on unified dark matter with constant speed of sound. Phys. Rev. D 2007, 76, 103519. [Google Scholar] [CrossRef]
- Avelino, P.P.; Ferreira, V.M.C. Constraints on the dark matter sound speed from galactic scales: The cases of the Modified and Extended Chaplygin Gas. Phys. Rev. D 2015, 91, 083508. [Google Scholar] [CrossRef]
- De Haro, J.; Cai, Y.-F. An Extended Matter Bounce Scenario: Current status and challenges. Gen. Relat. Gravit. 2015, 47, 95. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. ΛCDM Bounce Cosmology without ΛCDM: The case of modified gravity. Phys. Rev. D 2015, 91, 064036. [Google Scholar] [CrossRef]
- Lehners, J.-L.; Wilson-Ewing, E. Running of the scalar spectral index in bouncing cosmologies. J. Cosmol. Astropart. Phys. 2015, 2015, 038. [Google Scholar] [CrossRef]
- Ferreira, P. C.; Pavon, D. Thermodynamics of nonsingular bouncing universes. Eur. Phys. J. C 2016, 76, 37. [Google Scholar] [CrossRef]
- Brandenberger, R.H.; Cai, Y.-F.; Das, S.R.; Ferreira, E.G.M.; Morrison, I.A.; Wang, Y. Fluctuations in a Cosmology with a Space-Like Singularity and their Gauge Theory Dual Description. arXiv 2016. [Google Scholar]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Bounce universe history from unimodular F(R) gravity. Phys. Rev. D 2016, 93, 084050. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Deformed Matter Bounce with Dark Energy Epoch. Phys. Rev. D 2016, 94, 064022. [Google Scholar] [CrossRef]
- Bozza, V.; Bruni, M. A Solution to the anisotropy problem in bouncing cosmologies. J. Cosmol. Astropart. Phys. 2009, 2009, 014. [Google Scholar] [CrossRef]
- Cai, Y.-F.; Easson, D.A.; Brandenberger, R. Towards a Nonsingular Bouncing Cosmology. J. Cosmol. Astropart. Phys. 2012, 1208, 020. [Google Scholar] [CrossRef]
- Cai, Y.-F.; Brandenberger, R.; Peter, P. Anisotropy in a Nonsingular Bounce. Class. Quantum Gravity 2013, 30, 075019. [Google Scholar] [CrossRef]
- Levy, A.M. Fine-tuning challenges for the matter bounce scenario. arXiv 2016. [Google Scholar]
- Mukhanov, V.F.; Feldman, H.; Brandenberger, R.H. Theory of cosmological perturbations. Phys. Rep. 1992, 215, 203–333. [Google Scholar] [CrossRef]
- Mukhanov, V. Physical Foundations of Cosmology; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Cai, Y.-F.; Brandenberger, R.; Zhang, X. Preheating a bouncing universe. Phys. Lett. B 2011, 703, 25–33. [Google Scholar] [CrossRef]
- Quintin, J.; Cai, Y.-F.; Brandenberger, R.H. Matter creation in a nonsingular bouncing cosmology. Phys. Rev. D 2014, 90, 063507. [Google Scholar] [CrossRef]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753–1936. [Google Scholar] [CrossRef]
- Cai, Y.-F.; Saridakis, E.N.; Setare, M.R.; Xia, J.-Q. Quintom Cosmology: Theoretical implications and observations. Phys. Rep. 2010, 493, 1–60. [Google Scholar] [CrossRef]
- Li, M.; Li, X.-D.; Wang, S.; Wang, Y. Dark Energy. Commun. Theor. Phys. 2011, 56, 525–604. [Google Scholar] [CrossRef]
- Chimento, L.P.; Jakubi, A.S.; Pavon, D.; Zimdahl, W. Interacting quintessence solution to the coincidence problem. Phys. Rev. D 2003, 67, 083513. [Google Scholar] [CrossRef]
- Amendola, L. Coupled quintessence. Phys. Rev. D 2000, 62, 043511. [Google Scholar] [CrossRef]
- Comelli, D.; Pietroni, M.; Riotto, A. Dark energy and dark matter. Phys. Lett. B 2003, 571, 115–120. [Google Scholar] [CrossRef]
- Zhang, X. Coupled quintessence in a power-law case and the cosmic coincidence problem. Mod. Phys. Lett. A 2005, 20, 2575–2582. [Google Scholar] [CrossRef]
- Cai, R.-G.; Wang, A. Cosmology with interaction between phantom dark energy and dark matter and the coincidence problem. J. Cosmol. Astropart. Phys. 2005, 2005, 002. [Google Scholar] [CrossRef]
- Guo, Z.-K.; Cai, R.-G.; Zhang, Y.-Z. Cosmological evolution of interacting phantom energy with dark matter. J. Cosmol. Astropart. Phys. 2005, 2005, 007. [Google Scholar] [CrossRef]
- Delubac, T.; Bautista, J.E.; Rich, J.; Kirkby, D.; Bailey, S.; Font-Ribera, A.; Aubourg, É. Baryon acoustic oscillations in the Lyα forest of BOSS DR11 quasars. Astron. Astrophys. 2015, 574, A59. [Google Scholar] [CrossRef]
- Salvatelli, V.; Said, N.; Bruni, M.; Melchiorri, A.; Wands, D. Indications of a late-time interaction in the dark sector. Phys. Rev. Lett. 2014, 113, 181301. [Google Scholar] [CrossRef] [PubMed]
- Abdalla, E.; Ferreira, E.G.M.; Quintin, J.; Wang, B. New evidence for interacting dark energy from BOSS. arXiv 2014. [Google Scholar]
- Väliviita, J.; Palmgren, E. Distinguishing interacting dark energy from wCDM with CMB, lensing, and baryon acoustic oscillation data. J. Cosmol. Astropart. Phys. 2015, 2015, 015. [Google Scholar] [CrossRef]
- Donà, P.; Marcianò, A.; Zhang, Y.; Antolini, C. Yang-Mills condensate as dark energy: A nonperturbative approach. Phys. Rev. D 2016, 93, 043012. [Google Scholar] [CrossRef]
- Addazi, A.; Donà, P.; Marcianò, A. Dark Energy and Dark Matter from Yang-Mills Condensate and the Peccei-Quinn mechanism. arXiv 2016. [Google Scholar]
- Alexander, S.; Marcianò, A.; Yang, Z. Invisible QCD as Dark Energy. arXiv 2016. [Google Scholar]
- Addazi, A.; Marciano, A.; Alexander, S. A Unified picture of Dark Matter and Dark Energy from Invisible QCD. arXiv 2016. [Google Scholar]
- Valiviita, J.; Majerotto, E.; Maartens, R. Instability in interacting dark energy and dark matter fluids. J. Cosmol. Astropart. Phys. 2008, 2008, 020. [Google Scholar] [CrossRef]
- He, J.-H.; Wang, B.; Abdalla, E. Stability of the curvature perturbation in dark sectors’ mutual interacting models. Phys. Lett. B 2009, 671, 139–145. [Google Scholar] [CrossRef]
- Costa, A.A.; Xu, X.-D.; Wang, B.; Ferreira, E.G.M.; Abdalla, E. Testing the Interaction between Dark Energy and Dark Matter with Planck Data. Phys. Rev. D 2014, 89, 103531. [Google Scholar] [CrossRef]
- Cabass, G.; Di Valentino, E.; Melchiorri, A.; Pajer, E.; Silk, J. Constraints on the running of the running of the scalar tilt from CMB anisotropies and spectral distortions. Phys. Rev. D 2016, 94, 0235239. [Google Scholar] [CrossRef]
- Cai, Y.-F. Exploring Bouncing Cosmologies with Cosmological Surveys. Sci. China Phys. Mech. Astron. 2014, 57, 1414–1430. [Google Scholar] [CrossRef]
- Kobayashi, T.; Takahashi, F. Running Spectral Index from Inflation with Modulations. J. Cosmol. Astropart. Phys. 2011, 2011, 026. [Google Scholar] [CrossRef]
- Kogut, A.; Fixsen, D.J.; Chuss, D.T.; Dotson, J.; Dwek, E.; Halpern, M.; Spergel, D.N. The Primordial Inflation Explorer (PIXIE): A Nulling Polarimeter for Cosmic Microwave Background Observations. J. Cosmol. Astropart. Phys. 2011, 2011, 025. [Google Scholar] [CrossRef]
- Cai, Y.-F.; Zhang, X. Probing the origin of our universe through primordial gravitational waves by Ali CMB project. Sci. China Phys. Mech. Astron. 2016, 59, 670431. [Google Scholar] [CrossRef]
- Cai, Y.-F.; Xue, W.; Brandenberger, R.; Zhang, X. Non-Gaussianity in a Matter Bounce. J. Cosmol. Astropart. Phys. 2009, 2009, 011. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Arroja, F.; Ashdown, M.; Aumont, J.; Bartolo, N. Planck 2015 results. XVII. Constraints on primordial non-Gaussianity. Astron. Astrophys. 2016, 594, A17. [Google Scholar]
- Li, Y.B.; Quintin, J.; Wang, D.G.; Cai, Y.F. Matter bounce cosmology with a generalized single field: Non-Gaussianity and an extended no-go theorem. arXiv 2016. [Google Scholar]
- Qian, P.; Cai, Y.-F.; Easson, D. A.; Guo, Z.-K. Magnetogenesis in bouncing cosmology. Phys. Rev. D 2016, 94, 083524. [Google Scholar] [CrossRef]
- Li, C.; Brandenberger, R.H.; Cheung, Y.-K.E. Big-Bounce Genesis. Phys. Rev. D 2014, 90, 123535. [Google Scholar] [CrossRef]
- Cheung, Y.-K.E.; Kang, J.U.; Li, C. Dark matter in a bouncing universe. J. Cosmol. Astropart. Phys. 2014, 2014, 001. [Google Scholar] [CrossRef] [PubMed]
- Cheung, Y.-K.E.; Vergados, J.D. Direct dark matter searches—Test of the Big Bounce Cosmology. J. Cosmol. Astropart. Phys. 2015, 2015, 014. [Google Scholar] [CrossRef]
- Hawking, S.W.; Ellis, G.F.R. The Large Scale Structure of Space-Time; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Brandenberger, R. Matter Bounce in Horava-Lifshitz Cosmology. Phys. Rev. D 2009, 80, 043516. [Google Scholar] [CrossRef]
- Cai, Y.-F.; Saridakis, E.N. Non-singular cosmology in a model of non-relativistic gravity. J. Cosmol. Astropart. Phys. 2009, 2009, 020. [Google Scholar] [CrossRef]
- Bamba, K.; Makarenko, A.N.; Myagky, A.N.; Odintsov, S.D. Bouncing cosmology in modified Gauss-Bonnet gravity. Phys. Lett. B 2014, 732, 349–355. [Google Scholar] [CrossRef]
- Cai, Y.-F.; Chen, S.-H.; Dent, J.B.; Dutta, S.; Saridakis, E.N. Matter Bounce Cosmology with the f(T) Gravity. Class. Quantum Gravity 2011, 28, 215011. [Google Scholar] [CrossRef]
- Cai, Y.-F.; Capozziello, S.; De Laurentis, M.; Saridakis, E.N. f(T) Teleparallel Gravity and Cosmology. Rept. Prog. Phys. 2016, 79, 106901. [Google Scholar] [CrossRef] [PubMed]
- Roshan, M.; Shojai, F. Energy-Momentum Squared Gravity. Phys. Rev. D 2016, 94, 044002. [Google Scholar] [CrossRef]
- Cai, Y.-F.; Qiu, T.-T.; Brandenberger, R.; Zhang, X.-M. A Nonsingular Cosmology with a Scale-Invariant Spectrum of Cosmological Perturbations from Lee-Wick Theory. Phys. Rev. D 2009, 80, 023511. [Google Scholar] [CrossRef]
- Ashtekar, A.; Pawłowski, T.; Singh, P. Quantum Nature of the Big Bang: Improved dynamics. Phys. Rev. D 2006, 74, 084003. [Google Scholar] [CrossRef]
- Wands, D.; Malik, K.A.; Lyth, D.H.; Liddle, A.R. A New approach to the evolution of cosmological perturbations on large scales. Phys. Rev. D 2000, 62, 043527. [Google Scholar] [CrossRef]
- Wilson-Ewing, E. Lattice loop quantum cosmology: Scalar perturbations. Class. Quantum Gravity 2012, 29, 215013. [Google Scholar] [CrossRef]
- Kounnas, C.; Partouche, H.; Toumbas, N. Thermal duality and non-singular cosmology in d-dimensional superstrings. Nucl. Phys. B 2012, 855, 280–307. [Google Scholar] [CrossRef]
- Kounnas, C.; Partouche, H.; Toumbas, N. S-brane to thermal non-singular string cosmology. Class. Quantum Gravity 2012, 29, 095014. [Google Scholar] [CrossRef]
- Kounnas, C.; Toumbas, N. Aspects of String Cosmology. arXiv 2013. [Google Scholar]
- Brandenberger, R.H.; Kounnas, C.; Partouche, H.; Patil, S.P.; Toumbas, N. Cosmological Perturbations Across an S-brane. J. Cosmol. Astropart. Phys. 2014, 2014, 015. [Google Scholar] [CrossRef]
- Khoury, J.; Ovrut, B.A.; Seiberg, N.; Steinhardt, P.J.; Turok, N. From big crunch to big bang. Phys. Rev. D 2002, 65, 086007. [Google Scholar] [CrossRef]
- Lehners, J.-L.; McFadden, P.; Turok, N. Colliding Branes in Heterotic M-theory. Phys. Rev. D 2007, 75, 103510. [Google Scholar] [CrossRef]
- Shtanov, Y.; Sahni, V. Bouncing brane worlds. Phys. Lett. B 2003, 557, 1–6. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Faraoni, V. f(R) Theories Of Gravity. Rev. Mod. Phys. 2010, 82, 451–497. [Google Scholar] [CrossRef]
- Carloni, S.; Dunsby, P.K.S.; Solomons, D.M. Bounce conditions in f(R) cosmologies. Class. Quantum Gravity 2006, 23, 1913–1922. [Google Scholar] [CrossRef]
- Barragan, C.; Olmo, G.J.; Sanchis-Alepuz, H. Bouncing Cosmologies in Palatini f(R) Gravity. Phys. Rev. D 2009, 80, 024016. [Google Scholar] [CrossRef]
- Bamba, K.; Makarenko, A.N.; Myagky, A.N.; Nojiri, S.; Odintsov, S.D. Bounce cosmology from F(R) gravity and F(R) bigravity. J. Cosmol. Astropart. Phys. 2014, 2014, 008. [Google Scholar] [CrossRef] [PubMed]
- Paul, N.; Chakrabarty, S.N.; Bhattacharya, K. Cosmological bounces in spatially flat FRW spacetimes in metric f(R) gravity. J. Cosmol. Astropart. Phys. 2014, 2014, 009. [Google Scholar] [CrossRef] [PubMed]
- Odintsov, S.; Oikonomou, V. Matter Bounce Loop Quantum Cosmology from F(R) Gravity. Phys. Rev. D 2014, 90, 124083. [Google Scholar] [CrossRef]
- Lin, C.; Brandenberger, R.H.; Perreault Levasseur, L. A Matter Bounce By Means of Ghost Condensation. J. Cosmol. Astropart. Phys. 2011, 2011, 019. [Google Scholar] [CrossRef]
- Koehn, M.; Lehners, J.-L.; Ovrut, B.A. Cosmological super-bounce. Phys. Rev. D 2014, 90, 025005. [Google Scholar] [CrossRef]
- Deffayet, C.; Pujolas, O.; Sawicki, I.; Vikman, A. Imperfect Dark Energy from Kinetic Gravity Braiding. J. Cosmol. Astropart. Phys. 2010, 2010, 026. [Google Scholar] [CrossRef]
- Battarra, L.; Koehn, M.; Lehners, J.-L.; Ovrut, B.A. Cosmological Perturbations Through a Non-Singular Ghost-Condensate/Galileon Bounce. J. Cosmol. Astropart. Phys. 2014, 2014, 007. [Google Scholar] [CrossRef] [PubMed]
- Qiu, T.; Evslin, J.; Cai, Y.-F.; Li, M.; Zhang, X. Bouncing Galileon Cosmologies. J. Cosmol. Astropart. Phys. 2011, 2011, 036. [Google Scholar] [CrossRef]
- Easson, D.A.; Sawicki, I.; Vikman, A. G-Bounce. J. Cosmol. Astropart. Phys. 2011, 2011, 021. [Google Scholar] [CrossRef]
- Ijjas, A.; Steinhardt, P.J. Classically stable non-singular cosmological bounces. Phys. Rev. Lett. 2016, 117, 121304. [Google Scholar] [CrossRef] [PubMed]
- Dubovsky, S.; Gregoire, T.; Nicolis, A.; Rattazzi, R. Null energy condition and superluminal propagation. J. High Energy Phys. 2006, 2006, 025. [Google Scholar] [CrossRef]
- Libanov, M.; Mironov, S.; Rubakov, V. Generalized Galileons: Instabilities of bouncing and Genesis cosmologies and modified Genesis. J. Cosmol. Astropart. Phys. 2016, 2016, 037. [Google Scholar] [CrossRef]
- Kobayashi, T. Generic instabilities of nonsingular cosmologies in Horndeski theory: A no-go theorem. Phys. Rev. D 2016, 94, 043511. [Google Scholar] [CrossRef]
- Koehn, M.; Lehners, J.-L.; Ovrut, B. Nonsingular bouncing cosmology: Consistency of the effective description. Phys. Rev. D 2016, 93, 103501. [Google Scholar] [CrossRef]
- Cai, Y.-F.; Wilson-Ewing, E. Non-singular bounce scenarios in loop quantum cosmology and the effective field description. J. Cosmol. Astropart. Phys. 2014, 2014, 026. [Google Scholar] [CrossRef]
- Shapiro, I.L. Physical aspects of the space-time torsion. Phys. Rep. 2002, 357, 113–213. [Google Scholar] [CrossRef]
- Hammond, R.T. Torsion gravity. Rep. Prog. Phys. 2002, 65, 599–649. [Google Scholar] [CrossRef]
- Trautman, A. Einstein-Cartan theory. In Encyclopedia of Mathematical Physics; Françoise, J.-P., Naber, G.L., Tsou, S.T., Eds.; Elsevier: Oxford, UK, 2006; Volume 2, pp. 189–195. [Google Scholar]
- Perez, A.; Rovelli, C. Physical effects of the Immirzi parameter. Phys. Rev. D 2006, 73, 044013. [Google Scholar] [CrossRef]
- Freidel, L.; Minic, D.; Takeuchi, T. Quantum gravity, torsion, parity violation and all that. Phys. Rev. D 2005, 72, 104002. [Google Scholar] [CrossRef]
- Bambi, C.; Malafarina, D.; Marcianò, A.; Modesto, L. Singularity avoidance in classical gravity from four-fermion interaction. Phys. Lett. B 2014, 734, 27–30. [Google Scholar] [CrossRef]
- Alexander, S.; Biswas, T. The Cosmological BCS mechanism and the Big Bang Singularity. Phys. Rev. D 2009, 80, 023501. [Google Scholar] [CrossRef]
- Popławski, N.J. Nonsingular, big-bounce cosmology from spinor-torsion coupling. Phys. Rev. D 2012, 85, 107502. [Google Scholar] [CrossRef]
- Alexander, S.; Bambi, C.; Marcianò, A.; Modesto, L. Fermi-bounce Cosmology and scale invariant power-spectrum. Phys. Rev. D 2014, 90, 123510. [Google Scholar] [CrossRef]
- Alexander, S.; Cai, Y.-F.; Marcianò, A. Fermi-bounce cosmology and the fermion curvaton mechanism. Phys. Lett. B 2015, 745, 97–104. [Google Scholar] [CrossRef]
- Alexander, S.; Biswas, T.; Calcagni, G. Cosmological Bardeen-Cooper-Schrieffer condensate as dark energy. Phys. Rev. D 2010, 81, 043511. [Google Scholar] [CrossRef]
- Donà, P.; Marcianò, A. A note on the semiclassicality of cosmological perturbations. arXiv 2016. [Google Scholar]
- Addazi, A.; Alexander, S.; Cai, Y.F.; Marcianò, A. Dark matter and baryogenesis in the Fermi-bounce curvaton mechanism. arXiv 2016. [Google Scholar]
- Brahma, S.; Donà, P.; Marcianò, A. Non Bunch Davies group coherent states, and their quantum signatures in CMB observables. arXiv 2016. [Google Scholar]
- Donà, P.; Gan, X.; Marcianò, A. Loop corrections in fermion cosmology. 2016; in preparation. [Google Scholar]
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, Y.-F.; Marcianò, A.; Wang, D.-G.; Wilson-Ewing, E. Bouncing Cosmologies with Dark Matter and Dark Energy. Universe 2017, 3, 1. https://doi.org/10.3390/universe3010001
Cai Y-F, Marcianò A, Wang D-G, Wilson-Ewing E. Bouncing Cosmologies with Dark Matter and Dark Energy. Universe. 2017; 3(1):1. https://doi.org/10.3390/universe3010001
Chicago/Turabian StyleCai, Yi-Fu, Antonino Marcianò, Dong-Gang Wang, and Edward Wilson-Ewing. 2017. "Bouncing Cosmologies with Dark Matter and Dark Energy" Universe 3, no. 1: 1. https://doi.org/10.3390/universe3010001
APA StyleCai, Y.-F., Marcianò, A., Wang, D.-G., & Wilson-Ewing, E. (2017). Bouncing Cosmologies with Dark Matter and Dark Energy. Universe, 3(1), 1. https://doi.org/10.3390/universe3010001






