Anisotropic Particle Creation from the T-Vacuum in the Radiation-Dominated Universe

Abstract

We further investigate novel features of the T-vacuum state, originally defined in the context of quantum field theory in a (1+1)-dimensional radiation-dominated universe. Here, we extend the previous work to a realistic (3+1)-dimensional setup and show that the T-vacuum gives rise to an anisotropic particle creation phenomenon in the radiation-dominated early universe. Unlike the Hawking or Unruh effect, where the particle content is thermal and asymptotically defined, here, it is non-thermal and instantaneous. This novel example of particle creation is interesting because these particles are detected in the frame of physical or cosmological observers, who envision the T-vacuum as a particle-excited state. Such results have the potential to be eventually compared with the observed anisotropies from the early universe and may provide new insights into cosmological particle creation.

1. Introduction

Within the framework of quantum field theory in curved spacetime (QFTCS), under certain symmetries of spacetime, there may exist non-unique, unitarily inequivalent decompositions of quantum fields, which are usually expressed using distinct coordinates. It is not guaranteed that every curved spacetime will offer such quantizations in Fock space, but when they do, a direct notable consequence is the existence of non-unique vacuum states corresponding to different observers who are, in general, non-inertial with respect to each other. Therefore, the meaning of particle is not universally accepted—vacuum states for a set of observers could manifest as particle-excited quantum states for another set of observers. The only observers that agree with the notion of a particle are the inertial observers in Minkowski/flat spacetime, who are related by Lorentz transformations. However, no such unique global notion of particles can be attributed to observers in curved spacetime, including the cosmological setting.

This novel difference between the standard description of quantum field theory (QFT) in flat and curved space has inspired a generation of physicists to look into various aspects of QFT in curved space and obtain interesting results on particle excitation in various settings. Among them, the most well-known are particle creation by black holes [1,2], in a cosmological setting [3,4,5], as well as by accelerated observers in flat spacetime (i.e., the Unruh effect [6]). The work of Unruh showed that an accelerated observer in Minkowski spacetime (with uniform four-acceleration $a^{\mu }$) detects particles created by the excitation of the Minkowski vacuum. Furthermore, the resulting radiation flux follows a thermal distribution with a well-defined temperature $T=\left|a\right|/2\pi$ (in natural units). It is understood that the energy required to put the observer into accelerated motion is also responsible for disturbing the Minkowski vacuum and producing particles. Although important, the details of how to put the observer and the detector in accelerated motion are not essential for understanding the basic result of the Unruh effect. A nice review of the Unruh effect and related works can be found in [7]. Apart from the above seminal works, subsequent studies based on QFTCS are often focused, but not limited, to operational detector probes of curvature and entanglement (Unruh–DeWitt type, entangling power, and coherent control) [8,9,10,11]; statistics-driven effects where Dirac fields differ from bosons [12,13,14]; adiabatic particle-production phenomenology and renormalization frameworks for interacting spin-1/2 fields [15,16,17]; and quantum/nonclassical signatures in primordial gravitational waves, including squeezed relic gravitons and HBT-style tests [18,19,20].

Recently, one of us showed [21] that an analogous situation can be contemplated in the radiation-dominated early universe, where physical/cosmological observers detect radiation flux as a result of an excitation of a novel “T-vacuum state”. This is analogous to the case where accelerated observers detect particles created by the Minkowski vacuum state. Although similar, there exists an important difference with the Unruh effect. In the Unruh effect, the source of energy driving the accelerated observer is not included, but in the radiation-dominated universe, there is a gravitational force, and various observers have their own proper frames that are not globally inertial. In fact, this T-vacuum is a natural state for a new set of observers first introduced in [22] who experience the radiation-dominated universe as a spherically symmetric, inhomogeneous, and anisotropic spacetime. Various geometric aspects of the said metric were also highlighted in [21,22]. In [23], in a relatively different study, we provided a cosmic identity of the observers for whom such a metric appears natural. We showed that the natural observers inhabiting such a spherically symmetric form of the metric can be traced back and identified with the static de Sitter observers in the previous (inflationary) epoch. In other words, the T-vacuum state turns out to also be a natural vacuum state for the static de Sitter observers when the universe transitions to the next (radiation) epoch and the spacetime is no longer inflationary but dominated by radiation. On the field theory side, regarding particle creation, a pointwise comparison was also made in a (1+1)-dimensional case [21] to clearly state the similarities and differences with the Unruh effect. These studies on the geometric and field-theoretic aspects of the radiation-dominated universe are part of a broader motivation to understand various subtleties associated with QFT in a realistic universe with multiple epochs [24,25] of expansion. In [21], we also showed that the T-vacuum state is Hadamard (no divergences or other pathological behaviors present) in (1+1) dimensions.

While the geometric construction of the above studies in the context of the radiation-dominated universe was performed in (3+1) dimensions, the field-theoretic formulation of particle creation and renormalization was confined only to (1+1) dimensions. In this work, we extend the particle creation by the T-vacuum in a (3+1)-dimensional setup and leave the renormalization properties for future work [26]. First, considering a massless scalar field, we derive various field equations and quantize the field separately in the cosmological and spherically symmetric metrics describing the radiation-dominated universe. Some relational aspects of the Hubble horizon in the two metrics are carefully mentioned. We then explicitly calculate the Bogolyubov coefficients and particle number density within the s-wave approximation and compare the results with the two-dimensional case. Finally, we consider waves with arbitrary $l>0$ and manage to calculate particle number densities analytically for the deep sub-Hubble modes. Naturally, the particle distribution is a function of the conformal time $\eta$ (or the scale factor a). Thus, our result confirms an anisotropic, time-dependent particle creation by the T-vacuum in the early universe and in the radiation-dominated universe. In principle, this particle creation may have an imprint on the cosmic microwave background (CMB), especially because it takes place after inflation, and there is no such process (like inflation) that may completely wipe out the residuals of these tiny anisotropies. It will also be interesting to see what other cosmological implications may arise due to this gravitational particle creation. In this work, we do not delve into such issues; rather, we set a solid platform from which further questions may be asked, and we shall address them separately elsewhere [26].

The paper is organized as follows: In Section 2, we present a brief review of the various geometric features related to the spherically symmetric form of the radiation-dominated universe. It includes the coordinate transformation, identification of cosmological observers’ trajectories, spacetime foliation, comparison of the Hubble radius, and the connection with the static de Sitter metric. In Section 3 and Section 4, we quantize a massless scalar field in the two frames relevant to this study. Section 5 provides the main result of particle creation separately for the s-wave approximation and beyond the s-wave. Finally, we conclude in Section 6. In Appendix A and Appendix B, we calculate the normalization constants and Bogolyubov coefficients.

2. Novel Geometric Features of the Radiation-Dominated Early Universe

In this section, we review the key results of some of our recent works, which are essential for the main study of particle creation in the radiation-dominated universe presented in the subsequent sections of this article.

2.1. Conformal vs. Spherically Symmetric Forms of the Radiation Stage

Let us start from the spatially flat FRW metric in comoving coordinates:

$$d{s}^2=d{t}^2-a^2\left(t\right)[d{r}^2+r^2(d{\theta }^2+{sin}^2\theta d{\varphi }^2)],$$

(1)

which can be expressed in a conformally flat form:

$$d{s}^2=a^2\left(\eta \right)[d{\eta }^2-d{r}^2+r^2(d{\theta }^2+{sin}^2\theta d{\varphi }^2)].$$

(2)

which we call here the “cosmological frame” $(\eta , r, \theta , \varphi )$, where $\eta =\int {\displaystyle \frac{dt}{a\left(t\right)}}$ is the conformal/cosmological time. In our convention, the scale factor $a\left(t\right)$ has a dimension of length, while $\eta$ is dimensionless (t has the dimension of time). Thus, except for the conformal factor, everything is dimensionless in (2).

We are working in the radiation-dominated stage of the universe, which follows the inflationary epoch. Considering the scale factors for these two stages, one can determine the time at which this transition takes place [24]. The idea is to make the scale factor equal and differentiable at some transition point. That is, if we consider $a_{inf}=e^{\mathcal{H}t}$ and $a_{rd}=a_0{t}^{1/2}$ and make them continuous and differentiable at some $t=t_r$, we can fix $t_r=1/2\mathcal{H}$ and $a_0=\sqrt{2\mathcal{H}e}$ (where $\mathcal{H}$ is the inflationary Hubble constant). Substituting both, we obtain the value of the scale factor $a_{inf}=a_{rd}=\sqrt{e}$, the length scale where the early universe transits from the inflationary to the radiation-dominated stage. The metric (2) will later be used in the construction of a quantum field theory.

Now, we want to express the radiation-dominated universe in a spherically symmetric and conformally static form, which was discovered in [22]. First, we rewrite (2) by defining the light-cone coordinates $u=\eta -r$ and $v=\eta +r$, so that Equation (2) is as follows:

$$d{s}^2=a^2(u,v)\left[dudv-{\displaystyle \frac{{(v-u)}^2}{4}}(d{\theta }^2+{sin}^2\theta d{\varphi }^2)\right].$$

(3)

Then, we perform the following conformal transformation of the cosmological null coordinates for $a\left(t\right)\propto t^{1/2}$, as given in [22]:

$$U\equiv T-R=\pm {\displaystyle \frac{\mathcal{H}e}{2}}{u}^2,V\equiv T+R={\displaystyle \frac{\mathcal{H}e}{2}}{v}^2,$$

(4)

where the + and − signs stand for $u\ge 0$ and $u\le 0$, respectively. This transformation gives the following metrics for the sub-Hubble (I) and super-Hubble ($II$) regions, described as

$$d{s}^2=F_I(T,R)(d{T}^2-d{R}^2)-R^{2}d{\mathsf{\Omega }}^2,$$

(5)

for $U\ge 0$ ($T\ge R$), and

$$d{s}^2=F_{II}(T,R)(d{T}^2-d{R}^2)-T^{2}d{\mathsf{\Omega }}^2,$$

(6)

for $U\le 0$ ($T\le R$), with the functions $F_I$ and $F_{II}$ given as

$$F_I(T,R)={\displaystyle \frac{{(\sqrt{T+R}+\sqrt{T-R})}^2}{4\sqrt{T^2-R^2}}},$$

(7)

$$F_{II}(T,R)={\displaystyle \frac{{(\sqrt{R+T}-\sqrt{R-T})}^2}{4\sqrt{R^2-T^2}}}.$$

(8)

The relationship between $(T,R)$ and $(\eta ,r)$ frames is given by

$$\begin{array}{cc}\hfill T& ={\displaystyle \frac{V+U}{2}}={\displaystyle \frac{\mathcal{H}e}{2}}({\eta }^2+r^2),\hfill \\ \hfill R& ={\displaystyle \frac{V-U}{2}}=\mathcal{H}e\eta r,\hfill \end{array}$$

(9)

for region I, and

$$\begin{array}{cc}\hfill T& ={\displaystyle \frac{V+U}{2}}=\mathcal{H}e\eta r,\hfill \\ \hfill R& ={\displaystyle \frac{V-U}{2}}={\displaystyle \frac{\mathcal{H}e}{2}}({\eta }^2+r^2),\hfill \end{array}$$

(10)

for region $II$. The flipping of the temporal and radial coordinates is somewhat analogous to that which appears in the Kruskal coordinates for the maximally extended Schwarzschild spacetime, but differs in that it is not a causal boundary.

We can also express the conformal factors $F_I(T,R)$ and $F_{II}(T,R)$ as functions of the Hubble parameter for radiation stage $H={\left({\displaystyle \frac{\dot{a}}{a}}\right)}_{RD}$ [22]. These are

$$F_I(H,R)={\displaystyle \frac{1}{1-H^2{R}^2}},$$

(11)

and

$$F_{II}(H,T)={\displaystyle \frac{1}{H^2{T}^2-1}}.$$

(12)

The light-cone boundary $T=R$ for these observers is translated into the comoving Hubble radius at $R=1/H$.

These new metrics, (5) and (6), are static up to a dynamical conformal factor, and they exhibit spherical symmetry. We shall refer to this coordinate system as the $(T,R)$ frame in order to meaningfully express our thoughts. The spherical symmetry in the $(T,R)$ frame has some interesting geometric and field-theoretic implications. We shall discuss them in detail in the remainder of this work.

2.2. Identification of Cosmological Observers in the $(T,R)$ Frame

We want to identify the physical cosmological observers in the $(T,R)$ frame, since their frame is often used in cosmology. It was shown in [21] that for the sub-Hubble region (I) a worldline of the form

$$T=G\left(R\right)={\alpha }_1{R}^2+{\beta }_1$$

(13)

with ${\beta }_1=1/4{\alpha }_1=\mathcal{H}e{\eta }_0^2/2$ is identified as the cosmological static frame (at rest at an arbitrary sub-Hubble point $r=r_0$). These observers have a radial velocity ${\displaystyle \frac{dR}{dT}}={\displaystyle \frac{1}{2{\alpha }_{1}R}}$ and a non-zero, position-dependent deceleration ${\displaystyle \frac{d^{2}R}{d{T}^2}}=-{\displaystyle \frac{1}{4{\alpha }_1^2{R}^3}}$. For the super-Hubble region ($II$), cosmological observers at constant $r=r_0$ are described by the following worldline:

$$R=G\left(T\right)={\alpha }_1{T}^2+{\beta }_1$$

(14)

with ${\beta }_1=1/4{\alpha }_1=\mathcal{H}e{r}_0^2/2$. The radial velocity is time-dependent, ${\displaystyle \frac{dR}{dT}}=2{\alpha }_{1}T$, while the acceleration is constant ${\displaystyle \frac{d^{2}R}{d{T}^2}}=2{\alpha }_1$ for this case. Therefore, if we see the journey of the cosmological observer, in the $(T,R)$ frame, starting from the super-Hubble region, we find that the said observers accelerate at a constant rate, which lasts up to the Hubble entry. After the Hubble entry, they start decelerating and come to a rest, even in the $(T,R)$ frame, as they approach ${\mathcal{I}}^{+}$. As expected, the cosmological observers do not encounter any horizon (due to a coordinate singularity), although the metric (5) and (6) are fragmented into the sub-Hubble and super-Hubble regions.

2.3. Cosmological Foliation in $(T,R)$ Frame

While the cosmological frame $(\eta , r, \theta , \varphi )$ has a straightforward foliation of time and space slices with $\eta$ = const. and r = const., one has a slightly nontrivial case in the $(T,R)$ frame, where new time and space slices are identified with T = const. and R = const. For a well-defined initial value formulation, it is necessary that any spacetime be foliated by Cauchy slices. Since we already have the Cauchy problem well defined in the cosmological frame, we can prove that the same is true in the $(T,R)$ frame if we can embed cosmological time and space slices using the $(T,R)$ metric. This task was also completed in [21].

The first step is to identify time slices $\eta ={\eta }_0$ for the sub-Hubble region,

$$T={\displaystyle \frac{R^2}{2\mathcal{H}e{\eta }_0^2}}+{\displaystyle \frac{1}{2}}\mathcal{H}e{\eta }_0^2,$$

(15)

taking into account only the portion below the semi-latus rectum (SLR) of the above parabola. For the super-Hubble region, the time slices will be a portion of the following parabola, as follows:

$$R={\displaystyle \frac{T^2}{2\mathcal{H}e{\eta }_0^2}}+{\displaystyle \frac{1}{2}}\mathcal{H}e{\eta }_0^2$$

(16)

starting from the point where the SLR of (15) meets the Hubble horizon. Joining these two slices along the Hubble horizon provides an embedding of the full cosmological time slice in the $(T,R)$ frame. These are depicted in Figure 1 in red.

The space slices (timelike hypersurfaces) are constructed in a similar way, by taking $r=r_0$. In region I, the space slice is given by

$$T={\displaystyle \frac{R^2}{2\mathcal{H}e{r}_0^2}}+{\displaystyle \frac{1}{2}}\mathcal{H}e{r}_0^2$$

(17)

while for region $II$, the space slice is

$$R={\displaystyle \frac{T^2}{2\mathcal{H}e{r}_0^2}}+{\displaystyle \frac{1}{2}}\mathcal{H}e{r}_0^2,$$

(18)

again joining at the Hubble radius. The union of these two portions is made by joining the upper portion (of the SLR) of the parabola (17) with the left portion (of the SLR) of the parabola (18). These are depicted in Figure 1 in blue.

With these cosmological Cauchy slices, we can now foliate the full spacetime in the $(T,R)$ plane. There is no horizon for cosmological observers, as expected. Looking at the blue curves in Figure 1, we can now confirm that cosmological observers start radially accelerating in the asymptotic past while viewed from the $(T,R)$ frame, which is valid in the super-Hubble region. After entering the Hubble radius, they start decelerating and come to rest in the asymptotic future at ${\mathcal{I}}^{+}$. Here, we first obtain an impression that a vacuum state in the $(T,R)$ frame cannot be a vacuum for cosmological observers, since these observers are non-inertially connected to each other.

2.4. Hubble Parameter and Horizon Behavior in the $(T,R)$ Frame

It is important to realize that the transformed metrics (5) and (6), representing the radiation-dominated universe, are both inhomogeneous and anisotropic since they depend on both T and R. A direct consequence of this is that the value of the Hubble parameter depends not only on the new time T but also on the position of the observer R. We expect the Hubble horizon to manifest in a nontrivial manner when expressed in these new coordinates.

The Hubble parameter is calculated from the knowledge of the scale factor $a\left(t\right)$ and its derivative ($H={\displaystyle \frac{\dot{a}}{a}}$), meaning that an observer in any part of the universe can measure the same value if they are in the same time slice. In the case of the radiation-dominated universe, we have $H\left(t\right)={\displaystyle \frac{1}{2t}}$, but since we are working on the cosmological frame ($\eta ={\displaystyle \frac{2}{a_0}}{t}^{1/2}$, where we use $a_0=\sqrt{2\mathcal{H}e}$), the value of this parameter becomes

$$H={\displaystyle \frac{2}{a_0^2{\eta }^2}}={\displaystyle \frac{1}{\mathcal{H}e{\eta }^2}}.$$

(19)

Since $\eta$ has different expressions in the sub- and super-Hubble regions due to (9) and (10), in the $(T,R)$ frame, we will have different expressions for the Hubble parameter in those regions. In region I, using the coordinate transformations in (9), we can express $\eta$ as

$$\eta ={\displaystyle \frac{1}{\sqrt{2\mathcal{H}e}}}\left(\sqrt{T+R}+\sqrt{T-R}\right).$$

(20)

Using (19) and simplifying, we obtain

$$H_I(T,R)={\displaystyle \frac{1}{T+\sqrt{T^2-R^2}}}$$

(21)

for region I, i.e., for $R<T$. For region $II$, we use the coordinate transformation given in (10), and obtain a similar expression for $\eta$. By conducting a similar process, we obtain the value of the Hubble parameter for this region as

$$H_{II}(T,R)={\displaystyle \frac{1}{R+\sqrt{R^2-T^2}}}.$$

(22)

This expression is valid for $R>T$.

We can easily observe that these expressions are continuous on $T=R$, coinciding with the value $H={\displaystyle \frac{1}{T}}={\displaystyle \frac{1}{R}}$. As expected, these expressions are functions of the T and R coordinates, so, in general, any two observers at different points in space or time measure different values of the Hubble parameter. This is due to the nature of the metric, which defines the $(T,R)$ spacetime and breaks homogeneity and isotropy.

As we have the expression for the Hubble parameter in terms of the new T and R coordinates, we can express the radii for these two regions in both the sub-Hubble and super-Hubble spacetime sections, which are simply

$$L_H^I=L_P^I=T_0+\sqrt{T_0^2-R_0^2}$$

(23)

for region I ($R<T$) and

$$L_H^{II}=L_P^{II}=R_0+\sqrt{R_0^2-T_0^2}$$

(24)

for region II ($R>T$). We can observe that we now need to measure both the current time and radial position to determine the radii, rather than just measuring the current time in the cosmological frame. In the new frame, the Hubble radius and particle horizon depend on the position and time at which they are measured.

2.5. The Relationship Between the $(T,R)$ Frame and the Static de Sitter Frame

In a previous work involving one of us [23], we showed an interesting property of the metric (5) representing the $(T,R)$ frame. The point is that (5) can be traced back and matched with the static de Sitter frame in the preceding inflationary epoch with a time redefinition. Therefore, static de Sitter observers in the inflationary epoch will find themselves closely related to the $(T,R)$ frame when a transition to the radiation epoch has already taken place. This identification will be helpful later, when we discuss particle creation. Most importantly, this observation provides a valuable “cosmic identity” of these new observers in the radiation-dominated universe. To demonstrate how this happens mathematically, it was shown in [23] that the de Sitter universe in the static frame, given by

$$d{s}^2=(1-{\mathcal{H}}^2{R}^2)d{\tau }^2-{\displaystyle \frac{d{R}^2}{1-{\mathcal{H}}^2{R}^2}}-R^{2}d{\mathsf{\Omega }}^2,$$

(25)

smoothly transits into the following metric in the radiation epoch:

$$d{s}^2={\displaystyle \frac{4e^2{e}^{4\mathcal{H}\tau }d{\tau }^2-d{R}^2}{1-H^2{R}^2}}-R^{2}d{\mathsf{\Omega }}^2$$

(26)

a transition that takes place at the comoving time $t_r=1/2\mathcal{H}$, which in $\tau ,R$ coordinates translates to $R=a\left(t_r\right)r$ and $\tau ={\displaystyle \frac{1}{2\mathcal{H}}}log\left|{\displaystyle \frac{1}{2}}({\mathcal{H}}^2{r}^2-1/e)\right|$. We may call (26) the de Sitter “post-static” frame, as described in the radiation stage of the universe. We suggest that interested readers consult Section 5 of [23] for technical details. The static de Sitter metric, as represented in (26), has a striking similarity with the metric (5). If we redefine the de Sitter time

$$\tau ={\displaystyle \frac{1}{2\mathcal{H}}}log(\mathcal{H}T/e)$$

(27)

then we see that (26) matches exactly with (5). Therefore, one may interpret that (5) is actually the de Sitter static frame living in the radiation epoch with a logarithmic scaling of time. Note that (27) is purely temporal and does not mix the time with space coordinates, which plays a crucial role in interpreting particle creation even in this de Sitter post-static frame, as discussed in the subsequent sections of the paper.

3. Field Modes in Conformally Flat FRW

Now that we have a geometric understanding of the radiation-dominated universe in both frames, we turn our attention to the construction of quantum field theory in them. In this section, we consider the cosmological frame (2), where the metric is conformally flat.

Consider a massless scalar field with arbitrary coupling in the radiation stage and solve the Klein–Gordon equation $\square \mathsf{\Phi }=0$ (simply because $R=0$ and all fields become minimally coupled). We can express the scalar field ansatz using the separation of variables as

$$\mathsf{\Phi }(\eta ,r,\theta ,\varphi )=\sum _{\mathsf{\ell },m}{\displaystyle \frac{f_{\mathsf{\ell }}\left(r\right)}{r}}g\left(\eta \right)Y_{\mathsf{\ell }m}(\theta ,\varphi )$$

(28)

where the angular part $Y_{\mathsf{\ell }m}$ denotes the spherical harmonics and the $(\eta ,r)$-dependent parts satisfy the following equations:

$${\eta }^2{\displaystyle \frac{d^{2}g}{d{\eta }^2}}+2\eta {\displaystyle \frac{dg}{d\eta }}+{\omega }^2{\eta }^{2}g=0,$$

(29)

$${\displaystyle \frac{d^2{f}_{\mathsf{\ell }}}{d{r}^2}}+\left({\omega }^2-{\displaystyle \frac{\mathsf{\ell }(\mathsf{\ell }+1)}{r^2}}\right)f_{\mathsf{\ell }}=0.$$

(30)

The time-dependent variable $g\left(\eta \right)$ satisfies the well-known spherical Bessel equation, and we can use a Fourier mode decomposition and then sum over all modes to calculate $g\left(\eta \right)$.

At this point, we shall separate our study into the $\mathsf{\ell }=0$ or s-waves and higher values of $\mathsf{\ell }>0$ to make the comparison clear with the spherically symmetric case.

3.1. Field Modes for the s-Wave Approximation

Considering the s-wave approximation ($\mathsf{\ell }=0$), we can read from (28) the individual mode functions ${\mathsf{\Phi }}_{\omega }={\displaystyle \frac{f_0\left(r\right)}{r}}{g}_{\omega }\left(\eta \right)Y_{00}$. It is easy to solve (29) and (30) (with $\mathsf{\ell }=0$) to find the mode function ${\mathsf{\Phi }}_{\omega }$, and then sum over all modes to express the field $\mathsf{\Phi }$ as

$$\begin{array}{cc}\hfill \mathsf{\Phi }& =\sum _{\omega }𝒩{\displaystyle \frac{f_0\left(r\right)}{r}}{g}_{\omega }\left(\eta \right)Y_{00}(\theta ,\varphi )\hfill \\ \hfill & =\sum _{\omega }𝒩\left({\displaystyle \frac{e^{-i\omega (\eta -r)}}{2\sqrt{\pi }\omega \eta r}}{a}_{\omega }^{in}+{\displaystyle \frac{e^{-i\omega (\eta +r)}}{2\sqrt{\pi }\omega \eta r}}{a}_{\omega }^{out}\right)+\mathrm{h}.\mathrm{c}.\hfill \end{array}$$

(31)

where $𝒩$ is a normalization constant determined by the orthogonality condition between the field modes, which is given by $𝒩={\displaystyle \frac{\sqrt{\omega }}{\sqrt{4\pi }\mathcal{H}e}}$. The superscripts in and out imply the usual ingoing and outgoing modes. The field expansion for $\mathsf{\Phi }$ in the integral form can be written as

$$\mathsf{\Phi }=\int d^3\omega (u_{\omega }{a}_{\omega }^{in}+v_{\omega }{a}_{\omega }^{out})+\mathrm{h}.\mathrm{c}.$$

(32)

with the field modes $u_{\omega }$ and $v_{\omega }$ being

$$u_{\omega }={\displaystyle \frac{e^{-i\omega (\eta -r)}}{4\pi \mathcal{H}e\sqrt{\omega }\eta r}}$$

(33)

and

$$v_{\omega }={\displaystyle \frac{e^{-i\omega (\eta +r)}}{4\pi \mathcal{H}e\sqrt{\omega }\eta r}}.$$

(34)

3.2. Field Modes Beyond the s-Wave Approximation

The general solution to Equation (30) when $\mathsf{\ell }\ne 0$ has the form

$$f\left(r\right)=\sqrt{r}(C_1{J}_{\mathsf{\ell }+1/2}\left(\omega r\right)+C_2{Y}_{\mathsf{\ell }+1/2}\left(\omega r\right))$$

(35)

where $J_{\mathsf{\ell }+1/2}$ and $Y_{\mathsf{\ell }+1/2}$ are Bessel functions of the first and second kind, respectively. The Bessel function of the second kind, $Y_{\mathsf{\ell }+1/2}\left(r\right)$, blows up at $r\to 0$, so we must choose $C_2=0$ and let us rename $C_1=𝒩$ so that

$$f_{\mathsf{\ell }}\left(r\right)=𝒩\sqrt{r}{J}_{\mathsf{\ell }+1/2}\left(\omega r\right),$$

(36)

where $𝒩$ is the normalization constant determined by the orthogonality condition between the field modes. The value of $𝒩$ is calculated in Appendix A, giving $𝒩=\omega /\sqrt{2}\mathcal{H}e$.

For further simplification, the Bessel function can be separated in terms of spherical Hankel functions such that

$$\begin{array}{cc}\hfill J_{\mathsf{\ell }+1/2}\left(\omega r\right)& =\sqrt{{\displaystyle \frac{2\omega r}{\pi }}}{j}_{\mathsf{\ell }}\left(\omega r\right)\hfill \\ \hfill & =\sqrt{{\displaystyle \frac{2\omega r}{\pi }}}{\displaystyle \frac{1}{2}}\left(h_{\mathsf{\ell }}^{\left(1\right)}\left(\omega r\right)+h_{\mathsf{\ell }}^{\left(2\right)}\left(\omega r\right)\right)\hfill \\ \hfill & =\sqrt{{\displaystyle \frac{\omega r}{2\pi }}}\left({\displaystyle \frac{e^{i\omega r}}{\omega r}}{Q}_{\mathsf{\ell }}\left(\omega r\right)+{\displaystyle \frac{e^{-i\omega r}}{\omega r}}{Q}_{\mathsf{\ell }}^{*}\left(\omega r\right)\right),\hfill \end{array}$$

where the spherical Hankel functions are expanded as

$$\begin{array}{cc}\hfill h_{\mathsf{\ell }}^{\left(1\right)}\left(x\right)& ={(-i)}^{\mathsf{\ell }+1}{\displaystyle \frac{e^{ix}}{x}}\sum _{s=0}^{\mathsf{\ell }}{\displaystyle \frac{{(i/2)}^s}{s!}}{\displaystyle \frac{(\mathsf{\ell }+s)!}{(\mathsf{\ell }-s)!}}{x}^{-s}\equiv {\displaystyle \frac{e^{ix}}{x}}{Q}_{\mathsf{\ell }}\left(x\right),\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill h_{\mathsf{\ell }}^{\left(2\right)}\left(x\right)& ={\left(i\right)}^{\mathsf{\ell }+1}{\displaystyle \frac{e^{-ix}}{x}}\sum _{s=0}^{\mathsf{\ell }}{\displaystyle \frac{{(-i/2)}^s}{s!}}{\displaystyle \frac{(\mathsf{\ell }+s)!}{(\mathsf{\ell }-s)!}}{x}^{-s}={\displaystyle \frac{e^{-ix}}{x}}{Q}_{\mathsf{\ell }}^{*}\left(x\right).\hfill \end{array}$$

(38)

Then, the complete field expansion is given by

$$\begin{array}{ccc}\hfill \mathsf{\Phi }& =& {\displaystyle \frac{1}{\mathcal{H}e\eta }}\sum _{\mathsf{\ell },m}\int d^3\omega \sqrt{{\displaystyle \frac{\omega }{4\pi }}}\left(a_{\omega lm}^{in}{\displaystyle \frac{e^{-i\omega (\eta -r)}}{\omega r}}{Q}_{\mathsf{\ell }}\left(\omega r\right)\right.\hfill \\ & & \left.+a_{\omega lm}^{out}{\displaystyle \frac{e^{-i\omega (\eta +r)}}{\omega r}}{Q}_{\mathsf{\ell }}^{*}\left(\omega r\right)\right)Y_{\mathsf{\ell }m}(\theta ,\varphi )+h.c.\hfill \end{array}$$

(39)

From the above expression, we can identify the mode functions

$$\begin{array}{ccc}\hfill u_{\omega lm}& =& \sqrt{{\displaystyle \frac{\omega }{4\pi }}}{\displaystyle \frac{e^{-i\omega u}}{\mathcal{H}e\omega \eta r}}{Q}_{\mathsf{\ell }}\left(\omega r\right)Y_{\mathsf{\ell }m}(\theta ,\varphi ),\hfill \end{array}$$

(40)

$$\begin{array}{ccc}\hfill v_{\omega lm}& =& \sqrt{{\displaystyle \frac{\omega }{4\pi }}}{\displaystyle \frac{e^{-i\omega v}}{\mathcal{H}e\omega \eta r}}{Q}_{\mathsf{\ell }}^{*}\left(\omega r\right)Y_{\mathsf{\ell }m}(\theta ,\varphi ).\hfill \end{array}$$

(41)

The above two equations show that, unlike the s-wave sector, the complete set of modes cannot be separated into an incoming and outgoing sector. The functions $Q_{\mathsf{\ell }}\left(\omega r\right)$ and $Q_{\mathsf{\ell }}^{*}\left(\omega r\right)$ multiply the incoming and outgoing modes, as expected in a situation where there is no spherical symmetry. This process of backscattering is nicely captured by the $Q_{\mathsf{\ell }}/Q_{\mathsf{\ell }}^{*}$ multiplication of the incoming and outgoing sectors.

4. Field Modes in Spherically Symmetric FRW

In this section, we quantize massless scalar fields in the background geometries, given by (5) and (6), representing spherically symmetric forms of the radiation-dominated universe in the sub- and super-Hubble scales. We present this calculation separately using the above metrics as backgrounds, also separating the s-waves and $\mathsf{\ell }>0$ cases.

4.1. Sub-Hubble Region

Since (5) is spherically symmetric, we can write the scalar field ansatz as

$${\mathsf{\Phi }}_{\mathsf{\Omega }}=\sum _{\mathsf{\ell },m}{\displaystyle \frac{{\mathsf{\Phi }}_{\mathsf{\Omega }}^{\mathsf{\ell }m}(T,R)}{R}}{Y}_{\mathsf{\ell }m}(\theta ,\varphi )$$

(42)

Then, the Klein–Gordon equation is

$$\left({\displaystyle \frac{{\partial }^2{\mathsf{\Phi }}_{\mathsf{\Omega }}^{\mathsf{\ell }m}}{\partial T^2}}-{\displaystyle \frac{{\partial }^2{\mathsf{\Phi }}_{\mathsf{\Omega }}^{\mathsf{\ell }m}}{\partial R^2}}\right)+{\displaystyle \frac{\mathsf{\ell }(\mathsf{\ell }+1)}{R^2(1-H^2{R}^2)}}{\mathsf{\Phi }}_{\mathsf{\Omega }}^{\mathsf{\ell }m}=0,$$

(43)

where we find an effective potential:

$$V_{\mathsf{\ell }}(R,H)={\displaystyle \frac{\mathsf{\ell }(\mathsf{\ell }+1)}{R^2(1-H^2{R}^2)}}.$$

(44)

For any $\mathsf{\ell }\ne 0$ modes, this potential has an interesting behavior—it diverges at $R=0$ and $R=1/H$, i.e., at the origin of the coordinate system and also at the Hubble radius. While the divergence at the origin is a characteristic of spherical waves due to the choice of coordinate system, the other divergence at $R=1/H$ is nontrivial. We need to understand this in finer detail. We know that whenever the potential tends to infinity at some value of the coordinate, the mode functions become confined within this limit. That is, no $\mathsf{\ell }\ne 0$ modes can pass to the super-Hubble region; they will always be trapped inside the Hubble radius, i.e., in the sub-Hubble region. Note that although our background spacetime is defined in the sub-Hubble region, mode functions are global and there is, in principle, no restriction to extend them beyond the Hubble scale. The peculiarity of the potential (44) is interesting in this regard. It must also be added that, although in these new coordinates it may appear that the Hubble horizon is behaving just like a black hole event horizon, where modes cannot escape from inside the event horizon, there is a crucial difference. The potential barrier is mode-specific, i.e., (44) tells us $V_{\mathsf{\ell }}(R,H)=0$ for $\mathsf{\ell }=0$ modes and, hence, the s-wave modes see no potential whatsoever, but other modes do feel the potential barrier, which is not a characteristic of an event horizon.

Given the peculiarity of the potential (44), we will now discuss the $\mathsf{\ell }=0$ and $\mathsf{\ell }>0$ modes in the following discussion.

4.1.1. Field Modes for the s-Wave Approximation

If we consider the $\mathsf{\ell }=0$ modes only, from (43), we have the following:

$$\left({\displaystyle \frac{{\partial }^2{\mathsf{\Phi }}_{\mathsf{\Omega }}^{00}}{\partial T^2}}-{\displaystyle \frac{{\partial }^2{\mathsf{\Phi }}_{\mathsf{\Omega }}^{00}}{\partial R^2}}\right)=0.$$

(45)

The field expansion is of the following form:

$$\mathsf{\Phi }=\int d^3\mathsf{\Omega }(U_{\mathsf{\Omega }}^{\mathrm{sub}}{b}_{\mathsf{\Omega }>{\mathsf{\Omega }}_H}^{in}+V_{\mathsf{\Omega }}^{\mathrm{sub}}{b}_{\mathsf{\Omega }>{\mathsf{\Omega }}_H}^{out})+\mathrm{h}.\mathrm{c}.$$

(46)

where the mode functions are

$$U_{\mathsf{\Omega }}^{\mathrm{sub}}={\displaystyle \frac{1}{4\pi \sqrt{\mathsf{\Omega }}R}}{e}^{-i\mathsf{\Omega }(T-R)}$$

(47)

and

$$V_{\mathsf{\Omega }}^{\mathrm{sub}}={\displaystyle \frac{1}{4\pi \sqrt{\mathsf{\Omega }}R}}{e}^{-i\mathsf{\Omega }(T+R)}$$

(48)

and are valid for $R\le 1/H$. The operator $b_{\mathsf{\Omega }>{\mathsf{\Omega }}_H}^{in}$ is defined for the incoming sub-Hubble modes, and the state annihilated by this operator is called the T-vacuum (for this sector), which satisfies $b_{\mathsf{\Omega }>{\mathsf{\Omega }}_H}^{in}{|0\rangle }_T^{in}=0$. Similarly, one can define a vacuum, $b_{\mathsf{\Omega }>{\mathsf{\Omega }}_H}^{out}{|0\rangle }_T^{out}=0$, for the outgoing sector.

Our focus in this paper is to calculate particle creation from the T-vacuum state when viewed from the cosmological frame described in the last section.

4.1.2. Field Modes Beyond the s-Wave Approximation

If we want to go beyond the s-waves, we need to solve (43) for arbitrary $\mathsf{\ell }>0$, which is clearly a difficult task since the Hubble parameter depends on space and time $H\equiv H(T,R)$. It makes the differential equation quite nontrivial to solve in an exact form.

However, we can consider a curious case by restricting our interest to the deep sub-Hubble region $R<<1/H$. In this case, (43) becomes

$$\left({\displaystyle \frac{{\partial }^2{\mathsf{\Phi }}_{\mathsf{\Omega }}^{\mathsf{\ell }m}}{\partial T^2}}-{\displaystyle \frac{{\partial }^2{\mathsf{\Phi }}_{\mathsf{\Omega }}^{\mathsf{\ell }m}}{\partial R^2}}\right)+{\displaystyle \frac{\mathsf{\ell }(\mathsf{\ell }+1)}{R^2}}{\mathsf{\Phi }}_{\mathsf{\Omega }}^{\mathsf{\ell }m}=0.$$

(49)

By decomposing ${\mathsf{\Phi }}_{\mathsf{\Omega }}^{\mathsf{\ell }m}(T,R)=\psi \left(T\right)\chi \left(R\right)$ and solving (49), it is found that

$$\begin{array}{cc}\hfill {\displaystyle \frac{d^2\psi }{d{T}^2}}& +{\mathsf{\Omega }}^2\psi =0\hfill \end{array}$$

(50)

$$\begin{array}{cc}\hfill {\displaystyle \frac{d^2\chi }{d{R}^2}}& +({\mathsf{\Omega }}^2-{\displaystyle \frac{\mathsf{\ell }(\mathsf{\ell }+1)}{R^2}})\chi =0.\hfill \end{array}$$

(51)

It is then clear that $\psi \left(T\right)\propto e^{\pm i\mathsf{\Omega }T}$, while the differential equation for $\chi \left(T\right)$ has the exact same form as (30), and its solution is the Bessel function of the first kind $\sqrt{R}{J}_{\mathsf{\ell }+1/2}\left(\mathsf{\Omega }R\right)$.

The exact calculation for the normalization constant is a bit nontrivial. This is because, since our field modes are only valid for a restricted region $R<<1/H$, we cannot use them to normalize over the entire spatial volume element within the Hubble radius. Therefore, the normalization constant calculated in Appendix A, using the above modes, is only an approximation. To account for this approximation, we include a factor ${𝒩}_{\mathrm{sub}}$ in the field decomposition, which is now accurately expressed as

$$\begin{array}{ccc}\hfill \mathsf{\Phi }& =& \sum _{\mathsf{\ell },m}\int d^3\mathsf{\Omega }{𝒩}_{\mathrm{sub}}\sqrt{{\displaystyle \frac{\mathsf{\Omega }}{4\pi }}}\left(b_{\mathsf{\Omega }\mathsf{\ell }m}^{in}{\displaystyle \frac{e^{-i\mathsf{\Omega }(T-R)}}{\mathsf{\Omega }R}}{Q}_{\mathsf{\ell }}\left(\mathsf{\Omega }R\right)\right.\hfill \\ & & \left.+b_{\mathsf{\Omega }\mathsf{\ell }m}^{out}{\displaystyle \frac{e^{-i\mathsf{\Omega }(T+R)}}{\mathsf{\Omega }R}}{Q}_{\mathsf{\ell }}^{*}\left(\mathsf{\Omega }R\right)\right)Y_{\mathsf{\ell }m}(\theta ,\varphi )+\mathrm{h}.\mathrm{c}.\hfill \end{array}$$

(52)

Determination of the normalization constant ${𝒩}_{sub}$ would require integration over the three-dimensional volume element and exact mode solutions for all values of R. For this work, we stay within the analytical limit and work with unnormalized modes, which do not limit our ability to discuss the anisotropic particle creation phenomena from the T-vacuum, which is our main goal in this work. We plan to solve Equation (43) numerically in a separate study. For now, it is sufficient to consider the above-mentioned unnormalized mode functions:

$$\begin{array}{ccc}\hfill U_{\mathsf{\Omega }\mathsf{\ell }m}& =& \sqrt{{\displaystyle \frac{\mathsf{\Omega }}{4\pi }}}{\displaystyle \frac{e^{-i\mathsf{\Omega }U}}{\mathsf{\Omega }R}}{Q}_{\mathsf{\ell }}\left(\mathsf{\Omega }R\right)Y_{\mathsf{\ell }m}(\theta ,\varphi ),\hfill \end{array}$$

(53)

$$\begin{array}{ccc}\hfill V_{\mathsf{\Omega }\mathsf{\ell }m}& =& \sqrt{{\displaystyle \frac{\mathsf{\Omega }}{4\pi }}}{\displaystyle \frac{e^{-i\mathsf{\Omega }V}}{\mathsf{\Omega }R}}{Q}_{\mathsf{\ell }}^{*}\left(\mathsf{\Omega }R\right)Y_{\mathsf{\ell }m}(\theta ,\varphi ).\hfill \end{array}$$

(54)

The functions $Q_{\mathsf{\ell }}$ and $Q_{\mathsf{\ell }}^{*}$ are already defined in (37). Once again, we see that these coefficients represent backscattering between the incoming and outgoing field modes in (52).

4.2. Super-Hubble Region

We follow the same procedure as in the previous case, but now with the metric (6) to obtain the following field equation for the super-Hubble region:

$${\mathsf{\Phi }}_{\mathsf{\Omega }}=\sum _{\mathsf{\ell },m}{\displaystyle \frac{{\mathsf{\Phi }}_{\mathsf{\Omega }}^{\mathsf{\ell }m}(T,R)}{T}}{Y}_{\mathsf{\ell }m}(\theta ,\varphi )$$

(55)

since the radius of the two spheres is now given by T and not R. With the above expansion, the $R,T$-dependent part of the field equation is given by

$$\left({\displaystyle \frac{{\partial }^2{\mathsf{\Phi }}_{\mathsf{\Omega }}^{\mathsf{\ell }m}}{\partial T^2}}-{\displaystyle \frac{{\partial }^2{\mathsf{\Phi }}_{\mathsf{\Omega }}^{\mathsf{\ell }m}}{\partial R^2}}\right)+{\displaystyle \frac{\mathsf{\ell }(\mathsf{\ell }+1)}{T^2(H^2{T}^2-1)}}{\mathsf{\Phi }}_{\mathsf{\Omega }}^{\mathsf{\ell }m}=0.$$

(56)

Notice that the potential has a different form, as expected, because of the change in the metric coefficients in the super-Hubble region, given by

$$V_{\mathsf{\ell }}(T,H)={\displaystyle \frac{\mathsf{\ell }(\mathsf{\ell }+1)}{T^2(H^2{T}^2-1)}}.$$

(57)

Once again, the potential diverges at the origin of the radial coordinate (which is simply T for this region) and also at $T=1/H$. If we solve $T=1/H(T,R)$, we end up with $R=1/H$, which again shows that there is a divergence at the Hubble radius. Consequently, we see a peculiar behavior just like in the sub-Hubble case—the $s=0$ modes do not see this potential, but for $\mathsf{\ell }>0$ all modes are confined outside the Hubble radius and cannot enter the sub-Hubble region.

4.2.1. Field Modes for the s-Wave Approximation

For $\mathsf{\ell }=0$, the solution to (56) is straightforward, and the mode expansion is

$$\mathsf{\Phi }=\int d^3\mathsf{\Omega }(U_{\mathsf{\Omega }}^{\sup }{b}_{\mathsf{\Omega }<{\mathsf{\Omega }}_H}^{in}+V_{\mathsf{\Omega }}^{\sup }{b}_{\mathsf{\Omega }<{\mathsf{\Omega }}_H}^{out})+\mathrm{h}.\mathrm{c}.$$

(58)

which is natural in the super-Hubble region. Particular expressions for the incoming and outgoing modes are

$$U_{\mathsf{\Omega }}^{\sup }={\displaystyle \frac{1}{4\pi \sqrt{\mathsf{\Omega }}T}}{e}^{-i\mathsf{\Omega }(T-R)}$$

(59)

and

$$V_{\mathsf{\Omega }}^{\sup }={\displaystyle \frac{1}{4\pi \sqrt{\mathsf{\Omega }}T}}{e}^{-i\mathsf{\Omega }(T+R)}.$$

(60)

Once again, the quantum state annihilated by $b_{\mathsf{\Omega }<{\mathsf{\Omega }}_H}^{in}$ and $b_{\mathsf{\Omega }<{\mathsf{\Omega }}_H}^{in}$ is the definition of the T-vacuum on the super-Hubble scale for the respective in and out sectors.

4.2.2. Field Modes Beyond the s-Wave Approximation

Just like in the sub-Hubble case, the form of the potential (57) makes the differential equation hard to solve in general, but it is simpler if we are interested in deep super-Hubble modes for which $T<<1/H$, and (56) takes the following form:

$$\left({\displaystyle \frac{{\partial }^2{\mathsf{\Phi }}_{\mathsf{\Omega }}^{\mathsf{\ell }m}}{\partial T^2}}-{\displaystyle \frac{{\partial }^2{\mathsf{\Phi }}_{\mathsf{\Omega }}^{\mathsf{\ell }m}}{\partial R^2}}\right)-{\displaystyle \frac{\mathsf{\ell }(\mathsf{\ell }+1)}{T^2}}{\mathsf{\Phi }}_{\mathsf{\Omega }}^{\mathsf{\ell }m}=0.$$

(61)

This is identical to (49) with an exchange $R\leftrightarrow T$, and therefore has the same solution (52)—we just need to replace R with T. The final expression, with an undetermined normalization constant ${𝒩}_{\sup }$, is now given by

$$\begin{array}{ccc}\hfill \mathsf{\Phi }& =& \sum _{\mathsf{\ell },m}\int d^3\mathsf{\Omega }{𝒩}_{\sup }\sqrt{{\displaystyle \frac{\mathsf{\Omega }}{2\pi }}}\left(b_{\mathsf{\Omega }\mathsf{\ell }m}^{in}{\displaystyle \frac{e^{-i\mathsf{\Omega }(T-R)}}{\mathsf{\Omega }T}}{Q}_{\mathsf{\ell }}^{*}\left(\mathsf{\Omega }T\right)\right.\hfill \\ & & \left.+b_{\mathsf{\Omega }\mathsf{\ell }m}^{out}{\displaystyle \frac{e^{-i\mathsf{\Omega }(T+R)}}{\mathsf{\Omega }T}}{Q}_{\mathsf{\ell }}\left(\mathsf{\Omega }T\right)\right)Y_{\mathsf{\ell }m}(\theta ,\varphi )+\mathrm{h}.\mathrm{c}.\hfill \end{array}$$

(62)

We can also extract the mode functions for the above expansion, which are

$$\begin{array}{ccc}\hfill U_{\mathsf{\Omega }\mathsf{\ell }m}& =& \sqrt{{\displaystyle \frac{\mathsf{\Omega }}{4\pi }}}{\displaystyle \frac{e^{-i\mathsf{\Omega }U}}{\mathsf{\Omega }T}}{Q}_{\mathsf{\ell }}^{*}\left(\mathsf{\Omega }T\right)Y_{\mathsf{\ell }m}(\theta ,\varphi ),\hfill \end{array}$$

(63)

$$\begin{array}{ccc}\hfill V_{\mathsf{\Omega }\mathsf{\ell }m}& =& \sqrt{{\displaystyle \frac{\mathsf{\Omega }}{4\pi }}}{\displaystyle \frac{e^{-i\mathsf{\Omega }V}}{\mathsf{\Omega }T}}{Q}_{\mathsf{\ell }}\left(\mathsf{\Omega }T\right)Y_{\mathsf{\ell }m}(\theta ,\varphi ).\hfill \end{array}$$

(64)

To conclude, we now have a complete set of mode functions for the spherically symmetric form of the radiation-dominated universe for the following cases—(i) exact expressions (47), (48), (59), and (60) for the s-waves in both the sub- and super-Hubble regions, and (ii) approximate analytical solutions (up to undetermined normalization constants) (53), (54), (63), and (64) for the deep sub-Hubble and deep super-Hubble modes with $\mathsf{\ell }>0$. We now move to the next section to use these results and calculate particle creation from the T-vacuum.

5. Particle Creation from the T-Vacuum

We are interested in calculating the number density of particles created by the T-vacuum when viewed from a cosmological frame of reference. The first step is to calculate the Bogolyubov coefficient ${\beta }_{\omega \mathsf{\Omega }}$ and then use it to determine the particle number density.

By definition, the Bogolyubov coefficient has the following forms [27]:

$${\beta }_{\omega \mathsf{\Omega }}^{in}=-(u_{\omega },U_{\mathsf{\Omega }}^{*})=i{\int }_{\mathsf{\Sigma }}d{\mathsf{\Sigma }}^{\mu }(u_{\omega }{\partial }_{\mu }{U}_{\mathsf{\Omega }}-U_{\mathsf{\Omega }}{\partial }_{\mu }{u}_{\omega }).$$

(65)

and

$${\beta }_{\omega \mathsf{\Omega }}^{out}=-(v_{\omega },V_{\mathsf{\Omega }}^{*})=i{\int }_{\mathsf{\Sigma }}d{\mathsf{\Sigma }}^{\mu }(v_{\omega }{\partial }_{\mu }{V}_{\mathsf{\Omega }}-v_{\mathsf{\Omega }}{\partial }_{\mu }{v}_{\omega }).$$

(66)

for the incoming and outgoing sectors. In the above expressions, $\mathsf{\Sigma }$ is a Cauchy hypersurface and $d{\mathsf{\Sigma }}^{\mu }=n^{\mu }d\mathsf{\Sigma }$; $d\mathsf{\Sigma }$ is the volume element associated with this Cauchy hypersurface, and $n^{\mu }$ is a future-directed unit normal vector to $\mathsf{\Sigma }$. In this case, we take into account the scalar field $\mathsf{\Phi }$, which can be expanded into field modes as expressed in cosmological and $(T,R)$ frames in Section 4.

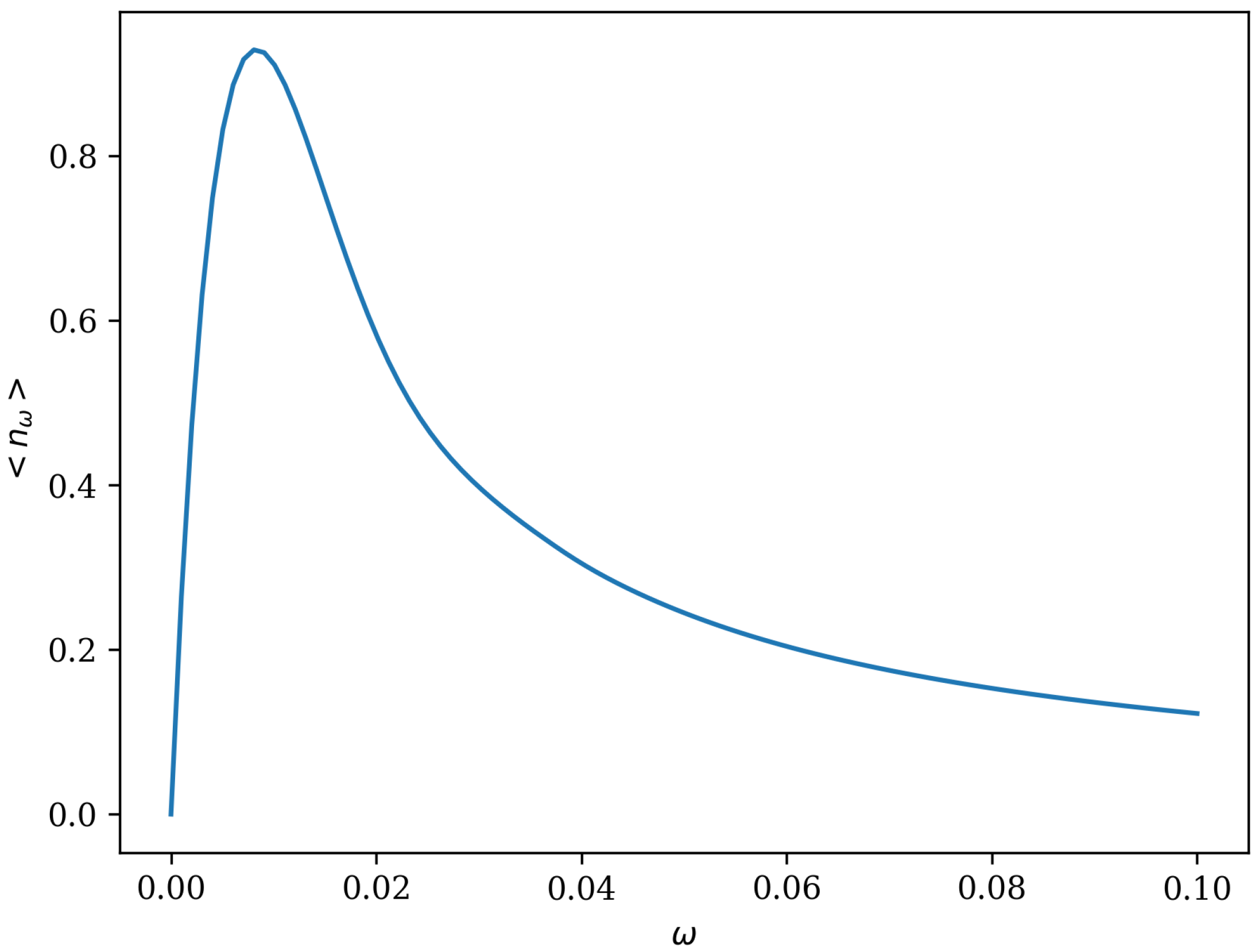
5.1. Particle Number Density for the s-Wave Approximation

Let us first consider the s-wave modes, which are given by (33) and (34) for the cosmological frame, whereas, for the $(T,R)$ frame, we have relevant expressions for the sub- and super-Hubble regions (appearing in (47), (48), (59), and (60)). Both coordinate modes are separated into incoming and outgoing sectors.

We first select the incoming modes, which are functions of the retarded light-cone coordinates u or U. Furthermore, we consider the sub-Hubble modes, for which we choose (33) and (47) for the calculation of the Bogolyubov coefficient. It is useful to consider the future null infinity ${\mathcal{I}}^{+}$ as the Cauchy hypersurface. This choice leads us to $d\mathsf{\Sigma }=a^2\left(\eta \right)r^{2}dud\overline{\mathsf{\Omega }}$, where $d\overline{\mathsf{\Omega }}$ is the solid angle element. Therefore,

$${\beta }_{\omega \mathsf{\Omega }}^{in}=-(u_{\omega },U_{\mathsf{\Omega }}^{*})=i{\int }_{{\mathcal{I}}^{+}}{a}^2\left(\eta \right)r^{2}dud\mathsf{\Omega }(u_{\omega }{\partial }_u{U}_{\mathsf{\Omega }}-U_{\mathsf{\Omega }}{\partial }_u{u}_{\omega }).$$

(67)

Conducting an integration by parts and taking the limit corresponding to the choice of the hypersurface ($\eta \to +\infty$ and $r\to +\infty$), we can write (67) as

$${\beta }_{\omega \mathsf{\Omega }}^{in}=2i{\int }_{{\mathcal{I}}^{+}}{a}^2\left(\eta \right)r^{2}dud\overline{\mathsf{\Omega }}{u}_{\omega }{\partial }_u\left(U_{\mathsf{\Omega }}\right).$$

(68)

with a scalar factor given by $a\left(\eta \right)=\mathcal{H}e\eta$. Simplifying (68) and taking into account that $U=\pm {\displaystyle \frac{\mathcal{H}e}{2}}{u}^2$ for $u\ge 0$ and $u\le 0$, respectively, we can express ${\beta }_{\omega \mathsf{\Omega }}$ as

$${\beta }_{\omega \mathsf{\Omega }}^{in}=I_1+I_2$$

(69)

where

$$I_1={\displaystyle \frac{\mathcal{H}e}{2\pi }}\sqrt{{\displaystyle \frac{\mathsf{\Omega }}{\omega }}}{\int }_0^{\infty }duu{e}^{-i(\omega u+{\displaystyle \frac{\mathsf{\Omega }\mathcal{H}e}{2}}{u}^2)}.$$

(70)

and

$$\begin{array}{cc}\hfill I_2& =-{\displaystyle \frac{\mathcal{H}e}{2\pi }}\sqrt{{\displaystyle \frac{\mathsf{\Omega }}{\omega }}}{\int }_{-\infty }^{0}duu{e}^{-i(\omega u-{\displaystyle \frac{\mathsf{\Omega }\mathcal{H}e}{2}}{u}^2)}\hfill \end{array}$$

(71)

$$\begin{array}{c}=I_1^{*}.\hfill \end{array}$$

(72)

Now, using the identity

$${\int }_{x_0}^{\infty }dx{x}^{s-1}{e}^{-bx}=e^{-s log b}\mathsf{\Gamma }[s,x_0];\mathrm{Re}\left(b\right),\mathrm{Re}\left(s\right)>0$$

(73)

where $b=-i+ϵ$ and $logb=log\left(1\right)-i\pi /2=-i\pi /2$, we can integrate $I_1$ to obtain

$$\begin{array}{cc}\hfill {\beta }_{\omega \mathsf{\Omega }}^{in}& ={\displaystyle \frac{1}{\pi \sqrt{\mathsf{\Omega }\omega }}}sin\left({\displaystyle \frac{{\omega }^2}{2\mathsf{\Omega }\mathcal{H}e}}\right)\mathsf{\Gamma }\left[1;{\displaystyle \frac{{\omega }^2}{2\mathsf{\Omega }\mathcal{H}e}}\right]\hfill \\ \hfill & -{\displaystyle \frac{1}{2\pi \mathsf{\Omega }}}\sqrt{{\displaystyle \frac{\omega }{\mathcal{H}e}}}{\left[1+sin\left({\displaystyle \frac{{\omega }^2}{\mathsf{\Omega }\mathcal{H}e}}\right)\right]}^{1/2}\mathsf{\Gamma }\left[{\displaystyle \frac{1}{2}};{\displaystyle \frac{{\omega }^2}{2\mathsf{\Omega }\mathcal{H}e}}\right].\hfill \end{array}$$

(74)

The squared value is now given by

$$\begin{array}{ccc}\hfill |{\beta }_{\omega \mathsf{\Omega }}^{in}{|}^2& =& {\displaystyle \frac{1}{{\pi }^2\mathsf{\Omega }\omega }}{sin}^2\left({\displaystyle \frac{{\omega }^2}{2\mathsf{\Omega }\mathcal{H}e}}\right){\mathsf{\Gamma }}^2\left[1;{\displaystyle \frac{{\omega }^2}{2\mathsf{\Omega }\mathcal{H}e}}\right]+{\displaystyle \frac{\omega }{4{\pi }^2{\mathsf{\Omega }}^2\mathcal{H}e}}\times \hfill \\ & & \times \left[1+sin\left({\displaystyle \frac{{\omega }^2}{\mathsf{\Omega }\mathcal{H}e}}\right)\right]{\mathsf{\Gamma }}^2\left[{\displaystyle \frac{1}{2}};{\displaystyle \frac{{\omega }^2}{2\mathsf{\Omega }\mathcal{H}e}}\right]-{\displaystyle \frac{1}{{\pi }^2{\mathsf{\Omega }}^{3/2}\sqrt{\mathcal{H}e}}}sin\left({\displaystyle \frac{{\omega }^2}{2\mathsf{\Omega }\mathcal{H}e}}\right)\times \hfill \\ & & \times {\left[1+sin\left({\displaystyle \frac{{\omega }^2}{\mathsf{\Omega }\mathcal{H}e}}\right)\right]}^{1/2}\mathsf{\Gamma }\left[1;{\displaystyle \frac{{\omega }^2}{2\mathsf{\Omega }\mathcal{H}e}}\right]\mathsf{\Gamma }\left[{\displaystyle \frac{1}{2}};{\displaystyle \frac{{\omega }^2}{2\mathsf{\Omega }\mathcal{H}e}}\right].\hfill \end{array}$$

(75)

We note that the above result for $|{\beta }_{\omega \mathsf{\Omega }}^{in}{|}^2$ is close (but not identical) to the (1+1)-dimensional problem calculated earlier in [21]. This was expected since radial modes in (3+1) dimensions are closest to a (1+1)-dimensional problem. The cross terms in (75) are a characteristic of the (3+1)-dimensional case.

The final step to determine the particle number density is to integrate the last equation

$$\langle 0|n_{\omega }{|0\rangle }_T=\int {\left|{\beta }_{\omega \mathsf{\Omega }}^{in}\right|}^{2}d\mathsf{\Omega }$$

(76)

which unfortunately does not provide a complete analytical solution. But it is easy to plot the average particle number density by performing a numerical integration. It is evident from (75) that the particle number density has an infrared (IR) divergence, which also appears in other cases of particle creation, such as moving-mirror scenarios [28,29]. We need to neglect modes with infinite wavelengths, and an IR cutoff is used to perform the integration numerically. It is not a problem for our case since the universe will transit to the matter-dominated stage after the radiation stage, and the size of the universe at the transition will set a natural UV cutoff for the modes originating in the radiation stage. To perform the integration, we set an ad hoc value $\mathsf{\Omega }=0.0001$ for the IR cutoff. Furthermore, we set $\mathcal{H}=1$ for the plot shown in Figure 2. We again see behavior closely analogous to the (1+1)-dimensional case reported previously [21]. It is easy to check that if one considers the outgoing modes (34) and (48) to calculate the Bogolyubov coefficient ${\beta }_{\mathsf{\Omega }\omega }^{out}$, and then uses it to calculate the particle content for the outgoing sector in the sub-Hubble region, we once again obtain a result identical to the incoming sector, and the plot in Figure 2 still applies.

Notice that this result is obtained from the contribution of sub-Hubble field modes $U_{\mathsf{\Omega }}^{\mathrm{sub}}$, and we can also look for the result in the super-Hubble sector. If we now conduct the same calculation for the super-Hubble modes, $U_{\mathsf{\Omega }}^{\sup }$ in (59) and (33), together with the corresponding transformation (10), we can realize that we obtain the same integral for the relevant Bogolyubov coefficient, and therefore, we obtain the same result, as depicted in Figure 2 for the incoming sector in the super-Hubble region. The same is true for the outgoing v-modes in the super-Hubble region. Therefore, we conclude that the plot in Figure 2 is generic and applies to both the sub- and super-Hubble regions, and to the incoming and outgoing sectors.

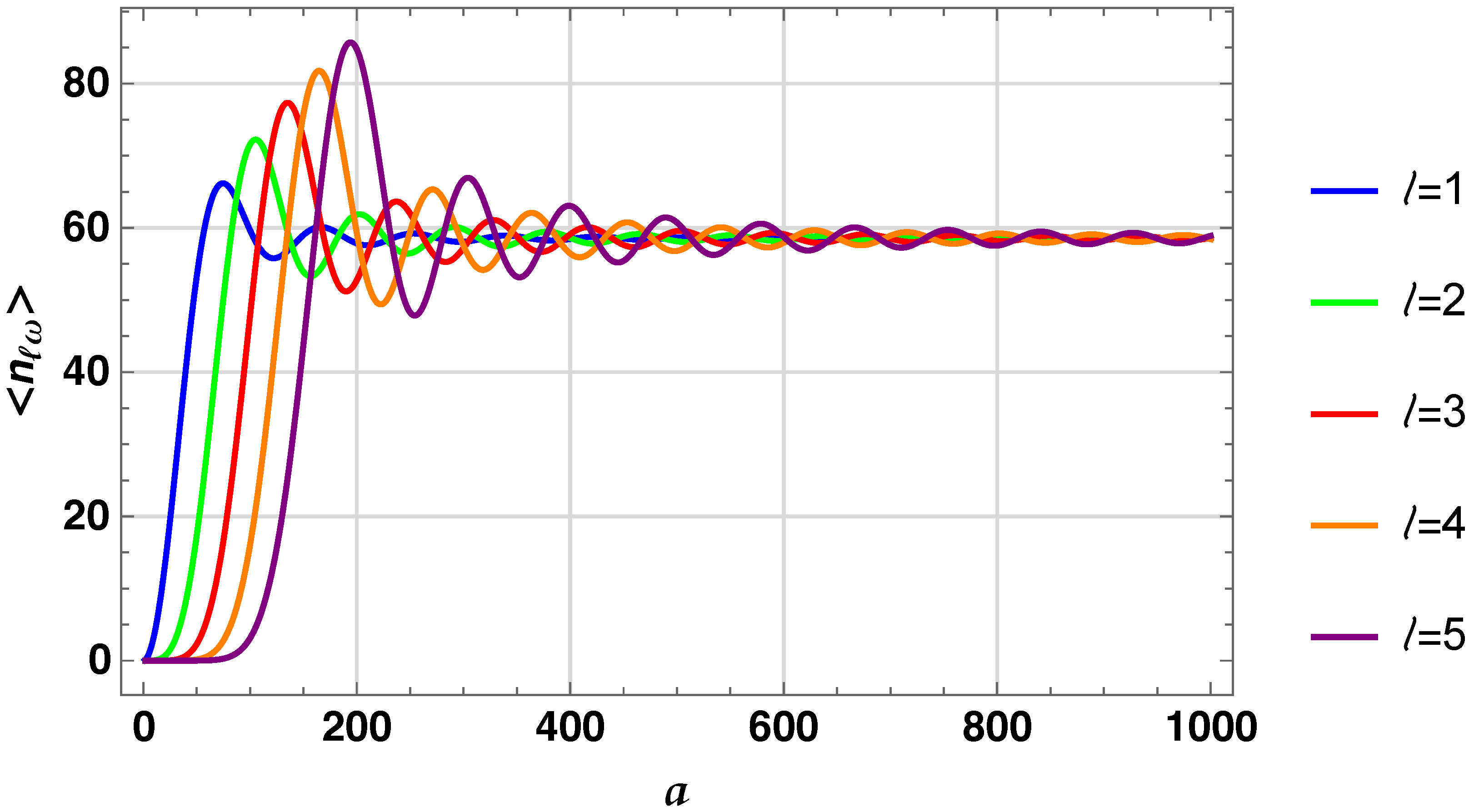
5.2. Particle Number Density Beyond the s-Wave Approximation

Let us now compute the particle number density for the most general case with $\mathsf{\ell }>0$. For this case, we do not have the luxury of calculating the Bogolyubov coefficients or the particle content with all generalities. The only situations where mode decomposition is possible in the $(T,R)$ frame are away from the Hubble radius, that is, for both the deep sub-Hubble and the deep super-Hubble modes ($R<<1/H$ and $R>>1/H$). These field expansions are shown in (52) and (62). On the other hand, in the cosmological coordinates, mode decomposition is valid for all sub-Hubble and super-Hubble scales as they appear in (39). Taking into account the incoming sector (u-modes) and the deep sub-Hubble region, we can express the Bogolyubov coefficient: 1

$${\beta }_{\omega \mathsf{\Omega }\mathsf{\ell }{\mathsf{\ell }}^{\prime }m{m}^{\prime }}^{in}=i\int a^2{r}^{2}drsin\theta d\theta d\varphi (u_{\omega \mathsf{\ell }m}{\partial }_{\eta }{U}_{\mathsf{\Omega }{\mathsf{\ell }}^{\prime }{m}^{\prime }}-U_{\mathsf{\Omega }{\mathsf{\ell }}^{\prime }{m}^{\prime }}{\partial }_{\eta }{u}_{\omega \mathsf{\ell }m}).$$

(77)

An explicit calculation of the integral (77) is lengthy, and it is performed in Appendix B. It is nice to see a closed-form analytical result, which is given by

$$\begin{array}{ccc}\hfill |{\beta }_{\omega \mathsf{\Omega }\mathsf{\ell } }^{in}{|}^2& =& {\displaystyle \frac{\eta {\omega }^2}{4\mathcal{H}e{\mathsf{\Omega }}^2}}{J}_{\mathsf{\ell }-1/2}^2\left(\eta \omega \right)-{\displaystyle \frac{2\mathsf{\ell }\omega }{4\mathcal{H}e{\mathsf{\Omega }}^2}}{J}_{\mathsf{\ell }-1/2}\left(\eta \omega \right)J_{\mathsf{\ell }+1/2}\left(\eta \omega \right)\hfill \\ & & +{\displaystyle \frac{{\mathsf{\ell }}^2+{\eta }^2{\omega }^2}{4\mathcal{H}e{\mathsf{\Omega }}^2\eta }}{J}_{\mathsf{\ell }+1/2}^2\left(\eta \omega \right).\hfill \end{array}$$

(78)

The average number density of particles created by the T-vacuum is given by

$$n_{\omega \mathsf{\ell }}=\int |{\beta }_{\omega \mathsf{\Omega }\mathsf{\ell } }^{in}{|}^{2}d\mathsf{\Omega }.$$

(79)

Considering (78), it is straightforward to integrate and obtain a closed-form expression for the particle content, given by

$$\begin{array}{ccc}\hfill \langle 0|n_{\omega \mathsf{\ell }}{|0\rangle }_T& =& {\displaystyle \frac{1}{4\mathcal{H}e{\mathsf{\Omega }}_0\eta }}\left({\eta }^2{\omega }^2{J}_{\mathsf{\ell }-1/2}^2\left(\eta \omega \right)\right.\hfill \\ & & \left.-2\mathsf{\ell }\omega \eta J_{\mathsf{\ell }-1/2}\left(\eta \omega \right)J_{\mathsf{\ell }+1/2}\left(\eta \omega \right)+({\mathsf{\ell }}^2+{\eta }^2{\omega }^2)J_{\mathsf{\ell }+1/2}^2\left(\eta \omega \right)\right),\hfill \end{array}$$

(80)

where ${\mathsf{\Omega }}_0$ is the IR cutoff introduced in the integration limit in Equation (79). As we discussed in the (1+1)-dimensional situation, the IR cutoff naturally applies here since the size of the universe in the radiation stage remains when it transitions to the matter-dominated stage just before producing the CMB radiation. We can therefore safely ignore modes of infinite wavelengths. Note that there is no ultraviolet divergence here, which is reassuring. Finally, we use the scale factor as the time parameter by using its relationship with the conformal time parameter, given by $a\left(\eta \right)=\mathcal{H}e\eta$ for the radiation stage, and then the expression (80) takes the following form:

$$\begin{array}{ccc}\hfill {\langle 0|}_T{n}_{\omega \mathsf{\ell }}{|0\rangle }_T& =& {\displaystyle \frac{1}{4a{\mathsf{\Omega }}_0}}\left({(a\omega /\mathcal{H}e)}^2{J}_{\mathsf{\ell }-1/2}^2(a\omega /\mathcal{H}e)-{\displaystyle \frac{2\mathsf{\ell }a\omega }{\mathcal{H}e}}{J}_{\mathsf{\ell }-1/2}(a\omega /\mathcal{H}e)J_{\mathsf{\ell }+1/2}(a\omega /\mathcal{H}e)\right.\hfill \\ & & \left.+({\mathsf{\ell }}^2+a^2{\omega }^2/{\mathcal{H}}^2{e}^2)J_{\mathsf{\ell }+1/2}^2(a\omega /\mathcal{H}e)\right).\hfill \end{array}$$

(81)

A few comments are needed regarding our final result (81). First and foremost, the particle content is manifestly anisotropic and is now known for any value of the angular momentum quantum number $\mathsf{\ell }>0$. This is a direct consequence of the fact that the T-vacuum is intrinsically anisotropic, as it is a natural state for observers who envision the radiation-dominated universe as such. Of course, these observers, who are the successors of static de Sitter observers, do not see any particles, as the quantum state is in a vacuum configuration for them. However, the cosmological observers with proper time $\eta$ are bombarded with particles due to their peculiar motion with respect to the $(T,R)$ frame. These particles are anisotropically distributed in the sky, and their distribution is given by (81). Evidently, this is not a blackbody distribution, and it is not at all a surprise since the relationship between the cosmological and $(T,R)$ frames does not invoke an exponential redshift relative to each other—rather, it is a power law and quadratic in nature. Furthermore, (81) is time-dependent, and it has an oscillatory behavior with the scale factor, which we depict in Figure 3.

Notice again that if we consider the outgoing v-modes in (34) and (54), we shall end up with the same result as (81). In addition, the result for the deep super-Hubble modes (63) and (64) leads us to an identical result (81). Thus, we can conclude that (81) and Figure 3 represent generic behaviors of the anisotropic particle creation by the T-vacuum in appropriate limits.

6. Discussions and Outlook

We have taken a significant step forward, making a case in favor of a physically appealing, anisotropic quantum vacuum state in the radiation-dominated stage of the early universe. To our knowledge, this is the only quantum vacuum state whose excitation naturally breaks homogeneity and isotropy for cosmological observers in the post-inflationary era. Our results are, however, valid in the sub- and super-Hubble regions away from the Hubble radius, which is interesting given our own location in the cosmos. We considered massless scalar fields for this study and quantized them in the two different reference frames—(i) the standard cosmological frame and (ii) a recently discovered spherically symmetric form of FRW defining the radiation stage. The latter frame was identified, by backtracking, with the static de Sitter frame in the inflationary stage. Quantum fields in curved spacetime are allowed to have non-unique vacuum states, although they might occupy only one of these physically allowed states while remaining unexcited. The presence of a T-vacuum and its excitation provides an observable angular variance in the radiation to a cosmological observer, and such observers are closely related to the comoving observers whose frame shapes our understanding of cosmological observations.

This particular nature of the T-vacuum raises a few interesting theoretical implications, and it is worth investigating further. One natural ambition might be calculating some definite imprints of these anisotropies originating from the T-vacuum and comparing them with the CMB map. This prospect is borne by the fact that the CMB map depicts the early universe in the matter-dominated stage, which is after the radiation stage, and, therefore, a suitable signature in the radiation stage, such as in (81), may have some residual imprint on the CMB map itself. It provides the exact number of particles (such as photons) corresponding to a given frequency and direction in the sky. This prediction is extremely precise and should not be confused with the statistical average, which is usually performed while analyzing CMB data, in the absence of a precise physical theory that might be producing the CMB radiation. Of course, we do not claim any connection between the observed CMB anisotropy and the anisotropy calculated in (81), yet, but, curiously, such an expression can be obtained from a first-principle theory in which an anisotropic photon background might be related to the symmetry of the quantum vacuum itself. This might require a careful study of how the future expansion stages (i.e., matter and dark energy) will affect the distribution of particles. Although the frequencies of the particles created by the T-vacuum will change due to gravitational redshift, their number will not be affected by future expansion stages, since this vacuum will not be a natural vacuum in those stages. It would be interesting to see if the calculated anisotropies generated by the T-vacuum can eventually be compared with CMB anisotropies, and in addition, if these new particles could play some part in reheating the early universe. We are currently investigating these aspects within a numerical setup and plan to report the outcomes in a future publication [26].