Probing the Cosmic Distance Duality Relation via Non-Parametric Reconstruction for High Redshifts
Abstract
1. Introduction
2. Data Sets
2.1. Transverse Baryon Acoustic Oscillations Data
2.2. Galaxy Clusters Data
- is the fractional temperature change of the CMB
- K is the present-day CMB temperature
- describes the spectral dependence of the effect (negative at GHz, positive at higher frequencies)
- is the Comptonization parameter along direction
- is Boltzmann’s constant, the electron mass, c the speed of light
- is the Thomson cross-section
- and are the electron number density (cm−3) and temperature (K) of the intracluster plasma
- The integral follows the line of sight through the cluster
- is the angular size of the cluster
- is the X-ray surface brightness in direction at energy E (typically 0.5–10 keV for clusters)
- z is the cluster redshift (accounting for cosmological dimming)
- is the radially-dependent electron number density (cm−3)
- is the X-ray cooling function (erg cm3 s−1), which depends on:
- –
- Electron temperature (typically – K for clusters)
- –
- Metallicity Z (primarily Fe, O, and Si lines)
- –
- Energy band E (continuum vs. line emission)
2.3. Type Ia Supernovae Data
2.4. Quasars Data
3. Methodology for Data Analysis
3.1. Data Binning Methodology
3.2. Gaussian Processes for Cosmological Parameter Reconstruction
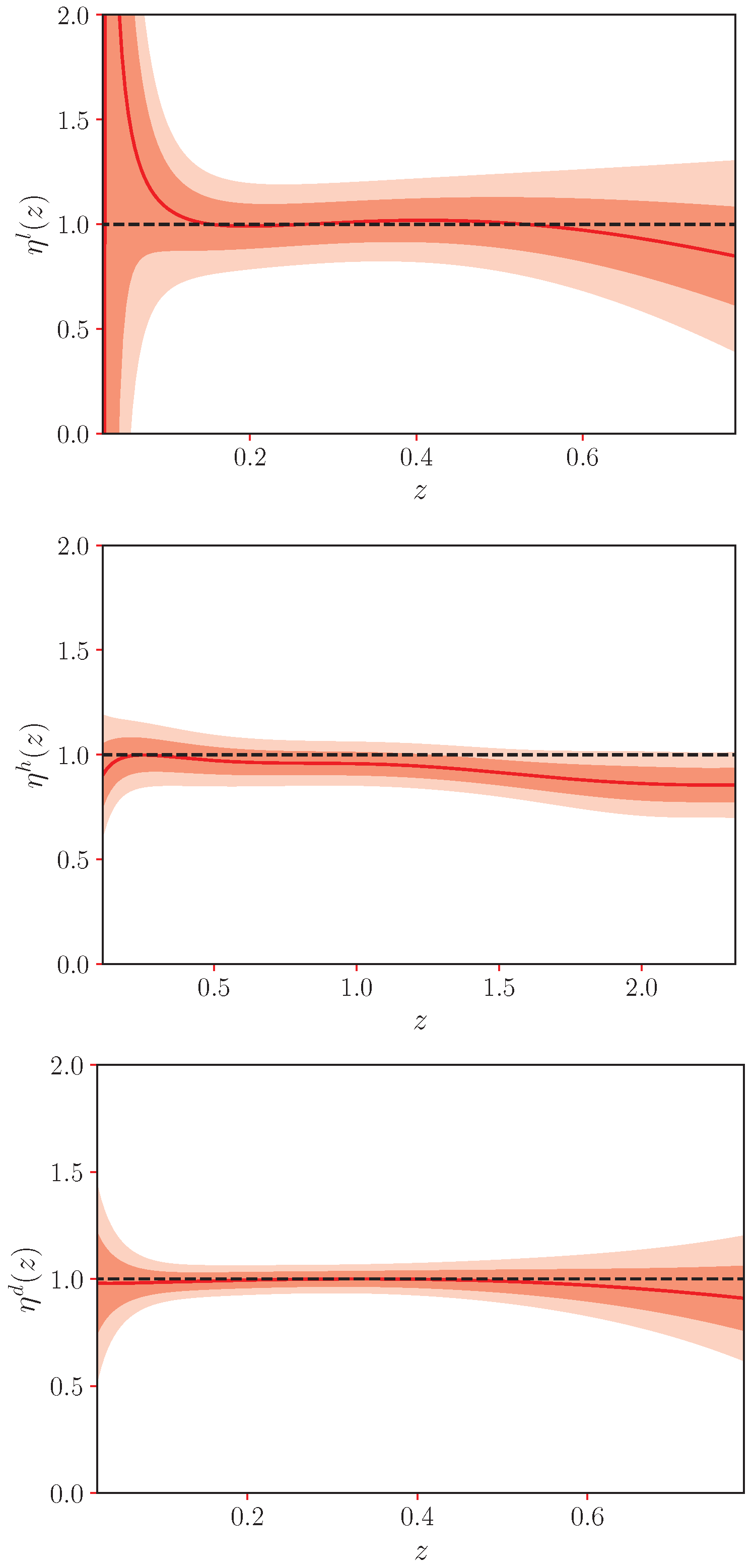
4. Results
- Low redshift combination (): obtained by combining the galaxy cluster (GC) measurements of with the full SNIa + QSO sample for ; both datasets for the redshift interval .
- High redshift combination (): based on the BAO-derived values combined with the SNIa + QSO data; both datasets for the redshift interval .
- Distance dual angular probe combination (): resulting from the combination of GC and BAO data alone, without involving luminosity distances; both datasets for the redshift interval .
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CDDR | Cosmic distance duality relation |
| CDM | cold dark matter |
| BAO | Baryon acoustic oscillations |
| GP | Gaussian processes |
| SZE | Sunyaev-Zel’dovich effect |
| CMB | Cosmic microwave background |
| 1 | |
| 2 | Note that . |
| 3 | https://github.com/JCGoran/GaPP, accessed on 3 July 2024. |
References
- Di Valentino, E.; Said, J.L.; Riess, A.; Pollo, A.; Poulin, V.; Gómez-Valent, A.; Weltman, A.; Palmese, A.; Huang, C.D.; van de Bruck, C.; et al. The CosmoVerse White Paper: Addressing observational tensions in cosmology with systematics and fundamental physics. arXiv 2025, arXiv:2504.01669. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Kamionkowski, M. The Physics of Cosmic Acceleration. Annu. Rev. Nucl. Part. Sci. 2009, 59, 397–429. [Google Scholar] [CrossRef]
- Weinberg, D.H.; Mortonson, M.J.; Eisenstein, D.J.; Hirata, C.; Riess, A.G.; Rozo, E. Observational probes of cosmic acceleration. Phys. Rep. 2013, 530, 87–255. [Google Scholar] [CrossRef]
- Perivolaropoulos, L.; Skara, F. Challenges for ΛCDM: An update. New Astron. Rev. 2022, 95, 101659. [Google Scholar] [CrossRef]
- Vagnozzi, S. Seven Hints That Early-Time New Physics Alone Is Not Sufficient to Solve the Hubble Tension. Universe 2023, 9, 393. [Google Scholar] [CrossRef]
- Etherington, I.M.H. On the Definition of Distance in General Relativity. Philos. Mag. 1933, 15, 761. [Google Scholar] [CrossRef]
- Ellis, G.F.R. On the definition of distance in general relativity: I. M. H. Etherington (Philosophical Magazine ser. 7, vol. 15, 761 (1933)). Gen. Relativ. Gravit. 2007, 39, 1047–1052. [Google Scholar] [CrossRef]
- Qin, J.; Melia, F.; Zhang, T.J. Test of the cosmic distance duality relation for arbitrary spatial curvature. Mon. Not. R. Astron. Soc. 2021, 502, 3500–3509. [Google Scholar] [CrossRef]
- Bassett, B.A.; Kunz, M. Cosmic distance-duality as a probe of exotic physics and acceleration. Phys. Rev. D 2004, 69, 101305. [Google Scholar] [CrossRef]
- Hees, A.; Minazzoli, O.; Larena, J. Breaking of the equivalence principle in the electromagnetic sector and its cosmological signatures. Phys. Rev. D 2014, 90, 124064. [Google Scholar] [CrossRef]
- Azevedo, R.P.L.; Avelino, P.P. Distance-duality in theories with a nonminimal coupling to gravity. Phys. Rev. D 2021, 104, 084079. [Google Scholar] [CrossRef]
- Levi Said, J.; Mifsud, J.; Parkinson, D.; Saridakis, E.N.; Sultana, J.; Zarb Adami, K. Testing the violation of the equivalence principle in the electromagnetic sector and its consequences in f(T) gravity. J. Cosmol. Astropart. Phys. 2020, 047. [Google Scholar] [CrossRef]
- Holanda, R.F.L.; Barros, K.N.N.O. Searching for cosmological signatures of the Einstein equivalence principle breaking. Phys. Rev. D 2016, 94, 023524. [Google Scholar] [CrossRef]
- Holanda, R.F.L.; Pereira, S.H.; Busti, V.C.; Bessa, C.H.G. Improved constraints on violations of the Einstein equivalence principle in the electromagnetic sector with complementary cosmic probes. Class. Quantum Gravity 2017, 34, 195003. [Google Scholar] [CrossRef]
- Kumar, D.; Rana, A.; Jain, D.; Mahajan, S.; Mukherjee, A.; Holanda, R.F.L. A non-parametric test of variability of Type Ia supernovae luminosity and CDDR. J. Cosmol. Astropart. Phys. 2022, 053. [Google Scholar] [CrossRef]
- Holanda, R.F.L.; Pereira, S.H.; Jain, D. Cosmic transparency and acceleration. Phys. Rev. D 2018, 97, 023538. [Google Scholar] [CrossRef]
- Combes, F. Properties of SN-host galaxies. New Astron. Rev. 2004, 48, 583–589. [Google Scholar] [CrossRef][Green Version]
- Shafieloo, A.; Majumdar, S.; Sahni, V.; Starobinsky, A.A. Searching for systematics in SNIa and galaxy cluster data using the cosmic duality relation. J. Cosmol. Astropart. Phys. 2013, 2013, 042. [Google Scholar] [CrossRef]
- Jesus, J.F.; Holanda, R.F.L.; Dantas, M.A. Testing the cosmic conservation of photon number with type Ia supernovae and ages of old objects. Gen. Relativ. Gravit. 2017, 49, 150. [Google Scholar] [CrossRef]
- Li, Z.; Wu, P.; Yu, H.; Zhu, Z.H. Cosmic opacity: Cosmological-model-independent tests and their impact on cosmic acceleration. Phys. Rev. D 2013, 87, 103013. [Google Scholar] [CrossRef]
- Liao, K.; Li, Z.; Ming, J.; Zhu, Z.H. Testing cosmic opacity from SNe Ia and Hubble parameter through three cosmological-model-independent methods. Phys. Lett. B 2013, 718, 1166–1170. [Google Scholar] [CrossRef]
- Rasanen, S.; Valiviita, J.; Kosonen, V. Testing distance duality with CMB anisotropies. J. Cosmol. Astropart. Phys. 2016, 4, 050. [Google Scholar] [CrossRef]
- Renzi, F.; Hogg, N.B.; Giarè, W. The resilience of the Etherington–Hubble relation. Mon. Not. Roy. Astron. Soc. 2022, 513, 4004–4014. [Google Scholar] [CrossRef]
- Qi, J.Z.; Jiang, Y.F.; Hou, W.T.; Zhang, X. Testing the Cosmic Distance Duality Relation Using Strong Gravitational Lensing Time Delays and Type Ia Supernovae. Astrophys. J. 2025, 979, 2. [Google Scholar] [CrossRef]
- Keil, F.; Nesseris, S.; Tutusaus, I.; Blanchard, A. Probing the Distance Duality Relation with Machine Learning and Recent Data. arXiv 2025, arXiv:2504.01750. [Google Scholar] [CrossRef]
- Rana, A.; Jain, D.; Mahajan, S.; Mukherjee, A. Revisiting the distance duality relation using a non-parametric regression method. J. Cosmol. Astropart. Phys. 2016, 7, 26. [Google Scholar] [CrossRef]
- Gahlaut, S. Model—Independent Probe of Cosmic Distance Duality Relation. Res. Astron. Astrophys. 2025, 25, 025019. [Google Scholar] [CrossRef]
- Mukherjee, P.; Mukherjee, A. Assessment of the cosmic distance duality relation using Gaussian process. Mon. Not. Roy. Astron. Soc. 2021, 504, 3938–3946. [Google Scholar] [CrossRef]
- More, S.; Niikura, H.; Schneider, J.; Schuller, F.P.; Werner, M.C. Modifications to the Etherington Distance Duality Relation and Observational Limits. arXiv 2016, arXiv:1612.08784. [Google Scholar] [CrossRef]
- Holanda, R.F.L.; Lima, J.A.S.; Ribeiro, M.B. Testing the Distance-Duality Relation with Galaxy Clusters and Type Ia Supernovae. Res. Astron. Astrophys. 2010, 722, L233–L237. [Google Scholar] [CrossRef]
- Avgoustidis, A.; Burrage, C.; Redondo, J.; Verde, L.; Jimenez, R. Constraints on cosmic opacity and beyond the standard model physics from cosmological distance measurements. J. Cosmol. Astropart. Phys. 2010, 2010, 024. [Google Scholar] [CrossRef]
- Holanda, R.F.L.; Busti, V.C.; Alcaniz, J.S. Probing the cosmic distance duality with strong gravitational lensing and supernovae Ia data. J. Cosmol. Astropart. Phys. 2016, 2016, 054. [Google Scholar] [CrossRef]
- Holanda, R.F.L.; Lima, J.A.S.; Ribeiro, M.B. Cosmic distance duality relation and the shape of galaxy clusters. Astron. Astrophys. 2011, 528, L14. [Google Scholar] [CrossRef]
- Holanda, R.F.L. The robustness of angular diameter distances to the lens in the B1608+656 and RXJ1131-1231 systems. Astropart. Phys. 2016, 84, 78–81. [Google Scholar] [CrossRef][Green Version]
- Li, Z.; Wu, P.; Yu, H. Cosmological-model-independent Tests for the Distance-Duality Relation from Galaxy Clusters and Type Ia Supernova. Astrophys. J. 2011, 729, L14. [Google Scholar] [CrossRef]
- Holanda, R.F.L.; Gonçalves, R.S.; Alcaniz, J.S. A test for cosmic distance duality. J. Cosmol. Astropart. Phys. 2012, 2012, 022. [Google Scholar] [CrossRef]
- Ellis, G.F.R.; Poltis, R.; Uzan, J.P.; Weltman, A. Blackness of the cosmic microwave background spectrum as a probe of the distance-duality relation. Phys. Rev. D 2013, 87, 103530. [Google Scholar] [CrossRef]
- Wu, P.; Li, Z.; Liu, X.; Yu, H. Cosmic distance-duality relation test using type Ia supernovae and the baryon acoustic oscillation. Phys. Rev. D 2015, 92, 023520. [Google Scholar] [CrossRef]
- Yang, T.; Holanda, R.F.L.; Hu, B. Constraints on the cosmic distance duality relation with simulated data of gravitational waves from the Einstein Telescope. Astropart. Phys. 2019, 108, 57–62. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, K.; Huang, Q. Probing cosmic opacity with the type Ia supernovae and Hubble parameter. Eur. Phys. J. C 2020, 80, 838. [Google Scholar] [CrossRef]
- da Silva, W.J.C.; Holanda, R.F.L.; Silva, R. Bayesian comparison of the cosmic duality scenarios. Phys. Rev. D 2020, 102, 063513. [Google Scholar] [CrossRef]
- Santos-da-Costa, S.; Busti, V.C.; Holanda, R.F.L. Two new tests to the distance duality relation with galaxy clusters. J. Cosmol. Astropart. Phys. 2015, 2015, 061. [Google Scholar] [CrossRef]
- Liu, T.; Cao, S.; Zhang, S.; Gong, X.; Guo, W.; Zheng, C. Revisiting the cosmic distance duality relation with machine learning reconstruction methods: The combination of HII galaxies and ultra-compact radio quasars. Eur. Phys. J. C 2021, 81, 903. [Google Scholar] [CrossRef]
- Teixeira, E.M.; Giarè, W.; Hogg, N.B.; Montandon, T.; Poudou, A.; Poulin, V. Implications of distance duality violation for the H0 tension and evolving dark energy. arXiv 2025, arXiv:2504.10464. [Google Scholar] [CrossRef]
- Holanda, R.F.L. Constraints on the Hubble Parameter from Galaxy Clusters and the Validity of the Cosmic Distance Duality Relation. Int. J. Mod. Phys. D 2012, 21, 1250008. [Google Scholar] [CrossRef]
- Afroz, S.; Mukherjee, S. Hint towards inconsistency between BAO and Supernovae Dataset: The Evidence of Redshift Evolving Dark Energy from DESI DR2 is Absent. arXiv 2025, arXiv:2504.16868. [Google Scholar] [CrossRef]
- de Carvalho, E.; Bernui, A.; Carvalho, G.C.; Novaes, C.P.; Xavier, H.S. Angular Baryon Acoustic Oscillation measure at z = 2.225 from the SDSS quasar survey. J. Cosmol. Astropart. Phys. 2018, 4, 064. [Google Scholar] [CrossRef]
- DESI Collaboration. DESI DR2 Results II: Measurements of Baryon Acoustic Oscillations and Cosmological Constraints. arXiv 2025, arXiv:2503.14738. [Google Scholar] [CrossRef]
- Sánchez, E.; Carnero, A.; García-Bellido, J.; Gaztañaga, E.; de Simoni, F.; Crocce, M.; Cabré, A.; Fosalba, P.; Alonso, D. Tracing the sound horizon scale with photometric redshift surveys. Mon. Not. Roy. Astron. Soc. 2011, 411, 277–288. [Google Scholar] [CrossRef]
- Menote, R.; Marra, V. Baryon acoustic oscillations in thin redshift shells from BOSS DR12 and eBOSS DR16 galaxies. Mon. Not. Roy. Astron. Soc. 2022, 513, 1600–1608. [Google Scholar] [CrossRef]
- de Carvalho, E.; Bernui, A.; Avila, F.; Novaes, C.P.; Nogueira-Cavalcante, J.P. BAO angular scale at zeff = 0.11 with the SDSS blue galaxies. Astron. Astrophys. 2021, 649, A20. [Google Scholar] [CrossRef]
- Planck Collaboration. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar] [CrossRef]
- Bonilla, A.; Kumar, S.; Nunes, R.C. Measurements of H0 and reconstruction of the dark energy properties from a model-independent joint analysis. Eur. Phys. J. C 2021, 81, 127. [Google Scholar] [CrossRef]
- Sunyaev, R.A.; Zeldovich, Y.B. The Observations of Relic Radiation as a Test of the Nature of X-Ray Radiation from the Clusters of Galaxies. Comments Astrophys. Space Phys. 1972, 4, 173. [Google Scholar]
- Birkinshaw, M. The Sunyaev-Zel’dovich effect. Phys. Rep. 1999, 310, 97–195. [Google Scholar] [CrossRef]
- Sarazin, C.L. X-ray emission from clusters of galaxies. Rev. Mod. Phys. 1986, 58, 1–115. [Google Scholar] [CrossRef]
- Reese, E.D.; Carlstrom, J.E.; Joy, M.; Mohr, J.J.; Grego, L.; Holzapfel, W.L. Determining the Cosmic Distance Scale from Interferometric Measurements of the Sunyaev-Zeldovich Effect. Astrophys. J. 2002, 581, 53–85. [Google Scholar] [CrossRef]
- Carlstrom, J.E.; Holder, G.P.; Reese, E.D. Cosmology with the Sunyaev-Zel’dovich Effect. Annu. Rev. Astron. Astrophys. 2002, 40, 643–680. [Google Scholar] [CrossRef]
- Uzan, J.P.; Aghanim, N.; Mellier, Y. Distance duality relation from x-ray and Sunyaev-Zel’dovich observations of clusters. Phys. Rev. D 2004, 70, 083533. [Google Scholar] [CrossRef]
- Holanda, R.F.L.; Alcaniz, J.S.; Carvalho, J.C. Cosmography with the Sunyaev-Zeldovich effect and X-ray data. J. Cosmol. Astropart. Phys. 2013, 2013, 033. [Google Scholar] [CrossRef][Green Version]
- Holanda, R.F.L.; Cunha, J.V.; Marassi, L.; Lima, J.A.S. Constraining H0 in general dark energy models from Sunyaev-Zeldovich/X-ray technique and complementary probes. J. Cosmol. Astropart. Phys. 2012, 2012, 035. [Google Scholar] [CrossRef]
- Colaço, L.R.; Ferreira, M.; Holanda, R.F.L.; Gonzalez, J.E.; Nunes, R.C. A Hubble constant estimate from galaxy cluster and type Ia SNe observations. J. Cosmol. Astropart. Phys. 2024, 2024, 098. [Google Scholar] [CrossRef]
- De Filippis, E.; Sereno, M.; Bautz, M.W.; Longo, G. Measuring the Three-dimensional Structure of Galaxy Clusters. I. Application to a Sample of 25 Clusters. Astrophys. J. 2005, 625, 108–120. [Google Scholar] [CrossRef]
- Bonamente, M.; Joy, M.K.; LaRoque, S.J.; Carlstrom, J.E.; Reese, E.D.; Dawson, K.S. Determination of the Cosmic Distance Scale from Sunyaev-Zel’dovich Effect and Chandra X-Ray Measurements of High-Redshift Galaxy Clusters. Astrophys. J. 2006, 647, 25–54. [Google Scholar] [CrossRef]
- Holanda, R.F.L.; Lima, J.A.S.; Ribeiro, M.B. Probing the cosmic distance-duality relation with the Sunyaev-Zel’dovich effect, X-ray observations and supernovae Ia. Astron. Astrophys. 2012, 538, A131. [Google Scholar] [CrossRef]
- Brout, D.; Scolnic, D.; Popovic, B.; Riess, A.G.; Zuntz, J.; Kessler, R.; Carr, A.; Davis, T.M.; Hinton, S.; Jones, D.; et al. The Pantheon+ Analysis: Cosmological Constraints. Astrophys. J. 2022, 938, 110. [Google Scholar] [CrossRef]
- Risaliti, G.; Lusso, E. A Hubble Diagram for Quasars. Astrophys. J. 2015, 815, 33. [Google Scholar] [CrossRef]
- Risaliti, G.; Lusso, E. Cosmological Constraints from the Hubble Diagram of Quasars at High Redshifts. Nat. Astron. 2019, 3, 272–277. [Google Scholar] [CrossRef]
- Lusso, E.; Risaliti, G.; Nardini, E.; Bargiacchi, G.; Benetti, M.; Bisogni, S.; Capozziello, S.; Civano, F.; Eggleston, L.; Elvis, M.; et al. Quasars as standard candles. III. Validation of a new sample for cosmological studies. Astron. Astrophys. 2020, 642, A150. [Google Scholar] [CrossRef]
- Raffai, P.; Pataki, A.; Böttger, R.L.; Karsai, A.; Dálya, G. Cosmic Chronometers, Pantheon+ Supernovae, and Quasars Favor Coasting Cosmologies over the Flat ΛCDM Model. Astrophys. J. 2025, 979, 51. [Google Scholar] [CrossRef]
- Li, X.; Keeley, R.E.; Shafieloo, A. Redshift Evolution of the X-Ray and Ultraviolet Luminosity Relation of Quasars: Calibrated Results from SNe Ia. Astrophys. J. 2025, 983, 141. [Google Scholar] [CrossRef]
- Seikel, M.; Clarkson, C.; Smith, M. Reconstruction of dark energy and expansion dynamics using Gaussian processes. J. Cosmol. Astropart. Phys. 2012, 2012, 036. [Google Scholar] [CrossRef]
- Seikel, M.; Clarkson, C. Optimising Gaussian processes for reconstructing dark energy dynamics from supernovae. arXiv 2013, arXiv:1311.6678. [Google Scholar] [CrossRef]
- Yang, T.; Guo, Z.K.; Cai, R.G. Reconstructing the interaction between dark energy and dark matter using Gaussian processes. Phys. Rev. D 2015, 91, 123533. [Google Scholar] [CrossRef]
- Gómez-Valent, A.; Amendola, L. H0 from cosmic chronometers and Type Ia supernovae, with Gaussian Processes and the novel Weighted Polynomial Regression method. J. Cosmol. Astropart. Phys. 2018, 2018, 051. [Google Scholar] [CrossRef]
- Zhang, M.J.; Li, H. Gaussian processes reconstruction of dark energy from observational data. Eur. Phys. J. C 2018, 78, 460. [Google Scholar] [CrossRef]
- Perenon, L.; Martinelli, M.; Maartens, R.; Camera, S.; Clarkson, C. Measuring dark energy with expansion and growth. Phys. Dark Universe 2022, 37, 101119. [Google Scholar] [CrossRef]
- Bonilla, A.; Kumar, S.; Nunes, R.C.; Pan, S. Reconstruction of the dark sectors’ interaction: A model-independent inference and forecast from GW standard sirens. Mon. Not. Roy. Astron. Soc. 2022, 512, 4231–4238. [Google Scholar] [CrossRef]
- Abedin, M.; Wang, G.J.; Ma, Y.Z.; Pan, S. In search of an interaction in the dark sector through Gaussian Process and ANN approaches. arXiv 2025, arXiv:2505.04336. [Google Scholar] [CrossRef]
- Jesus, J.F.; Valentim, R.; Escobal, A.A.; Pereira, S.H. Gaussian process estimation of transition redshift. J. Cosmol. Astropart. Phys. 2020, 2020, 053. [Google Scholar] [CrossRef]
- Mukherjee, P.; Banerjee, N. Revisiting a non-parametric reconstruction of the deceleration parameter from combined background and the growth rate data. arXiv 2020, arXiv:2007.15941. [Google Scholar] [CrossRef]
- Perenon, L.; Martinelli, M.; Ilić, S.; Maartens, R.; Lochner, M.; Clarkson, C. Multi-tasking the growth of cosmological structures. Phys. Dark Universe 2021, 34, 100898. [Google Scholar] [CrossRef]
- Avila, F.; Bernui, A.; Bonilla, A.; Nunes, R.C. Inferring S8(z) and γ (z) with cosmic growth rate measurements using machine learning. Eur. Phys. J. C 2022, 82, 594. [Google Scholar] [CrossRef]
- Calderón, R.; L’Huillier, B.; Polarski, D.; Shafieloo, A.; Starobinsky, A.A. Joint reconstructions of growth and expansion histories from stage-IV surveys with minimal assumptions. II. Modified gravity and massive neutrinos. Phys. Rev. D 2023, 108, 023504. [Google Scholar] [CrossRef]
- L’Huillier, B.; Shafieloo, A.; Polarski, D.; Starobinsky, A.A. Defying the laws of Gravity I: Model-independent reconstruction of the Universe expansion from growth data. Mon. Not. Roy. Astron. Soc. 2020, 494, 819–826. [Google Scholar] [CrossRef]
- Oliveira, F.; Avila, F.; Franco, C.; Bernui, A. Is ω0ωaCDM a good model for the clumpy Universe? Phys. Dark Universe 2025, 49, 101996. [Google Scholar] [CrossRef]
- Avila, F.; Bernui, A.; Nunes, R.C.; de Carvalho, E.; Novaes, C.P. The homogeneity scale and the growth rate of cosmic structures. Mon. Not. Roy. Astron. Soc. 2022, 509, 2994–3003. [Google Scholar] [CrossRef]
- Yin, Z.Y.; Wei, H. Non-parametric reconstruction of growth index via Gaussian processes. Sci. China Phys. Mech. Astron. 2019, 62, 999811. [Google Scholar] [CrossRef]
- Mu, Y.; Li, E.K.; Xu, L. Model-independent reconstruction of growth index via Gaussian process. Class. Quantum Gravity 2023, 40, 225003. [Google Scholar] [CrossRef]
- Oliveira, F.; Avila, F.; Bernui, A.; Bonilla, A.; Nunes, R.C. Reconstructing the growth index γ with Gaussian Processes. Eur. Phys. J. C 2024, 84, 636. [Google Scholar] [CrossRef]
- Escamilla, L.A.; Akarsu, O.; Di Valentino, E.; Özülker, E.; Vazquez, J.A. Exploring the Growth-Index (γ) Tension with ΛsCDM. arXiv 2025, arXiv:2503.12945. [Google Scholar]
- Sabogal, M.A.; Akarsu, O.; Bonilla, A.; Di Valentino, E.; Nunes, R.C. Exploring new physics in the late Universe’s expansion through non-parametric inference. Eur. Phys. J. C 2024, 84, 703. [Google Scholar] [CrossRef]
- Gao, S.; Gao, Q.; Gong, Y.; Lu, X. Null tests with Gaussian Process. arXiv 2025, arXiv:2503.15943. [Google Scholar] [CrossRef]
- Jiang, J.Q.; Pedrotti, D.; da Costa, S.S.; Vagnozzi, S. Nonparametric late-time expansion history reconstruction and implications for the Hubble tension in light of recent DESI and type Ia supernovae data. Phys. Rev. D 2024, 110, 123519. [Google Scholar] [CrossRef]
- Dinda, B.R.; Maartens, R. Model-agnostic assessment of dark energy after DESI DR1 BAO. J. Cosmol. Astropart. Phys. 2025, 01, 120. [Google Scholar] [CrossRef]
- Dinda, B.R.; Maartens, R.; Saito, S.; Clarkson, C. Improved null tests of ΛCDM and FLRW in light of DESI DR2. arXiv 2025, arXiv:2504.09681. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Q.; Li, C.; Yuan, P.; Ren, X.; Saridakis, E.N.; Cai, Y.F. Gaussian-process reconstructions and model building of quintom dark energy from latest cosmological observations. arXiv 2025, arXiv:2501.18336. [Google Scholar] [CrossRef]
- Dinda, B.R.; Banerjee, N. Model independent bounds on type Ia supernova absolute peak magnitude. Phys. Rev. D 2023, 107, 063513. [Google Scholar] [CrossRef]
- Ruiz-Zapatero, J.; García-García, C.; Alonso, D.; Ferreira, P.G.; Grumitt, R.D.P. Model-independent constraints on Ωm and H(z) from the link between geometry and growth. Mon. Not. Roy. Astron. Soc. 2022, 512, 1967–1984. [Google Scholar] [CrossRef]
- Escamilla, L.A.; Akarsu, Ö.; Di Valentino, E.; Vazquez, J.A. Model-independent reconstruction of the interacting dark energy kernel: Binned and Gaussian process. J. Cosmol. Astropart. Phys. 2023, 2023, 051. [Google Scholar] [CrossRef]
- Sun, W.; Jiao, K.; Zhang, T.J. Influence of the Bounds of the Hyperparameters on the Reconstruction of the Hubble Constant with the Gaussian Process. Astrophys. J. 2021, 915, 123. [Google Scholar] [CrossRef]
- Ó Colgáin, E.; Sheikh-Jabbari, M.M. Elucidating cosmological model dependence with H0. Eur. Phys. J. C 2021, 81, 892. [Google Scholar] [CrossRef]
- Ahlström Kjerrgren, A.; Mörtsell, E. On the use of galaxies as clocks and the universal expansion. Mon. Not. Roy. Astron. Soc. 2023, 518, 585–591. [Google Scholar] [CrossRef]
- Renzi, F.; Silvestri, A. A look at the Hubble speed from first principles. arXiv 2020, arXiv:2011.10559. [Google Scholar] [CrossRef]
- Calderón, R.; L’Huillier, B.; Polarski, D.; Shafieloo, A.; Starobinsky, A.A. Joint reconstructions of growth and expansion histories from stage-IV surveys with minimal assumptions: Dark energy beyond Λ. Phys. Rev. D 2022, 106, 083513. [Google Scholar] [CrossRef]
- Dinda, B.R. Analytical Gaussian process cosmography: Unveiling insights into matter-energy density parameter at present. Eur. Phys. J. C 2024, 84, 402. [Google Scholar] [CrossRef]
- Escamilla, L.A.; Özülker, E.; Akarsu, O.; Di Valentino, E.; Vázquez, J.A. Do we need wavelets in the late Universe? arXiv 2024, arXiv:2408.12516. [Google Scholar] [CrossRef]
- Velázquez, J.d.J.; Escamilla, L.A.; Mukherjee, P.; Vázquez, J.A. Non-Parametric Reconstruction of Cosmological Observables Using Gaussian Processes Regression. Universe 2024, 10, 464. [Google Scholar] [CrossRef]
- Gómez-Vargas, I.; Esquivel, R.M.; García-Salcedo, R.; Vázquez, J.A. Neural network reconstructions for the Hubble parameter, growth rate and distance modulus. Eur. Phys. J. C 2023, 83, 304. [Google Scholar] [CrossRef]
- Keeley, R.E.; Shafieloo, A.; Zhao, G.B.; Vazquez, J.A.; Koo, H. Reconstructing the Universe: Testing the Mutual Consistency of the Pantheon and SDSS/eBOSS BAO Data Sets with Gaussian Processes. Astron. J. 2021, 161, 151. [Google Scholar] [CrossRef]
- Zheng, J.; Qiang, D.C.; You, Z.Q.; Kumar, D. Quantifying the Impact of 2D and 3D BAO Measurements on the Cosmic Distance Duality Relation with HII Galaxy observation. arXiv 2025, arXiv:2507.17113. [Google Scholar] [CrossRef]
- Li, T.N.; Du, G.H.; Wu, P.J.; Qi, J.Z.; Zhang, J.F.; Zhang, X. Testing the cosmic distance duality relation with baryon acoustic oscillations and supernovae data. arXiv 2025, arXiv:2507.13811. [Google Scholar] [CrossRef]
- Yang, F.; Fu, X.; Xu, B.; Zhang, K.; Huang, Y.; Yang, Y. Testing the cosmic distance duality relation using Type Ia supernovae and BAO observations. Eur. Phys. J. C 2025, 85, 186. [Google Scholar] [CrossRef]
- Cosmai, L.; Fanizza, G.; Gasperini, M.; Tedesco, L. Discriminating different models of luminosity-redshift distribution. Class. Quant. Grav. 2013, 30, 095011. [Google Scholar] [CrossRef][Green Version]
- Wang, M.; Fu, X.; Xu, B.; Huang, Y.; Yang, Y.; Lu, Z. Testing the cosmic distance duality relation with Type Ia supernova and transverse BAO measurements. Eur. Phys. J. C 2024, 84, 702. [Google Scholar] [CrossRef]
- Hwang, S.g.; L’Huillier, B.; Keeley, R.E.; Jee, M.J.; Shafieloo, A. How to use GP: Effects of the mean function and hyperparameter selection on Gaussian process regression. J. Cosmol. Astropart. Phys. 2023, 2023, 014. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Y.C.; Zhang, T.J.; Zhang, T. Kernel Selection for Gaussian Process in Cosmology: With Approximate Bayesian Computation Rejection and Nested Sampling. Astrophys. J. Suppl. Ser. 2023, 266, 27. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; Adaptive Computation and Machine Learning; MIT Press: Cambridge, MA, USA, 2006; pp. 1–XVIII, 1–248. [Google Scholar]
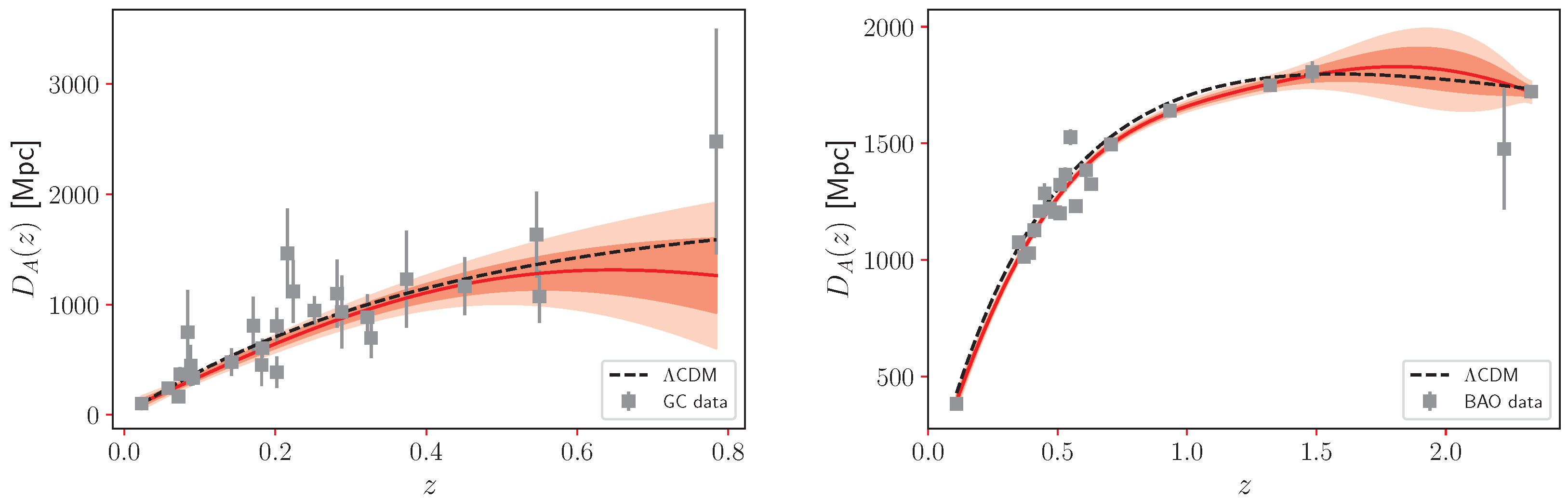


| Probe | Redshift Coverage | Number of Data Points |
|---|---|---|
| GC | 25 | |
| BAO | 22 | |
| SNe | 1701 | |
| QSO | 2195 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Avila, F.; Oliveira, F.; Franco, C.; Lopes, M.; Holanda, R.; Nunes, R.C.; Bernui, A. Probing the Cosmic Distance Duality Relation via Non-Parametric Reconstruction for High Redshifts. Universe 2025, 11, 307. https://doi.org/10.3390/universe11090307
Avila F, Oliveira F, Franco C, Lopes M, Holanda R, Nunes RC, Bernui A. Probing the Cosmic Distance Duality Relation via Non-Parametric Reconstruction for High Redshifts. Universe. 2025; 11(9):307. https://doi.org/10.3390/universe11090307
Chicago/Turabian StyleAvila, Felipe, Fernanda Oliveira, Camila Franco, Maria Lopes, Rodrigo Holanda, Rafael C. Nunes, and Armando Bernui. 2025. "Probing the Cosmic Distance Duality Relation via Non-Parametric Reconstruction for High Redshifts" Universe 11, no. 9: 307. https://doi.org/10.3390/universe11090307
APA StyleAvila, F., Oliveira, F., Franco, C., Lopes, M., Holanda, R., Nunes, R. C., & Bernui, A. (2025). Probing the Cosmic Distance Duality Relation via Non-Parametric Reconstruction for High Redshifts. Universe, 11(9), 307. https://doi.org/10.3390/universe11090307








