Spectral Analysis of Star-Forming Galaxies at z < 0.4 with FADO: Impact of Nebular Continuum on Galaxy Properties
Abstract
1. Introduction
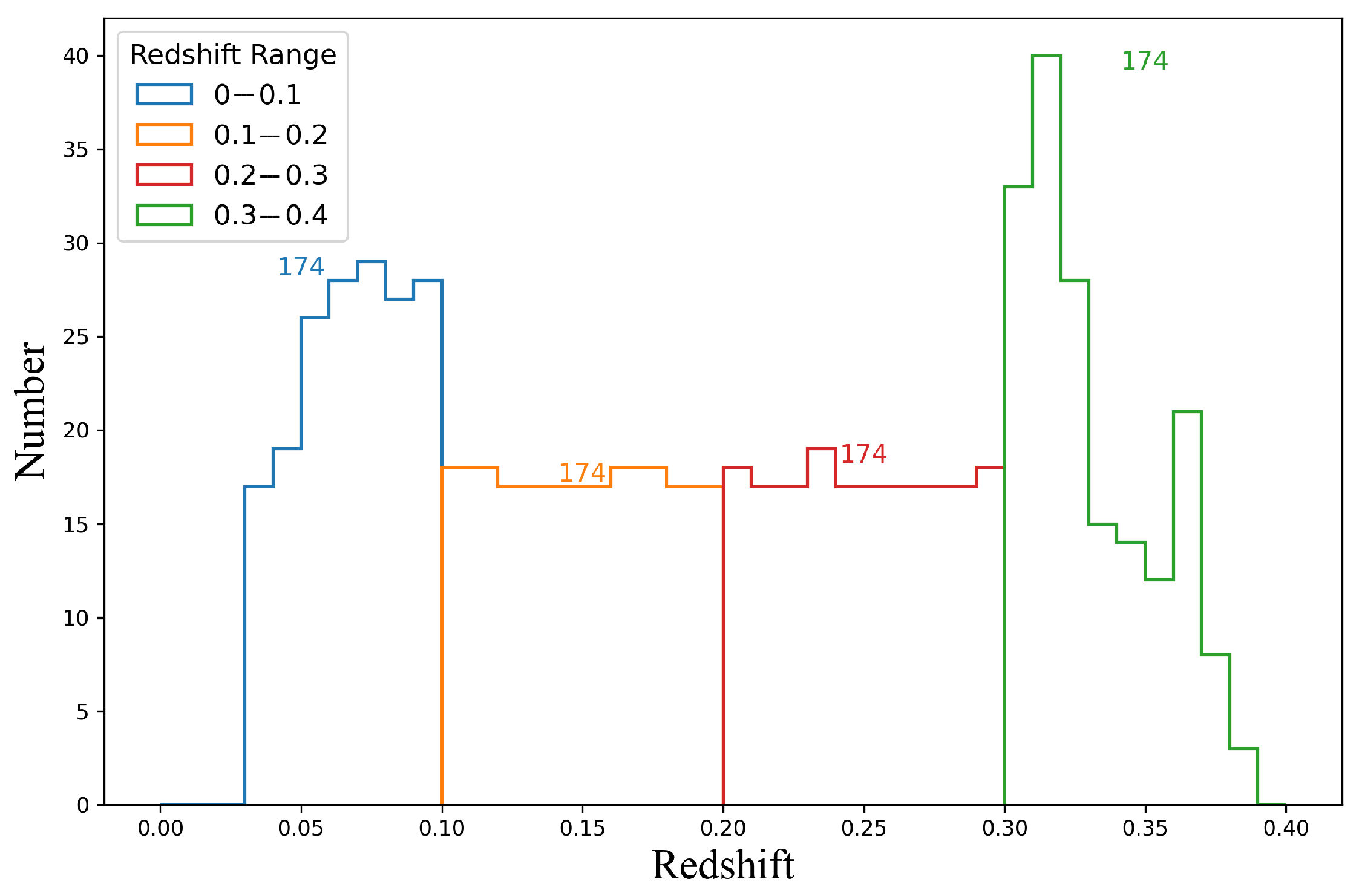
2. Sample Selection and Spectral Fitting
2.1. SQL Query
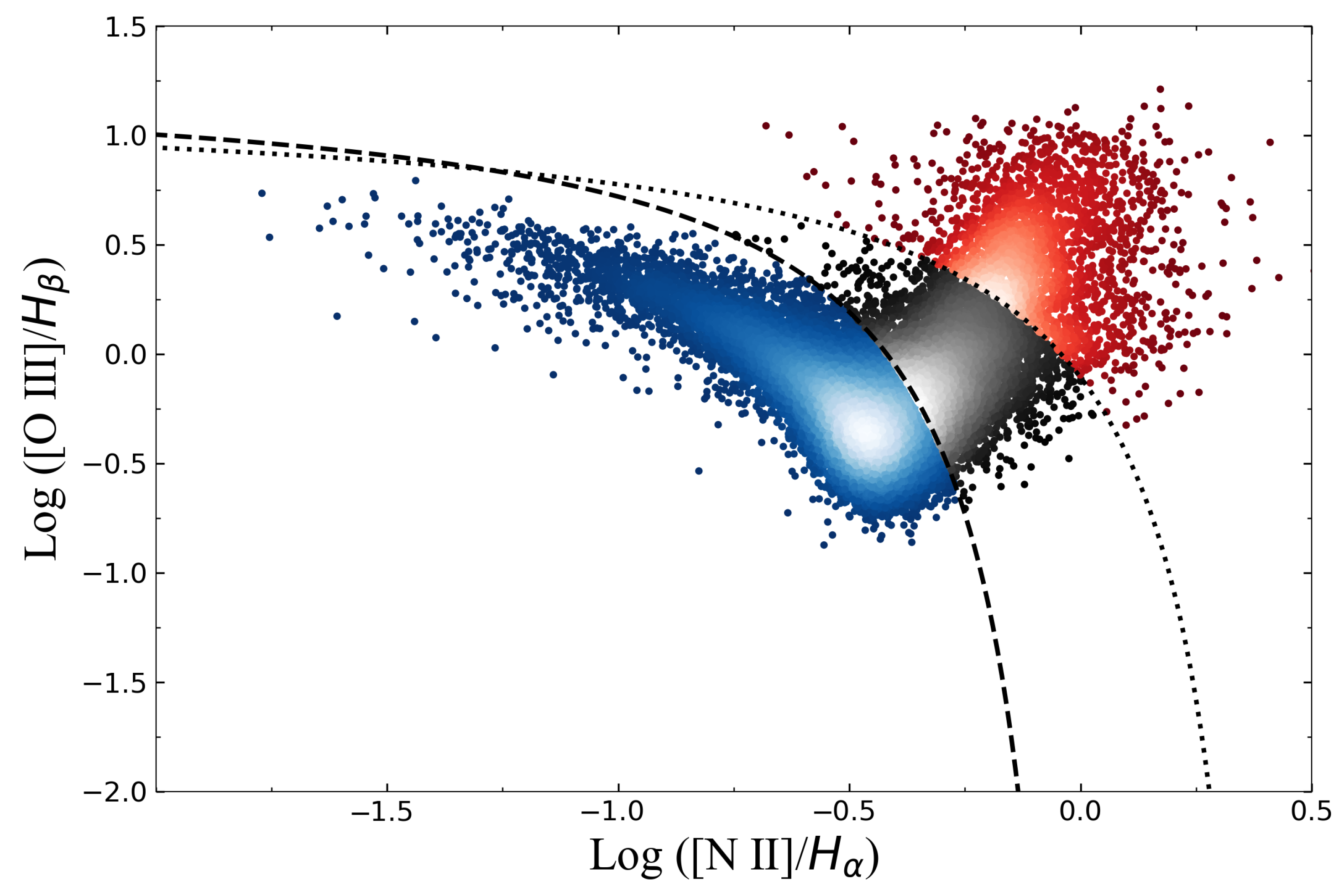
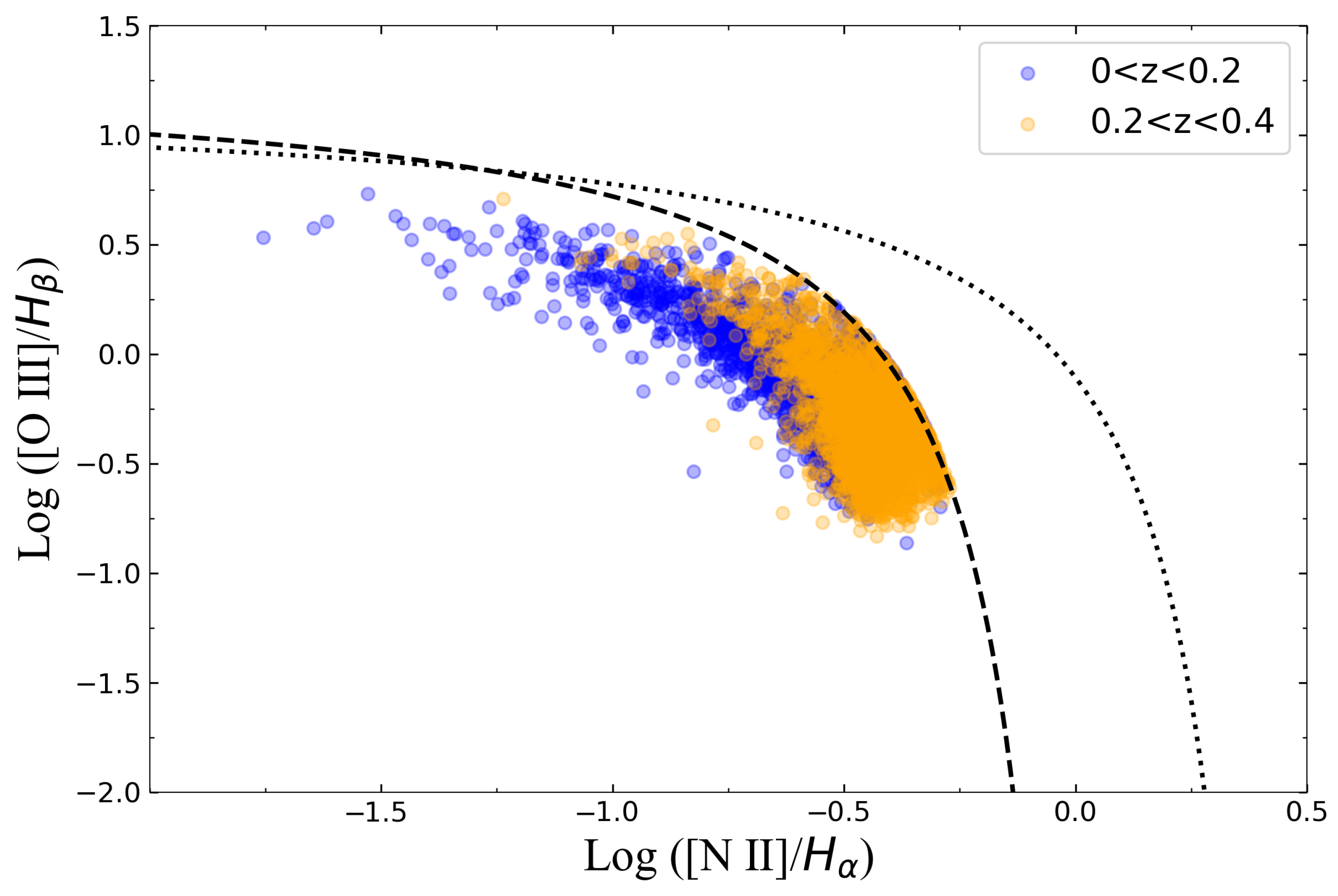
2.2. BPT Selection
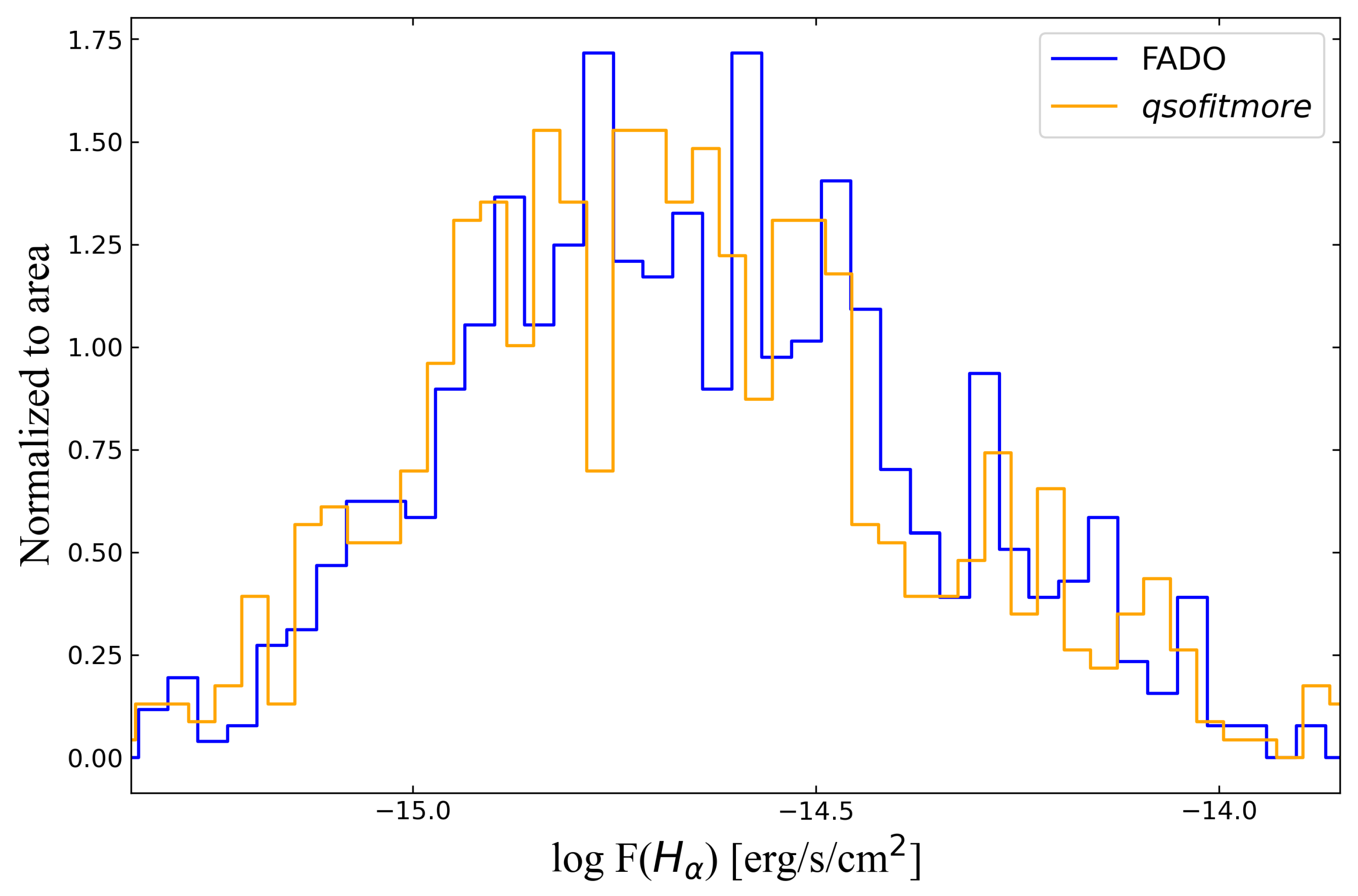
2.3. qsofitmore vs. FADO
- (i):
- Spectral Fitting Models: FADO employs population spectral synthesis (PSS) to decompose a galaxy spectrum into a linear combination of single stellar population (SSP) templates of different ages and metallicities, thereby inferring the fractional contributions of stellar populations. Additionally, FADO implements physically self-consistent coupling between stellar and nebular emission; it computes nebular continuum and Balmer emission line intensities based on the Lyman continuum (LyC) photon output from the fitted stellar populations and simultaneously fits these components with the observed spectrum. In contrast, qsofitmore performs linear fitting with PCA-based host galaxy templates [41]. These eigenspectra are derived from large observational samples, and implicitly include an average level of nebular emission inherited from the training set; however, they do not distinguish between the stellar and nebular continua of the target galaxy or adapt the nebular component to the specific physical conditions of the target. For emission line fitting, qsofitmore employs high-order Balmer series and complex Fe ii templates.
- (ii):
- Fitting Algorithms: FADO uses a differential evolution optimization (DEO) algorithm, which is a population-based evolutionary method that employs mutation, crossover, and selection operators to iteratively approach a global optimum. This approach enables multi-objective fitting, allowing several objectives to be optimized simultaneously and promoting physically meaningful solutions. Conversely, qsofitmore performs linear combination fitting using predefined spectral templates (SSPs, emission lines, and Fe ii complexes), minimizing the residuals via least-squares or similar linear optimization techniques.
- (iii):
- Treatment of Nebular Emissions: FADO implements self-consistent modeling of both the nebular continuum and Balmer emission lines, ensuring consistency between the nebular emission and the properties of the underlying stellar populations. On the other hand, qsofitmore does not compute nebular emission in a self-consistent manner. Instead, it employs PCA-derived galaxy templates in which the nebular emission is fixed at an invariant average level, which does not reflect the actual nebular emission of the target galaxy [40,41,45].Many studies have compared results from FADO and STARLIGHT, consistently reporting minor differences [20,29,30]. In this work, our comparison between FADO and qsofitmore for low-redshift SFGs tests whether a self-consistent treatment of nebular emission is necessary and whether spectral fits that include nebular emission self-consistently differ from those that treat it as fixed. For details of the two spectral fitting packages, see [28,40].
2.4. Spectral Fitting
2.5. Intrinsic Extinction Correction
3. Analysis and Results
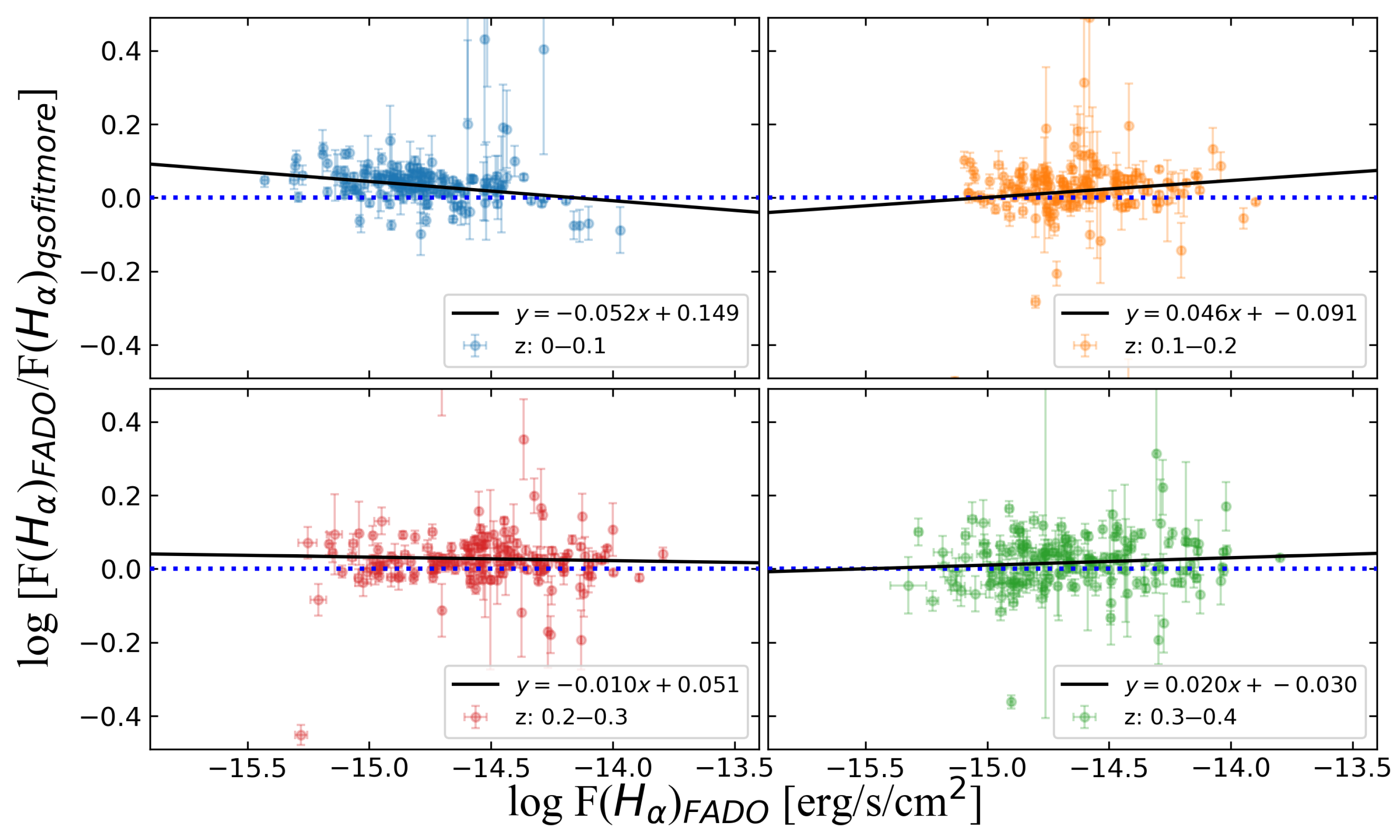
3.1. Comparison of Flux
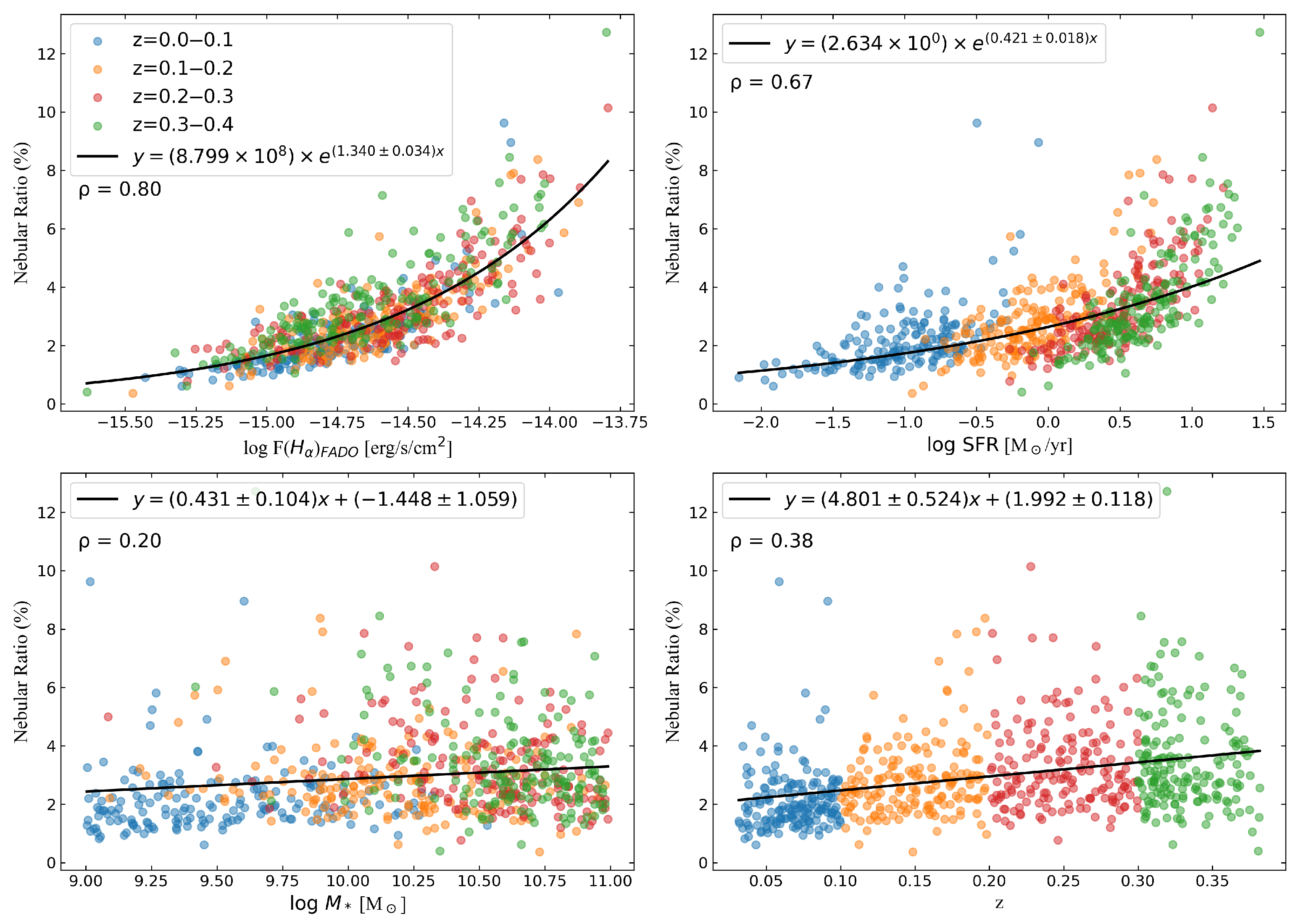
3.2. Nebular Ratio and Other Physical Parameters
3.3. Redshift vs. Nebular Ratio
4. Discussion
4.1. Comparison with Miranda’s Results and Uncertainty
4.2. Other Factors Affecting SFR Estimation
4.3. Sample Variation
5. Conclusions
- (1)
- This work compares the recently developed qsofitmore stellar population-based code with PCA-derived galaxy templates to the nebular-inclusive FADO code, aiming to evaluate their differences in fitting the emission. This comparison adds diversity to the evaluation between FADO and other consider nebula emission codes, supporting the robustness of FADO’s self-consistent approach for our sample. We find that FADO produces stable galaxy spectral fits within the low-redshift range (), showing only minor differences compared to models that treat nebular emission as a constant. Specifically, the median difference in flux between the two codes is approximately dex (corresponding to a linear difference of about ). This result is similar to the findings of Miranda et al. [20], who performed fitting using FADO and MAP-JHU. We infer that for -based SFR estimates at , the choice between self-consistent nebular modeling and an average nebular level has only a modest impact on the flux.
- (2)
- Statistical analysis indicates that for galaxies with and stellar masses in the range , both and SFR serve as reliable tracers of the nebular ratio, which itself shows weak sensitivity to stellar mass within this mass range. In particular, we observe an increasing trend of the nebular ratio with redshift, which is especially pronounced in the interval to . This finding underscores the necessity of adequately accounting for the nebular contribution in future spectroscopic analyses of higher-redshift star-forming galaxies. Such effects are expected to become increasingly significant under these conditions, particularly when investigating the active star-forming environments of the early universe.
- (3)
- This work presents a quantitative characterization of the increasing trend of the median nebular ratio with redshift in SFGs, which is largely insensitive (within uncertainties) to variations in stellar mass over –. Moreover, a quantitative model describing the dependence of the average nebular emission fraction on the redshift is established. This empirical relation provides a practical tool for estimating nebular contributions in low-redshift SDSS-like samples, and with appropriate calibration may inform assessments at higher redshifts. This framework provides a basis for quantitatively assessing nebular contributions in future studies of high-redshift galaxies, thereby supporting improved SFR inference and laying a solid foundation for future galaxy evolution studies utilizing large spectroscopic surveys.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. List of SQL Queries
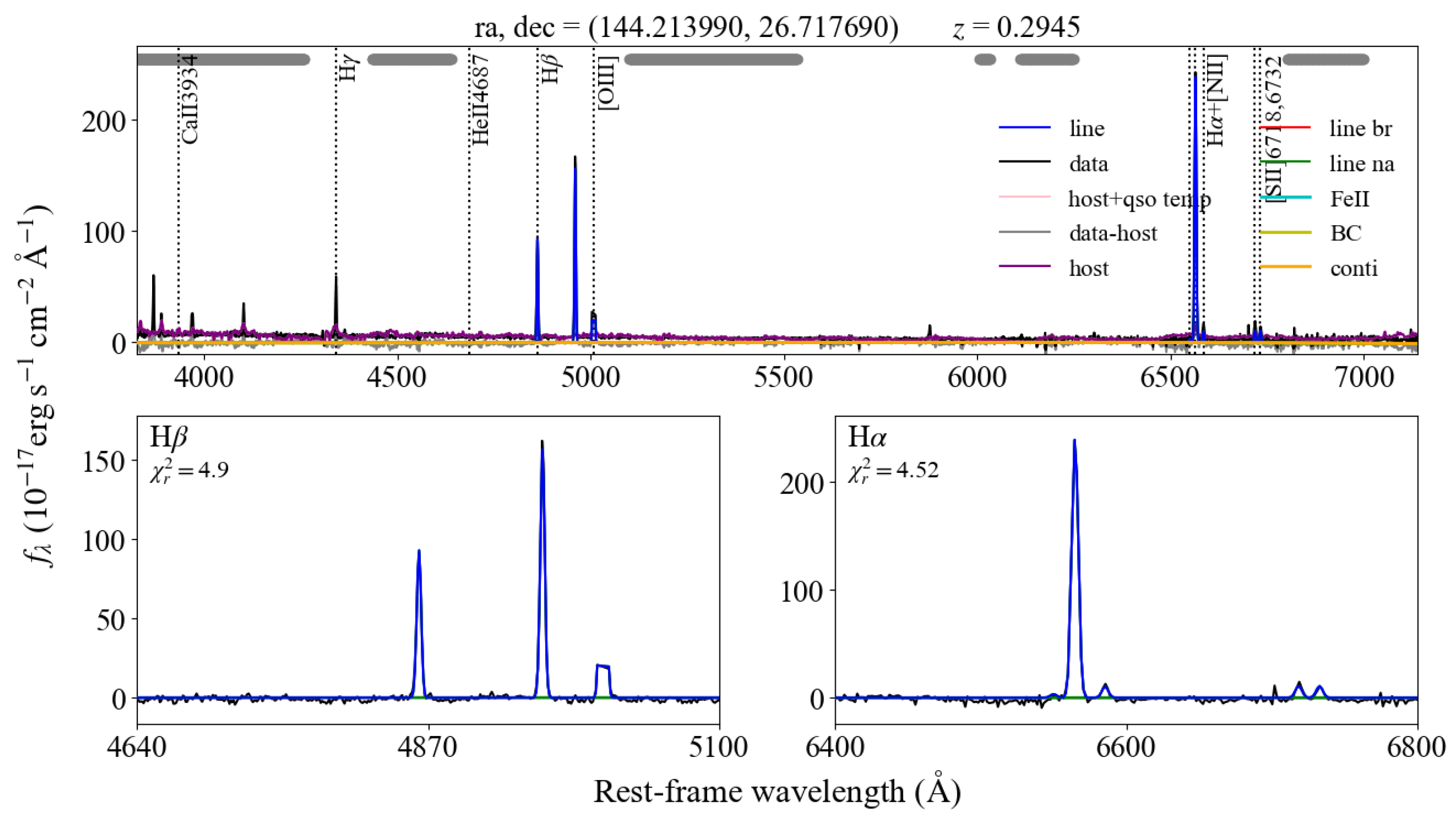
Appendix B. Example of qsofitmore and FADO Spectral Fitting

References
- Zhuang, M.Y.; Ho, L.C. Recalibration of [O II] λ3727 as a Star Formation Rate Estimator for Active and Inactive Galaxies. Astrophys. J. 2019, 882, 89. [Google Scholar] [CrossRef]
- Krumholz, M.R.; Dekel, A.; McKee, C.F. A Universal, Local Star Formation Law in Galactic Clouds, nearby Galaxies, High-redshift Disks, and Starbursts. Astrophys. J. 2012, 745, 69. [Google Scholar] [CrossRef]
- Mullaney, J.R.; Pannella, M.; Daddi, E.; Alexander, D.M.; Elbaz, D.; Hickox, R.C.; Bournaud, F.; Altieri, B.; Aussel, H.; Coia, D.; et al. GOODS-Herschel: The far-infrared view of star formation in active galactic nucleus host galaxies since z ≈ 3. Mon. Not. R. Astron. Soc. 2012, 419, 95–115. [Google Scholar] [CrossRef]
- Madau, P.; Dickinson, M. Cosmic Star-Formation History. Annu. Rev. Astron. Astrophys. 2014, 52, 415–486. [Google Scholar] [CrossRef]
- Lada, C.J.; Lada, E.A. Embedded Clusters in Molecular Clouds. Annu. Rev. Astron. Astrophys. 2003, 41, 57–115. [Google Scholar] [CrossRef]
- McKee, C.F.; Tan, J.C. Massive star formation in 100,000 years from turbulent and pressurized molecular clouds. Nature 2002, 416, 59–61. [Google Scholar] [CrossRef]
- Kirk, H.; Klassen, M.; Pudritz, R.; Pillsworth, S. The Role of Turbulence and Magnetic Fields in Simulated Filamentary Structure. Astrophys. J. 2015, 802, 75. [Google Scholar] [CrossRef]
- McKee, C.F.; Ostriker, E.C. Theory of Star Formation. Annu. Rev. Astron. Astrophys. 2007, 45, 565–687. [Google Scholar] [CrossRef]
- Di Matteo, T.; Springel, V.; Hernquist, L. Energy input from quasars regulates the growth and activity of black holes and their host galaxies. Nature 2005, 433, 604–607. [Google Scholar] [CrossRef] [PubMed]
- Springel, V.; Di Matteo, T.; Hernquist, L. Modelling feedback from stars and black holes in galaxy mergers. Mon. Not. R. Astron. Soc. 2005, 361, 776–794. [Google Scholar] [CrossRef]
- Wang, F.Y. The high-redshift star formation rate derived from gamma-ray bursts: Possible origin and cosmic reionization. Astron. Astrophys. 2013, 556, A90. [Google Scholar] [CrossRef]
- Robertson, B.E.; Ellis, R.S. Connecting the Gamma Ray Burst Rate and the Cosmic Star Formation History: Implications for Reionization and Galaxy Evolution. Astrophys. J. 2012, 744, 95. [Google Scholar] [CrossRef]
- Daigne, F.; Olive, K.A.; Vangioni-Flam, E.; Silk, J.; Audouze, J. Cosmic Star Formation, Reionization, and Constraints on Global Chemical Evolution. Astrophys. J. 2004, 617, 693–706. [Google Scholar] [CrossRef]
- Kennicutt, R.C.; Evans, N.J. Star Formation in the Milky Way and Nearby Galaxies. Annu. Rev. Astron. Astrophys. 2012, 50, 531–608. [Google Scholar] [CrossRef]
- York, D.G.; Adelman, J.; Anderson, J.E., Jr.; Anderson, S.F.; Annis, J.; Bahcall, N.A.; Bakken, J.A.; Barkhouser, R.; Bastian, S.; Berman, E.; et al. The Sloan Digital Sky Survey: Technical Summary. Astron. J. 2000, 120, 1579–1587. [Google Scholar] [CrossRef]
- Ellis, R.S.; McLure, R.J.; Dunlop, J.S.; Robertson, B.E.; Ono, Y.; Schenker, M.A.; Koekemoer, A.; Bowler, R.A.A.; Ouchi, M.; Rogers, A.B.; et al. The Abundance of Star-forming Galaxies in the Redshift Range 8.5-12: New Results from the 2012 Hubble Ultra Deep Field Campaign. Astrophys. J. Lett. 2013, 763, L7. [Google Scholar] [CrossRef]
- Wang, R.; Wagg, J.; Carilli, C.L.; Walter, F.; Lentati, L.; Fan, X.; Riechers, D.A.; Bertoldi, F.; Narayanan, D.; Strauss, M.A.; et al. Star Formation and Gas Kinematics of Quasar Host Galaxies at z ~ 6: New Insights from ALMA. Astrophys. J. 2013, 773, 44. [Google Scholar] [CrossRef]
- Cid Fernandes, R.; Mateus, A.; Sodré, L.; Stasińska, G.; Gomes, J.M. Semi-empirical analysis of Sloan Digital Sky Survey galaxies—I. Spectral synthesis method. Mon. Not. R. Astron. Soc. 2005, 358, 363–378. [Google Scholar] [CrossRef]
- Cappellari, M.; Emsellem, E. Parametric Recovery of Line-of-Sight Velocity Distributions from Absorption-Line Spectra of Galaxies via Penalized Likelihood. Publ. Astron. Soc. Pac. 2004, 116, 138–147. [Google Scholar] [CrossRef]
- Miranda, H.; Pappalardo, C.; Papaderos, P.; Afonso, J.; Matute, I.; Lobo, C.; Paulino-Afonso, A.; Carvajal, R.; Lorenzoni, S.; Santos, D. An investigation of the star-forming main sequence considering the nebular continuum emission at low-z. Astron. Astrophys. 2023, 669, A16. [Google Scholar] [CrossRef]
- Ahumada, R.; Allende Prieto, C.; Almeida, A.; Anders, F.; Anderson, S.F.; Andrews, B.H.; Anguiano, B.; Arcodia, R.; Armengaud, E.; Aubert, M.; et al. The 16th Data Release of the Sloan Digital Sky Surveys: First Release from the APOGEE-2 Southern Survey and Full Release of eBOSS Spectra. Astrophys. J. Suppl. Ser. 2020, 249, 3. [Google Scholar] [CrossRef]
- Krueger, H.; Fritze-v. Alvensleben, U.; Loose, H.H. Optical and near infrared spectral energy distributions. of blue compact galaxies from evolutionary synthesis. Astron. Astrophys. 1995, 303, 41. [Google Scholar]
- Salim, S.; Rich, R.M.; Charlot, S.; Brinchmann, J.; Johnson, B.D.; Schiminovich, D.; Seibert, M.; Mallery, R.; Heckman, T.M.; Forster, K.; et al. UV Star Formation Rates in the Local Universe. Astrophys. J. Suppl. Ser. 2007, 173, 267–292. [Google Scholar] [CrossRef]
- Schaerer, D.; de Barros, S. The impact of nebular emission on the ages of z ≈ 6 galaxies. Astron. Astrophys. 2009, 502, 423–426. [Google Scholar] [CrossRef]
- Pacifici, C.; da Cunha, E.; Charlot, S.; Rix, H.W.; Fumagalli, M.; Wel, A.v.d.; Franx, M.; Maseda, M.V.; van Dokkum, P.G.; Brammer, G.B.; et al. On the importance of using appropriate spectral models to derive physical properties of galaxies at 0.7 < z < 2.8. Mon. Not. R. Astron. Soc. 2015, 447, 786–805. [Google Scholar] [CrossRef]
- Izotov, Y.I.; Schaerer, D.; Guseva, N.G.; Thuan, T.X.; Worseck, G. Extremely strong C IV λ1550 nebular emission in the extremely low-metallicity star-forming galaxy J2229+2725. Mon. Not. R. Astron. Soc. 2024, 528, L10–L14. [Google Scholar] [CrossRef]
- Scoville, N.; Faisst, A.; Weaver, J.; Toft, S.; McCracken, H.J.; Ilbert, O.; Diaz-Santos, T.; Staguhn, J.; Koda, J.; Casey, C.; et al. Cosmic Evolution of Gas and Star Formation. Astrophys. J. 2023, 943, 82. [Google Scholar] [CrossRef]
- Gomes, J.M.; Papaderos, P. Fitting Analysis using Differential evolution Optimization (FADO): Spectral population synthesis through genetic optimization under self-consistency boundary conditions. Astron. Astrophys. 2017, 603, A63. [Google Scholar] [CrossRef]
- Cardoso, L.S.M.; Gomes, J.M.; Papaderos, P.; Pappalardo, C.; Miranda, H.; Paulino-Afonso, A.; Afonso, J.; Lagos, P. Revisiting stellar properties of star-forming galaxies with stellar and nebular spectral modelling. Astron. Astrophys. 2022, 667, A11. [Google Scholar] [CrossRef]
- Breda, I.; Vilchez, J.M.; Papaderos, P.; Cardoso, L.; Amorin, R.O.; Arroyo-Polonio, A.; Iglesias-Páramo, J.; Kehrig, C.; Pérez-Montero, E. Characterisation of the stellar content of SDSS EELGs through self-consistent spectral modelling. Astron. Astrophys. 2022, 663, A29. [Google Scholar] [CrossRef]
- Sobral, D.; Smail, I.; Best, P.N.; Geach, J.E.; Matsuda, Y.; Stott, J.P.; Cirasuolo, M.; Kurk, J. A large Hα survey at z = 2.23, 1.47, 0.84 and 0.40: The 11 Gyr evolution of star-forming galaxies from HiZELS. Mon. Not. R. Astron. Soc. 2013, 428, 1128–1146. [Google Scholar] [CrossRef]
- Kewley, L.J.; Geller, M.J.; Jansen, R.A. O II as a Star Formation Rate Indicator. Astron. J. 2004, 127, 2002–2030. [Google Scholar] [CrossRef]
- Kennicutt, R.C., Jr. Star Formation in Galaxies Along the Hubble Sequence. Annu. Rev. Astron. Astrophys. 1998, 36, 189–232. [Google Scholar] [CrossRef]
- Shapley, A.E.; Reddy, N.A.; Sanders, R.L.; Topping, M.W.; Brammer, G.B. JWST/NIRSpec Measurements of the Relationships between Nebular Emission-line Ratios and Stellar Mass at z 3–6. Astrophys. J. Lett. 2023, 950, L1. [Google Scholar] [CrossRef]
- Almeida, A.; Anderson, S.F.; Argudo-Fernández, M.; Badenes, C.; Barger, K.; Barrera-Ballesteros, J.K.; Bender, C.F.; Benitez, E.; Besser, F.; Bird, J.C.; et al. The Eighteenth Data Release of the Sloan Digital Sky Surveys: Targeting and First Spectra from SDSS-V. Astrophys. J. Suppl. Ser. 2023, 267, 44. [Google Scholar] [CrossRef]
- Pappalardo, C.; Cardoso, L.S.M.; Michel Gomes, J.; Papaderos, P.; Afonso, J.; Breda, I.; Humphrey, A.; Scott, T.; Amarantidis, S.; Matute, I.; et al. Self-consistent population spectral synthesis with FADO. II. Star formation history of galaxies in spectral synthesis methods. Astron. Astrophys. 2021, 651, A99. [Google Scholar] [CrossRef]
- Baldwin, J.A.; Phillips, M.M.; Terlevich, R. Classification parameters for the emission-line spectra of extragalactic objects. Publ. Astron. Soc. Pac. 1981, 93, 5–19. [Google Scholar] [CrossRef]
- Kewley, L.J.; Dopita, M.A.; Sutherland, R.S.; Heisler, C.A.; Trevena, J. Theoretical Modeling of Starburst Galaxies. Astrophys. J. 2001, 556, 121–140. [Google Scholar] [CrossRef]
- Kauffmann, G.; Heckman, T.M.; Tremonti, C.; Brinchmann, J.; Charlot, S.; White, S.D.M.; Ridgway, S.E.; Brinkmann, J.; Fukugita, M.; Hall, P.B.; et al. The host galaxies of active galactic nuclei. Mon. Not. R. Astron. Soc. 2003, 346, 1055–1077. [Google Scholar] [CrossRef]
- Fu, Y. QSOFITMORE: A Python Package for Fitting UV-Optical Spectra of Quasars; Zenodo: Geneva, Switzerland, 2021. [Google Scholar] [CrossRef]
- Fu, Y.; Wu, X.B.; Jiang, L.; Zhang, Y.; Huo, Z.Y.; Ai, Y.L.; Yang, Q.; Ma, Q.; Feng, X.; Joshi, R.; et al. Finding Quasars behind the Galactic Plane. II. Spectroscopic Identifications of 204 Quasars at ∣b∣ < 20°. Astrophys. J. Suppl. Ser. 2022, 261, 32. [Google Scholar] [CrossRef]
- Jin, J.J.; Wu, X.B.; Fu, Y.; Yao, S.; Ai, Y.L.; Feng, X.T.; He, Z.Q.; Ma, Q.C.; Pang, Y.X.; Zhu, R.; et al. The Large Sky Area Multi-Object Fiber Spectroscopic Telescope (LAMOST) Quasar Survey: Quasar Properties from Data Releases 6 to 9. Astrophys. J. Suppl. Ser. 2023, 265, 25. [Google Scholar] [CrossRef]
- Ding, X.; Onoue, M.; Silverman, J.D.; Matsuoka, Y.; Izumi, T.; Strauss, M.A.; Jahnke, K.; Phillips, C.L.; Li, J.; Volonteri, M.; et al. Detection of stellar light from quasar host galaxies at redshifts above 6. Nature 2023, 621, 51–55. [Google Scholar] [CrossRef]
- Chen, G.; Zheng, Z.; Zeng, X.; Zhang, L.; Xiao, H.; Liu, X.; Cui, L.; Fan, J. A Study of Broad Emission Line and Doppler Factor Estimation for Fermi Blazars. Astrophys. J. Suppl. Ser. 2024, 271, 20. [Google Scholar] [CrossRef]
- Yip, C.W.; Connolly, A.J.; Szalay, A.S.; Budavári, T.; SubbaRao, M.; Frieman, J.A.; Nichol, R.C.; Hopkins, A.M.; York, D.G.; Okamura, S.; et al. Distributions of Galaxy Spectral Types in the Sloan Digital Sky Survey. Astron. J. 2004, 128, 585–609. [Google Scholar] [CrossRef]
- Shen, Y.; Richards, G.T.; Strauss, M.A.; Hall, P.B.; Schneider, D.P.; Snedden, S.; Bizyaev, D.; Brewington, H.; Malanushenko, V.; Malanushenko, E.; et al. A Catalog of Quasar Properties from Sloan Digital Sky Survey Data Release 7. Astrophys. J. Suppl. Ser. 2011, 194, 45. [Google Scholar] [CrossRef]
- Shen, Y.; Hall, P.B.; Horne, K.; Zhu, G.; McGreer, I.; Simm, T.; Trump, J.R.; Kinemuchi, K.; Brandt, W.N.; Green, P.J.; et al. The Sloan Digital Sky Survey Reverberation Mapping Project: Sample Characterization. Astrophys. J. Suppl. Ser. 2019, 241, 34. [Google Scholar] [CrossRef]
- Rakshit, S.; Stalin, C.S.; Kotilainen, J. Spectral Properties of Quasars from Sloan Digital Sky Survey Data Release 14: The Catalog. Astrophys. J. Suppl. Ser. 2020, 249, 17. [Google Scholar] [CrossRef]
- Bruzual, G.; Charlot, S. Stellar population synthesis at the resolution of 2003. Mon. Not. R. Astron. Soc. 2003, 344, 1000–1028. [Google Scholar] [CrossRef]
- Abazajian, K.N.; Adelman-McCarthy, J.K.; Agüeros, M.A.; Allam, S.S.; Allende Prieto, C.; An, D.; Anderson, K.S.J.; Anderson, S.F.; Annis, J.; Bahcall, N.A.; et al. The Seventh Data Release of the Sloan Digital Sky Survey. Astrophys. J. Suppl. Ser. 2009, 182, 543–558. [Google Scholar] [CrossRef]
- Miranda, H.; Pappalardo, C.; Afonso, J.; Papaderos, P.; Lobo, C.; Paulino-Afonso, A.; Carvajal, R.; Matute, I.; Lagos, P.; Barbosa, D. Importance of modelling the nebular continuum in galaxy spectra. Astron. Astrophys. 2025, 694, A102. [Google Scholar] [CrossRef]
- Calzetti, D.; Armus, L.; Bohlin, R.C.; Kinney, A.L.; Koornneef, J.; Storchi-Bergmann, T. The Dust Content and Opacity of Actively Star-forming Galaxies. Astrophys. J. 2000, 533, 682–695. [Google Scholar] [CrossRef]
- Gaskell, C.M.; Ferland, G.J. Theoretical hydrogen-line ratios for the narrow-line regions of active galactic nuclei. Publ. Astron. Soc. Pac. 1984, 96, 393–397. [Google Scholar] [CrossRef]
- Hummer, D.G.; Storey, P.J. Recombination-line intensities for hydrogenic ions - I. Case B calculations for H I and He II. Mon. Not. R. Astron. Soc. 1987, 224, 801–820. [Google Scholar] [CrossRef]
- Cardelli, J.A.; Clayton, G.C.; Mathis, J.S. The Relationship between Infrared, Optical, and Ultraviolet Extinction. Astrophys. J. 1989, 345, 245. [Google Scholar] [CrossRef]
- Chabrier, G. The Galactic Disk Mass Function: Reconciliation of the Hubble Space Telescope and Nearby Determinations. Astrophys. J. Lett. 2003, 586, L133–L136. [Google Scholar] [CrossRef]
- Brinchmann, J.; Charlot, S.; White, S.D.M.; Tremonti, C.; Kauffmann, G.; Heckman, T.; Brinkmann, J. The physical properties of star-forming galaxies in the low-redshift Universe. Mon. Not. R. Astron. Soc. 2004, 351, 1151–1179. [Google Scholar] [CrossRef]
- Mannucci, F.; Cresci, G.; Maiolino, R.; Marconi, A.; Gnerucci, A. A fundamental relation between mass, star formation rate and metallicity in local and high-redshift galaxies. Mon. Not. R. Astron. Soc. 2010, 408, 2115–2127. [Google Scholar] [CrossRef]
- Behroozi, P.S.; Wechsler, R.H.; Conroy, C. The average star formation histories of galaxies in dark matter halos from z = 0–8. Astrophys. J. 2013, 770, 57. [Google Scholar] [CrossRef]
- Elbaz, D.; Leiton, R.; Nagar, N.; Okumura, K.; Franco, M.; Schreiber, C.; Pannella, M.; Wang, T.; Dickinson, M.; Díaz-Santos, T.; et al. Starbursts in and out of the star-formation main sequence. Astron. Astrophys. 2018, 616, A110. [Google Scholar] [CrossRef]
- Li, J.; Liu, C.; Zhang, Z.Y.; Tian, H.; Fu, X.; Li, J.; Yan, Z.Q. Stellar initial mass function varies with metallicity and time. Nature 2023, 613, 460–462. [Google Scholar] [CrossRef]
- Weilbacher, P.M.; Fritze-v. Alvensleben, U. On star formation rates in dwarf galaxies. Astron. Astrophys. 2001, 373, L9–L12. [Google Scholar] [CrossRef]
- Kewley, L.J.; Nicholls, D.C.; Sutherland, R.S. Understanding Galaxy Evolution Through Emission Lines. Annu. Rev. Astron. Astrophys. 2019, 57, 511–570. [Google Scholar] [CrossRef]
- Smith, J.D.T.; Draine, B.T.; Dale, D.A.; Moustakas, J.; Kennicutt, R.C., Jr.; Helou, G.; Armus, L.; Roussel, H.; Sheth, K.; Bendo, G.J.; et al. The Mid-Infrared Spectrum of Star-forming Galaxies: Global Properties of Polycyclic Aromatic Hydrocarbon Emission. Astrophys. J. 2007, 656, 770–791. [Google Scholar] [CrossRef]
- Rosario, D.J.; Mendel, J.T.; Ellison, S.L.; Lutz, D.; Trump, J.R. Local SDSS galaxies in the Herschel Stripe 82 survey: A critical assessment of optically derived star formation rates. Mon. Not. R. Astron. Soc. 2016, 457, 2703–2721. [Google Scholar] [CrossRef]
- Malmquist, K.G. On some relations in stellar statistics. Medd. Fran Lunds Astron. Obs. Ser. I 1922, 100, 1–52. [Google Scholar]
- Tasca, L.A.M.; Kneib, J.P.; Iovino, A.; Le Fèvre, O.; Kovač, K.; Bolzonella, M.; Lilly, S.J.; Abraham, R.G.; Cassata, P.; Cucciati, O.; et al. The zCOSMOS redshift survey: The role of environment and stellar mass in shaping the rise of the morphology-density relation from z ~ 1. Astron. Astrophys. 2009, 503, 379–398. [Google Scholar] [CrossRef]
- Ilbert, O.; McCracken, H.J.; Le Fèvre, O.; Capak, P.; Dunlop, J.; Karim, A.; Renzini, M.A.; Caputi, K.; Boissier, S.; Arnouts, S.; et al. Mass assembly in quiescent and star-forming galaxies since z = 4 from UltraVISTA. Astron. Astrophys. 2013, 556, A55. [Google Scholar] [CrossRef]
- Muzzin, A.; Marchesini, D.; Stefanon, M.; Franx, M.; McCracken, H.J.; Milvang-Jensen, B.; Dunlop, J.S.; Fynbo, J.P.U.; Brammer, G.; Labbé, I.; et al. The Evolution of the Stellar Mass Functions of Star-forming and Quiescent Galaxies to z = 4 from the COSMOS/UltraVISTA Survey. Astrophys. J. 2013, 777, 18. [Google Scholar] [CrossRef]
- Leja, J.; Johnson, B.D.; Conroy, C.; van Dokkum, P.; Speagle, J.S.; Brammer, G.; Momcheva, I.; Skelton, R.; Whitaker, K.E.; Franx, M.; et al. An Older, More Quiescent Universe from Panchromatic SED Fitting of the 3D-HST Survey. Astrophys. J. 2019, 877, 140. [Google Scholar] [CrossRef]
- Fumagalli, M.; Patel, S.G.; Franx, M.; Brammer, G.; van Dokkum, P.; da Cunha, E.; Kriek, M.; Lundgren, B.; Momcheva, I.; Rix, H.W.; et al. Hα Equivalent Widths from the 3D-HST Survey: Evolution with Redshift and Dependence on Stellar Mass. Astrophys. J. Lett. 2012, 757, L22. [Google Scholar] [CrossRef]
- Faisst, A.L.; Capak, P.; Hsieh, B.C.; Laigle, C.; Salvato, M.; Tasca, L.; Cassata, P.; Davidzon, I.; Ilbert, O.; Le Fèvre, O.; et al. A Coherent Study of Emission Lines from Broadband Photometry: Specific Star Formation Rates and [O III]/Hβ Ratio at 3 > z > 6. Astrophys. J. 2016, 821, 122. [Google Scholar] [CrossRef]
- Mármol-Queraltó, E.; McLure, R.J.; Cullen, F.; Dunlop, J.S.; Fontana, A.; McLeod, D.J. The evolution of the equivalent width of the Hα emission line and specific star formation rate in star-forming galaxies at 1 < z < 5. Mon. Not. R. Astron. Soc. 2016, 460, 3587–3597. [Google Scholar] [CrossRef]
- Reddy, N.A.; Shapley, A.E.; Sanders, R.L.; Kriek, M.; Coil, A.L.; Shivaei, I.; Freeman, W.R.; Mobasher, B.; Siana, B.; Azadi, M.; et al. The MOSDEF Survey: Significant Evolution in the Rest-frame Optical Emission Line Equivalent Widths of Star-forming Galaxies at z = 1.4–3.8. Astrophys. J. 2018, 869, 92. [Google Scholar] [CrossRef]
- Larson, R.L.; Hutchison, T.A.; Bagley, M.; Finkelstein, S.L.; Yung, L.Y.A.; Somerville, R.S.; Hirschmann, M.; Brammer, G.; Holwerda, B.W.; Papovich, C.; et al. Spectral Templates Optimal for Selecting Galaxies at z > 8 with the JWST. Astrophys. J. 2023, 958, 141. [Google Scholar] [CrossRef]
- Yan, H.; Li, H.; Wang, S.; Zong, W.; Yuan, H.; Xiang, M.; Huang, Y.; Xie, J.; Dong, S.; Yuan, H.; et al. Overview of the LAMOST survey in the first decade. Innov. 2022, 3, 100224. [Google Scholar] [CrossRef]
- DESI Collaboration; Abareshi, B.; Aguilar, J.; Ahlen, S.; Alam, S.; Alexander, D.M.; Alfarsy, R.; Allen, L.; Allende Prieto, C.; Alves, O.; et al. Overview of the Instrumentation for the Dark Energy Spectroscopic Instrument. Astron. J. 2022, 164, 207. [Google Scholar] [CrossRef]
- Dey, A.; Schlegel, D.J.; Lang, D.; Blum, R.; Burleigh, K.; Fan, X.; Findlay, J.R.; Finkbeiner, D.; Herrera, D.; Juneau, S.; et al. Overview of the DESI Legacy Imaging Surveys. Astron. J. 2019, 157, 168. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Y.; Chen, Q.; Jing, L.; Pappalardo, C.; Miranda, H. Spectral Analysis of Star-Forming Galaxies at z < 0.4 with FADO: Impact of Nebular Continuum on Galaxy Properties. Universe 2025, 11, 285. https://doi.org/10.3390/universe11090285
Yu Y, Chen Q, Jing L, Pappalardo C, Miranda H. Spectral Analysis of Star-Forming Galaxies at z < 0.4 with FADO: Impact of Nebular Continuum on Galaxy Properties. Universe. 2025; 11(9):285. https://doi.org/10.3390/universe11090285
Chicago/Turabian StyleYu, Yaosong, Qihang Chen, Liang Jing, Ciro Pappalardo, and Henrique Miranda. 2025. "Spectral Analysis of Star-Forming Galaxies at z < 0.4 with FADO: Impact of Nebular Continuum on Galaxy Properties" Universe 11, no. 9: 285. https://doi.org/10.3390/universe11090285
APA StyleYu, Y., Chen, Q., Jing, L., Pappalardo, C., & Miranda, H. (2025). Spectral Analysis of Star-Forming Galaxies at z < 0.4 with FADO: Impact of Nebular Continuum on Galaxy Properties. Universe, 11(9), 285. https://doi.org/10.3390/universe11090285







