Does Quantum Mechanics Breed Larger, More Intricate Quantum Theories? The Case for Experience-Centric Quantum Theory and the Interactome of Quantum Theories
Abstract
1. A Top-Down Introduction to an Interactome of Independent Quantum Theories
2. Quantum Simulation of a Larger Theory
2.1. Quantum Simulation Protocol
- (i)
- We first prepare a quantum statewhere , with being the first Pauli operator for spin- systems and on the basis of the eigenvectors of the third Pauli operator σ3. Here, δ is a sufficiently small real number (δ ≪ 1/|λΓ|). To perform the preparation, we note that the value of λ is not given. We are only given systems whose total state is what we call Γ, without even knowing (or needing to know) the state Γ itself. We also know the relation between λ and the unknown state Γ, which is given below Equation (3). To prepare the state , we use a modified “interferometric” quantum circuit, which has already been proposed to estimate nonlinear scalar functions of a state Γ, obviating the need for tomography of that state [9,15]—see Figure 1.
- (ii)
- Inspired by the density matrix exponentiation technique [12,19], we apply suitable controlled-swap gates (i.e., Fredkin gates) on a combined system composed of a system that is already prepared in , the simulator, and the two quantum systems with (unknown) states and ; hence, the total system is in the state . The suitable controlled-swap gates use the prepared system in as the control system and one of the systems in or and the simulator as the target systems. The gates are applied when the control system is in the state . In the next step, we perform a selective measurement on the control system on the basis and choose the output when it is in the state . Finally, we trace out over all of the ancillary systems, i.e., all of the systems other than the simulator. Up to this step, the (unnormalized) state of the simulator becomes . Interestingly, this is equivalent to simulating a state-dependent non-Hermitian Hamiltonian .
- (iii)
- To complete the simulation of the dynamics with the evolution , we simply need to repeat steps (i) and (ii) by preparing a new control system in(rather than ) and exchanging and , such that the state of the total system becomes .Parts (ii) and (iii) can be performed through the quantum circuit of Figure 2.
- (iv)
- We use the Trotter–Suzuki expansion to generalize the simulation to the general case of Hamiltonians of Equation (1) by repeating steps (i) through (iii) for each term in this state-history-dependent Hamiltonian.
2.2. Resource Analysis for Simulation
- (i)
- If the state-dependent Hamiltonian of interest (1) has M monomials, the above quantum circuit will have M interferometry circuits—one per each term in accordance with step (iv) of the simulation protocol.
- (ii)
- Assuming that depends on, at most, N states from the state history (e.g., ), each (and ) preparation part in the circuit of Figure 1 requires N past and present states.
- (iii)
- The quantum circuit for the simulation of dynamics generated by a term of factors, e.g., , will be similar to the half of the circuit in Figure 2, but with lines (labeled “” …“”) and l controlled-swap gates.
2.3. Simulation Protocol for a General State-History-Dependent Hamiltonian: Tomography Needed
- (i)
- Note that is typically small. The above protocol has achieved the evolution . In fact, is basically time-dependent through its dependence on the state history. Hence, the simulation of the evolution for longer times will need the time-ordered exponentialwhere , with and . This implies that a finite-time simulation of the true dynamics by the concatenation of also introduces further errors, which should be taken into account.
- (ii)
- Since is small, we also observe from Equation (20) that, for a given , does not need to be large. This is a favorable feature of this simulation: at any instant t, it does not require a large number of copies of to simulate .
- (iii)
- The simulation protocol described above implies that, given sufficient resources, one can, in principle, simulate general ECQT dynamics with the SQT framework. However, we should note that, in the above protocol, not only at any instant t do we need and copies of and , respectively, but we also need to perform tomography on at each time step. In fact, to prepare the relevant systems in , copies of the state at each time are needed for state tomography, where d is the dimension of the Hilbert space of the system. This implies that this protocol, indeed, can incur a significant resource overhead for simulation, which may render the very simulation infeasible or even impossible. This point will be important later in Section 4 for our discussion regarding the comparison of ECQT and SQT.
3. The Rosetta Stone of Experience-Centric Quantum Theory
- (i)
- the density operators in contribute in the construction of as part of its building blocks;
- (ii)
- takes, as part of its building blocks, some partial time-labeled information that is contained within the density operators constituting ;
- (iii)
- the structural composition of has any form of conditional dependence on some time-labeled information within .
4. SQT Versus ECQT
4.1. Reformulation of SQT Within ECQT: Basis-Dependent Recipe
4.1.1. EC Reformulation of a General One-Qubit System
4.1.2. EC Reformulation of Time-Independent One-Qubit SQT Hamiltonians
4.2. Reformulation of SQT by ECQT: Basis- and Decomposition-Independent Recipe
4.3. Inclusion Theorems
5. Behavioral Richness of EC Unitary Evolutions
5.1. Dynamics and Behavioral Phases
- Phase I: The wavefunction and its state history fidelity develop fixed-point attractors.
- Phase II: The wavefunction develops large regular simple periodic oscillations such that the state history fidelity has a fixed-point attractor, typically with tiny fluctuations.
- Phase III: The wavefunction and the state history fidelity feature large irregular oscillations.
- Phase IV: The wavefunction and the state history fidelity develop large structural oscillations in the form of sequential repetitions of temporally invariant behavioral modules that are marked with robustly ordered patterns.
- Phase V: The wavefunction features bistable attractor behavior of consecutively switching between two metastable states. These state swaps are in the form of sharp transitions. Accordingly, and in a manner that is synchronized with the wavefunction swaps, the state history fidelity features consecutive sharp minima, which equally parse the plateau of .
5.2. Deforming SQT Evolutions by Time-Local EC Hamiltonians
5.3. Global Wavefunction Localization by Near-Markovian Hybrid EC Hamiltonians
5.4. Deforming SQT Evolutions by Deeply Non-Markovian EC Hamiltonians
5.5. EC Hamiltonians Endowed with State-History-Dependent Couplings
- (i)
- The speed of wavefunction localization has a finite maximum value , for the whole spectrum of the deformation coupling. As one reads from the characteristic time scale of this EC evolution, (Equation (97)), the maximum speed is achieved at
- (ii)
- The fixed-point attractor of the unitary evolution—the moment at which the ground-state fidelity reaches the value 1—is infinitely distant. In other words, the dynamical attractor is asymptotic and the fidelity at any finite time has a value .
- (iii)
6. Characterization of General Quantum Behaviors and Phenomenological Significance of ECQT
- (i)
- The impacts of computational intelligence and cognition on the formulation of quantum theories in can be linked to a fundamental origin as follows. Information-theoretic constructions of quantum theories are ultimately based on observer-participatory networks (in the Wheelerian sense), where agentive decision making and inferential information processing are developed cooperatively. In effect, this “interactome” of agents functions as abstract cognitive machines performing inferential, probabilistic computations, which, in particular, construct (experiential representations of) the defining contexts of the alternative quantum theories. The bottomline of this reasoning is that mutual structural interactions between quantum and intelligent behaviors can be natural, fundamental, and multipurpose.
- (ii)
- The behavioral states and functional phases of complex many-body systems and neural networks can give rise to alternative quantum theories in , as their emergent descriptions. Thus, correspondingly, intelligent behavior can be the dominant determining factor in the defining structure of such quantum theories. This impact can manifest in either of the following forms: (a) the many-body complex system is itself a system with intelligent behavior by architecture, e.g., a classical or quantum neural network, or (b) it is some complex many-body system whose sufficiently rich behavioral phase diagram hosts specific states and phases that can feature intelligent behavior.
- (iii)
- One can formulate abstract, contextual quantum theories in , which, by definition and independently of any emergence mechanism, model abstract computational systems that solve goal-driven complex tasks, such as complex decision making, inference, or meta-learning.
- (i)
- Elementary quantum phenomena in agent-participatory networks: the elementary degrees of freedom, being the superposable “yes” or “no” (or even “no comment”) responses to the context-based-chosen queries that are posed by the associated agents in their participatory inferential networks. These information degrees of freedom, which are meaning-based (e.g., association-specifying), interact, evolve, and form Hilbert-space-representable experiential systems.
- (ii)
- Complementarity: the existence of nonempty classes of queries whose answers are informationally incompatible/nonadditive.
- (iii)
- Irreversibility of measurement actions: the registration of acquired information, meaning its retention in the absence of new informational incompatibilities.
- (iv)
- States: momentary states identified with density operators, encoding the complete sets of updated Bayesian predictions corresponding to agent–system pairs.
- (v)
- Distinctive role of the pure states: probability amplitudes encoded in pure states—being maximally informative density operators—with amplitudes identified by Born’s rule or its possible consistent generalizations or appropriate context-based deformations.
- (vi)
- Evolution: unitarity (or isometry) of the time evolution of the states of closed systems.
7. Foundations for Applications of ECQT
- ECQT can substantially impact the subfields of quantum information processing, including quantum computation, quantum communication, and quantum networks. In this respect, three points should be highlighted.(i) The standard disciplines of quantum information theory and quantum computation have thus far offered an abstract language for SQT. In the past few decades, the significant productivity of this language has proven itself in diverse areas of physics, such as condensed matter, holographic spacetimes, etc. However, beneath its abstractness, this language is bound to the contextual constraints of quantum mechanics, which renders it non-universal—with “universality” meant as faithful theoretical inclusivity, not simulational coverage. To bestow universality as such, one is required to revisit and generalize quantum information theory and quantum computation beyond this hidden mechanical context. This notion that quantum information and quantum computation should transcend quantum mechanics to be universal becomes more conspicuous when the computational units and processes are functional and emergent at higher levels. The computational modules and processes of such systems and states do not reflect the mechanisms that take place between the underlying elements at the anatomical level, nor do they bound themselves necessarily to the mechanistic constraints on the architectures. The QI and ECQT, by their nature and construction, do have the capacity and potency to develop a universal theory of fundamental and emergent information processing and computation. We shall return to this important point in the forthcoming applications of ECQT and .(ii) EC unitarities enable a larger space of observable quantities in which quantum information and computational elements can be implanted reliably. In particular, state history fidelities, their corresponding phase factors, and their many-point descendants (as defined in Equation (48)) can naturally encode a variety of evolving data. Indeed, there are numerous phases of EC unitary evolutions in which such time-nonlocal information encodings are highly robust. Concrete examples of such behavioral phases include Phases IV and V of the EC Hamiltonians of the one-qubit closed systems—see Figure 3—and their higher-order ramifications—see Figure 4.(iii) It has been shown that nonlinear unitarities can significantly enhance quantum computation [155] and quantum search algorithms [156,157,158]. The time nonlocality, the memory resource uses, and especially the EC steerability of EC unitary evolutions allow for the dissection, composition, development, and processing of quantum information in novel manners that are more complex and highly orchestrated. These features endow ECQT with the potential to enrich and enhance quantum computation, e.g., by enabling novel and structurally unprecedented quantum circuits, quantum walks, and quantum algorithms, which surpass the performance and limits of SQT.(iv) In ECQT systems of information processing, the computational units and modules can be continually redefined and updated according to the experience of the system and its subsystems (Element 2, Section 3). One can anticipate that this characteristic will bring about substantial advantages in computational processes and tasks that are highly complex. Once these points are appreciated, it becomes clear that one can develop significantly more powerful and versatile quantum information and quantum computation theories—which have the luxury of a universal, context-free framework—within ECQT. Moreover, the generalized families of EC Hamiltonians defined in Element 7 of Section 3 can not only further enrich these quantum computational systems but also provide natural candidates for novel quantum network architectures and quantum communication protocols that are more intricate and resourceful. Finally, we highlight that ECQT can naturally provide unique error correcting processes and protocols, with which the resilience of quantum computation becomes more easily achievable. Ultimately, these investigations should lead us to the computational landscape—e.g., in the sense of Ref. [159]—of ECQT and the QI, which are applicable in highly complex computations in broad disciplines and domains.
- Systematic EC generalizations of the standard theory of open quantum systems—and its different contextual realizations within —appear to be promising and can have potential profound impacts. In methodological similarity to quantum mechanics, ECQT has been initiated as a theory for closed quantum systems with their unitary evolutions. The next natural level will be moving toward its open-system descendant. The formulation begins with the EC unitary evolution of a closed composite system (composed of an open system interacting with an environment) and deducing the nonunitary dynamics of the open quantum system of interest. The closed-to-open transition in ECQT, however, brings about the following fundamental differences compared to SQT.(a) The innermost idea in ECQT is that nonunitarity (environmentally induced variations in the information content of open systems) and non-Markovianity (dynamical memory dependence) are essentially two independent aspects of general quantum behaviors in open quantum systems, including diverse contextual specializations. In fact, thinking reversely, the ECQT of closed quantum systems can be thought of as the dissipationless limit of a generalized open-system theory where—unlike SQT—non-Markovianity and nonunitarity can have their presences as independent variable aspects, while still impacting each other dynamically.(b) Indeed, this decoupling can be explicitly observed upon tracing out the environmental degrees of freedom of composite closed systems under EC unitary evolution. The EC open systems inherit their non-Markovianity from two independent sources, with the first source being the intrinsic non-Markovianity of their total closed systems and the second source—the one inducing nonunitarity—being correlations and interactions with the environment. This EC trinity of the nonunitarity and the two different kinds of non-Markovianity, in turn, results in rich mutual interactions between these variable aspects (bipartite and tripartite) beyond open-system SQT. Moreover, the EC Hamiltonian of the mother system—as, e.g., in the resolution-refined families of EC Hamiltonians presented in Section 3—typically contains inter-subsystem and environmental interactions of natures or forms that do not exist in SQT. In particular, due to the experience centricity of all these novel interactions, the information exchange between the interplaying parties (even including the mother system herself as one of these parties) can be even more constructive and orchestrated (resembling meaningful communications) than the information backflow in SQT.(c) The contextual realizations of EC open systems, relying on the above-mentioned characteristics, can naturally lead to diverse novel types of nonunitary quantum behaviors that are outstanding phenomenologically and empirically. As already witnessed in the smallest closed quantum system of one qubit, the experience centricity of the quantum dynamics leads to behavioral phases, transitions, and observable effects of diverse and unprecedented kinds. It is interesting to note that, already in the 4-dimensional open ECQT, which describes two open-system qubits, “Alice” and “Bob”, arising experientially from within their mother system, “Celine” (according to Element 2), become three-body interacting systems and generate highly rich behavioral phase diagrams. More generally, a plethora of even richer behavioral phases and observable effects emerge in more complex EC open-system evolutions. Indeed, even in a single EC open system, one has numerous phases, only some of which would qualitatively appear in a collection of distinct controlled SQT open systems. In particular, one can mention the following two natural features of EC open-system dynamics: recurrent phase revivals and complex cooperative learning on the basis of dynamically interactive exchanges of experience among agents.
- In recent years, an exciting progression of quantum computation theory has arisen in the form of quantum artificial intelligence and quantum machine learning. These disciplines apply the enriching techniques of quantum algorithms, quantum circuits, and open quantum dynamics within SQT to advance artificial intelligent systems, including machine learning and reinforcement learning [137,138]. Following the reasonings presented in Ref. [1], and in the above items (1) and (2), combined with the discussions presented in the forthcoming paragraphs about general cognitive processes, phenomena, and intelligent behaviors, we envision that ECQT can play a transformative role in all these disciplines and approaches. These ECQT applications include (structurally and functionally) novel generations of neural networks, deep learning, convolutional neural networks, Transformers, and large-language models. In a broader and even independent perspective, ECQT could lead to novel intelligent systems featuring meta-learning and meta-cognition toward artificial general intelligence.
- Prototypical spin, fermionic, and bosonic condensed matter systems such as quantum spin models, Hubbard models, and Bose–Hubbard models can be drastically generalized by allowing their internal interactions to become EC. In fact, the simplest example of this type was formulated in Ref. [1]. It would be exciting to obtain the enlarged phase diagrams and novel phase transitions of these EC condensed matter systems—for example, EC Hubbard models—whose SQT versions already capture some phenomenological aspects of strange metals, high-temperature superconductors, and emergent gauge fields. Along these lines, it would be intriguing to investigate novel aspects of nonequilibrium dynamics, effective thermalization, and especially the scrambling of information in EC quantum many-body systems.
- It is necessary to point out the possible applications of ECQT in cosmology and “beyond the standard model” physics. First, the discernment of possible ECQT observable phenomena in particle physics and cosmology mainly amounts to addressing novel empirical questions that are distinct from the established question sets traditionally addressed within the standard theories of particle physics and cosmology. Second, we highlight that the usual smallness of the empirical bounds on quantum nonlinearities does not necessarily render such ECQT-observable phenomena insignificant. Indeed, SQT perturbations with infinitesimally coupled Hermitian EC operators can accumulatively give rise to sizable observable effects over sufficiently long periods of time, which can be particularly relevant for cosmological scenarios. Moreover, as we have seen in Section 5, there are certain classes of slight EC perturbations of SQT that can generate non-negligible and phenomenologically interesting effects. One possible scenario for the investigation of such phenomena can be obtained via ECQT extensions of nonlinear quantum mechanics as in Ref. [62], possibly along the lines of Refs. [63,64].
- At the fundamental level, the QI and ECQT may lead to unprecedented, more plausible theories and models of quantum gravity. In this direction, it is primarily interesting to examine different approaches to formulating holographic models within ECQT—in particular, EC generalizations of AdS/CFT and its de Sitter-type variants [65] and matrix or tensor theories such as the BFSS model [66] and the SYK model [160] and its proposed dS-dual variants [161] stand out. Moreover, various independent proposals of quantum gravity, such as the ones introduced in Refs. [76,94,162], could benefit from suitable EC generalizations. In addition, revisiting quantum-information-theoretic aspects of causal horizons, including black holes and observer-dependent horizons, within the framework of EC unitary processing and computing sounds promising in the enhancement of existing models or the development of new models and formalisms. Finally, understanding that the ultimate and the only perfect closed system is the universe itself, it is natural to advance toward richer models of quantum cosmology using the resolution-refined versions of ECQT. Moving beyond this, one can use the QI and ECQT to revisit and reinvigorate formulations of grand unified theories, particularly within the context of “it-from-(qu)bit” paradigms—for example, in the spirit of Refs. [163,164].Thus far, we have suggested plausible applications of ECQT in various disciplines of quantum physics; however, these constitute a small fraction of the phenomenological coverage of ECQT and the QI. We are aware that there have been several remarkable investigations into diverse ways to generalize quantum mechanics; see, e.g., Refs. [27,28,43,165,166,167,168,169,170,171,172,173,174,175,176]. However, the overwhelming majority of this literature is marked by the following three characteristics: (i) it has been basically presumed (sometimes implicitly) that quantum theory is—by context—quantum mechanics, including its finite-dimensional reductions and quantum field-theoretical formulations; (ii) these generalizations are mostly motivated by the search for more fulfilling theories of quantum gravity with a sound conceptual basis and sharp, falsifiable, and predictive phenomenological outreach; (iii) typically, they are marked by giving precedence to structural generalizations of SQT that are mainly mathematical or kinematical or based on the formalism of measurement operators.However, the standpoints of ECQT and the QI are starkly different. In this regard, there are several major points that should be highlighted.(a) Quantum theory is not quantum mechanics. Quantum mechanics is quantum theory tailored to a specific context, i.e., the organizational theme: spacetime and spatiotemporal propagations, correlations, interactions, and observables. Otherwise, quantum theory—the theory of general quantum behaviors—is a multi-context grand theory that is vastly larger, richer, and more flexible than quantum mechanics.(b) Quantum gravity and, more generally, emergent spacetime have neither any privileged compass role nor any fundamental phenomenological precedence to guide generalizations of quantum mechanics.(c) In transcending quantum mechanics within ECQT, the primary direction in the generalization of SQT is dynamics rather than kinematics—merging the time evolution unitarity with non-Markovian experience centricity. Any other possible kinematical generalizations (including observables and measurements) should follow this dynamical generalization and be based on the context.(d) The fact that quantum mechanics has taken the role of identifying and representing quantum theory is mainly a historical (not principal) point. Quantum mechanics coexists and interacts with other structurally different context-based quantum theories that are independent and capable of predictive empirical success across domains and phenomena beyond the reach of traditional quantum physics. Indeed, the abstract fundamental nature of —participatory-agentive “it-from-(qu)bit” developing diverse contexts—together with the associated flexibility and generality of ECQT formalisms, places alternative contextual specializations and phenomenological domains of quantum theory on an equal footing. In this light, broader applications of ECQT are outlined selectively as follows.
- Formulating (“natural” or artificial) cognitive science [177,178]—that is, theoretical and empirical studies of general mental, cognitive, and intelligent phenomena and behaviors—and predicting its empirical observables are among the natural applications of ECQT. As such, cognitive quantum theories, as empirically predictive theories of general quantum intelligence and cognition, should correspond to particular context-based nodes of . By general agentive intelligence and cognition, we especially mean that the agent is able to cognize, form abstract representations of, and anticipate diverse (internal or external) situations; have meaningful thoughts, emotions, goal orientations, and decision-for-action abilities; process and (in principle) solve a general spectrum of problems of diverse kinds and levels, which, in particular, require general-scope learning, meta-learning, abstraction, predictions, and continual self-updating; and meaningfully communicate and interact with other agents. As we see and now explain, ECQT naturally leads to a universal theory of (emergent) general intelligent and cognitive phenomena and behaviors. One general prescription to formulate these phenomena and behaviors within ECQT is outlined in what follows.Consider a sufficiently complex (“natural” or artificial) classical many-body system , regardless of its microscopic units, interactions, and architecture. Moreover, suppose that (as is typical) interacts with a dynamical, sufficiently complex environment . To be general, it is assumed that - interactions can switch between “off” (passive) and “on” (active) states of arbitrary duration and that there can be considerable strength modulations or type variations in the environmental interactions during the “on” state. In general, can also include subsystems similar to . We stress that, as supposed, and form a classical closed system in total.We now suppose that the “mental” states of an emergent cognizant agent —whose cognitive behaviors fall within the broad definition of general quantum behaviors in (Section 6)—have (somehow) emerged from the internal mechanisms of . As such, the (classical) pair induces an interacting EC closed quantum system whose abstract information-theoretic degrees of freedom constitute the mental states of in the form of a complementary (and generally time-dependent) pair of intentional–extrospective open quantum systems. The intentional subsystem “” is composed of those quantum information degrees of freedom that constitute both introspective and intentional sub-states of ’s mind—those especially associated with ’s behavioral choices and their (re)organizations. The extrospective subsystem “” is composed of the complementary subset of quantum information degrees of freedom constituting ’s mental states by which—based on both perceived sensory stimuli and behavioral outcomes—the inferred internal representations, namely “cognitive maps”, together with predictive formal models of are formed. As such, , and , where and accommodate, respectively, the evolving quantum states and , identified as follows. The intentional sub-states encode ’s chosen probability distribution across its behavioral modes—’s behavioral “policy”—at every present moment t. These behavioral encodings can be time-local, namely inside , or time-nonlocal, namely within —for example, encoded in the state history n-point functions . The extrospective sub-states encode, at every present moment t, the last updated cognitive map that has (passively or actively) inferred about .There are seven points in order about the characterization of quantum degrees of freedom and their state spaces as presented above. (i) The time evolutions of extrospective and intentional sub-states are both centered on the integrated experiences of and follow Bayesian probabilistic reasoning under uncertainties, since we assume that, at typical moments t, has only partial knowledge of , due to complexity, practical, or epistemic restrictions. (ii) The extrospective Hilbert space can correspond to the effective low-dimensional reduction of an otherwise large Hilbert space, capturing only those environmental aspects that cares about. (iii) ’s cognitive processes (even when their motivations or contents have arisen environmentally) can also occur during the “off” state, resembling dreaming states or seclusive contemplative states of ’s mind. (iv) As is typical, there can be within the total closed system a set of noise variables that are particularly associated with the involved complexities. (v) As can include a number of subsystems , the considered agent can know about and interact with other agents in its surrounding world. We, however, focus on the single-agent scenario, while we emphasize that multi-agent scenarios have substantially enriching features. (vi) The time variable with respect to which the mental states and cognitive phenomena of the emergent evolve is typically distinct from the time variable with which the physical closed system evolves. This time variable, which can be called cognitive time, can be discrete or continuous and arises from the internal mechanisms of the physical system . The point is that this cognitive time is emergent and arises across higher levels. (vii) The cognitive bipartitioning of the mental Hilbert space into the subspace factors and can typically be time-dependent and experiential, as explained in Section 3. Moreover, these two Hilbert spaces and can further take experiential resolutions into cognitively meaningful subsystem Hilbert spaces depending on the empirical specificities.As we have laid out, the cognizant agent chooses its behaviors by going through introspective–extrospective cognitive computational processes that are centered on its (sensory and action–outcome) experiences. The adequate formulation of such general cognitive processes reflects the unitary or isometric time evolutions of ’s mental states , generated by the instantaneous Hamiltonians , which are EC, -resolution refined, and goal-oriented discriminative. In other words, the quantum information degrees of freedom constituting ’s mental states in evolve based on instantaneous Hamiltonians , which (at every present moment t) are directly (re)made from the triplet of the past-to-present quantum states , or the information contained therein. Thus, the structure of the cognitive EC Hamiltonians of ’s mental states, at every present moment of the (continuous or discrete) time “t”, reads asThe character specifications on the first and second lines are as follows: and are defined as in Elements 1 and 2; and are, respectively, sets of noise variables and state-history-dependent operators, some of which are induced by - interactions; are a set of goal operators depending on some subjective value parameters ; and are projection operators corresponding to the favorite eigenstates of the goal operators . In the third line of Equation (126), we have the same operators but now reduced to the behavioral Hilbert space , while denotes the history of ’s behavioral outcomes or “rewards” up to the present moment t.The cognitive EC Hamiltonians (126) can particularly be in the form of the three major classes introduced in Element 3 of Section 3. Accordingly, the forms of ’s EC Hamiltonians can (in part) resemble the numerous explicit examples throughout Elements 6–8 of Section 3. The central marker of the agent’s intelligence—the recurrent organization of its behavior and policy updates—is mirrored in the experiential recreations of the instantaneous operators , which are conjunct with or obtainable from the EC Hamiltonian upon a relevant state-space reduction . Finally, we wish to remark on cognitive quantum theories in that can be derived from ECQT.(i) Thus far, we have considered that the physical system and its environment are classical. Aside from concreteness, this assumption is motivated by the foremost examples of representing the body and brain, or, in the “artificial” realm, a sufficiently advanced classical neural network, and representing a large physical world surrounding it. This assumption is, however, by no means necessary. In fact, and can both or either be quantum mechanical systems or any type of classical–quantum hybrid. One returns in all of these cases to the central idea of the emergence paradigm [179,180,181], according to which a theory that describes the observable properties of a system at higher levels of organization in complex many-body systems can be a theory whose defining degrees of freedom, their interactions, and the dynamics are by nature distinct from their macroscopic ones. Cognitive quantum theories seek to formulate general cognitive processes and predict their phenomena and observable quantities, which are emergent at higher levels.(ii) We have stated that emergent cognitive processes respect the principles of general quantum behaviors (Section 6), such that the ECQT formalism in Section 3 formulates them. We now highlight that these assumptions should not be taken as being restrictive. Indeed, it is plausible to consider cognitive processes that, across diverse internal–external situations, can appropriately be quantum, classical, or simultaneous mixtures of them. Still, all these cognitive processes can be formulated, in appropriate ways, within ECQT. Even when cognitive processes are purely classical, they can be flexibly formulated as classical derivatives of their general EC formulations (126).(iii) In SQT treatments of agentive behavioral processes, individual decision-making events are typically incorporated as quantum measurement operations. We now highlight that the ECQT formalism provides various additional ways to realize decisional action selections and events alike, which (a) are measurement-free and decoherence-scenario-independent; (b) naturally arise out of the experience centricity of quantum state evolutions, without external controls and without fine-tuning; and (c) can bring about substantial utility in the formulation of cognitive processes outlined in Equation (126). This leverage comes about because the total states, sub-states, and state history n-point autocorrelations (in all of which cognitive and behavioral data can be encoded appropriately) can develop harmoniously throughout their EC evolutions’ recurrent patterns of (perfect or effective) localization–delocalization profiles. One observes this fact in the one-qubit behavioral analyses in Section 5, throughout Section 5.1, Section 5.2, Section 5.3, Section 5.4 and Section 5.5, while appreciating that such behavioral features become more diverse and flexible in one-qubit scenarios with momentarily reconfigurable EC Hamiltonian operators () and (even substantially more) in EC multi-qubit scenarios. This point serves as a clear example of the broad technical possibilities that the ECQT formalism provides in modeling general and context-based quantum behaviors.Following the formulation of general cognitive processes within ECQT portrayed in Equation (126), one can move on to extract cognitive quantum theories as specific nodes of that can predict cognitive observables and phenomena successfully. These extractions require the discernment of additional principles beyond those of general quantum behaviors (presented in Section 6), which are specific to the defining context of (general or special) cognition. As the result of these complementary principles, the cognitive EC Hamiltonian (126) admits additional constraints and structures.In recent times, several exciting investigations and proposals for quantum-theoretical descriptions of cognitive processes and behaviors, mathematical psychology, human decision making, and consciousness have been put forth—see, e.g., Refs. [182,183,184,185,186,187,188,189,190,191,192,193,194]. As we envision, the contributions of this paper, together with Ref. [1], to the natural evolution of this profound research field—which develops a constructive dialog between quantum physics and cognitive science—are promising and substantial. From the perspective of ECQT and the QI, the cognitive quantum theories, namely distinct nodes of following the above general recipe (126), should not be taken merely as mathematical modeling. Rather, we highlight that (i) these cognitive quantum theories, being ECQT offspring, do necessarily differ from SQT in several drastic ways; (ii) what these theories (based on ECQT) are to the higher-level emergent realm of cognitive science and phenomena is what the standard theory of particle physics (based on quantum mechanics) is to the lower-level realm of elementary particles and their spatiotemporal phenomena; and (iii) by conception and construction, cognitive quantum theories are genuine quantum theories in which general quantum behaviors (Section 6) specialize in the general context of mental, cognitive, and intelligent processes and phenomena and (admitting all the involved complexities) are able to predict their empirical observables.
- The versatile and natural applications of ECQT—the major component of the QI that formulates abstract information-theoretic general and context-based quantum behaviors—can include quantum formulations of diverse formal and phenomenological areas in broader domains and disciplines such as linguistics, sociophysics, economics, and game theory. Earlier investigations have focused on mostly the mathematical modeling of such phenomena within (closed- and open-system) SQT—see, e.g., Refs. [195,196,197,198]. Advancing further, one can harness the advantageous predictive formulations of these complex phenomena, processes, and their observables within the profound generalization of SQT offered by ECQT. Moreover, novel means of formulating, modeling, or behaviorally simulating and computing nonlinear classical dynamical systems featuring chaos or turbulence, such as weather forecasts, can be investigated within ECQT. Finally, we point to the promising applications of ECQT in modeling classical probabilistic systems such as stochastic time series and hidden Markov systems.
- –
- An intriguing inter-theoretical inquiry is to address whether and how ECQT can emerge from SQT in novel Wilsonian frameworks as a larger quantum theory that stands on its own.
- –
- There have been various epistemic derivations of quantum mechanics and particular nonlinear deformations of SQT, or at least some of their main features, from classical statistical theories—see, e.g., Refs. [199,200,201]. Given the primacy of the Bayesian nature of EC quantum states, it would be interesting to obtain similar derivations of EC closed and open quantum systems.
- –
- One immediate direction to investigate is experimental realizations of EC unitary evolutions and the descendant open-system dynamics. Indeed, our proof-of-principle quantum simulation protocol presented in Section 2 already demonstrates that a considerable class of phenomenologically interesting EC unitary evolutions can, in principle, be simulated using novel SQT quantum circuits. However, one can seek to design alternative, more resource-efficient quantum simulation networks with enhanced performance and broader coverage of ECQT processes. Independently, based on the understanding of EC quantum behaviors as higher-level functional emergences and their prevalence in natural systems, a promising alternative way to experimentally realize ECQT processes and phenomena is by synthesizing machines that—e.g., in the form of classical neural networks—serve as artificial cognitive connectomes.
- –
- It would be significant to explore novel features of entanglement dynamics under EC unitary evolutions and their open-system derivatives. For example, one can begin with two-qubit EC quantum systems or the ECQT versions of the Heisenberg or Hubbard models.
- –
- It it natural to discern ECQT gates, circuits, and algorithms motivated as follows. From an abstract general perspective, information-theoretic computations can ultimately be reduced to a finite number of elementary input–output operations, which, upon composing the developed modules of information, generate new processed information modules. As such, one envisions abstract quantum circuits as formal dynamical systems of information-theoretic grammar and meaningful text generation, which function based on experience centricity. Along these lines, ECQT algorithms can be naturally developed, resembling transitions from Turing machines to computational circuits in computer science. Moreover, in the context of quantum cognitive theories, mental and cognitive processes, and especially thought development, should naturally be based on such abstract elementary gates and circuits. In the paradigm of computational cognition, discerning versatile, finite formal systems of cognitive computation is also practically relevant due to the finiteness of the available physical resources for the underlying machines, such as the brain. Consequently, this leads to the generalization and enhancement of standard theories of quantum logic and quantum computation within ECQT. Independently, from an experimental point of view, it would be interesting to design and investigate gates, circuits, and networks for ECQT.
- –
- ECQT can generate distinct spatiotemporal sub-theories in , which nevertheless are larger and more flexible than in quantum mechanics. This requires sub-theories of ECQT with spatiotemporal causality, where one example could be EC extensions of causal nonlinear quantum mechanics as in Ref. [62]. A fundamental way to develop such causal spatiotemporal sub-theories is to formulate abstract information-theoretic degrees of freedom whose EC interactions are constrained by appropriate adjacency matrices of an abstract incomplete graph. In such scenarios, there can be analog variants of Lieb–Robinson bounds—especially their abstract variants [202]—from which spatiotemporal locality and causality can emerge. It is evident that, from a technical point of view, some structural elements of the so-called “quantum graphity” models can be relevant [89].
- –
- It is evident that ECQT can generate various novel families of classical theories in its appropriate mechanisms or limits of classicalization. For example, unprecedented models of classical random systems can be deduced from the classical limits of the EC Hamiltonians and their generalizations and ramifications, as presented in Section 5 throughout Section 5.1, Section 5.2, Section 5.3, Section 5.4 and Section 5.5. Along these lines, it would be interesting to explicitly derive various deformed versions of the Fokker–Planck equations, Langevin equations, and classical neural networks, within ECQT classicalizations. Independently, EC classicalization procedures can lead to novel classical nonlinear differential equations—such as drastically deformed Navier–Stokes equations—especially for hydrodynamics, which could help to capture a range of phenomena in fluid systems. Moreover, it is particularly relevant to derive purely classical formulations of cognitive processes and intelligent behaviors obtainable from the classical limits of general cognitive EC Hamiltonians (126).
- –
- In the present paper, as a matter of convenience, we have focused on finite-dimensional quantum systems even in the very context of SQT. The reason has been three-fold. First, the message and main results of this paper are insensitive to the dimensionality of the Hilbert space of the system. Second, finite-dimensional quantum systems are more crucial in abstract information-theoretic computations and inferential versions of quantum theory. However, certainly, it is interesting to directly investigate the distinct properties of EC closed and open quantum systems with infinitely many degrees of freedom. Furthermore, formulating EC quantum field theories requires systems with continua of degrees of freedom.
- –
- Some crystalized features of quantum mechanics, such as the no-cloning theorem [203] and violations of Bell’s inequalities [204], should be revisited within the much broader scope of ECQT and the QI. As we recall, by conception and construction, ECQT formulates emergent or fundamental general quantum behaviors alongside its various context-based specializations, as presented in Section 6. Such behaviors, being typically marked by experience centricity, are described by generalized quantum dynamics in which the inherent time-nonlocality and nonlinearity are merged with isometry and unitarity. Thus, since some of the assumptions or structural settings underlying quantum no-cloning and Bell’s inequalities lose fundamental ground in ECQT, a major revisit of these quantum mechanical properties becomes relevant. The quantum no-cloning theorem has already been revisited in works such as Ref. [205], while experience centricity provides a much larger space for scrutiny and generalization. Furthermore, we highlight that the ECQT reconsiderations of these aspects can be double-faceted, bringing distinctive technicalities with conceptual foundations. In particular, one notes in revisiting Bell’s inequalities in cognitive quantum theories formulated within the general formulation (126) the following points. Within the totality of the abstract information-theoretic degrees of freedom that comprise the emergent mental states in (regardless of their partitioning into introspective–extrospective subsystems), the traditional boundaries between ontic vs. epistemic and local vs. nonlocal characteristics disappear.
- –
- All foundational landmarks and techniques of SQT can be naturally revisited in ECQT. This list especially includes EC generalizations of uncertainty relations [206,207] for general and context-based quantum behaviors; quantum reference frames [208,209,210,211,212] formulated within ECQT and the QI; formulating second-quantized (and third-quantized) descendants of ECQT; and developing EC quantum field theories.
- –
- Following the significance of the adiabatic evolutions, processes, and computations in quantum systems, it is relevant both phenomenologically and technologically to formulate and investigate EC adiabatic phenomena and investigate their properties. Moreover, in a similar vein but independently, it is of immediate interest and relevance to formulate and investigate generalized quantum walks [213] with EC unitarity and their open-system variants.
- –
- Quantifying experience centricity (i.e., the interfusion of non-Markovianity and unitarity) in the generalized quantum dynamics proposed in Ref. [1] and in the present paper is of special interest. This requires the formulation of observables that can witness or measure, locally or globally, deviations of EC unitary evolution away from SQT.
- –
- To initiate broader applications of ECQT in domains beyond the traditional disciplines of SQT, as we have explained in this section, we suggest formulating and investigating sufficiently rich models of (a) human decision making within ECQT to advance earlier models, such as those of Refs. [183,185]; (b) quantum games [214] enriched within ECQT; and (c) EC social phenomena, expanding on earlier models, e.g., as in Ref. [215]. Moreover, it is of special interest to formulate and investigate self-organized complex structures in multi-agent decision-making networks—such as in Ref. [216]—within ECQT.
- –
- In this work and in Ref. [1], we have focused on investigating the behaviors of EC Hamiltonians whose chosen experience resources (chosen state histories) do not involve subsystem resolution refinement. It is crucial to advance our understanding of the distinctive behaviors of EC evolutions based on resolution-refined Hamiltonians for closed quantum systems [217].
8. Closing Remarks on a Portal to a Paradigm Shift
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. A Useful Identity
- (i)
- : The real-valued -dimensional vector defined aswhose elements areHere, superscript T denotes transposition.
- (ii)
- : The -dimensional real-valued vector that consists of all couplings of the EC Hamiltonian,
- (iii)
- : The state-history-made real-valued matrix, which collects all traces of the pairwise products of the state history monomials and whose elements areThis matrix provides a dynamical EC characterization of the closed quantum system. Hence, its elements can be fully determined as specific time-dependent functions of the state history two-point functions .
References
- Tavanfar, A.; Parvizi, A.; Pezzutto, M. Unitary evolutions sourced by interacting quantum memories: Closed quantum systems directing themselves using their state histories. Quantum 2023, 7, 1007. [Google Scholar] [CrossRef]
- Kadanoff, L.P. More is the same; phase transitions and mean field theories. J. Stat. Phys. 2009, 137, 777. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864. [Google Scholar] [CrossRef]
- White, S.R. Density Matrix Formulation for Quantum Renormalization Groups. Phys. Rev. Lett. 1992, 69, 2863. [Google Scholar] [CrossRef]
- Rahimi-Keshari, S.; Ralph, T.C.; Caves, C.M. Sufficient conditions for efficient classical simulation of quantum optics. Phys. Rev. X 2016, 6, 021039. [Google Scholar] [CrossRef]
- Feynman, R.P. Simulating physics with computers. Int. J. Theor. Phys. 1982, 21, 467. [Google Scholar] [CrossRef]
- Lloyd, S. Universal quantum simulators. Science 1996, 273, 1073. [Google Scholar] [CrossRef]
- Altman, E.; Brown, K.R.; Carleo, G.; Carr, L.D.; Demler, E.; Chin, C.; DeMarco, B.; Economou, S.E.; Eriksson, M.A.; Fu, K.-M.C.; et al. Quantum simulators: Architectures and opportunities. PRX Quantum 2021, 2, 017003. [Google Scholar] [CrossRef]
- Ekert, A.K.; Alves, C.M.; Oi, D.K.L.; Horodecki, M.; Horodecki, P.; Kwek, L.C. Direct Estimations of Linear and Nonlinear Functionals of a Quantum State. Phys. Rev. Lett. 2002, 88, 217901. [Google Scholar] [CrossRef]
- Hagan, M.; Wiebe, N. Composite quantum simulations. arXiv 2022, arXiv:2206.06409. [Google Scholar] [CrossRef]
- Poulin, D.; Qarry, A.; Somma, R.; Verstraete, F. Quantum Simulation of Time-Dependent Hamiltonians and the Convenient Illusion of Hilbert Space. Phys. Rev. Lett. 2011, 106, 170501. [Google Scholar] [CrossRef]
- Lloyd, S.; Mohseni, M.; Rebentrost, P. Quantum principal component analysis. Nat. Phys. 2014, 10, 631. [Google Scholar] [CrossRef]
- Kjaergaard, M.; Schwartz, M.E.; Greene, A.; Samach, G.O.; Bengtsson, A.; O’Keeffe, M.; McNally, C.M.; Braumüller, J.; Kim, D.K.; Krantz, P.; et al. Demonstration of density matrix exponentiation using a superconducting quantum processor. Phys. Rev. X 2022, 12, 011005. [Google Scholar] [CrossRef]
- Richard, J.-P. Time delay systems: An overview of some recent advances and open problems. Automatica 2003, 39, 1667. [Google Scholar] [CrossRef]
- Ericsson, M. Geometric and Topological Phases with Applications to Quantum Computation. Ph.D. Thesis, Uppsala University, Uppsala, Sweden, 2002. [Google Scholar]
- Oi, D.K.L. Interference of Quantum Channels. Phys. Rev. Lett. 2003, 91, 067902. [Google Scholar] [CrossRef] [PubMed]
- Oi, D.K.L.; Åberg, J. Fidelity and Coherence Measures from Interference. Phys. Rev. Lett. 2006, 97, 220404. [Google Scholar] [CrossRef]
- Kanjilal, S.; Pandey, V.; Pati, A.K. Entanglement meter: Estimation of entanglement with single copy in interferometer. New J. Phys. 2023, 25, 043026. [Google Scholar] [CrossRef]
- Marvian, I.; Lloyd, S. Universal quantum emulator. arXiv 2016, arXiv:1606.02734. [Google Scholar]
- Alicki, R.; Fannes, M.; Pogorzelska, M. Quantum generalized subsystems. Phys. Rev. A 2009, 79, 052111. [Google Scholar] [CrossRef]
- Duarte, C.; Carvalho, G.D.; Bernardes, N.K.; de Melo, F. Emerging dynamics arising from coarse-grained quantum systems. Phys. Rev. A 2017, 96, 032113. [Google Scholar] [CrossRef]
- Singh, A.; Carroll, S.M. Quantum decimation in Hilbert space: Coarse graining without structure. Phys. Rev. A 2018, 97, 032111. [Google Scholar] [CrossRef]
- Agon, C.; Balasubramanian, V.; Kasko, S.; Lawrence, A. Coarse grained quantum dynamics. Phys. Rev. D 2018, 98, 025019. [Google Scholar] [CrossRef]
- Kabernik, O.; Pollack, J.; Singh, A. Quantum state reduction: Generalized bipartitions from algebras of observables. Phys. Rev. A 2020, 101, 032303. [Google Scholar] [CrossRef]
- Cotler, J.; Strominger, A. The universe as a quantum encoder. arXiv 2022, arXiv:2201.11658. [Google Scholar]
- Kornyak, V.V. Mathematical modeling of finite quantum systems. In Mathematical Modeling and Computational Science, MMCP 2011; Adam, G., Buša, J., Hnatič, M., Eds.; Springer: Berlin, Germany, 2012; p. 79. [Google Scholar]
- Kornyak, V. Modeling quantum behavior in the framework of permutation groups. EPJWeb Conf. 2018, 173, 01007. [Google Scholar]
- Banks, T. Finite deformations of quantum mechanics. arXiv 2020, arXiv:2001.07662. [Google Scholar]
- Pitaevskii, L.; Stringari, S. Bose-Einstein Condensation; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Weinberg, S. Precision Tests of Quantum Mechanics. Phys. Rev. Lett. 1989, 62, 485. [Google Scholar] [CrossRef]
- Weinberg, S. Testing quantum mechanics. Ann. Phys. 1989, 194, 336. [Google Scholar] [CrossRef]
- Wheeler, J.A. The computer and the universe. Int. J. Theor. Phys. 1982, 21, 557. [Google Scholar] [CrossRef]
- Wheeler, J.A. World as system self-synthesized by quantum networking. IBM J. Res. Dev. 1988, 32, 4. [Google Scholar] [CrossRef]
- Wheeler, J.A. Information, physics, quantum: The search for links. In Complexity, Entropy, and the Physics of Information; Zurek, W.H., Ed.; Addison-Wesley: Redwood, CA, USA, 1990; p. 354. [Google Scholar]
- Fuchs, C.A.; Stacey, B.C. Qbism: Quantum theory as a hero’s handbook. In Proceedings of the International School of Physics “Enrico Fermi”; IOS Press: Amsterdam, The Netherlands, 2019; Volume 197, p. 133. [Google Scholar]
- Fuchs, C.A. On participatory realism. In Information and Interaction; Durham, I., Rickles, D., Eds.; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Fuchs, C.A. Quantum foundations in the light of quantum information. In Decoherence and its Implications in Quantum Computation and Information Transfer; Gonis, A., Turchi, P.E.A., Eds.; IOS Press: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Engelbrecht, A.P. Computational Intelligence: An Introduction; Wiley: Chichester, UK, 2007. [Google Scholar]
- Kochenderfer, M.J.; Wheeler, T.A.; Wray, K.H. Algorithms for Decision Making; MIT Press: London, UK, 2022. [Google Scholar]
- Gisin, N. Weinberg’s non-linear quantum mechanics and supraluminal communication. Phys. Lett. A 1990, 143, 1. [Google Scholar] [CrossRef]
- Peres, A. Nonlinear Variants of Schrödinger’s Equation Violate the Second Law of Thermodynamics. Phys. Rev. Lett. 1989, 63, 1114. [Google Scholar] [CrossRef] [PubMed]
- Jordan, T.F. Why quantum dynamics is linear. J. Phys. Conf. Ser. 2009, 196, 012010. [Google Scholar] [CrossRef]
- Mielnik, B. Generalized quantum mechanics. Commun. Math. Phys. 1974, 37, 221. [Google Scholar] [CrossRef]
- Weinberg, S. Weinberg replies. Phys. Rev. Lett. 1989, 63, 1115. [Google Scholar] [CrossRef]
- Polchinski, J. Weinberg’s Nonlinear Quantum Mechanics and the Einstein-Podolsky-Rosen Paradox. Phys. Rev. Lett. 1991, 66, 397. [Google Scholar] [CrossRef]
- Czachor, M. Mobility and non-separability. Found. Phys. Lett. 1991, 4, 351. [Google Scholar] [CrossRef]
- Jordan, T.F. Reconstructing a nonlinear dynamical framework for testing quantum mechanics. Ann. Phys. 1993, 225, 83. [Google Scholar] [CrossRef]
- Czachor, M. Nonlocal-looking equations can make nonlinear quantum dynamics local. Phys. Rev. A 1998, 57, 4122. [Google Scholar] [CrossRef]
- Bóna, P. Extended quantum mechanics. Acta Phys. Slov. 2000, 50, 1. [Google Scholar]
- Aerts, D.; Czachor, M.; Durt, T. (Eds.) Probing the Structure of Quantum Mechanics: Nonlinearity, Nonlocality, Computation and Axiomatics; World Scientific: Singapore, 2002. [Google Scholar]
- Ferrero, M.; Salgado, D.; Sánchez-Gómez, J.L. Nonlinear quantum evolution does not imply supraluminal communication. Phys. Rev. A 2004, 70, 014101. [Google Scholar] [CrossRef]
- Ferrero, M.; Salgado, D.; Sánchez-Gómez, J.L. On nonlinear evolution and supraluminal communication between finite quantum systems. Int. J. Quantum Inf. 2005, 3, 257. [Google Scholar] [CrossRef]
- Kent, A. Nonlinearity without superluminality. Phys. Rev. A 2005, 72, 012108. [Google Scholar] [CrossRef]
- Jordan, T.F. Assumptions that imply quantum dynamics is linear. Phys. Rev. A 2006, 73, 022101. [Google Scholar] [CrossRef]
- Pienaar, J. Causality Violation and Nonlinear Quantum Mechanics. Ph.D. Thesis, The University of Queensland, Melbourne, Australia, 2013. [Google Scholar]
- Kent, A. Testing quantum gravity near measurement events. Phys. Rev. D 2021, 103, 064038. [Google Scholar] [CrossRef]
- Beretta, G.P. Nonlinear extensions of Schrödinger-von Neumann quantum dynamics: A list of conditions for compatibility with thermodynamics. Mod. Phys. Lett. A 2005, 20, 977. [Google Scholar] [CrossRef]
- Helou, B.; Chen, Y. Different interpretations of quantum mechanics make different predictions in non-linear quantum mechanics, and some do not violate the no-signaling condition. J. Phys. Conf. Ser. 2017, 880, 012021. [Google Scholar] [CrossRef]
- Giulini, D.; Großardt, A.; Schwartz, P.K. Coupling quantum matter and gravity. arXiv 2022, arXiv:2207.05029. [Google Scholar]
- Rembieliński, J.; Caban, P. Nonlinear evolution and signaling. Phys. Rev. Res. 2020, 2, 012027. [Google Scholar] [CrossRef]
- Ray, R.K.; Beretta, G.P. No-signaling in steepest entropy ascent: A nonlinear non-local non-equilibrium quantum dynamics of composite systems. arXiv 2023, arXiv:2301.11548. [Google Scholar]
- Kaplan, D.E.; Rajendran, S. Causal framework for nonlinear quantum mechanics. Phys. Rev. D 2022, 105, 055002. [Google Scholar] [CrossRef]
- Polkovnikov, M.; Gramolin, A.V.; Kaplan, D.E.; Rajendran, S.; Sushkov, A.O. Experimental Limit on Non-Linear State- Dependent Terms in Quantum Theory. Phys. Rev. Lett. 2023, 130, 040202. [Google Scholar] [CrossRef]
- Broz, J.; You, B.; Khan, S.; Häffner, H.; Kaplan, D.E.; Rajendran, S. Test of Causal Nonlinear Quantum Mechanics by Ramsey Interferometry with a Trapped Ion. Phys. Rev. Lett. 2023, 130, 200201. [Google Scholar] [CrossRef] [PubMed]
- Maldacena, J. The large-N limit of superconformal field theories and supergravity. Int. J. Theor. Phys. 1999, 38, 1113. [Google Scholar] [CrossRef]
- Banks, T.; Fischler, W.; Shenker, S.H.; Susskind, L. M theory as a matrix model: A conjecture. Phys. Rev. D 1997, 55, 5112. [Google Scholar] [CrossRef]
- Seiberg, N. Emergent spacetime. In The Quantum Structure of Space and Time—Proceedings of the 23rd Solvay Conference on Physics, Brussels, Belgium, 1–3 December 2005; Gross, D., Henneaux, M., Sevrin, A., Eds.; World Scientific: Singapore, 2007; p. 163. [Google Scholar]
- Raamsdonk, M.V. Building up spacetime with quantum entanglement. Gen. Relativ. Gravit. 2010, 42, 2323. [Google Scholar] [CrossRef]
- Swingle, B. Entanglement renormalization and holography. Phys. Rev. D 2012, 86, 065007. [Google Scholar] [CrossRef]
- Nozaki, M.; Ryu, S.; Takayanagi, T. Holographic geometry of entanglement renormalization in quantum field theories. J. High Energy Phys. 2012, 2012, 193. [Google Scholar] [CrossRef]
- Hartnoll, S.A.; Lucas, A.; Sachdev, S. Holographic Quantum Matter; MIT Press: Cambridge, UK, 2016. [Google Scholar]
- Bao, N.; Cao, C.; Carroll, S.M.; Chatwin-Davies, A. de Sitter space as a tensor network: Cosmic no-hair, complementarity, and complexity. Phys. Rev. D 2017, 96, 123536. [Google Scholar] [CrossRef]
- Lee, S.S. Emergent gravity from relatively local Hamiltonians and a possible resolution of the black hole information puzzle. J. High Energy Phys. 2018, 2018, 43. [Google Scholar] [CrossRef]
- Lee, S.S. A model of quantum gravity with emergent spacetime. J. High Energy Phys. 2020, 2020, 70. [Google Scholar] [CrossRef]
- Cao, C.; Carroll, S.M.; Michalakis, S. Space from Hilbert space: Recovering geometry from bulk entanglement. Phys. Rev. D 2017, 95, 024031. [Google Scholar] [CrossRef]
- Carroll, S.M. Completely discretized, finite quantum mechanics. arXiv 2023, arXiv:2307.11927. [Google Scholar] [CrossRef]
- Oriti, D. Approaches to Quantum Gravity: Toward a New Understanding of Space, Time and Matter; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Oriti, D. Disappearance and emergence of space and time in quantum gravity. Stud. Hist. Philos. Mod. Phys. 2014, 46, 186. [Google Scholar] [CrossRef]
- Patton, C.M.; Wheeler, J.A. Is physics legislated by cosmogony? In Quantum Gravity: An Oxford Symposium; Isham, C.J., Penrose, R., Sciama, D.W., Eds.; Clarendon Press: Oxford, UK, 1975; p. 538. [Google Scholar]
- Wheeler, J.A. Pregeometry: Motivations and prospects. In Quantum Theory and Gravitation; Marlow, A.R., Ed.; Academic Press: New York, NY, USA, 1980. [Google Scholar]
- Dadić, I.; Pisk, K. Dynamics of discrete-space structure. Int. J. Theor. Phys. 1980, 18, 345. [Google Scholar] [CrossRef]
- Bombelli, L.; Lee, J.; Meyer, D.; Sorkin, R.D. Space-Time as a Causal Set. Phys. Rev. Lett. 1987, 59, 521. [Google Scholar] [CrossRef]
- Antonsen, F. Pregeometry. Master’s Thesis, University of Copenhagen, Copenhagen, Denmark, 1992. [Google Scholar]
- Surya, S. The causal set approach to quantum gravity. Living Rev. Relativ. 2019, 22, 5. [Google Scholar] [CrossRef]
- Hawkins, E.; Markopoulou, F.; Sahlmann, H. Evolution in quantum causal histories. Class. Quantum Grav. 2003, 20, 16. [Google Scholar] [CrossRef]
- Lloyd, S. A theory of quantum gravity based on quantum computation. arXiv 2005, arXiv:quant-ph/0501135. [Google Scholar]
- Konopka, T.; Markopoulou, F.; Severini, S. Quantum graphity: A model of emergent locality. Phys. Rev. D 2008, 77, 104029. [Google Scholar] [CrossRef]
- Hamma, A.; Markopoulou, F.; Premont-Schwarz, I.; Severini, S. Lieb-Robinson Bounds and the Speed of Light from Topological Order. Phys. Rev. Lett. 2009, 102, 017204. [Google Scholar] [CrossRef] [PubMed]
- Hamma, A.; Markopoulou, F.; Lloyd, S.; Caravelli, F.; Severini, S.; Markström, K. Quantum Bose-Hubbard model with an evolving graph as a toy model for emergent spacetime. Phys. Rev. D 2010, 81, 104032. [Google Scholar] [CrossRef]
- Crowther, K. Appearing Out of Nowhere: The Emergence of Spacetime in Quantum Gravity. Ph.D. Thesis, The University of Sydney, Sydney, Australia, 2014. [Google Scholar]
- Trugenberger, C.A. Combinatorial quantum gravity: Geometry from random bits. J. High Energy Phys. 2017, 2017, 45. [Google Scholar] [CrossRef]
- Cao, C.; Carroll, S.M. Bulk entanglement gravity without a boundary: Towards finding Einstein’s equation in Hilbert space. Phys. Rev. D 2018, 97, 086003. [Google Scholar] [CrossRef]
- Minic, D.; Tze, C.-H. Background independent quantum mechanics and gravity. Phys. Rev. D 2003, 68, 061501(R). [Google Scholar] [CrossRef]
- Berglund, P.; Hübsch, T.; Mattingly, D.; Minic, D. Gravitizing the quantum. Int. J. Mod. Phys. D 2022, 31, 2242024. [Google Scholar] [CrossRef]
- Berglund, P.; Geraci, A.; Hübsch, T.; Mattingly, D.; Minic, D. Triple interference, non-linear Talbot effect and gravitization of the quantum. arXiv 2023, arXiv:2303.15645. [Google Scholar] [CrossRef]
- Ashtekar, A.; Schilling, T.A. Geometrical formulation of quantum mechanics. In On Einstein’s Path; Harvey, A., Ed.; Springer: New York, NY, USA, 1999. [Google Scholar]
- Harlow, D. Jerusalem lectures on black holes and quantum information. Rev. Mod. Phys. 2016, 88, 15002. [Google Scholar] [CrossRef]
- Horowitz, G.T.; Maldacena, J. The black hole final state. J. High Energy Phys. 2004, 2004, 008. [Google Scholar] [CrossRef]
- Svetlichny, G. Nonlinear quantum mechanics at the planck scale. Int. J. Theor. Phys. 2005, 44, 2051. [Google Scholar] [CrossRef]
- Bousso, R. Complementarity is not enough. Phys. Rev. D 2013, 87, 124023. [Google Scholar] [CrossRef]
- Marolf, D.; Polchinski, J. Gauge/Gravity Duality and the Black Hole Interior. Phys. Rev. Lett. 2013, 111, 171301. [Google Scholar] [CrossRef] [PubMed]
- Marolf, D.; Polchinski, J. Violations of the Born rule in cool state-dependent horizons. J. High Energy Phys. 2016, 2016, 8. [Google Scholar] [CrossRef]
- Papadodimas, K.; Raju, S. State-dependent bulk-boundary maps and black hole complementarity. Phys. Rev. D 2014, 89, 086010. [Google Scholar] [CrossRef]
- Lloyd, S.; Preskill, J. Unitarity of black hole evaporation in final-state projection models. J. High Energy Phys. 2014, 2014, 126. [Google Scholar] [CrossRef]
- Susskind, L. Entanglement is not enough. Fortschr. Phys. 2016, 64, 49. [Google Scholar] [CrossRef]
- Maldacena, J. Quantum mechanics and the geometry of spacetime. In Proceedings of the Strings 2015 Talk, 100th Anniversary of General Relativity Session, Bangalore, India, 22–26 June 2015. [Google Scholar]
- Bousso, R.; Dong, X.; Engelhardt, N.; Faulkner, T.; Hartman, T.; Shenker, S.H.; Stanford, D. Snowmass white paper: Quantum aspects of black holes and the emergence of spacetime. arXiv 2022, arXiv:2201.03096. [Google Scholar]
- Hardy, L. Quantum theory from five reasonable axioms. arXiv 2001, arXiv:quant-ph/0101012. [Google Scholar]
- Hardy, L. Reconstructing quantum theory. In Quantum Theory: Informational Foundations and Foils; Chiribella, G., Spekkens, R., Eds.; Springer: Dordrecht, The Netherlands, 2016. [Google Scholar]
- Goyal, P. From information geometry to quantum theory. New J. Phys. 2010, 12, 023012. [Google Scholar] [CrossRef]
- Dakić, B.; Brukner, Č. Quantum theory and beyond: Is entanglement special? In Deep Beauty: Understanding the Quantum World through Mathematical Innovation; Halvorson, H., Ed.; Cambridge University Press: New York, NY, USA, 2011; p. 365. [Google Scholar]
- Chiribella, G.; D’Ariano, G.; Perinotti, P. Informational derivation of quantum theory. Phys. Rev. A 2011, 84, 012311. [Google Scholar] [CrossRef]
- Masanes, L.; Müller, M.P. A derivation of quantum theory from physical requirements. New J. Phys. 2011, 13, 063001. [Google Scholar] [CrossRef]
- de la Torre, G.; Masanes, L.; Short, A.J.; Müller, M.P. Deriving quantum theory from its local structure and reversibility. Phys. Rev. Lett. 2012, 109, 090403. [Google Scholar] [CrossRef] [PubMed]
- Masanes, L.; Müller, M.P.; Augusiak, R.; Pérez-García, D. Existence of an information unit as a postulate of quantum theory. Proc. Natl. Acad. Sci. USA 2013, 110, 16373. [Google Scholar] [CrossRef] [PubMed]
- Barnum, H.; Müller, M.P.; Ududec, C. Higher-order interference and single-system postulates characterizing quantum theory. New J. Phys. 2014, 16, 123029. [Google Scholar] [CrossRef]
- Krumm, M.; Barnum, H.; Barrett, J.; Müller, M.P. Thermodynamics and the structure of quantum theory. New J. Phys. 2017, 19, 043025. [Google Scholar] [CrossRef]
- Höhn, P.A. Toolbox for reconstructing quantum theory from rules on information acquisition. Quantum 2017, 1, 38. [Google Scholar] [CrossRef]
- Höhn, P.A.; Wever, C.S.P. Quantum theory from questions. Phys. Rev. A 2017, 95, 012102. [Google Scholar] [CrossRef]
- Appleby, M.; Fuchs, C.A.; Stacey, B.C.; Zhu, H. Introducing the qplex: A novel arena for quantum theory. Eur. Phys. J. D 2017, 71, 197. [Google Scholar] [CrossRef]
- Wootters, W.K. The Acquisition of Information from Quantum Measurements. Ph.D. Thesis, University of Texas at Austin, Austin, TX, USA, 1980. [Google Scholar]
- Adler, S.L. Quantum Theory as an Emergent Phenomenon: The Statistical Mechanics of Matrix Models as the Precursor of Quantum Field Theory; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- ’t Hooft, G. Emergent quantum mechanics and emergent symmetries. AIP Conf. Proc. 2007, 957, 154. [Google Scholar]
- ’t Hooft, G. The Cellular Automaton Interpretation of Quantum Mechanics; Springer: Cham, Switzerland, 2016. [Google Scholar]
- ’t Hooft, G. Fast vacuum fluctuations and the emergence of quantum mechanics. Found. Phys. 2021, 51, 63. [Google Scholar] [CrossRef]
- Elze, H.-T. Qubit exchange interactions from permutations of classical bits. Int. J. Quantum Inf. 2015, 17, 1941003. [Google Scholar] [CrossRef]
- Wetterich, C. Probabilistic cellular automata for interacting fermionic quantum field theories. Nucl. Phys. B 2021, 963, 115296. [Google Scholar] [CrossRef]
- Wetterich, C. Fermionic quantum field theories as probabilistic cellular automata. Phys. Rev. D 2022, 105, 074502. [Google Scholar] [CrossRef]
- Minic, D.; Pajevic, S. Emergent “quantum” theory in complex adaptive systems. Mod. Phys. Lett. B 2016, 30, 1650201. [Google Scholar] [CrossRef] [PubMed]
- Smolin, L. Quantum mechanics and the principle of maximal variety. Found. Phys. 2016, 46, 736. [Google Scholar] [CrossRef]
- Vanchurin, V. Entropic mechanics: Towards a stochastic description of quantum mechanics. Found. Phys. 2020, 50, 40. [Google Scholar] [CrossRef]
- Katsnelson, M.I.; Vanchurin, V. Emergent quantumness in neural networks. Found. Phys. 2021, 51, 94. [Google Scholar] [CrossRef]
- Filk, T. The quantum-like behavior of neural networks. In From Electrons to Elephants and Elections; Wuppuluri, S., Stewart, I., Eds.; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Slagle, K.; Preskill, J. Emergent quantum mechanics at the boundary of a local classical lattice model. Phys. Rev. A 2023, 108, 012217. [Google Scholar] [CrossRef]
- Wittek, P. Quantum Machine Learning: What Quantum Computing Means to Data Mining; Academic Press: San Diego, CA, USA, 2014. [Google Scholar]
- Schuld, M.; Sinayskiy, I.; Petruccione, F. The quest for a quantum neural network. Quantum Inf. Process. 2014, 13, 2567. [Google Scholar] [CrossRef]
- Biamonte, J.; Wittek, P.; Pancotti, N.; Rebentrost, P.; Wiebe, N.; Lloyd, S. Quantum machine learning. Nature 2017, 549, 195. [Google Scholar] [CrossRef]
- Dunjko, V.; Briegel, H.J. Machine learning and artificial intelligence in the quantum domain: A review of recent progress. Rep. Prog. Phys. 2018, 81, 074001. [Google Scholar] [CrossRef] [PubMed]
- Garg, S.; Ramakrishnan, G. Advances in quantum deep learning: An overview. arXiv 2020, arXiv:2005.04316. [Google Scholar]
- Cerezo, M.; Verdon, G.; Huang, H.-Y.; Cincio, L.; Coles, P.J. Challenges and opportunities in quantum machine learning. Nat. Comput. Sci. 2022, 2, 567. [Google Scholar] [CrossRef] [PubMed]
- O’Reilly, R.C.; Munakata, Y.; Frank, M.J.; Hazy, T.E. Computational Cognitive Neuroscience; Spring: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- van Gerven, M.A.J. Computational foundations of natural intelligence. Front. Comput. Neurosci. 2017, 11, 1. [Google Scholar] [CrossRef]
- Feynman, R.P. Space-time approach to non-relativistic quantum mechanics. Rev. Mod. Phys. 1948, 20, 367. [Google Scholar] [CrossRef]
- Feynman, R.P. Space-time approach to quantum electrodynamics. Phys. Rev. 1949, 76, 769. [Google Scholar] [CrossRef]
- Müller, M.P. How Spacetime Constrains the Structure of Quantum Theory, Virtual Seminar, 17 March 2023. Available online: https://www.youtube.com/watch?v=NSZ7gtMhnSI (accessed on 10 May 2025).
- Garner, A.J.P.; Müller, M.P.; Dahlsten, O.C.O. The complex and quaternionic quantum bit from relativity of simultaneity on aninterferometer. Proc. R. Soc. A 2017, 473, 20170596. [Google Scholar] [CrossRef]
- Jones, C.L.; Ludescher, S.L.; Aloy, A.; Müller, M.P. Theory-independent randomness generation with spacetime symmetries. arXiv 2022, arXiv:2210.14811. [Google Scholar]
- Alipour, S.; Rezakhani, A.T.; Babu, A.P.; Mølmer, K.; Möttönen, M.; Ala-Nissila, T. Correlation-Picture Approach to Open- Quantum-System Dynamics. Phys. Rev. X 2020, 10, 041024. [Google Scholar] [CrossRef]
- Smith, A.R.H.; Ahmadi, M. Quantizing time: Interacting clocks and systems. Quantum 2019, 3, 160. [Google Scholar] [CrossRef]
- Höhn, P.A.; Smith, A.R.H.; Lock, M.P.E. Trinity of relational quantum dynamics. Phys. Rev. D 2021, 104, 066001. [Google Scholar] [CrossRef]
- Oreshkov, O. Time-delocalized quantum subsystems and operations: On the existence of processes with indefinite causal structure in quantum mechanics. Quantum 2019, 3, 206. [Google Scholar] [CrossRef]
- Guŕrin, P.A.; Brukner, Č. Observer-dependent locality of quantum events. New J. Phys. 2018, 20, 103031. [Google Scholar] [CrossRef]
- Castro-Ruiz, E.; Giacomini, F.; Belenchia, A.; Brukner, Č. Quantum clocks and the temporal localisability of events in the presence of gravitating quantum systems. Nat. Commun. 2020, 11, 2672. [Google Scholar] [CrossRef]
- Paiva, I.L.; Nowakowski, M.; Cohen, E. Dynamical nonlocality in quantum time via modular operators. Phys. Rev. A 2022, 105, 042207. [Google Scholar] [CrossRef]
- Abrams, D.S.; Lloyd, S. Nonlinear Quantum Mechanics Implies Polynomial-Time Solution for NP-Complete and #P Problems. Phys. Rev. Lett. 1998, 81, 3992. [Google Scholar]
- Childs, A.M.; Young, J. Optimal state discrimination and unstructured search in nonlinear quantum mechanics. Phys. Rev. A 2016, 93, 022314. [Google Scholar] [CrossRef]
- Meyer, D.A.; Wong, T.G. Nonlinear quantum search using the Gross–Pitaevskii equation. New J. Phys. 2013, 15, 063014. [Google Scholar] [CrossRef]
- Wong, T.G. Nonlinear Quantum Search. Ph.D. Thesis, University of California San Diego, San Diego, CA, USA, 2014. [Google Scholar]
- Barrett, J.; de Beaudrap, N.; Hoban, M.J.; Lee, C.M. The computational landscape of general physical theories. npj Quantum Inf. 2019, 5, 41. [Google Scholar] [CrossRef]
- Chowdhury, D.; Georges, A.; Parcollet, O.; Sachdev, S. Sachdev-Ye-Kitaev models and beyond: Window into non-Fermi liquids. Rev. Mod. Phys. 2022, 94, 035004. [Google Scholar] [CrossRef]
- Susskind, L. De Sitter space, double-scaled SYK, and the separation of scales in the semiclassical limit. arXiv 2022, arXiv:2209.09999. [Google Scholar]
- Banks, T. Old ideas for new physicists: 1. arXiv 2022, arXiv:2208.08959. [Google Scholar]
- Wen, X.-G. Quantum Field Theory of Many-Body Systems: From the Origin of Sound to an Origin of Light and Electrons; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Wen, X.-G. Four revolutions in physics and the second quantum revolution—A unification of force and matter by quantum information. Int. J. Mod. Phys. B 2018, 32, 1830010. [Google Scholar] [CrossRef]
- Kibble, T.W.B. Geometrization of quantum mechanics. Commun. Math. Phys. 1979, 65, 189. [Google Scholar] [CrossRef]
- Sorkin, R.D. Quantum mechanics as quantum measure theory. Mod. Phys. Lett. A 1994, 09, 3119. [Google Scholar] [CrossRef]
- Adler, S.L.; Millard, A.C. Generalized quantum dynamics as pre-quantum mechanics. Nucl. Phys. B 1996, 473, 199. [Google Scholar] [CrossRef]
- Atmanspacher, H.; Römer, H.; Walach, H. Weak quantum theory: Complementarity and entanglement in physics and beyond. Found. Phys. 2002, 32, 379. [Google Scholar] [CrossRef]
- Atmanspacher, H.; Filk, T.; Römer, H. Weak quantum theory: Formal framework and selected applications. AIP Conf. Proc. 2006, 810, 34. [Google Scholar]
- Hartle, J.B. Glafka 2004: Generalizing quantum mechanics for quantum gravity. Int. J. Theor. Phys. 2006, 45, 1390. [Google Scholar] [CrossRef][Green Version]
- Giddings, S.B. Universal quantum mechanics. Phys. Rev. D 2008, 78, 084004. [Google Scholar] [CrossRef]
- The Quantum Landscape 2013 Conference, Perimeter Institute, May 27–31, 2013, Waterloo, Canada. Available online: https://www2.perimeterinstitute.ca/conferences/quantum-landscape (accessed on 10 May 2025).
- Hartle, J. Generalized quantum mechanics. arXiv 2021, arXiv:2110.11268. [Google Scholar]
- Müller, M.P. Probabilistic theories and reconstructions of quantum theory. SciPost Phys. Lect. Notes 2021, 28. [Google Scholar] [CrossRef]
- Kent, A. The measurement postulates of quantum mechanics are not redundant. arXiv 2023, arXiv:2307.06191. [Google Scholar]
- Masanes, L.; Galley, T.D.; Müller, M.P. Response to “The measurement postulates of quantum mechanics are not redundant”. arXiv 2023, arXiv:2309.01650. [Google Scholar] [CrossRef]
- Friedenberg, J.D.; Silverman, G.W. Cognitive Science: An Introduction to the Study of Mind; Sage: Thousand Oaks, CA, USA, 2015. [Google Scholar]
- Poeppel, D.; Mangun, G.R.; Gazzaniga, M.S. (Eds.) The Cognitive Neurosciences; MIT Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Anderson, P.W. More is different. Science 1972, 177, 393. [Google Scholar] [CrossRef]
- Gu, M.; Weedbrook, C.; Perales, Á.; Nielsen, M.A. More really is different. Physica D 2009, 238, 835. [Google Scholar] [CrossRef]
- Ellis, G.F.R. Emergence in solid state physics and biology. Found. Phys. 2020, 50, 1098. [Google Scholar] [CrossRef]
- Busemeyer, J.R.; Bruza, P.D. Quantum Models of Cognition and Decision; Cambridge University Press: New York, NY, USA, 2012. [Google Scholar]
- Martínez-Martínez, I.; Sánchez-Burillo, E. Quantum stochastic walks on networks for decision-making. Sci. Rep. 2016, 6, 23812. [Google Scholar]
- Kent, A. Quanta and qualia. Found. Phys. 2018, 48, 1021. [Google Scholar] [CrossRef]
- Li, J.-A.; Dong, D.; Wei, Z.; Liu, Y.; Pan, Y.; Nori, F.; Zhang, X. Quantum reinforcement learning during human decision-making. Nat. Hum. Behav. 2020, 4, 294. [Google Scholar] [CrossRef]
- Khrennikov, A. Quantum-like model for unconscious–conscious interaction and emotional coloring of perceptions and other conscious experiences. Biosystems 2021, 208, 104471. [Google Scholar] [CrossRef]
- Pothos, E.M.; Busemeyer, J.R. Quantum cognition. Annu. Rev. Psychol. 2022, 73, 749. [Google Scholar] [CrossRef] [PubMed]
- Aerts, D.; Arguëlles, J.A. Human perception as a phenomenon of quantization. Entropy 2022, 24, 1207. [Google Scholar] [CrossRef]
- Khrennikov, A.Y. Open Quantum Systems in Biology, Cognitive and Social Sciences; Springer: Cham, Switzerland, 2023. [Google Scholar]
- Conte, E.; Khrennikov, A.Y.; Todarello, O.; Federici, A.; Mendolicchio, L.; Zbilut, J.P. Mental states follow quantum mechanics during perception and cognition of ambiguous figures. Open Syst. Inf. Dyn. 2009, 16, 85. [Google Scholar] [CrossRef]
- DeBrota, J.B.; Love, P.J. Quantum and classical Bayesian agents. Quantum 2022, 6, 713. [Google Scholar] [CrossRef]
- Busemeyer, J.; Zhang, Q.; Balakrishnan, S.; Wang, Z. Application of quantum—Markov open system models to human cognition and decision. Entropy 2020, 22, 990. [Google Scholar] [CrossRef] [PubMed]
- Aerts, D.; Arguëlles, J.A.; Beltran, L.; Geriente, V.; de Bianchi, M.S.; Sozzo, S.; Veloz, T. Quantum entanglement in physical and cognitive systems: A conceptual analysis and a general representation. Eur. Phys. J. Plus 2019, 134, 493. [Google Scholar] [CrossRef]
- Brody, D.C. Quantum formalism for cognitive psychology. arXiv 2023, arXiv:2303.06055. [Google Scholar]
- Heunen, C.; Sadrzadeh, M.; Grefenstette, E. (Eds.) Quantum Physics and Linguistics: A Compositional, Diagrammatic Discourse; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Surov, I.A.; Semenenko, E.; Platonov, A.V.; Bessmertny, I.A.; Galofaro, F.; Toffano, Z.; Khrennikov, A.Y.; Alodjants, A.P. Quantum semantics of text perception. Sci. Rep. 2021, 11, 4193. [Google Scholar] [CrossRef]
- Haven, E.; Khrennikov, A. Quantum Social Science; Cambridge University Press: New York, NY, USA, 2013. [Google Scholar]
- Orrell, D. Quantum Economics and Finance: An Applied Mathematics Introduction; Panda Ohana: New York, NY, USA, 2020. [Google Scholar]
- Hausmann, L.; Nurgalieva, N.; del Rio, L. A consolidating review of Spekkens’ toy theory. arXiv 2021, arXiv:2105.03277. [Google Scholar]
- Budiyono, A.; Dipojono, H.K. Nonlinear Schrödinger equations and generalized Heisenberg uncertainty principle from estimation schemes violating the principle of estimation independence. Phys. Rev. A 2020, 102, 012205. [Google Scholar] [CrossRef]
- Budiyono, A.; Rohrlich, D. Quantum mechanics as classical statistical mechanics with an ontic extension and an epistemic restriction. Nat. Commun. 2017, 8, 1306. [Google Scholar] [CrossRef]
- Koochakie, M.M.R.; Alipour, S.; Rezakhani, A.T. Lieb-Robinson bound and adiabatic evolution. arXiv 2013, arXiv:1307.3726. [Google Scholar]
- Scarani, V.; Iblisdir, S.; Gisin, N.; Acín, A. Quantum cloning. Rev. Mod. Phys. 2005, 77, 1225. [Google Scholar] [CrossRef]
- Brunner, N.; Cavalcanti, D.; Pironio, S.; Scarani, V.; Wehner, S. Bell nonlocality. Rev. Mod. Phys. 2014, 86, 419. [Google Scholar] [CrossRef]
- Hu, Y.; Tomamichel, M. Fundamental limits on quantum cloning from the no-signalling principle. arXiv 2023, arXiv:2305.02002. [Google Scholar]
- Busch, P.; Heinonen, T.; Lahti, P. Heisenberg’s uncertainty principle. Phys. Rep. 2007, 452, 155. [Google Scholar] [CrossRef]
- Coles, P.J.; Berta, M.; Tomamichel, M.; Wehner, S. Entropic uncertainty relations and their applications. Rev. Mod. Phys. 2017, 89, 015002. [Google Scholar] [CrossRef]
- Bartlett, S.D.; Rudolph, T.; Spekkens, R.W. Reference frames, superselection rules, and quantum information. Rev. Mod. Phys. 2007, 79, 555. [Google Scholar] [CrossRef]
- Giacomini, F.; Castro-Ruiz, E.; Brukner, Č. Quantum mechanics and the covariance of physical laws in quantum reference frames. Nat. Commun. 2019, 10, 494. [Google Scholar] [CrossRef]
- Vanrietvelde, A.; Höhn, P.A.; Giacomini, F.; Castro-Ruiz, E. A change of perspective: Switching quantum reference frames via a perspective-neutral framework. Quantum 2020, 4, 225. [Google Scholar] [CrossRef]
- Fields, C.; Glazebrook, G.F.; Levin, M. Neurons as hierarchies of quantum reference frames. Biosystems 2022, 219, 104714. [Google Scholar] [CrossRef] [PubMed]
- Fields, C.; Friston, K.; Glazebrook, J.F.; Levin, M. A free energy principle for generic quantum systems. Prog. Biophys. Mol. Biol. 2022, 173, 36. [Google Scholar] [CrossRef] [PubMed]
- Venegas-Andraca, S.E. Quantum walks: A comprehensive review. Quantum Inf. Process. 2012, 11, 1015. [Google Scholar] [CrossRef]
- Khan, F.S.; Solmeyer, N.; Balu, R.; Humble, T.S. Quantum games: A review of the history, current state, and interpretation. Quantum Inf. Process. 2018, 309, 17. [Google Scholar]
- Manrique, P.D.; Huo, F.Y.; Oud, S.E.; Zheng, M.; Illari, L.; Johnson, N.F. Shockwavelike Behavior across Social Media. Phys. Rev. Lett. 2023, 130, 237401. [Google Scholar] [CrossRef]
- Ziepke, A.; Maryshev, I.; Aranson, I.S.; Frey, E. Multi-scale organization in communicating active matter. Nat. Commun. 2022, 13, 6727. [Google Scholar] [CrossRef]
- Tavanfar, A.; et al. Experience-Centric, Multi-Level Quantum Systems. in preparation.
- Trudeau, R.J. The Non-Euclidean Revolution; Birkhäuser: Boston, MA, USA, 2008. [Google Scholar]
- Tavanfar, A.; et al. Understanding the Principle of Inclusive Experience Centricity in Nature. in preparation.


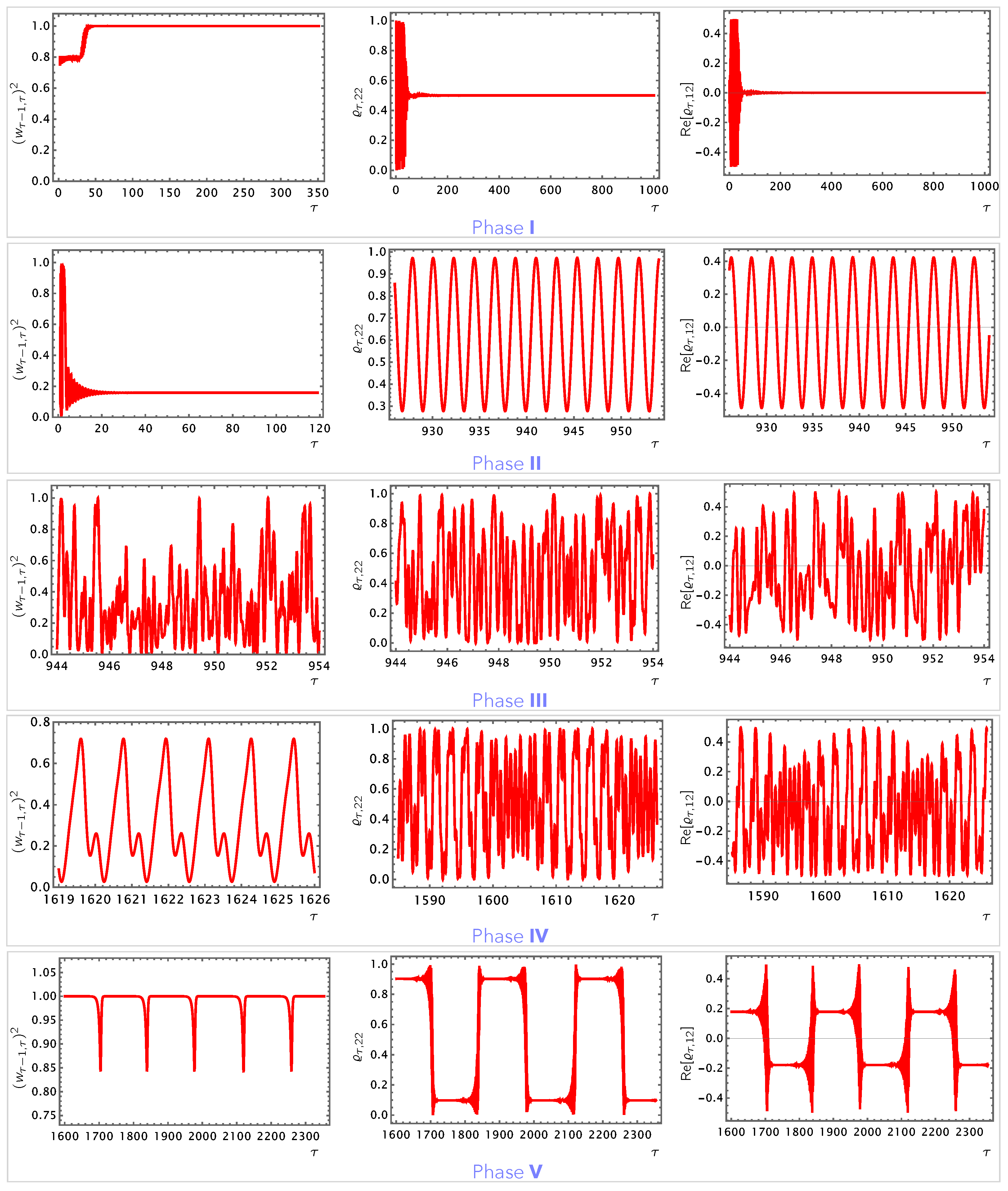
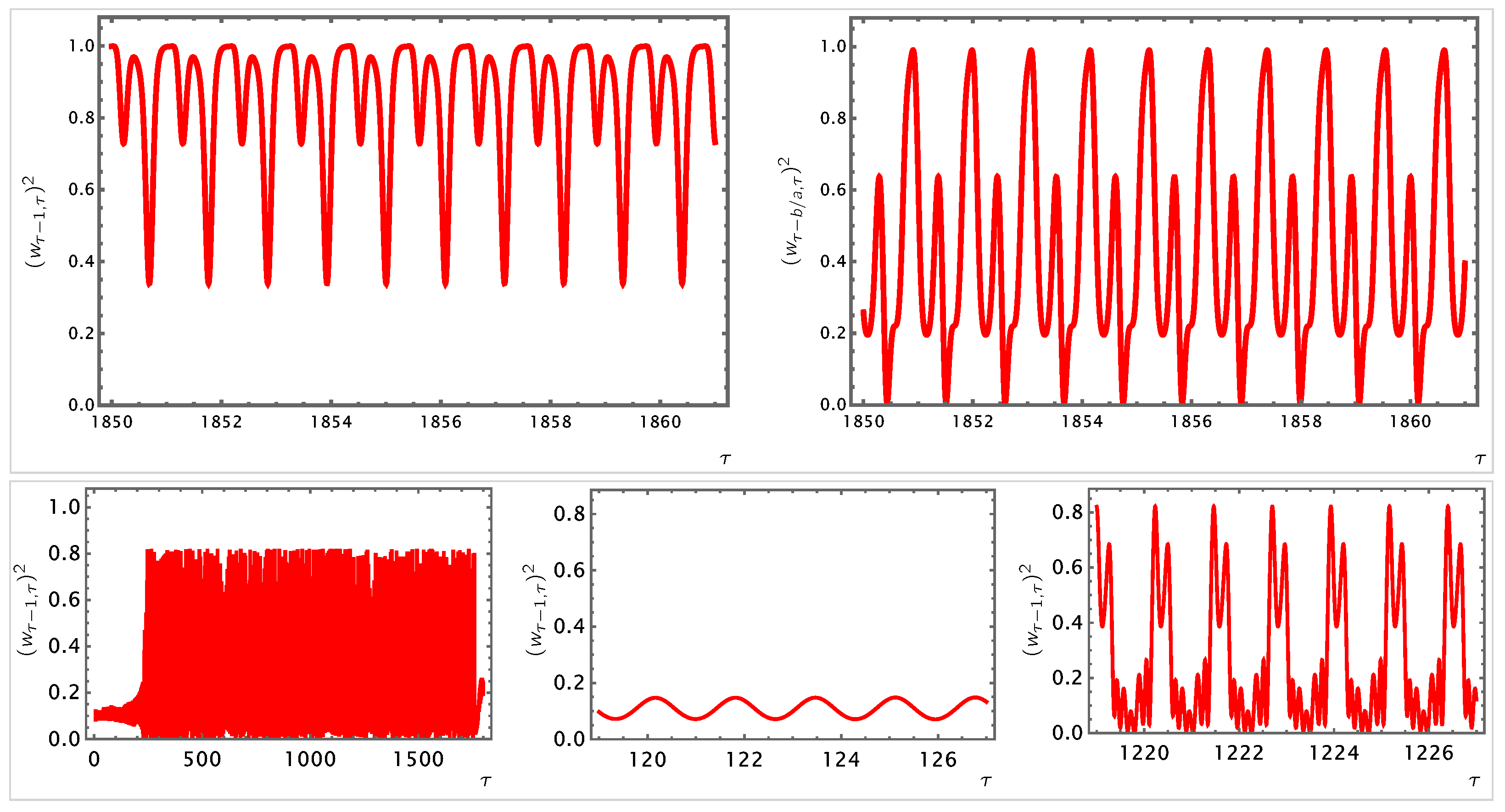
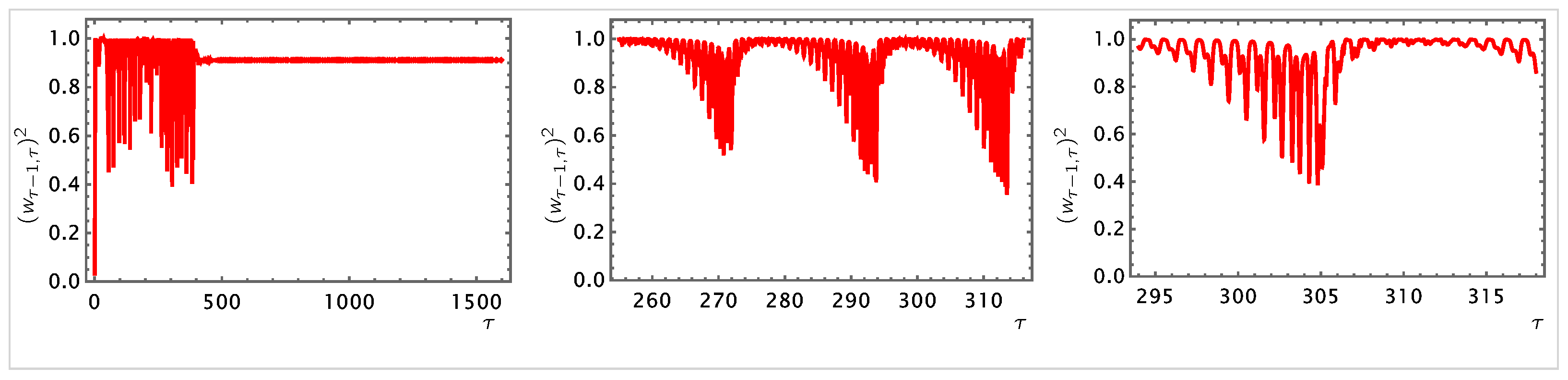

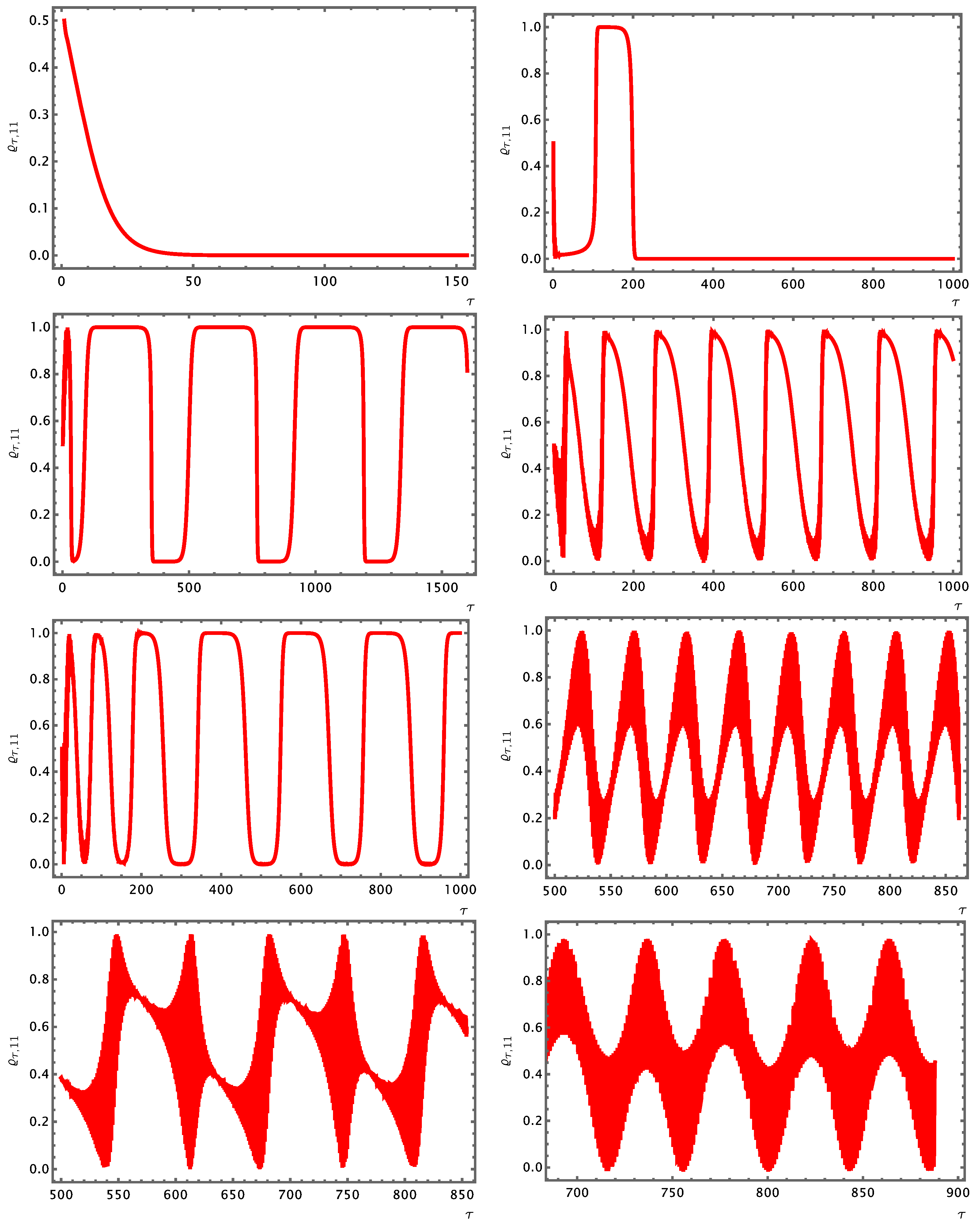

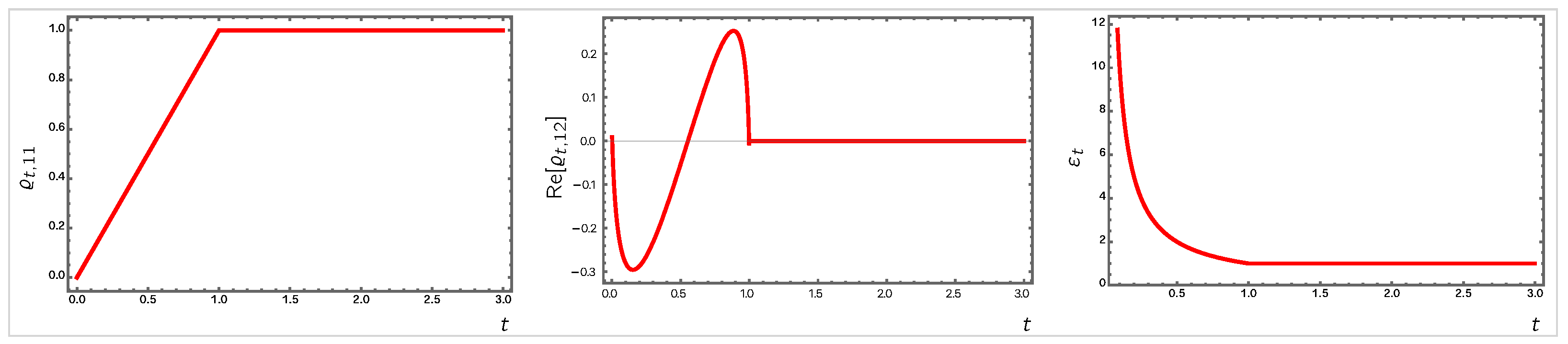
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tavanfar, A.; Alipour, S.; Rezakhani, A.T. Does Quantum Mechanics Breed Larger, More Intricate Quantum Theories? The Case for Experience-Centric Quantum Theory and the Interactome of Quantum Theories. Universe 2025, 11, 162. https://doi.org/10.3390/universe11050162
Tavanfar A, Alipour S, Rezakhani AT. Does Quantum Mechanics Breed Larger, More Intricate Quantum Theories? The Case for Experience-Centric Quantum Theory and the Interactome of Quantum Theories. Universe. 2025; 11(5):162. https://doi.org/10.3390/universe11050162
Chicago/Turabian StyleTavanfar, Alireza, Sahar Alipour, and Ali T. Rezakhani. 2025. "Does Quantum Mechanics Breed Larger, More Intricate Quantum Theories? The Case for Experience-Centric Quantum Theory and the Interactome of Quantum Theories" Universe 11, no. 5: 162. https://doi.org/10.3390/universe11050162
APA StyleTavanfar, A., Alipour, S., & Rezakhani, A. T. (2025). Does Quantum Mechanics Breed Larger, More Intricate Quantum Theories? The Case for Experience-Centric Quantum Theory and the Interactome of Quantum Theories. Universe, 11(5), 162. https://doi.org/10.3390/universe11050162






