Reconciling the Waiting Time Peaks Variations of Repeating FRBs with an Eccentric Neutron Star–White Dwarf Binary

Abstract

Fast radio bursts (FRBs) are luminous radio transients with millisecond duration. For some active repeaters, such as FRBs 20121102A and 20201124A, more than a thousand bursts have been detected by the Five-hundred-meter Aperture Spherical radio Telescope (FAST). The waiting time (WT) distributions of both repeaters, defined as the time intervals between adjacent (detected) bursts, exhibit a bimodal structure well-fitted by two log-normal functions. Notably, the time scales of the long-duration WT peaks for both repeaters show a decreasing trend over time. These similar burst features suggest that there may be a common physical mechanism for FRBs 20121102A and 20201124A. In this paper, we revisit the neutron star (NS)–white dwarf (WD) binary model with an eccentric orbit to account for the observed changes in the long-duration WT peaks. According to our model, the shortening of the WT peaks corresponds to the orbital period decay of the NS-WD binary. We consider two mass transfer modes, namely, stable and unstable mass transfer, to examine how the orbital period evolves. Our findings reveal distinct evolutionary pathways for the two repeaters: for FRB 20121102A, the NS-WD binary likely undergoes a combination of common envelope (CE) ejection and Roche lobe overflow, whereas for FRB 20201124A the system may experience multiple CE ejections. These findings warrant further validation through follow-up observations.

1. Introduction

Fast radio bursts (hereafter, FRBs) are luminous transients with millisecond duration (see reviews, e.g., [1,2,3]). Because the dispersion measures of FRBs exceed the contributions of our Galaxy, and certain FRB host galaxies have been identified at redshifts in the range $z\simeq 0.03-1$ (e.g., [4,5]), FRBs are thought to be extragalactic origins (except FRB 20200428 detected from the Galactic magnetar SGR J1935+2154; [6,7]). Based on the quantity of detected bursts, FRBs can be classified as repeating FRBs and apparently one-off (hereafter, simply “one-off”) FRBs. Recently, nearly 500 unique FRB sources have been detected by the Canadian Hydrogen Intensity Mapping Experiment (CHIME) (i.e., the CHIME/FRB Catalog 11. This sample is excellent for exploring the statistical properties of FRBs. Some statistical differences between one-off FRBs and repeating ones have been found based on this sample, including the differences in the distributions of the peak fluxes [8], the spectral indices [9], and the luminosities [10,11]. Additionally, the time–frequency drift (“sad-trombone” effect) commonly seen in repeating FRBs (e.g., [12]) is mostly absent in one-offs. All of these differences strongly suggest that one-off and repeating FRBs likely have distinct emission mechanisms and progenitors (e.g., [13,14]).

Periodic activities are an interesting property of repeaters that can provide important clues for revealing their physical mechanisms. Analysis of the burst arrival times of FRB 20180916B shows a ∼5-day activity window2 that recurs every 16.35 days [16]. FRB 20121102A, the first detected repeater coincident with a compact persistent radio source [17,18], was found to exhibit a candidate periodicity of ∼160 days [19,20]. Some models have been proposed to explain these long activity periods, including orbital motion (e.g., [21,22,23,24,25,26]), rotational period (e.g., [27]), and precession-based mechanisms (e.g., [28,29,30,31]).

The Five-hundred-meter Aperture Spherical radio Telescope (FAST) has conducted continuous monitoring of several active repeating FRBs, including FRBs 20121102A and 20201124A (e.g., [32,33,34]). Over the course of 59.5 h of observation time between 29 August 2019 and 29 October 2019, Li et al. [32] detected 1652 independent burst events from FRB 20121102A. These bursts have a bimodal energy distribution that can be well-fitted by combining a log-normal function with a Cauchy function [32]. Moreover, the distribution of the waiting time, defined as the time interval between two adjacent (detected) bursts, demonstrates a bimodal structure. The two fitted peak waiting times are ∼$3.4$ ms and ∼70 s (the fitted peak of the waiting time distribution of the high-energy component ($E>{10}^{38}\mathrm{erg}$) is ∼220 s; [32]). For FRB 20201124A3, 1863 separate burst have been detected by FAST during a total observation time of 82 h from 1 April 2021 to 29 May 2021 [33]. The waiting time distribution of FRB 20201124A similarly reveals a bimodal structure, which can be well-fitted by two log-normal functions peaking at 39 ms and 106.7 s, respectively [33]. Despite the detection of thousands of bursts, no significant periods have been found in the millisecond to the second range for either FRBs 20121102A or 20201124A (e.g., [32,33,36]).

For FRB 20121102A, a total of 478 independent burst events were detected by the 305-m Arecibo telescope4 over 59 h of observation between December 2015 and October 2016 [37]. The waiting time distribution of these bursts similarly exhibits a bimodal structure, which can be fitted by two log-normal functions peaking at ∼24 ms and ∼95 s, respectively [37]. For FRB 20201124A, following the detection of a new burst by CHIME/FRB on 21 September 20215, Zhang et al. [34] used FAST to monitor this source, initiating observations on 25 September 2021. In all, 8816 independent burst events from FRB 20201124A were detected in the first four days (i.e., from 25 September 2021 to 28 September 2021; [34]) of the 17-day monitoring campaign. The waiting time distribution of these bursts can also be fitted by two log-normal functions peaking at 51.22 ms and 10.05 s, respectively [34]. The time scales of the long-duration (second-level) peaks of the waiting time distributions of these two active repeaters both decrease with time, which would be a sign that both FRB sources are becoming increasingly active.

These observed similarities in burst characteristics suggest that a common physical mechanism likely exists for both FRBs 20121102A and 20201124A. In this paper, we explain the common features observed in two repeaters using the NS-WD binary model with an eccentric orbit [22]. We consider that the time intervals between adjacent bursts correspond to the orbital period of the NS-WD binary, as the intermittent type of Roche lobe overflow can commonly occur in the semi-detached systems. Consequently, the decreases in the long-duration wait time peaks are linked to the decreases in the orbital periods of the NS-WD binary. To investigate the evolution of the NS-WD binary, we consider two distinct forms of mass transfer, namely, stable and unstable mass transfer.

The remainder of this article is organized as follows: the NS-WD binary model with an eccentric orbit is illustrated in Section 2; the evolution of the NS-WD binary with stable mass transfer is studied in Section 3; the evolution of the binary with a massive WD based on a form of unstable mass transfer is shown in Section 4; finally, conclusions and discussion are presented in Section 5.

2. NS-WD Binary Model

Gu et al. [22] proposed a compact binary model with an eccentric orbit to explain the periodic activity observed in repeating FRBs. The system contains a magnetic WD and an NS with strong dipolar magnetic fields. At the periastron, the mass transfer occurs from the WD to the NS through the inner Lagrange point $L_1$ when the WD fills its Roche lobe. At other positions along the eccentric orbit, no mass transfer is supplied, as the Roche lobe is not filled. When the accreted magnetized materials approach the NS surface, magnetic reconnection is triggered, releasing strong electromagnetic radiation via curvature radiation as the electrons move along the NS magnetic field lines. The WD may be kicked away after a Roche lobe overflow process if $q<2/3$ [40], where q is the mass ratio defined as $q=M_{\mathrm{WD}}/M_{\mathrm{NS}}$, with $M_{\mathrm{NS}}$ and $M_{\mathrm{WD}}$ respectively denoting the masses of the NS and WD. The WD can replenish its Roche lobe through gravitational radiation; therefore, the next transfer process can recur. The intermittent nature of Roche lobe overflow appears to be a common phenomenon in the semi-detached NS-WD system, as the NS mass is normally larger than $1.4M_{\odot }$ and the WD mass distribution peaks at $0.6M_{\odot }$. According to this model, the duty cycle of the burst activity is related to the orbital period of the binary. An extremely high eccentricity ($e>0.95$) of orbit is required to explain the 16.35-day periodicity of FRB 20180916B [22].

The wait time distributions of the active repeaters FRBs 20121102A and 20201124A both exhibit a bimodal structure, i.e., a millisecond peak and a tens-of-second peak. A possible explanation for the millisecond peak is that due to the high time resolution of the radio telescopes, e.g., the 98.304-$\mathsf{\mu }$s sampling resolution of FAST [32], the individual burst events with long-duration pulse widths and multi-component pulse profiles (e.g., FRB 20191221A including 3-second duration and nine components; [41]) can be considered to be multiple separate bursts. Following the spirit of Gu et al. [22], these bursts with multiple pulse components can be produced in the mass transfer process. Specifically, the viscous processes during mass transfer are necessary to help the accreted materials lose angular momentum and eventually fall onto the surface of the NS. During this process, some massive accreted materials may be fragmented into a number of smaller portions. When the fragmented materials originating from the same initial bulk of material approach the NS at different times, multiple bursts with short intervals may be triggered, which can be regarded as a single burst event containing multiple sub-bursts.

For the tens-of-second peaks, an intriguing phenomenon is that the long-duration peaks decay with time. In our hypothesis, these peak waiting times may correspond to the orbital periods $P_{\mathrm{orb}}$ of the NS-WD binary. As a result, the variations in the orbital periods of the NS-WD binary induced by the mass transfer are hypothesized to induce variations in the long-duration wait time peaks of repeating FRBs. The reasons for this are as follows. For the semi-detached NS-WD system, the intermittent type of Roche lobe overflow may be a common phenomenon (e.g., [22,40,42]). The time interval between adjacent mass transfer processes $T_{\mathrm{mt}}$ is proportional to the mass of the transferred material from the WD $\Delta M_{\mathrm{WD}}$ [26]. For $M_{\mathrm{WD}}\sim 0.6M_{\odot }$, it can be evaluated that $T_{\mathrm{mt}}\lesssim P_{\mathrm{orb}}$ (see Equation (9) of [26]). Moreover, the supply of the accreted materials to the NS is expected to exhibit a uniform temporal lag. Therefore, the time interval between two adjacent bursts should be equivalent to $P_{\mathrm{orb}}$.

On the other hand, due to the remaining angular momentum, some of the fragmented materials cannot not fall to the surface of the NS while surrounding it; that is, even though no mass transfer occurs in the binary system, some materials surrounding the NS arrive on its surface episodically, where they stochastically produce radio bursts with wait times ranging from a few seconds to thousands of seconds.

3. Stable Mass Transfer

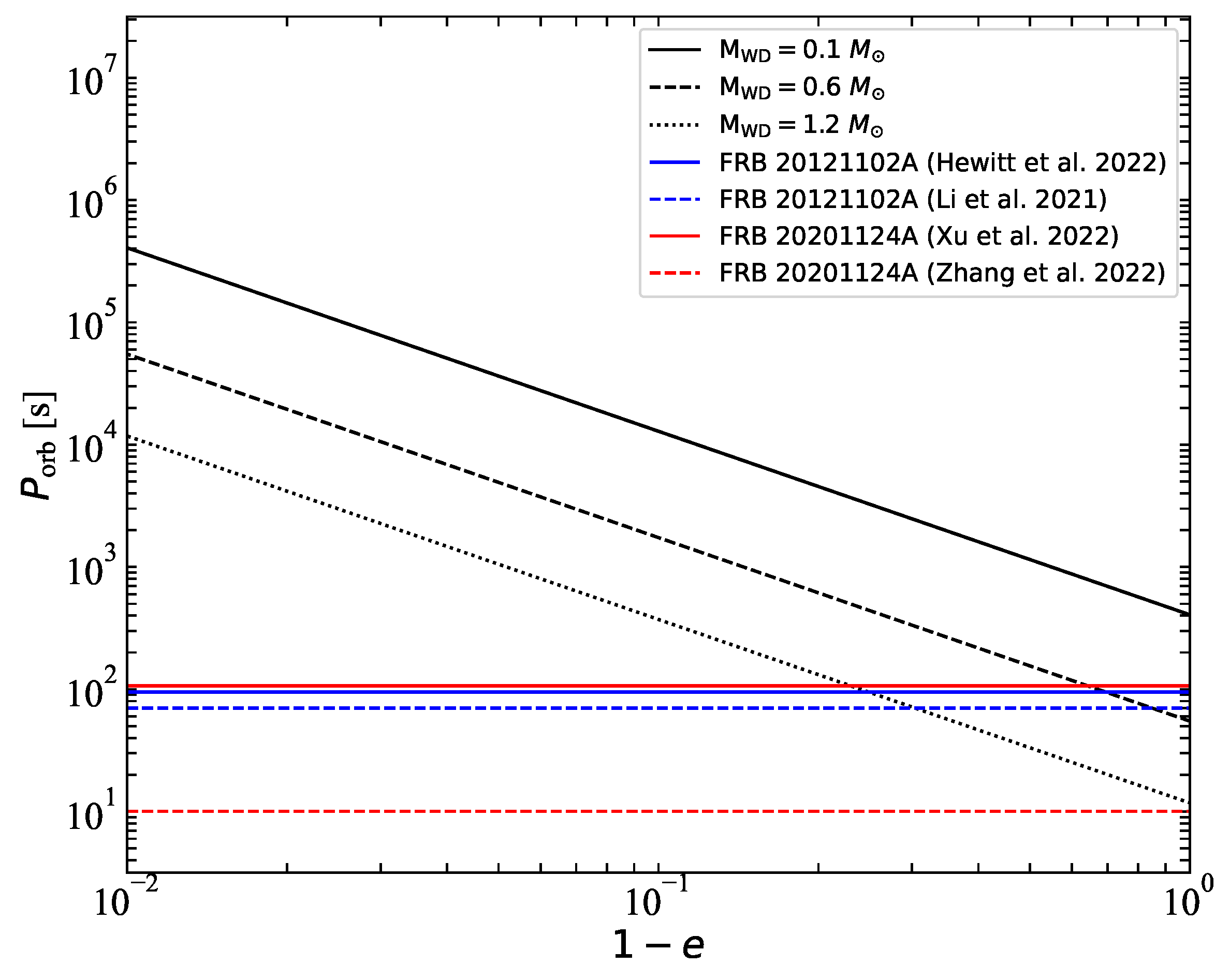
3.1. Orbital Period

The dynamic equation of the NS-WD binary system is provided by

$${\displaystyle \frac{G\left(M_{\mathrm{NS}}+M_{\mathrm{WD}}\right)}{a^3}}={\displaystyle \frac{4{\pi }^2}{P_{\mathrm{orb}}^2}},$$

(1)

where G is the gravitational constant and a is the semimajor axis of the eccentric orbit. The Roche lobe radius for the WD $R_{\mathrm{L}2}$ at the periastron can take the following form [43]:

$${\displaystyle \frac{R_{\mathrm{L}2}}{a\left(1-e\right)}}=0.462{\left({\displaystyle \frac{M_{\mathrm{WD}}}{M_{\mathrm{NS}}+M_{\mathrm{WD}}}}\right)}^{1/3}$$

(2)

where e is the eccentricity of the orbit. The WD radius $R_{\mathrm{WD}}$ can be expressed as [44]

$$R_{\mathrm{WD}}=0.0114R_{\odot }{\left[{\left({\displaystyle \frac{M_{\mathrm{WD}}}{M_{\mathrm{Ch}}}}\right)}^{-2/3}-{\left({\displaystyle \frac{M_{\mathrm{WD}}}{M_{\mathrm{Ch}}}}\right)}^{2/3}\right]}^{1/2}\times {\left[1+{\displaystyle \frac{7}{2}}{\left({\displaystyle \frac{M_{\mathrm{WD}}}{M_{\mathrm{p}}}}\right)}^{-2/3}+{\left({\displaystyle \frac{M_{\mathrm{WD}}}{M_{\mathrm{p}}}}\right)}^{-1}\right]}^{-2/3},$$

(3)

where $M_{\mathrm{Ch}}=1.44M_{\odot }$ is the Chandrasekhar mass limit and $M_{\mathrm{p}}=0.00057M_{\odot }$ [45].

At the periastron, it is assumed that the WD fills its Roche lobe, i.e., $R_{\mathrm{WD}}=R_{\mathrm{L}2}$. The orbital period $P_{\mathrm{orb}}$ can be derived by Equations (1)–(3) after $M_{\mathrm{NS}}$, $M_{\mathrm{WD}}$, and e are given. The relationships between the orbital period $P_{\mathrm{orb}}$ and the eccentricity e of the orbit for the distinct WD masses are shown in Figure 1. The black lines represent different WD masses, i.e., $0.1M_{\odot }$ (solid line), $0.6M_{\odot }$ (dashed line), and $1.2M_{\odot }$ (dotted line). The blue and red lines correspond to the peak waiting times of FRBs 20121102A and 20201124A, respectively, at the distinct activity epochs. It can be seen from Figure 1 that the orbital period $P_{\mathrm{orb}}$ of the NS-WD binary shortens with decreasing eccentricity e for a constant WD mass.

Observations of the active repeating FRBs 20121102A and 20201124A reveal that the long-duration wait time peaks both shorten over time. In the NS-WD binary model, the WD mass remains quasi-constant for short-term (e.g., a few years) stable mass transfer processes, whereas the eccentricity e of the NS-WD binary system can gradually decrease, as the dynamical mass transfer and gravitational radiation may cause orbital circularization. Thus, the orbital period $P_{\mathrm{orb}}$ can decrease gradually. As shown in Figure 1, the orbital period $P_{\mathrm{orb}}$ varies from hundreds to tens of seconds as the eccentricity decreases when $M_{\mathrm{WD}}\gtrsim 0.6M_{\odot }$, which is comparable to the variations in the long-duration peaks of the wait time distributions of FRBs 20121102A and 20201124A.

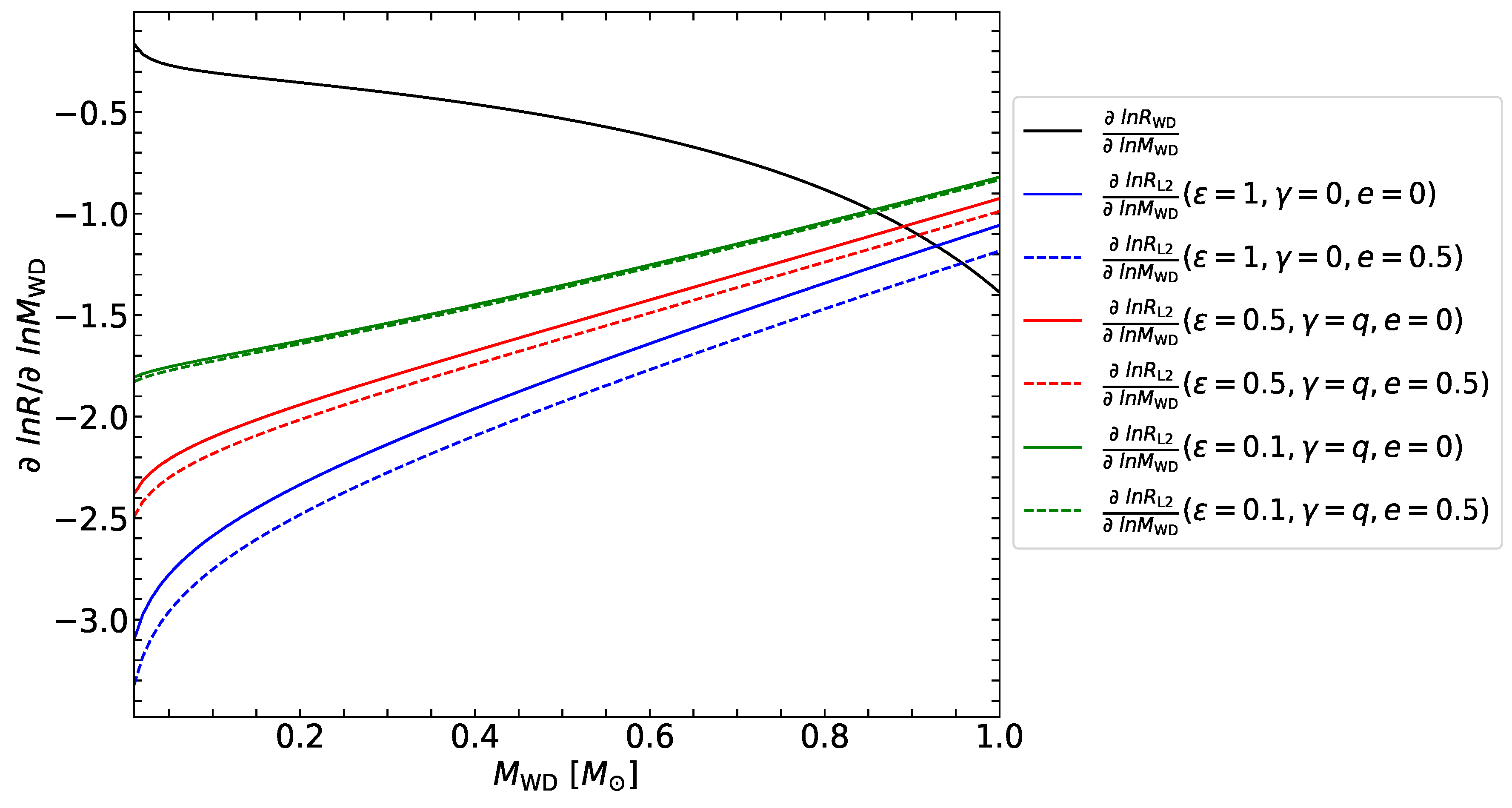
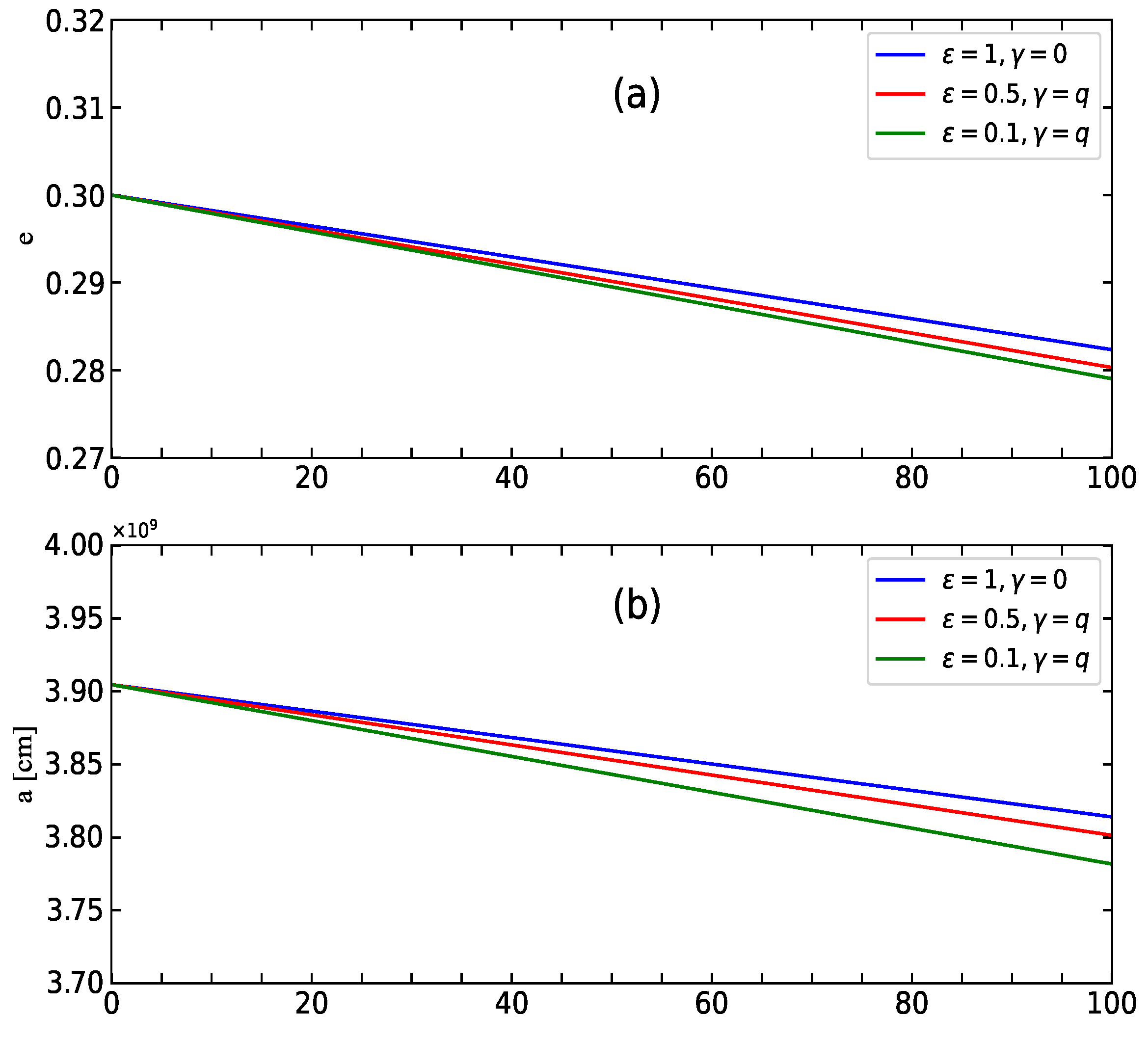
3.2. Orbital Evolution of NS-WD Binary

The orbital angular momentum of the NS-WD binary is provided by [46]

$$J_{\mathrm{orb}}=M_{\mathrm{NS}}{M}_{\mathrm{WD}}{\left[{\displaystyle \frac{Ga(1-e^2)}{M_{\mathrm{tot}}}}\right]}^{1/2},$$

(4)

where $M_{\mathrm{tot}}=M_{\mathrm{NS}}+M_{\mathrm{WD}}$ is the total mass of the binary. The orbital angular momentum evolution of a compact binary is dominated by the changes due to the gravitational wave radiation (${\dot{J}}_{\mathrm{GW}}$), mass transfer (${\dot{J}}_{\mathrm{mt}}$), and coupling between the spin of the (primary) accretor and the orbit (${\dot{J}}_{\mathrm{so}}$) (e.g., [45]). The changes in the orbital angular momentum can be expressed as follows:

$${\dot{J}}_{\mathrm{orb}}={\dot{J}}_{\mathrm{GW}}+{\dot{J}}_{\mathrm{mt}}+{\dot{J}}_{\mathrm{so}}.$$

(5)

Because the magnitude of the orbital angular velocity of eccentric binaries is a periodic function of time, it is unlikely for the stellar rotation rate to be synchronized with the orbital motion during all orbital phases [47]. Therefore, for NS-WD binaries with an eccentric orbit, we ignore the effect of the coupling between the spin of the NS and the orbit on the evolution of the orbital angular momentum.

We can deduce the time derivative of the orbital angular momentum ${\dot{J}}_{\mathrm{orb}}$ based on Equation (4), i.e.,

$${\displaystyle \frac{{\dot{J}}_{\mathrm{orb}}}{J_{\mathrm{orb}}}}={\displaystyle \frac{1}{2}}{\displaystyle \frac{\dot{a}}{a}}+{\displaystyle \frac{{\dot{M}}_{\mathrm{NS}}}{M_{\mathrm{NS}}}}+{\displaystyle \frac{{\dot{M}}_{\mathrm{WD}}}{M_{\mathrm{WD}}}}-{\displaystyle \frac{1}{2}}{\displaystyle \frac{{\dot{M}}_{\mathrm{tot}}}{M_{\mathrm{tot}}}}-{\displaystyle \frac{e\dot{e}}{1-e^2}},$$

(6)

where ${\dot{M}}_{\mathrm{tot}}={\dot{M}}_{\mathrm{NS}}+{\dot{M}}_{\mathrm{WD}}$ and ${\dot{M}}_{\mathrm{WD}}<0$. The change of the orbital angular momentum caused by the gravitational wave radiation is provided by [46]

$${\displaystyle \frac{{\dot{J}}_{\mathrm{GW}}}{J_{\mathrm{orb}}}}=-{\displaystyle \frac{32}{5}}{\displaystyle \frac{G^3}{c^5}}{\displaystyle \frac{M_{\mathrm{NS}}{M}_{\mathrm{WD}}{M}_{\mathrm{tot}}}{a^4}}{\displaystyle \frac{\left(1+\frac{7}{8}{e}^2\right)}{{\left(1-e^2\right)}^{5/2}}}.$$

(7)

When the NS-WD binary is a detached system, the gravitational wave radiation can shrink the orbital separation by dissipating the angular momentum of the system. With orbital decay due to gravitational wave radiation, the radius of the Roche lobe gradually decreases. Eventually, mass transfer occurs from the WD to the NS through the inner Lagrange point $L_1$ when the WD fills its Roche lobe at the periastron. The angular momentum transferred from the WD to the neighborhood of the accreting NS along with the transferred matter can induce a change in the orbital angular momentum, which is provided by [44,48]

$${\dot{J}}_{\mathrm{mt}}=-\sqrt{G{M}_{\mathrm{NS}}{R}_{\mathrm{h}}}{\dot{M}}_{\mathrm{NS}},$$

(8)

where $R_{\mathrm{h}}$ is an equivalent radius of the accreted matter orbiting the accreting NS. This radius $R_{\mathrm{h}}$ can be written as [44]

$${\displaystyle \frac{R_{\mathrm{h}}}{a}}=r_{\mathrm{h}}=0.0883-0.04858\log q+0.011489{\log }^{2}q+0.020475{\log }^{3}q,$$

(9)

where ${10}^{-3}<q<1$. In the case of a fully developed accretion disk around the accreting NS, the angular momentum caused by the mass flow is canceled by a reverse flow [44,48,49], i.e., $R_{\mathrm{h}}=0$.

On the other hand, as one of the most active repeating FRBs to date, the isotropic peak luminosities of FRB 20201124A are very high (e.g., from $5\times {10}^{37}\mathrm{erg}{\mathrm{s}}^{-1}$ to $3\times {10}^{40}\mathrm{erg}{\mathrm{s}}^{-1}$; [33]), indicating that the emission mechanism of this FRB source should be efficient. Based on the bursts reported by Xu et al. [33] and Zhang et al. [34], the average accretion rates of two active episodes can be estimated to be ∼$1.4\times {10}^{-4}{M}_{\odot }{\mathrm{yr}}^{-1}$ and ∼$5.2\times {10}^{-5}{M}_{\odot }{\mathrm{yr}}^{-1}$, respectively, assuming that $L=0.1{\dot{M}}_{\mathrm{NS}}{c}^2$. Thus, the outflows should be taken into account in the NS-WD binary with super-Eddington accretion rates (${\dot{M}}_{\mathrm{Edd}}\sim {10}^{-8}{M}_{\odot }{\mathrm{yr}}^{-1}$). We use the accretion efficiency $ϵ$ to describe the fraction of the matter lost by the WD that is accreted by the NS, i.e.,

$${\dot{M}}_{\mathrm{NS}}=-ϵ{\dot{M}}_{\mathrm{WD}}$$

(10)

and

$${\dot{M}}_{\mathrm{tot}}=\left(1-ϵ\right){\dot{M}}_{\mathrm{WD}},$$

(11)

where $0\le ϵ\le 1$. If $ϵ=1$, then all matter transferred from the WD is accreted by the NS, that is, the total mass of the system is conserved (i.e., ${\dot{M}}_{\mathrm{NS}}=-{\dot{M}}_{\mathrm{WD}}$ and ${\dot{M}}_{\mathrm{tot}}=0$). The only way to lose orbital angular momentum in this case is through gravitational wave radiation. If $ϵ<1$, then the binary gradually loses mass. In addition to the gravitational wave radiation, the system can lose angular momentum along with the ejected matter:

$${\displaystyle \frac{{\dot{J}}_{\mathrm{loss}}}{J_{\mathrm{orb}}}}=\gamma {\displaystyle \frac{{\dot{M}}_{\mathrm{tot}}}{M_{\mathrm{tot}}}}.$$

(12)

In the particular case where the ejected matter carries the specific orbital angular momentum of the accretor, $\gamma =q$ (e.g., [48]).

Combining Equations (6)–(12), the change of the semimajor axis of the eccentric NS-WD binary during the mass transfer process can be written as follows:

$${\displaystyle \frac{\dot{a}}{2a}}={\displaystyle \frac{{\dot{J}}_{\mathrm{GW}}}{J_{\mathrm{orb}}}}-{\displaystyle \frac{{\dot{M}}_{\mathrm{WD}}}{M_{\mathrm{WD}}}}\left[\left(1-ϵq\right)-{\displaystyle \frac{\left(1-ϵ\right)q}{1+q}}\left(\gamma +{\displaystyle \frac{1}{2}}\right)-ϵ\sqrt{{\displaystyle \frac{\left(1+q\right)r_{\mathrm{h}}}{1-e^2}}}\right]+{\displaystyle \frac{e\dot{e}}{1-e^2}}.$$

(13)

It is seen that the orbital separation can decay due to the gravitational wave radiation, mass loss, and orbital circularization.

At the periastron, the mass transfer from the WD to the NS occurs through the inner Lagrange point $L_1$ when the WD fills its Roche lobe. The radii of WD and its Roche lobe can change due to the mass loss of the WD. To ensure the stability of mass transfer, the change in the Roche lobe radius of the WD $R_{\mathrm{L}2}$ should exceed the change in its radius $R_{\mathrm{WD}}$, i.e.,

$${\dot{R}}_{\mathrm{L}2}\gtrsim {\dot{R}}_{\mathrm{WD}}.$$

(14)

By dividing both sides of Equation (14) by $R_{\mathrm{L}2}=R_{\mathrm{WD}}$ and ${\dot{M}}_{\mathrm{WD}}/M_{\mathrm{WD}}<0$, a well known criterion for the stability of mass transfer can be obtained (e.g., [44,50]):

$${\zeta }_{\mathrm{L}2}\lesssim {\zeta }_{\mathrm{WD}}$$

(15)

where ${\zeta }_{\mathrm{L}2}=\partial \ln R_{\mathrm{L}2}/\partial \ln M_{\mathrm{WD}}$ is the response of the Roche lobe radius of the WD to the mass loss and ${\zeta }_{\mathrm{WD}}=\partial \ln R_{\mathrm{WD}}/\partial \ln M_{\mathrm{WD}}$ is the response of the WD radius to the mass loss. If the WD does not obey this criterion to start transferring matter via Roche lobe overflow, then the increase in WD radius after mass loss is larger than the effective expansion of its Roche lobe. In this case, the Roche lobe overflow tends to be unstable.

Based on Equation (3), the logarithmic differentiation of WD radius ${\zeta }_{\mathrm{WD}}$ can be written as

$${\zeta }_{\mathrm{WD}}={\displaystyle \frac{\partial \ln R_{\mathrm{WD}}}{\partial \ln M_{\mathrm{WD}}}}=-{\displaystyle \frac{1}{3}}\left[{\displaystyle \frac{1+{\left(\frac{M_{\mathrm{WD}}}{M_{\mathrm{Ch}}}\right)}^{4/3}}{1-{\left(\frac{M_{\mathrm{WD}}}{M_{\mathrm{Ch}}}\right)}^{4/3}}}\right]+{\displaystyle \frac{2}{3}}\left[{\displaystyle \frac{1+\frac{7}{3}{\left(\frac{M_{\mathrm{WD}}}{M_{\mathrm{p}}}\right)}^{1/3}}{1+\frac{7}{2}{\left(\frac{M_{\mathrm{WD}}}{M_{\mathrm{p}}}\right)}^{1/3}+\left(\frac{M_{\mathrm{WD}}}{M_{\mathrm{p}}}\right)}}\right].$$

(16)

The factor ${\zeta }_{\mathrm{L}2}$ can be derived by logarithmic differentiation of Equation (2). We can deduce the critical mass ratio at which the unstable mass transfer occurs based on ${\zeta }_{\mathrm{L}2}\lesssim {\zeta }_{\mathrm{WD}}$. Figure 2 shows the logarithmic change in the radii of the WD and its Roche lobe due to mass transfer. In the NS-WD binary, we set the WD mass in the range of $0.01-1M_{\odot }$ and $M_{\mathrm{NS}}=1.4M_{\odot }$. The black and colored lines describe the logarithmic change in the WD radius and Roche lobe radius, respectively, while the solid and dashed lines represent the NS-WD binary with circular and eccentric orbits (e.g., $e=0.5$), respectively. The blue lines describe the logarithmic change in the Roche lobe radius when the total mass of the system is conserved, i.e., $ϵ=1$. The red and green lines describe the logarithmic changes in the Roche lobe radius when the total mass of the system gradually decreases, i.e., $ϵ=0.5$ (red) and $ϵ=0.1$ (green). Unstable mass transfer occurs when the black line describing the response of the WD radius falls below the colored lines describing the changes in the Roche lobe radius. As shown in Figure 2, mass transfer is dynamically unstable if $M_{\mathrm{WD}}>0.9M_{\odot }$, corresponding to $q\gtrsim 2/3$ (e.g., [40,48]). Moreover, the critical WD mass $M_{\mathrm{c}}$ in a NS-WD binary with an eccentric orbit is larger than that in a binary with a circular orbit. We can find that the critical WD mass decreases as the accretion efficiency $ϵ$ decreases, i.e., $ϵ=0.5$, $M_{\mathrm{c}}\sim 0.85M_{\odot }$, and $ϵ=0.1$, $M_{\mathrm{c}}\sim 0.8M_{\odot }$.

Based on the criterion ${\zeta }_{\mathrm{L}2}\lesssim {\zeta }_{\mathrm{WD}}$, the change of the eccentricity e during the stable mass transfer process can be written as

$${\displaystyle \frac{\dot{e}}{1+e}}\lesssim {\displaystyle \frac{2{\dot{J}}_{\mathrm{GW}}}{J_{\mathrm{orb}}}}-{\displaystyle \frac{2{\dot{M}}_{\mathrm{WD}}}{M_{\mathrm{WD}}}}\left[\left({\displaystyle \frac{5}{6}}-ϵq\right)-{\displaystyle \frac{\left(1-ϵ\right)q}{1+q}}\left(\gamma +{\displaystyle \frac{1}{3}}\right)-ϵ\sqrt{{\displaystyle \frac{\left(1+q\right)r_{\mathrm{h}}}{1-e^2}}}-{\displaystyle \frac{\partial \ln R_{\mathrm{WD}}}{\partial \ln M_{\mathrm{WD}}}}\right].$$

(17)

Therefore, we can combine Equations (13) and (17) to evaluate the orbital evolution of the NS-WD binary during the stable mass transfer process.

3.3. Mass Transfer Rate

For the NS-WD binary with an eccentric orbit, mass transfer from the WD to the NS occurs when the WD fills its Roche lobe at the periastron, i.e., $R_{\mathrm{WD}}=R_{\mathrm{L}2}$. We can define the overfill factor to indicate how much the donor overfills its Roche lobe by, i.e.,

$$\Delta =R_{\mathrm{WD}}-R_{\mathrm{L}2}.$$

(18)

Mass transfer occurs when $\Delta >0$. The adiabatic approximation of the mass transfer rate of the donor can be written as [45]

$${\dot{M}}_{\mathrm{WD}}=-f\left(M_{\mathrm{NS}},M_{\mathrm{WD}},a,R_{\mathrm{WD}}\right){\Delta }^3,$$

(19)

which increases monotonically with $\Delta$. As the system evolves, the mass transfer rate changes, leading to variations in the overfill factor. The change of the overfill factor is provided by [45]

$${\displaystyle \frac{d\Delta }{dt}}=R_{\mathrm{WD}}\left[\left({\zeta }_{\mathrm{WD}}-{\zeta }_{\mathrm{rL}}\right){\displaystyle \frac{{\dot{M}}_{\mathrm{WD}}}{M_{\mathrm{WD}}}}-{\displaystyle \frac{\dot{a}}{a}}\right],$$

(20)

where ${\zeta }_{\mathrm{rL}}=\partial \ln (R_{\mathrm{L}2}/a)/\partial \ln M_{\mathrm{WD}}$. A good approximation for the mass transfer rate can be obtained by setting the right-hand side of Equation (20) to 0 [45,51]. Therefore, we obtain

$${\displaystyle \frac{{\dot{M}}_{\mathrm{WD}}}{M_{\mathrm{WD}}}}={\displaystyle \frac{{\dot{J}}_{\mathrm{GW}}/J_{\mathrm{orb}}}{\frac{\left({\zeta }_{\mathrm{WD}}-{\zeta }_{\mathrm{rL}}\right)}{2}+\left(1-ϵq\right)-\frac{\left(1-ϵ\right)q}{1+q}\left(\gamma +\frac{1}{2}\right)-ϵ\sqrt{\frac{\left(1+q\right)r_{\mathrm{h}}}{1-e^2}}}}.$$

(21)

In the case of mass transfer in eccentric orbits, the evolution of the mass transfer rate has a Gaussian-like (or delta function) behavior, with the maximum mass transfer rate occurring at periastron [47,52,53]. Thus, we assume that Roche lobe outflow occurs only at periastron. The duration of the Roche lobe overflow can be evaluated as follows (e.g., [54]):

$$t_{\mathrm{RLOF}}\simeq R_{\mathrm{p}}/v_{\mathrm{p}}={\left({\displaystyle \frac{R_{\mathrm{p}}^3}{2G{M}_{\mathrm{NS}}}}\right)}^{1/2},$$

(22)

where $R_{\mathrm{p}}=a(1-e)$ is the distance between the binary components when the WD approaches periastron and $v_{\mathrm{p}}={(2G{M}_{\mathrm{NS}}/R_{\mathrm{p}})}^{1/2}$ is the WD’s orbital speed at $R_{\mathrm{p}}$. Combining Equations (21) and (22), we can estimate the transferred mass from the WD during periastron passage.

3.4. Results

We numerically integrate Equations (13), (17) and (21), starting from the onset of mass transfer. The short-term evolution (about one hundred years) of the NS-WD binary with an eccentric orbit is shown in Figure 3. We assume that the original system consists of a $1.4M_{\odot }$ NS and a $0.6M_{\odot }$ WD with an eccentricity $e=0.3$. In this case, the initial orbital period of the binary is ∼94 s, comparable to the long-duration peaks of the wait time distributions of FRBs 20121102A [37] and 20201124A [33].

In Figure 3, the different colored lines represent the evolution of the physical parameters under various accretion efficiencies $ϵ$ and $\gamma$, i.e., $ϵ=1,\gamma =0$ (blue), $ϵ=0.5,\gamma =q$ (red), and $ϵ=0.1,\gamma =q$ (green). For $ϵ=1$ and $\gamma =0$, the total mass of the system is conserved and all matter transferred from the WD is accreted by the NS. In this case, the only mechanism for losing orbital angular momentum is gravitational wave radiation. For the other two cases, the ejected matter provides an additional way to lose orbital angular momentum, resulting in a more significant reduction in both the orbital period and the eccentricity of the NS-WD binary. It can be seen from Figure 3 that the physical parameters of the NS-WD binary, including the orbital eccentricity e, semimajor axis a, and orbital period $P_{\mathrm{orb}}$ (panels a, b, and d of Figure 3, respectively), can be significantly reduced during the mass transfer process; moreover, the variations of these parameters in the two cases of $ϵ=0.5$ and $ϵ=0.1$ are greater than those in the case of $ϵ=1$. On the other hand, the WD mass loss rate ${\dot{M}}_{\mathrm{WD}}$ for the binary system with mass ejection is greater than that for the mass-conserving system (see panel c of Figure 3).

Although the orbital period of the NS-WD binary can be significantly reduced by the short-term Roche lobe overflow, the magnitude of the orbital period shrinkage is still smaller than that of the reductions in the long-duration waiting-time peaks of FRBs 20121102A and 20201124A (see panel d of Figure 3).

4. Unstable Mass Transfer

As shown in Figure 1, in the case of $M_{\mathrm{WD}}=1.2M_{\odot }$ (dotted line), the range of the orbital periods of the NS-WD binaries with different eccentricities is consistent with the range of variations in the long-duration wait time peaks of both repeaters. The presence of a $1.2M_{\odot }$ WD suggests that the binary system undergoes an unstable mass transfer process (see Figure 2), i.e., ${\zeta }_{\mathrm{L}2}>{\zeta }_{\mathrm{WD}}$, leading to evolution on dynamical time-scales. In this case, the WD would expand dramatically over about tens of orbital periods [55], inducing a sharp increase in the mass transfer rate (e.g., ${\dot{M}}_{\mathrm{WD}}\gtrsim 100M_{\odot }{\mathrm{yr}}^{-1}$; [55]). The NS is unable to accrete all the transferred materials, which subsequently pile up on the surface of the NS and begin to expand, eventually overfilling its Roche lobe. This results in the binary system becoming engulfed by a common envelope (CE). Due to the friction drag within the CE, the orbital energy of the embedded binary is reduced and deposited in the CE. If the total deposited energy can overcome the binding energy of the envelope, then orbital decay occurs, producing a binary with a very short orbital period following CE ejection. In contrast, if the CE fails to eject, then the inner binary coalesces into a single fast-rotating star (e.g., [56,57]).

The standard CE equation (known as the $\alpha$-mechanism) based on energy conservation can be written as [58,59]

$${\alpha }_{\mathrm{CE}}\left({\displaystyle \frac{G{M}_2{M}_{1,\mathrm{f}}}{2a_{\mathrm{f}}}}-{\displaystyle \frac{G{M}_{1,\mathrm{i}}{M}_2}{2a_{\mathrm{i}}}}\right)={\displaystyle \frac{G{M}_{1,\mathrm{i}}\left(M_{1,\mathrm{i}}-M_{1,\mathrm{f}}\right)}{\lambda R_1}},$$

(23)

where $M_{1,\mathrm{i}}$ and $M_2$ are the initial masses of the donor and the accretor, respectively, $M_{1,\mathrm{f}}$ is the final mass of the donor that lost its envelope, $a_{\mathrm{i}}$ and $a_{\mathrm{f}}$ are the initial and final binary separations, respectively, and $R_1$ is the radius of the donor at the onset of CE. The left-hand term of Equation (23) is the energy $\Delta E_{\mathrm{orb}}$ released from orbital shrinkage, the right-hand term of Equation (23) is the binding energy, and $\lambda$ is a parameter describing the structure of the envelope. The CE ejection efficiency ${\alpha }_{\mathrm{CE}}$ is defined as the fraction of reduced orbital energy that is used in ejecting the CE. This $\alpha$-mechanism can be used to explain the formation and evolution of some close interacting binaries, including cataclysmic variables, low-mass X-ray binaries [60], and double-degenerate WD binaries [59]. However, some uncertainties exist in the $\alpha$-mechanism; for example, the exact values of ${\alpha }_{\mathrm{CE}}$ and $\lambda$ are hardly determined, and the exact boundary between the stellar envelope and its core is hard to constrain (e.g., [57]).

If the angular momentum of the orbit is so large that the common envelope can easily be made to co-rotate with the orbit, then there are no drag forces anymore [61]. In this case, it is assumed that the entire envelope is lost completely from the binary system [61,62]. The mass loss process reduces the angular momentum of the system in a linear way, which can be written as follows:

$${\displaystyle \frac{J_{\mathrm{i}}-J_{\mathrm{f}}}{J_{\mathrm{i}}}}={\gamma }_{\mathrm{CE}}{\displaystyle \frac{\Delta M}{M_{\mathrm{tot}}}}$$

(24)

where $\Delta J=J_{\mathrm{i}}-J_{\mathrm{f}}$ is the decrease in the angular momentum due to CE ejection and $\Delta M$ is the envelope mass lost from the binary. This $\gamma$-mechanism is based on the angular momentum conservation, which was used in [61] to reconstruct the evolutionary histories of three double-He WDs with ${\gamma }_{\mathrm{CE}}$ in the range of 1.4 to 1.7. The change in orbital period is provided by [61,62]

$${\displaystyle \frac{P_{\mathrm{f}}}{P_{\mathrm{i}}}}={\left({\displaystyle \frac{M_{1,\mathrm{f}}{M}_{2,\mathrm{f}}}{M_{1,\mathrm{i}}{M}_{2,\mathrm{i}}}}\right)}^{-3}\left({\displaystyle \frac{M_{1,\mathrm{f}}+M_{2,\mathrm{f}}}{M_{1,\mathrm{i}}+M_{2,\mathrm{i}}}}\right){\left(1-{\gamma }_{\mathrm{CE}}{\displaystyle \frac{\Delta M}{M_{1,\mathrm{i}}+M_{2,\mathrm{i}}}}\right)}^3,$$

(25)

where $P_{\mathrm{i}}$ and $P_{\mathrm{f}}$ are the orbital periods of the binary system before and after CE ejection, respectively, and $M_{2,\mathrm{i}}$ and $M_{2,\mathrm{f}}$ are the initial and final masses of the accretor, respectively.

Based on Equation (25), we can obtain the relationship between the ratio of the final to the initial orbital period $P_{\mathrm{f}}/P_{\mathrm{i}}$ and the mass loss $\Delta M_{\mathrm{WD}}$ due to CE ejection (Figure 4). The component masses of the NS-WD binary at the onset of CE are $M_{\mathrm{NS}}=1.4M_{\odot }$ and $M_{\mathrm{WD}}=1.2M_{\odot }$, respectively. As shown in Figure 4, different colored lines represent different ${\gamma }_{\mathrm{CE}}$, i.e., ${\gamma }_{\mathrm{CE}}=1$ (black), 2 (blue), 3 (green), and 4 (orange). A larger value of ${\gamma }_{\mathrm{CE}}$ indicates that a greater fraction of the angular momentum of the initial binary is carried away by the ejected material [61]. The red and purple dashed lines indicate the ratios of the peak waiting times in two different activity phases for FRBs 20121102A and 20201124A, respectively.

4.1. FRB 20121102A

To make the change in the orbital period of the NS-WD binary comparable to the variation in the wait time peaks of FRB 20121102A, the mass of the ejected material $\Delta M_{\mathrm{WD}}$ should range from ∼$0.5M_{\odot }$ to ∼$0.7M_{\odot }$ when ${\gamma }_{\mathrm{CE}}$ varies between 3 and 4 (see the red dashed line in Figure 4). After CE ejection, the remaining WD mass ($M_{\mathrm{WD}}\sim 0.5–0.7M_{\odot }$) falls below the critical mass ($M_{\mathrm{c}}\sim 0.9M_{\odot }$) and the mass transfer process of the NS-WD binary becomes stable. Subsequently, the eccentricity e of both the orbit and the orbital period decrease as the orbital angular momentum decreases.

The possible evolutionary history of FRB 20121102A is as follows. A massive WD ($M_{\mathrm{WD}}=1.2M_{\odot }$) may be tidally captured by the NS (e.g., [63]), as large eccentricity e of the orbit is required to interpret the initial orbital period of the system. After the formation of a detached NS-WD binary, the orbital separation can be reduced by the gravitational wave radiation, resulting in a steady decrease in the Roche lobe radius of the WD. In this stage, mass loss from the WD may occur through a tidally enhanced wind (e.g., [64]). The interaction between the wind and the magnetosphere of the NS could produce coherent radio emissions [65]. When the WD fills its Roche lobe, dynamic unstable mass transfer occurs. A fraction of the transferred material approaches the NS surface, producing strong electromagnetic radiation by curvature radiation [22], whereas the majority of the transferred material cannot be accreted by the NS, leading to the formation of a CE. The angular momentum and the orbital period of the NS-WD binary both decrease due to the CE ejection. Therefore, the time interval between two adjacent bursts decreases as the orbital period shortens. After the CE ejection, the residual mass of the WD falls below the critical mass $M_{\mathrm{c}}$. Stable mass transfer can occur when the WD fills its Roche lobe at the periastron. Radio emissions can be produced when the accreted materials approach the surface of the NS. This burst phase could correspond to the burst storm observed by Arecibo [37] and FAST [32]. The orbital angular momentum of the NS-WD binary system is further reduced due to gravitational wave radiation and mass loss. When the eccentric orbit of the NS-WD binary system turns into a circular orbit, the mass transfer process always proceeds if the WD fills its Roche lobe. The FRB source may enter an extremely active phase, leading to a shorter time interval between two adjacent bursts.

In summary, the NS-WD binary model with an eccentric orbit can reconstruct the change in the burst activity of FRB 20121102A through the combined effects of CE ejection and Roche lobe overflow.

4.2. FRB 20201124A

For FRB 20201124A, as shown in Figure 4, the mass of the ejected material exceeds $1M_{\odot }$ when ${\gamma }_{\mathrm{CE}}=3–4$, which can account for the changes in the waiting time peaks. After CE ejection, the binary system containing an NS and a naked O-Ne WD [55] is in a circular orbit. Because the envelope of the WD is completely ejected, the mass transfer rate of the remaining component ($M_{\mathrm{WD}}<0.2M_{\odot }$, ${\dot{M}}_{\mathrm{WD}}\sim {10}^{-7}{M}_{\odot }{\mathrm{yr}}^{-1}$; [55]) is lower than that of the previous activity episodes, leading to a sharp decrease in the event rate of FRB 20201124A [66].

Nelemans et al. [61] considered two CE episodes to reconstruct the evolutionary histories of three double He WDs with ${\gamma }_{\mathrm{CE}}$ ranging from 1.4 to 1.7. In our model, the NS-WD binary system may also undergo two or more CE episodes with ${\gamma }_{\mathrm{CE}}$ ranging from 3 to 4, which would account for the variations in the wait time peaks of FRB 20201124A. After a CE ejection, the orbital separation decreases as the orbital angular momentum is reduced by the ejected material. Then, the Roche lobe radius of the WD would be reduced due to the gravitational wave radiation, causing the WD to fill its Roche lobe and triggering the next unstable mass transfer. In this scenario, the orbital period of the NS-WD binary becomes comparable to the waiting time peak after two or more CE episodes.

The orbital angular momentum of the evolved NS-WD binary is further reduced by gravitational wave radiation. Finally, the NS-WD binary merges. If the final remnant is a magnetar, then the NS-WD merged channel could produce one-off FRBs (e.g., FRB 20180924B; [67]).

5. Conclusions and Discussion

In this paper, we have revisited the NS-WD binary model with an eccentric orbit to explain the observed variations in the long-duration wait time peaks of FRBs 20121102A and 20201124A. In our model, the decreases in the wait time peaks correspond to the decays in the orbital periods of the binary system. We consider two modes of mass transfer, namely, stable and unstable, to study the evolution of the orbital period of the binary system. Our main results are summarized as follows:

• In the case of stable mass transfer (e.g., $M_{\mathrm{WD}}=0.6M_{\odot }$), although the short-term Roche lobe overflow can significantly shorten the orbital period of the NS-WD binary, the magnitude of the orbital period shrinkage cannot fully account for the observed reductions in the long-duration wait time peaks of FRBs 20121102A and 20201124A (see Section 3).
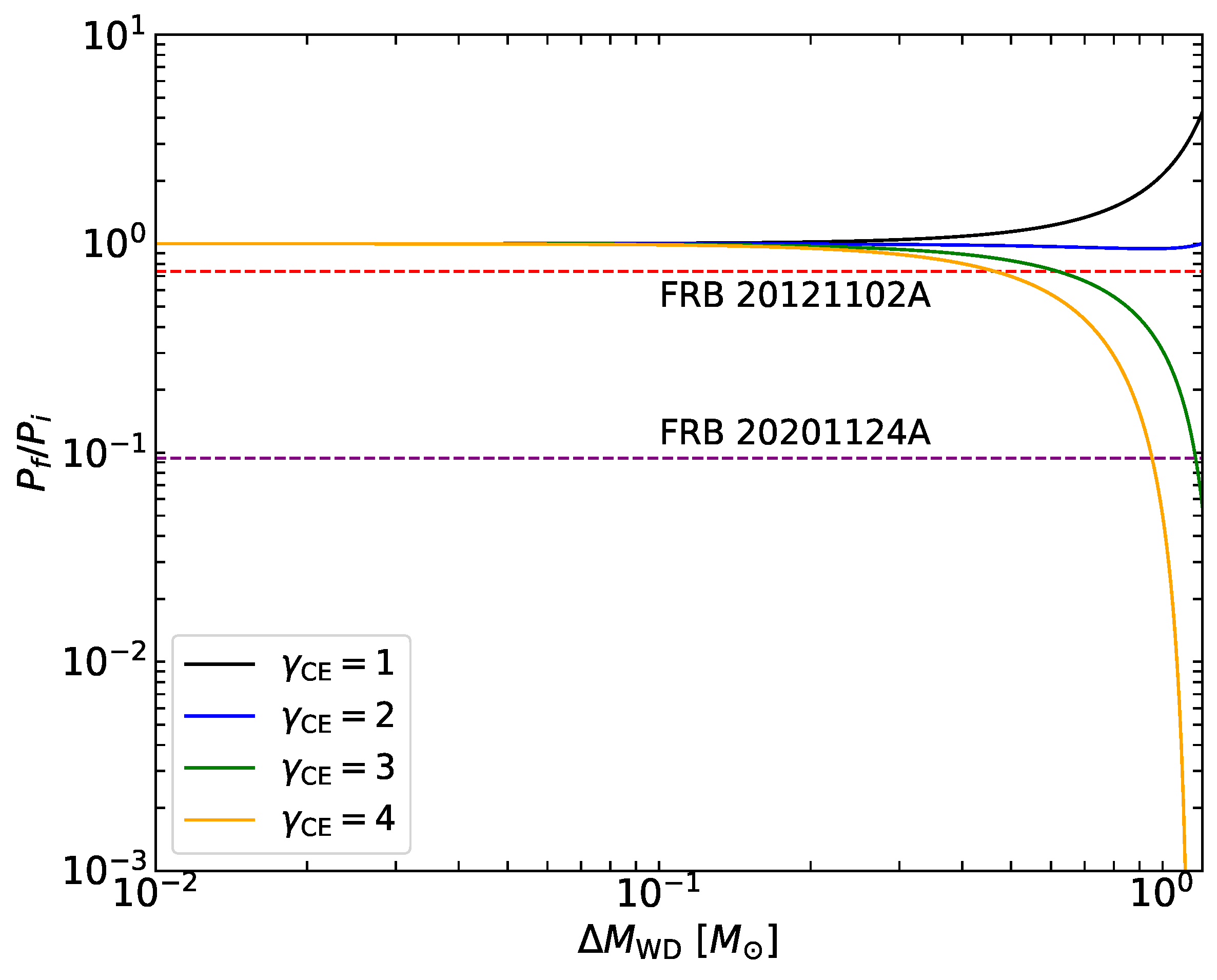
• The CE ejections provide an additional and more efficient mechanism for angular momentum loss in the system with a massive WD (e.g., $M_{\mathrm{WD}}=1.2M_{\odot }$). By applying the $\gamma$-mechanism to the CE ejections, the variations in the orbital period of the NS-WD binary, which are comparable to the changes in the wait time peaks of two repeaters, can be reconstructed with ${\gamma }_{\mathrm{CE}}$ ranging between 3 and 4. Furthermore, our analysis also suggests distinct evolutionary pathways for the two sources; for FRB 20121102A, the binary likely undergoes a combination of CE ejection and Roche lobe overflow, while for FRB 20201124A the system may experience multiple CE ejections (see Figure 4, Section 4).
• For FRB 20121102A, the remnant WD mass falls below the critical mass $M_{\mathrm{c}}$ after the CE phase. Stable mass transfer occurs when the WD fills its Roche lobe at the periastron. For FRB 20201124A, the final binary system consisting of an NS and a stripped O-Ne WD should be in a circular orbit. Following the complete ejection of the WD envelope, the remaining mass transfer rate decreases significantly, leading to a sharp decrease in the event rate of FRB 20201124A (see Section 4.1 and Section 4.2).

The observations of the two burst episodes for FRBs 20121102A and 20201124A are discontinuous [32,33,34,37], suggesting that the variations in the fitted wait time peaks across different activity epochs are also discontinuous. Thus, uncertainties remain in determining the evolutionary stage of the NS-WD binary based on the wait time peaks, such as estimating the WD mass before and after mass transfer.

Our evaluations indicate that the critical WD mass distinguishing stable from unstable mass transfer is $M_{\mathrm{c}}\sim 0.9M_{\odot }$. Furthermore, ejecting a sufficient amount of transferred material from the system could reduce the stability of mass transfer. Many studies have explored the stability of mass transfer in WD-NS systems. For example, Verbunt & Rappaport [44] showed that if the transferred angular momentum is efficiently returned to the binary orbit by an accretion disk (i.e., $R_{\mathrm{h}}=0$), then the critical WD mass is ∼$0.6M_{\odot }$. In contrast, the critical WD mass without an accretion disk drops to around $0.3M_{\odot }$. Taking into account the isotropic re-emission mass transfer, van Haaften et al. [48] suggested a WD mass limit of ∼$0.8M_{\odot }$. Based on hydrodynamic simulations, given that the angular momentum of the binary is lost by the disk wind, Bobrick et al. [55] reported a significantly lower critical WD mass of ∼$0.2M_{\odot }$.

In addition to the variations in the long-duration wait time peaks, FRB 20201124A exhibits dramatic variations in the Faraday rotation measure on a day timescale, similar to FRB 20121102A (e.g., [68]). These findings suggest the presence of a complex, dynamically evolving, and magnetized environment within the host galaxy [33]. Wang et al. [69] proposed that FRB 20201124A may be produced by a binary system containing a magnetar and a Be star surrounded by a decretion disk. The orbital period is assumed to be 80 days, with orbital eccentricity $e=0.75$. The interactions between radio bursts, the decretion disk, and various magnetic field components can naturally explain the variable rotation measures. In our model, the violent and unstable accretion process combined with the interactions between the radio bursts, the materials of the common envelope, and the magnetic field could explain the varying rotation measures [70]. After CE ejection, a non-evolving rotation measure can also be expected due to the vanishing of the CE [38].

Moreover, a massive WD-NS merger could produce some gamma ray bursts (GRBs), e.g., GRB 211211A [71,72]. A millisecond magnetar is a likely outcome of such a merger if the magnetic field of the post-merger product is amplified through a mechanism such as an $\alpha$–$\Omega$ dynamo. Then, at least a subset of FRB 180924-like FRBs could be produced by the magnetar within the framework of flaring magnetars [67]. On the other hand, due to their short orbital periods, NS-WD binaries are important sources of gravitational waves. The relationship between the gravitational wave frequency and the orbital period is given by $f=2/P_{\mathrm{orb}}$. Thus, the gravitational wave frequency of the closest NS-WD binary lies in the range of ${10}^{-2}$–${10}^{-1}$ Hz, which will potentially be observable by the Laser Interferometer Space Antenna (LISA) (${10}^{-4}$–${10}^{-1}$ Hz; [73]) in the future.

Similar to FRBs 20121102A and 20201124A, the wait time distributions of the active repeaters FRBs 20220912A and 20240114A also exhibit bimodal structures [74,75]. Double-peaked profiles of the wait time distributions seem to be a universal feature of active repeating FRBs. Xiao et al. [76] suggested that this asymmetric shape can be explained by the propagation effect in the magnetosphere of magnetars. Luo et al. [77] considered a rotation-modulated starquake model in magnetars to construct the wait time distribution. In future work, we aim to provide a detailed explanation of this bimodal structure based on the NS-WD binary system.