Next Article in Journal
The Impact of the Eccentricity on the Collapse of an Ellipsoid into a Black Hole
Previous Article in Journal
Bounce Cosmology in a Locally Scale Invariant Physics with a U(1) Symmetry
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Universe
Volume 11
Issue 3
10.3390/universe11030094
universe-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Communication

Predicting Ground-Level Enhancement Events and >500 MeV Proton Intensity Using Proton and Electron Observations

by
Marlon Núñez
Department of Languages and Computer Sciences, Universidad de Málaga, 29016 Málaga, Spain
Universe 2025, 11(3), 94; https://doi.org/10.3390/universe11030094
Submission received: 19 December 2024 / Revised: 2 March 2025 / Accepted: 5 March 2025 / Published: 12 March 2025
Browse Figures
Versions Notes

Abstract

:
Ground-Level Enhancements (GLEs) pose a potential hazard for crew and passengers on polar routes. The accurate estimation of the integral proton flux of Solar Energetic Particle (SEP) events is crucial for assessing the expected radiation dose. This paper describes a new approach that predicts the occurrence of GLEs and the associated >500 MeV intensity using proton and electron data. The new approach utilizes the Geostationary Operational Environmental Satellites (GOESs) for proton observations and the Advanced Composition Explorer (ACE) satellite for electron observations. Núñez et al. proposed a GLE occurrence predictor called the High Energy Solar Particle Events foRecastIng and Analysis (HESPERIA) University of Málaga Solar particle Event Predictor (UMASEP-500), which did not include a model for predicting the >500 MeV integral proton intensity. This paper presents a comparison in terms of the GLE event occurrence between the HESPERIA UMASEP-500 and a new approach called UMASEP-500. Although the new approach shows a slightly better critical success index (CSI), which combines the probability of detection (POD) and false alarm ratio (FAR), the difference is not statistically significant. The main advantage of the new UMASEP-500 is its ability to predict the expected >500 MeV proton intensity. This study provides initial insight into a new era of electron and proton telescopes that will be available at L1 in the coming years.

1. Introduction

Solar eruptions can accelerate particles to high relativistic energies. These energetic particles can reach Earth, penetrate its magnetic field, and enter its atmosphere [1,2]. The arrival of high-energy particles in the atmosphere increases the radiation environment. These events generate intricate cascades of atmospheric particles composed of secondary particles, which can be recorded by ground-based instruments like neutron monitors. When these devices detect a significant increase in particle counts, it is recognized as a Ground-Level Enhancement (GLE) [3]. GLEs pose a particular hazard at aviation altitudes where pilots, crew, and passengers can be exposed to dangerous levels of radiation [4,5,6,7]. The associated Solar Energetic Particle (SEP) events in space may damage spacecraft’s electronic components and confer a significantly high risk of cancer to astronauts [8,9,10].
Timely and accurate GLE warnings may provide airplanes the opportunity to reroute their flights to lower latitudes [6], and space launch operators may reschedule or postpone a launch [8]. Current GLE alert systems are based either on ground observations (neutron and/or muon counters) or proton observations by Geostationary Operational Environmental Satellites (GOESs). When neutron monitors are used, GLE alert systems [11,12,13,14,15,16,17] require the reception of several (usually three) station alerts, so their warnings can be emitted when the GLE event has already started and is being recorded on Earth. Núñez et al. [18] proposed the first proton-data-based GLE occurrence predictor, called the High Energy Solar Particle Events foRecastIng and Analysis (HESPERIA) University of Málaga Solar particle Event Predictor (UMASEP)-500, which is able to issue warnings a few minutes earlier than neutron-data-based GLE alert systems for approximately half of the events.
Electron observations have not been used so far in GLE nowcasting or prediction systems. Posner [19] found that near-relativistic electrons arrive earlier than protons during SEP events. In this study, the introduced tool, called UMASEP-500, assesses the use of Advanced Composition Explorer (ACE) electrons in addition to GOES protons for predicting the occurrence of GLE events and the >500 MeV peak proton intensity.
Several approaches have been applied to empirically predict SEP proton intensity: using a database with the characteristics of the parent solar flare and pre-calculated SEP peak flux of hundreds of SEP events [20]; or by using the predicted shock speed at Earth from the Shock ARrival Model (SARM) [21] as a proxy for predicting the integral proton flux of >10 MeV SEP events. In this paper, UMASEP-500 uses a novel approach that involves training a machine learning (ML) model with historical >500 MeV SEP peak fluxes.
Besides the prediction of GLE events, it is crucial to estimate the associated human radiation exposure from the Earth’s surface to deep space. It is well recognized that there is a strong relationship between the radiation dose at aviation altitudes and the associated particle measurements, either by neutron monitor stations or proton observations from GOESs. This provides a scientific basis for using any of these particle measurements as useful proxies for forecasting radiation doses experienced by flight crews and passengers [4,5], helping mitigate the risks that GLEs pose to human health.
Currently, there are a number of models for assessing radiation exposure that are available to the aviation community, including the CARI-7A (Civil Aeromedical Research Institute) model [22], the PANDOCA (Professional Aviation Dose Calculator) model [23], and the Nowcast of Aerospace Ionizing Radiation System (NAIRAS) [24,25]. For applications in space, the Acute Radiation Risks Tool (ARTT) [26] is also able to predict the radiation dose and the biological effects for astronauts on the ORION capsule for NASA’s Artemis missions. If proton intensity predictions associated with very energetic SEP events are predicted before the occurrence of the corresponding event, then earlier real-time radiation dose predictions are also possible before the detection of the corresponding event. Thus, Hu et al. [27] studied the feasibility of making radiation dose predictions onboard the ORION capsule by coupling the capabilities of the ARTT and UMASEP-100 [28], with UMASEP-100 being used to predict >100 MeV SEP events and provide proton intensity estimations. Mertens et al. [29] proposed the prediction of global atmospheric ionizing radiation exposure at commercial airline altitudes by coupling the NAIRAS with the >500 MeV SEP intensity predictions made by a preliminary prototype of the UMASEP-500. The aforementioned prototype has been refined and its forecast capability is introduced in this study.
This paper is organized as follows: Chapter 2 explains a new occurrence model that is different from that used in the HESPERIA UMASEP-500 and introduces the >500 MeV intensity prediction approach of the UMASEP-500. Chapter 3 compares the proposed proton-electron-based UMASEP-500 tool with the proton-based HESPERIA UMASEP-500 in terms of GLE occurrence predictions. Since the HESPERIA UMASEP-500 does not make intensity predictions, this chapter presents the intensity prediction forecast capability of the UMASEP-500 only. Chapter 4 presents some discussions about the results, and Chapter 5 presents the conclusions.

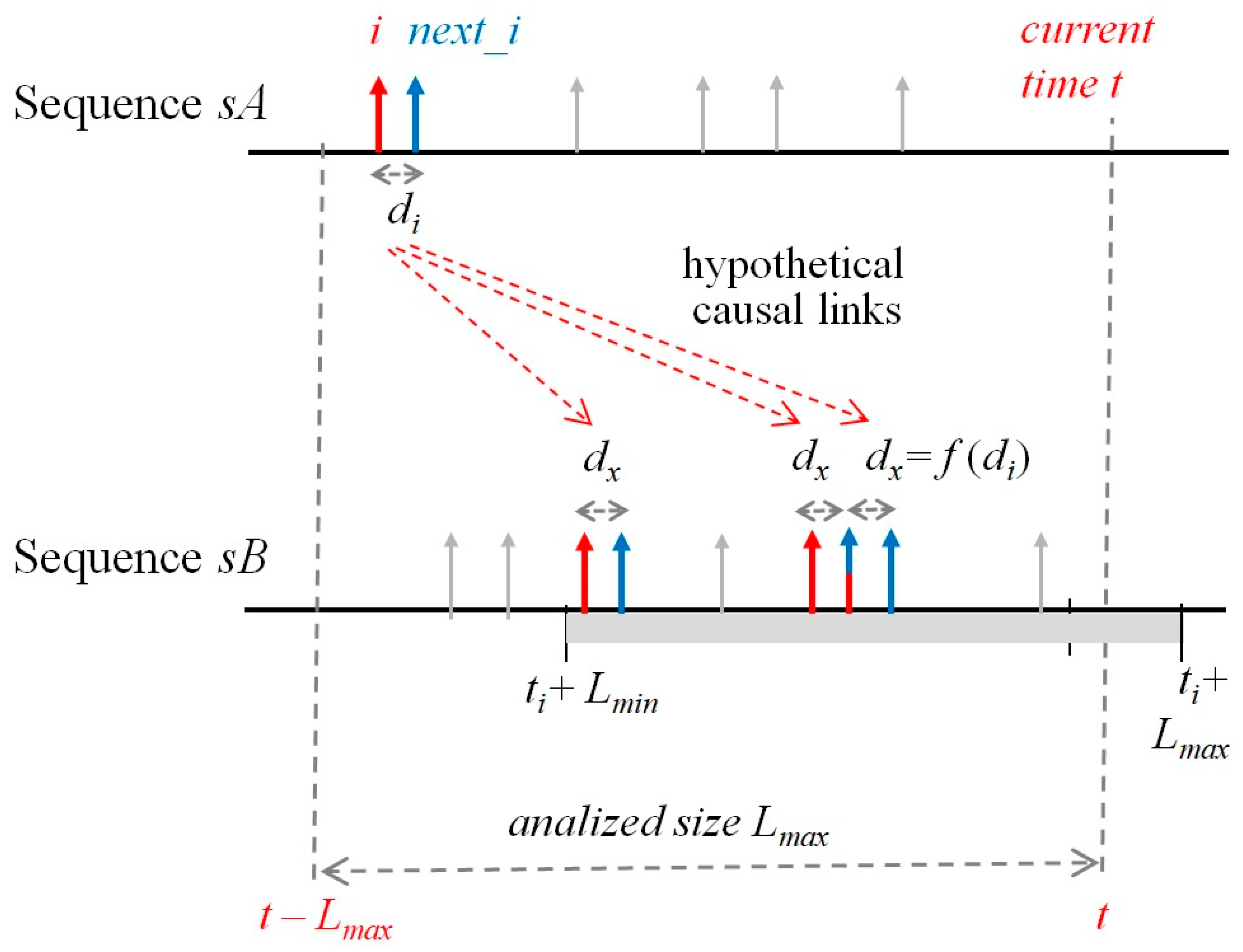
2. Materials and Methods

UMASEP-500 is founded on the Well-Connected events Prediction model—version 2 (WCP2) [30]. In contrast, HESPERIA UMASEP-500 utilizes an earlier version, the WCP1 model [31]. In this paper, the WCP2 model predicts well-connected >500 MeV SEP events, but its internal parameters are calibrated to maximize the critical success index (CSI) for predicting GLE events, that is, maximizing the number of hits and minimizing false alarms with respect to GLE events. The dates and times of GLEs were taken from the first time a neutron monitor station detected an event. The onset times were collected by Gopalswamy et al. [32,33,34] and the Neutron Monitor Database (NMDB) Nest page [35].

2.1. The GLE Occurrence Prediction Model

The physical processes that accelerate GLE and SEPs are associated with Coronal Mass Ejection (CME)-driven shocks [1,3,32,33,34], but CMEs and shocks are often observed tens of minutes or hours after the occurrence of GLEs, which normally arrive within minutes. Therefore, CME-driven shocks are not reliable for forecasting the occurrence of GLEs in real time. Given that strong flares are commonly observed in conjunction with CMEs, the UMASEP approach utilizes soft X-ray (SXR) flares as a proxy to represent the strength of the physical processes near the Sun. If a strong SXR flare precedes an increase in GOES protons, we may hypothesize that the particles that were accelerated by the strong physical solar event are traveling along a magnetic connection between the particle acceleration source (e.g., the interplanetary shock) and the Earth. It is important to mention that some strong flares alone (even from the western hemisphere) are not related to GLE events [36]. For this reason, the UMASEP-500 approach requires the fulfillment of two conditions: the occurrence of a strong flare and the existence of a subsequent particle enhancement near Earth.
For the case of UMASEP-500, the WCP2 model assumes that a magnetic connection is occurring when there is a lag correlation between the soft X-ray (SXR) flux and either the GOES > 500 MeV proton flux or a near-relativistic electron flux. The electron observations are obtained from the 0.175–0.375 MeV electron channel of the Electron Proton Alpha Monitor (EPAM) on board the Advanced Composition Explorer (ACE), which was operational at the time of this paper’s publication but will soon be decommissioned. For future versions of UMASEP-500, the electron fluxes will be obtained from other satellites such as NASA’s Interstellar Mapping and Acceleration Probe (IMAP) and/or NOAA’s Space Weather Follow-On (SWFO-L1), planned to be launched in late 2025.
In summary, WCP2 converts the SXR time series and the particle-related time series (proton and electron fluxes) into bit-based sequences. A “1” in a sequence signifies that the slope (i.e., the difference between the flux at time t and the flux at t-5 min) is extreme in the corresponding time series; a “0” indicates that no extreme slope occurs in the time series. An extreme slope is defined as one that exceeds a percentage p of the maximum slope in the current sequence of size L. If WCP2 identifies a lag correlation between the SXR and either the proton- or electron-based sequence, it suggests evidence of a Sun–Earth magnetic connection. Additionally, if a flare has recently occurred (during the recent L-size interval) and its SXR peak has exceeded a threshold f, a well-connected SEP event prediction is issued. For more details on how these bit-based sequences are derived, refer to [30].
The prediction model WCP1 [31] used by HESPERIA UMASEP-500 [18] assumes that an extreme SXR-related slope could be linked with a single extreme proton enhancement, whereas the WCP2 model [30] used by UMASEP-500 analyses multiple extreme proton enhancements. That is, the new version, WCP2, assumes that an extreme SXR-related slope could be linked with several extreme proton/electron flux enhancements during the occurrence of a magnetic connection. Based on this assumption, an SXR/particle lag correlation is deduced when WCP2 posits that an SXR-related “1” is associated with multiple particle-related “1”s. WCP2 formulates a causal hypothesis from the recent L-size sequences and endeavors to estimate the maximum number of potential cause–consequence pairs. If the hypothetical maximum number of pairs surpasses a threshold n, WCP2 concludes that a magnetic connection exists and some particles are traveling along that magnetic connection. The methodology for identifying cause–consequence pairs can be summarized as follows: suppose a subsequence i of two consecutive SXR-related “1”s, separated by di time steps, is followed after dp time steps by a subsequence x of two consecutive particle-related “1”s separated by dx time steps. The set of dx temporal distances is averaged to derive an important prediction inference called Lag. We consider the i–x pair valid if dx = di (see Figure 1). Subsequently, WCP2 verifies whether the number of identified cause–consequence pairs exceeds the threshold n and whether an SXR flare has surpassed a threshold f during the recent L-size interval. If either of these conditions is not met, WCP2 predicts an “all clear” situation.
Figure 1 depicts the magnetic connection detection method. Based on the assumption that during a magnetic connection taking place at the current (real) time t, an extreme SXR enhancement is linked to at least one extreme particle flux enhancement, WCP2 examines the most recent L-size sequence. If the hypothetical maximum number of pairs exceeds a threshold n, WCP2 concludes that a magnetic connection exists at the current time t. These thresholds are empirically determined to maximize the CSI forecasting index. As a result of the model optimization of UMASEP-500, the obtained values for the thresholds were as follows: L was 1 h, p was 91%, n was 3, and f was 2.9 × 10−4 Watt m−2.

2.2. UMASEP-500 Intensity Model

The intensity model is a multivariable regression model trained with information collected (i.e., a set of variables) during the execution of the WCP2 model for the historical GLE events in Table 1 and the corresponding >500 MeV SEP peak flux. During the execution of the WCP2 model, several attributes are collected: the magnetic connectivity estimation, the SXR/particle Lag, the log10 of the SXR peak, and several time-integrated SXR measurements. Regarding the last set of factors, we found that five 5 min measurements of the log10 of the time-integrated SXR were enough to obtain optimal results. If there is no value associated with one of the five time-integrated SXR variables, a “Missing” value is assigned. For example, during the first microprediction, only the first time-integrated SXR attribute is available; therefore, the values of the remaining four are “Missing”. The multivariable regression model we used can handle missing values. We used the Weka tool [37] to choose a multivariable regression method. After testing several regression methods, we selected M5P [38,39], which generates a tree where each leaf contains a multivariable linear model.
Linear regression models are used to explain observations of a dependent variable, typically represented by y, through the observed values of m independent variables, usually denoted by x1, x2, …, xm. That is, y = c + k1 x1 + k2 x2 + … + km xm, where c is the error term, and k1, …, km are the regression coefficients used to minimize the sum of squared errors over a set of training examples. Linear regression is suitable when the relationship between variables is linear. However, many real-world scenarios exhibit some degree of nonlinearity, complicating the modeling process. A model tree, which is a decision tree with a linear regression model in each leaf, can approximate a nonlinear function. The concept behind model trees [38,39] is to break down the task of learning the potential nonlinear relationship between the dependent and independent variables into n smaller subproblems, each focusing on a specific dimension or component. To divide a problem into n subproblems, a condition is required, represented by an internal node in the tree. Each internal node contains a splitting decision based on the input variables x1, …, xm, which divides the data into two subsets, corresponding to the left and right sub-trees. Model trees, constructed using the M5 algorithm [38,39], can have multivariate linear models in the leaves. M5 is efficient and can handle tasks with very high dimensionality (up to hundreds of attributes).
The final model tree to be used in real time was trained with the historical >500 MeV proton flux of the SEP events associated with the GLEs in Table 1. Regarding these proton fluxes, with the exception of the current GOES-R satellites, the >500 MeV proton flux was not part of the measurements of the GOESs before 2020, when most GLE events took place. For this reason, the peak >500 MeV integral proton flux intensities used for the machine learning of the new tool resulted from the application of a formula designed by Juan Rodriguez (private communication, 2016) from NOAA/NCEI: P500 = (a ⋅ P10 + b ⋅ P11)/c, where P500 is the >500 MeV integral proton flux; P10 (i.e., 510–700 MeV) and P11 (i.e., >700 MeV) are the real-time measurements of the High Energy Proton and Alpha Particles Detector (HEPAD) onboard GOESs 08–15; a is the geometrical factor of the proton channel P10, which was 162; b is the P11 geometrical factor, which was 1565; and c is the integral factor applied on the P10 and P11 channels, which was 0.56067.
The training table used for generating the regression tree is composed of a set of attributes consisting of real-time measurements and intermediate inferences from the WCP2 approach, and the target values, which were the corresponding >500 MeV peak flux intensities, calculated with the aforementioned formula by Juan Rodriguez. All the aforementioned training tasks were carried out using the aforementioned Weka tool v3.8.
In real time, the ML-based intensity prediction model extracts all the values of all the attributes of the M5P regression model trees, and makes the prediction of a single real value (the blue point in the graphical outputs), which is the expected peak > 500 MeV proton flux in the following hours. An uncertainty range associated with this predicted value is presented in the corresponding (JSON and graphical) prediction output.

3. Results

In order to show the forecasting performance of the UMASEP-500, this section presents Table 1 with the corresponding predictions, the forecast outputs of the successfully predicted events, and the final forecast results in terms of several forecasting performance metrics (Section 4).
Table 1 presents the summary of the occurrence and intensity prediction for all the GLE events in the period 2000–2023. Column 1 lists the event ID; column 2 presents the GLE start onset time (UTC) according to the NMDB list of events (nmdb.eu); column 3 presents the times of the UMASEP-500 predictions; column 4 lists the >500 MeV peak proton flux of the associated SEP, calculated by using the Juan Rodríguez formula described in Section 2; column 5 presents the predicted >500 MeV proton flux, which is the average of the intensities of the tool micropredictions (represented by the blue points); column 6 presents the forecasting results in terms of hits and misses; and column 7 presents the Warning Times. Section 4 presents the definitions of these counters and measures.
This section presents graphical prediction outputs of UMASEP-500. Figure 2 shows the prediction of the GLE on 10 September 2017. Figure 3 presents the GLE prediction for 29 October 2003, and Figure 4 depicts the prediction for 14 July 2000. Every microprediction starts at the time when it was triggered and presents a shape, whose color depends on the predicted intensity value (normally yellow). At the extreme right of each microprediction, there is a blue point, which presents the intensity value predicted by the intensity model.

4. Discussion

In this section, we aim to separate the analysis of the performance of both models (i.e., UMASEP-500 and HESPERIA UMASEP-500) in the most important aspect of this study: the GLE occurrence performance and the >500 MeV intensity prediction performance.
Table 1 shows that for the period 2000–2023, the WCP2 prediction model of the UMASEP-500 is able to make a prediction before the first alarm of the neutron monitor stations in 9 out of 15 events and issues 4 false alarms. That is, a hit for the UMASEP-500 occurs when its prediction is issued before the earliest GLE alert onset time detected by any neutron monitor station. The time of the earliest GLE onset time is taken from the GLE list of the NMDB website [35]. We define a, b, c, and d as representing the number of hits, false alarms, misses, and correct nulls, respectively. These kinds of counts are commonly used in the evaluation of meteorological models to provide information about the success or failure of the forecasts in a particular dataset (an account of this methodology is provided in the work of Schaefer [40]). Based on these counts, several forecast skill scores [41] commonly used by the meteorological community in analyzing data are individually described in Table 2, where, for the present study, the elements (a, b, c, and d) required to calculate individual formulae are included.
Table 3 presents the comparison results between UMASEP-500 and HESPERIA UMASEP-500. Regarding the GLE occurrence prediction performance, we see that although the UMASEP-500 achieved better performance than HESPERIA UMASEP-500 in terms of POD (i.e., 60.0% vs. 53.3%, respectively), the FAR was worse (i.e., 30.7% vs. 27.3%). These disparate scores do not allow for a definitive comparison. In terms of the CSI, HSS, GSS, and AWT, we observe that these metrics yield similar scores (47.3% vs. 44.4%), (0.638 vs. 0.624), (0.468 vs. 0.439), and (10.8 min vs. 10 min), respectively, indicating that both systems have an overall similar GLE prediction performance. To improve the GLE occurrence prediction, the ACE electron energy range (0.175–0.375 MeV) will be greatly extended in the future IMAP and SWFO satellites, which will certainly be more convenient for the earlier detection of GLE events. That is, although, currently, the GLE prediction performance is similar to that of the HESPERIA UMASEP-500, the new electron observations will likely provide better POD values and Warning Times than those provided when using the ACE.
The most significant achievement of the new tool, UMASEP-500, is evident in the intensity performance metric, MAE. UMASEP-500 achieves a satisfactory score, while the HESPERIA UMASEP-500 does not have an MAE value because it does not predict intensities. Because of this characteristic, the UMASEP-500, along with the UMASEP-100 [28], are the only systems that currently are coupled with radiation dose nowcast systems, such as the two NASA systems NAIRAS and ARTT, respectively, for making real-time radiation dose predictions.

5. Conclusions

The UMASEP-500 tool has been introduced. This tool predicts the occurrence of GLE events and the >500 MeV proton intensity. This tool makes a prediction when a magnetic connection is empirically detected, by estimating a lag correlation between GOES SXR fluxes and both the GOES > 500 MeV proton flux and the 0.175–0.315 MeV ACE EPAM electron fluxes. When either correlation is large and a recent SXR flare (greater than X2.9) occurs, a GLE prediction is issued.
By using the GLE events and the associated >500 MeV proton flux of 15 GLE events in the period 2000–2023, this paper presents the prediction results and compares them with those of the HESPERIA UMASEP-500 tool, which has been operating since 2017. In terms of the POD, the UMASEP-500 achieved a better POD but worse FAR. We also found that both systems have a similar AWT, CSI, Heidke, and Gilbert skill scores, which lead us to conclude that both systems have an overall similar GLE occurrence prediction performance.
The most significant difference between the UMASEP-500 and HESPERIA UMASEP-500 lies in the UMASEP-500’s ability to predict intensities with a satisfactory mean absolute error (0.303 log10 pfu). This unique characteristic allows the UMASEP-500 to be integrated with radiation dose nowcast systems, such as NASA’s NAIRAS, making this integration [29] an important tool for real-time predictions of global atmospheric ionizing radiation exposure at commercial airline altitudes. In the future, we also hope that the UMASEP-500 will process electron data from the future IMAP and SWFO satellites, enabling it to better serve in making preventive predictions for future missions to the moon and cislunar space.

Funding

The optimization and calibration process of the intensity prediction model of UMASEP-500 was funded by NASA’s Integrated Solar Energetic Proton Alert/Warning System (ISEP) project under the contract POTXS0149902 with the company KBR/Wyle Labs. The development of the WCP2 model of UMASEP-500 was funded by the Plan Propio de Investigación of Universidad de Málaga/Campus de Excelencia Internacional Andalucía Tech, reference 8.06/5475336.

Data Availability Statement

The original contributions presented in the study are included in the article. Further inquiries can be directed to the corresponding author.

Acknowledgments

The solar soft X-ray and near-Earth proton data were obtained from the United States NOAA’s National Centers for Environmental Information https://www.ncei.noaa.gov/data/goes-space-environment-monitor/access/avg (accessed on 1 March 2024). The author acknowledges NASA’s Integrated Space Weather Analysis (ISWA) system for providing the integral proton data https://iswa.ccmc.gsfc.nasa.gov/iswa_data_tree/observation/magnetosphere/goes_p/particle (accessed on 1 March 2024). Special thanks go to Caltech and the Johns Hopkins University Applied Physics Laboratory (JHU/APL) for their contributions to the Advanced Composition Explorer (ACE) Electron, Proton, and Alpha Monitor (EPAM) data. The ACE/EPAM data processing and analysis were supported by NASA and facilitated by the resources at JHU/APL https://izw1.caltech.edu/ACE/ASC/DATA/level3/epam (accessed on 1 March 2024). The author is also grateful to all the institutions and teams involved for their invaluable efforts in supplying the data used for the calibration and validation of the tool presented in this paper. Additionally, the author acknowledges the detailed and constructive feedback provided by the referees and appreciates the editor’s efforts in coordinating the review process.

Conflicts of Interest

The author declares no conflicts of interest.

References

  1. Reames, D.V. Solar energetic particle variations. Adv. Space Res. 2004, 34, 381–390. [Google Scholar] [CrossRef]
  2. Dorman, L.; Pustilnik, L.A.; Sternlieb, A.; Zukerman, I.G.; Belov, A.V.; Eroshenko, E.A.; Yanke, V.G.; Mavromichalaki, H.; Sarlanis, C.; Souvatzoglou, G.; et al. Monitoring and forecasting of great solar proton events using the neutron monitor network in real-time. IEEE Trans. Plasma Sci. 2004, 32, 1478–1488. [Google Scholar] [CrossRef]
  3. Aschwanden, M. GeV particle acceleration in solar flares and ground level enhancement (GLE) events. Space Sci. Rev. 2012, 171, 3–21. [Google Scholar] [CrossRef]
  4. Wilson, J.W. Overview of radiation environments and human exposures. Health Phys. 2000, 79, 470–494. [Google Scholar] [CrossRef]
  5. IEC/TS 62396-1:2006(E); Process Management for Avionics—Atmospheric Radiation Effects—Part 1: Accommodation of Atmospheric Radiation Effects Via Single Event Effects within Avionics Electronic Equipment. International Electrotechnical Commission: Geneva, Switzerland, 2006.
  6. Beck, P.; Latocha, M.; Rollet, S.; Stehno, G. TEPC reference measurements at aircraft altitudes during a solar storm. Adv. Space Res. 2005, 16, 1627–1633. [Google Scholar] [CrossRef]
  7. Mertens, C.J.; Kress, B.T.; Wiltberger, M.; Blattnig, S.R.; Slaba, T.S.; Solomon, S.C.; Engel, M. Geomagnetic influence on aircraft radiation exposure during a solar energetic particle event in October 2003. Space Weather 2010, 8, S03006. [Google Scholar] [CrossRef]
  8. Shea, M.A.; Smart, D.F. Space weather and the ground-level solar proton events of the 23rd solar cycle. Space Sci. Rev. 2012, 171, 161–188. [Google Scholar] [CrossRef]
  9. Durante, M.; Cucinotta, F.A. Physical basis of radiation protection in space travel. Rev. Mod. Phys. 2011, 83, 1245. [Google Scholar] [CrossRef]
  10. Ho, J.L.; Townsend, L.W.; Zapp, E.N. Interplanetary crew doses and dose equivalents: Variations among di erent bone marrow and skin sites. Adv. Space Res. 2004, 34, 1347–1352. [Google Scholar]
  11. Mavromichalaki, H.; Souvatzoglou, G.; Sarlanis, C.; Mariatos, G.; Papaioannou, A.; Belov, A.; Eroshenko, E.; Yanke, V.; the NMDB team. Implementation of the ground level enhancement alert software at NMDB database. New Astron. 2010, 15, 744–748. [Google Scholar] [CrossRef]
  12. Mavromichalaki, H.; Paschalis, P.; Gerontidou, M.; Tezari, A.; Papailiou, M.-C.; Lingri, D.; Livada, M.; Stassinakis, A.; Crosby, N.; Dierckxsens, M. An Assessment of the GLE Alert++ Warning System. Atmosphere 2024, 15, 345. [Google Scholar] [CrossRef]
  13. Mariatos, G.; Mavromichalaki, H.; Sarlanis, C.; Souvatzoglou, G. Alert system for ground level cosmic-ray enhancements prediction at the Athens Neutron Monitor Network in real-time. Int. J. Mod. Phys. 2005, 20, 6711–6713. [Google Scholar] [CrossRef]
  14. Kuwabara, T.; Bieber, J.W.; Clem, J.; Evenson, P.; Pyle, R.; Munakata, K.; Yasue, S.; Kato, C.; Akahane, S.; Koyama, M.; et al. Real-time cosmic ray monitoring system for space weather. Space Weather 2006, 4, S08001. [Google Scholar] [CrossRef]
  15. Souvatzoglou, G.; Mavromichalaki, H.; Sarlanis, C.; Mariatos, G.; Belov, A.; Eroshenko, E.; Yanke, V. Yanke, Real-time GLE alert for the December 13, 2006 event, at the ANMODAP center. Adv. Space Res. 2009, 43, 728–734. [Google Scholar] [CrossRef]
  16. Anashin, V.; Belov, A.V.; Eroshenko, E.; Kryakunova, O.; Mavromichalaki, H.; Ishutin, I.; Sarlanis, C.; Souvatsoglou, G.; Vashenyuk, E.; Yanke, V. The ALERT signal of ground level enhancements of solar cosmic rays: Physics basis, the ways of realization and development. In Proceedings of the 31st International Cosmic Ray Conference, Łód’z, Poland, 7–15 July 2009. [Google Scholar]
  17. Souvatzoglou, G.; Papaioannou, A.; Mavromichalaki, H.; Dimitroulakos, J.; Sarlanis, C. Optimizing the real-time ground level enhancement alert system based on neutron monitor measurements: Introducing GLE Alert Plus. Space Weather 2014, 12, 633–649. [Google Scholar] [CrossRef]
  18. Núñez, M.; Reyes-Santiago, P.J.; Malandraki, O.E. Real-time prediction of the occurrence of GLE events. Space Weather 2017, 15, 861–873. [Google Scholar] [CrossRef]
  19. Posner, A. Up to 1-hour forecasting of radiation hazards from solar energetic ion events with relativistic electrons. Space Weather 2007, 5, 5. [Google Scholar] [CrossRef]
  20. Papaioannou, A.; Sandberg, I.; Anastasiadis, A.; Kouloumvakos, A.; Georgoulis, M.K.; Tziotziou, K.; Tsiropoula, G.; Jiggens, P.; Hilgers, A. Solar Flares, Coronal Mass Ejections and Solar Energetic Particle Event Characteristics. J. Space Weather. Space Clim. 2016, 6, A42. [Google Scholar] [CrossRef]
  21. Núñez, M.; Nieves-Chinchilla, T.; Pulkkinen, A. Prediction of Shock Arrival Times from CME and Flare Data. Space Weather 2016, 14, 8. [Google Scholar] [CrossRef]
  22. Copeland, K. CARI-7A: Development and validation. Radiat. Prot. Dosim. 2017, 178, 419–431. [Google Scholar] [CrossRef]
  23. Matthiä, D.; Meier, M.M.; Reitz, G. Numerical calculation of the radiation exposure from galactic cosmic rays at aviation altitudes with the PANDOCA core model. Space Weather 2014, 12, 161–171. [Google Scholar] [CrossRef]
  24. Mertens, C.J.; Meier, M.M.; Brown, S.; Norman, R.B.; Xu, X. NAIRAS aircraft radiation model development, dose climatology, and initial validation. Space Weather 2013, 11, 603–635. [Google Scholar] [CrossRef] [PubMed]
  25. Mertens, C.J.; Gronoff, G.P.; Zheng, Y.; Buhler, J.; Willis, E.; Petrenko, M. NAIRAS Atmospheric and Space Radiation Environment Model. IEEE Trans. Nucl. Sci. 2023, 71, 618–625. [Google Scholar] [CrossRef]
  26. Hu, S.; Monadjemi, S.; Barzilla, J.E.; Semones, E. ARRT development for the upcoming human exploration missions. Space Weather 2020, 18, e2020SW002586. [Google Scholar] [CrossRef]
  27. Hu, S.; Barzilla, J.E.; Núñez, M.; Semones, E. Semones, E. Real-time dose prediction for Artemis missions. J. Space Weather Space Clim. 2025, 15, 1. [Google Scholar] [CrossRef]
  28. Núñez, M. Real-time prediction of the occurrence and intensity of the first hours of >100 MeV solar energetic proton events. Space Weather 2015, 13, 11. [Google Scholar] [CrossRef]
  29. Mertens, C.; Gronoff, G.; Phoenix, D.; Zheng, Y.; Núñez, M. Forecasting SEP Atmospheric and Space Radiation Using UMASEP and NAIRAS Models. In Proceedings of the American Geophysical Union (AGU) Fall 2024, Washington, DC, USA, 9–13 December 2024. [Google Scholar]
  30. Núñez, M. Evaluation of the UMASEP-10 version 2 tool for predicting all >10 MeV SEP events of solar cycles 22, 23 and 24. Universe 2022, 8, 35. [Google Scholar] [CrossRef]
  31. Núñez, M, Predicting solar energetic proton events (E > 10 MeV). Space Weather 2011, 9, S07003. [CrossRef]
  32. Gopalswamy, N.; Xie, H.; Yashiro, S.; Usoskin, I. Coronal Mass Ejections and Ground Level Enhancements. In Proceedings of the 29th International Cosmic Ray Conference, Pune, India, 3–11 August 2005; pp. 101–104. [Google Scholar]
  33. Gopalswamy, N.; Yashiro, S.; Mäkelä, P.; Xie, H.; Akiyama, S.; Monstein, C. Extreme Kinematics of the 2017 September 10 Solar Eruption and the Spectral Characteristics of the Associated Energetic Particles. Astrophys. J. Lett. 2018, 863, L39. [Google Scholar] [CrossRef]
  34. Gopalswamy, N.; Xie, H.; Yashiro, S.; Akiyama, S.; Mäkelä, P.; Usoskin, I.G. Properties of Ground Level Enhancement Events and the Associated Solar Eruptions During Solar Cycle 23. Space Sci. Rev. 2012, 171, 23–60. [Google Scholar] [CrossRef]
  35. Neutron Monitor Data Base/Nest Page. Available online: http://nmdb.eu/nest/gle_list.php (accessed on 1 February 2025).
  36. Waterfall, C.O.G.; Dalla, S.; Raukunen, O.; Heynderickx, D.; Jiggens, P.; Vainio, R. High Energy Solar Particle Events and Their Relationship to Associated Flare, CME and GLE Parameters. Space Weather 2023, 21, e2022SW003334. [Google Scholar] [CrossRef]
  37. Frank, E.; Hall, M.A.; Witten, I.H. The WEKA Workbench. Online Appendix for “Data Mining: Practical Machine Learning Tools and Techniques”. In Morgan Kaufmann, 4th ed.; The University of Waikato: Hamilton, New Zealand, 2016. [Google Scholar]
  38. Quinlan, J.R. Learning with continuous classes. In Proceedings of the 5th Australian Joint Conference on Artificial Intelligence, Canberra, Australia, 1–5 December 1992; Adams, A., Sterling, L., Eds.; World Scientific: Singapore, 1992; pp. 343–348. [Google Scholar]
  39. Wang, Y.; Witten, I.H. Induction of model trees for predicting continuous classes. In Proceedings of the 9th European Conference on Machine Learning, Prague, Czech Republic, 23–25 April 1997. [Google Scholar]
  40. Schaefer, J.T. Critical success index as an indication of warning skill. Weather Forecast. 1990, 3, 570–575. [Google Scholar] [CrossRef]
  41. McKenna-Lawlor, S.M.P.; Dryer, M.; Kartalev, M.D.; Smith, Z.; Fry, C.D.; Sun, W.; Deehr, C.S.; Kecskemety, K.; Kudela, K. Near real-time predictions of the arrival at Earth of flare-related shocks during Solar Cycle 23. J. Geophys. Res. 2006, 11, A11103. [Google Scholar] [CrossRef]
Universe 11 00094 g001
Figure 1. Illustration of the search of cause–consequence pairs of the WCP2 algorithm.
Figure 1. Illustration of the search of cause–consequence pairs of the WCP2 algorithm.
Universe 11 00094 g001
Universe 11 00094 g002
Figure 2. Prediction for the GLE event that took place on 10 September 2017.
Figure 2. Prediction for the GLE event that took place on 10 September 2017.
Universe 11 00094 g002
Universe 11 00094 g003
Figure 3. Prediction for the GLE event that took place on 29 October 2003.
Figure 3. Prediction for the GLE event that took place on 29 October 2003.
Universe 11 00094 g003
Universe 11 00094 g004
Figure 4. Prediction for the GLE event that took place on 14 July 2000.
Figure 4. Prediction for the GLE event that took place on 14 July 2000.
Universe 11 00094 g004
Table 1. Forecasting results for GLE events from 2000 to 2023.
Table 1. Forecasting results for GLE events from 2000 to 2023.
GLE Event IDGLE Start Onset Time (UTC)GLE Forecast Time (UTC)>500 MeV Peak Proton Flux
(pfu)		Predicted >500 MeV Proton Flux
(pfu) b		Forecasting Result aWarning Time (min) a
GLE-5914 July 2000 10:3014 July 2000 10:2210.53.89Hit8
GLE-6015 April 2001 14:0015 April 2001 13:5221.83.3Hit8
GLE-6118 April 2001 02:35 Miss
GLE-6204 November 2001 17:00 Miss
GLE-6326 December 2001 05:30 Miss
GLE-6424 August 2002 01:1824 August 2002 01:121.82.2Hit6
GLE-6528 October 2003 11:2228 October 2003 11:111.62.6Hit11
GLE-6629 October 2003 21:3029 October 2003 20:492.83.13Hit41
GLE-6702 November 2003 17:3002 November 2003 17:222.73.89Hit8
GLE-6817 January 2005 09:5517 January 2005 09:540.83.89Hit1
GLE-6920 January 2005 06:51 Miss
GLE-7013 December 2006 02:4513 December 2006 02:356.34.01Hit10
GLE-7117 May 2012 01:43 Miss
GLE-7210 September 2017 16:0810 September 2017 16:042.01.67Hit4
GLE-7328 December 2021 15:50 Miss
a Warning Times are estimated considering that a prediction is successful if it is triggered before the earliest GLE Alert Onset Time detected by any neutron monitor station. b Average of the intensity micropredictions, whose central values are represented by the blue points at the extreme right of each (usually yellow) shape. See graphical outputs in Section 3.
Table 2. Definition of prediction performance metrics.
Table 2. Definition of prediction performance metrics.
Performance MetricAbrev.FormulaDescription
Prob. of detection PODa/(a + c)Proportion of GLE observations that were correctly forecast
False alarm ratioFARb/(a + b)Proportion of GLE forecasts that were incorrect
Critical success indexCSIa/(a + b + c)Proportion of hits that were either forecast or observed
Heidke skill score aHSS(a + d – C1)/(N − C1)Percent correct, corrected by those expected correct by chance
Gilbert skill score aGSS(a − C2)/(a + b + c − C2)CSI, corrected by number of hits expected by chance (C2)
Mean absolute error bMAEAverage (AE)Average of absolute errors (AEs) of successful predictions
Average Warning Time cAWTAverage (WT)Average of Warning Times (WTs) of successful predictions
a N = (a + b + c + d) is total number of events, C1 = C2 + (b + d)(c + d)/N is number expected to be correct by chance, and C2 = (a + c)(a + b)/N is number of hits expected by chance. b Warning Time (WT) is the difference between the time of the GLE start time and the time of the model prediction. c Absolute error (AE) is the difference between the log10 of the observed Proton Flux Units at certain times and the log10 of the >500 MeV integral proton flux predicted by the model.
Table 3. Comparison between UMASEP-500 and HESPERIA UMASEP-500.
Table 3. Comparison between UMASEP-500 and HESPERIA UMASEP-500.
Performance MetricsUMASEP-500HESPERIA UMASEP-500
Probability of detection (POD)60.0% (9/15)53.3% (8/15)
False alarm ratio (FAR)30.7% (4/13)27.3% (3/11)
Critical success index (CSI)47.3%44.4%
Heidke skill score (HSS)0.6380.624
Gilbert skill score (GSS)0.4680.439
Average Warning Time (AWT) 10.8 min10 min
Mean Average Error (MAE)0.303n/a
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Núñez, M. Predicting Ground-Level Enhancement Events and >500 MeV Proton Intensity Using Proton and Electron Observations. Universe 2025, 11, 94. https://doi.org/10.3390/universe11030094

AMA Style

Núñez M. Predicting Ground-Level Enhancement Events and >500 MeV Proton Intensity Using Proton and Electron Observations. Universe. 2025; 11(3):94. https://doi.org/10.3390/universe11030094

Chicago/Turabian Style

Núñez, Marlon. 2025. "Predicting Ground-Level Enhancement Events and >500 MeV Proton Intensity Using Proton and Electron Observations" Universe 11, no. 3: 94. https://doi.org/10.3390/universe11030094

APA Style

Núñez, M. (2025). Predicting Ground-Level Enhancement Events and >500 MeV Proton Intensity Using Proton and Electron Observations. Universe, 11(3), 94. https://doi.org/10.3390/universe11030094

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop