Abstract
Alternative scenarios where the Big Bang singularity of the standard cosmological model is replaced by a bounce, or by an early almost static phase (known as emergent universe) have been frequently studied. We investigate the role of the spinor degrees of freedom in overcoming the initial singularity. We introduce a model which generalizes the Einstein–Cartan–Dirac theory, including local phase invariance of the spinor field supported by a gauge scalar field and certain couplings to the torsion. A natural gauge choice reduces the field equations to that of the Einstein–Dirac theory with a Dirac field potential that has polar and axial spinor currents. We identify a new potential term proportional to the square of the ratio of Dirac scalar and axial scalar, which provides a dark energy contribution dominating in the late-time Universe. In addition, the presence of spinor currents in the potential may induce the bounce of a contracting universe.
1. Introduction
Inflationary cosmology is able to explain the conceptual issues of standard cosmology, and also provide a nearly scale-invariant primordial power spectrum consistent with the observation of Cosmic Microwave Background fluctuation [1,2]. However, this model suffers from a singularity problem [3], meaning that the earliest moment of the evolution of the Universe is not understood. Hence, alternative scenarios have been proposed, where the initial singularity is avoided.
In the emergent universe scenarios, the universe originates from a past eternal Einstein static spacetime, after which it enters the normal thermal expanding phase [4,5,6]. This was realized originally in string gas cosmology [4], but it can be realized in a closed Friedmann universe with a scalar field that has asymptotically flat potential in general relativity [5,6]. However, the Einstein static universe is unstable against scalar perturbations; as a result, the initial singularity cannot be completely removed. In order to alleviate this problem, emergent universe scenarios were investigated in alternative theories of gravitation, for example, in Hořava–Lifshitz-like -gravity [7], in a scalar–tensor theory containing a scalar field with derivative coupling [8,9], in massive gravitational models [10,11], in degenerate higher-order scalar–tensor theory [12] and in mimetic gravity [13]. In the Jordan–Brans–Dicke theory, this scenario was realized through quantum tunneling, where the scalar field decays from a false vacuum state into a true vacuum state [14]. Recently, it has been shown that emergent cosmology may also arise in general relativity in the presence of an exotic, nonlinear electrodynamic field [15]. The emergent universe scenario can also be constructed based on the fermionic sector. The Dirac field in general relativity with a potential depending nonlinearly on can also support this genesis [16,17]. Moreover, this scenario can also be implemented both in the Einstein–Cartan theory of gravitation [18] and in the Einstein–Cartan–Brans–Dicke theory [19].
The bouncing cosmological models suggest that the universe was contracting, which stopped at a nonvanishingly small value of the scale factor, and this was followed by a phase of expansion leading to the formation of the known universe. Bouncing cosmology may occur when the matter violates the null energy condition or general relativity is modified. The bouncing scenario occurs in higher-order curvature models with limited curvature invariants [20,21,22]. The limited curvature and the bouncing evolution of the Friedmann universe can also be achieved within a mimetic theory [23] (the mimetic, constrained scalar field was introduced in the Einstein theory to induce mimetic dark matter by making the longitudinal degree of freedom of the gravitational field dynamical [24]). However, some of these limiting curvature models suffer from instabilities [25,26,27]. Bouncing evolution is also supported by certain potentials of the mimetic matter [28]. Bouncing cosmology with a matter-dominated phase of contraction can provide a scale-invariant spectrum of curvature fluctuations in agreement with the recent CMB observations [1,2]. In this matter bounce scenario, instabilities may also develop [29,30], depending on the proposed model governing the evolution around the bounce. The null energy condition can be violated by Quintom matter, which is a set of two scalar fields [31,32]. One of them obeys the weak energy condition, while the other one has a negative kinetic term. The bounce is supported by the Quintom matter; however, the negative kinetic term leads to an instability problem [33]. The ghost instability problem resulted from the fact that the negative kinetic term can be cured by introducing higher powers of the kinetic term into the action in order to create a stable fixed point. Bounce may also occur as a result of a scalar field which undergoes ghost condensation [34]. The original ekpyrotic bouncing model was based on colliding braneworlds in heteoric M-theory. [35]. The bounce is caused by an effective scalar field with large equation-of-state parameter values () in the contracting phase. This can be realized with a scalar field that has a negative exponential potential. In the original ekpyrotic scenario, no scale-invariant adiabatic fluctuations are obtained [36,37]. However, this can be rectified within Horndeski theory [38] or in the S-brane model [39]. Bouncing cosmological models were also obtained in other alternative gravitational models (see, for example, the recent papers [40,41,42,43,44,45,46,47,48,49]). Most of the bounce scenarios are based on the bosonic sector of the universe; however, they can also be supported by the fermionic sector. The Dirac field, through minimal coupling to the torsion, gives a negative contribution to the energy density, which may induce a bounce [50]. Moreover, the singularity may be avoided when the coupling of the Dirac field is non-minimal in the Einstein–Cartan theory [51,52]. Recently, it has been shown that a self-interacting fermionic field within Brans–Dicke scalar–tensor gravitational theory may also support the bouncing evolution of the scale factor [53]. For comprehensive reviews of bouncing cosmological models, the interested reader may consult Refs. [54,55].
The literature on dark energy is far richer than on bouncing cosmologies (see e.g., Refs. [56,57,58] and the references therein). The simplest form of dark energy is the cosmological constant with an equation of state . In this paper, we present a Dirac field potential term, which leads to the conclusion that the Dirac field contribution can mimic an effective cosmological constant during late-time cosmological evolution.
In this paper, we introduce a spinor model, which can provide a bouncing universe scenario and behaves as dark energy in the late-time universe. In Section 2, we summarize the useful formulae for the Einstein–Cartan theory and for the covariant derivative of the Dirac field. Then, we introduce a new model which generalizes the Einstein–Cartan–Dirac theory, including local phase invariance of the spinor field supported by a gauge scalar and certain couplings to the torsion. In a natural gauge, the field equations simplify significantly, and they correspond to that of the Einstein–Dirac theory with a potential that has polar and axial spinor currents. In our model, the Dirac field potential includes three types of contributions: (i) mass, (ii) spinor currents, and (iii) a term proportional to the square of the ratio of the spinor axial scalar and spinor scalar.
In Section 3, the evolution of flat Friedmann universes is considered. The analytical results are presented when one type of potential term is only nonvanishing. Numerical investigations are carried out when all three types of potential terms occur. The spinor model is also compared to a flat CDM model and observations related to low redshifts, where mostly dark energy dominates. Finally, Section 4 contains the conclusions.
Throughout the paper, we work in units of , where c is the speed of light.
2. A Spinor–Scalar–Tensor (SST) Model with a Gauge Scalar Singlet
2.1. Connection and Curvature
Like in Einstein–Cartan theory, we use a metric-compatible covariant derivative allowing the presence of torsion. Then, the affine connection is decomposed (see Refs. [59,60,61,62]) as follows:
where is the Christoffel symbol, while represents the contorsion tensor relating to the torsion tensor as
By construction, the contorsion tensor is antisymmetric in the first two indices . We use the convention where the second lower index of the connection is the derivative index, e.g., for any vector field ,
where is associated with the torsion-free part, hence being the Levi-Civita covariant derivative.
The torsion tensor can be decomposed into three irreducible parts as follows:
where is the totally antisymmetric volume element (), while
and obeys
The curvature tensor is defined as
leading to the following expression of the Ricci scalar [61]1:
where stands for the torsion-free part.
2.2. Covariant Derivative of the Dirac Spinor Field
We define the Dirac–Pauli matrices () to obey the anticommutation relations and the Hermiticity condition . Here, is the inverse of the Minkowski metric , I stands for the unit matrix, and the superscript + stands for the Hermitian conjugate. Such a representation for is given in Ref. [63], which we will use2. Denoting the tetrad field as , the “curved spacetime” Dirac–Pauli matrices are , obeying
The covariant derivative of the Dirac spinor field is introduced as
and
where stands for the spinor connection. As usual, we require the compatibility with the covariant derivatives of tensor fields. Introducing the Dirac conjugate as , where i is the imaginary unit3, and the relation results in
while gives [63]4
Then, holds, which can be checked using (9). In addition, we impose , leading to the following form of spinor connection:
where is an arbitrary real four vector,
and [65]
with a torsion-free part
Note that the usual Fock–Ivanenko covariant derivative is defined by
with
It can be shown that ; hence, is implied.
Throughout this paper, the four-vector in (13) will be chosen as
The invariance of Dirac action under local phase variation is usually maintained by coupling the Dirac field to the electromagnetic field. In the next subsection, we introduce an alternative gravitational model in which the coupling of the Dirac field to torsion will ensure this property through Equation (19). This ansatz corresponds to the non-minimal coupling presented in Ref. [61].
2.3. Action, Gauge Transformations and Field Equations
The action describing a modified Einstein–Cartan–Dirac theory is given by
The first term stands for the Einstein–Cartan action
where with the gravitational constant G. The second term in Equation (20) is a scalar field action
coupled to the torsion . The third term is the action for the Dirac field:
with a reduced Placnk constant ℏ, a mass parameter and a potential
where and are real constants, while has the dimension of 1/length squared. In addition5,
and
are real vector and axial vector currents, respectively. Here . The decomposition of into and torsional parts implies the following form of :
Hence, the Dirac field is coupled to both and . Finally, denotes the matter action.
Motivation for the above-presented action relies on the following. The coupling of the scalar field to torsion will maintain the invariance of total action under the local phase variation of the Dirac field in a natural way. The Dirac field will give three different kinds of contributions to the total energy density. The ratio will be responsible for a dark energy contribution, the current terms for the singularity avoidance, while the mass term for a dark matter like contribution, respectively.
Using the decomposition of the Ricci scalar (8), the total action can be written as6
where we have defined the gauge derivative as
The action (29) is invariant under the local phase variation of the Dirac field
provided and transform as
while and do not change.
The variations in the action with respect to , and result in the following equations of motion:
and the Dirac conjugation of (35), respectively. The Cartan equations arise from the variation in the action with respect to . After using the irreducible decomposition of the torsion tensor, these read as
and
At this point it is worth mentioning that since both and are gauge-invariant quantities, the gauge transformation rule for implies the desired variation for through Equation (37). The modified Einstein equations obtained from the variation in the action with respect to are given by
Here, is the energy momentum tensor of matter fields, is the Einstein tensor associated with the Christoffel symbols, and stands for the following torsional part
The contributions of the scalar and the Dirac field are
and
with
Note that the relations (35) and (36) have been used in the derivation of Equation (39).
Since is a pure gauge field, its equation of motion cannot be independent from the other ones. The modified Dirac Equation (35) using implies
Substituting the expression of from the Cartan Equation (37) into (44), we arrive at the scalar field Equation (34).
Finally, using the Cartan equations, the modified Einstein equations can be written in a more compact form as
As a check, it can be shown that all field equations are invariant under the gauge transformation.
Eliminating the Scalar Field
Writing the Dirac field multiplet in the form
and choosing the gauge condition
the contributions from the phase and from the scalar field cancel each other out in the field equations, resulting in . Hence, the modified Dirac equation reads as
while the modified Einstein equation simplifies to
Here, we have introduced two constants, and , which parameterize different theories. The above-introduced SST theory corresponds to . The theory, where the Dirac field does not couple to (i.e., ) and there is no scalar field contribution (i.e., const), corresponds to and . Finally, the field equations of a torsionless theory without a scalar field can be obtained by taking .
Hence, the field equations of the original Einstein–Cartan–Dirac theory are obtained as a subcase with , , , and . This theory coincides with a torsionless Einstein–Dirac theory that has the parameters , , , and . Of course, this equivalence holds only when one Dirac field is present. In addition, the introduced SST theory is equivalent to an Einsten–Dirac model with rescaled parameters , .
3. Cosmological Evolution
In the comoving coordinates t, x, y and z, the line element squared of a flat Friedmann spacetime is
with the scale factor . We assume that the matter energy momentum tensor describes a perfect fluid with energy density and pressure p. In addition, we impose for the Dirac field. Then, the modified Dirac Equation (48) becomes
where the dot stands for the derivative with respect to t, and . The modified Einstein equations (49) read as
with an effective energy density
and
with an effective pressure
We note that the ansatz for the Dirac field is compatible with the metric (50). This is because the ansatz implies that the matrices and the currents and are only time-dependent; hence, all terms in the field equations are too.
From the modified Dirac field equations, such a system can be derived for real variables: , , , and
which determine the source terms in and , and become closed together with the modified Einstein equations. Here and hereafter, the greek indices, like , take values of . The mentioned system for the real Dirac field is given in the Appendix A. The 16 real variables (, , , , , ) introduced to replace are too many, as only contains 8 real functions. This means that not all the variables are independent, which has to be taken into account in choosing the initial values, or equivalently, a much simpler system should be obtained.
Using the parametrization
where T stands for the transpose, and the representation of is given in Ref. [63], we obtain
with and . Hence, is positive, while is negative. In addition, a direct computation results in
and
The above identities highly reduce the number of necessary Dirac field variables, thus we are left with
The effective energy density and pressure associated with the Dirac field become
with
where
and
respectively. Finally, the evolution equations for the Dirac field variables (61) are
and
These form a closed system together with the modified Einstein equations. Since Equation (68) can simply be integrated, can also be expressed as
with a positive integration constant .
3.1. Integrable Examples
3.1.1. Subcase I (Dust): , and
In this case, only the field contributes to the right hand side of the modified Einstein equation through , and its evolution is described by
Both and are proportional to . It is worth mentioning that this result can also be obtained from the Dirac field continuity equation when vanishes. Hence, the Dirac field contributes to the dust.
3.1.2. Subcase II (Cosmological Constant): , and
Now only a term proportional to contributes to the energy density and pressure. Since , and are constants. The equation of state is like that of the cosmological constant. Hence, the Dirac field behaves like dark energy.
3.1.3. Subcase III (Bounce): , and
The field equations for the source terms in simplify to
resulting in
Note that the equation of state is , which, together with the continuity equation, also leads to (73).
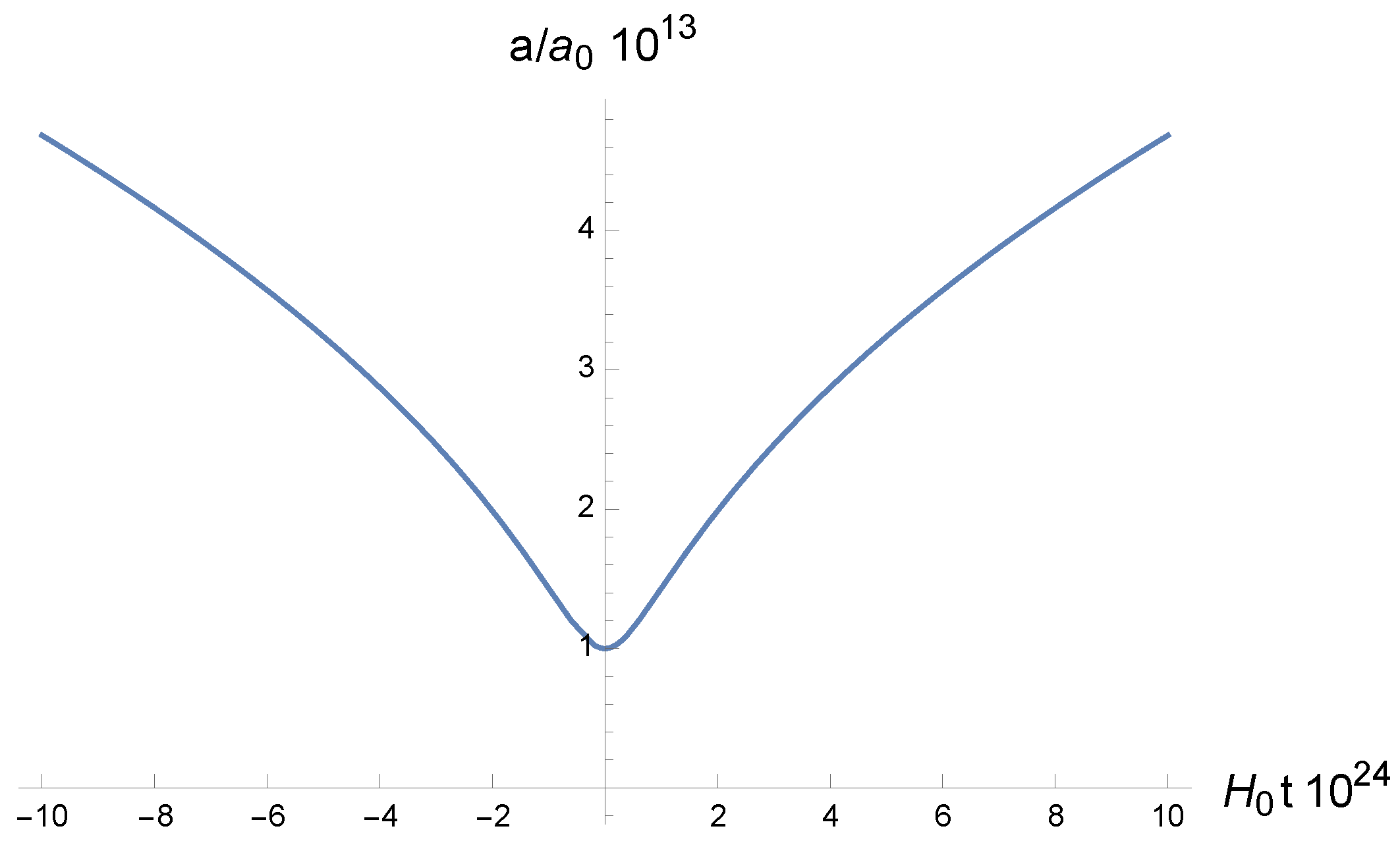
Since the radiation and the dust energy densities scale as and , respectively, the contribution of to the total energy density can only be significant in the early universe. In case of a negative , when , the total energy density vanishes for a corresponding small value of the scale factor, or equivalently, for a high value of redshift z. When this happens, Equations (52) and (54) give and , respectively; hence, the scale factor takes its minimal value. A contracting universe cannot reach a Big Crunch singularity in this model; instead, it undergoes a nonsingular bounce.
More particularly, near the bounce, where any other matter component is negligible with respect to the radiation, Equation (52) leads to
where the prime stands for the derivative with respect to with Hubble constant . We have introduced cosmological parameters characterizing the amount of the Dirac field and the radiation (including both background photons and neutrinos) in this equation as follows:
where the subscript 0 denotes the present value of the respective quantity. Equation (74) can be rewritten as
showing that must satisfy
The turning point can only occur at the equality, where vanishes. Hence, we can introduce a new variable as follows
without the loss of generality. Substitution of this parameterization into Equation (76) leads to
where we have assumed that . The integration of this equation results in
with the requirement that for . The solution of this transcendental equation gives the function .
The evolution of the scale factor near the bounce is shown in Figure 1. Such a spinor-driven bounce is stable against the linear order perturbation proven in an Einstein–Cartan–Holst model [66,67].
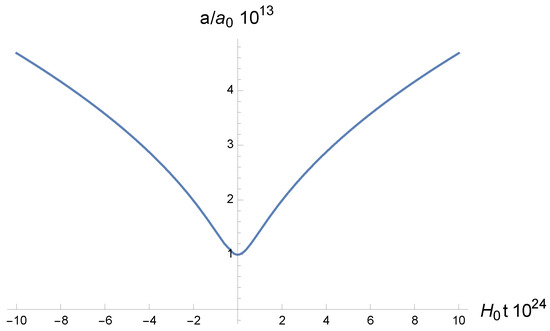
Figure 1.
The evolution of the scale factor near the bounce.
Similar bouncing evolution for closed Friedmann universes was presented in Ref. [50]. However, there is an important difference in what causes this bounce. The usual Einstein–Cartan–Dirac model corresponds to , , , and . Equivalently, when there is only one Dirac field under consideration, the usual Einstein–Cartan–Dirac model also corresponds to , , , and , as we have noted in the section Eliminating the Scalar Field. Then, the contribution of the Dirac field to the energy density is
as can be seen from Equation (49). The last term, arising from the spin–torsion coupling, corresponds to the second one on the right hand side of Equation (9) in Ref. [50]. There, the first term on the right hand side of Equation (9) was handled as a radiation component in the early universe. Evolving the field equations backward in time, the negative term arising from the spin–torsion coupling becomes comparable in terms of absolute value with the energy density of the radiation. At a certain time, when the total energy density vanishes, a bounce occurs. Hence, in Ref. [50], the bounce is a consequence of the spin–torsion coupling. However, when considering a space-independent spinor field in a flat Friedmann universe as in Ref. [16], the first term in can neither be considered as a pure radiation component nor neglected. Using the Dirac field equation, we obtain
The second term on the right hand side gives a similar contribution to the energy density when compared to the second term in Equation (81) and originates from the spin–torsion coupling through the Dirac equations. The energy density of the Dirac field becomes
The total contribution of the spin–torsion coupling is strictly positive; hence, it cannot cause a bounce. In contrast, in the model presented above, the bounce is caused by the spinor current terms in the potential. A simple case where a bounce occurs is , , , and , which is not the subcase equivalent to the Einstein–Cartan–Dirac model.
3.2. Numerical Examples
The evolution of the system is described by Equations (52), (62)–(67) and (70). The initial values will be chosen at the present time, where the scale factor is . The energy density contributions of the Dirac field are given by three components listed in Equation (63). In addition to the Dirac field, we include dust (baryonic and dark matter), radiation and a cosmological constant in the consideration with energy densities of , and , respectively. To characterize the amount of different components, we introduce dimensionless energy densities by multiplying them with . These dimensionless quantities will be distinguished by a hat, for instance, . The sum of , , , , and gives , which determines the large-scale cosmological evolution of the Friedmann universe. The present values of these dimensionless energy densities coincide with the usual cosmological parameters denoted by capital omegas, like with redshift z.
We choose ; hence, with an initial value parametrized as
Here, determines the present value of the energy density of the radiation component. Since and dominate for small values of the scale factor, gives approximately the redshift of a bounce, where . The initial values will be chosen in the following way. We fix the parameters , and . The contribution of the cosmological constant is derived from . Then, the parameter follows from the relation
Choosing , the value of determines . The present values of , and will be chosen to satisfy
which corresponds to the following initial Dirac field configuration:
Then, the values of the parameters and are obtained from and , respectively.
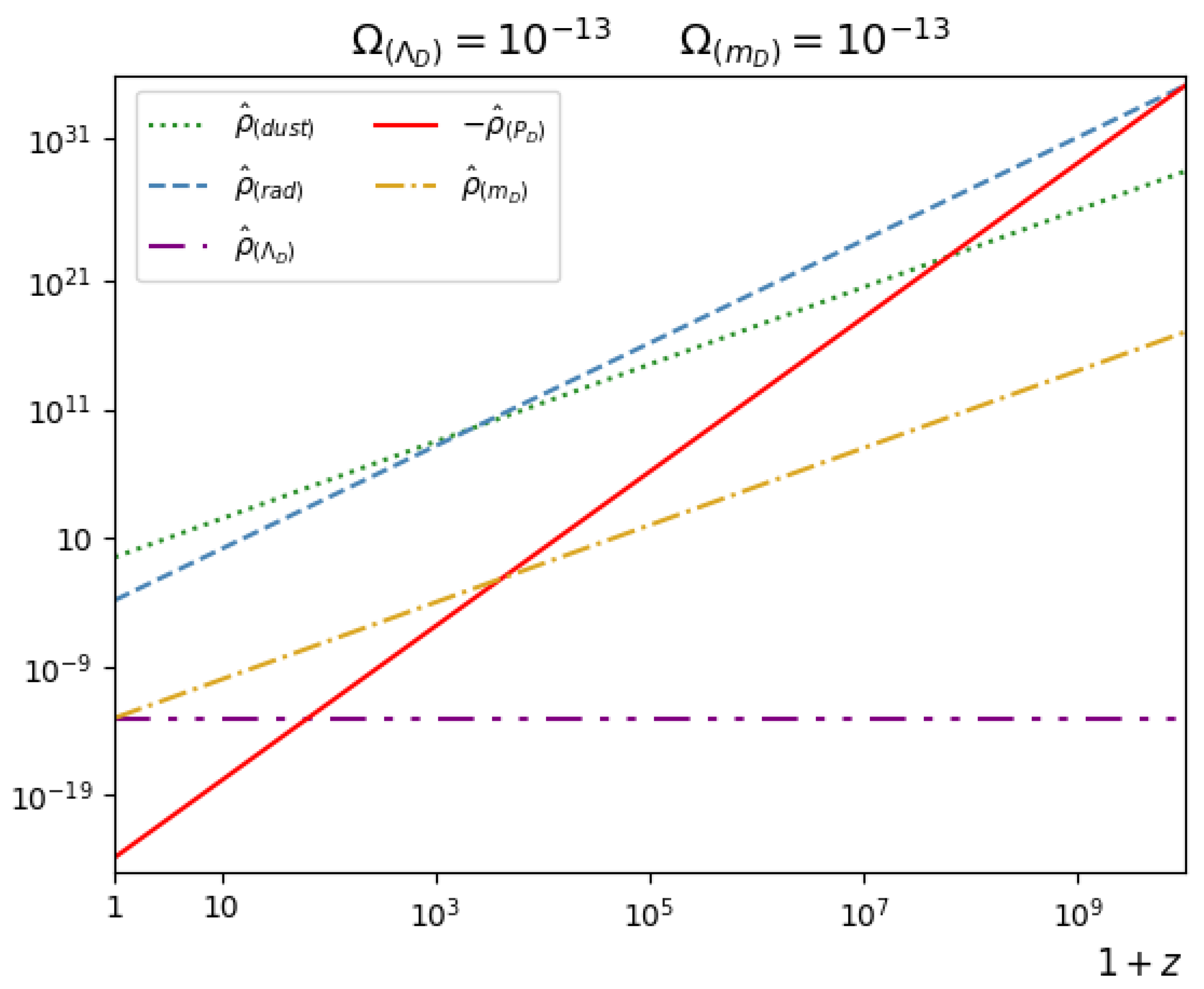
In the case of small and , Figure 2 shows the evolutions of , , , and as functions of the redshift. All Dirac field contribution to is negligible with respect to and except for . Hence, this model only predicts differences with respect to the CDM one at high redshifts, where the contribution from the current terms cancels the radiation component (at , where the blue and the red lines cross each other), inducing a bounce.
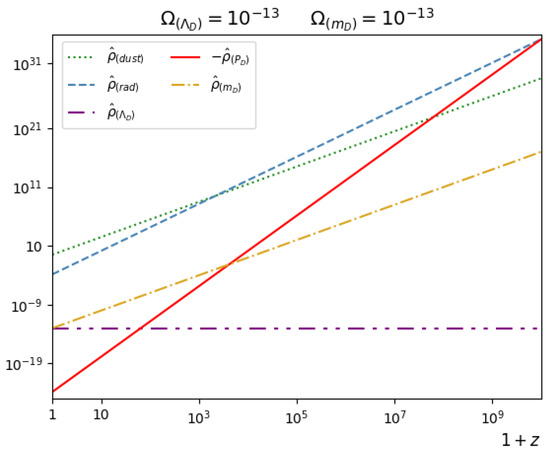
Figure 2.
The evolutions of (dotted green), (dashed blue), (dashed–dotted purple), (red) and (dashed–dotted yellow) are presented as functions of the redshift z, in the case of , and .
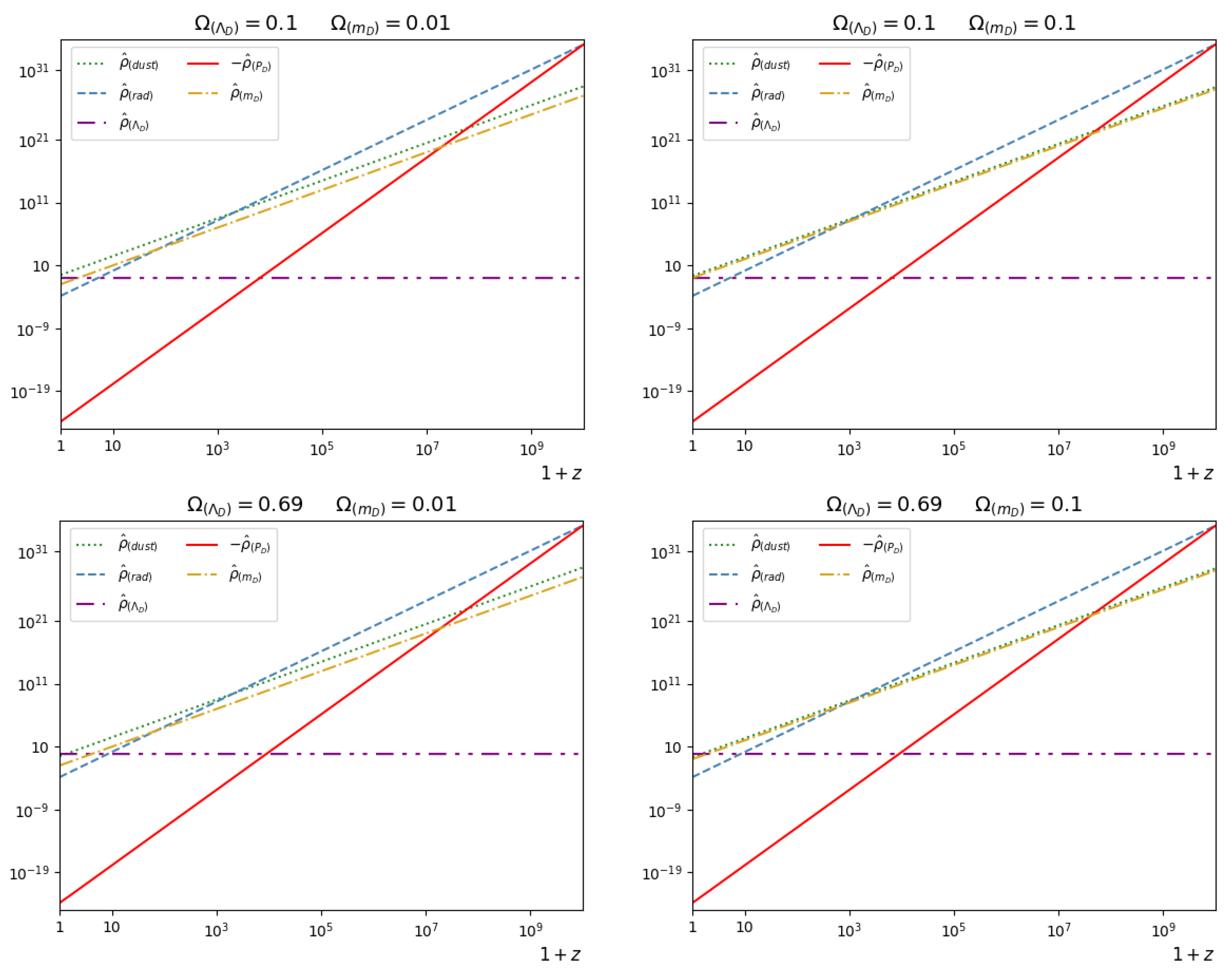
For higher values of and , Figure 3 presents the evolutions of different dimensionless energy density contributions. Similarly to the integrable subcases, we may conclude the following. Since the evolutions of and are described by roughly parallel lines, the term behaves similarly to a cold dark matter component. The term gives a constant contribution which may be responsible for dark energy (see the second line of Figure 3 with and ). Note that all dark energy contribution comes from the Dirac field on the panels shown in the second line of Figure 3. The current term contributes significantly at high redshifts, where it causes a bounce.
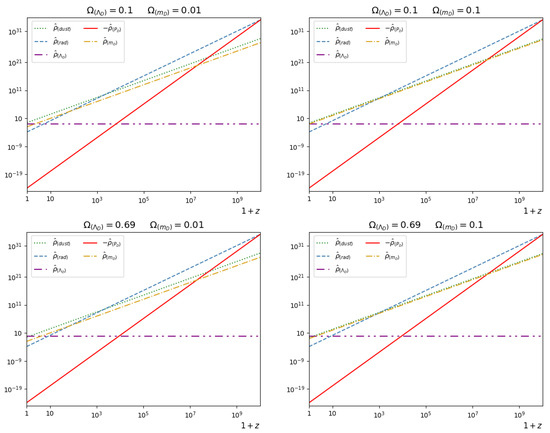
Figure 3.
The evolutions of (dotted green), (dashed blue), (dashed–dotted purple), (red) and (dashed–dotted yellow) are presented as functions of the redshift z, with . In the first row, is set to , while in the second line, it is set to . The parameter is in the left column, and in the right column.
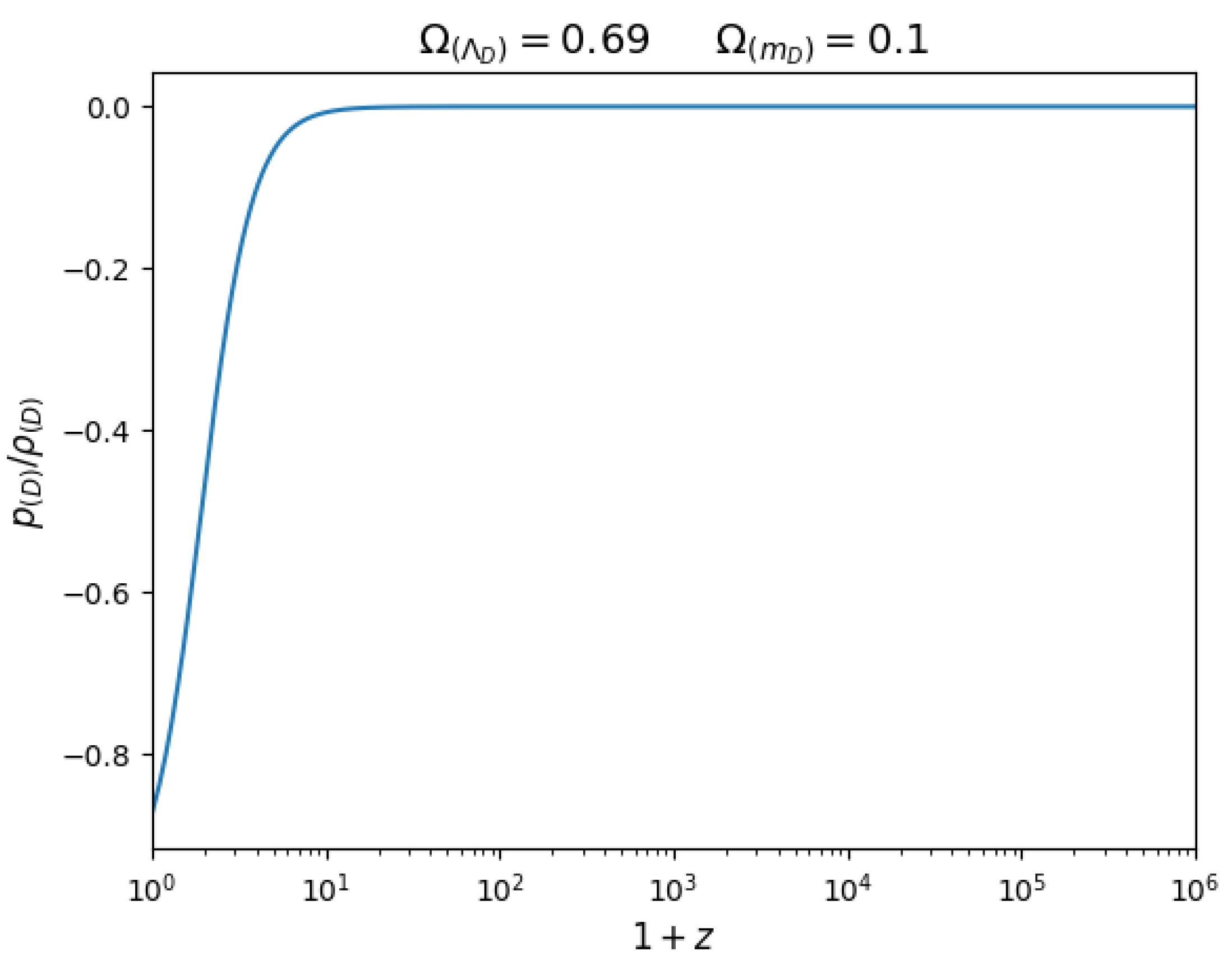
The equation of state of the Dirac field is shown in Figure 4 in the range of with the parameters and corresponding to the last case presented in Figure 3. The Dirac field behaves like dark energy and cold dark matter at low and high redshifts, respectively. However, when the current term contribution becomes significant, there is a redshift ( in this case (see Figure 3)), where the energy density of the Dirac field vanishes leading to a divergence in the equation of state. At even higher redshift values, where the current term dominates, the equation of state of the Dirac field becomes 1 due to Equation (64).
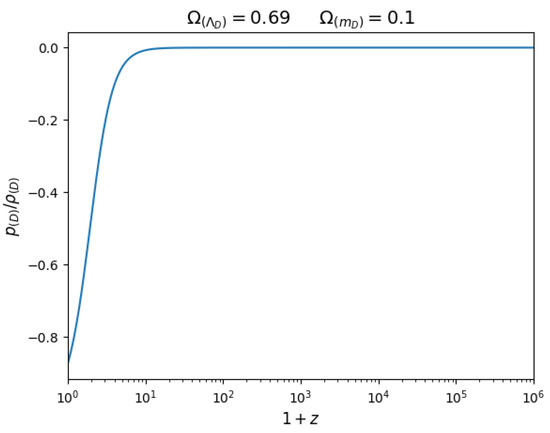
Figure 4.
Evolution of the Dirac field’s equation of state.
3.3. Comparison with a Flat CDM Model and Observations
In this subsection, we compare two subcases of the SST model with a flat CDM model. The first subcase, which will be referred to as SST-1, corresponds to the last case presented in Figure 3, for which the evolution of the equation of state is shown in Figure 4. For the second case, referred to as SST-2, the cosmological parameters are chosen as follows:
with a baryonic matter component . Hence, the Dirac field is only responsible for dark energy and the dust-like component (apart from the baryonic matter contribution). The CDM model parameters are and . In this CDM model, the dark energy–matter equality happens at , while the matter–radiation equality happens at .
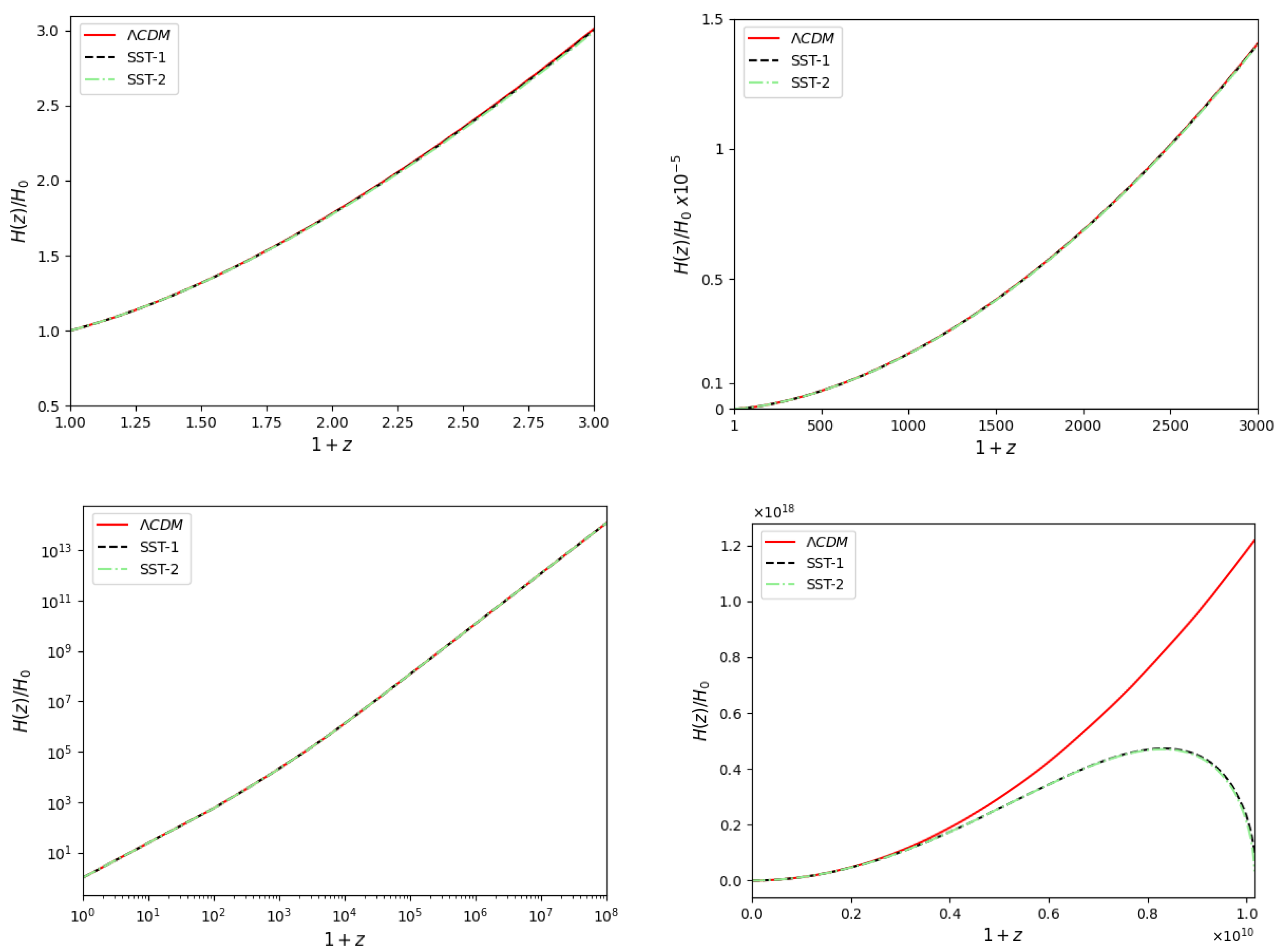
The evolution of the dimensionless Hubble parameter is presented in Figure 5. Apart from the very high redshifts, the Hubble parameter values almost coincide for the three models. However, the Hubble parameter starts to decrease when the negative energy contribution arising from the Dirac field current becomes significant for the SST models. The Hubble parameter tends to zero, and a bounce happens, where it vanishes.
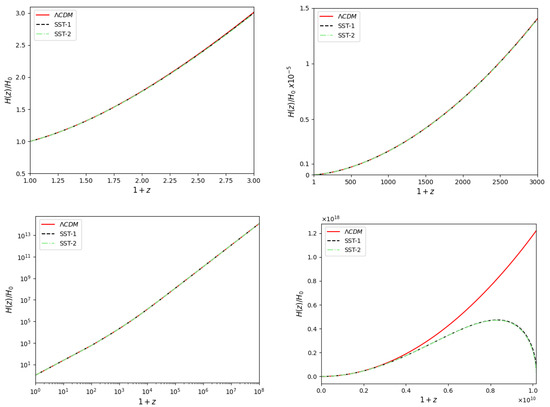
Figure 5.
Evolution of Hubble parameter is depicted for CDM (red), SST-1 (dashed black) and SST2 (dashed–dotted green) models in different redshift intervals.
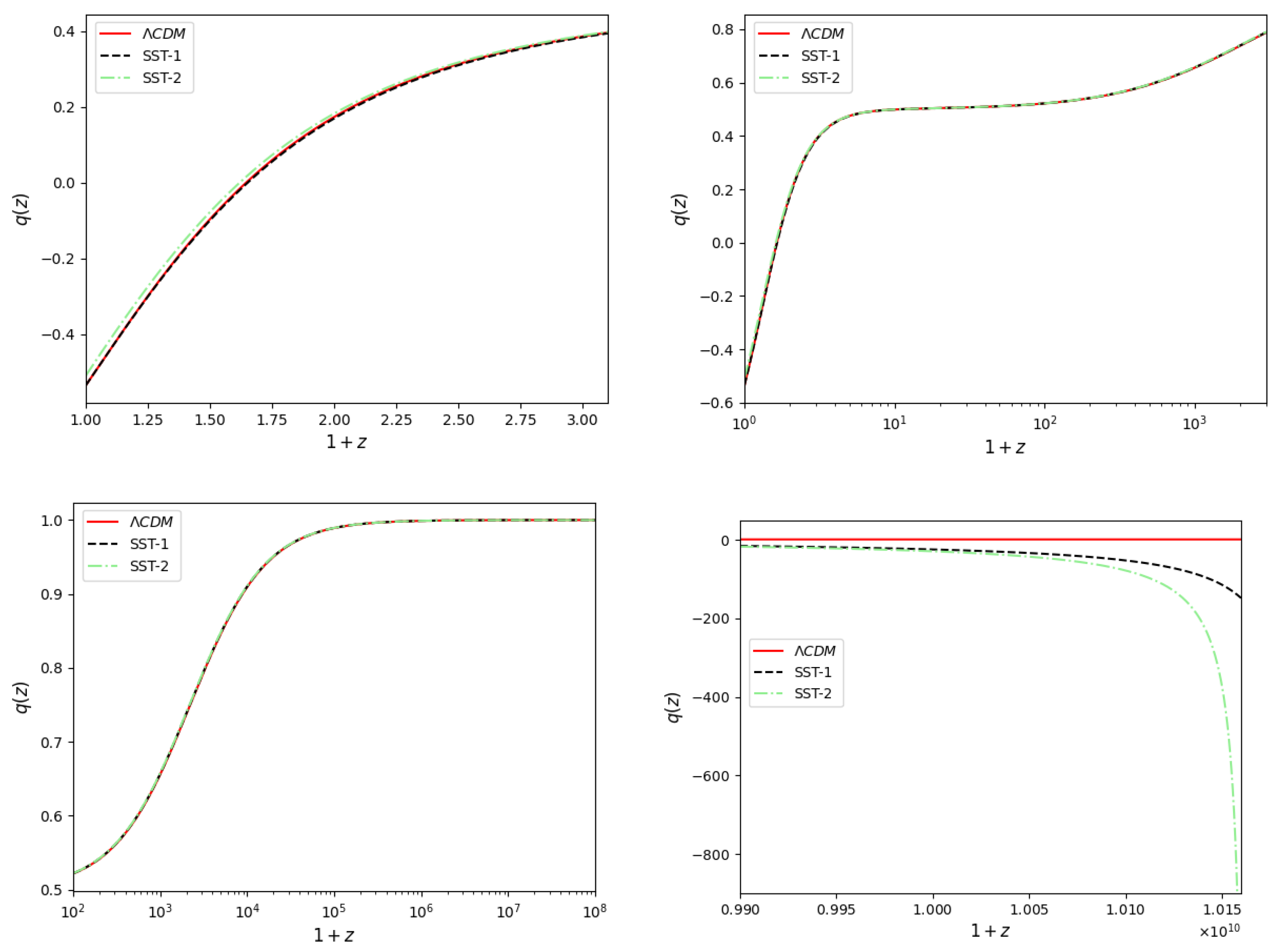
The behavior of the deceleration parameter is another important characteristic of a cosmological model, and is defined as
The evolution of this parameter is presented in Figure 6. The SST-2 model indicates somewhat higher deceleration than the SST-1 and CDM models at low redshifts. Significant differences with respect to the CDM model occur at high redshifts, where for the SST models. This is because vanishes at the bounce, while p is finite and negative. Nevertheless, the three models give the same deceleration in the intermediate evolution regime.
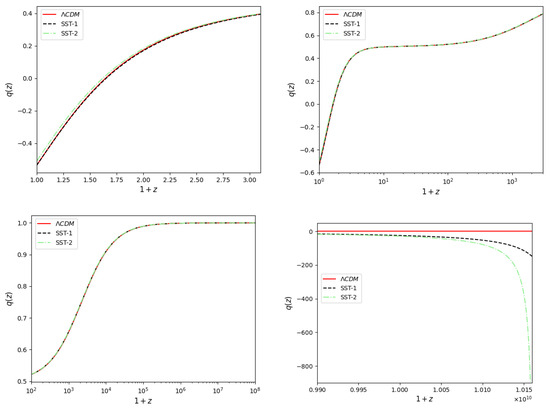
Figure 6.
Evolution of deceleration parameter is depicted for CDM (red), SST-1 (dashed black) and SST2 (dashed–dotted green) models in different redshift intervals.
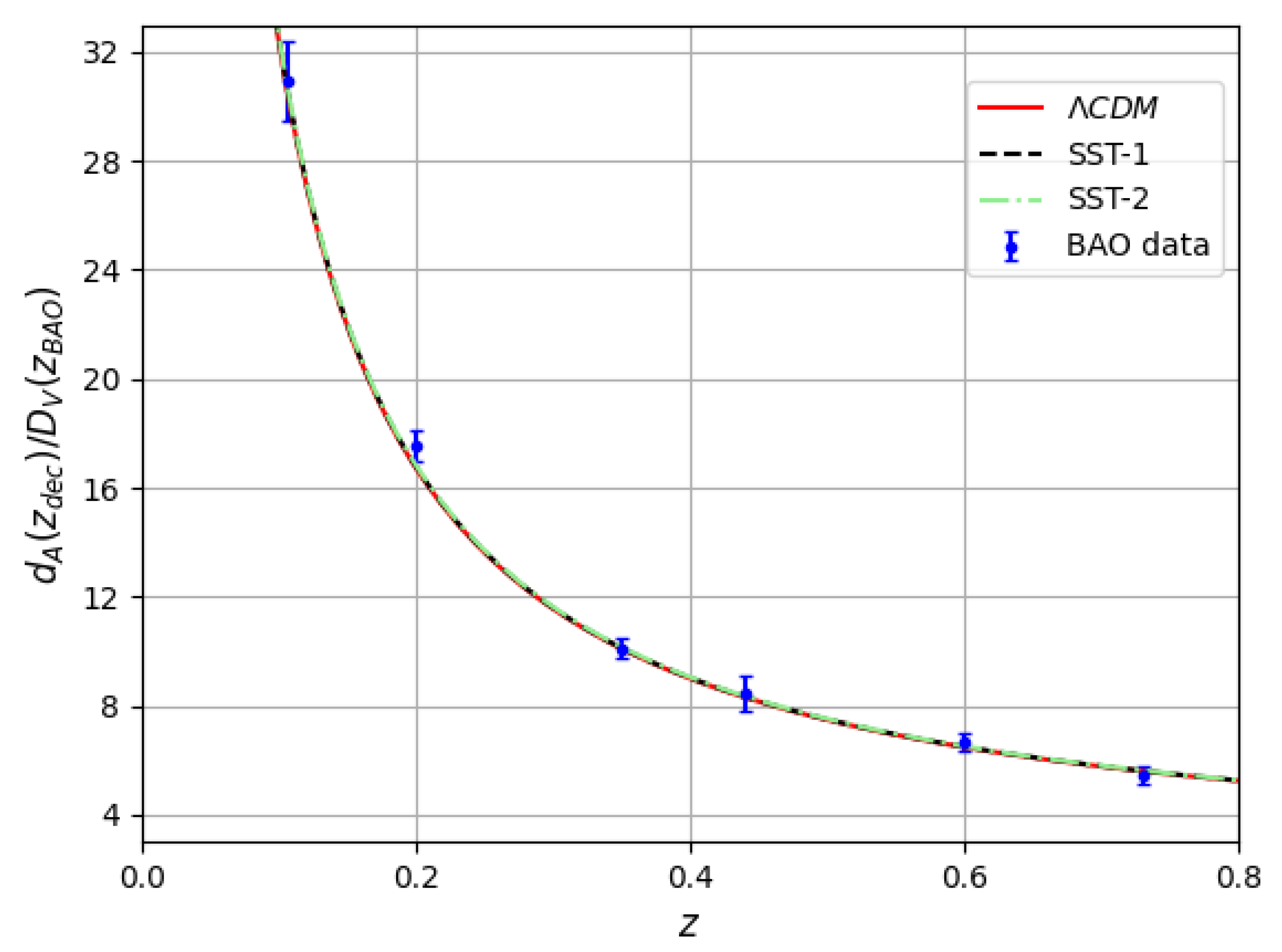
The cosmological evolution at low redshifts, where mostly dark energy dominates, can be tested using the data sets on baryon acoustic oscillations (BAOs), Hubble parameter and distance modulus. We do not carry out a test for the SST model looking for the best fit parameters; we only show that the presented SST-1 and SST-2 models fit as well with these data sets as the flat CDM model. One test with BAO data relies on calculating the ratio of the angular diameter evaluated at the epoch of photon decoupling ()
and the dilation scale
evaluated at the BAO redshift [68]. The BAO data set is given in Table 3 of Ref. [68]. The evolution of together with the data set is presented in Figure 7.
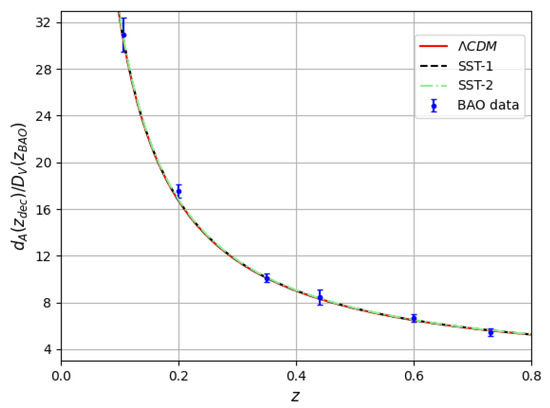
Figure 7.
Comparison of CDM (red), SST-1 (dashed black) and SST2 (dashed–dotted green) models with BAO data set.
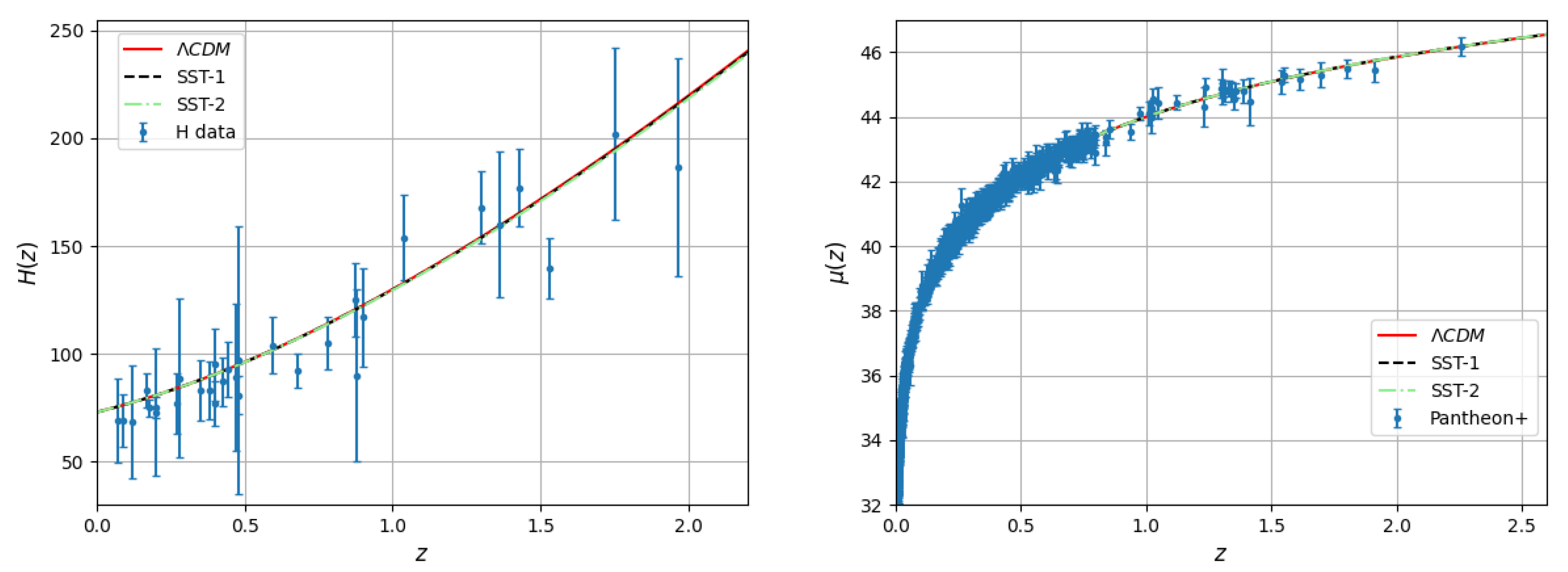
The Hubble parameter and the distance modulus
(with ) depend on , which we set to 73 km/sec/Mpc. The functions and together with the data sets are presented in Figure 8, where we have used Table 2 of Ref. [68] for the Hubble parameter, and the Pantheon+ data set [69] for the distance modulus.
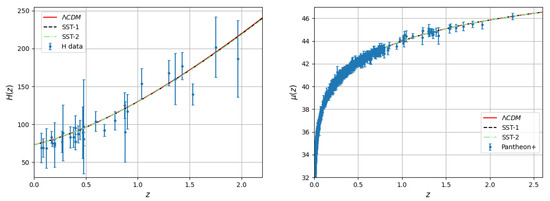
Figure 8.
Comparison of CDM (red), SST-1 (dashed black) and SST2 (dashed–dotted green) models with Hubble parameter (left) and distance modulus (right) data sets.
4. Conclusions
We introduced a model generalizing the Einstein–Cartan–Dirac theory, including local phase invariance of the spinor field supported by a gauge scalar and certain couplings to the torsion. The role of the scalar field is somewhat similar to that of the Dirac gauge function in the Weyl–Dirac theory [70,71]. In a natural gauge, the field equations correspond to that of an Einstein–Dirac theory with a potential that has polar and axial spinor currents. Dropping the local phase invariance and, hence, the scalar field and the coupling between the spinor and the trace of the torsion, the proposed model reduces to the usual Einstein–Cartan–Dirac theory. In this subcase, we showed that the Einstein–Cartan–Dirac theory with one Dirac field is equivalent to the Einstein–Dirac theory, where the Dirac field potential has a term with a spinor axial current . In our model, the Dirac field potential includes three types of contributions: (i) a mass term ( being the spinor scalar), (ii) a term containing the spinor currents , and finally (iii) the term ( being the spinor axial scalar).
We considered the evolution of a flat Friedmann spacetime. Our analytical investigation showed that the term in the potential provides a cosmological constant for and . For and , the contributions of the spinor current terms to the energy density and pressure scale as (a being the scale factor). Hence, they count only in the early universe, where they cause a cosmological bounce for . The observations from the analytical investigations are also confirmed by the numerical examples with nonvanishing , and . The known cosmological evolution can be reproduced even if the Dirac field contributes significantly to the dark energy through the -term. The spinor current contributions to both the energy density and pressure are significant only at small values of the scale factor. In the case of , they are responsible for the avoidance of a cosmological singularity occurring in the standard model, replacing it with a bounce. In addition, two subcases of the SST model are compared to a flat CDM model. Finally, the comparison with BAOs, Hubble parameters and Pantheon+ data sets indicates that the evolution is compatible with the observations even if the total amount of dark energy is related to the presented unconventional Dirac field.
Author Contributions
Conceptualization: Z.K.; Investigation and writing: B.F. and Z.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Publicly available data sets were used in this paper.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Equation of System Derived from Modified Dirac Equation
The system closed together with the Einstein field equations is given by
Here, we have introduced the 3-dimensional Levi–Civita tensor as
Note that Equation (A3) is a consequence of the global phase invariance of the modified Dirac action, which implies a conserved four-current , i.e., . In addition, the Dirac field obeys the continuity equation
which can be checked directly using the field equations.
Notes
| 1 | Note that the coefficient of the term in Equation (2.17) of Ref. [61] should be instead of . The notation correspondence between Ref. [61] and this article is given by {,,}→{,,}. |
| 2 | The representation for the Dirac gamma matrices is given [63] by |
| 3 | This definition of the Dirac conjugate carries an extra imaginary unit factor with respect to Refs. [63,64]. |
| 4 | Note that is introduced with an extra minus factor in Ref. [63]. |
| 5 | The global phase invariance of the Dirac field action implies a conserved, real 4-current . The integration of the perpendicular component of this current to a three-dimensional spacelike hypersurface over gives a conserved charge Q. Upon quantization Q is interpreted as the fermion number inside . Here, we have defined the conserved 4-current including an extra factor , which must be taken into account when relating to the particle number. |
| 6 | We have dropped the boundary term resulting from in the expression of the Ricci scalar. |
References
- Hinshaw, G.; Larson, D.; Komatsu, E.; Spergel, D.N.; Bennett, C.; Dunkley, J.; Nolta, M.R.; Halpern, M.; Hill, R.S.; Odegard, N.; et al. [WMAP Collaboration]. Nine-year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Parameter Results. Astrophys. J. Suppl. Ser. 2013, 208, 19. [Google Scholar] [CrossRef]
- Collaboration, P.; Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; et al. [Planck Collaboration]. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar]
- Borde, A.; Vilenkin, A. Eternal inflation and the initial singularity. Phys. Rev. Lett. 1994, 72, 3305. [Google Scholar] [CrossRef]
- Brandenberger, R.H.; Vafa, C. Superstrings in the early universe. Nucl. Phys. B 1989, 316, 391. [Google Scholar] [CrossRef]
- Ellis, G.F.R.; Maartens, R. The Emergent Universe: Inflationary cosmology with no singularity. Class. Quantum Grav. 2004, 21, 223. [Google Scholar] [CrossRef]
- Ellis, G.F.R.; Murugan, J.; Tsagas, C.G. The emergent universe: An explicit construction. Class. Quantum Grav. 2004, 21, 233. [Google Scholar] [CrossRef]
- Khodadi, M.; Heydarzade, Y.; Darabi, F.; Saridakis, E.N. Emergent universe in Horava-Lifshitz-like F(R) gravity. Phys. Rev. D 2016, 93, 124019. [Google Scholar] [CrossRef]
- Huang, Q.; Wu, P.; Yu, H. Stability of Einstein static universe in gravity theory with a non-minimal derivative coupling. Eur. Phys. J. C 2018, 78, 51. [Google Scholar] [CrossRef]
- Huang, Q.; Huang, H.; Chen, J.; Kang, S. On the stability of Einstein static universe in general scalar–tensor theory with non-minimal derivative coupling. Ann. Phys. 2018, 399, 124. [Google Scholar] [CrossRef]
- Paul, B.C.; Majumdar, A.S. Emergent universe with wormholes in massive gravity. Class. Quantum Grav. 2018, 35, 065001. [Google Scholar] [CrossRef]
- Li, S.-L.; Lü, H.; Wei, H.; Wu, P.; Yu, H. Emergent universe scenario, bouncing universes, and cyclic universes in degenerate massive gravity. Phys. Rev. D 2019, 99, 104057. [Google Scholar] [CrossRef]
- Ilyas, A.; Zhu, M.; Zheng, Y.; Cai, Y.-F. Emergent Universe and Genesis from the DHOST Cosmology. J. High Energy Phys. 2021, 2101, 141. [Google Scholar] [CrossRef]
- Huang, Q.; Xu, B.; Huang, H.; Tu, F.; Zhang, R. Emergent scenario in mimetic gravity. Class. Quantum Grav. 2020, 37, 195002. [Google Scholar] [CrossRef]
- Labraña, P.; Cossio, H. Emergent universe by tunneling in a Jordan-Brans-Dicke theory. Eur. Phys. J. C 2019, 79, 303. [Google Scholar]
- Sarkar, P.; Das, P.K. Emergent cosmology in models of nonlinear electrodynamics. New Astron. 2023, 101, 102003. [Google Scholar] [CrossRef]
- Cai, Y.-F.; Li, M.; Zhang, X. Emergent Universe Scenario via Quintom Matter. Phys. Lett. B 2012, 718, 248. [Google Scholar] [CrossRef]
- Cai, Y.-F.; Wan, Y.; Zhang, X. Cosmology of the Spinor Emergent Universe and Scale-invariant Perturbations. Phys. Lett. B 2014, 731, 217. [Google Scholar] [CrossRef]
- Huang, Q.; Wu, P.; Yu, H. Emergent scenario in the Einstein-Cartan theory. Phys. Rev. D 2015, 91, 103502. [Google Scholar] [CrossRef]
- Shabani, H.; Ziaie, A.H. Stability of the Einstein static Universe in Einstein–Cartan–Brans–Dicke gravity. Eur. Phys. J. C 2019, 79, 270. [Google Scholar] [CrossRef]
- Mukhanov, V.; Brandenberger, R. A nonsingular universe. Phys. Rev. Lett. 1992, 68, 1969. [Google Scholar] [CrossRef]
- Brandenberger, R.; Mukhanov, V.; Sornborger, A. Cosmological theory without singularities. Phys. Rev. D 1993, 48, 1629. [Google Scholar] [CrossRef] [PubMed]
- Abramo, L.R.; Yasuda, I.; Peter, P. onsingular bounce in modified gravity. Phys. Rev. D 2010, 81, 023511. [Google Scholar] [CrossRef]
- Chamseddine, A.H.; Mukhanov, V. Resolving cosmological singularities. J. Cosmol. Astropart. Phys. 2017, 2017, 009. [Google Scholar] [CrossRef]
- Chamseddine, A.H.; Mukhanov, V. Mimetic Dark Matter. J. High Energy Phys. 2013, 1311, 131. [Google Scholar] [CrossRef]
- Chaichian, M.; Kluson, J.; Oksanen, M.; Tureanu, A. Mimetic dark matter, ghost instability and a mimetic tensor-vector-scalar gravity. J. High Energy Phys. 2014, 1412, 102. [Google Scholar] [CrossRef]
- Firouzjahi, H.; Gorji, M.A.; Mansoori, S.A.H. Instabilities in mimetic matter perturbations. J. Cosmol. Astropart. Phys. 2017, 1707, 031. [Google Scholar] [CrossRef]
- Yoshida, D.; Quintin, J.; Yamaguchi, M.; Brandenberger, R. Cosmological perturbations and stability of nonsingular cosmologies with limiting curvature. Phys. Rev. D 2017, 96, 043502. [Google Scholar] [CrossRef]
- Chamseddine, A.H.; Mukhanov, V.; Vikman, A. Cosmology with Mimetic Matter. J. Cosmol. Astropart. Phys. 2014, 1406, 017. [Google Scholar] [CrossRef]
- Brandenberger, R.H. Alternatives to the inflationary paradigm of structure formation. Int. J. Mod. Phys. Conf. Ser. 2011, 1, 67. [Google Scholar] [CrossRef]
- Cartier, C.; Durrer, R.; Copeland, E.J. Cosmological perturbations and the transition from contraction to expansion. Phys. Rev. D 2003, 67, 103517. [Google Scholar] [CrossRef]
- Cai, Y.F.; Qiu, T.; Zhang, X.; Piao, Y.S.; Li, M. Bouncing universe with Quintom matter. J. High Energy Phys. 2007, 0710, 071. [Google Scholar] [CrossRef]
- Cai, Y.F.; Qiu, T.; Brandenberger, R.; Piao, Y.S.; Zhang, X. On Perturbations of Quintom Bounce. J. Cosmol. Astropart. Phys. 2008, 0803, 013. [Google Scholar] [CrossRef]
- Cline, J.M.; Jeon, S.; Moore, G.D. The phantom menaced: Constraints on low-energy effective ghosts. Phys. Rev. D 2004, 70, 043543. [Google Scholar] [CrossRef]
- Lin, C.; Brandenberger, R.H.; Levasseur, L.P. A Matter Bounce By Means of Ghost Condensation. J. Cosmol. Astropart. Phys. 2011, 1104, 019. [Google Scholar] [CrossRef]
- Khoury, J.; Ovrut, B.A.; Steinhardt, P.J.; Turok, N. Ekpyrotic universe: Colliding branes and the origin of the hot big bang. Phys. Rev. D 2001, 64, 123522. [Google Scholar] [CrossRef]
- Brandenberger, R.; Finelli, F. On the Spectrum of Fluctuations in an Effective Field Theory of the Ekpyrotic Universe. J. High Energy Phys. 2001, 0111, 056. [Google Scholar] [CrossRef][Green Version]
- Lyth, D.H. The primordial curvature perturbation in the ekpyrotic Universe. Phys. Lett. B 2002, 524, 1. [Google Scholar] [CrossRef]
- Cai, Y.-F.; Easson, D.A.; Brandenberger, R. Towards a nonsingular bouncing cosmology. J. Cosmol. Astropart. Phys. 2012, 1208, 020. [Google Scholar] [CrossRef]
- Brandenberger, R.; Wang, Z. Ekpyrotic cosmology with a zero-shear S-brane. Phys. Rev. D 2020, 101, 063522. [Google Scholar] [CrossRef]
- Houndjo, M.J.S. Unimodular f(G) gravity. Eur. Phys. J. C 2017, 77, 607. [Google Scholar] [CrossRef][Green Version]
- Casalino, A.; Sebastiani, L.; Zerbini, S. Note on nonsingular Einstein-Aether cosmologies. Phys. Rev. D 2020, 101, 104059. [Google Scholar] [CrossRef]
- Caruana, M.; Farrugia, G.; Said, J.L. Cosmological bouncing solutions in f(T, B) gravity. Eur. Phys. J. C 2020, 80, 640. [Google Scholar] [CrossRef]
- Ilyas, A.; Zhu, M.; Zheng, Y.; Cai, Y.-F.; Saridakis, E.N. DHOST bounce. J. Cosmol. Astropart. Phys. 2020, 2009, 002. [Google Scholar] [CrossRef]
- Casalino, A.; Sanna, B.; Sebastiani, L.; Zerbini, S. Bounce models within teleparallel modified gravity. Phys. Rev. D 2021, 103, 023514. [Google Scholar] [CrossRef]
- Ilyas, M.; Rahman, W.U. Bounce cosmology in f(R) gravity. Eur. Phys. J. C 2021, 81, 160. [Google Scholar] [CrossRef]
- Chakraborty, S.; Gregoris, D. Cosmological evolution with quadratic gravity and nonideal fluids. Eur. Phys. J. C 2021, 81, 944. [Google Scholar] [CrossRef]
- Polarski, D.; Starobinsky, A.A.; Verbin, Y. Bouncing Cosmological Isotropic Solutions in Scalar-Tensor Gravity. J. Cosmol. Astropart. Phys. 2022, 2201, 052. [Google Scholar] [CrossRef]
- Ganiou, M.G.; Houndjo, M.J.S.; Aïnamon, C.; Ayivi, L.; Kanfon, A. Reconstruction method applied to bounce cosmology and inflationary scenarios in cosmological f(G) gravity. Eur. Phys. J. P 2022, 137, 208. [Google Scholar] [CrossRef]
- Kolář, I.; Torralba, F.J.M.; Mazumdar, A. New nonsingular cosmological solution of nonlocal gravity. Phys. Rev. D 2022, 105, 044045. [Google Scholar] [CrossRef]
- Poplawski, N. Nonsingular, big-bounce cosmology from spinor-torsion coupling. Phys. Rev. D 2012, 85, 107502. [Google Scholar] [CrossRef]
- Bambi, C.; Malafarina, D.; Marciano, A.; Modesto, L. Singularity avoidance in classical gravity from four-fermion interaction. Phys. Lett. B 2014, 734, 27. [Google Scholar] [CrossRef]
- Alexander, S.; Bambi, C.; Marciano, A.; Modesto, L. Fermi-bounce cosmology and scale-invariant power spectrum. Phys. Rev. D 2014, 90, 123510. [Google Scholar] [CrossRef]
- Molinari, P.A.P.; Devecchi, F.P.; Ribas, M.O. Brans-Dicke accelerated cosmologies with fermionic sources. Phys. Rev. D 2022, 105, 043527. [Google Scholar] [CrossRef]
- Battefeld, D.; Peter, P. A critical review of classical bouncing cosmologies. Phys. Rept. 2015, 571, 1. [Google Scholar] [CrossRef]
- Brandenberger, R.; Peter, P. Bouncing Cosmologies: Progress and Problems. Found. Phys. 2017, 47, 797. [Google Scholar] [CrossRef]
- Yoo, J.; Watanabe, Y. Theoretical Models of Dark Energy. Int. J. Mod. Phys. D 2012, 21, 1230002. [Google Scholar] [CrossRef]
- Arun, K.; Gudennavar, S.B.; Sivaram, C. Dark matter, dark energy, and alternate models: A review. Adv. Space Res. 2017, 60, 166. [Google Scholar] [CrossRef]
- Motta, V.; García-Aspeitia, M.A.; Hernández-Almada, A.; Magaña, J. Verdugo, Tomás Taxonomy of Dark Energy Models. Universe 2021, 7, 163. [Google Scholar] [CrossRef]
- Hehl, F.W.; von der Heyde, P.; Kerlick, G.D.; Nester, J.M. General relativity with spin and torsion: Foundations and prospects. Rev. Mod. Phys. 1976, 48, 393. [Google Scholar] [CrossRef]
- Belyaev, A.S.; Shapiro, I.L. Torsion action and its possible observables. Nucl. Phys. B 1999, 543, 20. [Google Scholar] [CrossRef]
- Shapiro, I.L. Physical Aspects of the Space-Time Torsion. Phys. Rept. 2002, 357, 113. [Google Scholar] [CrossRef]
- Aldrovandi, R.; Pereira, J.G. An Introduction to Geometrical Physics, Chapter 36: Einstein–Cartan Theory, 2nd ed.; World Scientific: Singapore, 2016. [Google Scholar]
- Dolan, S.R.; Dempsey, D. Bound states of the Dirac equation on Kerr spacetime. Class. Quantum Grav. 2015, 32, 184001. [Google Scholar] [CrossRef]
- Herdeiro, C.A.R.; Pombo, A.M.; Radu, E. Asymptotically flat scalar, Dirac and Proca stars: Discrete vs. continuous families of solutions. Phys. Lett. B 2017, 773, 654. [Google Scholar] [CrossRef]
- Cabral, F.; Lobo, F.S.N.; Rubiera-Garcia, D. Cosmological bounces, cyclic universes, and effective cosmological constant in Einstein-Cartan-Dirac-Maxwell theory. Phys. Rev. D 2020, 102, 083509. [Google Scholar] [CrossRef]
- Magueijo, J.; Zlosnik, T.G.; Kibble, T.W.B. Cosmology with a spin. Phys. Rev. D 2013, 87, 063504. [Google Scholar] [CrossRef]
- Farnsworth, S.; Lehners, J.-L.; Qiu, T. Spinor driven cosmic bounces and their cosmological perturbations. Phys. Rev. D 2017, 96, 083530. [Google Scholar] [CrossRef]
- Myrzakulov, N.; Koussour, M.; Gogoi, D.J. A New Om(z) Diagnostic of Dark Energy in General Relativity Theory. Eur. Phys. J. C 2023, 83, 594. [Google Scholar] [CrossRef]
- Scolnic, D.M.; Jones, D.O.; Rest, A.; Pan, Y.C.; Chornock, R.; Foley, R.J.; Huber, M.E.; Kessler, R.; Narayan, G.; Riess, A.G.; et al. The Complete Light-curve Sample of Spectroscopically Confirmed SNe Ia from Pan-STARRS1 and Cosmological Constraints from the Combined Pantheon Sample. Astrophys. J. 2018, 859, 101. [Google Scholar] [CrossRef]
- Dirac, P.A.M. Long range forces and broken symmetries. Proc. R. Soc. Lond. A 1973, 33, 403. [Google Scholar]
- Rosen, N. Weyl’s geometry and physics. Found. Phys. 1982, 12, 213. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).