Abstract
We explore the evolutionary link between Galactic Be X-ray binaries (BeXBs) and Galactic field double neutron stars (DNSs) based on the properties of the NS spin period—P and binary orbital period—. First, both BeXB and DNS sources show positive correlation trends in P versus relation ( diagram), which may relate to the influence of the accretion evolution. Secondly, the two types of sources exhibit similar bi-modal P/ distributions with the gaps of s/ days for BeXBs and ms/ day for DNSs, respectively. We propose a possibility that Galactic BeXBs may transfer the bi-modal P/ classifications to Galactic field DNSs during the evolution process. Furthermore, based on the bi-modal gaps, we infer the contraction factors of P (by ) and (by ) valuesin the evolution from Galactic BeXBs to Galactic field DNSs. We find that the scaled P or values of Galactic BeXBs share the similar bi-modal distributions to that of Galactic field DNSs, and these results can offer a reference to trace the classification and evolution between the two types of sources.
1. Introduction
Be X-ray binaries (BeXBs) are composed of a neutron star (NS) and a massive B-type star with emission lines [1,2,3,4,5], which are the young populations of high-mass X-ray binaries (HMXBs) and originate from the binaries of two massive stars [6,7,8,9]. These objects usually show the wide ranges of a binary orbital period— and eccentricity— [3,10], and are mostly transient sources with several types of X-ray outbursts [11]: (I). Type I outburst, which occurs when NS of the system crosses the circum-stellar disk of its companion at periastron [11,12]. (II). Type II outburst or giant X-ray outburst, which exhibits the luminosity up to the Eddington limit, and is not clearly related to the orbital phase [5].
BeXBs show a positive correlation trend in the relation of NS spin period—P versus binary orbital period— (i.e., diagram or Corbet diagram [13,14]), which is explained by the accretion effect, i.e., the shorter orbit can cause the more efficient angular momentum transfer from the companion matter to NS by accretion [15]. Knigge, Coe, and Podsiadlowski (2011) found the bi-modal P and distributions of BeXBs [16], and attributed them to the two types of supernovas, where electron-capture supernovas preferentially produce BeXBs with short orbital periods and low eccentricities, while iron-core collapse supernovas produce BeXBs with long orbital periods and high eccentricities [16]. However, some authors indicated that the bi-modal classification of BeXBs may be related to the different accretion effects, which is based on the fact that the BeXB group with / share a higher X-ray luminosity and more Type II outbursts than the other group sources with / [17,18].
Double-neutron stars (DNSs) are the binaries containing two NSs, i.e., a recycled one and a non-recycled one [19,20]. This kind of system was firstly discovered in 1974 [21], and there are about ∼25 DNSs at present that have been detected in the Galactic field [22]. In theory, DNSs are suggested to originate from NS-HMXBs [8,20,23,24,25,26], where NS in the system accretes the companion matter to be accelerated to the faster spin period (i.e., the recycled NS), while its companion can become an NS with the relatively slower spin period (i.e., the non-recycled NS) through the supernova explosion. Therefore, the formation of DNSs is proposed to relate to the processes of supernova explosion [20,27,28,29,30,31], stellar evolution, binary mass transfer, common envelope [32,33,34,35,36], and the accretion-induced spin-up and magnetic field decay of NSs, etc. [18,37]. Moreover, it is also proposed in theory that some DNSs may finally merge into single stars by emitting gravitational wave radiation, making them the particular objects to test the general relativity [38,39,40,41,42,43,44]. The previous investigations of DNSs usually focus on the physical property analysis such as the distributions of , and mass, etc., as well as the theoretical study such as the birth, evolution, and merging of systems [22,45,46,47,48,49]. For example, Andrews and Mandel (2019) divided DNSs into the different types based on Ecc- distribution [47].
The evolutionary link between BeXBs and DNSs may induce the similar physical properties or classifications between the two types of sources [50]. For example, BeXBs show bi-modal features in distributions [16,17,18], and DNSs can be divided into different subgroups according to distribution [47]. In fact, Zhou et al. [50] proposed that the similar bi-modal classifications may be the evidence of an evolutionary link between the two group sources. In this paper, we try to explore the evolution correlation between BeXBs and DNSs by analyzing their properties, and the contents of the paper are arranged as follows: in Section 2, we show BeXB and DNS samples, as well as P/ values. Then, in Section 3, we analyze and compare the properties between BeXBs and DNSs. In Section 4, we probe the spin and orbital evolution from BeXBs to DNSs, and further infer the corresponding contraction factors of P/ values. Last, in Section 5, we summary the discussions and conclusions.
2. Samples of BeXBs and DNSs
We search the published literature for BeXBs in the Milky Way and DNSs in the Galactic field, and then collect their parameter values of the NS spin period—P and binary orbital period—. First, we refer to the catalogues of [3,6,10,51,52,53] and collect 94 Galactic BeXBs, which include 63 P and 60 data. In addition, 48 BeXBs among the previous 94 samples have both P and values. Secondly, we collect 25 field DNSs in the Galactic field from the published paper (see the reference in Table 1), where PSR J0737-3039 is a double neutron star system with PSR J0737-3039A/PSR J0737-3039B being the recycled/non-recycled NS [54]. Then, we also collect P and values of these DNS sources, as shown in Table 1. It should be noticed from Table 1 that PSR J1755-2550 ( s) and PSR J1906+0746 ( s) are suggested as the non-recycled DNSs in the binary systems [55,56,57,58]. As we only consider the recycled NSs in DNS systems, we can trace the influence of the accretion-induced spin-up process. Therefore, the two DNS systems detected with the non-recycled NSs are removed from the samples in the following analysis.

Table 1.
NS spin period—P and binary orbital period— of Galactic field DNSs.
3. P and Porb Distributions
We try to trace the evolutionary links between Galactic BeXBs and Galactic field DNSs based on the relation between P and .
3.1. Diagram
Figure 1 shows the relation of 48 Galactic BeXBs and 23 Galactic field DNSs. It can be seen that both the two types of sources exhibit a positive correlation trend between P and . In fact, the correlation coefficient of the relation for BeXBs in the elliptical region of Figure 1 is ∼0.58, while the corresponding correlation coefficient for 23 DNSs is ∼0.72. Moreover, it should also be noticed from Figure 1 that Galactic BeXBs show potential gaps of s and day in relation, which are also noticed by Knigge, Coe, and Podsiadlowski (2011) [16]. Similarly, Galactic field DNSs show the potential gaps of ms and day in Figure 1, as also being noticed by and Andrews and Mandel (2019) [46].
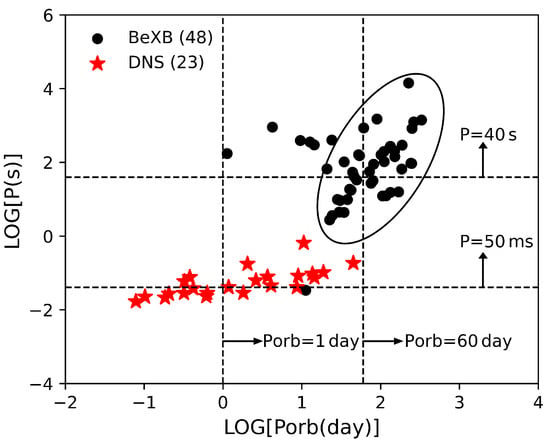
Figure 1.
diagram of Galactic BeXBs and Galactic field DNSs (only retain the recycled NSs), where the gaps of s/ days for bi-modal BeXBs and the gaps of ms/ day for bi-modal DNSs are also indicated.
3.2. P Distribution
Figure 2a,b show the P distributions of Galactic BeXBs and Galactic field DNSs, respectively. It can be seen that Galactic BeXBs show a bi-modal feature in P distribution divided by s. We apply double-Gaussian function to fit this P distribution, and obtain the fitted bi-modal peaks as s and s, respectively, (see Table 2). Similarly, Galactic field DNSs also show a bi-modal feature in P distribution divided by ms, and the double-Gaussian function fitting gives the bi-modal peaks as ms and ms, respectively, (see Table 2).
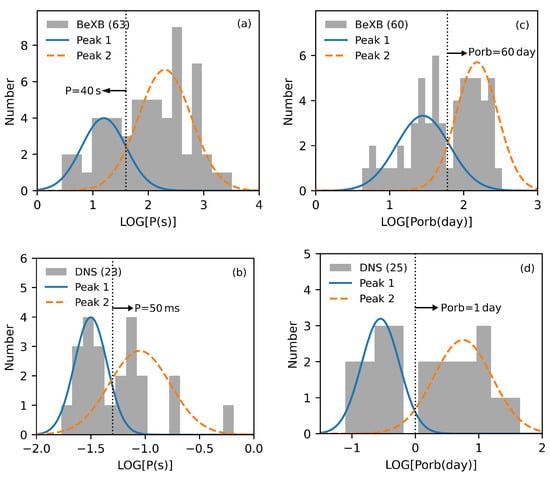
Figure 2.
(a) Histogram of the NS spin period P of Galactic BeXBs. (b) Histogram of NS spin period P of Galactic field DNSs. (c) Histogram of binary orbital period— of Galactic BeXBs. (d) Histogram of binary orbital period— of Galactic field DNSs. The curves in the figure are the double-Gaussian function fittings for the P and values (see also Table 2).

Table 2.
Double-Gaussian function fittings for bi-modal BeXBs and DNSs.
3.3. Distribution
Figure 2c,d show distributions of Galactic BeXBs and Galactic field DNSs. It can be seen that Galactic BeXBs show a bi-modal feature of distribution divided by day. We apply double-Gaussian function to fit this distribution, and obtain the fitted bi-modal peaks as days and days, respectively, (see Table 2). Similarity, Galactic field DNSs also show a bi-modal feature of distribution divided by day, and the double-Gaussian function fitting gives the bi-modal peaks as days and days, respectively, (see Table 2).
4. Spin and Orbital Evolution from BeXBs to DNSs
Theoretically, BeXBs are suggested as the progenitors of DNSs [8,20,24,25]. Then, the similar bi-modal classifications of the two types of sources may be the evidence for this evolutionary link, i.e., Galactic BeXBs transfer the bi-modal classification to Galactic field DNSs. Moreover, this evolution scenario also predicts the contraction of values from BeXBs to DNSs. Then, we try to study the evolutionary links between Galactic BeXBs and Galactic field DNSs by the P/ relations.
4.1. Diagram
Figure 3 shows the diagram of Galactic BeXBs and Galactic field DNSs. Then, we infer the contraction factors of values between the two types of sources by the gaps of the bi-modal classifications: as the evolution from Galactic BeXBs to Galactic field DNSs, the gaps of s/ days for bi-modal BeXBs transfer to the gaps of / for bi-modal DNSs, which infer the contraction factor of P values as , and the contraction factor of values as . We show the scaled P values (by ) and scaled values (by ) of Galactic BeXBs in Figure 3. It can be seen that the scaled relation of Galactic BeXBs share a similar range to Galactic field DNSs. Moreover, both scaled Galactic BeXBs and Galactic field DNSs show positive correlation trends in relation.
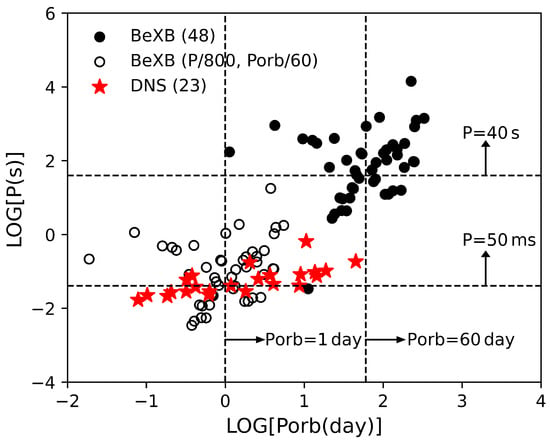
Figure 3.
diagram of Galactic BeXBs and Galactic field DNSs (only retain the recycled NSs), where the scaled P values (by ) and scaled values (by ) of Galactic BeXBs are also shown in the figure.
4.2. P Distribution
Figure 4a,b show the P distributions of Galactic BeXBs and Galactic field DNSs, respectively, in which the P values of Galactic BeXBs are scaled to . Moreover, the double-Gaussian function fitting gives the bi-modal peaks of scaled P distributions for Galactic BeXBs as ms and ms, respectively, (see Table 2). It can be seen that scaled Galactic BeXBs and Galactic field DNSs exhibit the P distributions with the similar gaps of the bi-modal features.
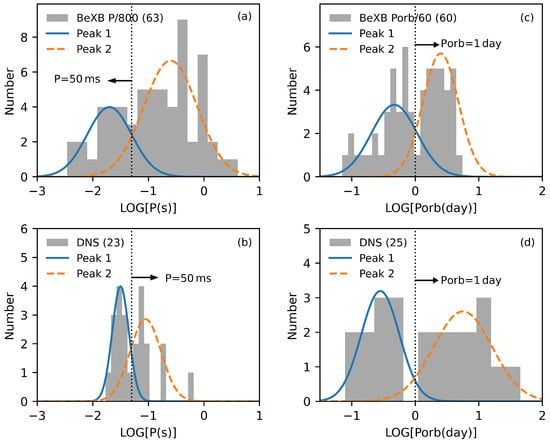
Figure 4.
(a) Histogram of the scaled NS spin period P (by ) of Galactic BeXBs. (b) Histogram of the NS spin period P of Galactic field DNSs. (c) Histogram of the scaled binary orbital period (by ) of Galactic BeXBs. (d) Histogram of the binary orbital period— of Galactic field DNSs. The curves in the figure are the double-Gaussian function fittings for the P and values (see also Table 2).
4.3. Distribution
Figure 4c,d show the distribution of Galactic BeXBs and Galactic field DNSs, respectively, in which the values of Galactic BeXBs are scaled to . Moreover, the double-Gaussian function fitting gives the bi-modal peaks of scaled distributions for Galactic BeXBs as days and days, respectively, (as can be seen in Table 2). It can be seen that scaled Galactic BeXBs and Galactic field DNSs exhibit the distributions with similar gaps and peaks in the bi-modal features.
5. Discussions and Conclusions
We the analyze P and distributions of Galactic BeXBs and Galactic field DNSs, and find similar bi-modal classifications between the two types of sources. These results may suggest an evolutionary link between Galactic BeXBs and Galactic field DNSs, which can further infer the spin and binary orbital evolution between them. The detailed discussions and conclusions are summarized as follows.
- Both Galactic BeXBs and Galactic field DNSs show the positive correlation trends in relation (see Figure 1), which may relate to the influence of accretion evolution, i.e., the shorter binary orbit may result in the more efficient angular momentum transfer as NS accretes the companion matter [15]. Moreover, the two types of sources also show similar bi-modal classifications in P or distributions (see Figure 2), which has also been noticed by Zhou et al. [50]. In theory, BeXBs are the young populations of NS-HMXBs with orbits which have not obviously evolved, and it is suggested that DNSs are the evolutionary products of NS-HMXBs [8,20,24,25]. Therefore, the similar relations and bi-modal classifications of the two types of sources support the evolution scenario from BeXBs to DNS. In fact, Zhou et al. [50] suggested the possibility that Galactic BeXBs may transfer the bi-modal classifications to DNSs during the accretion evolution process. Moreover, Zhou et al. [50] also indicated that, as the accretion effects can cause the spin-up of NS and the contraction of binary orbit [82,83,84,85], then BeXBs with shorter orbital periods will preferentially evolve into DNSs with faster spin periods and shorter orbits than those with longer orbits.
- It is noticed that the similar bi-modal P/ distributions in BeXBs and DNSs may not only arise from an evolutionary relationship, but may also be affected by the influence from other processes, such as variations in initial conditions or differences in supernova mechanisms. For example, the supernova explosion of the donor stars may significantly affect the evolution from NS-HMXBs to DNSs [31]. First, a binary like NS-HMXBs remains bound only if less than half of the total mass of the system is explosively ejected in the supernova [27]. Secondly, a NS-HMXB will disrupt its orbit if the critical angle— during the supernova satisfies [29]. Thirdly, the high-velocity kick of the donor star supernova in a NS-HMXB can lengthen the binary orbit and cause high eccentricity, or even disrupt the system [28]. However, it is noticed that a considerable fraction of DNSs is detected with quite low orbital eccentricities, implying that the second-born NSs seem to receive on average smaller kicks at birth [20]. In fact, it is theoretically suggested that these low-velocity kick NSs may either have been formed by electron-capture collapse, or by the collapse of ultra-stripped iron cores with a small kick formed though the Case BB Roche-lobe overflow process [20,30]. Therefore, compared to the accretion evolution process, these low-energy supernova with low-velocity kicks of the progenitors of the second-born NSs may be not the dominated factors for the formation of the bi-modal DNSs.
- The common envelope phase is another process that may significantly affect the evolution from BeXBs to DNSs [86]. Theoretically, in the latter evolution of a NS-HMXB, the unstable Roche lobe overflow of the companion can engulf NS and form a common envelope, and it is suggested that the formation of DNSs may have experienced at least one common envelope episode during their progenitor evolution [5,9,34]. The models of a common envelope usually consider the interaction between the binary and envelope, and predict several possible phases, e.g., the plunge-in, based on the multiple physical processes on various of timescales [35,36]. However, the predicted common envelope phase has not been observed until now, which may be due to the short duration time of the envelope phase (∼ y, see, e.g., Meurs and van den Heuvel (1989) [87]) compared to the lifetime of a massive star (∼ y, see, e.g., Chaty (2013) [5]). Moreover, the current simulations of the common envelope phase cannot give the consensus on a thorough understanding of this evolution on all the relevant spatial and timescales [26,34,35,36]. As for the evolution from NS-HMXBs to DNSs, Taam (1996) [88] and Taam and Sandquist (2000) [32] suggested that only a NS-HMXB starting out with the long orbit can survive the common envelope evolution and may then form a DNS. On the contrary, a NS-HMXB with the short initial orbit will finally lead to the merge of the binary into a single Thorne–Zytkow star [32]. However, the predicted Thorne–Zytkow star has not been observed until now [8]. Meanwhile, it is indicated by Taam and Sandquist (2000) [32] that, if the envelope matter is ejected out from the system during the common envelope stage due to the binary interaction, the system can also form a DNS with a short binary orbit. Therefore, both NS-HMXBs with short or long orbits have the opportunity to survive and form a DNS if the envelope matter is effectively ejected out from the system.
- It should be noted that potential uncertainties introduced from the sample selections may affect our conclusions. First, we only analyze BeXBs in the Milky Way, and do not consider the sources in the large Magellanic cloud or small Magellanic cloud, which are based on the following considerations: (I). Knigge et al. [16] and Zhou et al. [50] indicated that all three BeXB groups, i.e., those detected in the Milky Way, large Magellanic clouds, and small Magellanic clouds, exhibit positive correlations in the relation, as well as the similar bi-modal classifications in P and distributions. (II). The detected DNSs at present are all discovered in the Milky Way, and then the evolution analysis between BeXBs and DNSs should be constrained in the same host galaxy to maintain consistency. Secondly, as for DNSs, we only retain the sources in the Galactic field of the Milky Way, and discard those in the global clusters. The reason is that cluster DNSs constitute most candidates, and are suggested to have experienced more complicated formation and evolution processes than those in the Galactic field. Finally, it is also noticed that there are selection biases in the detections of binary orbital periods of BeXBs, since, for the longer orbit sources, the X-ray outbursts are less frequent, and the pulse timing is not easy to implement [89].
- In order to explore the evolutionary link between BeXBs and DNSs, we assume that Galactic BeXBs transfer the bi-modal P/ classifications to Galactic field DNSs through the accretion process. Moreover, we also assume that the Galactic BeXB group that corresponds to the short orbit sources ( days) of bi-modal classifications will preferentially evolve into the Galactic field DNS group that corresponds to the sources with a fast spin ( ms) and short orbit ( day) in the bi-modal classifications. Furthermore, we infer the spin (P values are scaled by ) and orbital ( values are scaled by ) contraction factors, which are inferred by the gaps ( s and days for Galactic BeXBs, and ms and day for Galactic field DNSs, as can be seen in Figure 2) showing the bi-modal classifications of the two types of sources. It can be seen from Figure 3 that the scaled P and values of Galactic BeXBs and Galactic field DNSs show similar positive correlation trends in the relation. In addition, it can be also noticed from Figure 4 and Table 2 that the scaled P and values of Galactic BeXBs share the similar bi-modal distributions to those of Galactic field DNSs. It is noticed that these contraction factors of P/ values are derived in a statistical way, which may cause uncertainties due to the limit of the sample numbers. In fact, it can be seen from Figure 4a,b and Table 2 that the two peaks of bi-modal P distributions of scaled Galactic BeXBs and Galactic field DNSs are not quite symmetric, which may be due to influence of the binary accretion-induced spin-up evolution. Moreover, the contraction of NS spin and binary orbit from Galactic BeXBs to Galactic field DNSs may be also affected by other physical factors. In fact, it is indicated by Zhou et al. [50] that BeXBs with short orbits of days on average share faster NS spin periods, lower NS magnetic field strengths [18], lower binary orbital eccentricities, and more high energy outbursts (Type II outbursts) with higher average peak X-ray luminosities than those sources with longer orbits of days. Moreover, Zhou et al. [50] also indicated that DNSs with short orbits of day on average share faster NS spin periods, higher spin-down powers, and higher binary accretion rates than those sources with longer orbits of day. Therefore, the potential evolution relation and channels from BeXBs to DNSs may need further observation confirmation and theoretical analysis, e.g., the larger samples, and the detailed modeling of binary evolution. However, the inferred contraction factors of P and can offer a reference for the binary evolution from BeXBs and DNSs, which can also offer a tool to trace the classification of the two types of sources.
Author Contributions
Y.Z. and D.W. wrote the main manuscript, including the text, tables, and figures. D.W. and C.Z. proposed a theoretical model and reasoned in detail, analyzed the conclusions, and put forward relevant suggestions. All authors reviewed the manuscript, and then discussed and revised the paper together, and finally agreed to submit the paper. All authors have read and agreed to the final version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China (Grant Nos. 12163001, 12463007 and U1938117), and the New Academic Seedling Foundation of Guizhou Normal University (Grant No. [2022]05).
Data Availability Statement
The BeXBs data are based on the following websites: in Raguzova & Popov (2005) at ref. [51]; in Liu, van Paradijs & van den Heuvel (2006) at ref. [6]; in Reig (2011) at ref. [3]; in Walter et al. (2015) at ref. [52]; in Reig & Zezas (2018) at ref. [53]; in Fortin et al. (2023) at ref. [10]. The DNSs data are based on the following websites: in Yang et al. (2023) at ref. [22]; in Zhao et al. (2024) at ref. [68]; in Colom i Bernadich et al. (2023) at ref. [69]; in Padmanabh et al. (2023) at ref. [74]; in Swiggum et al. (2023) at ref. [76]; in Wu et al. (2023) at ref. [77]; in Su et al. (2024) at ref. [79].
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Maraschi, L.; Treves, A.; van den Heuvel, E.P.J. B-emission Stars and X-ray sources. Nature 1976, 259, 292. [Google Scholar] [CrossRef]
- Rappaport, S.; van den Heuvel, E.P.J. X-ray observations of Be stars. Symp.-Int. Astron. Union 1982, 98, 327–344. [Google Scholar] [CrossRef]
- Reig, P. Be/X-ray binaries. Astrophys. Space Sci. 2011, 332, 1–29. [Google Scholar] [CrossRef]
- Chaty, S. Nature, Formation, and Evolution of High Mass X-Ray Binaries. In Evolution of Compact Binaries; Schmidtobreick, L., Schreiber, M.R., Tappert, C., Eds.; Astronomical Society of the Pacific Conference Series; Astronomical Society of the Pacific: San Francisco, CA, USA, 2011; Volume 447, p. 29. [Google Scholar] [CrossRef]
- Chaty, S. Optical/infrared observations unveiling the formation, nature and evolution of High-Mass X-ray Binaries. Adv. Space Res. 2013, 52, 2132–2142. [Google Scholar] [CrossRef]
- Liu, Q.Z.; van Paradijs, J.; van den Heuvel, E.P.J. Catalogue of high-mass X-ray binaries in the Galaxy (4th edition). Astron. Astrophys. 2006, 455, 1165–1168. [Google Scholar] [CrossRef]
- Chaty, S. High mass X-ray binaries: Progenitors of double neutron star systems. In Proceedings of the Fourteenth Marcel Grossmann Meeting—MG14, Rome, Italy, 12–18 July 2015; Bianchi, M., Jansen, R.T., Ruffini, R., Eds.; World Scientific Publishing: Singapore, 2018; pp. 1883–1888. [Google Scholar] [CrossRef]
- Van den Heuvel, E.P.J. High-Mass X-ray Binaries: Progenitors of double compact objects. In High-Mass X-Ray Binaries: Illuminating the Passage from Massive Binaries to Merging Compact Objects; Oskinova, L.M., Bozzo, E., Bulik, T., Gies, D.R., Eds.; Cambridge University Press: Cambridge, UK, 2019; Volume 346, pp. 1–13. [Google Scholar] [CrossRef]
- Chaty, S. Accreting Binaries; Nature, Formation, and Evolution; IOP Publishing: Bristol, UK, 2022. [Google Scholar] [CrossRef]
- Fortin, F.; García, F.; Simaz Bunzel, A.; Chaty, S. A catalogue of high-mass X-ray binaries in the Galaxy: From the INTEGRAL to the Gaia era. Astron. Astrophys. 2023, 671, A149. [Google Scholar] [CrossRef]
- Stella, L.; White, N.E.; Rosner, R. Intermittent Stellar Wind Acceleration and the Long-Term Activity of Population I Binary Systems Containing an X-Ray Pulsar. Astrophys. J. 1986, 308, 669. [Google Scholar] [CrossRef]
- Rivinius, T.; Carciofi, A.C.; Martayan, C. Classical Be stars. Rapidly rotating B stars with viscous Keplerian decretion disks. Astron. Astrophys. Rev. 2013, 21, 69. [Google Scholar] [CrossRef]
- Corbet, R.H.D. Be/neutron star binaries: A relationship between orbital period and neutron star spin period. Astron. Astrophys. 1984, 141, 91–93. [Google Scholar]
- Corbet, R.H.D. The three types of high-mass X-ray pulsator. Mon. Not. R. Astron. Soc. 1986, 220, 1047–1056. [Google Scholar] [CrossRef]
- Waters, L.B.F.M.; van Kerkwijk, M.H. The relation between orbital and spin periods in massive X-ray binaries. Astron. Astrophys. 1989, 223, 196–206. [Google Scholar]
- Knigge, C.; Coe, M.J.; Podsiadlowski, P. Two populations of X-ray pulsars produced by two types of supernova. Nature 2011, 479, 372–375. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Z.Q.; Shao, Y.; Li, X.D. On the Spin Period Distribution in Be/X-Ray Binaries. Astrophys. J. 2014, 786, 128. [Google Scholar] [CrossRef]
- Ye, C.Q.; Wang, D.H.; Zhang, C.M.; Zhang, J.W. Exploring the accretion-induced evolution of the spin period and magnetic field strength of Be/X-ray Pulsars. Astrophys. Space Sci. 2020, 365, 126. [Google Scholar] [CrossRef]
- Lorimer, D.R.; Kramer, M. Handbook of Pulsar Astronomy; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Tauris, T.M.; Kramer, M.; Freire, P.C.C.; Wex, N.; Janka, H.T.; Langer, N.; Podsiadlowski, P.; Bozzo, E.; Chaty, S.; Kruckow, M.U.; et al. Formation of Double Neutron Star Systems. Astrophys. J. 2017, 846, 170. [Google Scholar] [CrossRef]
- Hulse, R.A.; Taylor, J.H. Discovery of a pulsar in a binary system. Astrophys. J. Lett. 1975, 195, L51–L53. [Google Scholar] [CrossRef]
- Yang, Y.Y.; Zhang, C.M.; Li, D.; Chen, L.; Zhang, J.W.; Wang, D.H.; Jiang, L.Y.; Cui, X.H. Investigating the distribution of double neutron stars and unconventional component mass. Mon. Not. R. Astron. Soc. 2023, 521, 4669–4678. [Google Scholar] [CrossRef]
- Podsiadlowski, P.; Langer, N.; Poelarends, A.J.T.; Rappaport, S.; Heger, A.; Pfahl, E. The Effects of Binary Evolution on the Dynamics of Core Collapse and Neutron Star Kicks. Astrophys. J. 2004, 612, 1044–1051. [Google Scholar] [CrossRef]
- Stairs, I.H. Pulsars in Binary Systems: Probing Binary Stellar Evolution and General Relativity. Science 2004, 304, 547–552. [Google Scholar] [CrossRef] [PubMed]
- van den Heuvel, E.P.J. Formation of Double Neutron Stars, Millisecond Pulsars and Double Black Holes. J. Astrophys. Astron. 2017, 38, 45. [Google Scholar] [CrossRef]
- Vigna-Gómez, A.; Neijssel, C.J.; Stevenson, S.; Barrett, J.W.; Belczynski, K.; Justham, S.; de Mink, S.E.; Müller, B.; Podsiadlowski, P.; Renzo, M.; et al. On the formation history of Galactic double neutron stars. Mon. Not. R. Astron. Soc. 2018, 481, 4009–4029. [Google Scholar] [CrossRef]
- Blaauw, A. On the origin of the O- and B-type stars with high velocities (the “run-away” stars), and some related problems. Bull. Astron. Institutes Neth. 1961, 15, 265. [Google Scholar]
- Flannery, B.P.; van den Heuvel, E.P.J. On the origin of the binary pulsar PSR 1913+16. Astron. Astrophys. 1975, 39, 61–67. [Google Scholar]
- Tauris, T.M.; van den Heuvel, E.P.J. Formation and evolution of compact stellar X-ray sources. In Compact Stellar X-ray Sources; Lewin, W.H.G., van der Klis, M., Eds.; Cambridge University Press: Cambridge, UK, 2006; Volume 39, pp. 623–665. [Google Scholar] [CrossRef]
- Tauris, T.M.; Langer, N.; Podsiadlowski, P. Ultra-stripped supernovae: Progenitors and fate. Mon. Not. R. Astron. Soc. 2015, 451, 2123–2144. [Google Scholar] [CrossRef]
- Alsabti, A.W.; Murdin, P. Handbook of Supernovae; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Taam, R.E.; Sandquist, E.L. Common Envelope Evolution of Massive Binary Stars. Annu. Rev. Astron. Astrophys. 2000, 38, 113–141. [Google Scholar] [CrossRef]
- Taam, R.E.; Ricker, P.M. Common envelope evolution. New Astron. Rev. 2010, 54, 65–71. [Google Scholar] [CrossRef]
- Vigna-Gómez, A.; MacLeod, M.; Neijssel, C.J.; Broekgaarden, F.S.; Justham, S.; Howitt, G.; de Mink, S.E.; Vinciguerra, S.; Mandel, I. Common envelope episodes that lead to double neutron star formation. Publ. Astron. Soc. Aust. 2020, 37, e038. [Google Scholar] [CrossRef]
- Ivanova, N.; Justham, S.; Chen, X.; De Marco, O.; Fryer, C.L.; Gaburov, E.; Ge, H.; Glebbeek, E.; Han, Z.; Li, X.D.; et al. Common envelope evolution: Where we stand and how we can move forward. Astron. Astrophys. Rev. 2013, 21, 59. [Google Scholar] [CrossRef]
- Ivanova, N.; Justham, S.; Ricker, P. Common Envelope Evolution; IOP Publishing: Bristol, UK, 2020. [Google Scholar] [CrossRef]
- Zhang, C.M.; Kojima, Y. The bottom magnetic field and magnetosphere evolution of neutron star in low-mass X-ray binary. Mon. Not. R. Astron. Soc. 2006, 366, 137–143. [Google Scholar] [CrossRef]
- Kramer, M. The Double Pulsar: A Unique Lab for Relativistic Plasma Physics and Tests of General Relativity. In Neutron Stars and Pulsars; Becker, W., Ed.; Astrophysics and Space Science Library; Springer: Berlin/Heidelberg, Germany, 2009; Volume 357, p. 73. [Google Scholar] [CrossRef]
- Miller, M.C.; Miller, J.M. The masses and spins of neutron stars and stellar-mass black holes. Phys. Rep. 2015, 548, 1–34. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Wex, N. Neutron Stars as Probes for General Relativity and Gravitational Waves. In Handbook of Supernovae; Alsabti, A.W., Murdin, P., Eds.; Springer: Cham, Switzerland, 2017; p. 1447. [Google Scholar] [CrossRef]
- Becker, W.; Kramer, M.; Sesana, A. Pulsar Timing and Its Application for Navigation and Gravitational Wave Detection. Space Sci. Rev. 2018, 214, 30. [Google Scholar] [CrossRef]
- Kramer, M.; Stairs, I.H.; Manchester, R.N.; Wex, N.; Deller, A.T.; Coles, W.A.; Ali, M.; Burgay, M.; Camilo, F.; Cognard, I.; et al. Strong-Field Gravity Tests with the Double Pulsar. Phys. Rev. X 2021, 11, 041050. [Google Scholar] [CrossRef]
- Burgay, M.; Perrodin, D.; Possenti, A. General Relativity Measurements from Pulsars. In Timing Neutron Stars: Pulsations, Oscillations and Explosions; Belloni, T.M., Méndez, M., Zhang, C., Eds.; Astrophysics and Space Science Library; Springer: Berlin/Heidelberg, Germany, 2021; Volume 461, pp. 53–95. [Google Scholar] [CrossRef]
- Özel, F.; Freire, P. Masses, Radii, and the Equation of State of Neutron Stars. Annu. Rev. Astron. Astrophys. 2016, 54, 401–440. [Google Scholar] [CrossRef]
- Andrews, J.J.; Zezas, A. Double neutron star formation: Merger times, systemic velocities, and travel distances. Mon. Not. R. Astron. Soc. 2019, 486, 3213–3227. [Google Scholar] [CrossRef]
- Andrews, J.J.; Mandel, I. Double Neutron Star Populations and Formation Channels. Astrophys. J. Lett. 2019, 880, L8. [Google Scholar] [CrossRef]
- Farrow, N.; Zhu, X.J.; Thrane, E. The Mass Distribution of Galactic Double Neutron Stars. Astrophys. J. 2019, 876, 18. [Google Scholar] [CrossRef]
- Zhang, C.; Yang, Y. The masses of 18 pairs of double neutron stars and implications for their origin. In High-Mass X-ray Binaries: Illuminating the Passage from Massive Binaries to Merging Compact Objects; Oskinova, L.M., Bozzo, E., Bulik, T., Gies, D.R., Eds.; Cambridge University Press: Cambridge, UK, 2019; Volume 346, pp. 474–477. [Google Scholar] [CrossRef]
- Zhou, Y.G.; Wang, D.H.; Zhang, C.M. Be X-ray Binaries as Progenitors of Double Neutron Stars: Evidence of Similar bi-modal Classifications. Publ. Astron. Soc. Pac. 2024, 136, 114202. [Google Scholar] [CrossRef]
- Raguzova, N.V.; Popov, S.B. Be X-ray binaries and candidates. Astron. Astrophys. Trans. 2005, 24, 151–185. [Google Scholar] [CrossRef]
- Walter, R.; Lutovinov, A.A.; Bozzo, E.; Tsygankov, S.S. High-mass X-ray binaries in the Milky Way. A closer look with INTEGRAL. Astron. Astrophys. Rev. 2015, 23, 2. [Google Scholar] [CrossRef]
- Reig, P.; Zezas, A. Discovery of X-ray pulsations in the Be/X-ray binary IGR J06074+2205. Astron. Astrophys. 2018, 613, A52. [Google Scholar] [CrossRef]
- Lyne, A.G.; Burgay, M.; Kramer, M.; Possenti, A.; Manchester, R.N.; Camilo, F.; McLaughlin, M.A.; Lorimer, D.R.; D’Amico, N.; Joshi, B.C.; et al. A Double-Pulsar System: A Rare Laboratory for Relativistic Gravity and Plasma Physics. Science 2004, 303, 1153–1157. [Google Scholar] [CrossRef] [PubMed]
- Lorimer, D.R.; Stairs, I.H.; Freire, P.C.; Cordes, J.M.; Camilo, F.; Faulkner, A.J.; Lyne, A.G.; Nice, D.J.; Ransom, S.M.; Arzoumanian, Z.; et al. Arecibo Pulsar Survey Using ALFA. II. The Young, Highly Relativistic Binary Pulsar J1906+0746. Astrophys. J. 2006, 640, 428–434. [Google Scholar] [CrossRef]
- van Leeuwen, J.; Kasian, L.; Stairs, I.H.; Lorimer, D.R.; Camilo, F.; Chatterjee, S.; Cognard, I.; Desvignes, G.; Freire, P.C.C.; Janssen, G.H.; et al. The Binary Companion of Young, Relativistic Pulsar J1906+0746. Astrophys. J. 2015, 798, 118. [Google Scholar] [CrossRef]
- Ng, C.; Champion, D.J.; Bailes, M.; Barr, E.D.; Bates, S.D.; Bhat, N.D.R.; Burgay, M.; Burke-Spolaor, S.; Flynn, C.M.L.; Jameson, A.; et al. The High Time Resolution Universe Pulsar Survey - XII. Galactic plane acceleration search and the discovery of 60 pulsars. Mon. Not. R. Astron. Soc. 2015, 450, 2922–2947. [Google Scholar] [CrossRef]
- Ng, C.; Kruckow, M.U.; Tauris, T.M.; Lyne, A.G.; Freire, P.C.C.; Ridolfi, A.; Caiazzo, I.; Heyl, J.; Kramer, M.; Cameron, A.D.; et al. PSR J1755-2550: A young radio pulsar with a massive, compact companion. Mon. Not. R. Astron. Soc. 2018, 476, 4315–4326. [Google Scholar] [CrossRef]
- Stovall, K.; Freire, P.C.C.; Chatterjee, S.; Demorest, P.B.; Lorimer, D.R.; McLaughlin, M.A.; Pol, N.; van Leeuwen, J.; Wharton, R.S.; Allen, B.; et al. PALFA Discovery of a Highly Relativistic Double Neutron Star Binary. Astrophys. J. Lett. 2018, 854, L22. [Google Scholar] [CrossRef]
- Cameron, A.D.; Champion, D.J.; Kramer, M.; Bailes, M.; Barr, E.D.; Bassa, C.G.; Bhandari, S.; Bhat, N.D.R.; Burgay, M.; Burke-Spolaor, S.; et al. The High Time Resolution Universe Pulsar Survey - XIII. PSR J1757-1854, the most accelerated binary pulsar. Mon. Not. R. Astron. Soc. 2018, 475, L57–L61. [Google Scholar] [CrossRef]
- Lazarus, P.; Freire, P.C.C.; Allen, B.; Aulbert, C.; Bock, O.; Bogdanov, S.; Brazier, A.; Camilo, F.; Cardoso, F.; Chatterjee, S.; et al. Einstein@Home Discovery of a Double Neutron Star Binary in the PALFA Survey. Astrophys. J. 2016, 831, 150. [Google Scholar] [CrossRef]
- Ferdman, R.D.; Freire, P.C.C.; Perera, B.B.P.; Pol, N.; Camilo, F.; Chatterjee, S.; Cordes, J.M.; Crawford, F.; Hessels, J.W.T.; Kaspi, V.M.; et al. Asymmetric mass ratios for bright double neutron-star mergers. Nature 2020, 583, 211–214. [Google Scholar] [CrossRef] [PubMed]
- Martinez, J.G.; Stovall, K.; Freire, P.C.C.; Deneva, J.S.; Jenet, F.A.; McLaughlin, M.A.; Bagchi, M.; Bates, S.D.; Ridolfi, A. Pulsar J0453+1559: A Double Neutron Star System with a Large Mass Asymmetry. Astrophys. J. 2015, 812, 143. [Google Scholar] [CrossRef]
- Weisberg, J.M.; Nice, D.J.; Taylor, J.H. Timing Measurements of the Relativistic Binary Pulsar PSR B1913+16. Astrophys. J. 2010, 722, 1030–1034. [Google Scholar] [CrossRef]
- Weisberg, J.M.; Huang, Y. Relativistic Measurements from Timing the Binary Pulsar PSR B1913+16. Astrophys. J. 2016, 829, 55. [Google Scholar] [CrossRef]
- Lynch, R.S.; Swiggum, J.K.; Kondratiev, V.I.; Kaplan, D.L.; Stovall, K.; Fonseca, E.; Roberts, M.S.E.; Levin, L.; DeCesar, M.E.; Cui, B.; et al. The Green Bank North Celestial Cap Pulsar Survey. III. 45 New Pulsar Timing Solutions. Astrophys. J. 2018, 859, 93. [Google Scholar] [CrossRef]
- Fonseca, E.; Stairs, I.H.; Thorsett, S.E. A Comprehensive Study of Relativistic Gravity Using PSR B1534+12. Astrophys. J. 2014, 787, 82. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, N.; Yuan, J.P.; Li, D.; Wang, P.; Xue, M.Y.; Zhu, W.W.; Miao, C.C.; Yan, W.M.; Wang, J.B.; et al. A Relativistic Double Neutron Star Binary PSR J1846-0513. Astrophys. J. Lett. 2024, 964, L7. [Google Scholar] [CrossRef]
- Colom i Bernadich, M.; Balakrishnan, V.; Barr, E.; Berezina, M.; Burgay, M.; Buchner, S.; Champion, D.J.; Chen, W.; Desvignes, G.; Freire, P.C.C.; et al. The MPIfR-MeerKAT Galactic Plane Survey. II. The eccentric double neutron star system PSR J1208-5936 and a neutron star merger rate update. Astron. Astrophys. 2023, 678, A187. [Google Scholar] [CrossRef]
- Haniewicz, H.T.; Ferdman, R.D.; Freire, P.C.C.; Champion, D.J.; Bunting, K.A.; Lorimer, D.R.; McLaughlin, M.A. Precise mass measurements for the double neutron star system J1829+2456. Mon. Not. R. Astron. Soc. 2021, 500, 4620–4627. [Google Scholar] [CrossRef]
- Sengar, R.; Balakrishnan, V.; Stevenson, S.; Bailes, M.; Barr, E.D.; Bhat, N.D.R.; Burgay, M.; Bernadich, M.C.i.; Cameron, A.D.; Champion, D.J.; et al. The High Time Resolution Universe Pulsar Survey - XVII. PSR J1325-6253, a low eccentricity double neutron star system from an ultra-stripped supernova. Mon. Not. R. Astron. Soc. 2022, 512, 5782–5792. [Google Scholar] [CrossRef]
- Agazie, G.Y.; Mingyar, M.G.; McLaughlin, M.A.; Swiggum, J.K.; Kaplan, D.L.; Blumer, H.; Chawla, P.; DeCesar, M.; Demorest, P.B.; Fiore, W.; et al. The Green Bank Northern Celestial Cap Pulsar Survey. VI. Discovery and Timing of PSR J1759+5036: A Double Neutron Star Binary Pulsar. Astrophys. J. 2021, 922, 35. [Google Scholar] [CrossRef]
- Martinez, J.G.; Stovall, K.; Freire, P.C.C.; Deneva, J.S.; Tauris, T.M.; Ridolfi, A.; Wex, N.; Jenet, F.A.; McLaughlin, M.A.; Bagchi, M. Pulsar J1411+2551: A Low-mass Double Neutron Star System. Astrophys. J. Lett. 2017, 851, L29. [Google Scholar] [CrossRef]
- Padmanabh, P.V.; Barr, E.D.; Sridhar, S.S.; Rugel, M.R.; Damas-Segovia, A.; Jacob, A.M.; Balakrishnan, V.; Berezina, M.; Bernadich, M.C.; Brunthaler, A.; et al. The MPIfR-MeerKAT Galactic Plane Survey—I. System set-up and early results. Mon. Not. R. Astron. Soc. 2023, 524, 1291–1315. [Google Scholar] [CrossRef]
- Janssen, G.H.; Stappers, B.W.; Kramer, M.; Nice, D.J.; Jessner, A.; Cognard, I.; Purver, M.B. Multi-telescope timing of PSR J1518+4904. Astron. Astrophys. 2008, 490, 753–761. [Google Scholar] [CrossRef]
- Swiggum, J.K.; Pleunis, Z.; Parent, E.; Kaplan, D.L.; McLaughlin, M.A.; Stairs, I.H.; Spiewak, R.; Agazie, G.Y.; Chawla, P.; DeCesar, M.E.; et al. The Green Bank North Celestial Cap Survey. VII. 12 New Pulsar Timing Solutions. Astrophys. J. 2023, 944, 154. [Google Scholar] [CrossRef]
- Wu, Q.D.; Wang, N.; Yuan, J.P.; Li, D.; Wang, P.; Xue, M.Y.; Zhu, W.W.; Miao, C.C.; Yan, W.M.; Wang, J.B.; et al. PSR J2150+3427: A Possible Double Neutron Star System. Astrophys. J. Lett. 2023, 958, L17. [Google Scholar] [CrossRef]
- Keith, M.J.; Kramer, M.; Lyne, A.G.; Eatough, R.P.; Stairs, I.H.; Possenti, A.; Camilo, F.; Manchester, R.N. PSR J1753-2240: A mildly recycled pulsar in an eccentric binary system. Mon. Not. R. Astron. Soc. 2009, 393, 623–627. [Google Scholar] [CrossRef]
- Su, W.Q.; Han, J.L.; Yang, Z.L.; Wang, P.F.; Yuan, J.P.; Wang, C.; Zhou, D.J.; Wang, T.; Yan, Y.; Jing, W.C.; et al. The FAST Galactic Plane Pulsar Snapshot Survey - V. PSR J1901+0658 in a double neutron star system. Mon. Not. R. Astron. Soc. 2024, 530, 1506–1511. [Google Scholar] [CrossRef]
- Ferdman, R.D.; Stairs, I.H.; Kramer, M.; Janssen, G.H.; Bassa, C.G.; Stappers, B.W.; Demorest, P.B.; Cognard, I.; Desvignes, G.; Theureau, G.; et al. PSR J1756-2251: A pulsar with a low-mass neutron star companion. Mon. Not. R. Astron. Soc. 2014, 443, 2183–2196. [Google Scholar] [CrossRef]
- Swiggum, J.K.; Rosen, R.; McLaughlin, M.A.; Lorimer, D.R.; Heatherly, S.; Lynch, R.; Scoles, S.; Hockett, T.; Filik, E.; Marlowe, J.A.; et al. PSR J1930-1852: A Pulsar in the Widest Known Orbit around Another Neutron Star. Astrophys. J. 2015, 805, 156. [Google Scholar] [CrossRef]
- Melatos, A. Spin-down of an oblique rotator with a current-starved outer magnetosphere. Mon. Not. R. Astron. Soc. 1997, 288, 1049–1059. [Google Scholar] [CrossRef]
- Bisnovatyi-Kogan, G.S. PHYSICS OF OUR DAYS: Binary and recycled pulsars: 30 years after observational discovery. Phys. Uspekhi 2006, 49, 53–67. [Google Scholar] [CrossRef]
- Bisnovatyi-Kogan, G. Binary recycled pulsars: A powerful physical laboratory. Mem. Soc. Astron. Ital. 2010, 81, 258. [Google Scholar]
- Di Salvo, T.; Sanna, A. Accretion Powered X-ray Millisecond Pulsars. In Millisecond Pulsars; Bhattacharyya, S., Papitto, A., Bhattacharya, D., Eds.; Astrophysics and Space Science Library; Springer: Cham, Switzerland, 2022; Volume 465, pp. 87–124. [Google Scholar] [CrossRef]
- Paczynski, B. Common Envelope Binaries. Symp.-Int. Astron. Union 1976, 73, 75. [Google Scholar] [CrossRef]
- Meurs, E.J.A.; van den Heuvel, E.P.J. The number of evolved early-type close binaries in the galaxy. Astron. Astrophys. 1989, 226, 88–107. [Google Scholar]
- Taam, R.E. Common-Envelope Evolution, the Formation of CVs, LMXBs, and the Fate of HMXBs. Symp.-Int. Astron. Union 1996, 165, 3. [Google Scholar] [CrossRef]
- Vinciguerra, S.; Neijssel, C.J.; Vigna-Gómez, A.; Mandel, I.; Podsiadlowski, P.; Maccarone, T.J.; Nicholl, M.; Kingdon, S.; Perry, A.; Salemi, F. Be X-ray binaries in the SMC as indicators of mass-transfer efficiency. Mon. Not. R. Astron. Soc. 2020, 498, 4705–4720. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).