Abstract
Dark matter, one of the fundamental components of the universe, has remained mysterious in modern cosmology and particle physics, and hence, this field is of utmost importance at the present moment. One of the foundational questions in this direction is the origin of dark matter, which directly links to its creation. In the present article, we study the gravitational production of dark matter in two distinct contexts: firstly, when reheating occurs through gravitational particle production, and secondly, when it is driven by decay of the inflaton field. We establish a connection between the reheating temperature and the mass of dark matter, and from the reheating bounds, we determine the range of viable dark matter mass values.
1. Introduction
Dark matter, a fundamental component of the universe, remains one of the most profound mysteries in modern cosmology and particle physics. Despite its gravitational effects being observed across a variety of astrophysical scales, from galaxies to the cosmic microwave background, its origin and nature continue to elude us. Among the proposed mechanisms for dark matter generation, the gravitational production of dark matter stands out as a particularly compelling explanation, especially within the context of the early universe, see for instance [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20].
Gravitational dark matter production leverages the unique role of gravity, a universal interaction, as the primary mechanism for generating dark matter particles. This process requires no additional couplings or interactions with the Standard Model, relying solely on the dynamics of the expanding universe. Such production is especially relevant during the reheating phase following cosmic inflation, where the universe transits from an early inflationary epoch to a radiation-dominated era.
Two primary scenarios dominate discussions of gravitational dark matter production: one in which reheating occurs through the copious production of heavy particles [21] that subsequently decay into Standard Model particles, and another in which reheating results from the decay of the inflaton field directly into Standard Model particles [22]. These pathways connect the physics of inflation, reheating, and dark matter, establishing a relationship between the reheating temperature and the mass of dark matter. This connection allows us, through reheating constraints, to identify the range of viable dark matter masses.
This short note delves into the theoretical foundations of gravitational dark matter production studied in several works [1,2,3,4,5,6,7,8,9,10,12,13,14,15,16,17,18,19,20] emphasizing its dependence on inflationary reheating dynamics, its potential observational implications, and the range of viable dark matter masses within this framework. The rest of this short note is organized as follows. In Section 2, we present the gravitational reheating formulas. Section 3 describes the gravitational production of dark matter in the context of gravitational reheating. In Section 4, we discuss the gravitational production of dark matter and reheating through the decay of the inflaton field. Finally, in Section 5 we conclude the present note with a brief summary.
Throughout the article, we work under the assumption of the spatially flat Friedmann–Lemaître–Robertson–Walker (FLRW) geometry with (hereafter a) representing the expansion scale factor of the universe and we have used the following notations:
- 1.
- “END” denotes the end of inflation.
- 2.
- “0” denotes the present time.
- 3.
- “reh” denotes the reheating time.
- 4.
- denotes the energy density of the produced A-particles, at the end of inflation.
- 5.
- is the energy density of the background at the end of inflation ( is the reduced Planck mass), that is, it corresponds to the energy density of the inflaton field.
- 6.
- corresponds to the energy density of the radiation.
- 7.
- is the heating efficiency of the A-particles.
- 8.
- is the decay efficiency of the A-particles, where is the decay rate of the A-particles.
- 9.
- is the density parameter for radiation ( km/s/Mpc in which is the present day value of the Hubble constant).
- 10.
- is the density parameter of the A-particles.
Concerning the observational constraints on some of the parameters, we have used the following values [23]:
- 1.
- , where the Y-particles are the candidate for dark matter.
- 2.
- .
- 3.
- .
- 4.
- .
2. Gravitational Reheating Formulas
This section provides a detailed review of the results recently obtained in [24,25] (see also [21,26,27,28] to find some of the recent results in the context of gravitational reheating). To begin with, we consider a potential, which, near the minimum , behaves like (n is a natural number). We examine heavy massive X-particles, which are produced gravitationally due to the coupling of a X-field with the Ricci scalar (see, for instance, [21], and also [29,30] for the foundations of quantum field theory in curved spaces and its gravitational effects), and then they decay into Standard Model (SM) particles in order to reheat the universe. During the oscillations, close to the minimum, as the potential behaves like , hence, with the use of virial theorem, the effective Equation of State (EoS) parameter, , becomes . Note that is higher than for . This guarantees that the inflaton’s energy density decays faster than the energy density of the produced particles as well as their decay products, because, as a function of the scale factor, the energy density of matter decays as , the one of radiation as , and for the fluid with EoS parameter , it decays as , which in the case of the inflaton’s energy density becomes .1 As a consequence, the energy density of the latter products will eventually dominate and finally this will lead to a successful reheating of the universe. We shall concentrate on the class of inflationary potentials having similar behavior close to the minimum, e.g., Hyperbolic Inflation, Superconformal -Attractor E-models or Superconformal -Attractor T-models [31,32,33].
In order to clearly realize the mechanism of gravitational reheating, it is essential to understand the decay process. The decay process can be described with the use of the dynamics governed by the Boltzmann equations:
where stands for the energy density of the produced X-particles, is the energy density of the radiation (the energy density of the decay products), and is the decay rate of X-particles into SM particles and it is assumed to be a constant. For example, considering an interaction of the X-field with fermions, this leads to the decay of the X-particles with the decay rate , where is a dimensionless constant [34].
We proceed with the solution which describes the energy density of the heavy massive particles as follows
Here, this solution represents that the decay begins at the end of inflation, as discussed in [11]. This is due to the fact that the heavy X-particles are produced at the end of inflation, when the inflaton starts to oscillate. Consequently, the decay of these particles commences immediately upon their creation.
Now, inserting (2) into the second equation of (1) and considering the fact that decay starts at the end of inflation, one can obtain
We now proceed by defining as the time where decay ends, that is, when . This quickly gives , (), and we focus on the investigation of the evolution of the decay products for . We presume that the background dominates and with such an assumption, we have since . Now, bearing in mind that
where denotes Euler’s Gamma function, we reach the conclusion that for , the following approximation can be made
where we have used the definition of the decay efficiency of X-particles. Now, since, , the energy density of the background, that is, the energy density of the inflaton field, satisfies the equation , and thus, it evolves as
Therefore, since the universe becomes reheated when , we obtain
and as a result of which, the energy density of the decay products at the time of reheating is given by the following
Now, using the Stefan–Boltzmann law (here denotes the effective number of degrees of freedom in the SM), one obtains the following reheating temperature,
It is essential to calculate the range of values for . We first note that because the decay occurs well after the end of inflation. Additionally, we have assumed that the energy density of the background dominates at the end of decay, that means, . Therefore, using the relation , we obtain,
and inserting the above relation into , one arrives at
Moreover, combining (11) with the following bound of the reheating temperature, , which states that the reheating temperature remains in an interval consistent with the Big Bang Nucleosynthesis (BBN), which occurs at about ∼1 MeV scale, and attains an upper bound at about ∼109 GeV in order to mitigate the issues related to the gravitino problem [35,36,37,38] one obtains four distinct cases. However, the only viable case is the following
provided that the inequality
holds. Finally, we comment on the maximum value of the reheating temperature. The maximum reheating temperature is obtained at the epoch when the decay coincides with the end of the inflaton’s domination, which means, when . Now, considering Equation (8), one obtains
and inserting this into (9), the maximum reheating temperature becomes
where , due to the bounds of the reheating temperature, is constrained as follows
3. Gravitational Production of Dark Matter
This section deals with the gravitational production of dark matter in the framework of gravitational reheating. We consider two quantum scalar fields, X and Y, which are conformally coupled to the Ricci scalar. The X-field produces heavy X-particles with mass , which will decay into SM particles and reheat the universe. The Y-field produces Y-particles with mass , and they correspond to the present-day dark matter candidate.
3.1. Maximum Reheating Temperature
The case when the X-particles decay close to the onset of radiation leads to the maximum reheating temperature. We begin by considering the energy density of the dark matter at the present time which is given by
Now, with the use of the following
where the adiabatic expansion of the universe after reheating has been considered, i.e., , we now calculate
wherein we make use of [25], which arises under the assumptions of the background evolving as
and the decay of the X-particles is at the onset of radiation. With these, we find the following relation between the energy density of the Y-particles and the maximum reheating temperature
that is:
Now, inserting the value of the maximum reheating temperature and the observational values of and , one arrives at the following bound
Next, we deal with scalar particles conformally coupled to gravity (for the non-conformally coupled case, specially the minimally coupled case, see, for instance, [39,40]), when , because in this case one can use the Wentzel–Kramers–Brillouin (WKB) method in the complex plane in order to analytically calculate the -Bogoliubov coefficients, which is the key piece to finding the energy density of the produced particles. Using the results obtained in [25], we obtain
where we have used the usual value of the Hubble rate at the end of inflation, i.e., . Then, we obtain:
and taking into account the constraint, , coming from the BBN success, after substituting (15) into it, we obtain:
that is:
where we have used that . Finally, taking into account (15) and (24), the reheating temperature can be written as a function of the mass and the parameter n, as follows:
Finally, we close this section with Figure 1 and Figure 2. In Figure 1, we display the dependence of with as given in Equation (25) for different values of n. This clearly exhibits a pattern for increasing n. Similarly, in Figure 2 we show how the maximum reheating temperature, , depends on for different values of n. One can clearly notice that for a specific value of n, if increases, also increases. Additionally, one can further notice that for a particular value of , if n increases, then increases and it assumes the maximum value for .
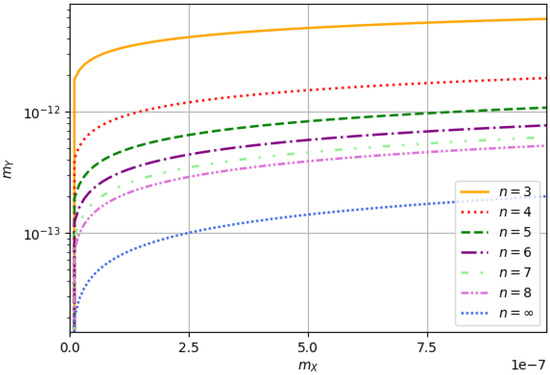
Figure 1.
The dependence of masses with has been shown for different values of n. We work with the units where .
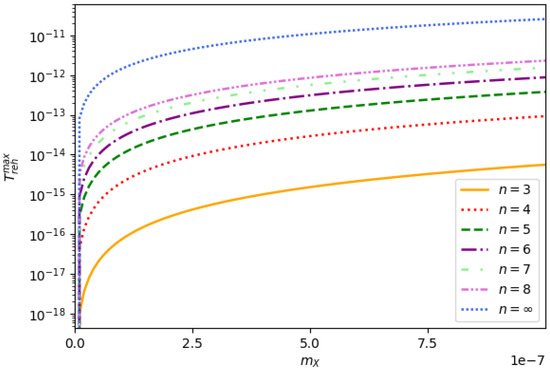
Figure 2.
The maximum reheating temperature versus the mass of the produced particles, for different values of n has been depicted. We work with the units where .
Quintessential Inflation
In this section, we discuss the bounds on the masses of X and Y particles in a special cosmological scenario, namely, the Quintessential Inflation [21,26,27,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56]—a unified cosmological model, where after inflation, the universe enters a kination phase, i.e., all the energy density is kinetic, which means that , and thus, it is equivalent to the case . Using the values of and , we have the following relation between the masses
which for , leads to
Conversely, the bound of the maximum reheating temperature leads to the following constraint
where we continue taking . Inserting the value of , we arrive at the following
which must be improved due to the fact that we have assumed , leading to,
Now, using this last constraint, we find the range of viable values of the mass of dark matter lies in the following region:
3.2. General Case: Decay Before the Onset of Radiation
When the decay is before the end of the domination of the inflaton, using (7) and (8), one has,
Therefore, from (17), (18) and (19), the energy density of the Y particles becomes
and taking into consideration the formula of the reheating temperature (9) one arrives at,
which in terms of the density parameters, takes the form
This coincides with the previous case when . Now, inserting the observational values, one obtains,
and from the expression of , we derive
with the following constraints (see for details [25]):
and
where we continue using . From this last constraint, it is also possible to obtain the bound for as,
with and
Quintessential Inflation
In the case with , the formulas simplify as follows. The reheating temperature in this case is given by
The relation between different heating efficiencies and the decay efficiency is given by
which leads to
with the constraints:
and
Finally, we have the following bound for the masses:
and
with . Taking into account the bound of , one can conclude that the viable masses for dark matter are of the order GeV.
4. Gravitational Production of Dark Matter + Reheating via Inflaton Decay
As we have already discussed, gravitational reheating works only for . The reason behind this is that the energy density of the background must decrease faster than that of the decay products for radiation to eventually dominate and for the universe to become reheated. As we have already discussed, this condition is satisfied only when, after inflation, the effective EoS parameter of the background is greater than , which corresponds to .
Here, we investigate the case with , where the potential behaves like near its minimum, corresponding to models such as Higgs or Starobinsky inflation. To achieve a successful reheating, we assume that the inflaton field decays into SM particles with a decay rate . In this scenario, we first assume that the decay is instantaneous, which means, all the energy stored in the inflaton field is immediately converted to radiation, which is quite different than a delayed decay as we will see in Section Delayed Decay. Reheating is achieved when , yielding a reheating temperature given by [57]:
Next, we consider the scalar Y-particles, which are created gravitationally and are responsible for the present dark matter. For , the background evolves as , and immediately after the decay, which coincides with the reheating time, this energy density transforms to . Then, following step by step the calculation carried out in Section 3.1, we obtain,
which coincides with the result used in [2]. By inserting the value of the reheating temperature along with the observational data, we obtain:
At this point, we note that for , when , we have [4,25,39]
where we have used . Therefore, , which leads to the following relation between and as
Finally, we derive the relation between the reheating temperature and the dark matter mass as
and taking this into account, the constraint of the reheating temperature we find to be,
where we have taken into account that . Therefore, the viable masses for dark matter are of the order: GeV.
Delayed Decay
This situation is more involved than the previous case because it requires the solving of the Boltzmann equations:
where for simplicity, we assume that the decay rate is constant. Following the reasoning depicted in [11], we can write the second equation as follows
and assuming that the decay occurs during the inflaton’s domination, i.e., when , one has
Next, following [11], we also assume that the background scales as , and inserting this into (61), which after integration leads to
where we can see that for , the energy density of radiation evolves as
which does not match with the real evolution of radiation at late times, which scales as . The problem in this approach is that the authors assume, for all the time, an evolution of the background that only holds at early times when as is discussed in the earlier works [2,28,58,59], because, as we can see from the first equation of (59), its exact evolution, for all time , is
which means that at very late times, since the right hand side of the second equation of (59) decays exponentially, it becomes , which is the conservation equation for radiation. Therefore, as we will demonstrate, the reheating temperature obtained in this work will differ slightly—by less than an order of magnitude—from the values reported in previous studies.
Having clarified this point, we now address the exact evolution of radiation, which is described by:
Equating both energy densities at the reheating time, one has,
which is impossible to solve analytically, because to find the evolution of the scale factor, one needs to analytically solve (59) with , which can only be solved numerically. Therefore, to find an approximate solution of (66), we follow the strategy of assuming that before the reheating, the evolution is dominated by the background, and thus, the evolution of the scale factor is given by:
which leads to
which under the assumption of can be approximated by
Therefore,
where we have assumed that . Taking into account that a primitive, which can be obtained integrating by parts, of the integrand is given by:
we have
For , the contribution of the term
appearing in (65) can be disregarded, which means that, at late times, .
Returning to (66), (69) and (72), after introducing the notation, , we find:
whose solution is , and leads to the following reheating temperature , which is of the same order, the difference is replacing by , from the result obtained in [11] using the method explained above. Having in mind all of these results, we calculate:
and write
obtaining:
Now, multiplying the right hand side by , we find,
where we have used that . Therefore, we conclude that the relation between the density parameters is,
and inserting the observational data, we obtain,
and using that , we find,
which is of the same order as the result obtained in the previous case of instantaneous decay. Consequently, the viable masses of dark matter are of the same order as those obtained in (58).
5. Conclusions
In this article, we have studied the gravitational production of dark matter particles resulting from the conformal coupling of a massive scalar field to the Ricci tensor in two distinct scenarios: (i) when the reheating occurs via gravitational production of heavy particles conformally coupled to gravity, which subsequently decay into SM particles, and (ii) when reheating is driven by the decay of the inflaton field into SM particles.
In both scenarios, we relate the reheating temperature to the mass of dark matter particles. By considering the constraints on the reheating temperature imposed by the success of the BBN, we identify the range of viable masses for dark matter particles, obtaining new bounds (see Section 3 and Section 4).
A significant result emerges when reheating is driven by the gravitational production of scalar particles conformally coupled to gravity. In this case, as described in Section 3, the range of viable dark matter masses is relatively low and narrow, depending on the effective EoS parameter during the oscillations of the inflaton field. For example, in the case of Quintessential Inflation, where , the maximum viable mass is below the TeV scale.
Conversely, in the second scenario where the potential is approximately quadratic near its minimum, as we have shown in Section 4, the viable mass range for dark matter particles is significantly higher, centered around GeV, though still within a narrow range. This highlights the strong dependence of viable dark matter properties on the specific dynamics of reheating in the early universe.
Author Contributions
Conceptualization and methodology, J.d.H.; software, S.P.; writing—original draft preparation, J.d.H.; writing—review and editing, J.d.H. and S.P. All authors have read and agreed to the published version of the manuscript.
Funding
J.d.H. is supported by the Spanish grants PID2021-123903NB-I00 and RED2022-134784-T funded by MCIN/AEI/10.13039/501100011033 and by ERDF “A way of making Europe”. S.P. has been supported by the Department of Science and Technology (DST), Govt. of India under the Scheme “Fund for Improvement of S&T Infrastructure (FIST)” (File No. SR/FST/MS-I/2019/41).
Data Availability Statement
We have not used any specific dataset to constrain the cosmological parameters considered in this work. All datasets that are mentioned here are publicly available.
Conflicts of Interest
The authors declare no conflicts of interest.
Note
| 1 | Without any loss of generality, we have set , the present-day value of the scale factor to be unity. |
References
- Chung, D.J.H. Classical Inflation Field Induced Creation of Superheavy Dark Matter. Phys. Rev. D 2003, 67, 083514. [Google Scholar] [CrossRef]
- Chung, D.J.H.; Crotty, P.; Kolb, E.W.; Riotto, A. On the Gravitational Production of Superheavy Dark Matter. Phys. Rev. D 2001, 64, 043503. [Google Scholar] [CrossRef]
- Markkanen, T.; Nurmi, S. Dark matter from gravitational particle production at reheating. J. Cosmol. Astropart. Phys. 2017, 2017, 008. [Google Scholar] [CrossRef]
- Ema, Y.; Nakayama, K.; Tang, Y. Production of Purely Gravitational Dark Matter. J. High Energy Phys. 2018, 2018, 135. [Google Scholar] [CrossRef]
- Ema, Y.; Nakayama, K.; Tang, Y. Production of purely gravitational dark matter: The case of fermion and vector boson. J. High Energy Phys. 2019, 2019, 60. [Google Scholar] [CrossRef]
- Haro, J. Gravitational production of dark matter in the Peebles–Vilenkin model. Eur. Phys. J. C 2020, 80, 257. [Google Scholar] [CrossRef]
- Haro, J.; Aresté Saló, L. Gravitational production of superheavy baryonic and dark matter in quintessential inflation: Nonconformally coupled case. Phys. Rev. D 2019, 100, 043519. [Google Scholar] [CrossRef]
- Cembranos, J.A.R.; Garay, L.J.; Sánchez Velázquez, J.M. Gravitational production of scalar dark matter. J. High Energy Phys. 2020, 2020, 84. [Google Scholar] [CrossRef]
- Babichev, E.; Gorbunov, D.; Ramazanov, S.; Reverberi, L. Gravitational reheating and superheavy Dark Matter creation after inflation with non-minimal coupling. J. Cosmol. Astropart. Phys. 2020, 2020, 059. [Google Scholar] [CrossRef]
- Karam, A.; Raidal, M.; Tomberg, E. Gravitational dark matter production in Palatini preheating. J. Cosmol. Astropart. Phys. 2021, 2021, 064. [Google Scholar] [CrossRef]
- Mambrini, Y.; Olive, K.A. Gravitational Production of Dark Matter during Reheating. Phys. Rev. D 2021, 103, 115009. [Google Scholar] [CrossRef]
- Bernal, N.; Zapata, O. Gravitational dark matter production: Primordial black holes and UV freeze-in. Phys. Lett. B 2021, 815, 136129. [Google Scholar] [CrossRef]
- Garcia, M.A.G.; Pierre, M.; Verner, S. Scalar dark matter production from preheating and structure formation constraints. Phys. Rev. D 2023, 107, 043530. [Google Scholar] [CrossRef]
- Bastero-Gil, M.; Ferraz, P.B.; Ubaldi, L.; Vega-Morales, R. Super heavy dark matter from inflationary Schwinger production. Phys. Rev. D 2024, 110, 095019. [Google Scholar] [CrossRef]
- Zhang, R.; Zheng, S. Gravitational dark matter from minimal preheating. J. High Energy Phys. 2024, 2024, 61. [Google Scholar] [CrossRef]
- Barman, B.; Datta, A. Testing axionic dark matter during gravitational reheating. Phys. Rev. D 2024, 109, 095029. [Google Scholar] [CrossRef]
- Bastero-Gil, M.; Ferraz, P.B.; Ubaldi, L.; Vega-Morales, R. Schwinger dark matter production. J. Cosmol. Astropart. Phys. 2024, 10, 078. [Google Scholar] [CrossRef]
- Belfiglio, A.; Luongo, O. Production of ultralight dark matter from inflationary spectator fields. Phys. Rev. D 2024, 110, 023541. [Google Scholar] [CrossRef]
- Bertuzzo, E.; Perez-Gonzalez, Y.F.; Salla, G.M.; Funchal, R.Z. Gravitationally produced dark matter and primordial black holes. J. Cosmol. Astropart. Phys. 2024, 2024, 059. [Google Scholar] [CrossRef]
- Wang, C.; Zhao, W. Gravitational Dark Matter Production in Supergravity α-Attractor Inflation. arXiv 2024, arXiv:2411.15030. [Google Scholar]
- Hashiba, S.; Yokoyama, J. Gravitational reheating through conformally coupled superheavy scalar particles. J. Cosmol. Astropart. Phys. 2019, 2019, 028. [Google Scholar] [CrossRef]
- Garcia, M.A.G.; Kaneta, K.; Mambrini, Y.; Olive, K.A. Inflaton Oscillations and Post-Inflationary Reheating. J. Cosmol. Astropart. Phys. 2021, 2021, 012. [Google Scholar] [CrossRef]
- Lahav, O.; Liddle, A.R. The Cosmological Parameters (2021). arXiv 2022, arXiv:2201.08666. [Google Scholar]
- de Haro, J.; Aresté Saló, L.; Pan, S. Gravitational reheating formulas and bounds in oscillating backgrounds. Phys. Rev. D 2024, 110, 123504. [Google Scholar] [CrossRef]
- de Haro, J.; Pan, S. Gravitational reheating formulas and bounds in oscillating backgrounds II: Constraints on the spectral index and gravitational dark matter production. arXiv 2024, arXiv:2411.06190. [Google Scholar]
- Chun, E.J.; Scopel, S.; Zaballa, I. Gravitational reheating in quintessential inflation. J. Cosmol. Astropart. Phys. 2009, 2009, 022. [Google Scholar] [CrossRef]
- de Haro, J.; Aresté Saló, L. Analytic formula to calculate the reheating temperature via gravitational particle production in smooth nonoscillating backgrounds. Phys. Rev. D 2023, 107, 063542. [Google Scholar] [CrossRef]
- Kaneta, K.; Mambrini, Y.; Olive, K.A. Radiative Production of Non-thermal Dark Matter. Phys. Rev. D 2019, 99, 063508. [Google Scholar] [CrossRef]
- Grib, A.A.; Mamayev, S.G.; Mostepanenko, V.M. Vacuum Quantum Effects in Strong Fields; Friedmann Laboratory Publishing: St. Petersburg, Russia, 1999. [Google Scholar]
- Parker, L.E.; Toms, D.J. Quantum Field Theory in Curved Spacetime. In Cambridge Monograph on Mathematical Physics; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Brown, A.R. Hyperbolic Inflation. Phys. Rev. Lett. 2018, 121, 251601. [Google Scholar] [CrossRef]
- Kallos, R.; Linde, A.; Roest, D. Superconformal Inflationary α-Attractors. J. High Energy Phys. 2013, 11, 198. [Google Scholar] [CrossRef]
- Kallos, R.; Linde, A. Non-minimal Inflationary Attractors. J. Cosmol. Astropart. Phys. 2013, 10, 033. [Google Scholar] [CrossRef]
- Felder, G.; Kofman, L.; Linde, A. Inflation and Preheating in NO models. Phys. Rev. D 1999, 60, 103505. [Google Scholar] [CrossRef]
- Ellis, J.R.; Linde, A.D.; Nanopoulos, D.V. Inflation Can Save the Gravitino. Phys. Lett. B 1982, 118, 59–64. [Google Scholar] [CrossRef]
- Khlopov, M.Y.; Linde, A.D. Is It Easy to Save the Gravitino? Phys. Lett. B 1984, 138, 265–268. [Google Scholar] [CrossRef]
- Kawasaki, M.; Kohri, K.; Moroi, T. Big-Bang nucleosynthesis and hadronic decay of long-lived massive particles. Phys. Rev. D 2005, 71, 083502. [Google Scholar] [CrossRef]
- Kawasaki, M.; Kohri, K.; Moroi, T.; Takaesu, Y. Revisiting Big-Bang Nucleosynthesis Constraints on Long-Lived Decaying Particles. Phys. Rev. D 2018, 97, 023502. [Google Scholar] [CrossRef]
- Kolb, E.W.; Long, A.J. Cosmological gravitational particle production and its implications for cosmological relics. Rev. Mod. Phys. 2024, 96, 045005. [Google Scholar] [CrossRef]
- Jenks, L.; Kolb, E.W.; Thyme, K. Gravitational Particle Production of Scalars: Analytic and Numerical Approaches Including Early Reheating. arXiv 2024, arXiv:2410.03938. [Google Scholar]
- Peebles, P.J.E.; Vilenkin, A. Quintessential inflation. Phys. Rev. D 1999, 59, 063505. [Google Scholar] [CrossRef]
- Giovannini, M. Production and detection of relic gravitons in quintessential inflationary models. Phys. Rev. D 1999, 60, 123511. [Google Scholar] [CrossRef]
- Dimopoulos, K.; Valle, J.W.F. Modeling quintessential inflation. Astropart. Phys. 2002, 18, 287–306. [Google Scholar] [CrossRef]
- Giovannini, M. Low scale quintessential inflation. Phys. Rev. D 2003, 67, 123512. [Google Scholar] [CrossRef]
- Sami, M.; Sahni, V. Quintessential inflation on the brane and the relic gravity wave background. Phys. Rev. D 2004, 70, 083513. [Google Scholar] [CrossRef]
- Rosenfeld, R.; Frieman, J.A. A Simple model for quintessential inflation. J. Cosmol. Astropart. Phys. 2005, 2005, 003. [Google Scholar] [CrossRef]
- Bento, M.C.; Gonzalez Felipe, R.; Santos, N.M.C. A simple quintessential inflation model. Int. J. Mod. Phys. A 2009, 24, 1639–1642. [Google Scholar] [CrossRef]
- Lankinen, J.; Vilja, I. Gravitational Particle Creation in a Stiff Matter Dominated Universe. J. Cosmol. Astropart. Phys. 2017, 2017, 025. [Google Scholar] [CrossRef]
- De Haro, J.; Aresté Saló, L. Reheating constraints in quintessential inflation. Phys. Rev. D 2017, 95, 123501. [Google Scholar] [CrossRef]
- Aresté Saló, L.; de Haro, J. Quintessential inflation at low reheating temperatures. Eur. Phys. J. C 2017, 77, 798. [Google Scholar] [CrossRef]
- Haro, J.; Yang, W.; Pan, S. Reheating in quintessential inflation via gravitational production of heavy massive particles: A detailed analysis. J. Cosmol. Astropart. Phys. 2019, 2019, 023. [Google Scholar] [CrossRef]
- de Haro, J.; Pan, S.; Aresté Saló, L. Understanding gravitational particle production in quintessential inflation. J. Cosmol. Astropart. Phys. 2019, 2019, 056. [Google Scholar] [CrossRef]
- Dimopoulos, K.; Karam, A.; Sánchez López, S.; Tomberg, E. Palatini R 2 quintessential inflation. J. Cosmol. Astropart. Phys. 2022, 10, 076. [Google Scholar] [CrossRef]
- de Haro, J. Reheating formulas in quintessential inflation via gravitational particle production. Phys. Rev. D 2024, 109, 023517. [Google Scholar] [CrossRef]
- Inagaki, T.; Taniguchi, M. Quintessential Inflation in Logarithmic Cartan F(R) Gravity. arXiv 2023, arXiv:2312.11776. [Google Scholar] [CrossRef]
- Giarè, W.; Di Valentino, E.; Linder, E.V.; Specogna, E. Testing α-attractor quintessential inflation against CMB and low-redshift data. arXiv 2024, arXiv:2402.01560. [Google Scholar] [CrossRef]
- Kofman, L.; Linde, A.D.; Starobinsky, A.A. Towards the theory of reheating after inflation. Phys. Rev. D 1997, 56, 3258–3295. [Google Scholar] [CrossRef]
- Garcia, M.A.G.; Kaneta, K.; Mambrini, Y.; Olive, K.A. Reheating and Post-inflationary Production of Dark Matter. Phys. Rev. D 2020, 101, 123507. [Google Scholar] [CrossRef]
- Giudice, G.F.; Kolb, E.W.; Riotto, A. Largest temperature of the radiation era and its cosmological implications. Phys. Rev. D 2001, 64, 023508. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).