Hadronic Molecules with Four Charm or Beauty Quarks
Abstract
1. Introduction
2. Formalism
2.1. The System
2.2. The and Systems
2.3. The and Systems
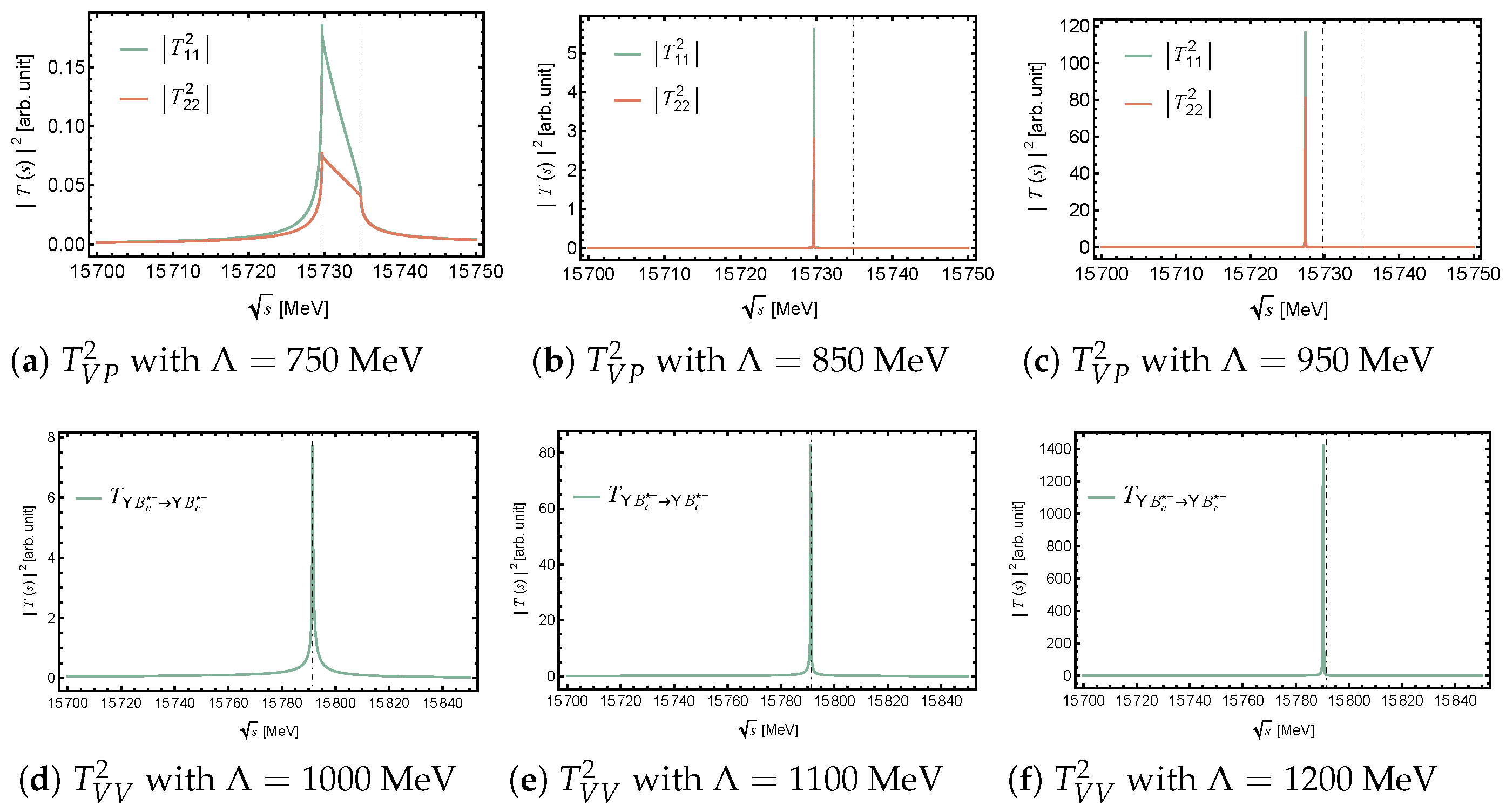
3. Numerical Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.R.; Chen, H.X.; Chen, W.; Liu, X.; Zhu, S.L. Pentaquark and Tetraquark States. Prog. Part. Nucl. Phys. 2019, 107, 237–320. [Google Scholar] [CrossRef]
- Chen, H.X.; Chen, W.; Liu, X.; Liu, Y.R.; Zhu, S.L. An updated review of the new hadron states. Rep. Prog. Phys. 2023, 86, 026201. [Google Scholar] [CrossRef]
- Guo, F.K.; Hanhart, C.; Meißner, U.G.; Wang, Q.; Zhao, Q.; Zou, B.S. Hadronic molecules. Rev. Mod. Phys. 2018, 90, 015004. [Google Scholar] [CrossRef]
- Brambilla, N.; Eidelman, S.; Hanhart, C.; Nefediev, A.; Shen, C.P.; Thomas, C.E.; Vairo, A.; Yuan, C.Z. The XYZ states: Experimental and theoretical status and perspectives. Phys. Rep. 2020, 873, 1–154. [Google Scholar] [CrossRef]
- Esposito, A.; Pilloni, A.; Polosa, A.D. Multiquark resonances. Phys. Rep. 2017, 668, 1–97. [Google Scholar] [CrossRef]
- Lebed, R.F.; Mitchell, R.E.; Swanson, E.S. Heavy-quark QCD exotica. Prog. Part. Nucl. Phys. 2017, 93, 143–194. [Google Scholar] [CrossRef]
- Ali, A.; Lange, J.S.; Stone, S. Exotics: Heavy pentaquarks and tetraquarks. Prog. Part. Nucl. Phys. 2017, 97, 123–198. [Google Scholar] [CrossRef]
- Oller, J.A.; Oset, E. Chiral symmetry amplitudes in the S wave isoscalar and isovector channels and the σ, f0(980), a0(980) scalar mesons. Nucl. Phys. A 1997, 620, 438–456. [Google Scholar] [CrossRef]
- Oller, J.A.; Oset, E.; Pelaez, J.R. Meson meson interaction in a nonperturbative chiral approach. Phys. Rev. D 1999, 59, 074001, Erratum in Phys. Rev. D 1999, 60, 099906; Phys. Rev. D 2007, 75, 099903. [Google Scholar] [CrossRef]
- Oset, E.; Ramos, A. Nonperturbative chiral approach to s wave anti-K N interactions. Nucl. Phys. A 1998, 635, 99–120. [Google Scholar] [CrossRef]
- Jido, D.; Oller, J.A.; Oset, E.; Ramos, A.; Meissner, U.G. Chiral dynamics of the two Lambda(1405) states. Nucl. Phys. A 2003, 725, 181–200. [Google Scholar] [CrossRef]
- Bruns, P.C.; Mai, M.; Meissner, U.G. Chiral dynamics of the S11(1535) and S11(1650) resonances revisited. Phys. Lett. B 2011, 697, 254–259. [Google Scholar] [CrossRef]
- Garcia-Recio, C.; Lutz, M.F.M.; Nieves, J. Quark mass dependence of s wave baryon resonances. Phys. Lett. B 2004, 582, 49–54. [Google Scholar] [CrossRef]
- Hyodo, T.; Nam, S.I.; Jido, D.; Hosaka, A. Flavor SU(3) breaking effects in the chiral unitary model for meson baryon scatterings. Phys. Rev. C 2003, 68, 018201. [Google Scholar] [CrossRef]
- Wu, J.J.; Molina, R.; Oset, E.; Zou, B.S. Prediction of Narrow N* and Λ* Resonances with Hidden Charm above 4 GeV. Phys. Rev. Lett. 2010, 105, 232001. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.J.; Molina, R.; Oset, E.; Zou, B.S. Dynamically generated N* and Λ* resonances in the hidden charm sector around 4.3 GeV. Phys. Rev. C 2011, 84, 015202. [Google Scholar] [CrossRef]
- Chen, H.X.; Geng, L.S.; Liang, W.H.; Oset, E.; Wang, E.; Xie, J.J. Looking for a hidden-charm pentaquark state with strangeness S = −1 from decay into J/ψK−Λ. Phys. Rev. C 2016, 93, 065203. [Google Scholar] [CrossRef]
- He, J. and interactions and the LHCb hidden-charmed pentaquarks. Phys. Lett. B 2016, 753, 547–551. [Google Scholar] [CrossRef]
- Xiao, C.W.; Nieves, J.; Oset, E. Combining heavy quark spin and local hidden gauge symmetries in the dynamical generation of hidden charm baryons. Phys. Rev. D 2013, 88, 056012. [Google Scholar] [CrossRef]
- Roca, L.; Nieves, J.; Oset, E. LHCb pentaquark as a Σc − molecular state. Phys. Rev. D 2015, 92, 094003. [Google Scholar] [CrossRef]
- Liu, X.H.; Wang, Q.; Zhao, Q. Understanding the newly observed heavy pentaquark candidates. Phys. Lett. B 2016, 757, 231–236. [Google Scholar] [CrossRef]
- Uchino, T.; Liang, W.H.; Oset, E. Baryon states with hidden charm in the extended local hidden gauge approach. Eur. Phys. J. A 2016, 52, 43. [Google Scholar] [CrossRef]
- Aaij, R. et al. [LHCb Collaboration] Observation of structure in the J/ψ-pair mass spectrum. Sci. Bull. 2020, 65, 1983–1993. [Google Scholar] [CrossRef]
- Aad, G. et al. [ATLAS Collaboration] Observation of an Excess of Dicharmonium Events in the Four-Muon Final State with the ATLAS Detector. Phys. Rev. Lett. 2023, 131, 151902. [Google Scholar] [CrossRef] [PubMed]
- Hayrapetyan, A. et al. [CMS Collaboration] Observation of new structure in the J/ψJ/ψ mass spectrum in proton-proton collisions at = 13 TeV. arXiv 2023, arXiv:hep-ex/2306.07164. [Google Scholar]
- Liu, M.S.; Liu, F.X.; Zhong, X.H.; Zhao, Q. Full-heavy tetraquark states and their evidences in the LHCb di-J/ψ spectrum. arXiv 2020, arXiv:hep-ph/2006.11952. [Google Scholar]
- Tiwari, R.; Rathaud, D.P.; Rai, A.K. Spectroscopy of all charm tetraquark states. arXiv 2021, arXiv:hep-ph/2108.04017. [Google Scholar] [CrossRef]
- Lü, Q.F.; Chen, D.Y.; Dong, Y.B. Masses of fully heavy tetraquarks in an extended relativized quark model. Eur. Phys. J. C 2020, 80, 871. [Google Scholar] [CrossRef]
- Faustov, R.N.; Galkin, V.O.; Savchenko, E.M. Masses of the tetraquarks in the relativistic diquark-antidiquark picture. Phys. Rev. D 2020, 102, 114030. [Google Scholar] [CrossRef]
- Zhang, J.R. 0+ fully-charmed tetraquark states. Phys. Rev. D 2021, 103, 014018. [Google Scholar] [CrossRef]
- Li, Q.; Chang, C.H.; Wang, G.L.; Wang, T. Mass spectra and wave functions of tetraquarks. Phys. Rev. D 2021, 104, 014018. [Google Scholar] [CrossRef]
- Bedolla, M.A.; Ferretti, J.; Roberts, C.D.; Santopinto, E. Spectrum of fully-heavy tetraquarks from a diquark+antidiquark perspective. Eur. Phys. J. C 2020, 80, 1004. [Google Scholar] [CrossRef]
- Weng, X.Z.; Chen, X.L.; Deng, W.Z.; Zhu, S.L. Systematics of fully heavy tetraquarks. Phys. Rev. D 2021, 103, 034001. [Google Scholar] [CrossRef]
- Liu, F.X.; Liu, M.S.; Zhong, X.H.; Zhao, Q. Higher mass spectra of the fully-charmed and fully-bottom tetraquarks. Phys. Rev. D 2021, 104, 116029. [Google Scholar] [CrossRef]
- Giron, J.F.; Lebed, R.F. Simple spectrum of states in the dynamical diquark model. Phys. Rev. D 2020, 102, 074003. [Google Scholar] [CrossRef]
- Karliner, M.; Rosner, J.L. Interpretation of structure in the di-J/ψ spectrum. Phys. Rev. D 2020, 102, 114039. [Google Scholar] [CrossRef]
- Zhao, Z.; Xu, K.; Kaewsnod, A.; Liu, X.; Limphirat, A.; Yan, Y. Study of charmoniumlike and fully-charm tetraquark spectroscopy. Phys. Rev. D 2021, 103, 116027. [Google Scholar] [CrossRef]
- Mutuk, H. Nonrelativistic treatment of fully-heavy tetraquarks as diquark-antidiquark states. Eur. Phys. J. C 2021, 81, 367. [Google Scholar] [CrossRef]
- Wang, G.J.; Meng, L.; Oka, M.; Zhu, S.L. Higher fully charmed tetraquarks: Radial excitations and P-wave states. Phys. Rev. D 2021, 104, 036016. [Google Scholar] [CrossRef]
- Wang, Z.G. Tetraquark candidates in the LHCb’s di-J/ψ mass spectrum. Chin. Phys. C 2020, 44, 113106. [Google Scholar] [CrossRef]
- Ke, H.W.; Han, X.; Liu, X.H.; Shi, Y.L. Tetraquark state X(6900) and the interaction between diquark and antidiquark. Eur. Phys. J. C 2021, 81, 427. [Google Scholar] [CrossRef]
- Zhu, R. Fully-heavy tetraquark spectra and production at hadron colliders. Nucl. Phys. B 2021, 966, 115393. [Google Scholar] [CrossRef]
- Jin, X.; Xue, Y.; Huang, H.; Ping, J. Full-heavy tetraquarks in constituent quark models. Eur. Phys. J. C 2020, 80, 1083. [Google Scholar] [CrossRef]
- Yang, G.; Ping, J.; Segovia, J. Exotic resonances of fully-heavy tetraquarks in a lattice-QCD insipired quark model. Phys. Rev. D 2021, 104, 014006. [Google Scholar] [CrossRef]
- Albuquerque, R.M.; Narison, S.; Rabemananjara, A.; Rabetiarivony, D.; Randriamanatrika, G. Doubly-hidden scalar heavy molecules and tetraquarks states from QCD at NLO. Phys. Rev. D 2020, 102, 094001. [Google Scholar] [CrossRef]
- Albuquerque, R.M.; Narison, S.; Rabetiarivony, D.; Randriamanatrika, G. Doubly hidden 0++ molecules and tetraquarks states from QCD at NLO. Nucl. Part. Phys. Proc. 2021, 312-317, 15289. [Google Scholar] [CrossRef]
- Wu, R.H.; Zuo, Y.S.; Wang, C.Y.; Meng, C.; Ma, Y.Q.; Chao, K.T. NLO results with operator mixing for fully heavy tetraquarks in QCD sum rules. arXiv 2022, arXiv:hep-ph/2201.11714. [Google Scholar]
- Asadi, Z.; Boroun, G.R. Masses of fully heavy tetraquark states from a four-quark static potential model. Phys. Rev. D 2022, 105, 014006. [Google Scholar] [CrossRef]
- Yang, B.C.; Tang, L.; Qiao, C.F. Scalar fully-heavy tetraquark states in QCD sum rules. Eur. Phys. J. C 2021, 81, 324. [Google Scholar] [CrossRef]
- Feng, F.; Huang, Y.; Jia, Y.; Sang, W.L.; Xiong, X.; Zhang, J.Y. Fragmentation production of fully-charmed tetraquarks at LHC. arXiv 2020, arXiv:hep-ph/2009.08450. [Google Scholar]
- Ma, Y.Q.; Zhang, H.F. Exploring the Di-J/ψ Resonances around 6.9 GeV Based on ab initio Perturbative QCD. arXiv 2020, arXiv:hep-ph/2009.08376. [Google Scholar]
- Maciuła, R.; Schäfer, W.; Szczurek, A. On the mechanism of T4c(6900) tetraquark production. Phys. Lett. B 2021, 812, 136010. [Google Scholar] [CrossRef]
- Gonçalves, V.P.; Moreira, B.D. Fully-heavy tetraquark production by γγ interactions in hadronic collisions at the LHC. Phys. Lett. B 2021, 816, 136249. [Google Scholar] [CrossRef]
- Wang, X.Y.; Lin, Q.Y.; Xu, H.; Xie, Y.P.; Huang, Y.; Chen, X. Discovery potential for the LHCb fully-charm tetraquark X(6900) state via annihilation reaction. Phys. Rev. D 2020, 102, 116014. [Google Scholar] [CrossRef]
- Esposito, A.; Manzari, C.A.; Pilloni, A.; Polosa, A.D. Hunting for tetraquarks in ultraperipheral heavy ion collisions. Phys. Rev. D 2021, 104, 114029. [Google Scholar] [CrossRef]
- Zhuang, Z.; Zhang, Y.; Ma, Y.; Wang, Q. The lineshape of the compact fully heavy tetraquark. arXiv 2021, arXiv:hep-ph/2111.14028. [Google Scholar] [CrossRef]
- Zhao, J.; Shi, S.; Zhuang, P. Fully-heavy tetraquarks in a strongly interacting medium. Phys. Rev. D 2020, 102, 114001. [Google Scholar] [CrossRef]
- Becchi, C.; Ferretti, J.; Giachino, A.; Maiani, L.; Santopinto, E. A study of tetraquark decays in 4 muons and in at LHC. Phys. Lett. B 2020, 811, 135952. [Google Scholar] [CrossRef]
- Sonnenschein, J.; Weissman, D. Deciphering the recently discovered tetraquark candidates around 6.9 GeV. Eur. Phys. J. C 2021, 81, 25. [Google Scholar] [CrossRef]
- Zhu, J.W.; Guo, X.D.; Zhang, R.Y.; Ma, W.G.; Li, X.Q. A possible interpretation for X(6900) observed in four-muon final state by LHCb—A light Higgs-like boson? arXiv 2020, arXiv:hep-ph/2011.07799. [Google Scholar]
- Wan, B.D.; Qiao, C.F. Gluonic tetracharm configuration of X(6900). Phys. Lett. B 2021, 817, 136339. [Google Scholar] [CrossRef]
- Gordillo, M.C.; De Soto, F.; Segovia, J. Diffusion Monte Carlo calculations of fully-heavy multiquark bound states. Phys. Rev. D 2020, 102, 114007. [Google Scholar] [CrossRef]
- Liu, M.Z.; Geng, L.S. Is X(7200) the heavy anti-quark diquark symmetry partner of X(3872)? Eur. Phys. J. C 2021, 81, 179. [Google Scholar] [CrossRef]
- Majarshin, A.J.; Luo, Y.A.; Pan, F.; Segovia, J. Bosonic algebraic approach applied to the tetraquarks. Phys. Rev. D 2022, 105, 054024. [Google Scholar] [CrossRef]
- Kuang, Z.; Serafin, K.; Zhao, X.; Vary, J.P. All-charm tetraquark in front form dynamics. Phys. Rev. D 2022, 105, 094028. [Google Scholar] [CrossRef]
- Wang, Q.N.; Yang, Z.Y.; Chen, W. Exotic fully-heavy tetraquark states in color configuration. Phys. Rev. D 2021, 104, 114037. [Google Scholar] [CrossRef]
- Chen, W.; Chen, H.X.; Liu, X.; Steele, T.G.; Zhu, S.L. Hunting for exotic doubly hidden-charm/bottom tetraquark states. Phys. Lett. B 2017, 773, 247–251. [Google Scholar] [CrossRef]
- Czarnecki, A.; Leng, B.; Voloshin, M.B. Stability of tetrons. Phys. Lett. B 2018, 778, 233–238. [Google Scholar] [CrossRef]
- Guo, Z.H.; Oller, J.A. Insights into the inner structures of the fully charmed tetraquark state X(6900). Phys. Rev. D 2021, 103, 034024. [Google Scholar] [CrossRef]
- Cao, Q.F.; Chen, H.; Qi, H.R.; Zheng, H.Q. Some remarks on X(6900). Chin. Phys. C 2021, 45, 103102. [Google Scholar] [CrossRef]
- Gong, C.; Du, M.C.; Zhao, Q.; Zhong, X.H.; Zhou, B. Nature of X(6900) and its production mechanism at LHCb. Phys. Lett. B 2022, 824, 136794. [Google Scholar] [CrossRef]
- Dong, X.K.; Baru, V.; Guo, F.K.; Hanhart, C.; Nefediev, A.; Zou, B.S. Is the existence of a J/ψJ/ψ bound state plausible? Sci. Bull. 2021, 66, 1577. [Google Scholar] [CrossRef] [PubMed]
- Ortega, P.G.; Entem, D.R.; Fernández, F. Exploring Tψψ tetraquark candidates in a coupled-channels formalism. Phys. Rev. D 2023, 108, 094023. [Google Scholar] [CrossRef]
- Wang, G.J.; Meng, Q.; Oka, M. S-wave fully charmed tetraquark resonant states. Phys. Rev. D 2022, 106, 096005. [Google Scholar] [CrossRef]
- Zhou, Q.; Guo, D.; Kuang, S.Q.; Yang, Q.H.; Dai, L.Y. Nature of the X(6900) in partial wave decomposition of J/ψJ/ψ scattering. Phys. Rev. D 2022, 106, L111502. [Google Scholar] [CrossRef]
- Liu, W.Y.; Chen, H.X. Fully-heavy hadronic molecules bound by fully-heavy mesons. arXiv 2023, arXiv:hep-ph/2312.11212. [Google Scholar]
- Bando, M.; Kugo, T.; Yamawaki, K. Nonlinear Realization and Hidden Local Symmetries. Phys. Rep. 1988, 164, 217–314. [Google Scholar] [CrossRef]
- Meissner, U.G. Low-Energy Hadron Physics from Effective Chiral Lagrangians with Vector Mesons. Phys. Rep. 1988, 161, 213. [Google Scholar] [CrossRef]
- Oset, E.; Ramos, A. Dynamically generated resonances from the vector octet-baryon octet interaction. Eur. Phys. J. A 2010, 44, 445–454. [Google Scholar] [CrossRef]
- Aceti, F.; Bayar, M.; Oset, E.; Martinez Torres, A.; Khemchandani, K.P.; Dias, J.M.; Navarra, F.S.; Nielsen, M. Prediction of an I = 1 state and relationship to the claimed Zc(3900), Zc(3885). Phys. Rev. D 2014, 90, 016003. [Google Scholar] [CrossRef]
- Geng, L.S.; Oset, E. Vector meson-vector meson interaction in a hidden gauge unitary approach. Phys. Rev. D 2009, 79, 074009. [Google Scholar] [CrossRef]
- Nagahiro, H.; Roca, L.; Hosaka, A.; Oset, E. Hidden gauge formalism for the radiative decays of axial-vector mesons. Phys. Rev. D 2009, 79, 014015. [Google Scholar] [CrossRef]
- Molina, R.; Oset, E. The Y(3940), Z(3930) and the X(4160) as dynamically generated resonances from the vector-vector interaction. Phys. Rev. D 2009, 80, 114013. [Google Scholar] [CrossRef]
- Workman, R.L. et al. [Particle Data Group] Review of Particle Physics. Prog. Theor. Exp. Phys. 2022, 2022, 083C01. [Google Scholar] [CrossRef]
- Bečirević, D.; Duplančić, G.; Klajn, B.; Melić, B.; Sanfilippo, F. Lattice QCD and QCD sum rule determination of the decay constants of ηc, J/ψ and hc states. Nucl. Phys. B 2014, 883, 306–327. [Google Scholar] [CrossRef]
- Mathur, N.; Padmanath, M.; Mondal, S. Precise predictions of charmed-bottom hadrons from lattice QCD. Phys. Rev. Lett. 2018, 121, 202002. [Google Scholar] [CrossRef] [PubMed]
- McNeile, C.; Davies, C.T.H.; Follana, E.; Hornbostel, K.; Lepage, G.P. Heavy meson masses and decay constants from relativistic heavy quarks in full lattice QCD. Phys. Rev. D 2012, 86, 074503. [Google Scholar] [CrossRef]
- Aceti, F.; Bayar, M.; Dias, J.M.; Oset, E. Prediction of a Zc(4000) state and relationship to the claimed Zc(4025). Eur. Phys. J. A 2014, 50, 103. [Google Scholar] [CrossRef]
- Oset, E.; Roca, L. Exotic molecular meson states of B(*)K(*) nature. Eur. Phys. J. C 2022, 82, 882, Erratum in Eur. Phys. J. C 2022, 82, 1014. [Google Scholar] [CrossRef]
- Yu, Q.X.; Pavao, R.; Debastiani, V.R.; Oset, E. Description of the Ξc and Ξb states as molecular states. Eur. Phys. J. C 2019, 79, 167. [Google Scholar] [CrossRef]
- Lu, J.X.; Zhou, Y.; Chen, H.X.; Xie, J.J.; Geng, L.S. Dynamically generated JP = 1/2−(3/2−) singly charmed and bottom heavy baryons. Phys. Rev. D 2015, 92, 014036. [Google Scholar] [CrossRef]
- Ozpineci, A.; Xiao, C.W.; Oset, E. Hidden beauty molecules within the local hidden gauge approach and heavy quark spin symmetry. Phys. Rev. D 2013, 88, 034018. [Google Scholar] [CrossRef]

| Constituent | Sector | Sector | Sector |
|---|---|---|---|
| 15,725.3 − | 15,710.8 − | 15,685.2 − | ||||
| 15,790.3 − | 15,784.0 − |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.-Y.; Chen, H.-X. Hadronic Molecules with Four Charm or Beauty Quarks. Universe 2025, 11, 36. https://doi.org/10.3390/universe11020036
Liu W-Y, Chen H-X. Hadronic Molecules with Four Charm or Beauty Quarks. Universe. 2025; 11(2):36. https://doi.org/10.3390/universe11020036
Chicago/Turabian StyleLiu, Wen-Ying, and Hua-Xing Chen. 2025. "Hadronic Molecules with Four Charm or Beauty Quarks" Universe 11, no. 2: 36. https://doi.org/10.3390/universe11020036
APA StyleLiu, W.-Y., & Chen, H.-X. (2025). Hadronic Molecules with Four Charm or Beauty Quarks. Universe, 11(2), 36. https://doi.org/10.3390/universe11020036






