Artificial Intelligence Revolutionizing Time-Domain Astronomy

Abstract

Artificial intelligence (AI) applications have attracted widespread attention and have proven to be highly successful in understanding messages across various dimensions. These applications have the potential to assist astronomers in exploring the massive amounts of astronomical data. In fact, the integration of AI techniques with astronomy began some time ago, significantly advancing our understanding of the universe by aiding in exoplanet discovery, galaxy morphology classification, gravitational wave event analysis, and more. In particular, AI is now recognized as a crucial component in time-domain astronomy, particularly given the rapid evolution of targeting transients and the increasing number of candidates detected by powerful surveys. A notable success is SN 2023tyk, the first transient discovered and spectroscopically classified without human inspection, an achievement made even more remarkable given that it was identified by the Zwicky Transient Facility, which detects millions of alert sources every night. There is no doubt that AI will play a crucial role in future astronomical observations across various messenger channels, aiding in transient discovery and classification, and helping, or even replacing, observers in making real-time decisions. This review paper examines several cases where AI is transforming contemporary astronomy, especially time-domain astronomy. We discuss the AI algorithms and methodologies employed to date, highlight significant discoveries enabled by AI, and outline future research directions in this rapidly evolving field.

1. Introduction

In recent years, artificial intelligence (AI) has emerged as a powerful tool in various scientific disciplines, including astronomy. AI techniques, such as machine learning, deep learning, and data mining, have found diverse applications in astronomy, ranging from data analysis and source classification to predictive modeling and decision-making. Specifically, AI algorithms are employed to filter through vast amounts of observational data, identify patterns, and extract meaningful information from complex datasets. For example, machine learning algorithms can automate the process of classifying celestial objects based on their spectral characteristics, light curves, or morphological features. Moreover, AI techniques enable astronomers to make predictions about the behavior and properties of astronomical objects, facilitating the discovery of new phenomena and guiding observational campaigns.

It is worth nothing that in this review, we adopt a broad and functional definition of AI, encompassing classical machine-learning algorithms, modern deep-learning architectures, and emerging generative or large language model approaches. In astronomy, these methods share a common goal: to extract informative features from complex, multidimensional data and to enable automated or semi-automated decision-making that traditionally required human intervention. We acknowledge that the terminology surrounding AI, machine learning, and deep learning is often used interchangeably and sometimes ambiguously, reflecting historical cycles of enthusiasm and reevaluation within the broader AI community. Our focus here is therefore not on the algorithmic details themselves but on how these data-driven techniques are being applied in time-domain astronomy, what types of datasets most benefit from AI-assisted analysis, and how such approaches are reshaping transient discovery and classification pipelines.

The application of AI in astronomy has led to significant advancements in various subfields. By asking ChatGPT-4 [1] 1 about successful applications of AI in astronomy, we received the following responses:

• Exoplanet Discovery: AI algorithms analyze stellar data to identify patterns indicative of exoplanets orbiting distant stars. This has led to the discovery of numerous exoplanets, expanding our understanding of planetary systems beyond our own.
• Galaxy Morphology Classification: AI techniques, such as deep learning, are used to classify the shapes and structures of galaxies in large-scale surveys. This helps astronomers study galaxy evolution and formation.
• Gravitational Wave Detection: AI algorithms analyze data from gravitational wave observatories like LIGO and Virgo to detect and characterize gravitational wave signals emitted by cataclysmic cosmic events such as black hole mergers.
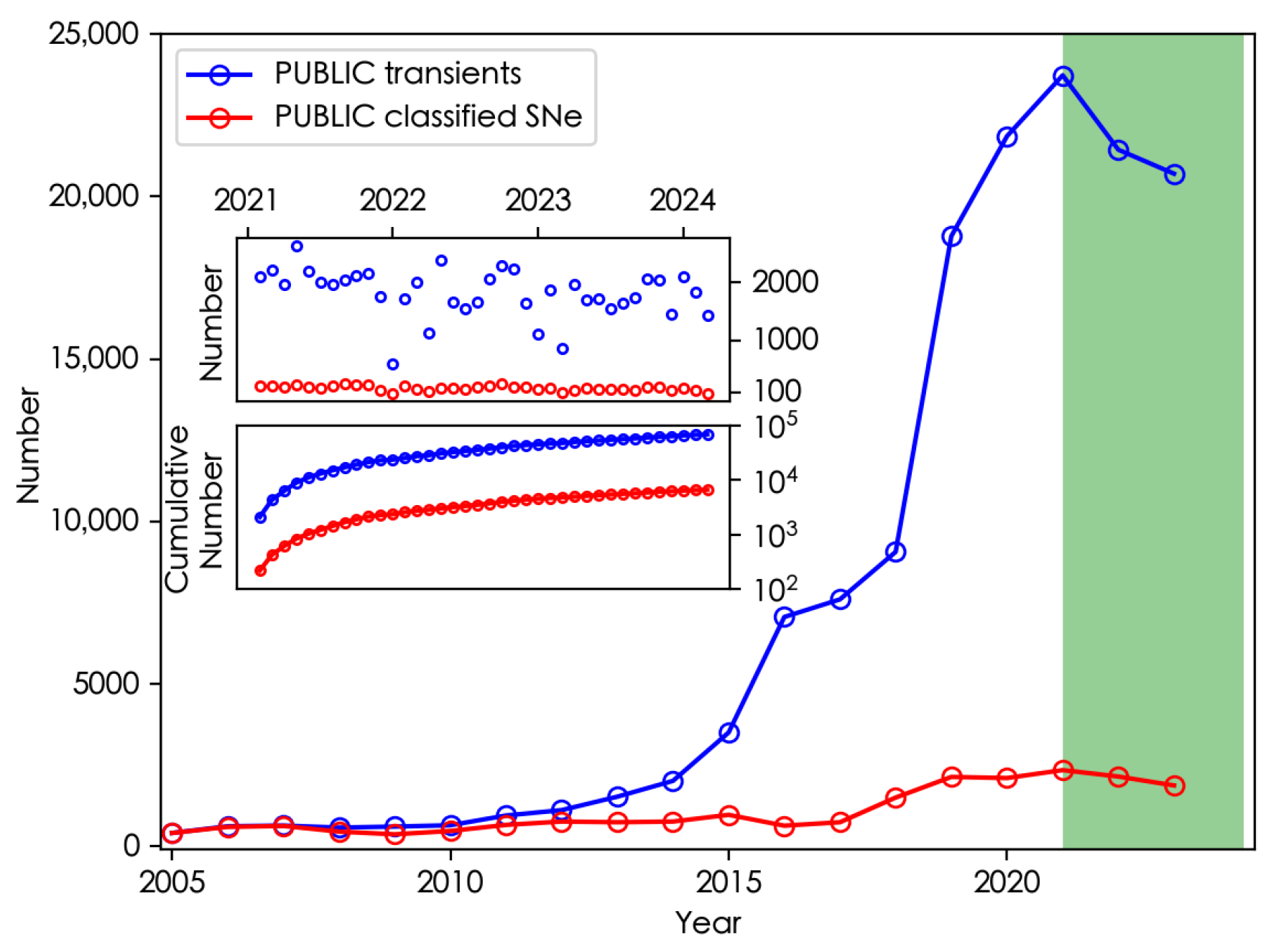
• Transient Detection and Classification: AI is used to automatically detect and classify transient events such as supernovae, gamma-ray bursts, and fast radio bursts in astronomical surveys, enabling rapid follow-up observations.
• Data Analysis and Interpretation: AI techniques are employed to analyze large datasets from telescopes and satellites, extracting valuable insights about the properties and behaviors of celestial objects.

From these answers, it can be seen that AI has a wide range of applications and prospects in astronomy. This review mainly focuses on describing the application of AI in time-domain astronomy, showing how it effectively assists astronomers in dealing with the opportunities and challenges brought about by instrument upgrades, ultimately facilitating revolutionary advancements in time-domain astronomy.

Time-domain astronomy focuses on the study of celestial events that vary or appear transiently over time. These events, known as transients, encompass a wide spectrum, ranging from dramatic cataclysmic events like supernovae (SNe) [2] and gamma-ray bursts (GRBs) [3] to compact stellar systems, including cataclysmic variables (CVs) [4] and X-ray binaries [5], to active galactic nuclei (AGNs) [6], whose brightness fluctuations trace accretion physics around supermassive black holes. Time-domain astronomy plays a crucial role in understanding the dynamic and evolving nature of the universe, offering insights into fundamental astrophysical processes, cosmology, and even the search for extraterrestrial intelligence.

Aiming to detect the variability of astronomical sources, particularly transients, modern synoptic surveys are designed to monitor large sky areas with high cadence. With the continuous increase in telescope aperture and the rapid advancement of detector technologies such as mosaic CCDs [7,8,9], the survey capability of current time-domain surveys has seen an exponential improvement compared to the past; for instance, the Pan-STARRS [10] and the Zwicky Transient Facility (ZTF) [11,12,13,14] cameras have a large field of view, i.e., 9 and 47 square degrees, respectively, and they can thus monitor the full northern sky with daily cadence. Consequently, the data volume of transient candidates detected each night far exceeds the capacity for human inspection, e.g., as shown in Figure 1, the number of public transients reported per year was relatively low between 2005 and 2012, allowing for classification by eye. After 2012, there was a rapid increase, reaching nearly 25,000 reported events per year. Of course, the reported candidates have already been pre-selected; in fact, the number of detected candidates is much larger than this figure. In the meantime, the number of classified supernovae remained relatively low, comparable to the earlier classification numbers. This is due to the scarcity of spectral resources. Thus, any tool aiding in the classification holds importance in time-domain astronomy research. AI, which encompasses a broad range of techniques and methodologies aimed at enabling machines to perform tasks that typically require human intelligence, can play a crucial role here. For instance, machine learning algorithms can be trained on labeled datasets to recognize patterns and anomalies associated with different types of transients, enabling rapid and accurate classification of new observations, even with multi-band photometry only. Furthermore, the integration of AI with time-domain astronomy holds the potential to uncover novel insights and discoveries that may have remained hidden using traditional approaches. By harnessing the power of AI to analyze multi-dimensional and time-varying data, astronomers can explore new parameter spaces and identify unexpected correlations or phenomena.

In the meantime, astronomers often do not have sufficient time to slowly process the vast amount of data and extract valuable insights from it. Compared to relatively common transients such as SNe, astronomers are now more inclined to explore rapidly evolving transients, aiming to unveil a broader spectrum of extreme astronomical phenomena such as kilonovae (KNe) [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32], fast blue optical transients (FBOTs) [33,34,35,36,37], and the shock breakout (SBO) emissions of SNe; e.g., the cooling tail of SBO might be caught in ultra-violet and optical wavelengths [38,39]. Therefore, observational instruments need to possess high temporal resolution. To overcome limitations imposed by the horizon and the atmosphere, astronomers have initiated the deployment of space telescopes like Kepler [40,41,42], TESS [43,44,45,46], GAIA [47], etc. However, considering the costs associated with construction, maintenance, and operational lifespan, a more feasible alternative involves establishing fully automated telescopes at various locations worldwide, thereby creating a network for time-domain astronomy observations, e.g., Las Cumbres Observatory Global Telescope (LCOGT) [48], Asteroid Terrestrial Last-Alert System (ATLAS) [49,50,51], All-Sky Automated Survey for Supernovae (ASAS-SN) [52], Distance Less Than 40 Mpc Survey (DLT40) [53], etc. The operation of multiple telescopes often requires a significant amount of manpower. Therefore, AI-based collaborative observation techniques and fully automated operation technologies for telescopes have become important tools in current research in time-domain astronomy. AI-driven predictive models can forecast the properties and evolution of transient events, guiding follow-up observations and maximizing scientific return.

In summary, the integration of AI with time-domain astronomy represents a significant methodological change in the way we explore the transient universe. By leveraging AI techniques to analyze vast amounts of observational data, astronomers can unlock the full potential of time-domain surveys and uncover the secrets of the dynamic cosmos. For instance, with the support of AI techniques, astronomers can now classify millions of alerts within just a few hours, compared to the days or even months once required for human verification in earlier surveys. This dramatic, order-of-magnitude improvement in latency and throughput enables astronomers to identify rare and unusual transient events that might otherwise have been missed. In this context, SN 2023tyk [54,55] is claimed as the first transient that required no human action from its discovery to its spectroscopic classification (type Ia supernova), being posted to TNS2. In this review paper, we use SN 2023tyk as a case illustrating successful applications of AI in astronomy. We explore the transformative impact of AI on time-domain astronomy with SN 2023tyk as an example in Section 2, demonstrating how meaningful features can be extracted from diverse datasets. In Section 3, we introduced various machine learning algorithms and evaluation criteria, and we summarize those that have been widely applied in time-domain astronomy. We highlight the key developments, challenges, and future directions in this rapidly evolving field in Section 4, and finally, we conclude this review paper in Section 5.

2. SN 2023tyk as a Case Illustrating the Application of AI in Time-Domain Astronomy

In Figure 2, we present a workflow diagram illustrating the monitoring process of the transient sky, including candidate detection, photometric and spectroscopic follow-up strategies, and the final diagnosis of the physical scenario. In this process, machine learning can primarily be applied in three parts, i.e., real bogus classification of candidates based on their images, pattern recognition based on the multi-band light curves, and automatic analysis based on spectral energy distributions (SEDs). Additionally, machine learning can also be utilized in various other ways, such as survey strategy optimization, although these applications are beyond the scope of this review.

Regarding SN 2023tyk, a.k.a. ZTF23abhvlji, it was automatically identified as a bright extragalactic transient in the ZTF public alert stream by BTSbot [56]. Due to its scientific interest, which was judged by the computer itself, it was subsequently and automatically observed by the Bright Transient Survey (BTS) [57,58] using the SED Machine [59]. A spectrum was robotically obtained, automatically reduced using pySEDM [60], and classified with SNIascore [61]. The classification was then routinely reported to the TNS server.

In this section, we use the discovery and follow-up story of SN 2023tyk as an example to illustrate the fully robotic pipeline developed within the ZTF ecosystem. In Section 2.1, we present how to distinguish between real and bogus candidates by relying on the image stamps, while in Section 2.2 and Section 2.3, we demonstrate how to distinguish different candidate types based on their observed fluxes and ultimately connect them to the underlying physical scenarios.

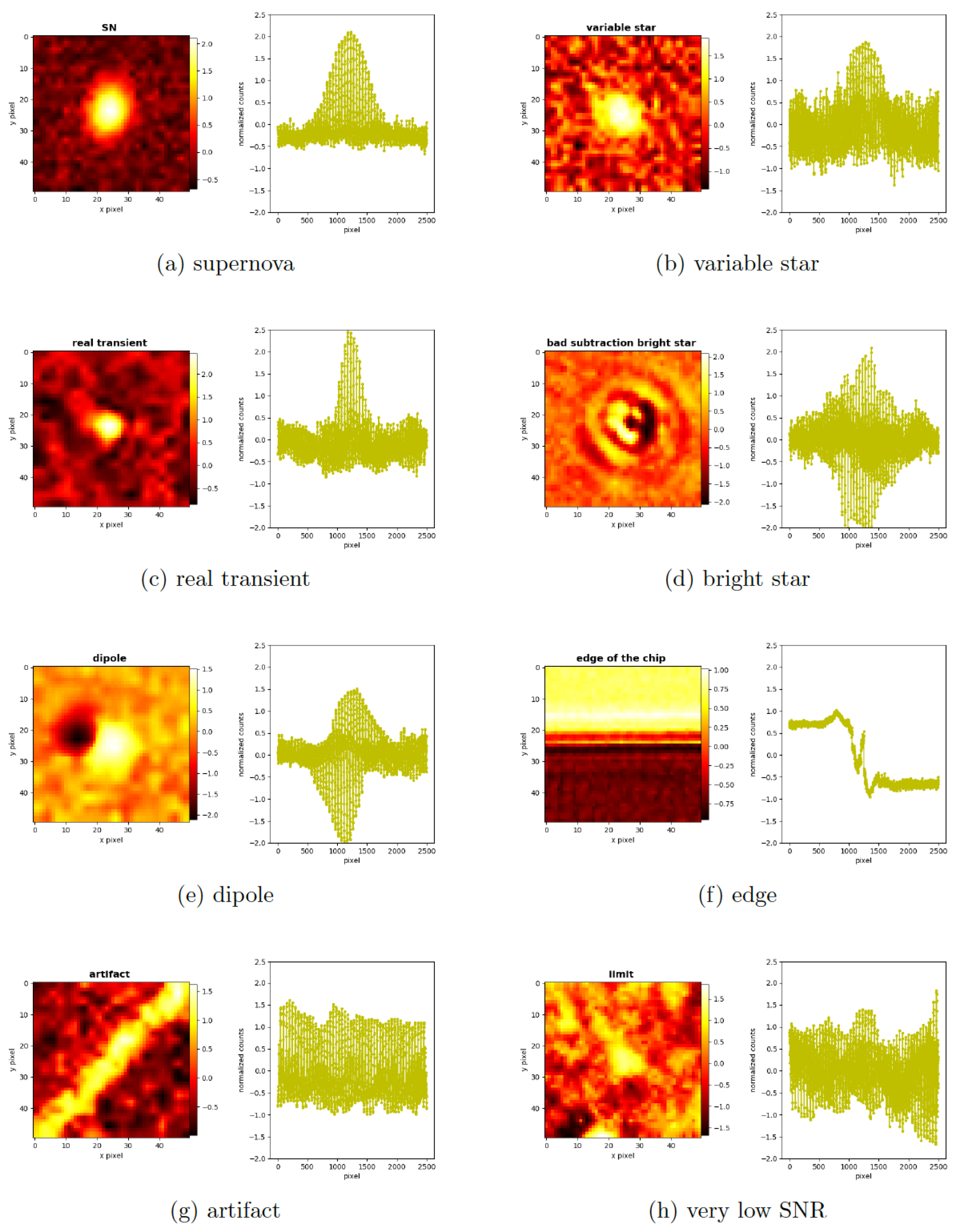
2.1. Real–Bogus Classification

Astronomers use telescopes to capture images of the sky and compare them with historical images of the same celestial region to detect new transients. Upon acquisition of images, the most effective method for transient detection involves subtracting search images from reference images captured previously. However, a major challenge with optical images from ground-based telescopes is that the Point Spread Function (PSF) varies at different epochs due to changing atmospheric conditions, such as variable seeing. To perform subtraction more effectively without atmospheric interference, the PSFs from two different epochs can be convolved to match each other using several publicly available codes, such as ISIS [62], HotPants [63], and ZOGY [64]. Once the images are properly subtracted, astronomers can identify residuals in the difference images using tools like SExtractor [65]. Sources exhibiting a Gaussian-like profile are likely real, while those that do not may be artifacts caused by various factors. Overall, owing to various issues associated with the detector and subtraction algorithms—such as alterations in the flux distribution kernel of point sources caused by atmospheric changes—the candidates identified from the resultant residual images are frequently tainted by a plethora of artifacts, see Figure 3, typically presenting a ratio of 100–1000 bogus candidates for every real one (depending on the threshold of signal-to-noise ratio).

As detailed in Section 1, advancements in observational facilities and techniques have significantly enhanced the capabilities of modern telescopes to monitor vast areas of the sky. As a result, they generate an overwhelming number of transient candidates each night—far beyond what astronomers can feasibly inspect manually. Human visual inspection becomes the bottleneck for rapid target identification. To address this challenge, AI has become an essential tool in the field, helping to alleviate the burden and enable efficient source identification.

Choosing informative, discriminating, and independent features is crucial to produce effective algorithms for pattern recognition, classification, and regression tasks. In fact, there are various approaches to constructing features for machine learning algorithms in addressing the real–bogus classification problem. One of the most commonly used methods, as proposed by [66], is to represent each transient candidate directly using its pixel data. As illustrated in Figure 3, for a given training example, a feature vector can be constructed by extracting a x by x pixel region centered on the transient (x is the size of square image stamp, which can vary depending on the seeing conditions; typically, a region spanning approximately five times the average seeing is used), shown as the left side in each subplot of Figure 3. Then, on the right-hand side of each subplot, a 1-D feature vector is created by sequentially shifting each column of the substamp and concatenating them to form a vector of pixel intensity values. To mitigate variations in pixel intensity across different images—variations that are not intrinsic to the transient source itself—a normalization procedure is typically applied. One commonly used approach is the log normalization method, as described in Equation (1) of [66]. This step ensures that amplitude differences arising from external factors (e.g., background noise, detector sensitivity) are minimized. After normalization, the machine learning algorithm can more effectively identify patterns in the feature vectors that are characteristic of real or bogus detections.

In addition to the feature extraction method described above, various alternative approaches have been explored. For instance, one can use source-fitting parameters obtained from tools like SExtractor, employ deep learning algorithms to automatically learn feature representations [68], or even apply image recognition models that operate directly on the raw images [69]. These different strategies have been adopted in several projects and have all demonstrated promising classification performance. A comprehensive overview and comparisons between these methods are beyond the scope of this paper.

In order to assist astronomers in identifying interesting celestial objects in the shortest possible time, allowing them ample time and confidence to prepare for subsequent deep observations with large-aperture telescopes, modern time-domain surveys such as the ZTF and Rubin LSST [70] have integrated tasks such as image processing, candidate source extraction, and machine learning-based real–bogus classification into streamlined, automated pipelines operated by expert teams. This enables the broader astronomical community to receive transient candidates, accompanied by essential contextual information, in real time. This need for rapid and accessible data dissemination is the key motivation behind the development of alert systems and dedicated broker platforms. Inspired by the data delivery architectures used in commercial applications—such as those employed by LinkedIn3 —and built upon frameworks like Apache Kafka [71], these surveys can efficiently distribute alert packets to multiple broker systems, including ALeRCE [72]4, Lasair [73]5, ANTARES [74]6, Fink [75]7, and Ampel [76]8, among others9. Each alert packet10 (see e.g., the ZTF alert documentation11) contains rich metadata and contextual information, including photometric measurements and image cutouts (science, reference, and difference images). This allows users to apply customized filters and algorithms to identify and prioritize transient events of interest. For example, one can refer to the Lasair’s filter page12, which provides a collection of community-designed filters aimed at identifying different types of transient and variable source candidates.

A variety of parameters, multi-epoch photometric data, and even image cutouts for each epoch are displayed on the dedicated Lasair webpage of SN 2023tyk13. All of this information is derived from the alert stream. For each epoch, the alert also provides associated parameters such as rb and drb, which represent the probabilities that the candidate is real, as computed using machine learning and deep learning algorithms, respectively. These values are designed to assist users in deciding whether a candidate merits follow-up observations, and which observational epochs, they provide reliable flux measurements.

BTSbot is a convolutional neural network designed to identify sources relevant to the BTS project. As shown in the Figure 1 of [56], BTSbot achieves this by assigning a bright transient score to each ZTF alert packet [77] based on the image cutouts and 14 selected numeric features, autonomously requesting follow-up observations for those most promising candidates. Follow-up observations can thus generate multi-band light curves and SEDs of candidate objects, providing astronomers with crucial data for classifying transients based on empirical knowledge. Additionally, machine learning algorithms, by comparing these observations with vast historical datasets, can significantly enhance the efficiency of identifying and prioritizing important candidates.

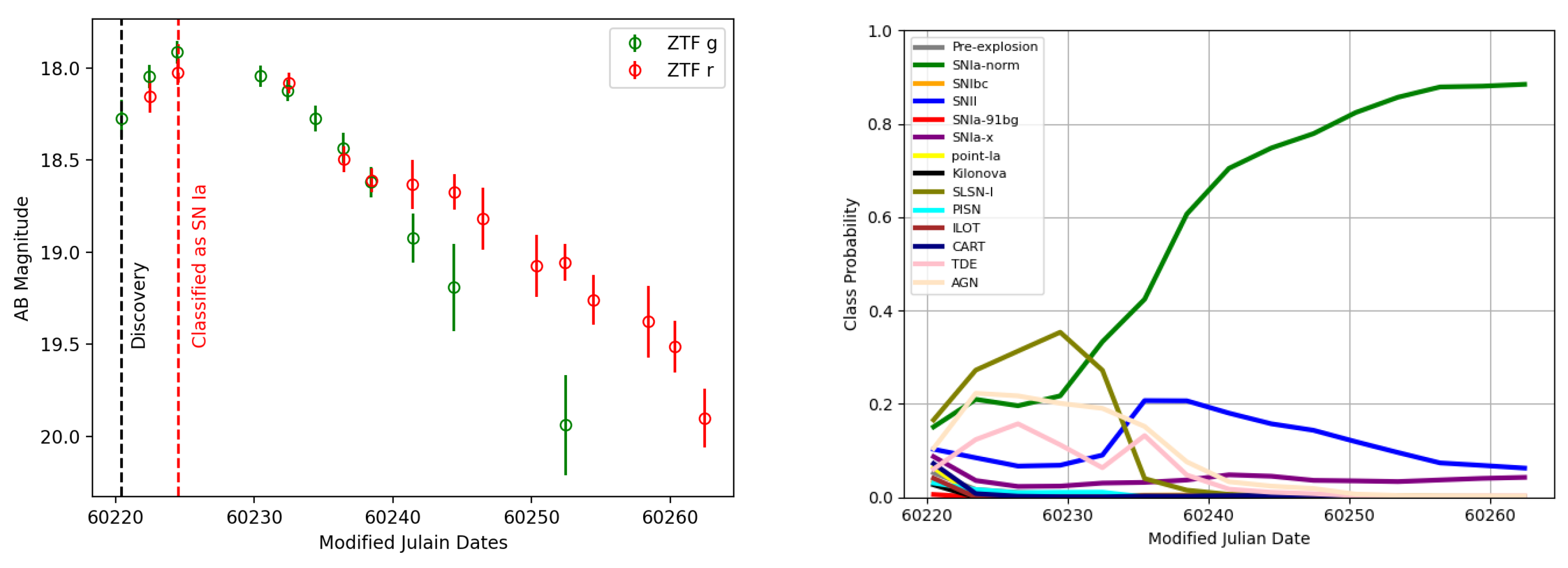
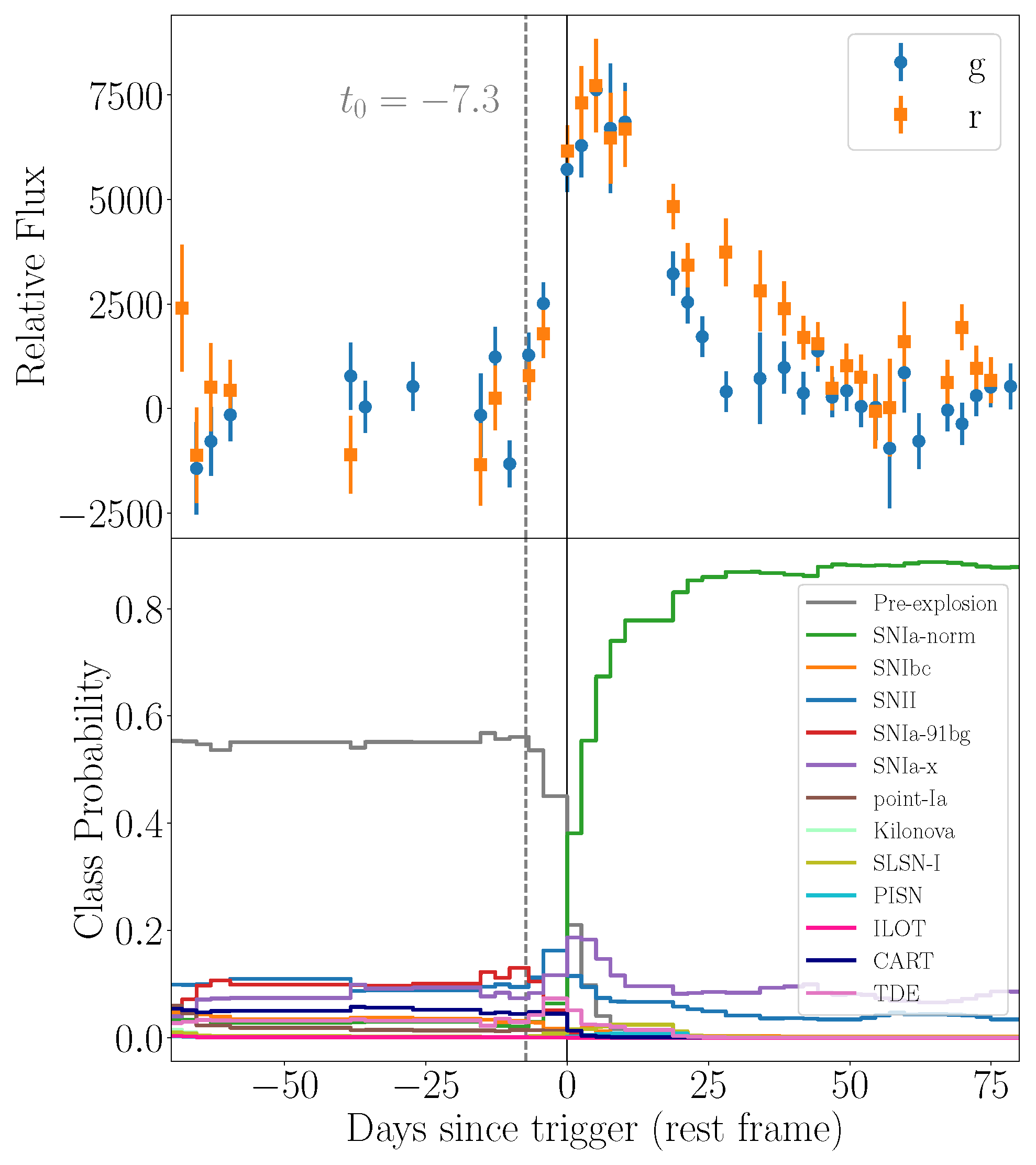
2.2. Multi-Band Photometric Lightcurves

Once astronomers identify an interesting real transient through alert filters, the next step typically involves gathering additional information about the candidate through various means. This may include checking for associations with multi-wavelength or multi-messenger sources, or evaluating whether follow-up observations with large-aperture telescopes are feasible to obtain a more detailed spectral energy distribution of the source. The spectroscopic observations from large-aperture telescopes are often crucial for astronomers to delve into the intricacies of these transients. However, observation time on large-aperture telescopes is extremely precious. Astronomers often require reliable and efficient tools to quickly discern the uniqueness and scientific value of alerts, thus bolstering confidence to utilize precious large-aperture telescope resources for uncharted exploration. Multiband photometric information from small-aperture telescopes—even citizen scientists, whose equipment may be less advanced—however, often obtain images with remarkably good cadence [78,79], to some extent reflecting the SED of candidates, making it a highly trusted tool for astronomers, e.g., extracting features such as color and brightness variation rates from multiband light curve data. Within diverse extracted features from photometry, astronomers can then employ various AI tools, such as machine learning algorithms, to compare with historical data or relevant models, thus assessing the potential underlying special physical eruption mechanisms of these sources behind those multi-band light curves.

As before, we take SN 2023tyk as an example. Figure 4 shows its ZTF light curves as well as its machine learning-based photometric classification of the transient. Remarkably, using only limited photometric information, AI identified the source as a potential Type Ia supernova—a prediction that was later confirmed by spectroscopic observations. At present, such light curve-based machine learning approaches are applicable to most classes of transients. However, there are still too few cases to robustly assess their accuracy in distinguishing between, for instance, Type Ib and Type Ic SNe, separating kilonovae from the SBO cooling tails of SNe, or determining whether a SNe is a superluminous event when distance information is unavailable.

Of course, the accuracy of light curve-based machine learning classification is strongly dependent on the completeness of the photometric sampling. Figure 5 illustrates the performance of astrorapid14, a deep recurrent neural network framework for real-time classification of multi-band light curves. During the earliest phases of an outburst, the classification scores of different supernova types are nearly uniform; however, within ∼5 days of the trigger, clear separation between Type Ia and non-Ia supernovae emerges. When light curves are well sampled—i.e., observed with sufficiently high cadence and across multiple filters—the predictive power of machine learning can approach that of direct spectroscopic classification. Nonetheless, as emphasized above, early-time SED observations are crucial, and in practice, astronomers often realize a transient’s importance only after this critical phase has passed. Rapid acquisition of rich early-time SED data therefore remains a major challenge for time-domain surveys. Two general strategies are currently pursued. One is to conduct large, indiscriminate spectroscopic campaigns, exemplified by projects such as LAMOST [80] and 7DT [81]. Such efforts, however, are rare and resource-intensive. More commonly, wide-field, high-cadence surveys rely on machine learning algorithms to classify transients from sparse photometric data. While this approach carries intrinsic risks, it can yield enormous scientific rewards when successful.

The challenge of classifying transients from photometric light curves has been recognized for more than a decade. In 2010, the Supernova Photometric Classification Challenge (SNPhotCC) [82,83] released a mixed dataset of simulated supernovae to test methods for distinguishing Type Ia supernovae from other classes. This initiative spurred the development of classification techniques in preparation for the Dark Energy Survey (DES) [84], ranging from template fitting to more advanced approaches such as light curve parameter fitting. Semi-analytic models, e.g., refs. [85,86], explored the possibility of reproducing SNe light curves with only a small number of hyperparameters. These models can be further embedded within other frameworks, such as the Gaussian processes [87], which may be applied for interpolation or parameter constraint, thereby providing informative features for transient classification. Many of these fitting and feature-extraction processes have been integrated into publicly available codes, allowing astronomers to conveniently extract analytic or physical parameters directly from observational data. Representative examples include HAFFET (easily public transient data access and various light curve/SED model fittings) [88], PISCOLA (SNe light curve interpolation for cosmology) [89], MOSFiT (physically motivated models such as magnetar or radioactive decay) [90], TigerFit (similar to MOSFIT but places greater emphasis on the circumstellar medium interaction-powered scenarios)15, RESSPECT (enables the construction of optimized training samples for the Rubin LSST) [91], and TransFit (improves upon previous physical models, enabling faster and more accurate reproduction of light curves) [92].

This effort was expanded in 2019 with the Photometric Luminous and Transient Classification Challenge (PLAsTiCC) [93]16, which simulated 19 classes of transients using tools such as SNANA [94] to evaluate classification strategies for LSST. These challenges attracted a broad community of astronomers and algorithm developers, fostering a variety of feature extraction techniques and machine learning approaches. Collectively, such developments have driven time-domain astronomy to a new level, enabling deeper exploration of the dynamic universe.

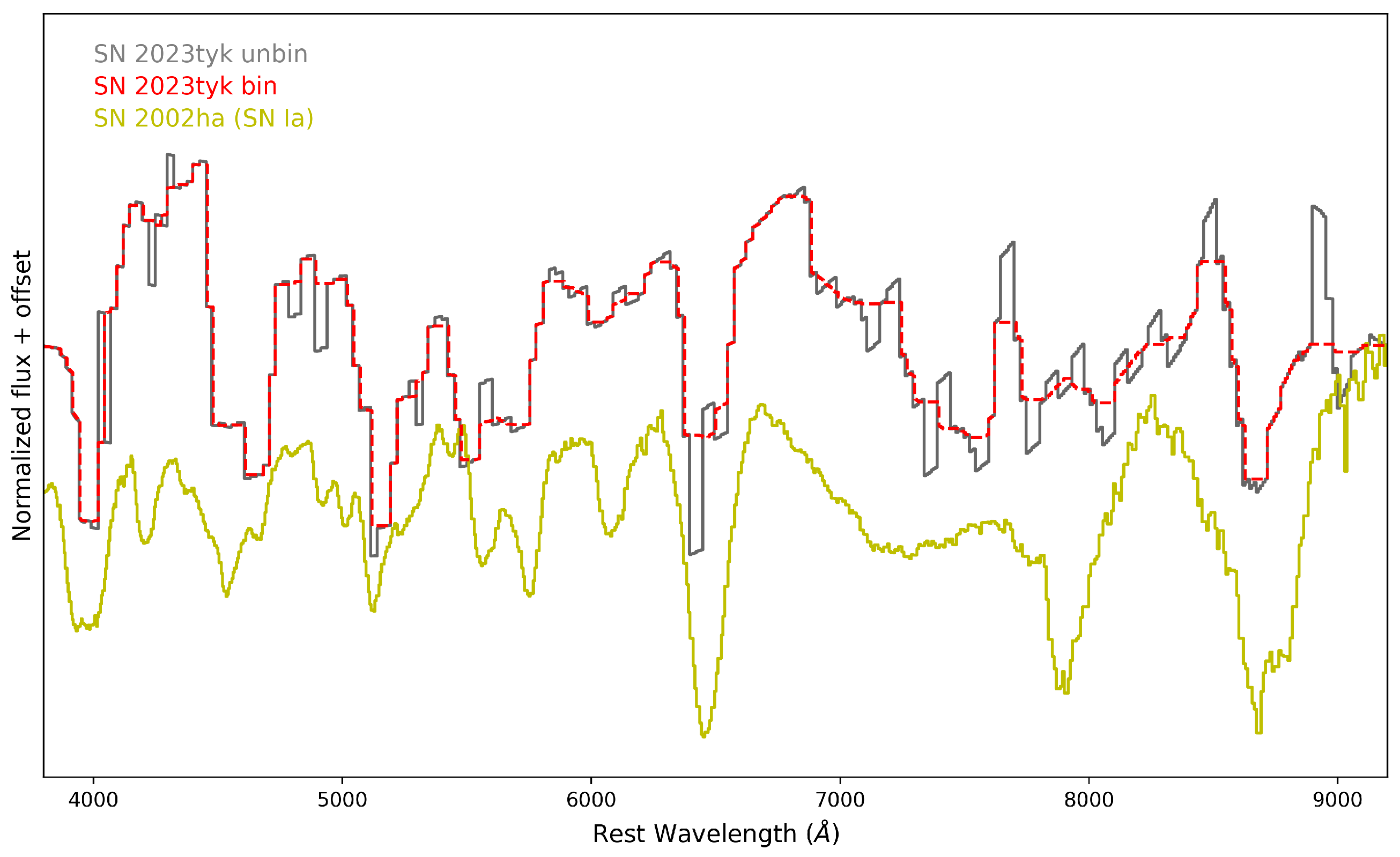
2.3. Spectral Energy Distributions

When a source is preliminarily identified as potentially significant—either through peculiar metadata (see Section 2.1) or early-time photometric behavior (see Section 2.2)—astronomers often announce the discovery via community networks such as the Gamma-ray Coordinates Network (GCN)17, Astronotes18, or the Astronomer’s Telegram (ATel)19. Once such announcements gain traction within the community, they typically trigger an intensive campaign of photometric and spectroscopic follow-up observations.

Although the light curve classification tools mentioned above are powerful in most cases, they may not be able to accurately classify SNe in certain specific situations, requiring spectroscopic identification. The SED describes the distribution of radiation energy of celestial bodies at different wavelengths, as shown in Figure 6. By analyzing the presence of hydrogen and helium in the spectrum, SNe can be further subdivided. 2023tyk is a widely studied SN candidate that, after confirmation by BTSbot, obtains a spectrum using the SED Machine and is classified by SNIascore. Similar to SNIascore, there is the CCSNscore [95] rating system, which quantifies the spectral features of different SNe to improve classification accuracy.

Currently, there are various automated classification tools such as Supernova Identification (SNID) [97]20, Generative Latent Textured Objects (GELATO) [98]21, Deep Automated Supernova and Host classifier (astrodash) [99]22, The Next Generation SuperFit (NGSF) [100]23, and the SNID SAGE24, which can quickly and accurately identify the types and relevant parameters of supernovae. SNID provides a spectroscopic classification method based on cross-correlation, effectively distinguishing SN Ia from other types of SNe and allowing for flexibility in adjustment when dealing with different spectral data. As shown in Figure 7, the observed spectra are compared with historic data via the SNID tool to identify the possible nature behind the sources. GELATO is a user-friendly online tool that can automatically compare input spectra with a rich template database to quickly identify the most similar SN spectra. Its intuitive interface and powerful backend algorithms enable even non-professional users to easily classify SNe. Additionally, astrodash provides a Python library that supports batch processing of SNe spectra, significantly improving data processing efficiency. NGSF has been integrated into the Weizmann Interactive Supernova Data Repository (WISeREP) [101] webpage25, allowing it to be executed directly on the spectral search page of the repository. By combining the strengths of these tools, utilizing machine learning techniques for the analysis and classification of SNe spectra is no longer a challenge, greatly improving the timeliness and accuracy of classifications.

3. Machine Learning Algorithms and Criteria

Building on Section 2, where we used the ZTF discovery and automated identification of SN 2023tyk as an example, we illustrated the broad applicability of machine learning techniques in time-domain astronomy. In the following section, we review the various machine learning algorithms and decision criteria that have been employed in this process. It is worth noting that machine learning has now developed into a highly systematic methodology. Its utility is not limited to astronomy; as long as meaningful features and reliable labels can be extracted, these algorithms can be readily applied across disciplines to perform large-scale data mining and uncover hidden patterns in complex datasets.

3.1. Machine Learning Concepts and Evaluation Standards

Machine learning is a discipline that studies how to improve algorithms and model performance through experience, i.e., the historic data. The core terminology in machine learning that provides the foundation for methodological development and application includes:

• Model: A model is an abstract representation of a computer program or algorithm used to process and analyze data, make decisions, or make predictions. A model can be seen as a decision center that learns patterns and rules from data to perform tasks like prediction or classification. In time-domain astronomy, models can be applied to process and analyze various types of data, such as tabular data, time series data, and image data, to explore and understand astronomical phenomena.
• Dataset: A dataset is a collection of information used to train and test models. In time-domain astronomy, datasets can include various types of data, such as astronomical images, astronomical light curves, and observational flux distributions. Typically, datasets are divided into training sets and test sets. The training set is used for the learning and training of the model, providing a large number of sample data points that enable the model to learn the features and patterns of the data. The test set is used to evaluate the model’s performance and generalization ability on unseen data, verifying whether the model has truly learned knowledge from the training data.
• Features and Labels: Features are attributes or characteristics used to describe data, such as color, shape, size, etc. In time-domain astronomy, features can be various numerical characteristics extracted from observational data. Labels are interpretations or tags assigned to data, similar to naming or classifying the data. By learning the associations between features and labels, models can classify or identify new observational data.

Depending on whether the input data are labeled, unlabeled, or require interaction with an environment, machine learning is typically divided into three main categories:

• Supervised Learning [103]: In this learning mode, models are trained using a set of input–output pairs, where the input consists of features and the output is the target variable. The goal of supervised learning is to master the mapping relationship between features and the target variable. Common algorithms include Decision Trees, Support Vector Machines (SVMs), and Random Forests (RFs). Typical application scenarios include classification (classifying spectra as stars or quasars [104]) and regression (estimating redshift from photometric measurements [105]).
• Unsupervised Learning [106]: Unsupervised learning is used to discover the intrinsic structure of unlabeled data. It does not rely on labels provided by humans but instead reveals patterns and relationships in the data through techniques such as clustering, dimensionality reduction, and anomaly detection. Unsupervised learning is particularly important in scientific research because it can extract new knowledge from existing datasets and drive new discoveries. Common unsupervised learning methods include clustering algorithms (e.g., K-means, HDBSCAN, DBSCAN) [107,108,109], dimensionality reduction techniques (e.g., PCA, t-SNE, UMAP) [110,111,112], and anomaly detection algorithms [113,114,115,116].
• Reinforcement learning (RL) [117]: RL is centered on the idea that an agent explores and exploits a specific environment, optimizing its decision-making process through trial and error. The goal is to learn how to take effective actions through interaction with the environment. Compared to the other two machine learning methods, RL significantly transforms the learning process into actual actions. Currently, in the field of astronomy, RL has been widely applied to telescope control [118,119,120,121,122] and hyperparameter tuning in radio astronomical data processing pipelines [123,124].

Evaluating model performance is undoubtedly a key step, and evaluation standards vary based on the nature of the task (classification or regression). In regression tasks, where the target variable is continuous, common evaluation metrics include Mean Absolute Error (MAE) and Mean Squared Error (MSE) [125]. The MAE measures the average absolute difference between predicted and actual values, making it suitable for scenarios where sensitivity to outliers needs to be minimized. The MSE calculates the average of the squared differences between predicted and actual values, making it more sensitive to outliers.

For classification tasks, where the target variable is discrete, evaluation standards typically include the Area Under the ROC Curve (AUC), confusion matrix, F₁ score, F₂ score, F_1/2 score, F_1/3 score, and accuracy.

• ROC (Receiver Operating Characteristic) Curve: The ROC curve displays the performance of a classifier at different thresholds, with the horizontal axis representing the false positive rate (FP) and the vertical axis representing the true positive rate (TP). The closer the curve is to the top left corner (point (0,1)), the better the classification performance. The AUC value, which represents the area under the ROC curve, ranges from 0 to 1; the closer the AUC value is to 1, the better the model’s performance.
• F₁ Score: The F₁ score is the harmonic mean of precision (P) and recall (R), calculated as follows:

  $$F_1={\displaystyle \frac{2·\mathrm{P}·\mathrm{R}}{\mathrm{P}+\mathrm{R}}}$$

  (1)
• F₂ Score: The F₂ score gives more weight to recall than precision, calculated as follows:

  $$F_2={\displaystyle \frac{5·\mathrm{P}·\mathrm{R}}{4·\mathrm{P}+\mathrm{R}}}$$

  (2)
• F_1/2 Score: The F_1/2 score emphasizes precision while considering recall, calculated as follows:

  $$F_{1/2}={\displaystyle \frac{3·\mathrm{P}·\mathrm{R}}{2·\mathrm{P}+\mathrm{R}}}$$

  (3)
• F_1/3 Score: The F_1/3 score puts a greater emphasis on recall, calculated as follows:

  $$F_{1/3}={\displaystyle \frac{4·\mathrm{P}·\mathrm{R}}{3·\mathrm{P}+\mathrm{R}}}$$

  (4)
• Accuracy: Accuracy measures the proportion of correct predictions (both true positives and true negatives) out of the total predictions made. It is calculated as follows:

  $$Accuracy={\displaystyle \frac{\mathrm{TP}+\mathrm{TN}}{\mathrm{TP}+\mathrm{TN}+\mathrm{FP}+\mathrm{FN}}}$$

  (5)

In these equations:

$$P={\displaystyle \frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}}}$$

(6)

$$R={\displaystyle \frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}}}$$

(7)

Finally, the confusion matrix is an intuitive tool for displaying the comparison between the model’s predictions and actual labels, with each row corresponding to a true class and each column corresponding to a predicted class. These evaluation metrics provide a comprehensive assessment of classification model performance, allowing for better decision-making based on specific needs and contexts.

3.2. Photometric Classification for Optical Transient Studies

In Section 2, we used SN 2023tyk as an example to illustrate how machine learning assists astronomers in identifying real sources in images and in classifying different source types through light curves and SEDs. In fact, the accuracy of machine learning algorithms on image vetting has already reached a very high level, e.g., a missed detection rate of around 10% by accepting a false positive rate of 1% [66], and for survey data such as that from ZTF, LSST, etc., it has been highly integrated into broker systems. At the same time, machine learning has significantly improved the accuracy of spectral classification of sources; however, spectroscopic data remain sparse and complex, meaning that expert analysis is still indispensable. As noted above, current surveys such as ZTF and LSST are extremely powerful, producing massive amounts of photometric data that can only be efficiently processed with machine learning algorithms. Methods to achieve this have varied, with differing levels of accuracy, and the development of improved approaches continues to be an active research area. Therefore, in this section, we systematically review, through a selection of representative studies, how astronomers have applied machine learning algorithms, e.g., Random Forests [126,127], Support Vector Machines [128], and Bayesian Neural Networks (BNNs) [129,130,131], to massive multi-band light curves in time-domain astronomy to carry out large-scale data mining.

In [86], the authors evaluated four feature extraction methods—model parameters, manually selected features, principal component analysis (PCA), and direct light curve inputs—together with two data-augmentation techniques (SMOTE and MVG) and three classification algorithms, i.e., SVM, RF, and Multi-Layer Perceptron (MLP). By combining these approaches into 24 distinct pipelines, they assessed the purity, accuracy, and completeness of transient classifications. Their analysis showed that the most successful pipeline—resulting in around 90% average accuracy, 70% average purity, and 80% average completeness for all SN classes—achieved the highest performance for Type Ia SNe and SLSNe, while the classification accuracy for Type Ib/c SNe remained comparatively poor. Convolutional Neural Networks (CNNs) have achieved significant success in image recognition [132,133,134], and their application to light curve data has also shown great potential. For example, the SCONE algorithm generates two-dimensional heat maps of light curves using Gaussian processes and utilizes CNNs for classification. Experimental results indicate that SCONE can classify six types of supernovae with over 98% accuracy without redshift information [135]. Recurrent neural networks (RNNs) are suitable for processing time-series data and have been widely used in light curve classification problems in recent years. Ref. [136] used long short-term memory networks (LSTM) to distinguish between Type Ia SNe and core-collapse SNe. With around 10,000 SNe used for training, the model achieves a Type Ia vs. non-Ia classification accuracy of 94.7%, an AUC of 0.986, and an F1 score of 0.64. For using the early-epoch data only, performance remains high with 93.1% accuracy, AUC = 0.977, and F1 = 0.58. A bidirectional RNN further distinguishes Types I, II, and III with 90.4% accuracy and AUC = 0.974, demonstrating competitive performance for large-scale photometric surveys. Ref. [137] trained classifiers using RNNs with a masking layer to fill arrays with zero entries, successfully identifying SNe, kilonovae, and other rare sources from simulated light curves of ZTF. Unlike previous methods, they adopted a new anomaly detection approach, combining multi-class isolation forests (MCIFs) to train separate forests for 17 categories of sources, avoiding the disadvantages of interpolation and discovering 41 ± 3 anomalies among the top 2000 ranked transient sources detected. Ref. [138] used the ELAsTiCC26 streaming dataset and the binary classifier in Fink broker to divide the dataset into five categories: SN-like, Periodic, Non-periodic, Long, and Fast. They built a deep learning light curve classification framework using LSTM recurrent neural networks to evaluate the performance of SuperNNova (SNN), finding stable classification performance for SN-like and Periodic transients. e.g., predicting within this framework, CATS achieves more than 93% precision for all classes except long (83%), while the best-performing binary classifier reaches more than 98% precision and 99% completeness for periodic sources.

On the other hand, unsupervised algorithms also demonstrate strong application potential in the classification of transient sources. Ref. [139] used the unsupervised clustering method HDBSCAN27 [108] and the isolation forest algorithm in the ASTRONOMALY28 Python package to explore seven unknown transient sources and two types of stellar flares on second-to-hour time scales. For time-series and tabular data, the initial method [140] simplified the data to a 2D representation for classification using deep learning. In a departure from traditional methods, Transformers [141], a new deep learning architecture, were applied by [142] to the PLAsTiCC dataset to handle multivariate time-series data, achieving excellent performance metrics. Ref. [143] developed ATAT, composed of two Transformer models, overcoming the resource-intensive nature of feature engineering (FE) [144]. They processed input data in two branches: time modulation and quantile feature marker mechanism, training the ATAT model with different combinations of light curves, metadata, and features, pioneering multi-modal applications.

3.3. Beyond the Optical: Classification of Transients Across the Spectrum

Of course, the applications of machine learning in time-domain astronomy extend far beyond those described in Section 3.2. In fact, many contemporary research areas in astronomy—such as gravitational-wave waveform recognition [145], exoplanet detection [146], and galaxy morphology classification [147]—rely heavily on machine learning techniques. More broadly, any discipline that involves large-scale data analysis can benefit from these methods. A comprehensive review of all such applications is beyond the scope of this paper. Instead, in this section, we highlight selected advances that illustrate how machine learning has been applied to transient astronomy beyond supernova studies, with particular emphasis on research frontiers involving gamma-ray bursts (GRBs) and fast radio bursts (FRBs).

FRBs are highly energetic millisecond-duration astrophysical phenomena typically categorized as repeaters or nonrepeaters. However, observational limitations may result in misclassifications, potentially leading to a higher proportion of repeaters than currently identified. Therefore, machine learning has been widely applied to the detection and analysis of FRBs [148,149,150,151,152,153,154]. With the first CHIME/FRB catalog, Refs. [155,156] identified 188 and 117 repeater candidates from 474 apparently nonrepeating FRBs through unsupervised learning, respectively. Ref. [157] reported 145 repeaters using FRB morphology as features, while [158] identified dozens of repeater candidates with various supervised learning methods. Moreover, refs. [158] found that brightness temperature and rest-frame frequency bandwidth are the most significant factors distinguishing repeaters from nonrepeaters, whereas refs. [159] suggested that spectral running may also play an important role. Some of the authors of this manuscript have also applied machine learning with 16 physical features to identify over a hundred repeater candidates, revealing distinct empirical relations between repeating and nonrepeating clusters, with all parameters in these empirical relations being mutually independent [160]. In addition, machine learning has been used to classify thousands of bursts from highly active repeaters, such as FRB 20121102 [161] and FRB 20201124A [162], in order to probe their possible radiation mechanisms.

GRBs are among the most energetic explosions in the universe, occurring in distant galaxies and outshining virtually all other astrophysical phenomena. They represent the brightest and most powerful class of cosmic transients, releasing immense amounts of energy within short timescales. GRBs exhibit durations that range from a few milliseconds to several hours and are conventionally classified into two populations based on their burst duration: short GRBs (≤2 s), which are typically associated with compact binary mergers, and long GRBs (≥2 s), which are generally linked to the collapse of massive stars [163]. However, in recent years, it has become increasingly clear that the traditional classification of GRBs by burst duration is not always reliable. A growing number of GRB events challenge this dichotomy. For example, according to standard theory, short GRBs are associated with compact binary mergers, which naturally produce r-process nucleosynthesis and are accompanied by kilonova emission. Yet, several long GRBs have recently been observed with candidate kilonova counterparts, e.g., GRB 191019A [164], GRB 211211A [165] and GRB 230307A [166]. This is puzzling, since long GRBs are thought to originate from the collapse of massive stars, a process typically accompanied by core-collapse SNe rather than kilonovae. These unexpected associations have raised serious questions about the adequacy of the duration-based classification scheme. In this context, applying machine learning algorithms to raw GRB data may provide new insights and reveal more physically motivated categories. Ref. [167] used dimensionality reduction algorithms t-SNE and UMAP based on four observational parameters (duration, peak energy, radiated energy and peak flux) to classify Fermi GRBs into two categories. They found that GRBs associated with kilonovae all belonged to Category I (except GRB 211211A [168] and GRB 230307A [169]), but this classification did not have a clear boundary compared to the traditional long–short classification. Ref. [170] proposed ClassiPyGRB, a machine learning-based tool for GRB classification and visualization. This tool uses the t-SNE algorithm for dimensionality reduction and visualization of GRB data, significantly improving the accuracy and efficiency of GRB classification. In the future, further integration of deep learning techniques and more complex feature engineering methods is expected to enhance classification outcomes further.

4. Future Directions and Challenges

As detailed above, while the application of ML and AI has already transformed time-domain astronomy, several important challenges and opportunities lie ahead. Here, we outline key directions for future research, emphasizing both the scientific potential and the technical barriers that must be addressed.

First, the classification of transients from photometric light curves remains a central task. Although supervised models trained on well-curated datasets (e.g., SNPhotCC and PLAsTiCC) have demonstrated promising results, their performance is often limited by incomplete or sparsely sampled light curves. Recent work, such as astrorapid, has shown that deep recurrent networks can achieve near-spectroscopic performance when light curves are densely sampled across multiple bands. However, in practice, early-phase SEDs are scarce, leaving significant uncertainties in classification. Large-scale, indiscriminate spectroscopic campaigns (e.g., LAMOST, 7DT) are one strategy, but resource constraints mean that ML-based classification from limited data will continue to play a critical role.

Second, the integration of multimodal data is an emerging frontier. Rather than relying solely on photometry, future systems will need to incorporate images, contextual metadata, and spectra into unified frameworks. For example, the AppleCiDEr system [171] combines photometry, image cutouts, metadata, and spectra to improve early classification performance, even for rare transients. Similarly, LAISS [172] leverages host-galaxy environment variables in addition to light curve features to identify anomalous transients in real-time through the ANTARES broker. These approaches demonstrate the power of multimodal integration in uncovering rare and scientifically valuable events.

Third, anomaly detection will remain a vital tool for discovering new classes of astrophysical phenomena. Traditional supervised classifiers are inherently biased toward known types, whereas unsupervised or semi-supervised methods can highlight sources that deviate from expectations. Multi-Class Isolation Forest (MCIF) [137] has shown excellent performance in surfacing rare transients such as kilonovae and unstable SNe from ZTF-like datasets. Similarly, LAISS has demonstrated the potential of combining anomaly detection with contextual filtering to reveal unclassified transients missed by conventional pipelines.

Fourth, real-time scalability is an urgent challenge in the LSST era, when tens of millions of alerts will be generated each night. Efficient algorithms for streaming data are critical to enable low-latency classification and follow-up. Efforts such as FINK’s kilonova science module [173] and representation-learning searches for fast X-ray transients in archival data [174] showcase how specialized modules and deep learning approaches can push real-time anomaly detection to new regimes. Looking forward, optimizing deep architectures (e.g., transformers, graph-based models) for irregular, sparse, and multimodal data streams will be essential.

Finally, interpretability and reproducibility remain key scientific concerns. While deep learning has proven powerful, its “black box” nature risks reducing trust in results. Transparent algorithms, uncertainty quantification, and community benchmarks will be critical for ensuring robustness. Furthermore, systematic biases—such as uneven sky coverage, incomplete spectroscopic training sets, or differences in host-galaxy populations—must be carefully addressed to prevent misleading scientific conclusions.

In summary, the future of AI in time-domain astronomy lies in multimodal integration, robust anomaly detection, real-time scalability, and transparent interpretability. With ongoing advances, AI will not only accelerate the discovery of known transients but also unlock entirely new classes of astrophysical phenomena, driving the field into an era of discovery that matches the unprecedented scale of upcoming surveys.

5. Conclusions

Artificial intelligence, particularly machine learning and deep learning technologies, has significantly enhanced the efficiency of transient event detection and classification in time-domain astronomy. By automating data processing and enabling rapid analysis, AI not only alleviates the workload of astronomers but also provides powerful tools for faster and more accurate exploration of the universe. This review paper discusses the transformative applications of AI in time-domain astronomy, especially its potential in processing and analyzing vast amounts of astronomical data. As the demand for research on transient celestial objects continues to grow, AI technologies have become indispensable for identifying, classifying, and predicting astronomical events. The case of SN 2023tyk particularly illustrates how AI has achieved the discovery and classification of transient objects without human intervention. Looking ahead, as data volumes continue to increase and technologies advance, the prospects for AI applications in time-domain astronomy are promising. However, challenges such as algorithm reliability, interpretability, and fairness also need to be addressed. By further integrating multimodal data, enhancing real-time processing capabilities, and developing automated systems, time-domain astronomy is poised to transcend traditional research methods, revealing more of the universe’s mysteries and advancing the field of astronomy further.