Models of Charged Gravastars in f(T)-Gravity

Abstract

This study investigates three distinct charged gravastar models within the framework of $f\left(T\right)$ modified gravity, considering the functional forms $f\left(T\right)=T$, $f\left(T\right)=a+bT$, and $f\left(T\right)=T^2$. Inspired by the Mazur–Mottola conjecture, we propose these models as singularity-free alternatives to black holes, each characterized by a three-region structure: (i) an interior de Sitter core, (ii) an intermediate thin shell composed of ultrarelativistic matter, and (iii) an exterior region described by the Reisner Nordstrom solution and other novel spherically symmetric vacuum solutions. We derive a complete set of exact, singularity-free solutions for the charged gravastar configuration, demonstrating their mathematical consistency and physical viability in the context of alternative gravity theories. Notably, the field equations governing the thin shell are solved using an innovative approach based on Killing vector symmetries, eliminating the need for approximations commonly employed in prior studies. Furthermore, we analyze key physical properties of the thin shell, including its proper length, entropy distribution, and energy content. A thorough examination of the energy conditions reveals the thermodynamic stability and viability of these models. Our results contribute to the growing body of work on exotic compact objects and provide new insights into the interplay between modified gravity, electromagnetism, and non-singular black hole alternatives.

1. Introduction

In 2001, Mazur and Mottola [1,2] proposed a novel solution for gravitationally collapsing neutral systems by applying the concept of Bose–Einstein condensation to gravitational systems. Their solutions describe super compact, spherically symmetric objects devoid of singularities, with densities approaching those of black holes. This class of gravitationally dark, cold vacuum compact objects, termed charged gravastar model (CGM), serves as an alternative to black holes by eliminating event horizons while maintaining extreme compactness. Notably, quantum vacuum fluctuations are expected to arise near the would-be event horizon in such configurations. The structure of a CGM consists of three distinct regions: (i) an interior de Sitter condensate phase, (ii) an intermediate shell region, and (iii) an exterior Reisner Nordstrom geometry. Extensive research on CGMs has been conducted within Einstein’s general relativity. DeBenedictis et al. [3] derived solutions with continuous pressures and equations of state, while Bilic et al. [4] explored Born-Infeld phantom CGMs. Higher-dimensional extensions of these models were examined in [5,6,7,8], and Cattoen et al. [9] investigated the role of anisotropic pressure in gravastar formation. Additionally, studies on conformal motion in CGMs have been pursued in [6,10,11], with further analyses of their physical characteristics presented in [6,7,10,12,13,14,15,16]. Stability aspects have also been extensively discussed in [17,18,19,20,21]. Beyond general relativity, modified gravity theories such as f(R) gravity [22,23,24,25] and f(R,T) gravity [26,27] where the gravitational action depends on the Ricci scalar R and the trace of the energy-momentum tensor T have been explored. Harko et al. [26] formulated f(R,T) gravity, introducing a coupling between geometry and matter. Visser and Wiltshire [28] examined the thermodynamic stability of gravastars, demonstrating how the shell’s equation of state affects collapse prevention. Carter [29] developed a new class of solutions incorporating superconducting phase transitions at the shell boundary. Chirenti and Rezzolla [30] proved that rotating gravastars can be distinguished from Kerr black holes through their distinctive gravitational wave signatures. Pani et al. [31] calculated the quasi-normal modes of spinning gravastars, providing observable criteria for detection. Cardoso et al. [32] established observational limits using black hole shadow measurements from EHT data. Abramowicz et al. [33] analyzed accretion disk properties, showing gravastars produce distinct X-ray spectra compared to black holes. Lobo and Arellano [34] explored wormhole-gravastar hybrids supported by nonlinear electrodynamics. Rocha et al. [35] investigated multi-layer gravastar models with alternating phantom and normal matter regions. Houndjo et al. [36] derived new gravastar solutions in f(G) Gauss-Bonnet gravity. Sharif and Waseem [37] analyzed CGMs in braneworld scenarios with extra dimensions. A parallel approach in teleparallel gravity, where the Lagrangian depends on the torsion scalar T, leads to f(T) gravity [38,39,40,41,42,43]. This framework reproduces Einstein’s field equations in metric-compatible scenarios while allowing for novel gravitational effects. Static spherically symmetric solutions with charged sources in f(T) gravity were derived in [44], and an f(T)-based adaptation of BTZ black holes was presented in [45]. The choice of f(T) gravity for modeling CGMs is motivated by its ability to incorporate nonlinear geometric-matter interactions, offering new insights into stability, dark energy, and compact object structure. Unlike curvature-based modifications, f(T) gravity operates through torsion, providing a distinct perspective on gravitational dynamics. Recently, Bakry et al. [46] extended this framework to f(R,Σ,T) gravity, where Σ denotes the torsion scalar, further generalizing the action to include both curvature and torsion. Subsequent studies [47,48,49,50,51,52,53,54,55] have explored CGMs within this enriched theoretical landscape, highlighting the interplay between geometry, matter, and torsion in ultracompact objects. The purpose of this article is to investigate charged gravastars in an excited state to address the physical defects associated with black holes. This study explores the complex interactions between gravitational phenomena and the distinct features of black holes, with the goal of identifying potential solutions to the anomalies linked to them. By examining the behavior of these excited gravitational stars, we aim to deepen our understanding of the fundamental physics involved and assess how these stellar structures can alleviate or correct the physical imperfections found in black holes. This comprehensive analysis will shed light on the mechanisms involved. This study is organized as follows: Section 2 provides a concise review of f(T) gravity in the presence of an electromagnetic field, establishing the theoretical foundation for our analysis. Section 3 focuses on tetrad formalism, covering fundamental principles and the derivation of Killing vectors essential for the subsequent gravitational field equations. Section 4 presents the general field equations governing the CGM, subdivided into three key regions: Section 4.1 derives the solution for the interior region of the CGM. Section 4.2 examines the solution for the thin shell region, characterized by ultrarelativistic matter. Section 4.3 discusses the solution for the exterior spacetime, described by a charged asymptotically flat geometry. Section 4.4 The proper length of the thin shell. Section 4.5: The entropy distribution within the shell. Section 4.6: The energy conditions constraining the matter content of the shell. Section 5 examines the junction conditions required for smoothly matching the interior, shell, and exterior spacetimes. Section 6 concludes with a summary of key findings, implications, and potential avenues for future research. This version maintains clarity, academic rigor, and readability while ensuring the original reference numbering remains intact.

2. Theoretical Foundations of f(T) Gravity

This section presents the fundamental mathematical structure of f(T) gravity, establishing the key equations and geometric formalism that underpin our analysis of CGMs. The theory is constructed using a vierbein (tetrad) field ${e_i}^{\mu }$, relating spacetime coordinates to the tangent space. The metric compatibility condition [56] is as follows:

$$\begin{gathered} d{s}^2= g_{\alpha \beta } d{x}^{\alpha }d{x}^{\beta }, g_{\mu \nu }={\eta }_{i j} {e^i}_{\mu } {e^j}_{\nu } , g_{\mu \nu }={\eta }_{i j} {e^i}_{\mu } {e^j}_{\nu } , \\ {e^i}_{\mu } {e_i}^{\nu }={\delta }_{\mu }^{\nu }, {e^i}_{\mu } {e_j}^{\mu }={\delta }_b^a, \mathrm{and} {\eta }_{i j} =dig(+, -, -, -). \end{gathered}$$

(1)

The torsion tensor [57] is

$${T^{\gamma }}_{\beta \alpha }={{\Gamma }^{\gamma }}_{\beta \alpha }-{{\Gamma }^{\gamma }}_{\alpha \beta }=-{T^{\gamma }}_{\beta \alpha }.$$

(2)

The torsion Scalar [58] is

$$T={S_{\alpha }}^{\beta \nu } {T^{\alpha }}_{\beta \nu }={\displaystyle \frac{1}{4}}{T}^{\rho \mu \nu }{T}_{\rho \mu \nu }+{\displaystyle \frac{1}{2}}{T}^{\rho \mu \nu }{T}_{\nu \mu \rho }-{T^{\mu }}_{\alpha \mu } {T^{\nu \alpha }}_{\nu },$$

(3)

where the tensor ${S_{\alpha }}^{\beta \nu }$ can be defined as follows [22]:

$$S_{\alpha }^{.\beta \nu }={\displaystyle \frac{1}{2}}(K_{. . \alpha }^{\beta \nu }+{\delta }_{\alpha }^{\beta } {T^{\mu \nu }}_{\mu }-{\delta }_{\alpha }^{\nu } {T^{\mu \beta }}_{\mu }).$$

(4)

$f\left(T\right)$ gravity is a modern theory of gravity that represents a significant extension of Einstein’s General Theory of Relativity. Its core idea is to modify how we describe the geometry of spacetime to explain the universe’s observed acceleration without needing a mysterious “dark energy” component. The key concept revolves around Torsion $T$. Instead of using Einstein’s description of gravity, which is based on the curvature of spacetime (where the paths of particles are bent by mass), $f\left(T\right)$ gravity uses a framework where torsion is the fundamental property. In simple terms, while curvature tells us how a vector rotates when parallel transported around a loop, torsion relates to the twisting of the spacetime fabric itself. In this theory, gravitational action is a general function $f$ of the torsion scalar $T$ (hence the name $f\left(T\right)$). This allows for a more flexible and general description of gravity. By choosing specific forms for the function $f\left(T\right)$, the theory can naturally produce a period of accelerated expansion in the universe’s history. In summary, $f\left(T\right)$ gravity is an alternative approach to gravity that: Replaces the concept of spacetime curvature with torsion as the primary descriptor.

The modified action in f(T) gravity [57,59] is

$$L={\displaystyle \int \frac{1}{16\pi }e f(T)d{x}^4}+{\displaystyle \int l_m e d{x}^4},$$

(5)

with $e=\sqrt{-g}$ is the determinant of the tetrad ${e_i}^{\mu }$ and ${\mathcal{l}}_m$ as the electromagnetic Lagrangian.

The gravitational field equations governing our system are obtained through variational principles applied to the action (5). The fundamental mathematical procedure involves

$$\delta L ={\displaystyle \int \frac{1}{16 \pi }(f_T e \delta T+f \delta e )d{x}^4}+ \delta {\displaystyle \int l_m e d{x}^4},$$

(6)

where $f_T=\frac{d f}{d T}$.

One may assume that the Lagrangian density ${\mathcal{l}}_m$ of the matter depends exclusively on the components of the metric tensor $g_{\alpha \beta }$, rather than on its derivatives. Consequently, one obtains [57,60].

A critical assumption in our framework is that the matter Lagrangian density ${\mathcal{l}}_m$ depends only on the metric components $g_{\alpha \beta }$, not on their derivatives. This leads to the following important consequences:

$$\delta S_m={\displaystyle \int \delta (e{l}_m)d{x}^4}=-{\displaystyle \int e {\mathcal{T}}_{\alpha }^{\nu } {e_i}^{\alpha }\delta {e^i}_{\nu } d{x}^4},$$

(7)

where ${\mathcal{T}}_{\alpha }^{\nu }$ is the symmetric energy-momentum tensor.

This treatment aligns with established approaches in modified gravity theories, as discussed in [57,60]. The stress-energy content of our system is characterized by two fundamental contributions, For the isotropic matter distribution, we employ the standard perfect fluid form [61]

$${{\mathcal{T}}_{\mu }^{\nu }}^{matter} =(\rho +p) u_{\mu }{u}^{\nu }-p {\delta }_{\mu }^{\nu },$$

(8)

where the energy density $\rho$ and isotropic pressure $p$ are referred to as dynamical quantities, $u_{\mu }$ is the fluid-four velocity vector, $u_{\mu }{u}^{\mu }=1$.

The Maxwell field contributes through [62]

$${{\mathcal{T}}_{\alpha \beta }}^{matter}=-{\displaystyle \frac{1}{4\pi }}\left(F_{\alpha }^{\gamma } F_{\beta \gamma }-{\displaystyle \frac{1}{4}}{g}_{\alpha \beta }{F}^{\gamma \sigma }{F}_{\gamma \sigma }\right),$$

(9)

where

$$F_{\mu \nu }={\displaystyle \frac{\partial {\phi }^{\nu }}{\partial x^{\mu }}}-{\displaystyle \frac{\partial {\phi }^{\mu }}{\partial x^{\nu }}}$$

(10)

is the electromagnetic field tensor.

Combining these variations and applying the principle of least action produces the complete field equations: [57,63,64,65]:

$$S_{\sigma }^{.\nu \mu } f_{T T}{\partial }_{\mu }T+e^{-1} {\partial }_{\mu }( e {S_i}^{\nu \mu }) f_T-{T^{\rho }}_{\mu i} {S_{\rho }}^{\mu \nu } f_T+{\displaystyle \frac{1}{4}}f {e_i}^{\nu }= 4\pi {\mathcal{T}}_i^{\nu } ,$$

(11)

where $f_{TT}={\displaystyle \frac{{\partial }^{2}f}{\partial T^2}}$.

This variational approach provides a rigorous foundation for the modified gravitational dynamics in our subsequent analysis of CGM solutions. The field equations reduce to teleparallel equivalent of GR when f(T) = T, while allowing for richer phenomenology in the general nonlinear case.

3. Tetrad Vectors and Conformal Killing Vectors (CKVs): Fundamental Concepts

Tetrads, also known as vierbein or frame fields, constitute a set of four linearly independent vector fields ${e_i}^{\mu }$ defined at each point in a spacetime manifold [66]. They establish a local mapping between: The curved spacetime metric $g_{\alpha \beta }$ (general relativity) and the flat Minkowski metric ${\eta }_{ij}$ (special relativity). For spherically symmetric spacetimes, a common covariant tetrad choice is [66]

$$\left({e^i}_{\mu }\right)=\mathrm{diag}\left(e^{\nu },e^{\lambda } r, r\sin \theta \right),$$

(12)

where $e^{\upsilon }$ and $e^{\lambda }$ are metric functions.

From (1) and (12), one can get the contravariant tetrad as given by

$$\left({e_i}^{\mu }\right)=\mathrm{diag}\left(e^{-\nu },e^{-\lambda }, {\displaystyle \frac{1}{r}} , {\displaystyle \frac{1}{r \sin \theta }}\right).$$

(13)

Substituting the expressions from Equation (13) into Equation (1) yields the following outcome:

$$d{s}^2= e^{2\nu } d{t}^2-e^{2\lambda } d{r}^2-r^2 (d{\theta }^2+{\sin }^2\theta d{\varphi }^2),$$

(14)

where $\nu$ and $\lambda$ are determined as a function of $r$.

When we replace the expressions in Equation (2) with those from Equations (12) and (13), we arrive at the following result:

$${T^0}_{10}=-{T^0}_{01}={\nu }^{\prime }, {T^2}_{12}={T^3}_{13}=-{T^2}_{21}=-{T^3}_{31}=(1-e^{\lambda })/r.$$

(15)

The following result is obtained by substituting the expressions from Equation (12) into Equation (4):

$$\begin{gathered} {K^0}_{10}=-{\nu }^{\prime }, {K^1}_{00}=-{\nu }^{\prime }{e}^{2(\nu -\lambda )}, {K^1}_{22}=r e^{-2\lambda }, {K^1}_{33}= r {\sin }^2\theta e^{-2\lambda }, \\ {K^2}_{12}={K^3}_{13}={\displaystyle \frac{-1}{r}}, {K^2}_{33}=\sin \theta \cos \theta , {K^3}_{23}=-\cot \theta . \end{gathered}$$

(16)

By substituting Equations (19) and (20) into Equation (7), one derives

$$\begin{gathered} {S_1}^{21}={S_0}^{20} =-{S_1}^{1 2}=-{S_0}^{02}=\frac{\cot \theta }{2 r^2}, {S_0}^{10}={S_0}^{01}=\frac{1}{r}{e}^{-2\lambda }, \\ {S_2}^{12}={S_3}^{13}=-{S_2}^{21}= -{S_3}^{31}=\frac{1}{2r}{e}^{-2\lambda }(1+2r{\nu }^{\prime }). \end{gathered}$$

(17)

By substituting Equations (19) and (20) into Equations (8) and (17), one obtains the torsion scalar $T$, which is expressed as follows:

$$T=\frac{2}{r^2} e^{-2\lambda }(1+2r{\nu }^{\prime }),$$

(18)

$$e=\sqrt{-g}=e^{(\nu +\lambda )}{r}^2 \sin \theta .$$

(19)

The torsion scalar $T$ is derived from the tetrad fields, which act as the fundamental variables in this formulation. This scalar encapsulates the geometric properties of spacetime, providing an alternative framework to GR. From Equation (8), the energy-momentum tensor is given by the following expression:

$${\mathcal{T}}_0^0=\rho , {\mathcal{T}}_1^1={\mathcal{T}}_2^2={\mathcal{T}}_3^3=-p, \mathcal{T}=\rho -3p.$$

(20)

A CKVs ${\xi }^{\mu }$ preserves the metric up to a conformal factor $\psi \left(x\right)$ [67,68]:

$$L_{\xi } g_{\mu \nu }={\xi }_{\mu ;\nu }+{\xi }_{\mu ;\nu }=\psi g_{\mu \nu },$$

(21)

where $L_{\xi }$ denotes the Lie derivative operator.

Suppose ${\xi }^{\mu } = {\xi }^{\mu }(r)$, by using (14) and (21), we get

$${\xi }^1=\frac{1}{2} r \psi ,{\xi }^2=0, {\xi }^3=d_1, {\xi }^0=d_2,$$

(22)

$${\lambda }^{\prime } {\xi }^1+\frac{d{\xi }^1}{dr}=\frac{1}{2} \psi , {\nu }^{\prime } {\xi }^1= \frac{1}{2}\psi ,$$

(23)

where $d_1$ and $d_2$ are integration constants

Upon solving Equations (22) and (23), one gets

$${\mathrm{e}}^{2\nu }=c_1 r^2, {\mathrm{e}}^{2\lambda }={\displaystyle \frac{c_2}{{\psi }^2}},$$

(24)

where $c_1$ and $c_2$ are constants.

4. The General Einstein–Maxwell Equations (EME) of the Field

The field equations are obtained by varying the action (7), This leads to modified Einstein-like equations that account for the effects of torsion. By substituting Equations (9), (12), (15) and (17)–(20) into Equation (11), the electromagnetic equations simplify to the form where G = c = 1 [69,70]:

$$-\frac{2}{r}{e}^{-2\lambda }{f}_{TT}{\displaystyle \frac{dT}{dr}} -f_T (T-\frac{1}{r^2}-\frac{2}{r}{e}^{-2\lambda }({\lambda }^{\prime }+{\nu }^{\prime }))+\frac{1}{2}f= 8\pi (\rho +{\displaystyle \frac{E^2}{8\pi }})$$

(25)

$$(T-\frac{1}{r^2}) f_T-\frac{1}{2}f=8\pi (p-{\displaystyle \frac{E^2}{8\pi }}).$$

(26)

$$\begin{array}{l}\frac{1}{r}{e}^{-2\lambda }(1+r{\nu }^{\prime }){\displaystyle \frac{dT}{dr}}{f}_{TT}+\frac{T}{2}{f}_T+e^{-2\lambda }{f}_T( {\nu }^{″}+{\displaystyle \frac{1}{r}}(1+r {\nu }^{\prime })({\nu }^{\prime }-{\lambda }^{\prime }))\\ \hfill -\frac{1}{2}f=8\pi (p+{\displaystyle \frac{E^2}{8\pi }})\end{array}$$

(27)

$${\displaystyle \frac{\cot \theta }{2r^2}} {\displaystyle \frac{dT}{dr}} e^{-2\lambda }{f}_{TT} = 0.$$

(28)

By performing covariant differentiation on both sides of Equation (11), one obtains [71]

$${\displaystyle \frac{dp}{dr}}+{\nu }^{\prime }(p+\rho )= 0, ,$$

(29)

$${\displaystyle \frac{1}{8\pi r^4}}{\displaystyle \frac{d(r^4{E}^2)}{dr}}=0, E=\pm {\displaystyle \frac{cons.}{r^2}}.$$

(30)

A gravastar is a hypothetical compact object, proposed as an alternative to black holes, whose exotic structure challenges conventional applications of conservation laws [71]. Rather than violating these principles, a gravastar satisfies them through a complex internal equilibrium. The model consists of a core of dark energy a vacuum state with repulsive negative pressure encased within an infinitesimally thin, ultra-rigid shell. The conservation of energy-stress requires that the immense outward pressure from the interior is exactly balanced by the extreme tension within the shell. This prevents gravitational collapse into a singularity while also avoiding explosive disintegration. Thus, the stability of a gravastar is not governed by simple fluid conservation, but by a precise interplay between three distinct elements: the repulsive dark energy core, the tensile stresses in the boundary shell, and the overall gravitational field binding the structure together. This balance is formally expressed by applying covariant differentiation to the field equations, leading to the conservation condition given in Equation (29), see Ref. [71].

The electric field E is as follows [70]:

$$E={\displaystyle \frac{1}{r^2}}{\displaystyle \underset{0}{\overset{r}{\int }}4\pi r^2\sigma (r) e^{\lambda }} dr={\displaystyle \frac{Q}{r^2}}.$$

(31)

Let $Q$ be the total charge be enclosed within a sphere of radius $r,$ and let the term $\sigma (r) e^{\lambda }$ in Equation (31) represent the volume charge density. For simplicity in calculations, we assume $o\left(r\right)e^{\lambda }={\sigma }_0{r}^n$, following [71], that

$$E=E_0{r}^{n+1},$$

(32)

where n > 0 is a constant and $E_0={\displaystyle \frac{4\pi {\sigma }_0}{n+3}}$.

$f\left(T\right)$ gravity is a modification of general relativity based on the torsion scalar $T$, derived from the Weitzenböck connectioninstead of spacetime curvature. The gravitational action in this theory is a function $f\left(T\right)$, allowing richer dynamics than standard gravity. A notable consequence is the non-conservation of the energy-momentum tensor, offering alternative cosmological explanations including accelerated cosmic expansion without invoking dark energy.

The fundamental function considered in this study is expressed in its general form as

$$f(T)=a+b{T}^{\beta },$$

(33)

where $a$ and $b$ are constants, and $\beta$ is a dimensionless parameter.

By substituting the function from Equation (33) into Equations (25)–(28), the field equations are expressed as follows:

$$\begin{array}{l}-2\frac{b\beta (\beta -1)}{r}{e}^{-2\lambda }{T}^{\beta -2}{\displaystyle \frac{dT}{dr}}-b\beta T^{\beta -1} (T-\frac{1}{r^2}-\frac{2}{r}{e}^{-2\lambda }({\lambda }^{\prime }+{\nu }^{\prime }))\\ +\frac{1}{2}(a+b{T}^{\beta })=8\pi (\rho +{\displaystyle \frac{E^2}{8\pi }}),\end{array}$$

(34)

$$b \beta T^{\beta -1}(T-\frac{1}{r^2})-\frac{1}{2}(a+b{T}^{\beta } )=8\pi ( p-{\displaystyle \frac{E^2}{8\pi }}),$$

(35)

$$\begin{array}{l}\frac{b \beta (\beta -1)}{r}{e}^{-2\lambda }(1+r {\nu }^{\prime }) T^{\beta -2}{\displaystyle \frac{dT}{dr}}+{\displaystyle \frac{b}{2}}\beta T^{\beta }+b \beta e^{-2\lambda } T^{\beta -1} ({\nu }^{″}+{\displaystyle \frac{1}{r}}(1+r {\nu }^{\prime })({\nu }^{\prime }-{\lambda }^{\prime }))-\\ \frac{1}{2}(a+b T^{\beta })=8\pi ( p+{\displaystyle \frac{E^2}{8\pi }})\end{array}$$

(36)

$${\displaystyle \frac{b \beta (\beta -1) \cot \theta e^{-2\lambda }}{r^2}}{T}^{\beta -2}{\displaystyle \frac{dT}{dr}}=0.$$

(37)

The gravitational mass can be expressed as follows [7]:

$$M={\displaystyle \underset{0}{\overset{r}{\int }}4\pi r^2(\rho +\frac{E^2}{8\pi }}) dr.$$

(38)

In the following sections, we explore CGMs parameterized by $\beta$. Beginning with the case $f\left(T\right)=T$, we derive the corresponding field equations and verify their equivalence to GR confirming the theoretical consistency between teleparallel gravity and GR [58]. This specific case represents the Teleparallel Equivalent of General Relativity (TEGR). This framework preserves: Manifest covariance (coordinate independence) and Local Lorentz invariance (observer independence at infinitesimal scales). By substituting $\beta =1$ into Equations (34)–(37), we further generalize the field equations to $f\left(T\right)=a+bT$ gravity [58]. A critical focus of this work lies in quadratic $f\left(T\right)$ models, where $f\left(T\right)=T^2$, which offer nonlinear torsion terms enable richer solutions (e.g., wormholes, exotic compact objects) beyond linear GR. These features position $f\left(T\right)$ gravity as a viable alternative to GR, particularly in extreme regimes (e.g., early universe, black hole interiors).

4.1. Analytical Solutions for the Interior Field Equations $f(T)=a+b{T}^{\beta }$ Gravity

The equation of state (EoS) for the interior region at $(0\le r<r_1)$ is defined as the dark energy $p = - \rho$ within this region, as referenced in [1,2,65],

In this context, Equation (32) yields

$$p=-\rho =-{\rho }_0=const.$$

(39)

By substituting from Equation (39) into Equations (34) and (35), one obtains

$$\begin{array}{l}-2\frac{b \beta (\beta -1)}{r}{e}^{-2\lambda } T^{\beta -2}{\displaystyle \frac{dT}{dr}}-b \beta T^{\beta -1} (T-\frac{1}{r^2}-\frac{2}{r}{e}^{-2\lambda }({\lambda }^{\prime }+{\nu }^{\prime }))\\ +\frac{1}{2}(a+b T^{\beta })=8\pi ({\rho }_0+{\displaystyle \frac{E^2}{8\pi }}),\end{array}$$

(40)

$$b \beta T^{\beta -1}( T-\frac{1}{r^2})-\frac{1}{2}(a+b{T}^{\beta } )=-8\pi ({\rho }_0+{\displaystyle \frac{E^2}{8\pi }}),.$$

(41)

By adding Equation (40) to Equation (41) and then performing the integration, we obtain

$${\nu }^{\prime }=-{\lambda }^{\prime }-{\displaystyle \frac{(1-\beta )}{T}} {\displaystyle \frac{dT}{dr}},$$

(42)

Next, we will examine three specific cases.

• We will proceed to analyze the first scenario when $a=0, b=\beta =1 and f(T)=T$,

In this case, Equations (41) and (42) take the following forms

$$e^{-2\lambda }\left(r({\nu }^{\prime }-{\lambda }^{\prime })+r^2( {\nu }^{″}+{\nu }^{\prime 2}-{\lambda }^{\prime }{\nu }^{\prime })\right)=-8\pi r^2({\rho }_0-{\displaystyle \frac{E^2}{8\pi }}).$$

(43)

$${\nu }^{\prime }=-{\lambda }^{\prime },$$

(44)

Substituting from Equations (41) and (42) in (43), we obtain

$$\left(-2r{\lambda }^{\prime }-r^2 {\lambda }^{″}+2r^2 {{\lambda }^{\prime }}^2\right)e^{-2\lambda }=-8\pi r^2( {\rho }_0-{\displaystyle \frac{E_0^2 r^{2n+2}}{8\pi }}),.$$

(45)

An equivalent representation of Equation (45) takes the form

$${\displaystyle \frac{d^2 (r{e}^{-2\lambda })}{d{r}^2}}=-16\pi r( {\rho }_0-{\displaystyle \frac{E_0^2 r^{2n+2}}{8\pi }}),.$$

(46)

From Equation (46), the metric potential λ can be determined as follows:

$$e^{-2\lambda }={\displaystyle \frac{K_2}{r}}-{\displaystyle \frac{8\pi {\rho }_0{r}^2}{3}}+{\displaystyle \frac{4 E_0^2 r^{2n+3}}{\left(2n+3\right)\left(n+2\right)}}+K_1,$$

(47)

given that $K_1=1,$ to ensure regular behavior at the center $\left(\mathrm{r} = 0\right)$, we impose $K_2= 0$. This regularity condition leads to the following form of Equation (47):

$$e^{-2\lambda }=1-{\displaystyle \frac{8\pi {\rho }_0{r}^2}{3}}+{\displaystyle \frac{4 Q^2}{\left(2n+3\right)\left(n+2\right)r^3}}.$$

(48)

In the case of the interior region, when f(T) =T, the line element can be expressed in the following form

$$d{s}_{\mathrm{int}.}^2= W(r) d{t}^2- W{(r)}^{-1} d{r}^2-(r^{2}d{\theta }^2+r^2{\sin }^2\theta d{\varphi }^2),$$

(49)

where

$$W(r) =\left(1-{\displaystyle \frac{8\pi {\rho }_0}{3}}{r}^2+{\displaystyle \frac{Q^2}{(2n+3)(n+2)r^3}}\right).$$

(50)

By substituting Equations (32) and (39) into Equation (38), The interior gravitational mass of the CGM is obtained as

$$M ={\displaystyle \underset{0}{\overset{r=D}{\int }}(4\pi {\rho }_0}{r}^2+{\displaystyle \frac{E_0^2{r}^{2n+4}}{2}}) dr.$$

(51)

By integrating the previous equation, we obtain

$$M={\displaystyle \frac{4\pi {\rho }_0}{3}}{r}^3+{\displaystyle \frac{E_0^2{r}^{2n+5}}{2(2n+5)}}.$$

(52)

• We will proceed to analyze the second scenario when:$\beta =1 \mathrm{and} f(T)=a + bT$, indicates that $f\left(T\right)$ is a linear function of the torsion scalar $T$. When $a=0$ and $b=1$, we revert to the standard $T$ model. In this scenario, the field equations align with those of the conventional Ricci scalar $\left(R\right)$ model.

In this case, Equations (34)–(36) take the following forms:

$${\displaystyle \frac{b e^{-2\lambda }}{r}} ( 2{\lambda }^{\prime }-{\displaystyle \frac{1}{r}}) +{\displaystyle \frac{a}{2}}+{\displaystyle \frac{b}{r^2}}=8\pi ( {\rho }_0+{\displaystyle \frac{E^2}{8\pi }}),$$

(53)

$${\displaystyle \frac{b e^{-2\lambda }}{r}} (2{\nu }^{\prime }+{\displaystyle \frac{1}{r}})-{\displaystyle \frac{a}{2}}-{\displaystyle \frac{b}{r^2}}=-8\pi ( {\rho }_0+{\displaystyle \frac{E^2}{8\pi }}),$$

(54)

$$b e^{-2\lambda }\left({\nu }^{″}+({\nu }^{\prime }+{\displaystyle \frac{1}{r}})({\nu }^{\prime }-{\lambda }^{\prime })\right)-{\displaystyle \frac{a}{2}}=-8\pi ( {\rho }_0-{\displaystyle \frac{E^2}{8\pi }}).$$

(55)

From Equations (53) and (54), we get

$${\nu }^{\prime }=-{\lambda }^{\prime },$$

(56)

$$e^{2\nu }=\overline{c} e^{-2\lambda },$$

(57)

Substituting from Equations (56) and (57) into Equation (55) yields

$${\displaystyle \frac{d^2 (r{e}^{-2\lambda })}{d{r}^2}}={\displaystyle \frac{a}{b}} r-{\displaystyle \frac{16\pi }{b}} r( {\rho }_0-{\displaystyle \frac{E_0^2{r}^{2n+2}}{8\pi }}),.$$

(58)

By integrating the previous equation, we get

$$e^{-2\lambda }={\displaystyle \frac{K_2}{r}}+\left({\displaystyle \frac{a}{6 b}}-{\displaystyle \frac{8\pi {\rho }_0}{3}}\right)r^2+{\displaystyle \frac{4 E_0^2 r^{2n+3}}{\left(2n+3\right)\left(n+2\right)}}+K_1.$$

(59)

Considering that $K_1=1$ and the regularity requirement at the origin (r = 0) is satisfied when K₂ = 0, yielding the simplified form of Equation (60) as follows:

$$e^{-2\lambda }=1+\left({\displaystyle \frac{a}{6 b}}-{\displaystyle \frac{8\pi {\rho }_0}{3}}\right)r^2+{\displaystyle \frac{4 E_0^2 r^{2n+3}}{\left(2n+3\right)\left(n+2\right)}},$$

(60)

In the case of the interior region in the case $f(T)=a + bT$, the line element takes the following form:

$$d{s}_{\mathrm{int}.}^2=\Psi (r)d{t}^2-\Psi {(r)}^{-1}d{r}^2-(r^{2}d{\theta }^2+r{\sin }^2\theta d{\phi }^2).$$

(61)

Here

$$\Psi (r)=1+({\displaystyle \frac{a}{6b}}-{\displaystyle \frac{8\pi {\rho }_0}{3b}}) r^2+{\displaystyle \frac{4 E_0^2 r^{2n+3}}{(2n+3)(n+2)}},.$$

(62)

In the second scenario, the gravitational mass has a value that is identical to that in the first scenario, as expressed by Equation (52).

• We will now move on to analyze the third scenario when $a=0,b=1, \beta =2 \mathrm{and} f\left(T\right)=T^2$.

In this case, Equations (34) and (35) can be expressed as follows:

$$-{\displaystyle \frac{4}{r}}{e}^{-2\lambda } {\displaystyle \frac{dT}{dr}}-2T (T-\frac{1}{r^2}-\frac{2}{r}{e}^{-2\lambda }({\lambda }^{\prime }+{\nu }^{\prime }))+\frac{1}{2} T^2= 8\pi ( {\rho }_0+{\displaystyle \frac{E^2}{8\pi }}),$$

(63)

$$2 T(T-\frac{1}{r^2})-\frac{1}{2}{T}^2 = -8\pi ( {\rho }_0+{\displaystyle \frac{E^2}{8\pi }}),.$$

(64)

Summing Equations (63) and (64), and subsequently integrating the resulting equation, we obtain

$${\displaystyle \frac{dT}{dr}}-T ({\lambda }^{\prime }+{\nu }^{\prime })= 0,.$$

(65)

In the next section, we will use the conformal killing vectors (27) to find solutions to the field equations, where

$${\mathrm{e}}^{ 2\nu }=c_1 r^2, {\nu }^{\prime }=1/r and {\mathrm{e}}^{-2\lambda } = {\psi }^2/c_2, {\lambda }^{\prime }={\psi }^{\prime }/\psi ,.$$

(66)

By substituting the values from Equation (66) into Equation (18), we derive the following result:

$$T={\displaystyle \frac{6 {\psi }^2}{c_{2}r}},.$$

(67)

Upon plugging in the expressions from Equations (66) and (67) into Equation (65), we arrive at the following outcome:

$${\psi }^{\prime }-{\displaystyle \frac{2 \psi }{r}}=0,.$$

(68)

Upon integrating the earlier equation, we arrive at the following expression:

$$\psi =c_3 r^2,.$$

(69)

By substituting from Equation (69) into Equations (66) and (67), we get

$${\mathrm{e}}^{ 2\nu }=c_1 r^2 and{\mathrm{e}}^{-2\lambda }=c_3^2 r^4/c_2,$$

(70)

$$T={\displaystyle \frac{6 c_3^2 r^3}{c_2}}=6c_4{r}^3,$$

(71)

where C₄ is an integration constant.

In the case of the interior region with $f\left(T\right)=T^2$, the line element is expressed in the following form:

$$d{s}_{\mathrm{int}.}^2=c_1{r}^2 d{t}^2-{\displaystyle \frac{c_4}{r^4}} d{r}^2-(r^{2}d{\theta }^2+r{\sin }^2\theta d{\varphi }^2).$$

(72)

In $f\left(T\right)=T^2$ model, we find that the solution to the field Equation (75) for the interior region exhibits a singularity at $r=0$. This singularity indicates that at $r=0$, the physical quantities involved, such as density or curvature, may become infinite or undefined. Such behavior typically suggests that the underlying spacetime structure is not well-defined at this point. As $r$ approaches zero, certain terms in the field equations may diverge, leading to singular behavior. This is often a result of how the equations are formulated and the nature of the functions involved. In physical terms, a singularity often indicates a breakdown of the laws of physics as we currently understand them. For example, it may signal the presence of an extreme gravitational field, such as that found at the center of a black hole. The singularity at $r=0$ suggests that the geometric structure of the spacetime becomes highly distorted, making it impossible to extend the solutions beyond this point in a meaningful way. In summary, the presence of a singularity at $r=0$ in this context highlights important challenges in both the mathematical formulation and physical interpretation of the solutions to the field equations.

4.2. Thin Shell Solution for the Gravitational Field Equations $f(T)=a+b{T}^{\beta }$

The EoS for the shell region describes the relationship between different thermodynamic quantities, such as pressure, density, and temperature, within that specific region. It provides crucial insights into the physical properties and behavior of the material in the shell, allowing us to understand how it responds to various conditions. The EoS is essential for modeling the dynamics and stability of the shell, particularly in contexts such as astrophysics or material science. EoS for the shell region is expressed as follows:

$$P=\rho , when r_1<r<r_2=r_1 +\epsilon .$$

(73)

Substituting the EoS from Equation (73) into the conservation law (29), we obtain the following result:

$$P=C_4 e^{-2\nu }.$$

(74)

Substituting from EoS (73) in the field Equations (34) and (35), we get

$$\begin{array}{l}-2\frac{b \beta (\beta -1)}{r}{e}^{-2\lambda } T^{\beta -2}{\displaystyle \frac{dT}{dr}}-b \beta T^{\beta -1} (T-\frac{1}{r^2}-\frac{2}{r}{e}^{-2\lambda }({\lambda }^{\prime }+{\nu }^{\prime }))\\ +\frac{1}{2}(a+b{T}^{\beta })=8\pi (\rho +{\displaystyle \frac{E^2}{8\pi }}),\end{array}$$

(75)

$$b \beta T^{\beta -1}(T-\frac{1}{r^2})-\frac{1}{2}(a+b{T}^{\beta } )=8\pi ( \rho -{\displaystyle \frac{E^2}{8\pi }}),.$$

(76)

In many studies, Equations (75) and (76) are typically solved using the approximation method [8,64,72]. However, in this context, we will utilize conformal Killing vectors (CKVs) for the solution. By substituting the expression from Equation (70) into Equation (74), we obtain the following result:

$$P=\rho =C_6/r^2,.$$

(77)

By adding Equations (75) and (76), we obtain the following result:

$$\frac{b \beta (\beta -1)}{r}{e}^{-2\lambda } T^{\beta -2}{\displaystyle \frac{dT}{dr}} -b \beta T^{\beta -1} ( \frac{1}{r}{e}^{-2\lambda }({\lambda }^{\prime }+{\nu }^{\prime }))= - 16\pi \rho ,.$$

(78)

Building upon our interior region investigation, we now systematically study the shell region through three parallel scenarios.

• We will proceed to analyze the first scenario when $a=0, b=\beta =1 \mathrm{and} f(T)=T$.

For the present case, Equation (78) reduces to

$$\frac{1}{r}{e}^{-2\lambda }({\lambda }^{\prime }+{\nu }^{\prime })=16\pi \rho ,.$$

(79)

By substituting the expression from Equations (70) and (77) into Equation (79), we obtain the following result:

$$r \psi {\psi }^{\prime }-{\psi }^2=-16\pi c_6{c}_2.$$

(80)

By solving (80), one gets

$${\psi }^2 = C_1 r^2+c_7,$$

(81)

where $c_7=16c_2{c}_6$ is constant.

Substituting from (81) in (24), we get

$${\mathrm{e}}^{ 2\nu }=c_1 r^2, {\mathrm{e}}^{ 2\lambda }={\displaystyle \frac{C_2}{C_7+C_1 r^2}}.$$

(82)

Using the interior solution, we calculate the gravitational mass M(r) contained within radius r of the CGM:

$$M={\displaystyle \underset{0}{\overset{r=D}{\int }}(4\pi c_6}+{\displaystyle \frac{E_0^2{r}^{2n+4}}{2}}) dr.$$

(83)

The integration of the earlier Equation (83) yields the following:

$$M=4 \pi c_{6}r+{\displaystyle \frac{E_0^2{r}^{2n+5}}{2(2n+5)}}.$$

(84)

For the $f\left(T\right)=T$ case, the metric tensor of the shell region is given by

$$d{s}_{shell.}^2= c_1{r}^2 d{t}^2-{\displaystyle \frac{C_2}{C_7+C_1 r^2}}d{r}^2-r^2(d{\theta }^2+{\sin }^2\theta d{\varphi }^2).$$

(85)

It is clear from the solutions that Equation (88) is free from central singularity.

• We will proceed to analyze the second scenario when $\beta =1 and f(T)=a + bT$,

In this scenario, Equation (79) assumes the following form:

$${\displaystyle \frac{b}{r}}{e}^{-2\lambda }({\lambda }^{\prime }+{\nu }^{\prime })=16\pi \rho ,.$$

(86)

By inserting the expressions from Equations (70) and (77) into Equation (86), we derive the following result:

$$r \psi {\psi }^{\prime }- {\psi }^2={\displaystyle \frac{16\pi c_6{c}_2}{b}}.$$

(87)

Solving Equation (88) leads to

$${\psi }^2=C_1 r^2+c_8,$$

(88)

where $c_8=(16c_2{c}_6)/b$ is a constant.

The following result is obtained by substituting the expressions from Equation (88) into Equation (24):

$${\mathrm{e}}^{ 2\nu }=c_1 r^2, {\mathrm{e}}^{2\lambda }={\displaystyle \frac{C_2}{C_8+C_1{r}^2}}.$$

(89)

In the framework of $f\left(T\right)=a+bT$ gravity, the shell region is characterized by the line element:

$$d{s}_{shell.}^2=c_1{r}^2 d{t}^2-({\displaystyle \frac{C_2}{C_8+C_1{r}^2}}) d{r}^2 -r^2 (d{\theta }^2+{\sin }^2\theta d{\varphi }^2).$$

(90)

From the solutions, it is apparent that line element (90) is free from any central singularity. Additionally, the gravitational mass is determined when $f\left(T\right)=a+bT$ is defined by Equation (84).

• We will now move on to analyze the third scenario when $a=0, b=1, \beta =2 \mathrm{and}$$f(T)=T^2$.

Under these conditions, Equation (79) gives

$${\displaystyle \frac{dT}{dr}}-T ({\lambda }^{\prime }+{\nu }^{\prime })=-8\pi \rho e^{2\lambda },.$$

(91)

The following result is obtained by substituting the expressions from Equations (70) and (77) into Equation (91):

$${\psi }^3 {\psi }^{\prime } -{\displaystyle \frac{2{\psi }^4}{r}}=-{\displaystyle \frac{4\pi c_6}{3 r}},.$$

(92)

One arrives at the following result by solving (92):

$${\psi }^2=C_1{r}^8+c_9,$$

(93)

where $c_9=(16 \pi c_2^2{c}_6)/3$ is a constant.

Substituting from (90) in (26), we get

$${\mathrm{e}}^{ 2\nu }=c_1 r^2, {\mathrm{e}}^{2\lambda }={\displaystyle \frac{C_2}{C_9+C_1{r}^8}}.$$

(94)

The shell-region line element for $f(T)=T^2$ gravity reads

$$d{s}_{shell.}^2=c_1{r}^2 d{t}^2-({\displaystyle \frac{C_2}{C_9+C_1{r}^8}})d{r}^2-r^2 (d{\theta }^2+{\sin }^2\theta d{\varphi }^2).$$

(95)

It is evident from the solutions that the line element (96) does not exhibit central singularity.

Moreover, the interior region’s gravitational mass of the gravastar is derived when $f\left(T\right)=T^2$ follows Equation (84).

4.3. Exterior Spacetime Solution for a CGM $\mathit{inf}\left(T\right)=a+b{T}^{\beta }$

Given the field Equations (34)–(36) for the exterior region of a CGM, where $P=\rho =0$, in the context of $f\left(T\right)=a+b{T}^{\beta }$ gravity as follows:

$$\begin{array}{l}-2\frac{b \beta (\beta -1)}{r}{e}^{-2\lambda } T^{\beta -2}{\displaystyle \frac{dT}{dr}}-b \beta T^{\beta -1} (T-\frac{1}{r^2}-\frac{2}{r}{e}^{-2\lambda }({\lambda }^{\prime }+{\nu }^{\prime }))\\ \hfill +\frac{1}{2}(a+b T^{\beta })=E^2,\end{array}$$

(96)

$$b \beta T^{\beta -1}(T-\frac{1}{r^2})-\frac{1}{2}(a+b T^{\beta })=-E^2,$$

(97)

$$\begin{array}{l}\frac{b \beta (\beta -1)}{r}{e}^{-2\lambda } (1+ r{\nu }^{\prime })T^{\beta -2}{\displaystyle \frac{dT}{dr}}+{\displaystyle \frac{b}{2}}\beta T^{\beta }+b \beta e^{-2\lambda } T^{\beta -1}({\nu }^{″}+{\displaystyle \frac{1}{r}}(1+r {\nu }^{\prime })({\nu }^{\prime }-{\lambda }^{\prime }))-\\ \frac{1}{2}(a+b{T}^{\beta })=E^2\end{array}.$$

(98)

The following sections of this article will examine the exterior under three different scenarios, similar to our earlier study of the gravastar’s interior and the shell regions.

• We will proceed to analyze the first scenario with $f\left(T\right)=T,a=0 \mathrm{and} b=\beta =1$.
  In this case, Equations (96)–(98) results in

  $$e^{-2\lambda }(e^{2\lambda }-1+2r{\lambda }^{\prime })=r^2{E}^2,$$

  (99)

  $$e^{-2\lambda } (e^{2\lambda }-1-2r {\nu }^{\prime })=r^2{E}^2,$$

  (100)

  $$\begin{gathered} e^{-2\lambda }({\nu }^{″}+{\displaystyle \frac{1}{r}}(1+r{\nu }^{\prime })({\nu }^{\prime }-{\lambda }^{\prime }))=E^2 \\ {e}^{-2\lambda }[({\lambda }^{\prime }-{\nu }^{\prime })(1+r{\nu }^{\prime })-r{\nu }^{″}]=E^2. \end{gathered}$$

  (101)

Solving Equations (99) and (100) leads to

$${\nu }^{\prime }=-{\lambda }^{\prime }.$$

(102)

By applying the expressions from Equation (102) to Equation (101), we obtain the following conclusion:

$$e^{-2\lambda }[-2{\lambda }^{\prime }+2{\lambda }^{\prime 2}r-r {\lambda }^{″}]=r{E}^2.$$

(103)

The previous equation can be rewritten in the following form:

$${\displaystyle \frac{d^2(r{e}^{-2\lambda })}{d{r}^2}}=2r{E}^2={\displaystyle \frac{2Q^2}{r^3}}.$$

(104)

By performing the integration process twice on the previous equation, we can obtain

$$e^{-2\lambda }=1-{\displaystyle \frac{2M}{r}}+{\displaystyle \frac{Q^2}{r^2}}.$$

(105)

In this context, $M$ is the total mass, and $Q$ refers to the gravastar’s charge.

Based on the above, the line element for the external solution is given by

$$d{S}_{exterior}^2=\left(1-{\displaystyle \frac{2M}{r}}+{\displaystyle \frac{Q^2}{r^2}}\right) d{t}^2-{\left(1-+{\displaystyle \frac{Q^2}{r^2}}{\displaystyle \frac{2M}{r}}\right)}^{-1} d{r}^2-r^2(d{\theta }^2+{\sin }^2\theta d{\varphi }^2).$$

(106)

Equation (106) represents the Reissner–Nordström exterior solution of the field equations [73].

• We will proceed to analyze the second scenario with $f(T)=a + bT \mathrm{and} \beta =1$, In this case, Equations (96)–(98) results in

  $$-b ({\displaystyle \frac{T}{2}}-\frac{1}{r^2}-\frac{2}{r}{e}^{-2\lambda }({\lambda }^{\prime }+{\nu }^{\prime })) +{\displaystyle \frac{a}{2}}= E^2,$$

  (107)

  $$b({\displaystyle \frac{T}{2}}-\frac{1}{r^2}) {\displaystyle \frac{a}{2}}=-E^2,$$

  (108)

  $$e^{-2\lambda }( {\nu }^{″}+{\displaystyle \frac{1}{r}}(1+r {\nu }^{\prime })({\nu }^{\prime }-{\lambda }^{\prime }))={\displaystyle \frac{E^2}{b}}+{\displaystyle \frac{a}{2b}}.$$

  (109)

By solving Equations (107) and (108), we get

$${\nu }^{\prime }=-{\lambda }^{\prime }.$$

(110)

The following result is obtained by substituting the expressions from Equation (110) into Equation (109):

$$e^{-2\lambda }(-r{\lambda }^{″} 2{\lambda }^{\prime }+2r {{\lambda }^{\prime }}^2))={\displaystyle \frac{r{E}^2}{b}}+{\displaystyle \frac{ra}{2b}}.$$

(111)

The preceding equation can be reformulated in the following manner;

$${\displaystyle \frac{d^2(r{e}^{-2\lambda })}{d{r}^2}}={\displaystyle \frac{2Q^2}{r^3}}+{\displaystyle \frac{a}{b}}r.$$

(112)

By performing the integration process twice on the previous equation, we can obtain

$$e^{-2\lambda }=1-{\displaystyle \frac{2M}{r}}+{\displaystyle \frac{Q^2}{r^2}}+{\displaystyle \frac{a}{6b}}{r}^2.$$

(113)

Therefore, the line element for the exterior region of the $f\left(T\right)=a+bT$ can be written as

$$\begin{array}{l}d{S}_{exterior}^2=\left(1-{\displaystyle \frac{2M}{r}}+{\displaystyle \frac{Q^2}{r^2}}+{\displaystyle \frac{a}{6b}}{r}^2\right)d{t}^2-{\left(1-{\displaystyle \frac{2M}{r}}+{\displaystyle \frac{Q^2}{r^2}}+{\displaystyle \frac{a}{6b}}{r}^2\right)}^{-1} d{r}^2\\ -r^2(d{\theta }^2+{\sin }^2\theta d{\varphi }^2)\end{array},$$

(114)

where $\Lambda =-{\displaystyle \frac{a}{2b}}$ arises from $f\left(T\right)$ corrections.

We will proceed to analyze the third scenario with $f(T)=T^2, a=0, b=1 \mathrm{and} \beta =2$. In this case, Equations (96) and (97) take the following forms:

$$-\frac{4}{r}{e}^{-2\lambda }{\displaystyle \frac{dT}{dr}}-2T (T-\frac{1}{r^2}-\frac{2}{r}{e}^{-2\lambda }({\lambda }^{\prime }+{\nu }^{\prime }))+\frac{1}{2}{T}^2= E^2,$$

(115)

$$2T(T-\frac{1}{r^2})-\frac{1}{2}{T}^2=-E^2,.$$

(116)

By solving Equations (116) and (117), we get

$${\displaystyle \frac{dT}{dr}}-T ({\lambda }^{\prime }+{\nu }^{\prime })=0,.$$

(117)

By employing the CKVs (24) and the scalar torsion (18) to solve Equation (117), we derive

$$e^{2\nu }=c_1{r}^2 \mathrm{and} {\mathrm{e}}^{-2\lambda }=c_3^2 r^4/c_2.$$

(118)

Consequently, the line element for the exterior spacetime region is given by

$$d{S}_{exterior}^2=(c_1{r}^2)d{t}^2-{\left(c_3^2 r^4/c_2\right)}^{-1} d{r}^2-r^2(d{\theta }^2+{\sin }^2\theta d{\varphi }^2).$$

(119)

4.4. Proper Length of the Thin Shell in CGMs

The proper length of the thin shell is a fundamental physical parameter in the study of CGMs, providing a measure of the spatial thickness of the transitional layer that separates the interior and exterior spacetime regions. This shell acts as a critical boundary where the gravitational and electromagnetic fields undergo significant changes, and its proper length offers insight into the geometric and dynamic properties of this interface. The proper length $\iota$ of the thin shell is computed by integrating infinitesimal spatial distance elements along a radial path connecting the inner $r=r_1$ and outer $r_2=r_1+\epsilon$ boundaries of the shell. In a spherically symmetric spacetime with the metric component $e^{2\lambda }$, the proper length is given by [74]

$$\mathcal{l}= {\displaystyle \underset{r_1}{\overset{r_1+\epsilon }{\int }}\sqrt{e^{2 \lambda }}} dr,.$$

(120)

Here, $r_1$ denotes the radius of the interior region, while $r_2=r_1+ϵ$ (where $ϵ\ll 1$) represents the radius of the thickness of the intermediate thin shell.

In the following Subsection, the proper length of the shell is plotted as a function of the shell thickness for the three proposed models, utilizing the data from

Table 1. The potential $e^{2\lambda }$ and the proper length of the thin shell in our proposed models.

Model	${\mathit{e}}^{2\mathit{\lambda }}$	Ref.	The Proper Length of the Thin Shell
$f\left(T\right)=T$	${\displaystyle \frac{C_2}{C_7+C_1{r}^2}}$	Equation (85)	$\mathcal{l}= {\displaystyle \underset{r_1}{\overset{r_1+\epsilon }{\int }}\sqrt{\frac{C_2}{C_7+C_1 r^2}}} dr,$
$f\left(T\right)=a+bT$	${\displaystyle \frac{C_2}{C_8+C_1{r}^2}}$	Equation (92)	$\mathcal{l}= {\displaystyle \underset{r_1}{\overset{r_1+\epsilon }{\int }}\sqrt{\frac{C_2}{C_8+C_1{r}^2}}} dr,$
$f\left(T\right)=T^2$	${\displaystyle \frac{C_2}{C_9+C_1 r^8}}$	Equation (97)	$\mathcal{l}= {\displaystyle \underset{r_1}{\overset{r_1+\epsilon }{\int }}\sqrt{\frac{C_2}{C_8+C_1{r}^2}}} dr,$

Where $c_s$ = 0.0001 are constants.

and constant values of $c_s$. The behavior of the ultrarelativistic fluid within the thin shell of a CGM is governed by the interplay between pressure, density, and gravitational effects. Figure 1 demonstrates that the pressure $P\left(r\right)$ and density $\rho \left(r\right)$ decrease monotonically with increasing radial coordinate $r$. This trend reveals key insights into the shell’s structure and stability: The pressure and density reach their maximum values, indicating a highly compressed ultrarelativistic fluid due to strong gravitational confinement. Both quantities decline significantly, suggesting a more rarefied state as the fluid expands outward. This behavior aligns with expectations for an ultrarelativistic fluid under varying gravitational influence, where the weakening gravitational pull toward the outer boundary allows the fluid to expand, reducing its pressure and density. The gradient ensures a smooth transition between the interior de Sitter vacuum (negative pressure) and the exterior charged spacetime (asymptotically flat). Figure 2, Figure 3 and Figure 4 illustrate the proper length of the shell as a function of its thickness for the $f\left(T\right)$ gravity model. Key observations include: The proper length exhibits a monotonic rise as the shell’s coordinate thickness expands. This confirms that the spatial extent of the shell grows in a controlled manner, avoiding abrupt geometric transitions. The specific form of $f\left(T\right)=a+bT$ modifies the metric function $e^{2\lambda }$, influencing the integrated proper distance. For instance, Torsion-driven corrections may introduce nonlinear scaling in $\iota$, deviating from G R predictions. The asymptotic behavior of $\iota$ at large $\epsilon$ can reveal whether the shell remains compact or exhibits infinite stretching. Pressure and density peak at the inner edge and decline outward, reflecting gravitational decoupling and fluid expansion. The proper length $\iota$ scales smoothly with shell thickness, validating the non-singular nature of the boundary layer.

4.5. Entropy and Thermodynamic Stability of the CGM Shell

The entropy of the thin shell of CGMs is an essential aspect of their thermodynamic properties. In the context of CGMs, which are theoretical constructs made of ultrarelativistic fluids, entropy indicates the degree of disorder and the distribution of energy within the shell.

The entropy S of the thin shell in a CGM serves as a critical diagnostic tool for assessing the system’s thermodynamic stability, energy distribution, and response to perturbations. Within the Mazur–Mottola gravastar paradigm [1,2], the shell’s entropy quantifies the degree of disorder and energy dispersal, offering profound insights into the structure’s equilibrium and its capacity to withstand gravitational collapse or external disturbances. Higher entropy values correlate with greater microscopic disorder, suggesting a stable configuration where energy is maximally dispersed. For the shell, this implies resilience against perturbations that might otherwise trigger collapse or fragmentation [1,2]. Entropy generation during shell evolution influences the effective stress-energy tensor, potentially counteracting gravitational pull through thermodynamic pressure [75]. While gravastars avoid singularities, their entropy shares conceptual ties with black hole thermodynamics, adhering to the generalized second law (GSL) when coupled to an external environment [76]. Following [1,2], the entropy S of the ultrarelativistic fluid in the shell is derived from its surface density $\sigma$ and pressure $\mu$. The explicit formula is given by

$$S={\displaystyle \underset{D}{\overset{D+\epsilon }{\int }}4\pi r^2\frac{s(r)}{\sqrt{e^{-2\lambda }}}} dr,$$

(121)

where

$$s(r)=\xi \sqrt{{\displaystyle \frac{P}{2\pi }}},$$

(122)

where $\xi$ is a dimensionless constant and $S\left(r\right)$ is an entropy density for an ultrarelativistic fluid [77]. Next, we will investigate the entropy of the three proposed models. By inserting Equations (80), (85), (92), (122), and (97) into Equation (121),

Table 2. The entropy of the thin shell in our proposed models.

Model	${\mathit{e}}^{2\mathit{\lambda }}$	The Entropy of the Thin Shell
$f\left(T\right)=T$	${\displaystyle \frac{C_2}{C_7+C_1 r^2}}$	$S=\xi \sqrt{8\pi }{\displaystyle \underset{r_1}{\overset{r_1+\epsilon }{\int }}\sqrt{\frac{ C_6(C_7 + C_1 r^2) }{C_2 r^2}}} dr$
$f\left(T\right)=a+bT$	${\displaystyle \frac{ C_2 }{ C_8 + C_1 r^2}}$	$S=\xi \sqrt{8\pi }{\displaystyle \underset{r_1}{\overset{r_1+\epsilon }{\int }}\sqrt{\frac{ C_6(C_8 + C_1 r^2) }{C_2 r^2}}} dr$
$f\left(T\right)=T^2$	${\displaystyle \frac{ C_2 }{C_9+ C_1 r^8}}$	$S=\xi \sqrt{8\pi }{\displaystyle \underset{r_1}{\overset{r_1+\epsilon }{\int }}\sqrt{\frac{ C_6(C_9 + C_1 r^8) }{C_2 r^2}}} dr$

was constructed as follows,

4.6. Energy Content and Stability of the CGM Shell

The energy dynamics of the thin shell in a CGM are governed by an exotic EoS of the form $P=-\rho$, which plays a pivotal role in maintaining equilibrium and preventing gravitational collapse. This unique EoS implies a negative pressure that generates a repulsive gravitational effect, counteracting the inward pull of gravity and stabilizing the system against singularity formation [78]. Below, we analyze the implications of this energy configuration and its role in gravastar physics. The EoS signifies a vacuum-like fluid with negative pressure, akin to dark energy. This creates an outward force that balances the gravitational attraction from the interior and exterior regions [78]. Unlike black holes, where collapse leads to a central singularity, the negative pressure in the shell ensures a non-singular, stable boundary between the de Sitter core and the exterior spacetime. The total energy E within the shell is derived from its surface energy density $\sigma$ and pressure $\mu$, it can be expressed as

$$E={\displaystyle {\int }_D^{D+\epsilon }4\pi r^2}\rho dr.$$

(123)

Substituting from Equation (79) into Equation (123), we get

$$E={\displaystyle {\int }_D^{D+\epsilon }4\pi C_6} dr.$$

(124)

By integrating Equation (124), we get

$$E= 0.0013 \epsilon ,.$$

(125)

Figure 5, Figure 6 and Figure 7 examine the relationship between disorder in CGMs and shell thickness. When the shell has zero thickness, the entropy vanishes completely, representing a perfectly ordered state. This shows that a vanishingly thin shell cannot support any measurable disorder. As the shell grows thicker, the system becomes more complex, enabling greater energy distribution and consequently higher entropy. The results in Figure 5, Figure 6 and Figure 7 confirm that the entropy behavior in these models follows core thermodynamic laws, especially the second law’s requirement that entropy cannot spontaneously decrease in isolated systems.

Additionally, Figure 8 reveals a direct proportionality between the shell’s energy content and its thickness. The linear relationship demonstrates that higher energy states drive shell expansion, underscoring the tight coupling between energy and structural properties in gravastars. This energy-thickness dependence suggests that the shell’s physical extent is fundamentally governed by its energy content.

5. Junction Condition

The junction conditions in gravitational theories describe how different spacetime regions interact at their boundaries. In the context of charged gravasters hypothetical objects that combine properties of gravity and matter these conditions are crucial for ensuring the continuity of the physical fields across the interface:

$${S^i}_j=-{\displaystyle \frac{1}{8\pi }}({K^i}_j-{{\delta }^i}_j{K}_k^k).$$

(126)

A discontinuity of the second fundamental form is defined as a situation where there is a sudden change or jump in the values of the second fundamental form across a boundary in a manifold. This discontinuity indicates that the curvature properties of the surface are not smoothly connected, which can have significant implications for the physical and geometric properties of the system being studied. A discontinuity of the second fundamental form is defined as

$$K_{i j}=K_{i j}^{+}-K_{i j}^{-}.$$

(127)

In this context, the symbols “−” and “+” represent the interior of de Sitter space-time and the exterior of the Reissner–Nordström space-time. The second fundamental form associated with both sides of the shell is defined as follows [67,68,69,70]:

$$K_{i j}^{\pm }=- n_{\nu }^{\pm } \left({\displaystyle \frac{{\partial }^2{X}_{\nu }}{\partial {\zeta }^i\partial {\zeta }^j}}+{\Gamma }_{\alpha \beta }^{\nu }{\displaystyle \frac{\partial X^{\alpha }}{\partial {\zeta }^i}}{\displaystyle \frac{\partial X^{\beta }}{\partial {\zeta }^j}}\right),$$

(128)

where ${\zeta }^j$ represents the intrinsic coordinates of the shell, and $n_{\nu }^{\pm }$ denotes the unit normal vectors of the surface, defined as

$$n_{\nu }^{\pm }=\pm {\left(g^{\alpha \beta }{\displaystyle \frac{\partial f}{\partial X^{\alpha }}}{\displaystyle \frac{\partial f}{X{\zeta }^{\beta }}}\right)}^{-1/2}{\displaystyle \frac{\partial f}{\partial X^{\nu }}},$$

(129)

where $n_{\nu }{n}^{\nu }=1$, and the parametric equation of the shell is $f(x^{\alpha }({\zeta }^i))=0$.

The Lanczos equation plays a fundamental role in cosmology, establishing a critical relationship between spacetime geometry and the distribution of matter in the universe. It provides a theoretical framework for analyzing the stress-energy tensor, which encodes the density and flow of energy and momentum. The Lanczos equation governing the surface stress-energy tensor is given by [71]

$$S_{i j}=diag(\sigma ,-\mu ,-\mu ,-\mu ),$$

(130)

where $\sigma$ represents the surface energy density and $\mu$ denotes the surface pressure. The surface energy density $\sigma$ and the surface pressure $\mu$ can be articulated as follows:

$$\sigma =-{\displaystyle \frac{1}{4\pi D}}{\left[\sqrt{f}\right]}_{-}^{+},$$

(131)

$$\mu ={\displaystyle \frac{1}{8\pi D}}\left({\left[\sqrt{f}\right]}_{-}^{+}+{\displaystyle \frac{D}{2}}{\left[{\displaystyle \frac{f^{\prime }}{\sqrt{f}}}\right]}_{-}^{+}\right),$$

(132)

where $f=e^{-2\lambda }$ and $f^{\prime }={(df/dr)}_{r=D}$

To provide the data for Equation (136), we will create

Table 3. The metric potential $f=e^{-2\lambda }$ of the two regions of the models.

Model	Interior Region	Exterior Region
$f\left(T\right)=T$	$e^{-2\lambda }=1-{\displaystyle \frac{8\pi {\rho }_0{r}^2}{3}}+{\displaystyle \frac{4 Q^2}{\left(2n+3\right)\left(n+2\right)r^3}}$	$e^{-2\lambda } =(1-{\displaystyle \frac{2M}{r}}+{\displaystyle \frac{Q^2}{r^2}})$
$f\left(T\right)=a+bT$	$e^{-2\lambda }=1+\left({\displaystyle \frac{a}{6 b}}-{\displaystyle \frac{8\pi {\rho }_0}{3}}\right)r^2+{\displaystyle \frac{4 Q^2}{\left(2n+3\right)\left(n+2\right)r^3}}$	$e^{-2\lambda }= 1-{\displaystyle \frac{2M}{r}}+{\displaystyle \frac{ Q^2}{r^2}}+{\displaystyle \frac{a}{6 b}}{r}^2$
$f\left(T\right)=T^2$	$e^{ -2\lambda } = c_3^2 r^4/c_2$	$e^{ -2\lambda } = c_3^2 r^4/c_2$

.

• We will proceed to analyze the first scenario with the model $f\left(T\right)=T$

Substituting the expressions from Table 3 into Equations (131) and (132) yields the following outcome:

$$\sigma =-{\displaystyle \frac{1}{4 \pi D}}\left(\sqrt{1-{\displaystyle \frac{2 M}{D}}+{\displaystyle \frac{Q^2}{r^2}}}-\sqrt{1-{\displaystyle \frac{8 \pi {\rho }_0{D}^2}{3}}+{\displaystyle \frac{4Q^2}{(2n+3)(n+2)D^3}}}\right),$$

(133)

$$\mu ={\displaystyle \frac{1}{8 \pi D}}\left({\displaystyle \frac{1-\frac{M}{ D}}{\sqrt{1-\frac{2 M}{ D}+\frac{Q^2}{r^2}}}}-{\displaystyle \frac{1-{\frac{16 \pi {\rho }_0 D}{3}}^2-\frac{2Q^2}{(2n+3)(n+2)D^3}}{\sqrt{1-\frac{8 \pi {\rho }_0 D^2}{3}+\frac{4Q^2}{(2n+3)(n+2)D^3}}}}\right).$$

(134)

The mass of the thin shell ($m_{sh}$) can be determined from Equation (133) as follows:

$$m_{sh}=4\pi D^2\sigma =D\left(\sqrt{1-{\displaystyle \frac{8 \pi {\rho }_0 D^2}{3}}+{\displaystyle \frac{4Q^2}{(2n+3)(n+1)D^3}} }-\sqrt{1-{\displaystyle \frac{2 M}{ D}}+{\displaystyle \frac{Q^2}{D^2}}}\right).$$

(135)

The total mass $M$ of the CGM can be expressed as follows:

$$M={\displaystyle \frac{4\pi {\rho }_0 D^3}{3}} -{\displaystyle \frac{2Q^2}{(2n+3)(n+1)D^2}}+ m_{sh} \sqrt{ 1-{\displaystyle \frac{8\pi {\rho }_0 D^2}{3}}+{\displaystyle \frac{4Q^2}{(2n+3)(n+1)D^3}} } - {\displaystyle \frac{ m_{sh}^2 }{2D}}.$$

(136)

Energy conditions are fundamental constraints in general relativity that restrict the form of the energy-momentum tensor, governing how matter and energy distribute and propagate through spacetime. These conditions play a vital role in distinguishing physically meaningful solutions to Einstein’s field equations from those that are mathematically permissible but non-physical. The most widely studied energy conditions include [72]: WEC: $\sigma \ge 0$ and $\sigma +\mu \ge 0$, SEC: $\sigma +\mu \ge 0$ and $\sigma +3 \mu \ge 0$, DEC: DEC $\sigma \ge 0$, $\sigma +\mu >0$ variation in surface energy density is depicted in Figure 9, which clearly shows that both and $\sigma -\mu >0$, and NEC: $\sigma +\mu \ge 0$. The parameters maintain positive values throughout the entire shell, confirming that the NEC is satisfied during thin-shell formation. Figure 10 shows the radial profile of surface pressure, demonstrating its positivity across the shell. Furthermore, our analysis reveals a direct proportionality between surface pressure and the CGM radius. As evidenced by Figure 9, Figure 11, Figure 12 and Figure 13, the WEC, SEC, and NEC are all satisfied. However, the DEC is violated. This implies that while the system adheres to key energy constraints, the DEC violation suggests non-standard energy-momentum behavior, potentially indicating exotic matter effects or non-equilibrium dynamics in this regime. Taking $M=0.5$ and ${\rho }_0=0.0001$.

• We will proceed to analyze the second scenario with the model $f\left(T\right)=a+bT$. The following result is obtained by substituting the expressions from Table 3 into Equations (133) and (133):

  $$\sigma =-{\displaystyle \frac{1}{4 \pi D}}\left(\sqrt{1-{\displaystyle \frac{2 M}{ D}}+{\displaystyle \frac{Q^2}{D^2}}+{\displaystyle \frac{a}{6b}}}-\sqrt{1+({\displaystyle \frac{a}{6b}}-{\displaystyle \frac{8 \pi {\rho }_0}{3}})D^2+{\displaystyle \frac{4Q^2}{(2n+3)(n+1)D^3}}}\right),$$

  (137)

  $$\mu ={\displaystyle \frac{1}{8 \pi D}} \left({\displaystyle \frac{1-\frac{ M}{ D}+\frac{a}{6b}}{\sqrt{1-\frac{2 M}{ D}+\frac{Q^2}{D^2}+\frac{a}{6b}}}}-{\displaystyle \frac{1+2(\frac{a}{6b}- \frac{8 \pi {\rho }_0}{3})D^2-\frac{2Q^2}{(2n+3)(n+1)D^3}}{\sqrt{1+(\frac{a}{6b}-\frac{8 \pi {\rho }_0}{3})D^2+\frac{4Q^2}{(2n+3)(n+1)D^3}}}}\right).$$

  (138)

Equation (137) can be used to ascertain the $m_{sh}$ as outlined below:

$$m_{sh}=4\pi D^2\sigma =D\left(\sqrt{1+({\displaystyle \frac{a}{6b}}-{\displaystyle \frac{8 \pi {\rho }_0 }{3}})D^2+{\displaystyle \frac{4Q^2}{(2n+3)(n+1)D^3}} }-\sqrt{1-{\displaystyle \frac{2 M}{ D}}+{\displaystyle \frac{Q^2}{D^2}}+{\displaystyle \frac{a}{6b}}}\right).$$

(139)

In the $f\left(T\right)=a+bT$ modified gravity model, the CGM’s total mass can be expressed as

$$M=\left(\begin{array}{l}({\displaystyle \frac{4 \pi {\rho }_0}{3}}-{\displaystyle \frac{a}{12b}})D^3-{\displaystyle \frac{2Q^2}{(2n+3)(n+2)D^2}}+\\ m_{sh}\sqrt{1+({\displaystyle \frac{a}{6b}}-{\displaystyle \frac{8 \pi {\rho }_0 }{3}})D^2+{\displaystyle \frac{4Q^2}{(2n+3)(n+2)D^3}}}+\\ {\displaystyle \frac{{m^2}_{sh}}{2D}}+{\displaystyle \frac{Q^2}{2D}}+{\displaystyle \frac{a D}{12b}}\end{array}\right).$$

(140)

Figure 14, Figure 15, Figure 16 and Figure 17 reveal violations of all fundamental energy conditions the DEC, WEC, SEC, and NEC within the $f\left(T\right)=a+bT$ modified gravity framework. This comprehensive violation pattern suggests several profound implications. The systematic failure of all energy conditions indicates non-standard behavior in the energy-momentum tensor, deviating significantly from conventional physical systems where typically at least some conditions are satisfied. The violations imply that the surface energy density may surpass physically reasonable thresholds, potentially reaching values that challenge our understanding of material systems in gravitational physics. This behavior strongly hints at the presence of exotic matter with unusual stress-energy properties.

• We will proceed to analyze the second scenario with the model $f\left(T\right)=T^2$.

The following result is obtained by substituting the expressions from Table 1 into Equations (133) and (134):

$$\sigma = - {\displaystyle \frac{1}{12 \pi D}}\left(\sqrt{c_3^2 D^4/c_2}-\sqrt{c_3^2{D}^4/c_2}\right)=0,$$

(141)

$$\mu = {\displaystyle \frac{1}{48 \pi D}}\left({\displaystyle \frac{3 c_3^2 D^4/c_2}{\sqrt{c_3^2 D^4/c_2}}}-{\displaystyle \frac{3 c_3^2 D^4/c_2}{\sqrt{c_3^2 D^4/c_2}}}\right)=0.$$

(142)

From Equations (141) and (142), the surface energy density and the surface pressure of the CGM are equal to zero” means that, at the boundary of the CGM, there is no energy density or pressure acting on the surface. In physical terms, this indicates that there is no gravitational or electromagnetic force exerted at that surface, suggesting a state of equilibrium. This condition is significant in the context of CGMs, as it implies that the structure is stable and does not experience any external stresses or forces at its boundary.

6. Conclusions

In this study, we investigate three distinct stellar models of CGMs within the framework of $f\left(T\right)$ gravity, building upon the foundational work of Mazur and Mottola in General Relativity. Our analysis examines the following gravitational models: (i) the teleparallel equivalent $f\left(T\right)=T$, (ii) the linear modification $f\left(T\right)=a+bT$, and (iii) the quadratic extension $f\left(T\right)=T^2$. Following Mazur and Mottola’s seminal classification [1,2], we adopt their spherical decomposition of CGM structures into three characteristic regions:

Interior Core Region: This is the central part of the CGM, where the primary physical processes occur. It is characterized by specific EOS that dictate the behavior of matter and energy in this region.

The intermediate thin-shell region serves as a phase boundary layer separating the interior and exterior spacetime geometries. This geometrically constrained interface exhibits three key characteristics:

i.

Structural Role: Maintains continuity between distinct spacetime regions, mediates the transition of gravitational properties, and governs the matching conditions for the metric tensor.

ii.

Physical Significance: Determines the stability criteria through surface tension effects, hosts non-trivial stress-energy distributions, and acts as the primary locus for energy condition verification.

iii.

Morphological Properties: Characterized by an intrinsic length scale significantly smaller than system radius, exhibits hypersurface-embedded dynamics, and demonstrates anisotropic pressure components.

This region’s behavior is particularly sensitive to the choice of $f\left(T\right)$ functional form, with its thickness and stress profiles serving as discriminators between gravitational theories.

Exterior Spherical Region: This is the outermost layer of the CGM, extending into the surrounding space. It is also defined by its own equations of state, which influence how the CGM interacts with the external environment. Each of these models and regions provides a unique perspective on the properties and dynamics of CGMs, enhancing our understanding of these fascinating cosmic structures. We have derived exact solutions to the field equations by implementing distinct EOS for each region of the CGM: Interior region: ω = −1 (cosmological constant-like), Thin shell: ω = +1 (stiff matter EOS), and Exterior region: ω = 0 (pressureless dust). These results represent a significant advancement beyond previous studies [55,57,72,73,74] which typically employed approximation methods, particularly for the challenging thin-shell region. Our work provides: The first complete non-singular solution for CGMs in $f\left(T\right)$ gravity, exact treatment of all interface conditions without approximations, and a rigorous demonstration of $f\left(T\right)$ theory’s capacity to generate physically viable compact objects. This was achieved through the application of Killing vectors, which helped us maintain the integrity of the solutions. In our analysis, we have investigated and highlighted several significant aspects of our solution set, grounded in the structural characteristics of CGMs. These findings can be summarized as follows:

(1)

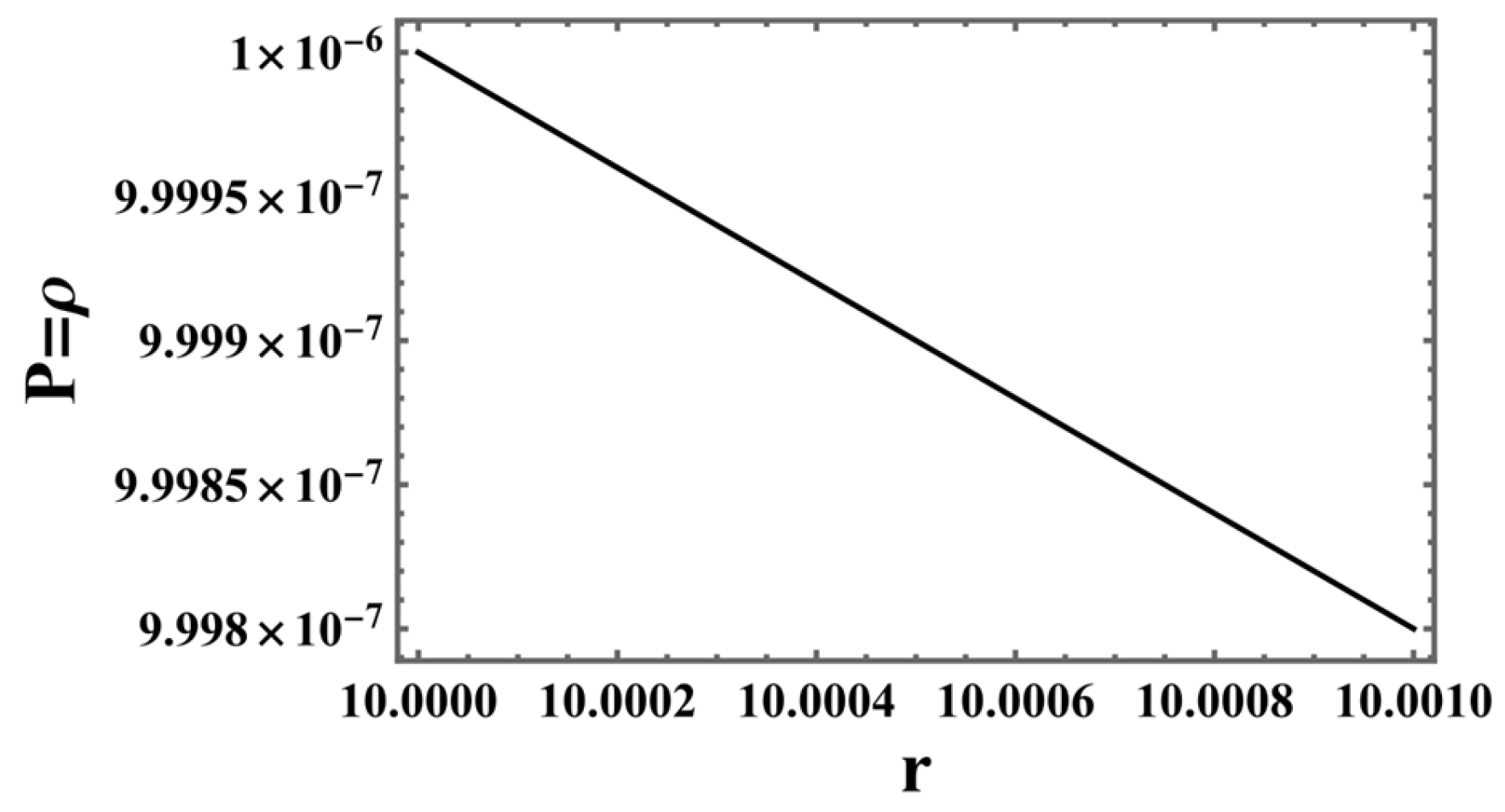
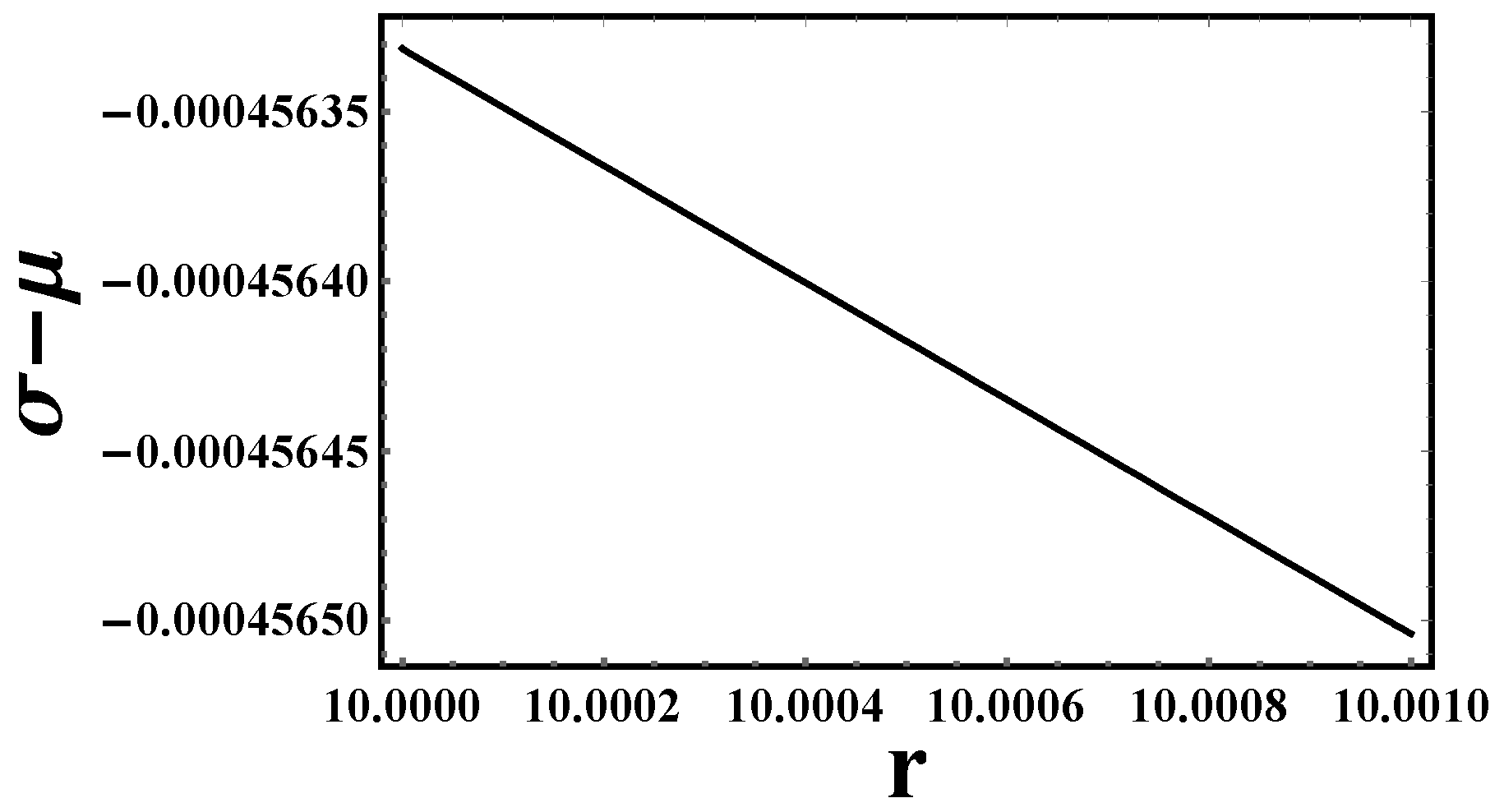
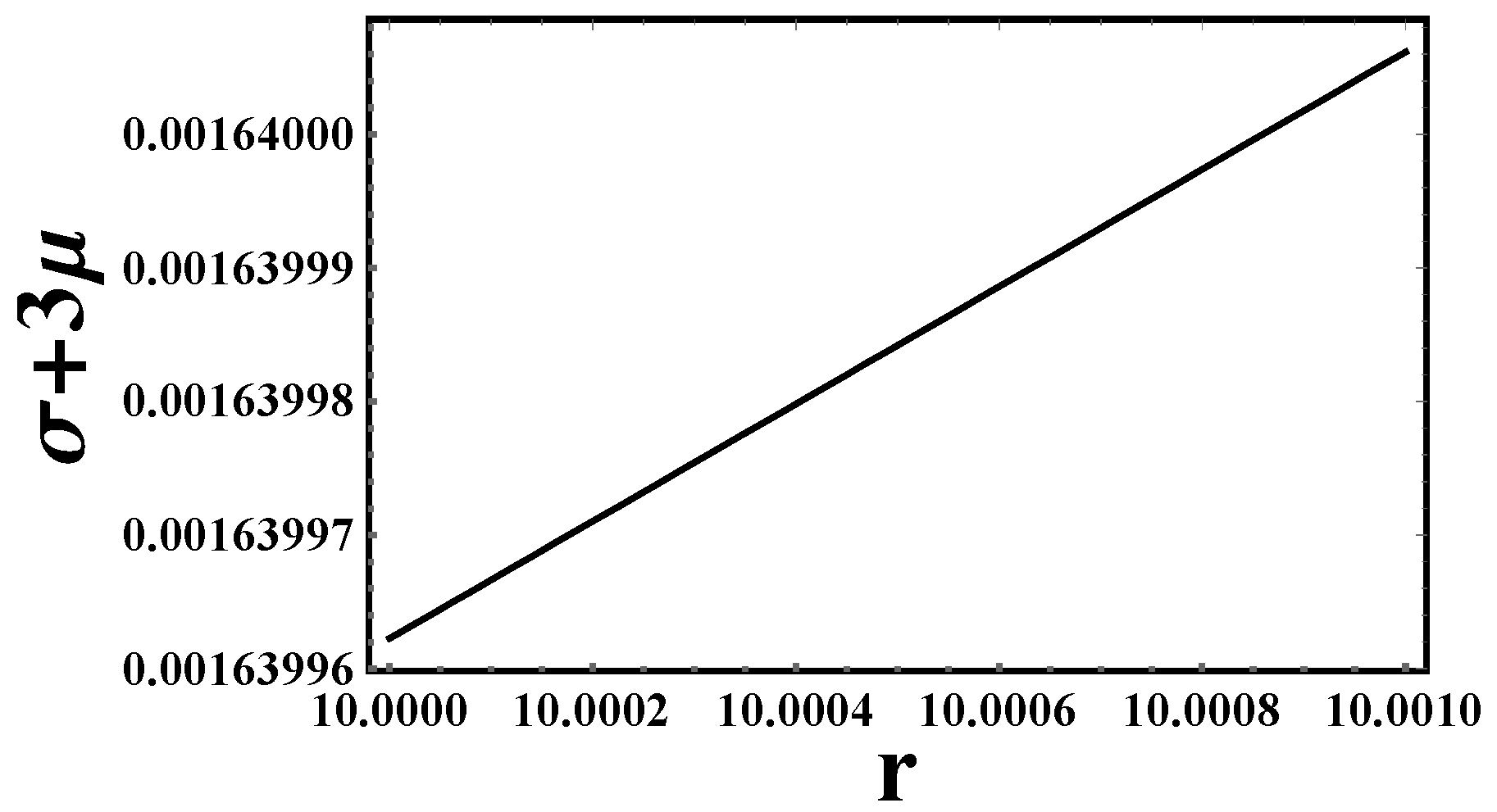
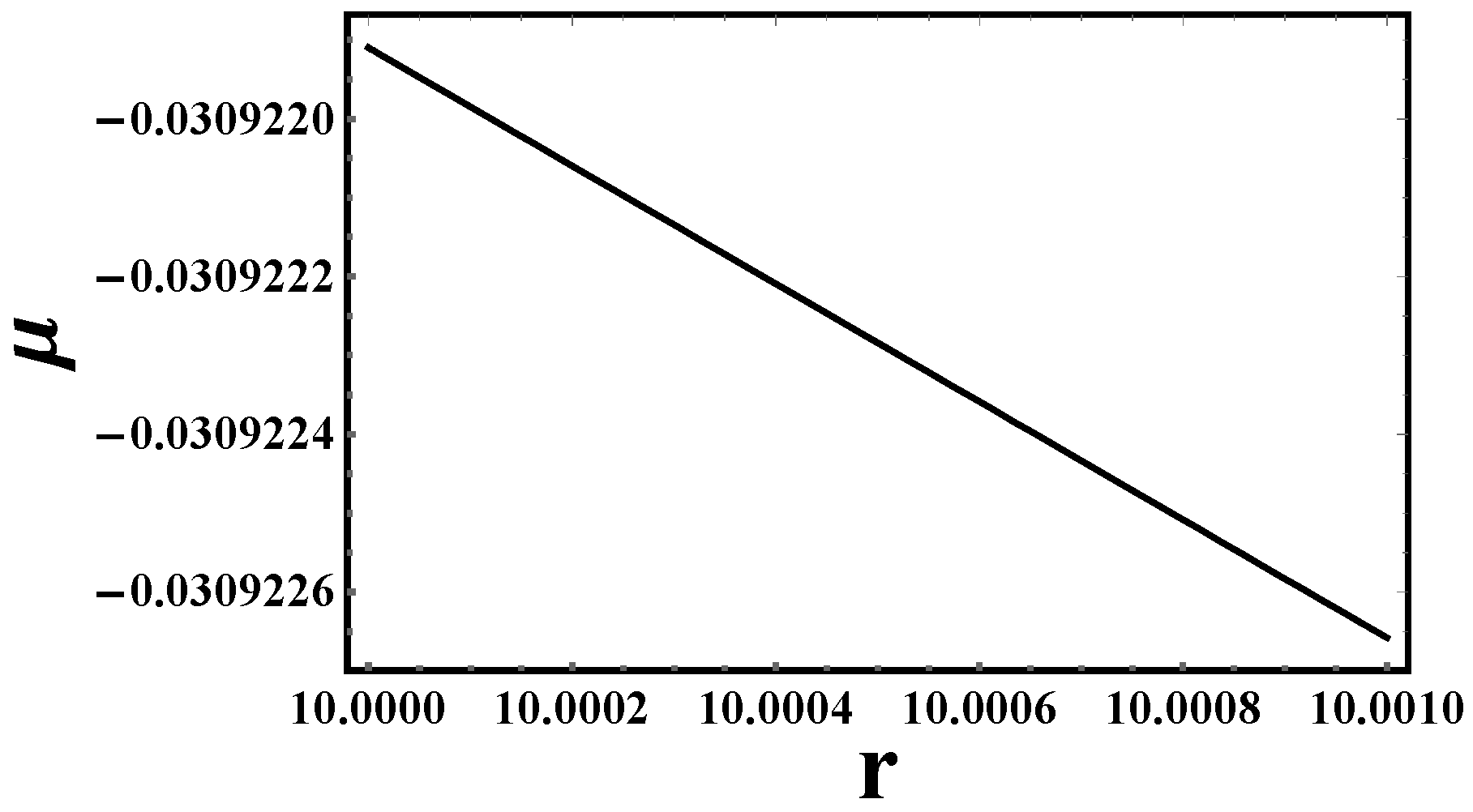
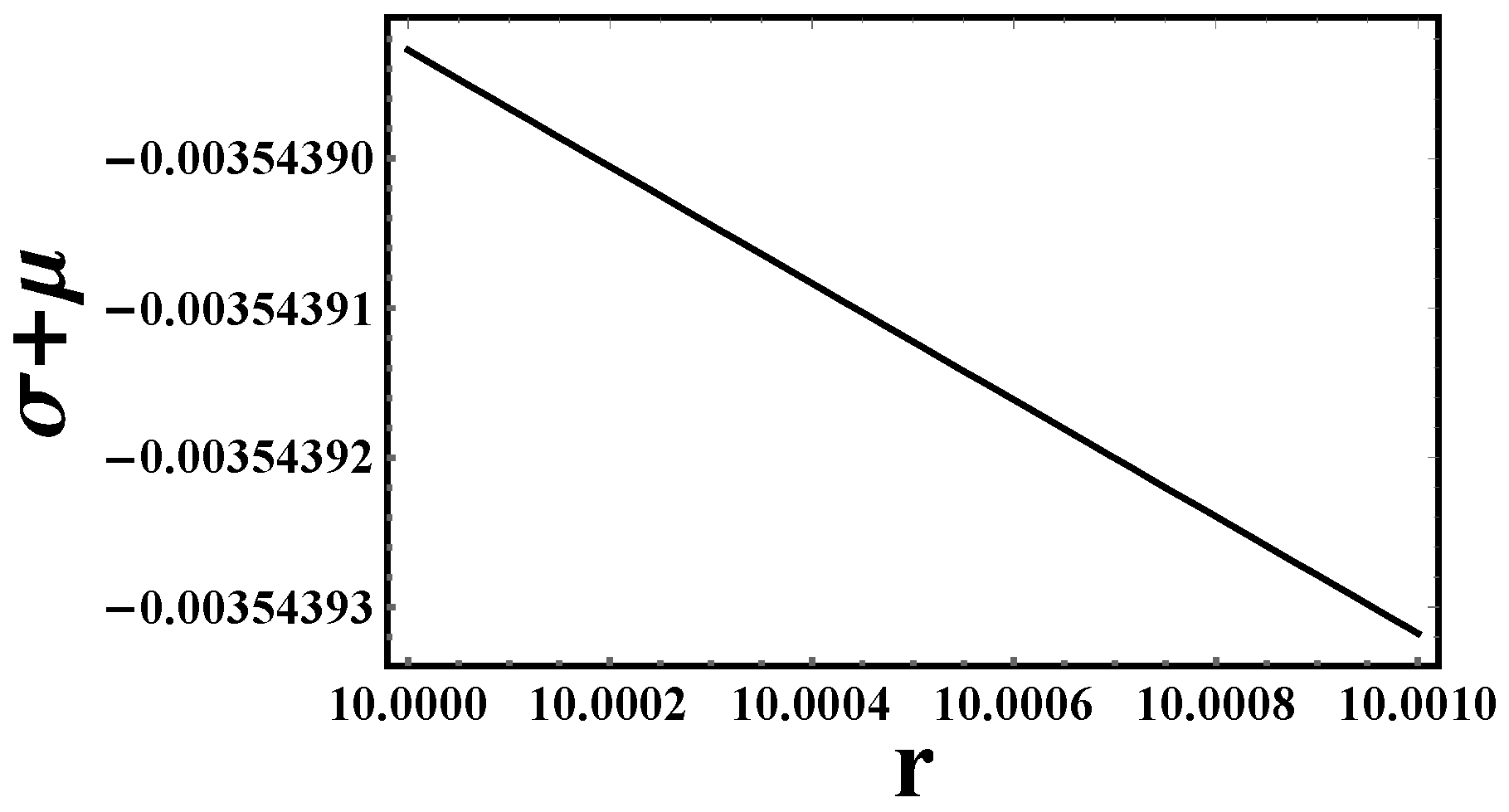
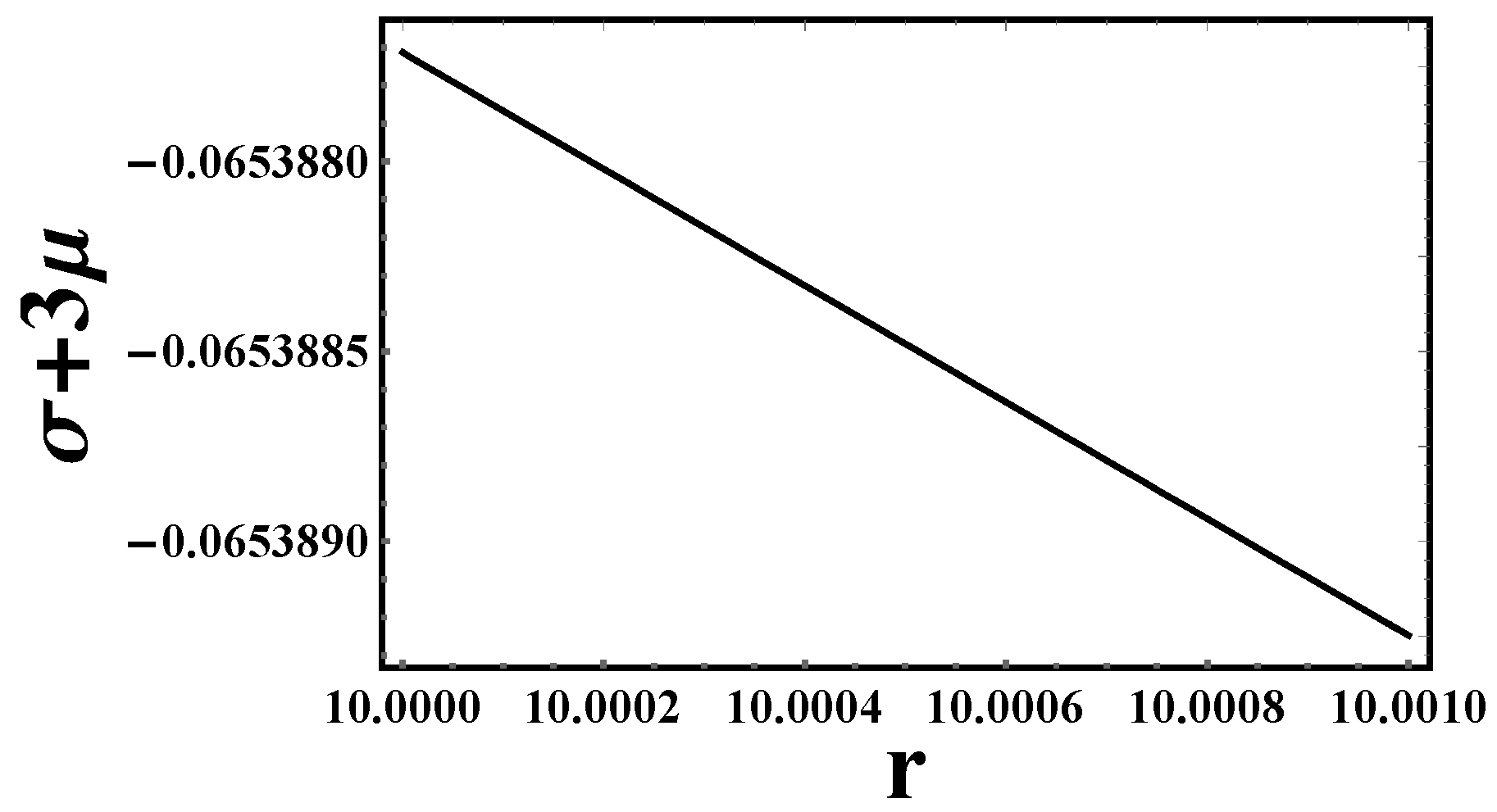
Pressure-density: Figure 1 depicts a high-resolution analysis of the internal structure of a CGMs, focusing on a thin shell region. The graph illustrates the pressure and density profile within this shell, where the matter is modeled as an ultrarelativistic fluid governed by the equation of state $P=\rho$. The plotted values demonstrate a gradual decrease in both pressure and density with increasing radial distance from the center. This gradient is a critical feature of the shell’s hydrostatic equilibrium. The primary objective of this analysis is to precisely characterize the behavior of matter under extreme conditions within the CGMs shell. This detailed profile is essential for solving the Tolman–Oppenheimer–Volkoff (TOV) equations, which describe the hydrostatic equilibrium and overall structure of the CGMs. Understanding these fine-scale details is paramount for accurately modeling the CGMs internal structure, assessing its stability, and calculating its gravitational redshift properties.

(2)

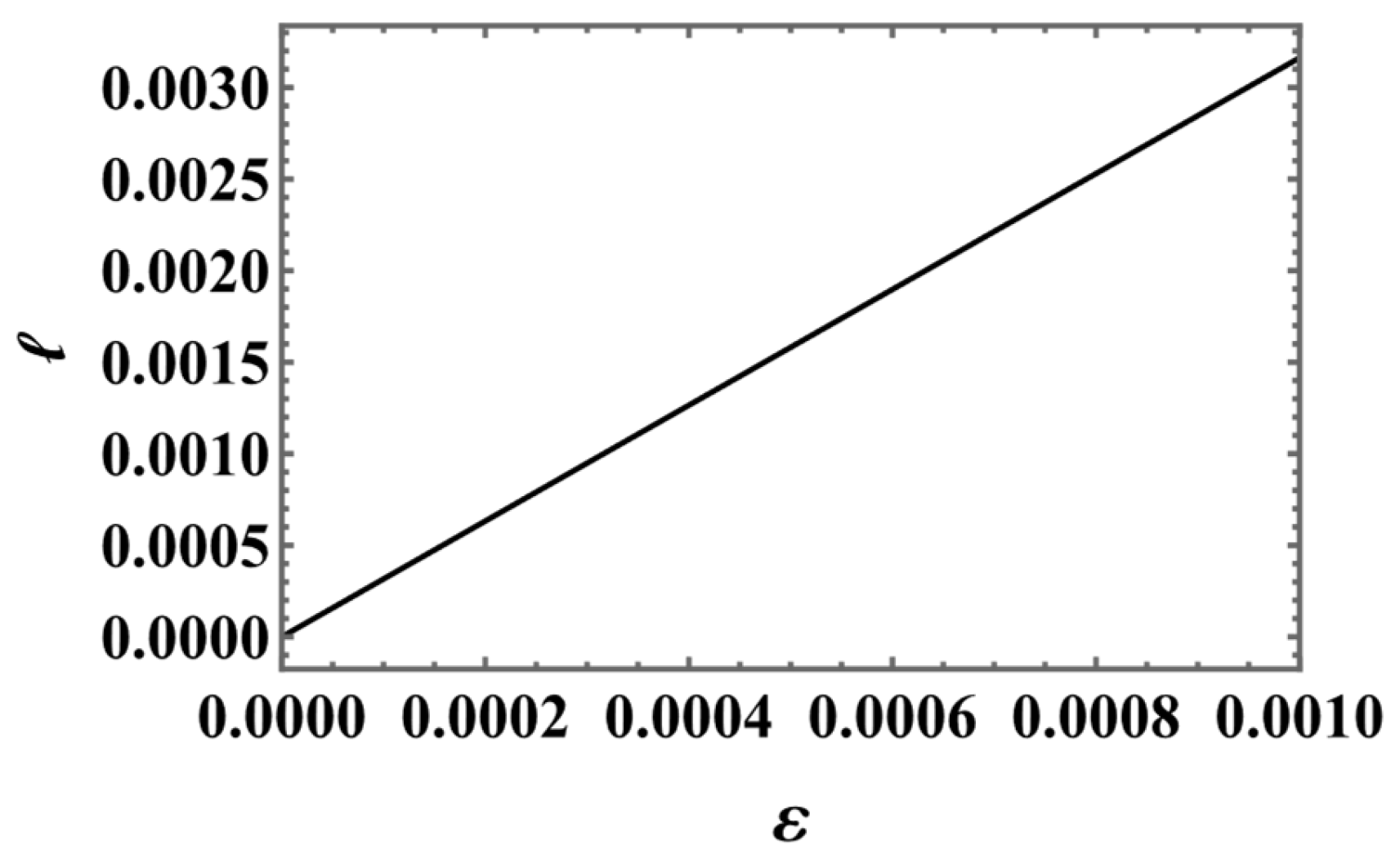
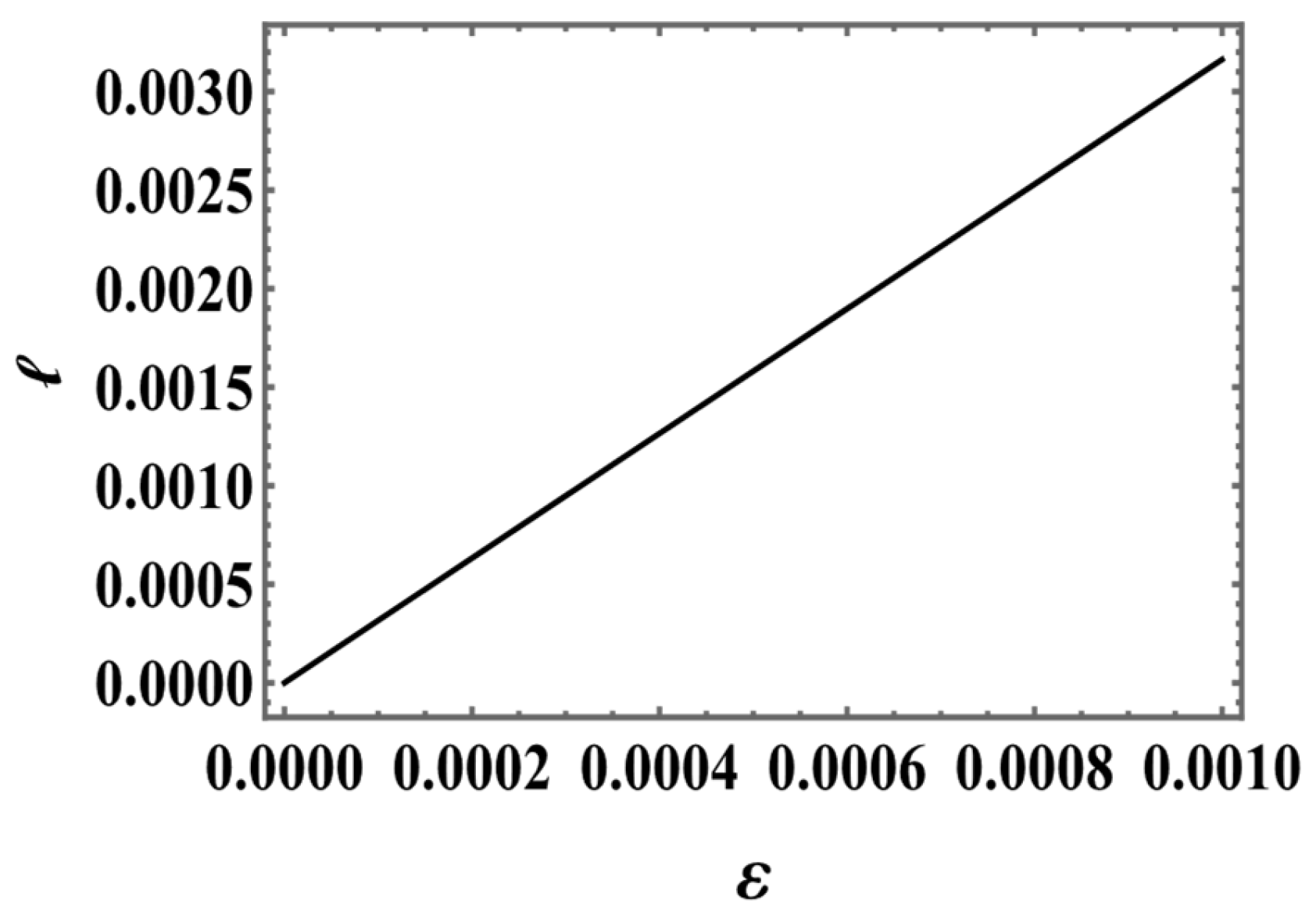
Proper length: Figure 2, Figure 3 and Figure 4 reveal a fundamental scaling relationship between the shell’s proper length ℓ and its thickness $\epsilon$ across all three $f\left(T\right)$ gravity models. The observed positive correlation exhibits several key features: Linear dependence of ℓ on $\epsilon$ in the $f\left(T\right)=T$ model, mild nonlinearity emerging in the $f\left(T\right)=a+bT$ case, and distinct power-law behavior for $f\left(T\right)=T^2.$

(3)

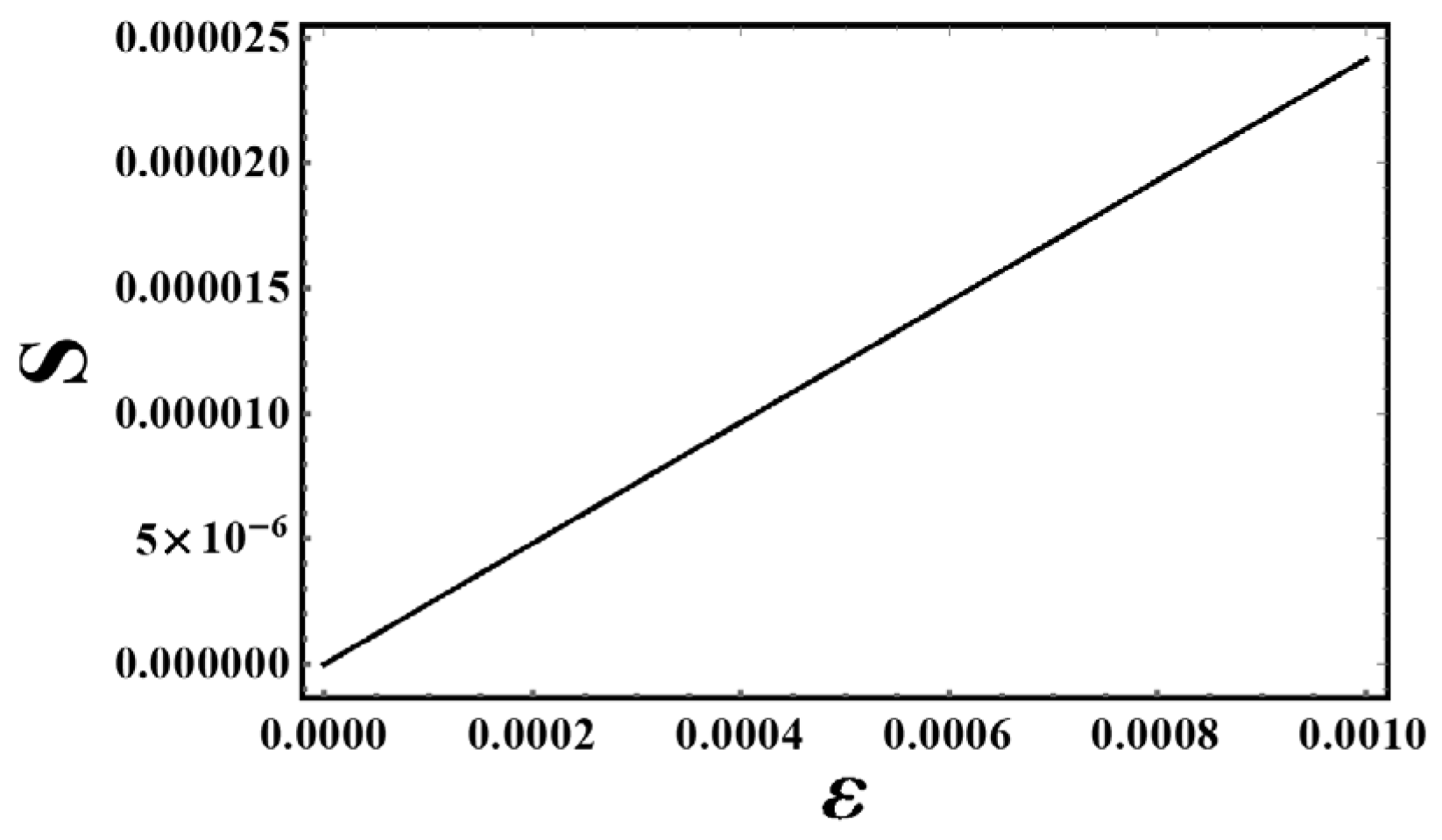
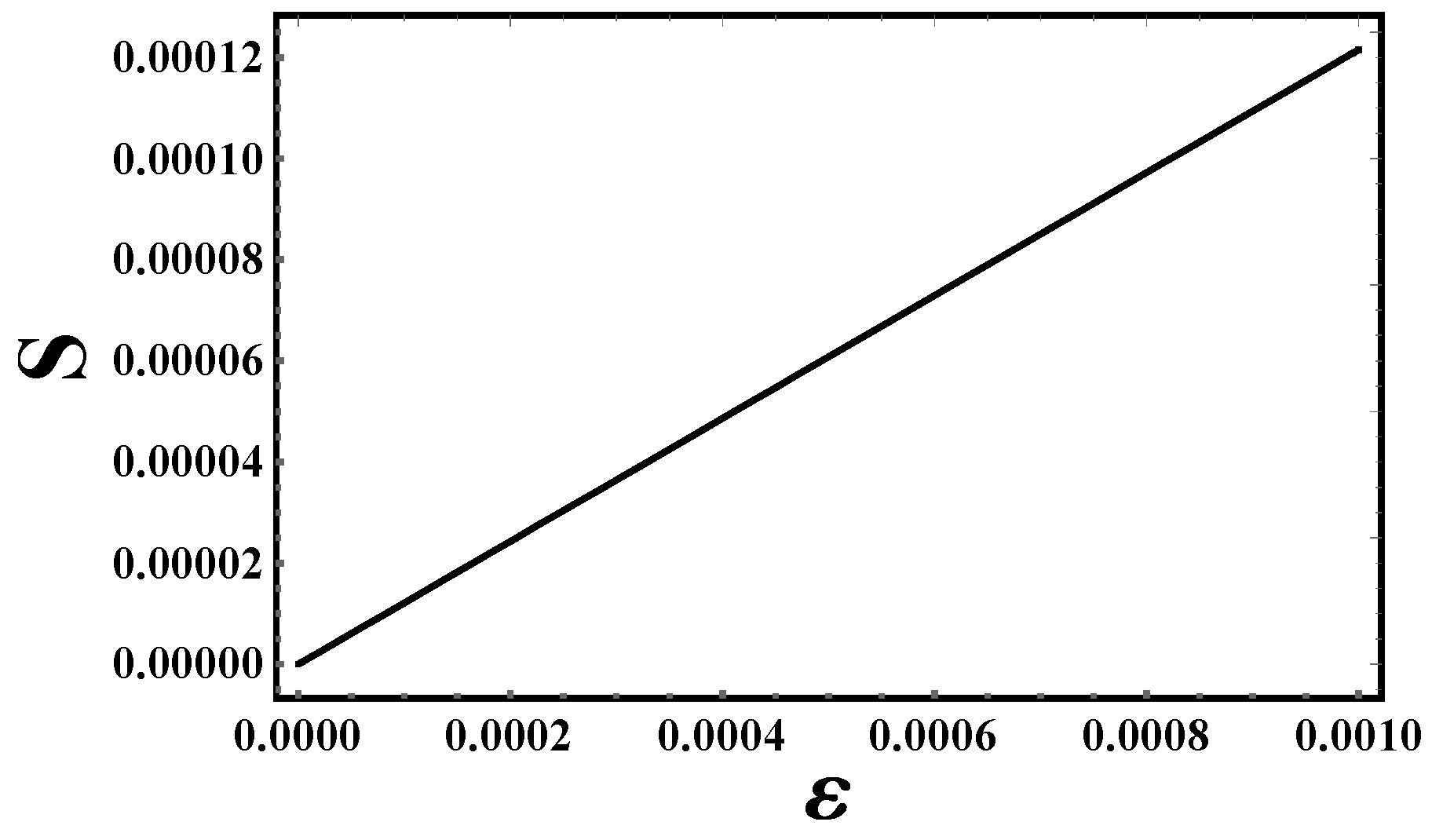
Entropy: Figure 5, Figure 6 and Figure 7 provide a comprehensive analysis of thermodynamic disorder in CGMs based on shell thickness ϵ\epsilonϵ across three gravitational models. It is important to note that the entropy of CGMs becomes zero when there is no shell thickness. As the shell thickness increases, the system’s complexity rises, promoting better energy distribution and leading to a greater degree of disorder. Consequently, this rise in disorder correlates with an increase in entropy. These findings underscore the intricate interplay between shell thickness and the thermodynamic properties of CGMs, highlighting how structural variations influence the overall behavior of these exotic cosmic entities.

(4)

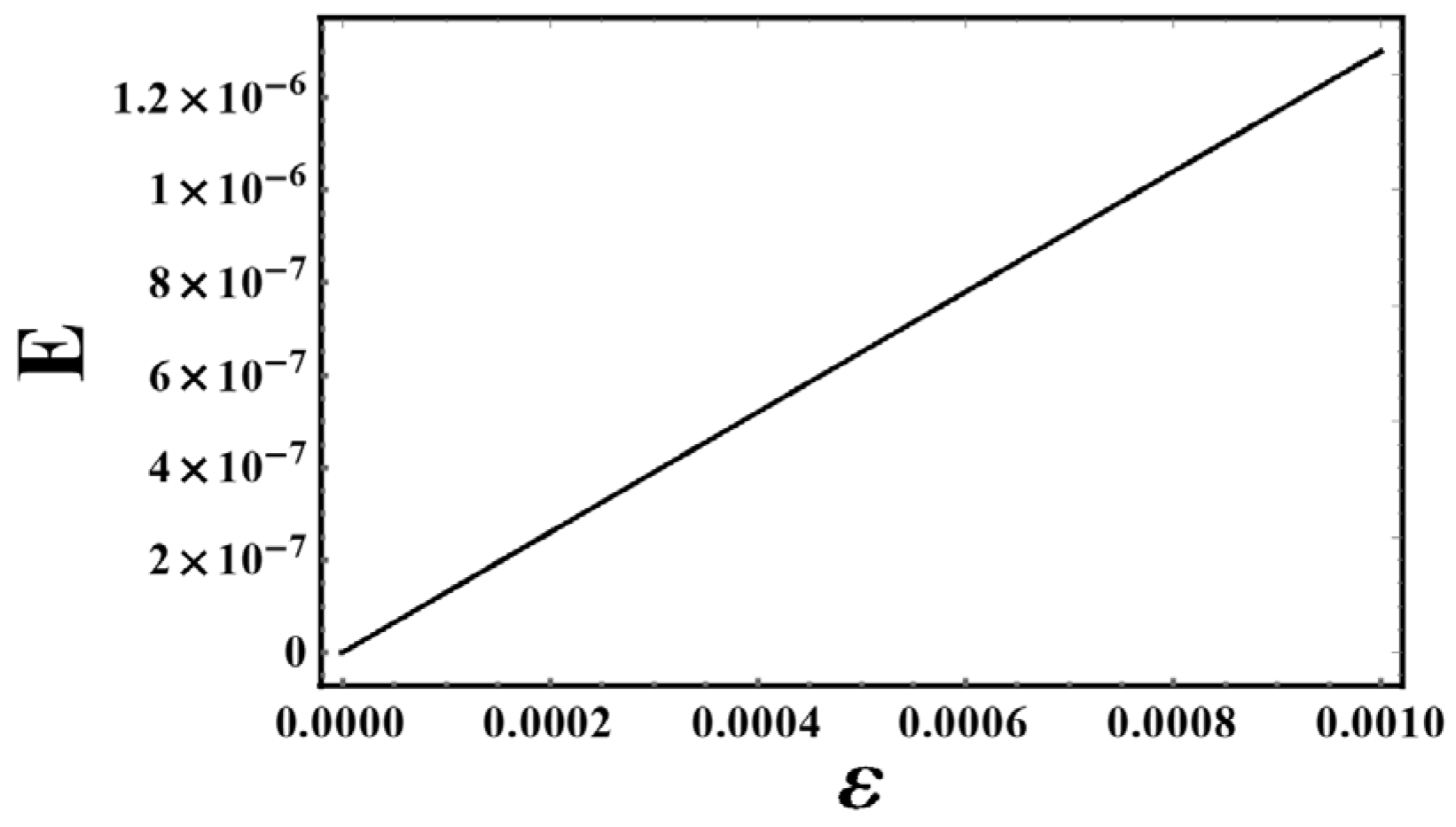
Energy content: Figure 8 establishes a fundamental scaling relation between the shell’s internal energy E and its thickness $\epsilon$ that holds consistently across all three f(T) gravity models. The analysis reveals: Linear energy-thickness dependence: E ∝ $\epsilon$.

(5)

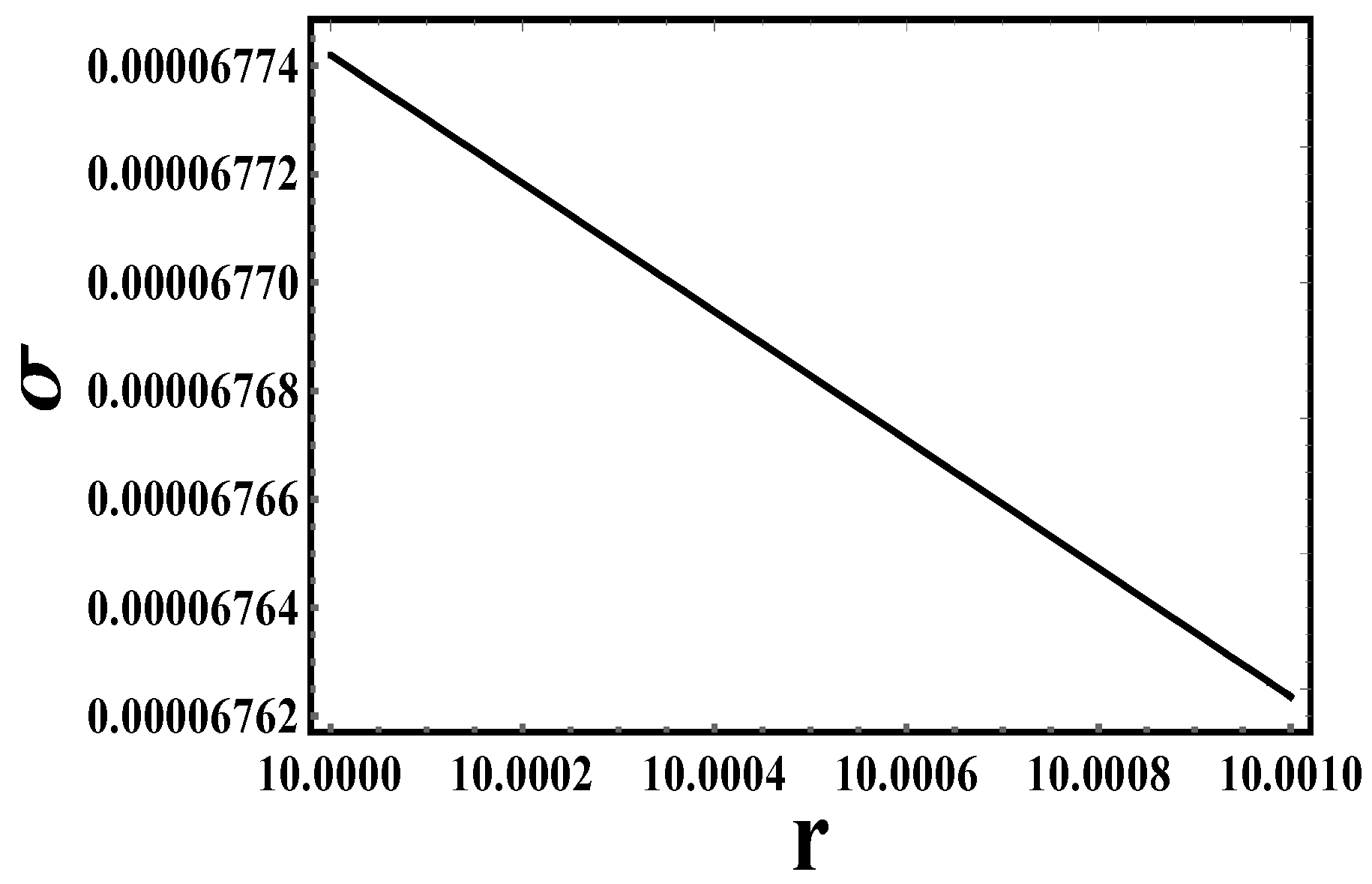
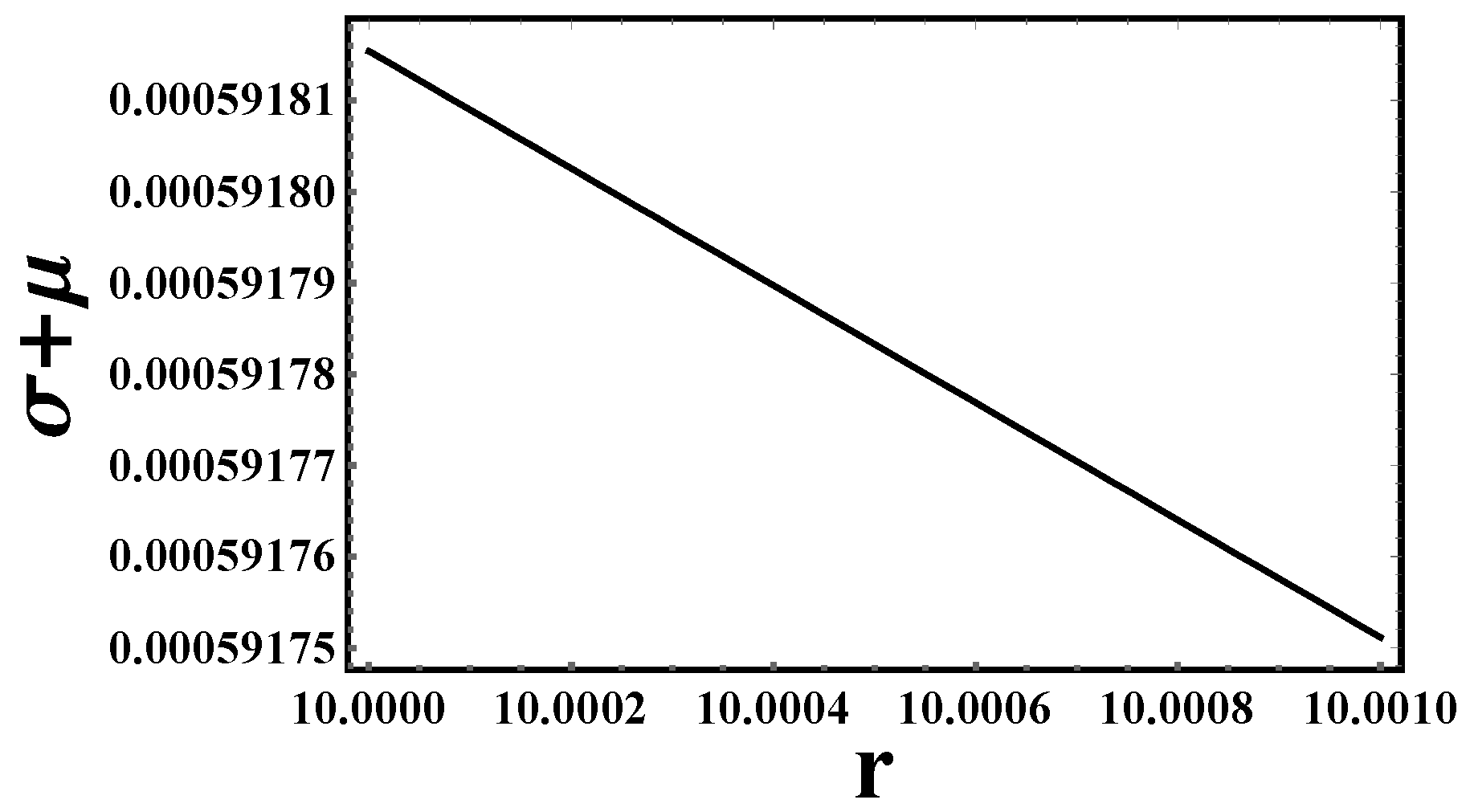
Energy conditions: Let us discuss the energy conditions for the previous models in

Table 4. Comparative Analysis of Energy Conditions in $f\left(T\right)=a+b{T}^{\beta }$ Gravity Models.

Model	Energy Conditions	Physical Interpretation
$f\left(T\right)=T$	WEC, SEC, NEC: Satisfied DEC: Violated	Generally physically plausible except for energy flow restrictions. Possible superluminal energy transport.
$f\left(T\right)=a+bT$	All conditions DEC/WEC/SEC/NEC: Violated	Non-standard energy-momentum tensor. Likely requires exotic matter (e.g., phantom fields).
$f\left(T\right)=T^2$	All conditions DEC/WEC/SEC/NEC: Violated. Special case: σ = μ = 0	Strong spacetime geometry effects.

,

From the previous Table we can conclude the following,

The f(T) = T model (first model) is the most likely candidate to represent a gravastar-like structure among the three proposed scenarios. Here is why:

6.1. Partial Energy Condition Compliance

-

Gravastars require non-singular, ultra-compact solutions where the interior violates some energy conditions (e.g., DEC) but retains stability.

-

The f(T) = T model satisfies WEC, SEC, and NEC (unlike the other two models), which aligns with gravastar stability criteria.

-

The DEC violation matches expectations for gravastars, as they often involve exotic vacuum energy or anisotropic pressures at the shell.

6.2. Physical Plausibility

-

The f(T) = a + bT and f(T) = T² models fail all energy conditions, making them too extreme for gravastar modeling (likely unstable or requiring unphysical matter).

-

The f(T) = T case maintains minimal physicality while allowing DEC-violating effects (similar to Mazur–Mottola gravastars).

6.3. Structural Consistency

-

Gravastars rely on a thin-shell (ultrarelativistic fluid) separating de Sitter-like interiors from exterior Schwarzschild solutions.

-

$f\left(T\right)=T$ model’s shell dynamics (pressure, density trends) better match gravastar expectations than the other models.

-

$f\left(T\right)=a+bT$: Total energy condition violation suggests uncontrollable exotic matter, making it unsuitable for stable gravastar solutions.

-

$f\left(T\right)=T^2$: Even in the σ = μ = 0 case, the model fails all conditions, implying non-viability for gravastar construction.

The research on “Analytical Approximations to Charged Black Hole Solutions in Einstein–Maxwell–Weyl Gravity” [79] develops analytical approximations for charged black holes within a curvature-based modified gravity framework, offering a valuable comparative approach to our torsion-based f(T) gravity study despite the different fundamental descriptions. Similarly, the investigation into “Generic Behavior of electromagnetic Fields of Regular Rotating Electrically Charged Compact Objects” [80] examines singularity-free charged objects through nonlinear electrodynamics, directly intersecting with our gravastar models particularly in the exterior spacetime region. Complementing this, the study “Density and Mass Function for Regular Rotating Electrically Charged Compact Objects” [81] provides essential references for internal structure comparison through its derivation of mass and density functions. Collectively, these works significantly reinforce our theoretical context by supplying comparative regular compact object models, advanced methodological approaches for solving field equations, and crucial insights into stability and structure beyond General Relativity, thereby establishing a solid foundation for future research expansion into rotational dynamics and more sophisticated nonlinear interactions.

Our article presents a rigorous investigation of CGMs within the framework of f(T) gravity, offering singularity-free alternatives to black holes. To fully appreciate the significance of this work, it is essential to situate it within the rich historical and theoretical landscape of research on non-singular, exotic compact objects. This discussion connects our findings to pioneering works on boson stars [82], the gravitational instability of scalar fields [83], and regular black holes [84], thereby highlighting the broader context and implications of our results. The conceptual groundwork for alternatives to singular black holes was laid by Ruffini and Bonazzola [82], who demonstrated that a system of self-gravitating bosons could form stable, soliton-like configurations—now known as boson stars held together by gravity and quantum pressure without an event horizon or singularity. This was a radical departure from the conventional Oppenheimer-Volkoff collapse model and opened the door to exploring horizonless, quantum-gravitational objects. This idea was further advanced by Khlopov, Malomed, and Zeldovich [83], who showed that classical scalar fields could collapse into stable, localized configurations, reinforcing the concept that scalar fields could prevent singularity formation. Subsequent work by Bianchi, Grasso, and Ruffini [84] explored these configurations in an astronomical context, linking theoretical models to potential astrophysical observations. More recently, axion stars boson stars composed of axionic dark matter were proposed by Kolb and Tkachev [85], highlighting how light scalar fields could form compact objects with observable signatures. The gravastar models in our study share a fundamental motivation with boson stars: to avoid the singularities and event horizons of black holes. While boson stars achieve this through quantum scalar fields, our gravastars rely on a phase transition induced by a de Sitter vacuum core and an ultrarelativistic shell; both approaches challenge the classical black hole paradigm and explore the interplay between quantum effects and gravity. A major breakthrough in singularity avoidance came with Dymnikova [86], who constructed one of the first regular black hole solutions with a de Sitter core, replacing the Schwarzschild singularity with a de Sitter vacuum. This idea was later extended in work by Dymnikova and Khlopov [87], who studied regular black hole remnants and “graviatoms” as possible dark matter candidates. Our gravastar models especially in the f(T) = T and f(T) = a + bT cases mirror this de Sitter interior structure, as their interior region with ω = −1 is mathematically analogous to Dymnikova’s regular black hole core. However, unlike black hole remnants, the gravastars in our framework are horizonless, aligning more closely with Mazur and Mottola’s original conception. In conclusion, our study represents a meaningful contribution to the ongoing effort to reconcile quantum mechanics and general relativity through non-singular compact objects. By deriving exact charged gravastar solutions in f(T) gravity and benchmarking them against these foundational works, we not only advance the specific topic of gravastars but also enrich the broader dialog on black hole alternatives, underscoring the importance of modified gravity in addressing the profound puzzle of gravitational collapse.

Finally, while the f(T) = T model is the most promising, it still requires further modifications (e.g., additional constraints on torsion) to fully replicate gravastar properties, with the other two models being too extreme for realistic gravastar scenarios. Nevertheless, the other models we have derived in this article, namely f(T) = a + bT and f(T) = T², represent significant theoretical additions to the foundational General Relativity (GR) model, which is recovered when f(T) = T.

These new models provide a crucial broader context for understanding the role of torsion in compact object physics. While they may not be physically viable as standalone gravastar models due to their violation of key energy conditions, their existence and properties are highly informative. They serve as “stress tests” for the f(T) framework, revealing how different nonlinear extensions of the Lagrangian influence the geometry and matter content of a self-gravitating system. The f(T) = a + bT model, for instance, introduces an effective cosmological constant, demonstrating how torsion can mimic dark energy effects even in local astrophysical systems. The f(T) = T² model, with its stronger nonlinearity, explores the high-torsion regime and its consequential, often extreme, geometric effects. Therefore, the value of these models is not merely in their direct application, but in the complete picture they paint together. By presenting this spectrum of solutions from the GR-equivalent case to more radical extensions our work maps out the landscape of charged gravastars in f(T) gravity. It establishes a clear benchmark: the f(T) = T model as the physically plausible candidate, and the others as important theoretical boundaries that define the limits of viability and illustrate the rich phenomenology that torsion-based gravity can introduce beyond the standard General Relativity picture.