Gravitational Wave Signatures of Warm Dark Matter in the Gauge Extensions of the Standard Model

Abstract

We studied the left-right symmetric extension of the standard model (LRSM), featuring a TeV-scale, right-handed (RH) gauge boson $W_R$ and three RH neutrinos. This setup naturally realizes the type-II seesaw mechanism for active neutrino masses. We identified the conditions that yield sufficient entropy dilution to reconcile the keV sterile neutrino dark matter energy density with observations while inducing an early matter domination (EMD) phase. These constrained the lightest active neutrino mass to $8.59\times {10}^{-10}\mathrm{eV}<m_{{\nu }_1}<5.06\times {10}^{-9}\mathrm{eV}$. The resulting frequency-dependent suppression of the stochastic gravitational wave (GW) background was set by the mass and lifetime of the heavier RH neutrinos. Computing the signal-to-noise ratio (SNR) for future detectors, we found that a blue-tilted primordial tensor spectrum can boost the GW signal to detectable levels (SNR > 10) in experiments such as LISA, BBO, and DECIGO.

1. Introduction

The gravitational wave (GW) background is one of the most significant predictions of the inflationary paradigm [1,2]. These stochastic GWs were generated by the quantum fluctuations of the metric stretched to cosmological scales during the rapid accelerated expansion of the early universe. The detailed time evolution of the Hubble rate during the expansion determines the transfer function that describes how the stochastic GWs at different frequencies were red-shifted to the present day. The resulting GW energy spectrum carries direct information about the physics of inflation and the evolution of the universe thereafter.

The shape and amplitude of the GW background are primarily determined by the primordial tensor power spectrum, which depends on two key parameters: the tensor initial amplitude $A_t$ and the spectral index $n_t$ [3,4]. These parameters are set by the inflationary dynamics and can vary for different inflationary scenarios. Furthermore, the spectrum is also affected by the subsequent thermal history of the universe, including the reheating phase and the radiation-dominated (RD) era [5].

In the standard slow-roll inflationary model, the GW energy spectrum is nearly scale-invariant across a wide range of frequencies. This behavior arises because the relativistic degrees of freedom remain approximately constant for modes re-entering the horizon during the RD era, resulting in minimal distortion of the spectrum. Consequently, the observation of a scale-invariant stochastic GW background would provide compelling evidence for inflation and impose constraints on both the inflationary potential and the reheating dynamics. Deviations from a scale-invariant GW spectrum can originate from two main sources: the tilt of the primordial tensor power spectrum [3,4,6], and modifications in the equation of the state of the early universe arising from the interaction properties of elementary particles during and after reheating [7,8].

One important effect is neutrino free-streaming, first analyzed in Ref. [9], which leads to a damping of the GW amplitude by approximately 35.5% in the frequency range ${10}^{-16}$–${10}^{-10}$ Hz. The extension of this analysis to include all standard model (SM) particles [10] demonstrates that successive changes in the number of relativistic degrees of freedom leave distinctive imprints on the GW energy spectrum.

Moreover, a detailed thermodynamic analysis of SM particles enabled the computation of the temperature dependence of the effective degrees of freedom throughout the expansion history, where the results are provided in the form of tabulated data and fitting functions [11]. In addition, full numerical simulations of the GW spectrum across a wide frequency range, incorporating the dynamics of the inflationary scalar field, its decay during reheating, the evolution of relativistic degrees of freedom, and the anisotropic stress from photons and neutrinos, were performed in Ref. [12].

Observation of gravitational waves from black hole mergers by the LIGO and Virgo collaborations [13,14], together with the GW signals detected by pulsar timing array (PTA) experiments [15,16,17], has stimulated the development of various beyond standard model (BSM) scenarios for GW production. These include studies on leptogenesis [18,19,20], modified cosmologies and non-thermal dark matter [21,22,23], GW spectra arising from electroweak phase transitions [24,25], and topological defects [26]. Other works have focused on primordial black hole (PBH) formation and their associated GW signatures [27], GW generation by vector and tensor fields [28,29], and GWs produced by particle interactions in the early universe plasma [30]. Comprehensive reviews of astrophysical sources and BSM particle physics can be found in Ref. [31], while Ref. [32] discusses how current and future GW detectors may discriminate between the astrophysical and cosmological BSM signatures in the GW background.

An early matter-dominated (EMD) epoch, which can leave imprints on the GW energy spectrum, arises naturally in many BSM scenarios, in which heavy particles temporarily dominate the energy density of the universe before decaying and initiating a radiation-dominated era prior to Big Bang Nucleosynthesis (BBN).

Such a phase frequently appears in models with hidden sectors [33,34,35,36]. During the EMD phase, various mechanisms for the production of massive particles can account for the observed dark matter (DM) abundance, leading to predictions that are testable through cosmological observations and DM direct detection experiments [18,20,37].

Among the various BSM scenarios for dark matter, a sterile neutrino with a mass in the keV range and a small mixing angle with active neutrinos constitutes a well-motivated Warm Dark Matter (WDM) candidate [38,39,40].

Emerging from a minimal extension of the standard model, the keV-scale sterile neutrino can simultaneously explain active neutrino oscillations, the observed dark matter abundance, and the matter–antimatter asymmetry of the universe [41,42].

Several production mechanisms for keV-scale sterile neutrinos have been proposed. One of the earliest is the Dodelson–Widrow (DW) scenario [43], in which sterile neutrinos are produced via non-resonant oscillations with active neutrinos (NRPs). However, this mechanism is now ruled out by structure formation constraints, as it produces sterile neutrino velocity distributions that are too hot [44,45].

An alternative is resonant production (RP), known as the Shi–Fuller mechanism [46], in which a large lepton asymmetry enables efficient active-to-sterile neutrino conversion [47]. In this scenario, the sterile neutrino parameters required to reproduce the observed dark matter abundance are broadly consistent with current cosmological observations, including constraints from the Local Group and high-redshift galaxy counts [47]. Nonetheless, some tension remains with Lyman-$\alpha$ forest data [48].

Additionally, keV sterile neutrino dark matter production via particle decays has been extensively discussed (see Ref. [49] and the references therein).

The lower mass limit of sterile neutrino dark matter is constrained by the universal Tremaine–Gunn bound [50], which applies when all dark matter is composed of sterile neutrinos. A more stringent constraint arises from analyses of the dark matter phase–space distribution in dwarf spheroidal galaxies, leading to $m_{N_1}>1.8$ keV for sterile neutrino non-resonant production (NRP) [51]. This bound was revisited in Ref. [52] in the frame of ΛCold+Warm Dark Matter (ΛCWDM) model, where WDM in the form of sterile neutrinos represents a fraction, $f_{DM}$, from the total DM.

From the combined analysis of WMAP5 and Lyman−α datasets, it was found that if $f_{DM}=1$ (pure Λ>WDM model), then the lower bound of sterile neutrino mass in the NRP case is $M_{N_1}>1.6$ keV (at 95%CL), which scales as $f_{DM}^{1/3}$ [53]. The same analysis shows that, below a certain threshold, $f_{DM}$ approach has a constant value because the contribution of WDM component become too small to be constrained by the data.

A combined analysis of the CMB anisotropy and lensing data, cosmic shear observations, and low-redshift BAO measurements [54] yields a sterile neutrino mass $M_{N_1}=7.88\pm 0.73$ keV (68%CL) and $f_{DM}=0.86\pm 0.07$ (68% CL), which is consistent with the Lyman-$\alpha$ forest constraints that exclude $f_{\mathrm{DM}}=1$ at $3\sigma$ [53]. A review of sterile neutrinos as a potential dark matter candidate can be found in Refs. [55,56].

Sterile neutrino dark matter is unstable. To serve as a viable dark matter candidate, its lifetime ${\tau }_{N_1}$ must exceed the age of the universe, ${\tau }_u\sim {10}^{17}$ s.

A more stringent constraint on ${\tau }_{N_1}$ arises from its radiative decay channel $N_1\to \nu \gamma$, in which a DM sterile neutrino decays into an active neutrino and a photon of energy $E_{\gamma }=M_{N_1}/2$. This photon lies within the sensitivity range of current and upcoming X-ray observatories [57,58,59,60,61]. The decay width of this process imposes an upper bound on the active–sterile neutrino mixing angle ${\theta }_1^2\le 1.8\times {10}^{-5}{(1\mathrm{keV}/M_{N_1})}^5$, leading to the DM sterile neutrino lifetime ${\tau }_{N_1}\sim {10}^{24}$ s, which is six times longer than the age of the universe [39,41].

For $M_{N_1}\ge 2$ keV, the resulting contribution of the DM sterile neutrino $N_1$ to the active neutrino masses, $\delta m_{\nu }\sim {\theta }_1^2{M}_{N_1}$, remains below the uncertainty in the solar neutrino mass-squared difference, as indicated by the global fits to neutrino oscillation data [62]. Consequently, two additional right-handed (RH) neutrinos, $N_2$ and $N_3$, are required to reproduce the observed neutrino oscillation pattern.

In this paper, we assume an inflationary reheating scenario consistent with the normal ordering (NO) of right-handed (RH) neutrino masses $M_{N_1}<M_{N_2}<M_{N_3}$. We further assume that DM sterile neutrino $N_1$ is thermally produced as a relativistic particle via freeze-out, while $N_2$ and $N_3$ decouple while relativistic and then decay out of equilibrium after the freeze-out of $N_1$.

This scenario can be realized within the left-right symmetric extension of the standard model (LRSM), which introduces a right-handed charged gauge boson $W_R$ with a mass at the TeV scale, as well as employs the type-II seesaw mechanism to generate active neutrino masses [63,64,65]. In this model, the mass spectrum of the RH neutrinos leads to the same hierarchical active neutrino spectrum. The presence of the $W_R$ boson plays a key role in accurately predicting the dark matter relic abundance, ensuring that, for RH neutrinos that decouple while relativistic, their freeze-out temperatures, and consequently their yields, are expected to coincide to a very good approximation [66].

Once the heavier RH neutrinos become non-relativistic, they behave as matter and, if they are sufficiently long-lived, can dominate the energy density of the universe. This results in an epoch of early matter domination (EMD), which ends with their decays and the associated release of a substantial amount of entropy.

We show that this entropy injection simultaneously dilutes the abundance of the DM sterile neutrino $N_1$, bringing it into agreement with observational constraints [39,66], and it also suppresses the GW energy density spectrum at scales that re-enter the horizon prior to, or during the decay of, the heavier RH neutrinos, leaving measurable imprints on the spectral shape of the gravitational wave background [18,20,37].

This paper is organized as follows. Section 2 presents the constraints and requirements for DM sterile neutrino production. Section 3 analyses the propagation of inflationary tensor perturbations as gravitational waves. Section 4 discusses the imprints left on the gravitational wave background spectrum by RH neutrino decay and evaluates the capability of various GW experiments in searching these specific signatures in terms of signal-to-noise ratio. Our conclusions are summarized in Section 5.

2. Constraints and Requirements for DM Sterile Neutrino Production

2.1. DM Sterile Neutrino Abundance

Inclusion of the RH-charged gauge boson $W_R$ with TeV mass introduces new annihilation channels and modifies the freeze-out dynamics of RH neutrinos. The scattering of RH neutrinos with the light SM fermions, mediated by the heavy gauge bosons, keeps them in thermal equilibrium. Their freeze-out (decoupling) temperature $T_f$ can be estimated from the out-of-equilibrium condition ${\mathrm{\Gamma }}_N=H\left(T_f\right)$, where ${\mathrm{\Gamma }}_N$ is the interaction rate of and $H\left(T_f\right)$ is the Hubble expansion rate in the radiation-dominated universe [56,66,67]:

$$\begin{array}{c}\hfill {\mathrm{\Gamma }}_N\left(T_f\right)\simeq G_F^2{T}_f^5{\left({\displaystyle \frac{M_W}{M_{W_R}}}\right)}^4,H\left(T_f\right)=\sqrt{{\displaystyle \frac{4\pi g_{\ast f}}{45}}}{\displaystyle \frac{T_f^2}{M_{pl}}},\end{array}$$

(1)

where $g_{{\ast }_f}$ counts the number of relativistic degrees of freedom at $T_f$ $G_F=1.66\times {10}^{-5}$ GeV⁻² is the Fermi constant, $M_W=80.34$ GeV is the mass of the W boson [68] and $M_{pl}=1.2\times {10}^{19}$ GeV is the Planck mass. The out-of-equilibrium condition leads to [67]:

$$\begin{array}{c}\hfill T_f\simeq 4\mathrm{MeV}{\left({\displaystyle \frac{g_{\ast f}}{10.75}}\right)}^{1/6}{\left({\displaystyle \frac{M_{WR}}{M_W}}\right)}^{4/3}.\end{array}$$

(2)

For RH neutrinos, which freeze out while relativistic, the number density per entropy density (the yield) at $T_f$ is as follows:

$$Y\left(T_f\right)={\displaystyle \frac{n_{N_1}\left(T_f\right)}{s\left(T_f\right)}}\simeq {\displaystyle \frac{1}{g_{\ast f}}}{\displaystyle \frac{123\zeta \left(3\right)}{4{\pi }^4}}.$$

(3)

If the gauge interactions of RH neutrinos are universal, their freeze-out temperatures, and consequently their yields, are expected to coincide.

The contribution of the keV sterile neutrino $N_1$ with present-day energy density ${\mathrm{\Omega }}_s$ to the present-day total dark matter energy density ${\mathrm{\Omega }}_{DM}$ is observationally constrained to the energy density fraction $f_{DM}\le 1$. Accordingly, using Equation (3) and taking into account that the yields of RH neutrinos are thermally conserved quantities, then $f_{DM}$ can be written as follows:

$$\begin{array}{c}\hfill f_{DM}={\displaystyle \frac{{\mathrm{\Omega }}_s}{{\mathrm{\Omega }}_{DM}}}={\displaystyle \frac{Y_{N_1}{s}_0}{{\mathrm{\Omega }}_{DM}{\rho }_c}}\left({\displaystyle \frac{M_{N_1}}{1\mathrm{keV}}}\right){\displaystyle \frac{1}{{\Delta }_S}},\end{array}$$

(4)

where $M_{N_1}$ is the sterile neutrino mass, $s_0=2889.2$ cm⁻³ is the present entropy density, and ${\rho }_c=1.05368\times {10}^{-5}$ h² GeV cm⁻³ is the critical energy density. Additionally, ${\mathrm{\Omega }}_{DM}$ is constrained by the cosmological observations to ${\mathrm{\Omega }}_{DM}=0.228\pm 0.005$ at $3\sigma$ [69].

In the following, we adopt the sterile neutrino masses $M_{N_1}$ in the range $1.6÷8$ keV, which is consistent with the observational mass bounds of the keV sterile neutrino [56].

The dilution factor ${\Delta }_s$ in Equation (4) accounts for the post freeze-out entropy injection needed to satisfy the observational constraint $f_{DM}\le 1$. The value of ${\Delta }_s$ is required to avoid the over closure of the universe, which is given by the following:

$${\Delta }_s={\displaystyle \frac{Y_{N_1}{s}_0}{{\mathrm{\Omega }}_{DM}{\rho }_c}}\left({\displaystyle \frac{M_{N_1}}{1\mathrm{keV}}}\right).$$

(5)

2.2. Early Matter Domination (EMD) Onset and the Entropy Dilution

The large entropy injection required to achieve the correct abundance of the sterile neutrino $N_1$ can be generated through the decay of a heavy, long-lived particle with a relatively short lifetime [70,71]. In the LRSM, the only particles capable of such late decays with a significant impact on entropy production are the RH neutrinos $N_2$ and $N_3$.

For simplicity, in what follows, we will focus on $N_2$ as the diluter. In this scenario, the RH neutrino $N_2$ reaches thermal equilibrium at early times through its interactions with the thermal bath. After becoming non-relativistic, it behaves as a matter component and, if sufficiently long-lived, can come to dominate the energy density of the universe.

This leads to a period of early matter domination (EMD), which ends once $N_2$ decays, restoring a radiation-dominated (RD) universe and setting the conditions for Big Bang Nucleosynthesis (BBN).

The important stages of the thermal history in this scenario and their requirements are as follows:

• In order to achieve enough dilution, the $N_2$ neutrino freeze-out temperature $T_f$ should exceed its mass; otherwise, the yield in Equation (3) receives a suppression factor $e^{-M_{N_2}/T_f}$:

  $$T_f>M_{N_2}.$$

  (6)
  As RH neutrino $N_2$ freeze out at temperature $T_f$ is given by Equation (2), Constraint (6) leads to the bound on the RH gauge boson mass $M_{WR}$:

  $$M_{WR}\ge 7\mathrm{TeV}{\displaystyle \frac{1}{g_{\ast f}^{1/8}}}{\left({\displaystyle \frac{M_{N_2}}{1\mathrm{GeV}}}\right)}^{3/4}.$$

  (7)
• The transition of $N_2$ to the non-relativistic regime is around at temperature $T=M_{N_2}$. At this stage, the $N_2$ energy density redshifts more slowly than that of radiation, scaling as ${\rho }_{N_2}\propto a^{-3}$ compared to ${\rho }_r\propto a^{-4}$, and $N_2$ can come to dominate the total energy density of the universe. We denote the temperature at which this transition occurs by $T_{dom}$, and the corresponding Hubble expansion rate by $H_{dom}$. The necessary condition for $N_2$ dominance is as follows:

  $${\mathrm{\Gamma }}_{N_2}<H_{dom}.$$

  (8)
  Condition ${\rho }_{N_2}\simeq {\rho }_r$ can be used to calculate $H_{dom}$ and $T_{dom}$ [37]:

  $$\begin{array}{c}\hfill H_{dom}={\displaystyle \frac{g_{\ast dom}^{2/3}}{g_N^{8/3}}}H(T=M_{N_2}),T_{dom}={\displaystyle \frac{7}{4}}{\displaystyle \frac{M_{N_2}}{g_{\ast }\left(T_{dec}\right)}}\simeq 2\%M_{N_2}.\end{array}$$

  (9)
  Here, $g_{\ast dom}$ and $g_{\ast }\left(T_{dec}\right)$ are the number of relativistic degrees of freedom at $T_{dom}$ and $T_{dec}$, while $g_{\ast N}=2$ accounts for the two degrees of freedom associated with the $N_2$ neutrino.
• Before decaying, $N_2$ becomes non-relativistic as long as its total decay width is smaller than the Hubble rate at temperatures around $M_{N_2}$, i.e., ${\mathrm{\Gamma }}_{N_2}\ll H\left(M_{N_2}\right)$. Assuming that the decay is instantaneous and the decay products thermalize quickly with the radiation bath, the decay temperature $T_{dec}$ can be estimated from the condition ${\mathrm{\Gamma }}_{N_2}=H\left(T_{dec}\right)$ as follows:

  $$\begin{array}{c}\hfill T_{dec}\simeq {\left({\displaystyle \frac{90}{8{\pi }^3{g}_{\ast }\left(T_{dec}\right)}}\right)}^{1/4}\sqrt{{\mathrm{\Gamma }}_{N_2}{M}_{pl}}.\end{array}$$

  (10)
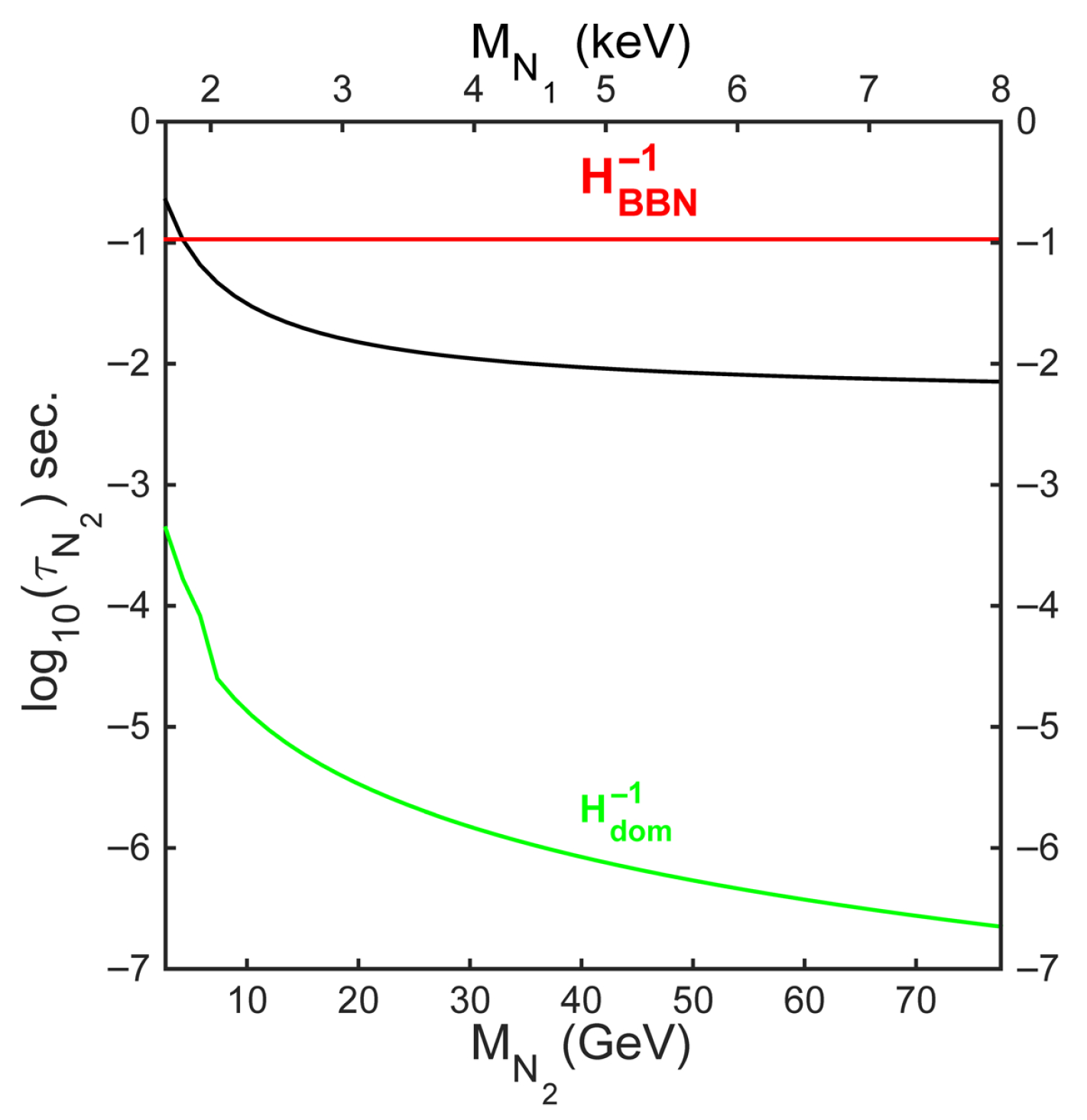
• The EMD era ends once $N_2$ decays and must be completed before the onset of the BBN. This constraint imposes a lower bound on the decay temperature, typically $T_{dec}>T_{BBN}=4$ MeV, corresponding to the following:

  $$\begin{array}{c}\hfill {\mathrm{\Gamma }}_{N_2}>H_{BBN}\sim 10s^{-1},\end{array}$$

  (11)

  leading to the $N_2$ lifetime bound ${\tau }_{N_2}={\mathrm{\Gamma }}_{N_2}^{-1}\sim 1s$.
• After $N_2$ decay is completed, EMD ends and the universe is reheated. The entropy injection associated with the decay products dilutes the pre-existing relics. This dilution is quantified by the entropy dilution factor ${\Delta }_s$, which is defined as the ratio entropy density before and after $N_2$ decay [18,20,37]:

  $$\begin{array}{c}\hfill {\Delta }_s\equiv {\displaystyle \frac{s_{after}}{s_{before}}},\end{array}$$

  (12)

  where $s_{before}$ is the entropy density of the radiation existing from prior stages at $H={\mathrm{\Gamma }}_{N_2}$, while $s_{after}$ is the entropy density generated by $N_2$ decay.
  Using the energy density conservation, we have the following:

  $$\begin{array}{c}\hfill M_{N_2}{Y}_{N_2}{s}_{before}={\displaystyle \frac{3}{4}}{s}_{after}{T}_{dec},\end{array}$$

  (13)

  and the dilution factor is obtained as

  $$\begin{array}{c}\hfill {\Delta }_s\simeq 1.8g_f^{1/4}{\displaystyle \frac{Y_{N_2}{M}_{N_2}}{\sqrt{{\mathrm{\Gamma }}_{N_2}{M}_{pl}}}}.\end{array}$$

  (14)
  Is worth noting that, in this scenario, the freeze-out temperatures of the DM sterile neutrino $N_1$ coincides with that of $N_2$.
  Combining Equations (5) and (14), we obtain the $N_2$ decay width as follows:

  $${\mathrm{\Gamma }}_{N_2}\simeq 0.38\times {10}^{-6}{g}_f^{-1/2}{\displaystyle \frac{M_{N_2}^2}{M_{pl}}}{\left({\displaystyle \frac{1\mathrm{keV}}{M_{N_1}}}\right)}^2.$$

  (15)
  Equation (15) provides the proper entropy dilution if $N_2$ decouples while still relativistic, as indicated in (6), and if it satisfies BBN constraint (11). These constraints translate into a bound on the mass of $N_2$:

  $$\begin{array}{c}\hfill M_{N_2}>\left({\displaystyle \frac{M_1}{1\mathrm{keV}}}\right)(1.7÷10)\mathrm{GeV}.\end{array}$$

  (16)

Figure 1 presents the temperature evolution in the $M_{N_1}-M_{N_2}$ parameter space across the different stages discussed above after imposing the conditions in Equations (6), (7), and (15). The $N_1$ energy density ${\mathrm{\Omega }}_s{h}^2$ is also presented. For reference, this should be compared with the present energy density of the active neutrinos ${\mathrm{\Omega }}_{\nu }\simeq 0.0011$.

In Figure 2, we show the conditions for the early matter domination (EMD) given in Equations (8) and (11).

In the left-right symmetric model (LRSM), where the active neutrino masses are generated by the type II seesaw mechanism, the mass spectrum of RH neutrinos leads to the same hierarchical spectrum for the active neutrinos, implying that the ratio of the mass eigenvalues of active and sterile neutrinos are identical [18,66]. For the normal mass ordering, this relation can be expressed as follows:

$${\displaystyle \frac{m_{{\nu }_1}}{m_{{\nu }_2}}}={\displaystyle \frac{M_{N_1}}{M_{N_2}}},{\displaystyle \frac{m_{{\nu }_2}}{m_{{\nu }_3}}}={\displaystyle \frac{M_{N_2}}{M_{N_3}}}.$$

(17)

The parameter space $M_{N_1}-M_{N_2}$ imposes bounds on the active neutrino mass $m_{{\nu }_1}$ and on the RH neutrino mass $M_{N_3}$. For the normal ordering, $m_{{\nu }_2}=\sqrt{{\Delta }^2{m}_{sol.}}\simeq 8.6\times {10}^{-3}$ eV and $m_{{\nu }_3}=\sqrt{{\Delta }^2{m}_{sol.}+{\Delta }^2{m}_{atm}}\simeq 0.05$ eV, where ${\Delta }^2{m}_{sol.}=7.{420}_{-0.20}^{+0.21}\times {10}^{-5}\mathrm{eV}$ and ${\Delta }^2{m}_{atm.}=2.{517}_{-0.028}^{+0.026}\times {10}^{-3}\mathrm{eV}$ are the solar and atmospheric neutrino mass-squared differences obtained, respectively, from the global fit to neutrino oscillation data [62], we obtain the following:

$$\begin{array}{ccc}\hfill 8.59\times {10}^{-10}\mathrm{eV}& <& m_{{\nu }_1}<5.06\times {10}^{-9}\mathrm{eV}\hfill \end{array}$$

(18)

$$\begin{array}{ccc}\hfill 15.21\mathrm{GeV}& <& M_{N_3}<450.57\mathrm{GeV}.\hfill \end{array}$$

(19)

3. The Spectrum of the Gravitational Waves

The gravitational wave (GW) energy density spectrum today can be written as follows [20,72]:

$$\begin{array}{c}\hfill {\mathrm{\Omega }}_{GW}\left(k\right)={\displaystyle \frac{1}{12H_0^2{a}_0^2}}{\left[T^{\prime }(k,{\tau }_0)\right]}^2\mathcal{P}\left(k\right),\end{array}$$

(20)

where k is the GW wave number, ${\tau }_0=2/H_0$ is the conformal time today, $\mathcal{P}\left(k\right)$ is the primordial power spectrum of the tensor modes, ${\left[T^{\prime }(k,{\tau }_0)\right]}^2$ is the derivative of the transfer function with respect to the conformal time, $a_0=1$ is the present-day scale factor, and $H_0\simeq 2.2\times {10}^{-4}$ Mpc⁻¹ is the present Hubble expansion rate [69].

In the sub-horizon regime relevant in this paper, i.e., $k{\tau }_0\gg 1$, one typically uses the approximation ${\left[T^{\prime }(k,{\tau }_0)\right]}^2\sim k^2{T}^2(k,{\tau }_0)$, leading to the following:

$${\mathrm{\Omega }}_{GW}\left(k\right)={\displaystyle \frac{1}{12}}{\left({\displaystyle \frac{k}{a_0{H}_0}}\right)}^2{T}^2\left(k\right)\mathcal{P}\left(k\right),$$

(21)

The primordial power spectrum of the tensor modes $\mathcal{P}\left(k\right)$ at the pivot scale $k_{*}$ can be parametrized in terms of the amplitude of the tensor modes $A_T$ and the tensor spectral index $n_T$ as follows:

$$\begin{array}{c}\hfill \mathcal{P}\left(k\right)=A_T\left(k_{*}\right){\left({\displaystyle \frac{k}{k_{*}}}\right)}^{n_T}.\end{array}$$

(22)

The amplitude of the tensor modes $A_T\left(k_{*}\right)$ is related to the amplitude of the scalar modes $A_s\left(k_{*}\right)$ through the following:

$$A_T\left(k_{*}\right)=A_s\left(k_{*}\right)r,$$

(23)

where r is the tensor-to-scalar ratio. In the standard slow-roll, inflation $n_T$ satisfies the consistency relation $n_T\simeq -r/8$, leading to a red-tilted spectrum $n_T<0$.

Alternative inflationary models and particle production models that allow departures from the consistency relation, leading to a blue-tilted spectrum ($n_T>0$), are also discussed in the literature [73,74].

In this analysis, we adopted $r=0.036$, as indicated by the combined Planck/BICEP2 observations [75], set $A_s\left(k_{*}\right)=2.0989\times {10}^{-9}$ at $k_{*}=0.05,{\mathrm{Mpc}}^{-1}$ [69], which take $n_T$ as the free parameter.

The transfer function $T^2\left(k\right)$ is given by the following:

$$T^2\left(k\right)={\mathrm{\Omega }}_m^2\left({\displaystyle \frac{g_{\ast }\left(T_{hc}\right)}{g_{*}^0}}\right){\left({\displaystyle \frac{g_{\ast s}^0}{g_{\ast s}\left(T_{in}\right)}}\right)}^{4/3}{\left({\displaystyle \frac{3j_1\left(z_k\right)}{z_k}}\right)}^{2}F\left(k\right),$$

(24)

where $g_{*}^0$ = 3.36 and $g_{\ast s}^0$ = 3.91 are the present time effective degrees of the freedom for energy density and entropy density, respectively; ${\mathrm{\Omega }}_m$ = 0.31 is the total matter energy density parameter [69]; $F\left(k\right)$ is a fitting function; $j_1\left(z_k\right)$ is the spherical Bessel function; and $z_k=k{\tau }_0$. For $z_k\gg 1$, $j_1\left(z_k\right)$ can be approximated by $j_1\left(z_k\right)\simeq 1/\left(\sqrt{2}{z}_k\right)$.

The horizon crossing temperature $T_{hc}$ associated with the scale k, can be expressed as [23]:

$$\begin{array}{c}\hfill T_{hc}={\displaystyle \frac{k{M}_{pl}}{1.66a_0{T}_0{g}_{*}^{1/2}\left(T_{hc}\right)}}{\left({\displaystyle \frac{g_{\ast s}\left(T_{hc}\right)}{g_{\ast s}^0}}\right)}^{1/3}.\end{array}$$

(25)

Taking $k=a_{hc}{H}_{hc}$ and applying the entropy conservation $g_{\ast s}{a}^3=$ const., the Hubble expansion rate at the horizon crossing $H_{hc}$ is obtained as follows:

$$H_{hc}={\displaystyle \frac{k^2}{a_0^2{T}_0^2}}{\displaystyle \frac{M_{pl}}{1.66}}{\displaystyle \frac{1}{g_{*}^{1/2}\left(T_{hc}\right)}}{\left({\displaystyle \frac{g_{\ast s}\left(T_{hc}\right)}{g_{\ast s}^0}}\right)}^{2/3}.$$

(26)

We use “0” and “hc” to denote quantities at the present time and at the horizon crossing, respectively, and $T_0\simeq 2.725$ K the present cosmic microwave temperature.

The frequency f corresponding to the mode k crossing the horizon at $T_{hc}$ is given by:

$$\begin{array}{c}\hfill f={\displaystyle \frac{k}{2\pi a_0}}={\displaystyle \frac{H_{hc}}{2\pi }}{\displaystyle \frac{a_{hc}}{a_0}}\simeq 2.65\times {10}^{-8}{\left({\displaystyle \frac{g_{*}\left(T_{hc}\right)}{106.75}}\right)}^{1/2}{\left({\displaystyle \frac{g_{\ast s}\left(T_{hc}\right)}{106.75}}\right)}^{-1/3}\left({\displaystyle \frac{T_{hc}}{1\mathrm{GeV}}}\right)\mathrm{Hz}.\end{array}$$

(27)

In the standard cosmological model, the fitting function $F\left(k\right)$ from Equation (24) is given by the following [3,23,74]:

$$\begin{array}{c}\hfill F_{st}\left(k\right)=T_1^2\left({\displaystyle \frac{k}{k_{eq}}}\right)T_2^2\left({\displaystyle \frac{k}{k_{RH}}}\right),\end{array}$$

(28)

where the wave numbers corresponding to the matter–radiation equality and the completion of reheating are, respectively, as follows:

$$\begin{array}{ccc}\hfill k_{eq}& =& 7.1\times {10}^{-2}{\mathrm{Mpc}}^{-1}{\mathrm{\Omega }}_m{h}^2,\hfill \end{array}$$

(29)

$$\begin{array}{ccc}\hfill k_{RH}& =& 1.7\times {10}^{14}{\mathrm{Mpc}}^{-1}{\left({\displaystyle \frac{g_{\ast s}\left(T_{RH}\right)}{g_{\ast s}^0}}\right)}^{1/6}\left({\displaystyle \frac{T_{RH}}{{10}^7\mathrm{GeV}}}\right).\hfill \end{array}$$

(30)

For $T_1^2\left(x\right)$, $T_2^2\left(x\right)$, we use following fitting functions [23,76]:

$$\begin{array}{ccc}\hfill T_1^2\left(x\right)& =& 1+1.57x+3.42x^2,T_2^2\left(x\right)={(1-0.22x^{3/2}+0.65x^2)}^{-1}.\hfill \end{array}$$

For the case with an early matter domination (EMD) phase, $F\left(k\right)$ takes the following form:

$$\begin{array}{c}\hfill F_{EMD}\left(k\right)=T_1^2\left({\displaystyle \frac{k}{k_{eq}}}\right)T_2^2\left({\displaystyle \frac{k}{k_{dec}}}\right)T_3^2\left({\displaystyle \frac{k}{k_{dec}^S}}\right)T_2^2\left({\displaystyle \frac{k}{k_{RH}^S}}\right),\end{array}$$

(31)

where

$$\begin{array}{ccc}\hfill k_{dec}& =& 1.7\times {10}^{14}{\mathrm{Mpc}}^{-1}{\left({\displaystyle \frac{g_{\ast s}\left(T_{dec}\right)}{g_{\ast s}^0}}\right)}^{1/6}\left({\displaystyle \frac{T_{dec}}{{10}^7\mathrm{GeV}}}\right)\hfill \end{array}$$

(32)

$$\begin{array}{ccc}\hfill k_{dec}^S& =& k_{dec}{\Delta }_s^{2/3},k_{RH}^S=k_{RH}{\Delta }_s^{-1/3},\hfill \end{array}$$

(33)

where $T_{dec}$ denotes the $N_2$ sterile neutrino decay temperature given in Equation (10), $T_{RH}$ represents the reheating temperature after inflation, and ${\Delta }_s$ is the entropy dilution factor defined in Equation (14).

For the fitting function $T_3^2\left(x\right)$ we used the following:

$$\begin{array}{c}\hfill T_3^2\left(x\right)=1+0.59x+0.65x^2.\end{array}$$

(34)

Characteristic scales $k_{dec}^S$ and $k_{RH}^S$ encode key information about the EMD phase, specifically its onset and the end of the associated entropy dilution.

4. Results

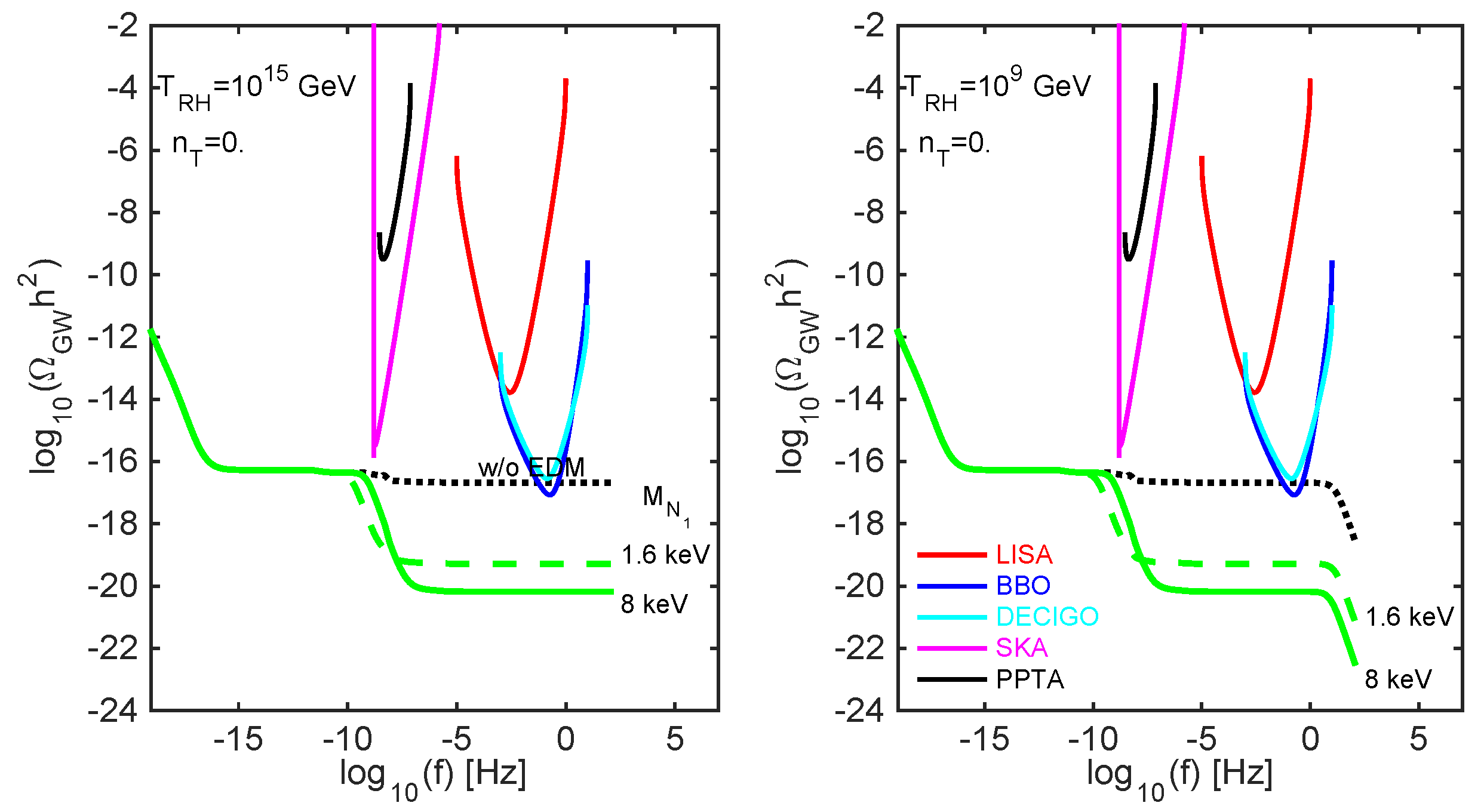
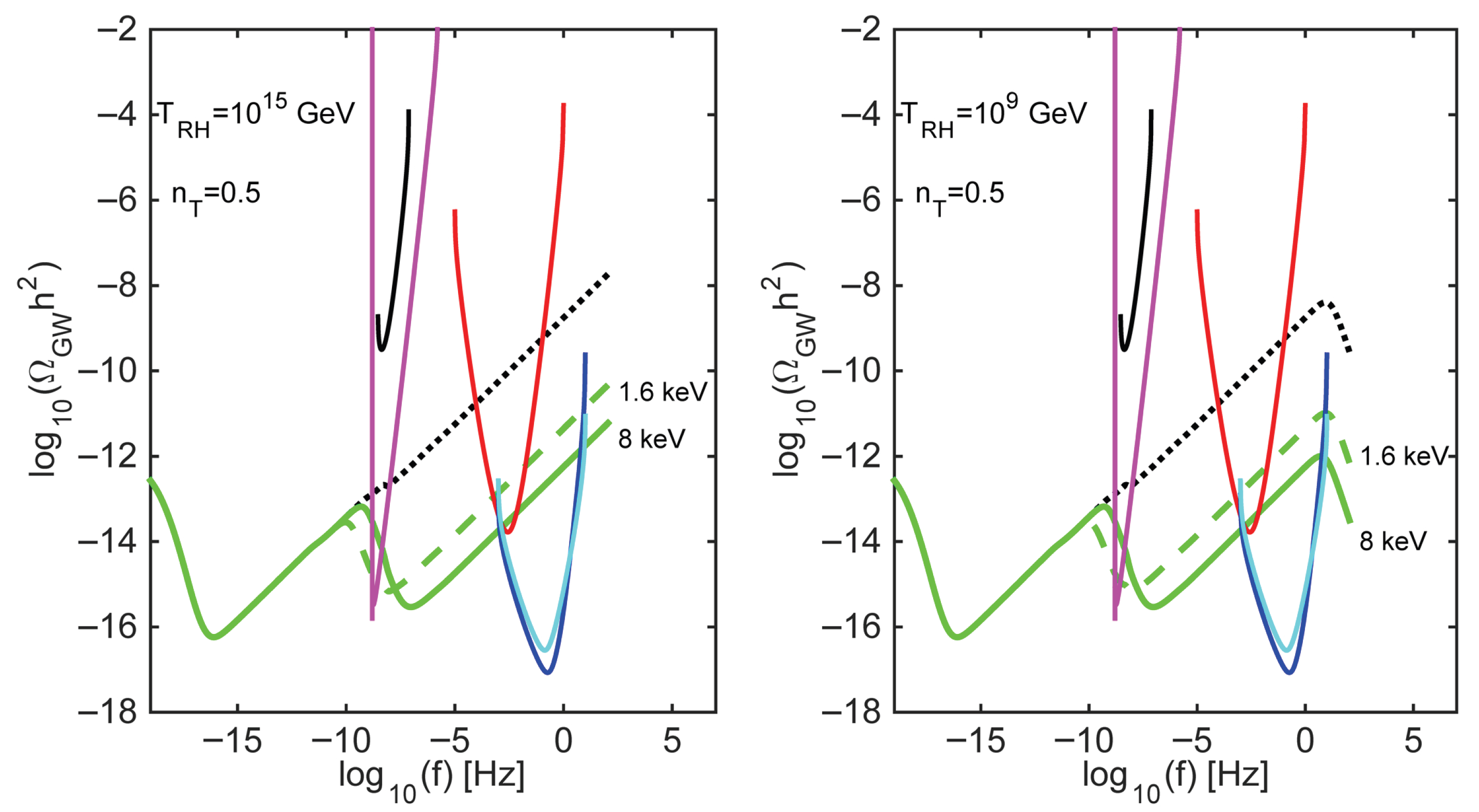
4.1. DM Signatures in the Gravitational Wave Background

We computed the energy density spectrum of the gravitational waves (GWs) for the standard model and for models with an early matter domination phase (EDM).

Figure 3 and Figure 4 present the GW energy density spectra obtained for tensor spectral index $n_T=0$ and $n_T=0.5$, respectively.

Both figures present the spectra for two benchmark reheating temperatures $T_{RH}={10}^{15}$ GeV and $T_{RH}={10}^9$ GeV. Each figure shows a characteristic suppression in the GW spectrum that arises when entropy dilution from $N_2$ decay dominates, as characterized by the $k_{dec}^S$ given in Equation (33). The suppression ends once the $N_2$ decay is completed at $T_{dec}$ and occurs at $k_{dec}$, as defined in Equation (33). This suppression is a direct consequence of the duration of the EMD phase, which is determined by the $N_2$ neutrino mass $M_{N_2}$ and is lifetime ${\tau }_N$.

A larger ${\tau }_N$ delays the $N_2$ decay, lowering $T_{dec}$ and extending the EMD duration. These dependencies are clearly illustrated in Figure 3 and Figure 4, where they are shown by green dashed lines.

In a similar way, increasing $M_{N_2}$ rises $T_{dec}$, enhancing the entropy dilution and increasing the suppression effect. These dependencies are shown in Figure 3 and Figure 4 by green continuous lines.

The high-frequency suppression for $T_{reh}={10}^9$ GeV arises from the inflationary reheating at the characteristic scale $k_{RH}$ given in Equation (30).

Figure 3 clearly shows that, for $n_T=0$, the prospect of detecting the GW spectrum by the current and upcoming missions is low. However, a blue-tilted spectrum can enhance the GW spectrum, as illustrated in Figure 4 for $n_T=0.5$.

In the standard inflationary models, the tensor spectral index is typically red, corresponding to a negative tensor tilt ($n_T<0$). However, a number of non-standard or modified early-universe scenarios allow for a blue tilt tensor spectral index ($n_T>0$). Examples include super-inflation [79,80], phantom inflation [81,82,83], Galileon inflation [84,85,86], and gas string inflation [87,88], as well as the multi-field and higher-curvature correction models of inflation [89,90].

A blue tilt spectral index $n_T>0$ can enhance the GW spectrum by increasing the effective number of the relativistic degrees of freedom $N_{eff}$ before recombination with its deviation $\Delta N_{eff}$ from the standard value $N_{eff}=3.046$ [68]. Thus, the GW spectrum is subject to an upper bound arising from $\Delta N_{eff}$ [91]:

$${\int }_{f_{min}}^{f_{max}}{\displaystyle \frac{\mathrm{d}f}{f}}{\mathrm{\Omega }}_{GW}\left(f\right)h^2\le 5.6\times {10}^{-6}\Delta N_{eff},$$

(35)

where $f_{min}$ is the ultraviolet cutoff that is typically ${10}^{-18}$ Hz for CMB and ${10}^{-10}$ Hz for BBN. The ultraviolet cutoff, $f_{max}$, represents the size of the horizon at the end of inflation and depends on the reheating temperature $T_{RH}$ [92]. Assuming instantaneous reheating with $T_{RH}\sim {10}^{15}$ GeV, one obtains $k_{end}\sim {10}^{23}$ Mpc⁻¹, leading to $f_{max}\simeq {10}^8$ Hz [93].

Current cosmological observations place upper limits on $\Delta N_{eff}$, which in turn constrain the tensor spectral index via Equations (20) and (35). Specifically, the bounds are $\Delta N_{eff}\le 0.28$ from CMB measurements [94] and $\Delta N_{eff}\le 0.4$ from BBN data [95].

Combining the CMB and BBN constraints yields an upper limit on the tensor spectral index $n_T\le 0.4$ (95% CL) within the standard cosmological model when assuming the current tensor-to-scalar ratio to be $r\le 0.035$ and $T_{RH}\simeq {10}^{15}$ GeV [96].

Direct measurements from ground-based interferometers, such as LIGO and VIRGO, constrain the GW energy density to ${\mathrm{\Omega }}_{GW}\le {10}^{-7}$ in the frequency range 20–85.8 Hz [97], which corresponds to an upper limit on the tensor spectral index of $n_T\le 0.52$ [94].

The tensor spectral index upper bounds are derived under the assumption that the primordial tensor power spectrum follows a power–law behavior, as given in Equation (22), which is an approach widely adopted in the literature. However, the frequencies probed by the GW experiments correspond to modes that exited the horizon near the end of inflation. Consequently, assuming a pure power–law form across all frequencies can render the estimation of $n_T$ unreliable [98,99].

Ref. [98] demonstrates that, at high frequencies, the primordial tensor power spectrum can exhibit a strong dependence on the running of the tensor spectral index ${\alpha }_T=\mathrm{d}{n}_T/\mathrm{d}lnk$, which parameterizes the scale dependence of the tensor tilt.

The sensitivity of upcoming CMB experiments, such as CMB-S4 [100], CMB-Bharat [101], and CMB-HD [102], are expected to significantly improve the constraints on the tensor-to-scalar ratio and $\Delta N_{eff}$. In particular, the CMB-S4 experiment aims to reach a sensitivity of $r\sim {10}^{-3}$ and $\Delta N_{eff}\le 0.05$ that, in turn, will improve the constraints on the tensor tilt.

The left panel of Figure 5 shows the tensor spectral index sensitivity curves for the future space-based interferometer experiments LISA [103,104], BBO [105,106], and DECIGO [107], and they were derived from the corresponding power–law-integrated sensitivity curves (PLISCs) that are available online in the Zenodo repository [77,78]. These results were obtained within the framework of standard cosmology for a reheating temperature of $T_{RH}={10}^{15}$ GeV and for two values of the tensor-to-scalar ratio: the current upper limit $r\le 0.035$ and the forecasted value $r\le 0.001$. We also include the current and projected upper bounds on $n_T$ from the CMB and BBN observations, as well as the tensor tilt constraint from VIRGO and LIGO.

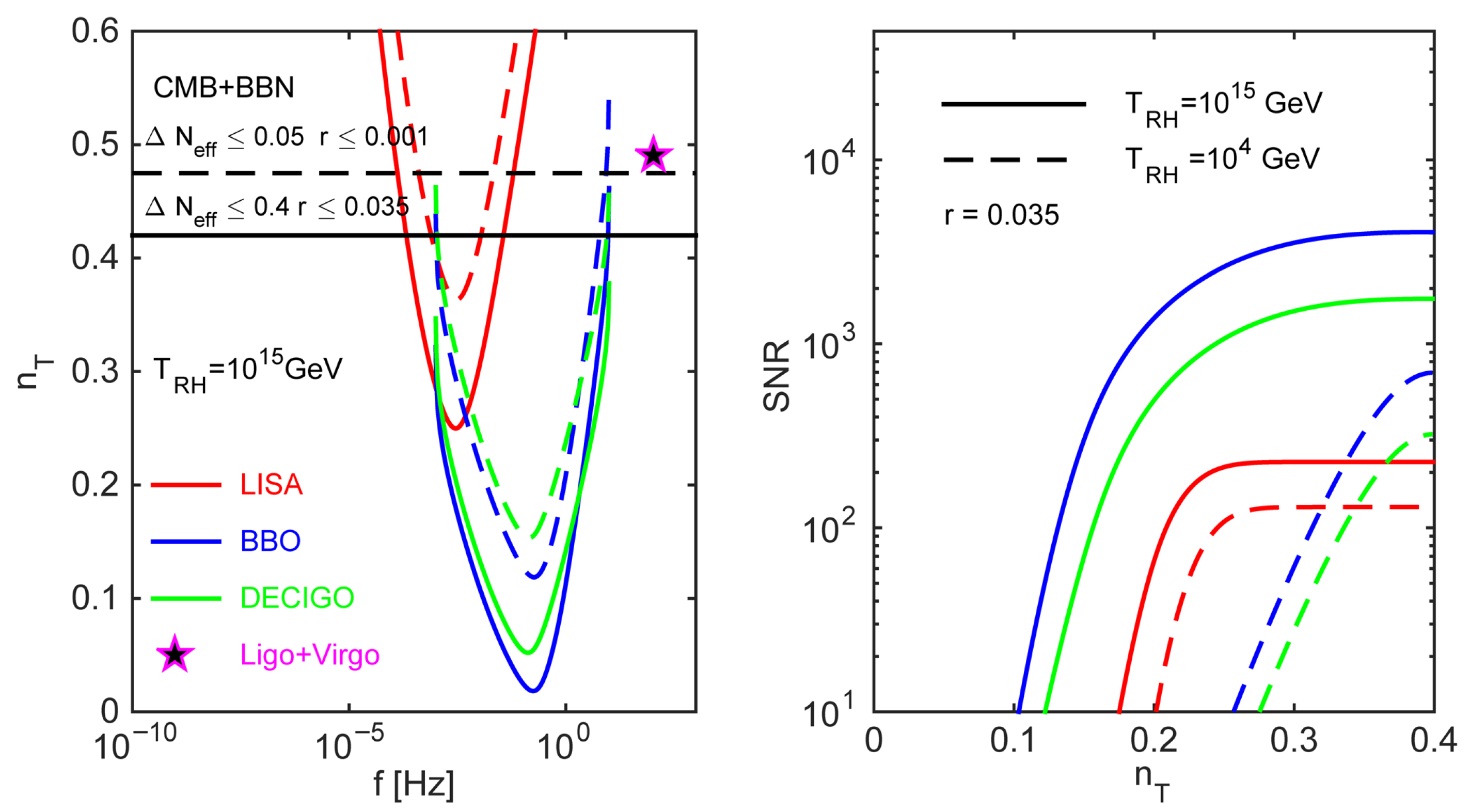
4.2. Signal-to-Noise Ratio for GW Experiments

To evaluate the capability of various GW experiments in searching for the specific early universe evolution imprints in the GW spectra described above, we computed the signal-to-noise ratio (SNR) using the PLISC files for the future space interferometers LISA, BBO, and DECIGO. The SNR is defined as follows:

$$\begin{array}{c}\hfill SNR\equiv \sqrt{{\tau }_{obs}{\int }_{f_{min}}^{f_{max}}\mathrm{d}f{\left({\displaystyle \frac{{\mathrm{\Omega }}_{GW}^{EDM}\left(f\right)h^2}{{\mathrm{\Omega }}_{GW}^{exp}\left(f\right)h^2}}\right)}^2},\end{array}$$

(36)

where ${\mathrm{\Omega }}_{GW}^{EDM}\left(f\right)$ are the GW energy density spectra discussed in the previous section, ${\mathrm{\Omega }}_{GW}^{exp}\left(f\right)$ denotes the energy density spectra derived from the PLISC signals, $f_{min}$ and $f_{max}$ define the operational frequency range corresponding to different experiments, and ${\tau }_{obs}$ is the total observation time. For a consistent sensitivity comparison, we adopted a common observation time of ${\tau }_{obs}=5$ years for all experiments and imposed the detection threshold at $SNR\ge 10$ [72].

In this analysis, we treated $n_T$ and $T_{RH}$ as free parameters within the region of parameter space allowed by the CMB and BBN constraints for $r\le 0.035$, starting from $T_{RH}={10}^{15}$ GeV. The lower limit of $T_{RH}={10}^4$ GeV was imposed by the requirement that the reheating temperature must exceed the mass of the heaviest right-handed (RH) neutrino, $M_{N_3}$. The right panel of Figure 5 shows the allowed region $(n_T,T_{RH})$ that yields the signal-to-noise ratio SNR $\ge 10$, which was obtained for the LISA, BBO, and DECIGO experiments. The high-frequency suppression of the ${\mathrm{\Omega }}_{GW}^{EDM}\left(f\right)$ resulting from the inflationary reheating at the characteristic scale $k_{RH}$ manifests as a decrease in the signal-to-noise ratio with decreasing $T_{RH}$. Since the SNR scales with $T_{RH}$, for clarity, the figure presents the results obtained for for $T_{RH}={10}^{15}$ GeV and $T_{RH}={10}^4$ GeV.

5. Conclusions

In this work, we considered the left-right symmetric extension of the standard model (LRSM), which introduces a right-handed charged gauge boson, $W_R$, with a mass at the TeV scale. This framework naturally accommodates the type-II seesaw mechanism for generating active neutrino masses.

The right-handed $W_R$ boson plays a central role in determining the dark matter relic abundance. For RH neutrinos that decouple while still relativistic, it ensures that, to a very good approximation, their freeze-out temperatures, and thus their yields, are identical.

At later times, once the heavier RH neutrinos become non-relativistic, they behave as matter and come to dominate the energy density of the universe. This leads to a period of early matter domination (EMD), which ends when the RH neutrinos decay, releasing a significant amount of entropy.

We analyzed the conditions required to achieve the appropriate entropy dilution that both aligns the sterile neutrino dark matter abundance with observational constraints and induces an early matter domination phase. The latter leaves a characteristic, frequency-dependent suppression in the spectral shape of the stochastic gravitational wave background. Furthermore, we found that these conditions impose bounds on the lightest active neutrino mass: $8.59\times {10}^{-10} \mathrm{eV}<m_{{\nu }_1}<5.06\times {10}^{-9} \mathrm{eV}$.

We demonstrate that the frequency-dependent suppression of the gravitational wave background arises directly from the duration of the early matter domination phase, which is governed by the mass and lifetime of the heavier RH neutrino. To assess the detectability of this suppression in the GW energy spectrum by the upcoming experiments, such as SKA, LISA, BBO, and DECIGO, we evaluated the corresponding signal-to-noise ratio (SNR).

We found that a blue-tilted primordial tensor power spectrum can significantly enhance the GW energy density, enabling detection with $SNR>10$ in experiments such as LISA, BBO, and DECIGO.

The main challenge faced in this model is the mass of right-handed gauge boson $M_{WR}\sim 10$ TeV. Theoretical considerations set a lower bound $M_{WR}>$ 2.5–4 TeV [67], while direct searches, such as ATLAS and CMS, continue to raise the experimental limits on $M_{W_R}$ [68]. Alternative approaches to avoid the overproduction of sterile neutrino dark matter within the LRSM have been proposed. For instance, Ref. [67] discusses a scenario in which all new gauge interactions are realized at the QCD scale.