Ringing of Reissner–Nordström Black Holes with a Non-Abelian Hair in Gravity’s Rainbow
Abstract
1. Introduction
2. Black Hole Solutions and Massless Scalar Perturbations
3. Quasinormal Modes
3.1. Asymptotically Flat Spacetime
3.2. Asymptotically dS Spacetime
4. Greybody Factors
5. Outlook and Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
| 1 | This is actually a physical assumption due to the fact that the test particles have much less energy far from the black hole compared to the particles close to the black hole, implying that as (or ). |
References
- Kokkotas, K.D.; Schmidt, B.G. Quasinormal modes of stars and black holes. Living Rev. Rel. 1999, 2, 2. [Google Scholar] [CrossRef] [PubMed]
- Nollert, H.P. Quasinormal modes: The characteristic sound of black holes and neutron stars. Class. Quantum Grav. 1999, 16, R159. [Google Scholar] [CrossRef]
- Berti, E.; Cardoso, V.; Starinets, A.O. Quasinormal modes of black holes and black branes. Class. Quantum Grav. 2009, 26, 163001. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zhidenko, A. Quasinormal modes of black holes: From astrophysics to string theory. Rev. Mod. Phys. 2011, 83, 793. [Google Scholar] [CrossRef]
- Berti, E.; Cardoso, V.; Will, C.M. Gravitational-wave spectroscopy of massive black holes with the space interferometer LISA. Phys. Rev. D 2006, 73, 064030. [Google Scholar] [CrossRef]
- Barack, L.; Cardoso, V.; Nissanke, S.; Sotiriou, T.P.; Askar, A.; Belczynski, C.; Bertone, G.; Bon, E.; Blas, D.; Brito, R.; et al. Black holes, gravitational waves and fundamental physics: A roadmap. Class. Quantum Grav. 2019, 36, 143001. [Google Scholar] [CrossRef]
- Momennia, M. Quasinormal modes of self-dual black holes in loop quantum gravity. Phys. Rev. D 2022, 106, 024052. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, C.; Ma, Y. Shadow and stability of quantum-corrected black holes. Eur. Phys. J. C 2023, 83, 619. [Google Scholar] [CrossRef]
- Yang, S.; Guo, W.D.; Tan, Q.; Liu, Y.X. Axial gravitational quasinormal modes of a self-dual black hole in loop quantum gravity. Phys. Rev. D 2023, 108, 024055. [Google Scholar] [CrossRef]
- Livine, E.R.; Montagnon, C.; Oshita, N.; Roussille, H. Scalar Quasi-Normal Modes of a Loop Quantum Black Hole. J. Cosmol. Astropart. Phys. 2024, 10, 037. [Google Scholar] [CrossRef]
- Gong, H.; Li, S.; Zhang, D.; Fu, G.; Wu, J.P. Quasinormal modes of quantum-corrected black holes. Phys. Rev. D 2024, 110, 044040. [Google Scholar] [CrossRef]
- Cao, L.M.; Chen, J.N.; Wu, L.B.; Xie, L.; Zhou, Y.S. The pseudospectrum and spectrum (in) stability of quantum corrected Schwarzschild black hole. Sci. China Phys. Mech. Astron. 2024, 67, 100412. [Google Scholar] [CrossRef]
- Dubinsky, A. Quantum gravitational corrections to the Schwarzschild spacetime and quasinormal frequencies. Int. J. Theor. Phys. 2025, 64, 203. [Google Scholar] [CrossRef]
- Malik, Z. Perturbations and quasinormal modes of the dirac field in effective quantum gravity. Ann. Phys. 2025, 479, 170046. [Google Scholar] [CrossRef]
- Chen, C.Y.; Chiang, H.W.; Tsao, J.S. Eikonal quasinormal modes and photon orbits of deformed Schwarzschild black holes. Phys. Rev. D 2022, 106, 044068. [Google Scholar] [CrossRef]
- Gwak, B. Quasinormal modes in near-extremal spinning C-metric. Eur. Phys. J. Plus 2023, 138, 582. [Google Scholar] [CrossRef]
- Lutfuoglu, B.C. Quasinormal Modes and Gray-Body Factors for Gravitational Perturbations in Asymptotically Safe Gravity. arXiv 2025, arXiv:2505.06966. [Google Scholar] [CrossRef]
- Myrzakulov, Y.; Myrzakulov, K.; Upadhyay, S.; Singh, D.V. Quasinormal modes and phase structure of regular AdS Einstein-Gauss-Bonnet black holes. Int. J. Geom. Meth. Mod. Phys. 2023, 20, 2350121. [Google Scholar] [CrossRef]
- Liu, D.; Yang, Y.; Wu, S.; Xing, Y.; Xu, Z.; Long, Z.W. Ringing of a black hole in a dark matter halo. Phys. Rev. D 2021, 104, 104042. [Google Scholar] [CrossRef]
- Gonzalez, P.A.; Papantonopoulos, E.; Saavedra, J.; Vasquez, Y. Quasinormal modes for massive charged scalar fields in Reissner-Nordström dS black holes: Anomalous decay rate. J. High Energy Phys. 2022, 6, 150. [Google Scholar] [CrossRef]
- Dubinsky, A.; Zinhailo, A. Asymptotic decay and quasinormal frequencies of scalar and Dirac fields around dilaton-de Sitter black holes. Eur. Phys. J. C 2024, 84, 847. [Google Scholar] [CrossRef]
- Skvortsova, M. Ringing of Extreme Regular Black Holes. Gravit. Cosmol. 2024, 30, 279. [Google Scholar] [CrossRef]
- Skvortsova, M. Long lived quasinormal modes of regular and extreme black holes. Eur. Phys. Lett. 2025, 149, 59001. [Google Scholar] [CrossRef]
- He, X.; Wang, B.; Chen, S.; Cai, R.G.; Lin, C.Y. Quasinormal modes in the background of charged Kaluza-Klein black hole with squashed horizons. Phys. Lett. B 2008, 665, 392. [Google Scholar] [CrossRef]
- Hendi, S.H.; Hajkhalili, S.; Jamil, M.; Momennia, M. Stability and phase transition of rotating Kaluza-Klein black holes. Eur. Phys. J. C 2021, 81, 1112. [Google Scholar] [CrossRef]
- Cao, L.M.; Wu, L.B.; Zhao, Y.; Zhou, Y.S. Quasinormal modes of tensor perturbations of Kaluza-Klein black holes in Einstein-Gauss-Bonnet gravity. Phys. Rev. D 2023, 108, 124023. [Google Scholar] [CrossRef]
- Momennia, M.; Hendi, S.H. Near-extremal black holes in Weyl gravity: Quasinormal modes and geodesic instability. Phys. Rev. D 2019, 99, 124025. [Google Scholar] [CrossRef]
- Momennia, M.; Hendi, S.H. Quasinormal modes of black holes in Weyl gravity: Electromagnetic and gravitational perturbations. Eur. Phys. J. C 2020, 80, 505. [Google Scholar] [CrossRef]
- Momennia, M.; Hendi, S.H.; Bidgoli, F.S. Stability and quasinormal modes of black holes in conformal Weyl gravity. Phys. Lett. B 2021, 813, 136028. [Google Scholar] [CrossRef]
- Konoplya, R.A. Conformal Weyl gravity via two stages of quasinormal ringing and late-time behavior. Phys. Rev. D 2021, 103, 044033. [Google Scholar] [CrossRef]
- Becar, R.; Gonzalez, P.A.; Moncada, F.; Vasquez, Y. Massive scalar field perturbations in Weyl black holes. Eur. Phys. J. C 2023, 83, 942. [Google Scholar] [CrossRef]
- Malik, Z. Quasinormal modes of the Mannheim-Kazanas black holes. Z. Naturforsch. A 2024, 79, 1063. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Khrabustovskyi, A.; Kriz, J.; Zhidenko, A. Quasinormal Ringing and Shadows of Black Holes and Wormholes in Dark Matter-Inspired Weyl Gravity. J. Cosmol. Astropart. Phys. 2025, 4, 062. [Google Scholar] [CrossRef]
- Lutfuoglu, B.C. Long-lived quasinormal modes and gray-body factors of black holes and wormholes in dark matter inspired Weyl gravity. Eur. Phys. J. C 2025, 85, 486. [Google Scholar] [CrossRef]
- Momennia, M. Novel echoes from black holes in conformal Weyl gravity. arXiv 2025, arXiv:2502.03706. [Google Scholar] [CrossRef]
- Yasskin, P.B. Solutions for gravity coupled to massless gauge fields. Phys. Rev. D 1975, 12, 2212. [Google Scholar] [CrossRef]
- Mazharimousavi, S.H.; Halilsoy, M. 5D black hole solution in Einstein-Yang-Mills-Gauss-Bonnet theory. Phys. Rev. D 2007, 76, 087501. [Google Scholar] [CrossRef]
- Mazharimousavi, S.H.; Halilsoy, M. Black Holes in Einstein-Maxwell-Yang-Mills Theory and their Gauss-Bonnet Extensions. J. Cosmol. Astropart. Phys. 2008, 12, 005. [Google Scholar] [CrossRef]
- Hendi, S.H.; Momennia, M. Thermodynamic description and quasinormal modes of adS black holes in Born-lnfeld massive gravity with a non-abelian hair. J. High Energy Phys. 2019, 10, 207. [Google Scholar] [CrossRef]
- Hendi, S.H.; Momennia, M. AdS charged black holes in Einstein-Yang-Mills gravity’s rainbow: Thermal stability and P-V criticality. Phys. Lett. B 2018, 777, 222. [Google Scholar] [CrossRef]
- Baxter, J.E.; Winstanley, E. On the stability of soliton and hairy black hole solutions of SU(N) Einstein-Yang-Mills theory with a negative cosmological constant. J. Math. Phys. 2016, 57, 022506. [Google Scholar] [CrossRef]
- Bizon, P. Stability of Einstein Yang-Mills black holes. Phys. Lett. B 1991, 259, 53. [Google Scholar] [CrossRef]
- Aichelburg, P.C.; Bizon, P. Magnetically charged black holes and their stability. Phys. Rev. D 1993, 48, 607. [Google Scholar] [CrossRef] [PubMed]
- Jusufi, K.; Azreg-Ainou, M.; Jamil, M.; Wei, S.; Wu, Q.; Wang, A. Quasinormal modes, quasiperiodic oscillations, and the shadow of rotating regular black holes in nonminimally coupled Einstein-Yang-Mills theory. Phys. Rev. D 2021, 103, 024013. [Google Scholar] [CrossRef]
- Pu, Y.; Yang, Y. Quasinormal ringing of regular Einstein-Yang-Mills black hole. Eur. Phys. Lett. 2023, 144, 49001. [Google Scholar] [CrossRef]
- Gogoi, D.J.; Ponglertsakul, S. Constraints on quasinormal modes from black hole shadows in regular non-minimal Einstein Yang-Mills gravity. Eur. Phys. J. C 2024, 84, 652. [Google Scholar] [CrossRef]
- Ji, Y. Quasinormal modes and Hawking radiation of a non-minimal Einstein-Yang-Mills regular black hole. Phys. Scr. 2025, 100, 085001. [Google Scholar] [CrossRef]
- Lutfuoglu, B.C. Non-minimal Einstein-Yang-Mills black holes: Fundamental quasinormal mode and grey-body factors versus outburst of overtones. Eur. Phys. J. C 2025, 85, 630. [Google Scholar] [CrossRef]
- Dubinsky, A. Long-Lived Quasinormal Modes and Quasi-Resonances around Non-Minimal Einstein-Yang-Mills Black Holes. Eur. Phys. J. C 2025, 85, 924. [Google Scholar] [CrossRef]
- Guo, Y.; Miao, Y. Scalar quasinormal modes of black holes in Einstein-Yang-Mills gravity. Phys. Rev. D 2020, 102, 064049. [Google Scholar]
- Guo, Y.; Miao, Y. Null geodesics, quasinormal modes, and the correspondence with shadows in high-dimensional Einstein-Yang-Mills spacetimes. Phys. Rev. D 2020, 102, 084057. [Google Scholar] [CrossRef]
- Amelino-Camelia, G. Doubly Special Relativity. Nature 2002, 418, 34. [Google Scholar] [CrossRef]
- Colladay, D.; Kostelecky, V.A. Lorentz-violating extension of the standard model. Phys. Rev. D 1998, 58, 116002. [Google Scholar] [CrossRef]
- Coleman, S.R.; Glashow, S.L. High-energy tests of Lorentz invariance. Phys. Rev. D 1999, 59, 116008. [Google Scholar] [CrossRef]
- Jacobson, T.A.; Liberati, S.; Mattingly, D.; Stecker, F.W. New limits on Planck scale Lorentz violation in QED. Phys. Rev. Lett. 2004, 93, 021101. [Google Scholar] [CrossRef] [PubMed]
- Magueijo, J.; Smolin, L. Gravity’s rainbow. Class. Quantum Grav. 2004, 21, 1725. [Google Scholar] [CrossRef]
- Galan, P.; Marugan, G.A.M. Entropy and temperature of black holes in a gravity’s rainbow. Phys. Rev. D 2006, 74, 044035. [Google Scholar] [CrossRef]
- Ali, A.F. Black hole remnant from gravity’s rainbow. Phys. Rev. D 2014, 89, 104040. [Google Scholar] [CrossRef]
- Santos, G.; Gubitosi, G.; Amelino-Camelia, G. On the initial singularity problem in rainbow cosmology. J. Cosmol. Astropart. Phys. 2015, 8, 005. [Google Scholar] [CrossRef]
- Hendi, S.H.; Panahiyan, S.; Panah, B.E.; Faizal, M.; Momennia, M. Critical behavior of charged black holes in Gauss-Bonnet gravity’s rainbow. Phys. Rev. D 2016, 94, 024028. [Google Scholar] [CrossRef]
- Dehghani, M. AdS4 black holes with nonlinear source in rainbow gravity. Phys. Lett. B 2020, 801, 135191. [Google Scholar] [CrossRef]
- Dehghani, M. Dilaton black holes with logarithmic source in gravity’s rainbow. Int. J. Geom. Meth. Mod. Phys. 2021, 18, 2150046. [Google Scholar] [CrossRef]
- Panah, B.E.; Zare, S.; Hassanabadi, H. Accelerating AdS black holes in gravity’s rainbow. Eur. Phys. J. C 2024, 84, 259. [Google Scholar] [CrossRef]
- Panah, B.E.; Heidari, N.; Soleimani, M.; Kaveh, M. Super-entropic black holes in gravity’s rainbow and determining constraints on rainbow functions. Eur. Phys. J. C 2025, 85, 650. [Google Scholar] [CrossRef]
- Momennia, M.; Herrera-Aguilar, A.; Nucamendi, U. Kerr black hole in de Sitter spacetime and observational redshift: Toward a new method to measure the Hubble constant. Phys. Rev. D 2023, 107, 104041. [Google Scholar] [CrossRef]
- Carroll, S.M. The Cosmological Constant. Living Rev. Rel. 2001, 4, 1. [Google Scholar] [CrossRef]
- Price, R.H. Nonspherical perturbations of relativistic gravitational collapse. I. Scalar and gravitational perturbations. Phys. Rev. D 1972, 5, 2419. [Google Scholar] [CrossRef]
- Brady, P.; Chambers, C.; Krivan, W.; Laguna, P. Telling tails in the presence of a cosmological constant. Phys. Rev. D 1997, 55, 7538. [Google Scholar] [CrossRef]
- Matzner, R.A. Scattering of Massless Scalar Waves by a Schwarzschild “Singularity”. J. Math. Phys. 1968, 9, 163. [Google Scholar] [CrossRef]
- Regge, T.; Wheeler, J.A. Stability of a Schwarzschild Singularity. Phys. Rev. 1957, 108, 1063. [Google Scholar] [CrossRef]
- Schutz, B.F.; Will, C.M. Black hole normal modes: A semianalytic approach. Astrophys. J. Lett. 1985, 291, L33. [Google Scholar] [CrossRef]
- Iyer, S.; Will, C.M. Black-hole normal modes: A WKB approach. I. Foundations and application of a higher-order WKB analysis of potential-barrier scattering. Phys. Rev. D 1987, 35, 3621. [Google Scholar] [CrossRef]
- Konoplya, R.A. Quasinormal behavior of the D-dimensional Schwarzschild black hole and the higher order WKB approach. Phys. Rev. D 2003, 68, 024018. [Google Scholar] [CrossRef]
- Matyjasek, J.; Opala, M. Quasinormal modes of black holes: The improved semianalytic approach. Phys. Rev. D 2017, 96, 024011. [Google Scholar] [CrossRef]
- Hawking, S.W. Black holes and thermodynamics. Phys. Rev. D 1976, 13, 191. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle creation by black holes. Commun. Math. Phys. 1975, 43, 199, Erratum in Commun. Math. Phys. 1976, 46, 206. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zhidenko, A.; Zinhailo, A.F. Higher order WKB formula for quasinormal modes and grey-body factors: Recipes for quick and accurate calculations. Class. Quantum Grav. 2019, 36, 155002. [Google Scholar] [CrossRef]
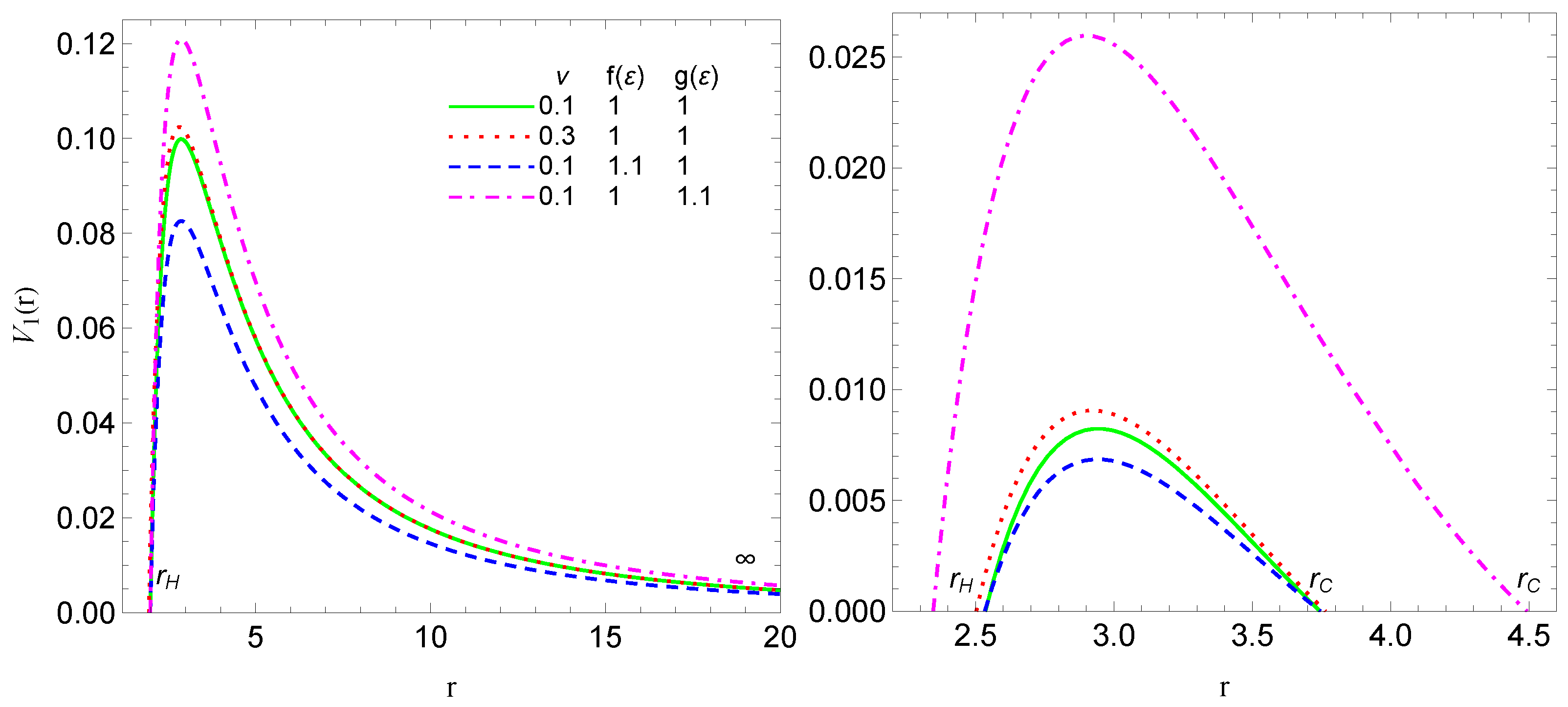
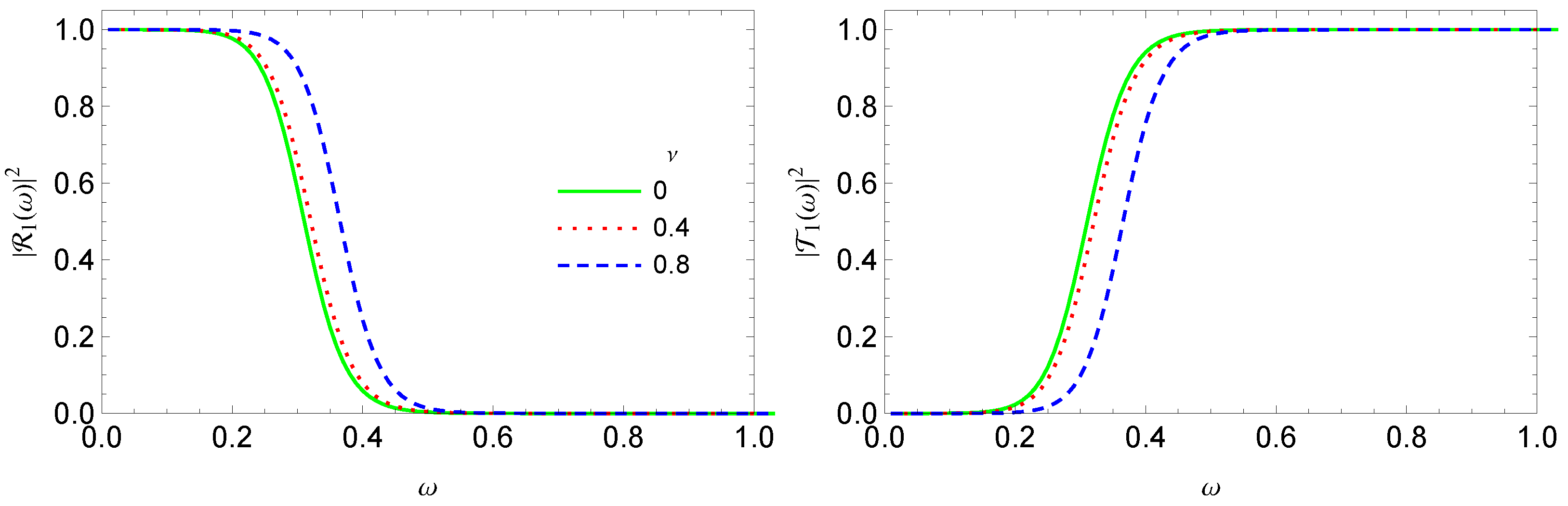

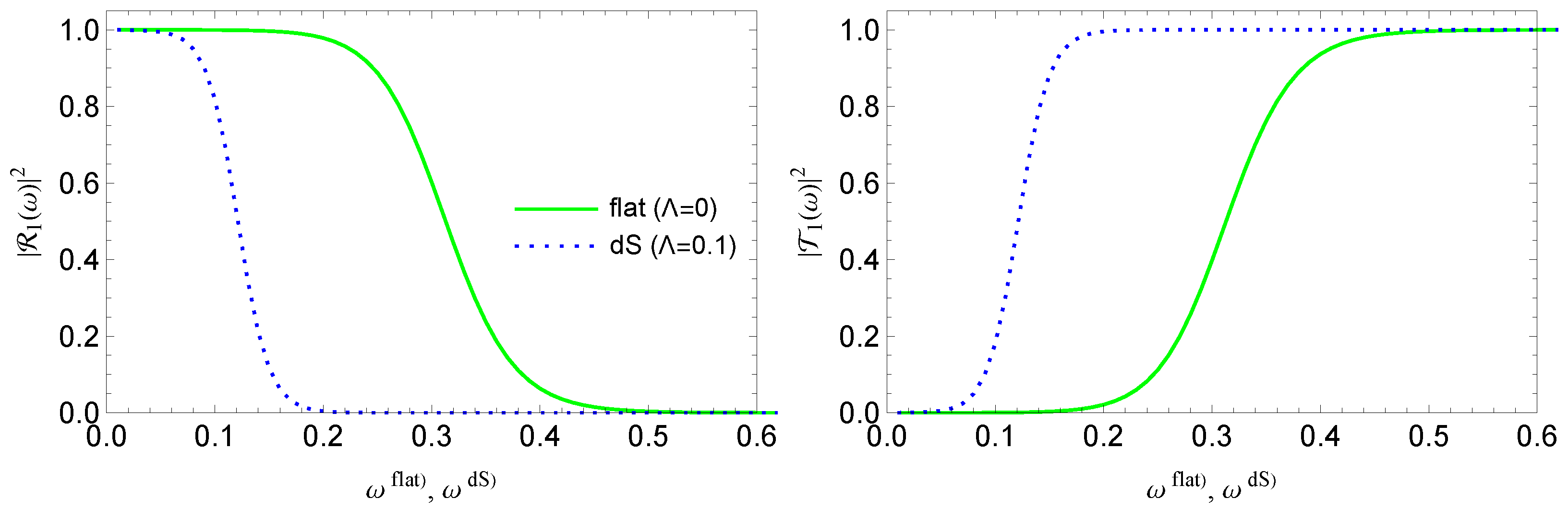
| ν | f(ε) | g(ε) | ω01 | ω02 |
|---|---|---|---|---|
| 0 | 1 | 1 | ||
| 1 | 1 | |||
| 1 | ||||
| 1 |
| ν | f(ε) | g(ε) | ω01 | ω02 |
|---|---|---|---|---|
| 0 | 1 | 1 | ||
| 1 | 1 | |||
| 1 | ||||
| 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Momennia, M. Ringing of Reissner–Nordström Black Holes with a Non-Abelian Hair in Gravity’s Rainbow. Universe 2025, 11, 341. https://doi.org/10.3390/universe11100341
Momennia M. Ringing of Reissner–Nordström Black Holes with a Non-Abelian Hair in Gravity’s Rainbow. Universe. 2025; 11(10):341. https://doi.org/10.3390/universe11100341
Chicago/Turabian StyleMomennia, Mehrab. 2025. "Ringing of Reissner–Nordström Black Holes with a Non-Abelian Hair in Gravity’s Rainbow" Universe 11, no. 10: 341. https://doi.org/10.3390/universe11100341
APA StyleMomennia, M. (2025). Ringing of Reissner–Nordström Black Holes with a Non-Abelian Hair in Gravity’s Rainbow. Universe, 11(10), 341. https://doi.org/10.3390/universe11100341







