Exploring the Enigma of Particle Dynamics and Plasma Lensing Using Einstein–Euler–Heisenberg Black Hole Geometry
Abstract
1. Introduction
2. Black Holes in Einstein–Euler–Heisenberg (EEH) Theory
3. Particle Dynamics Around Black Hole in EEH Theory
3.1. Massive Particle Motions Orbiting Black Holes in EEH Theory
3.2. Motion of Massless Particles (Photon)
4. Weak Gravitational Lensing in Einstein–Euler–Heisenberg Theory
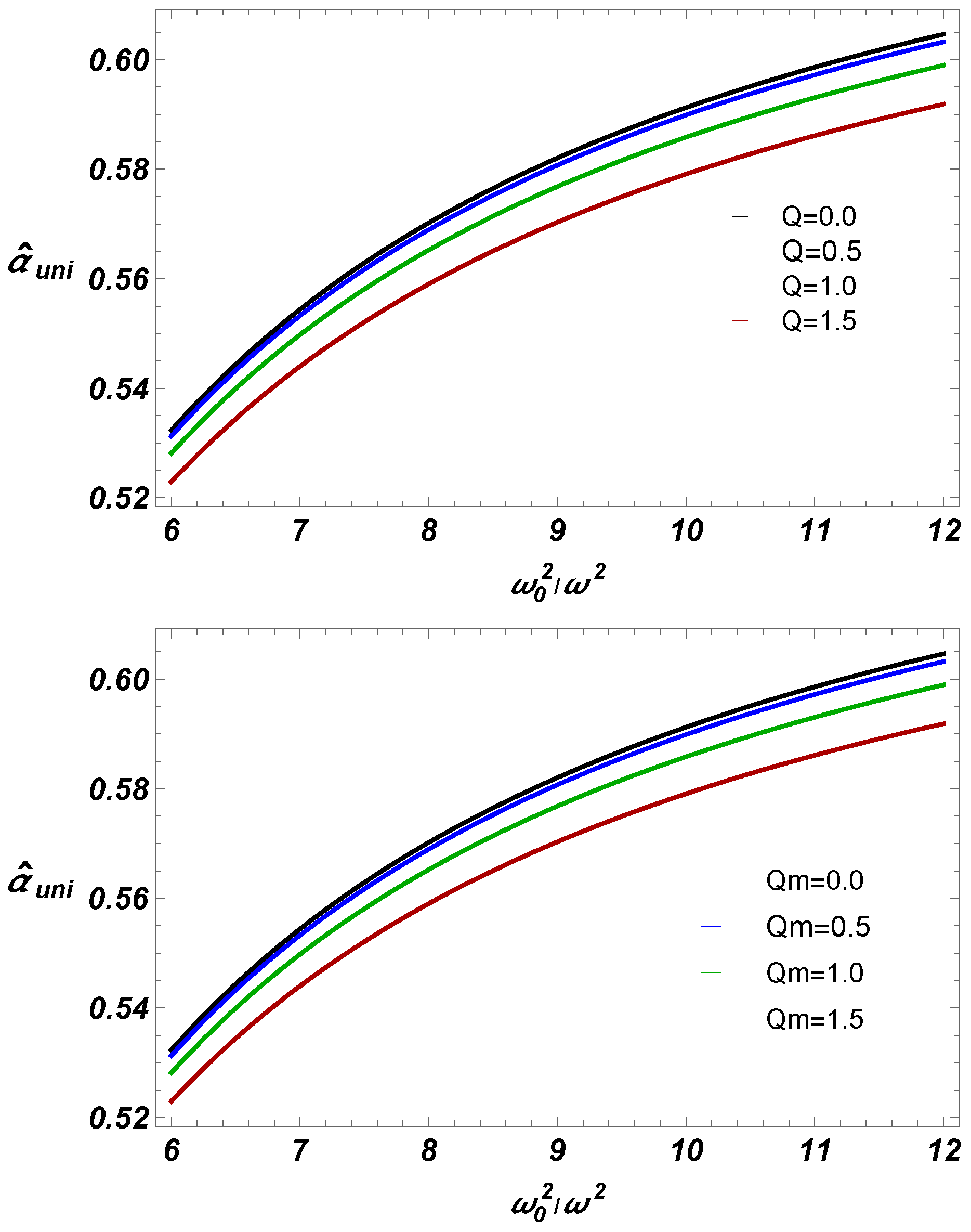
4.1. Case 1: In Presence of Uniform Plasma
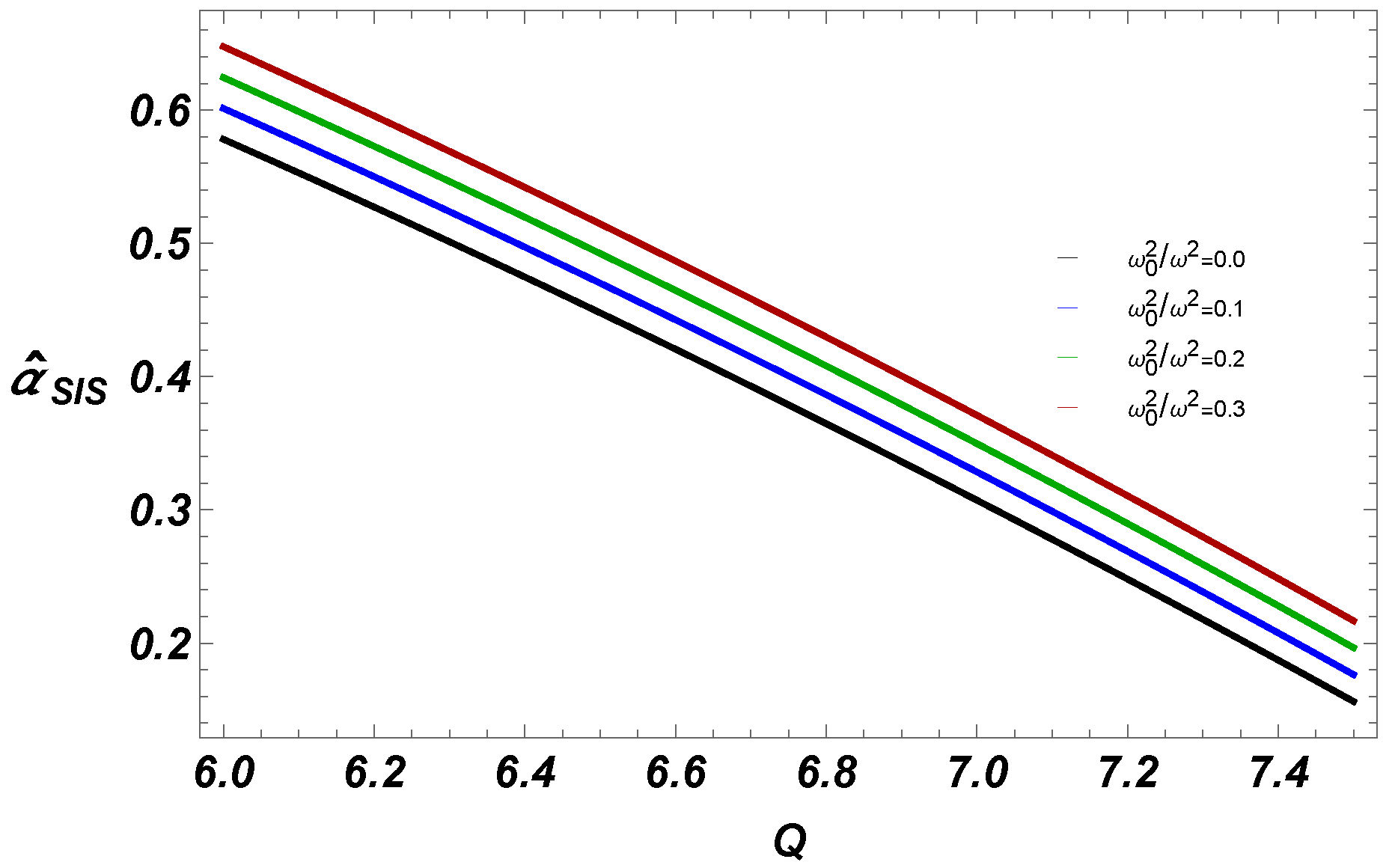
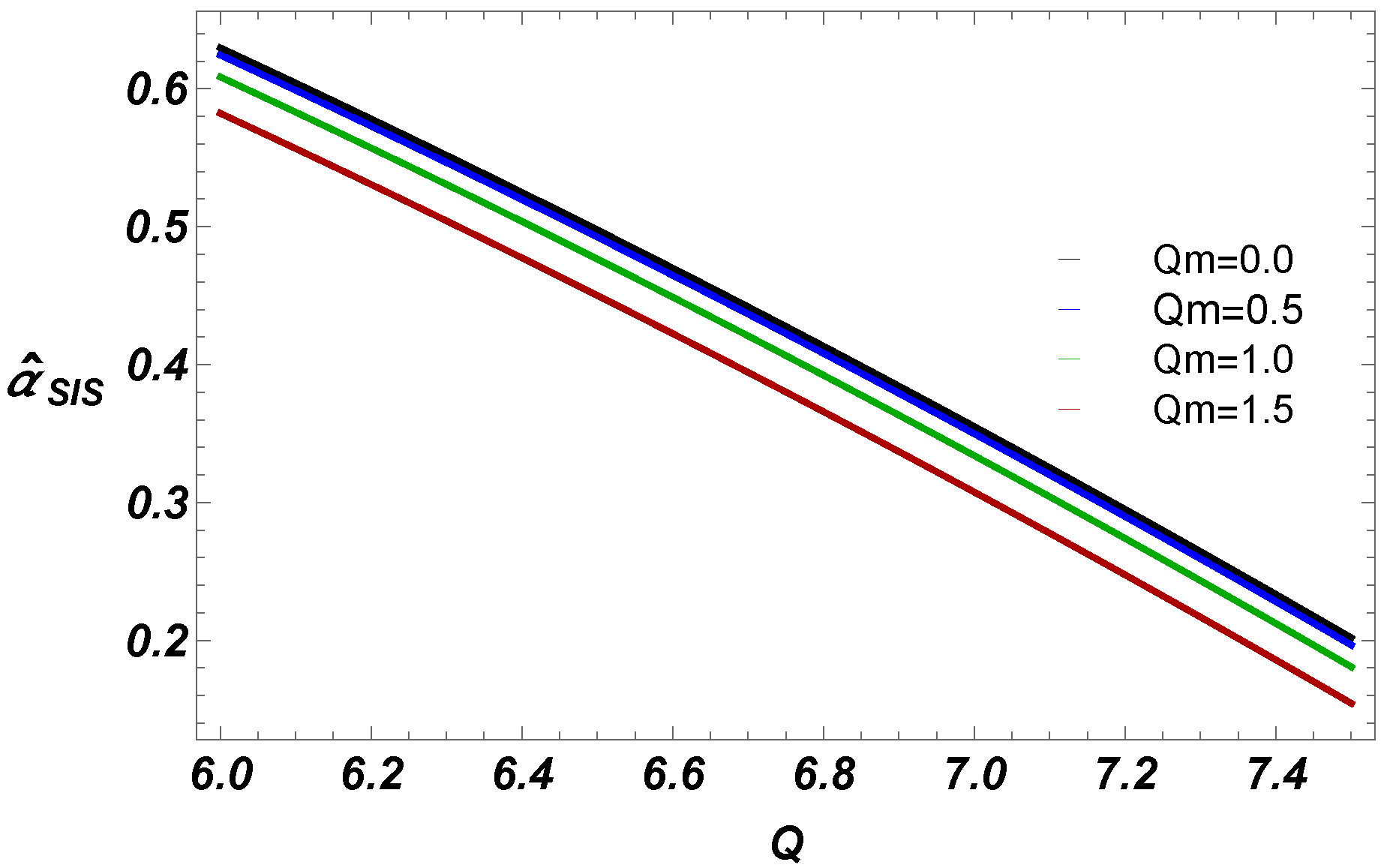
4.2. Case 2: In the Presence of Non-Uniform Plasma
5. Comparison
6. Summary
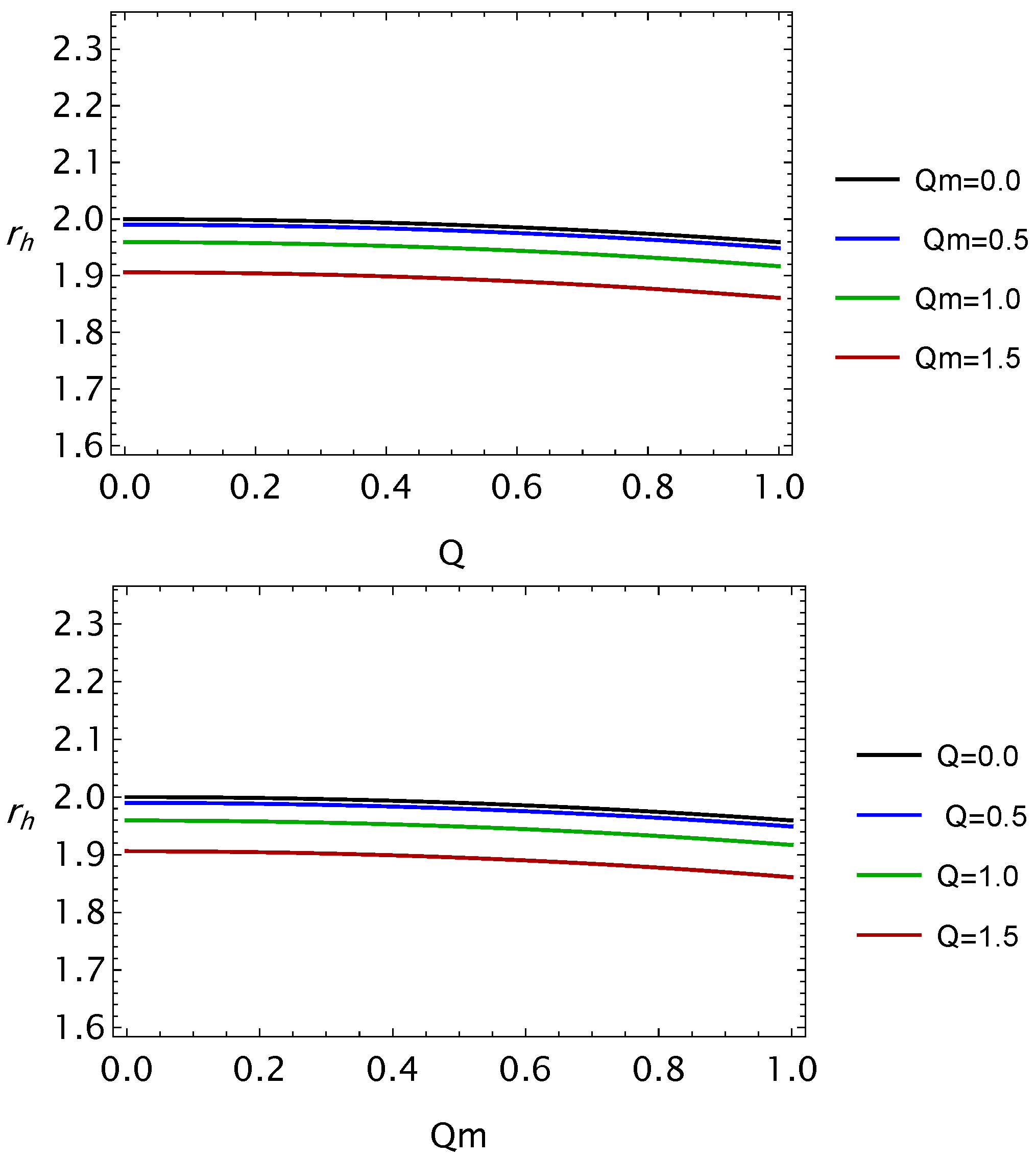
- We worked on BH’s horizon structure using the effective Lagrangian of EEH BH solution. The findings show that increasing the parameter Q and decreases the event horizon radius, as shown in Figure 1.
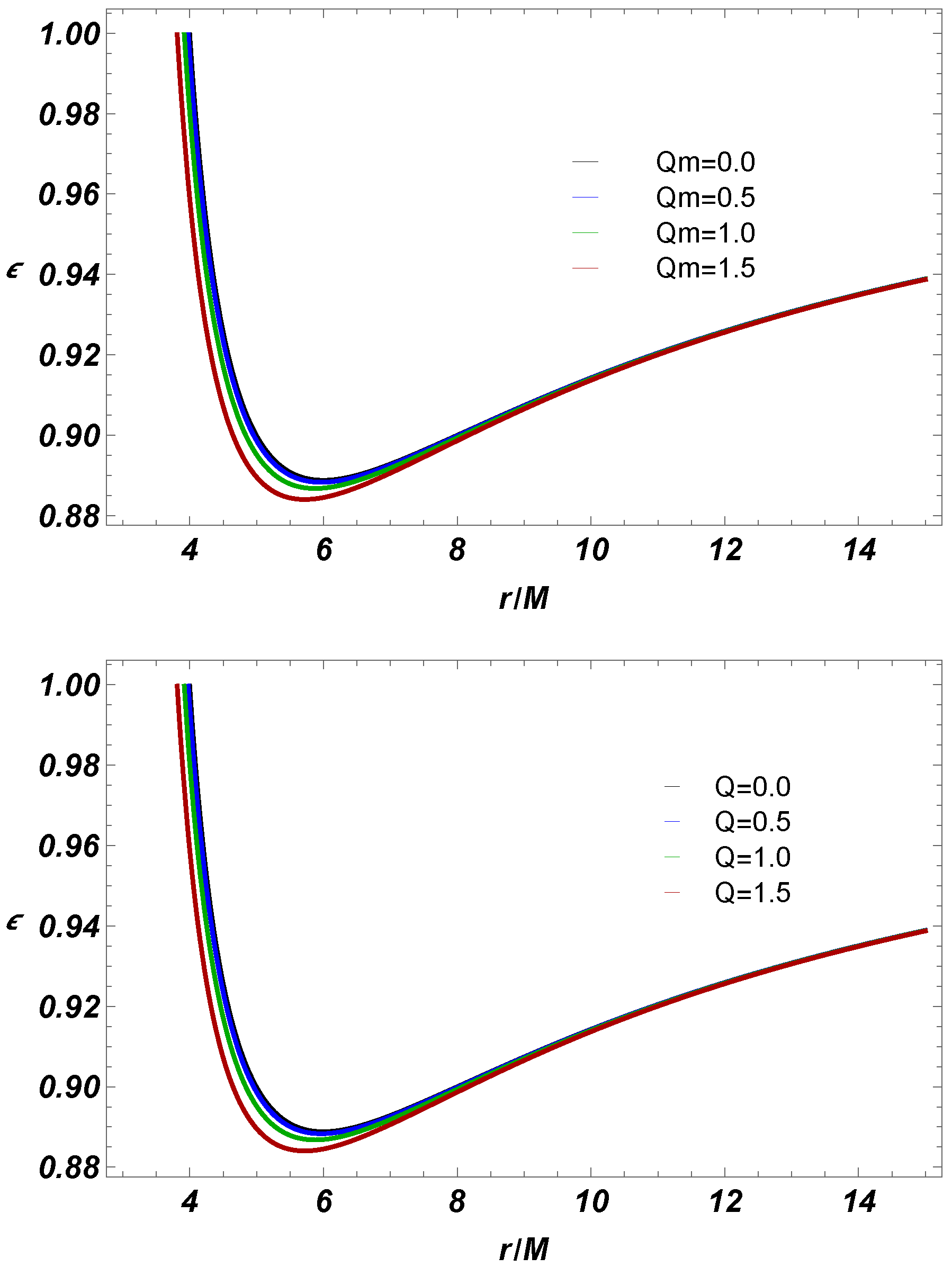
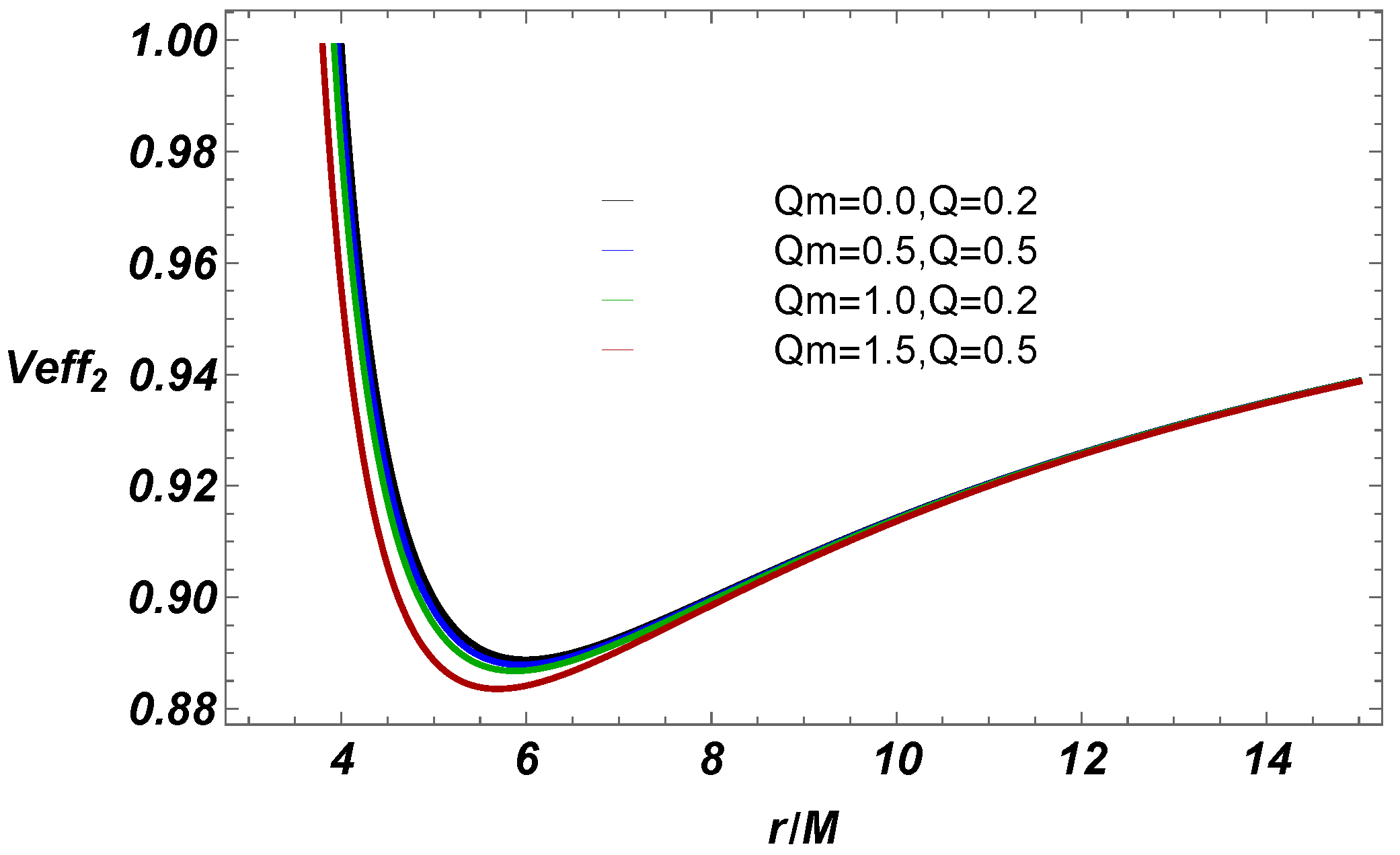
- We discussed the particle motion effective potential near BH. We investigated the relation between massive and massless particle effective potential along radial coordinate r for various values of EEH BH parameters Q and . We noticed that effective potential decreases by increasing these parameters.
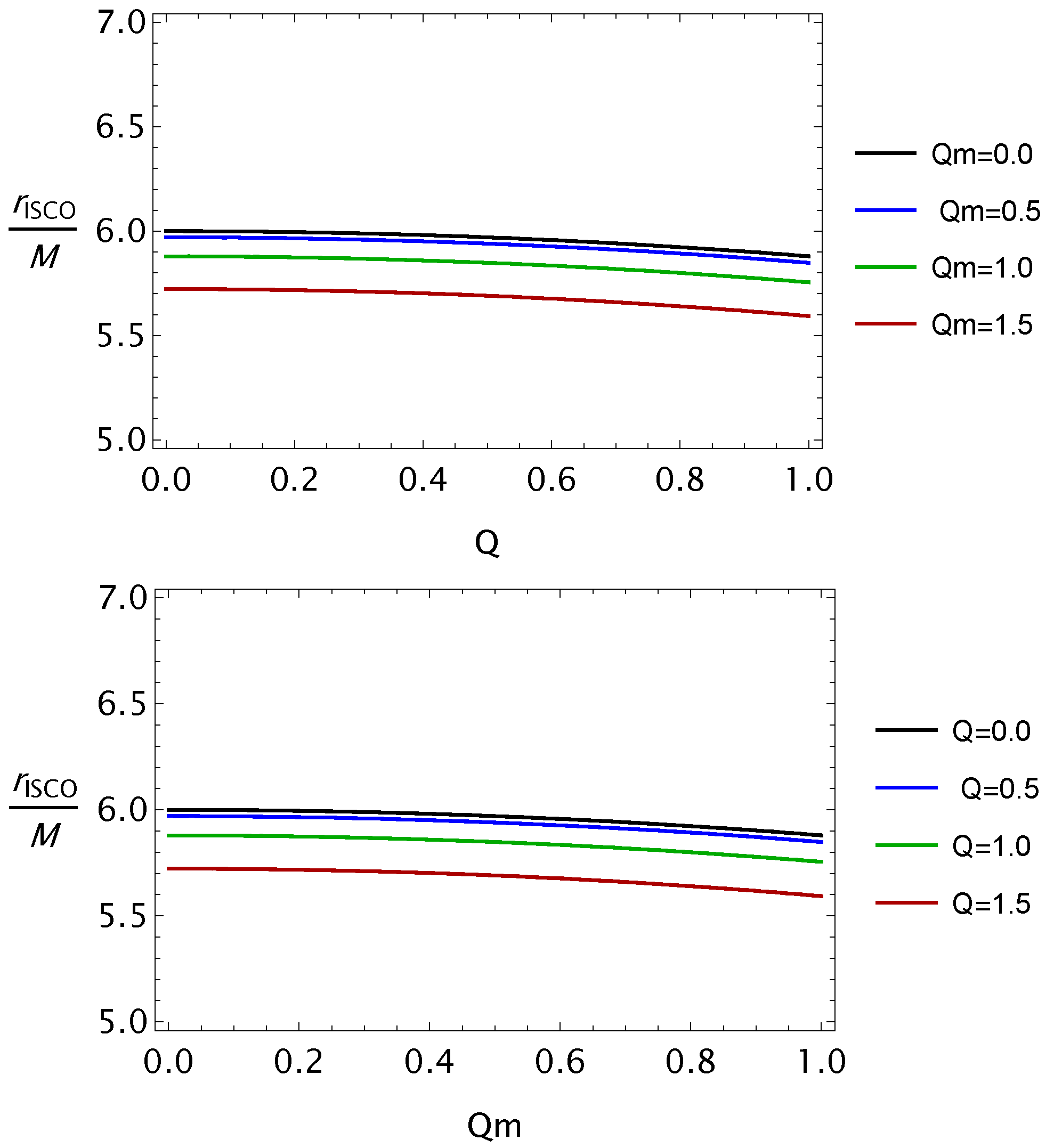
- We explored the ISCO radius for massive particles surrounding BH. It has been shown that with an increases in the values of EEH BH parameters Q and , the ISCO radius decreases (see Figure 5).
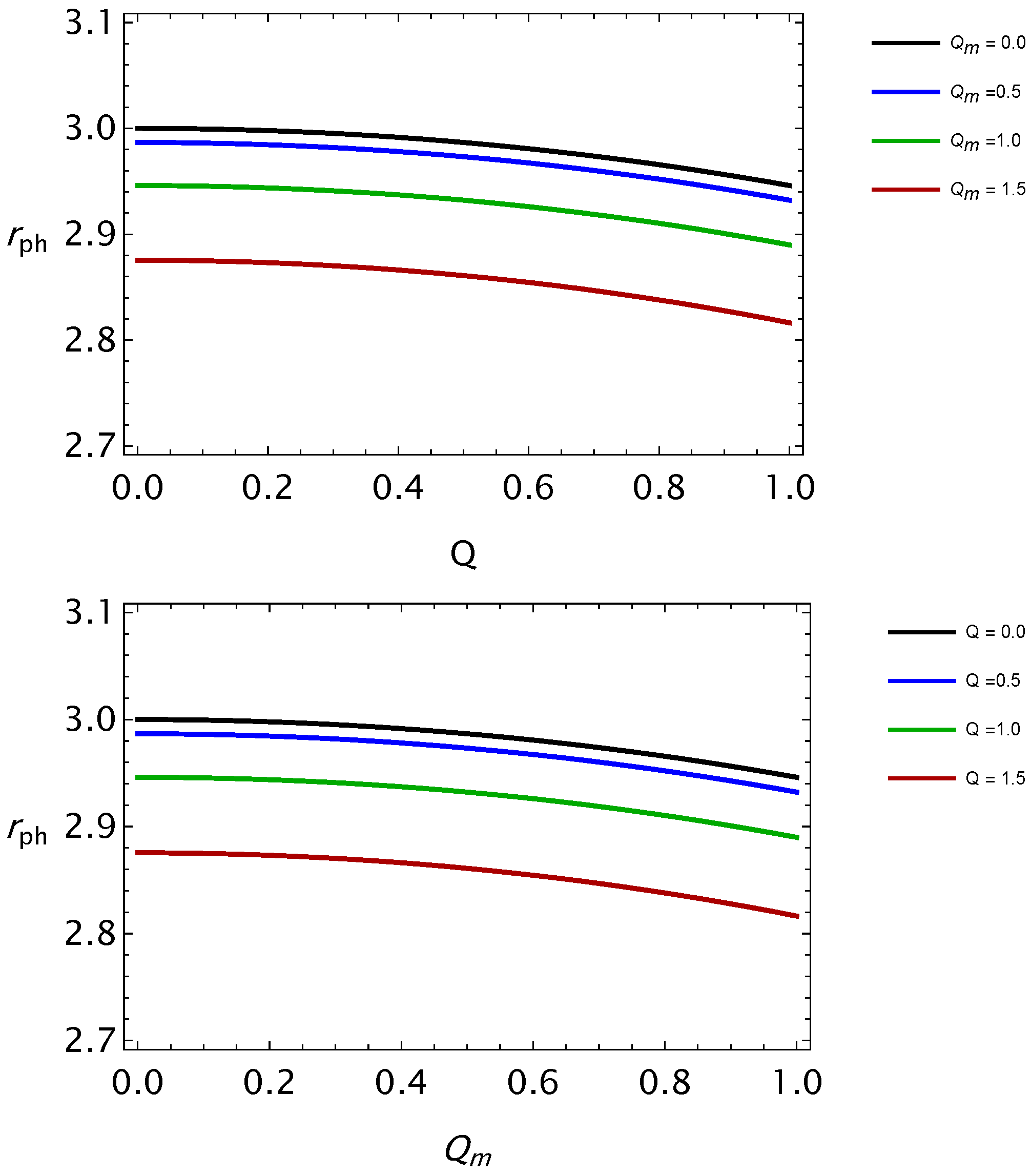
- The photon’s sphere radius is also studied near BH using the effective Lagrangian of EEH BH. Photon orbits decrease with increase in BH parameters, as shown in Figure 7.
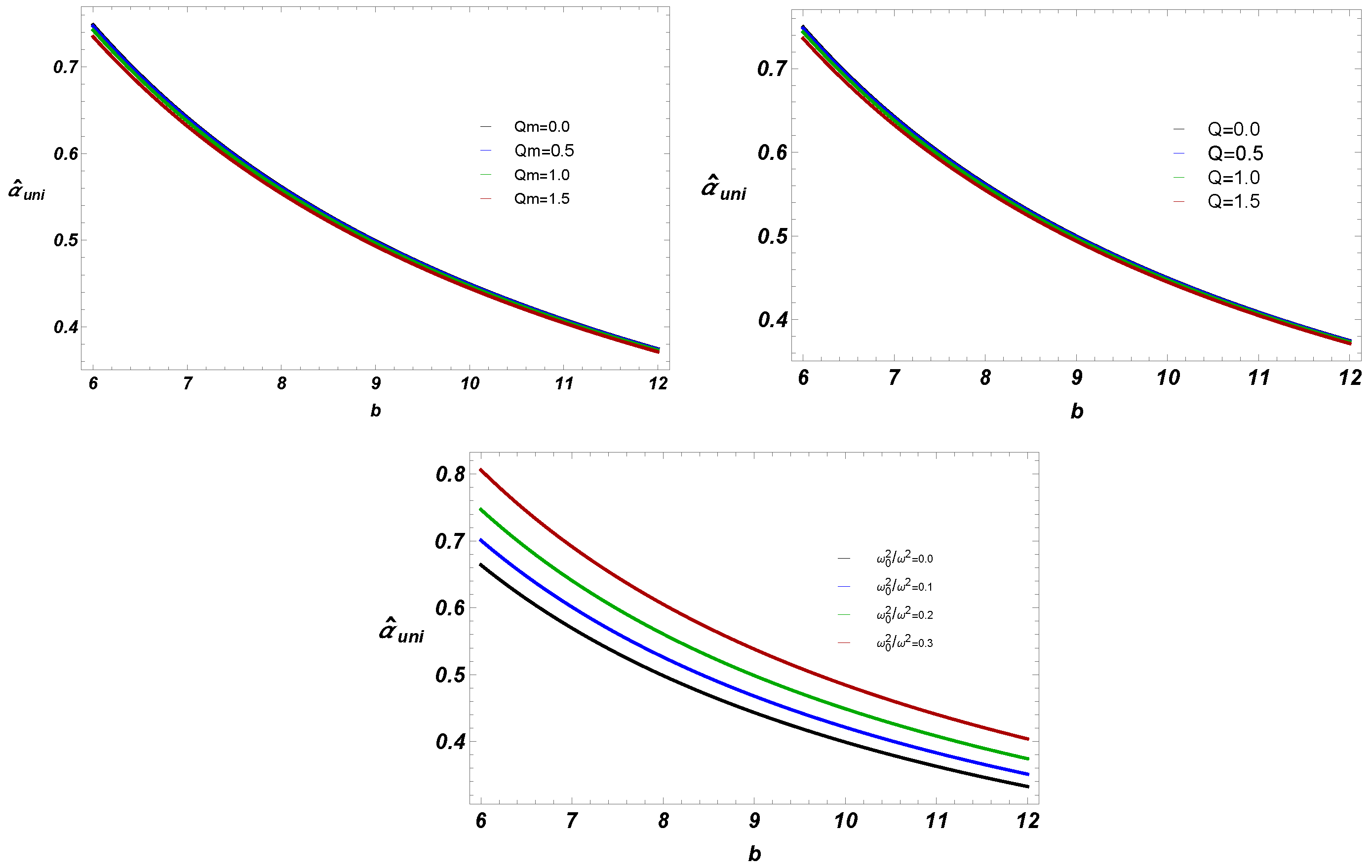
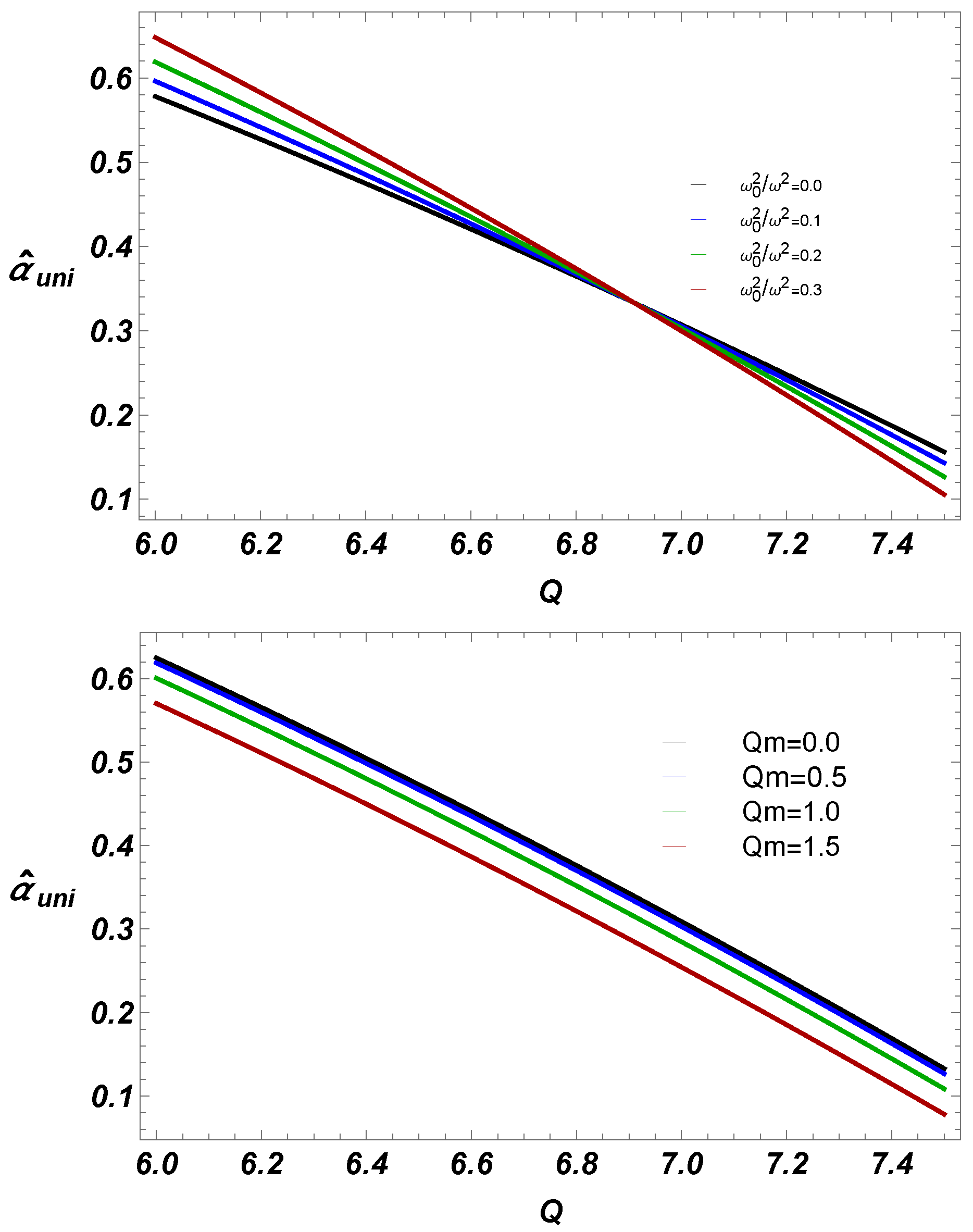
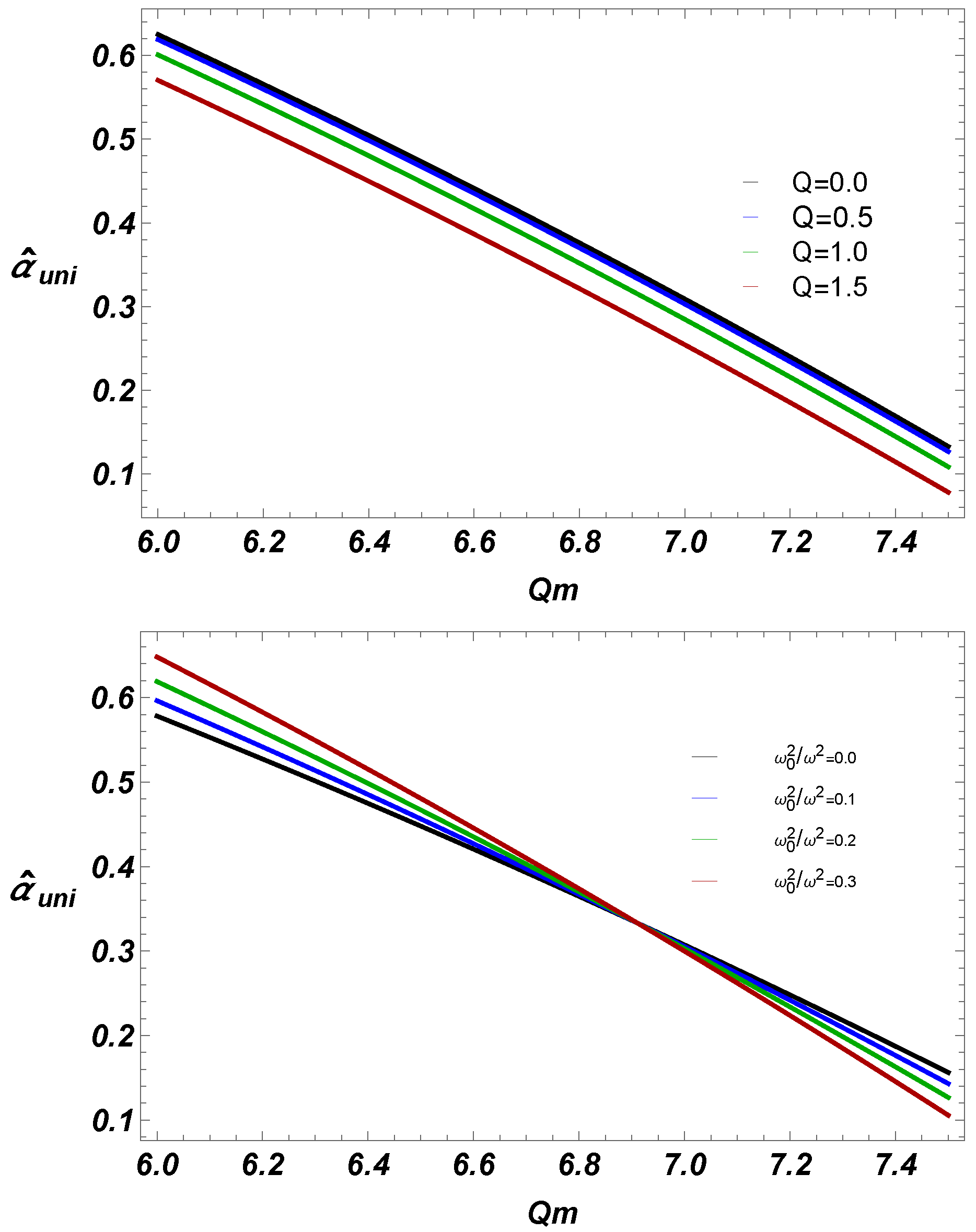
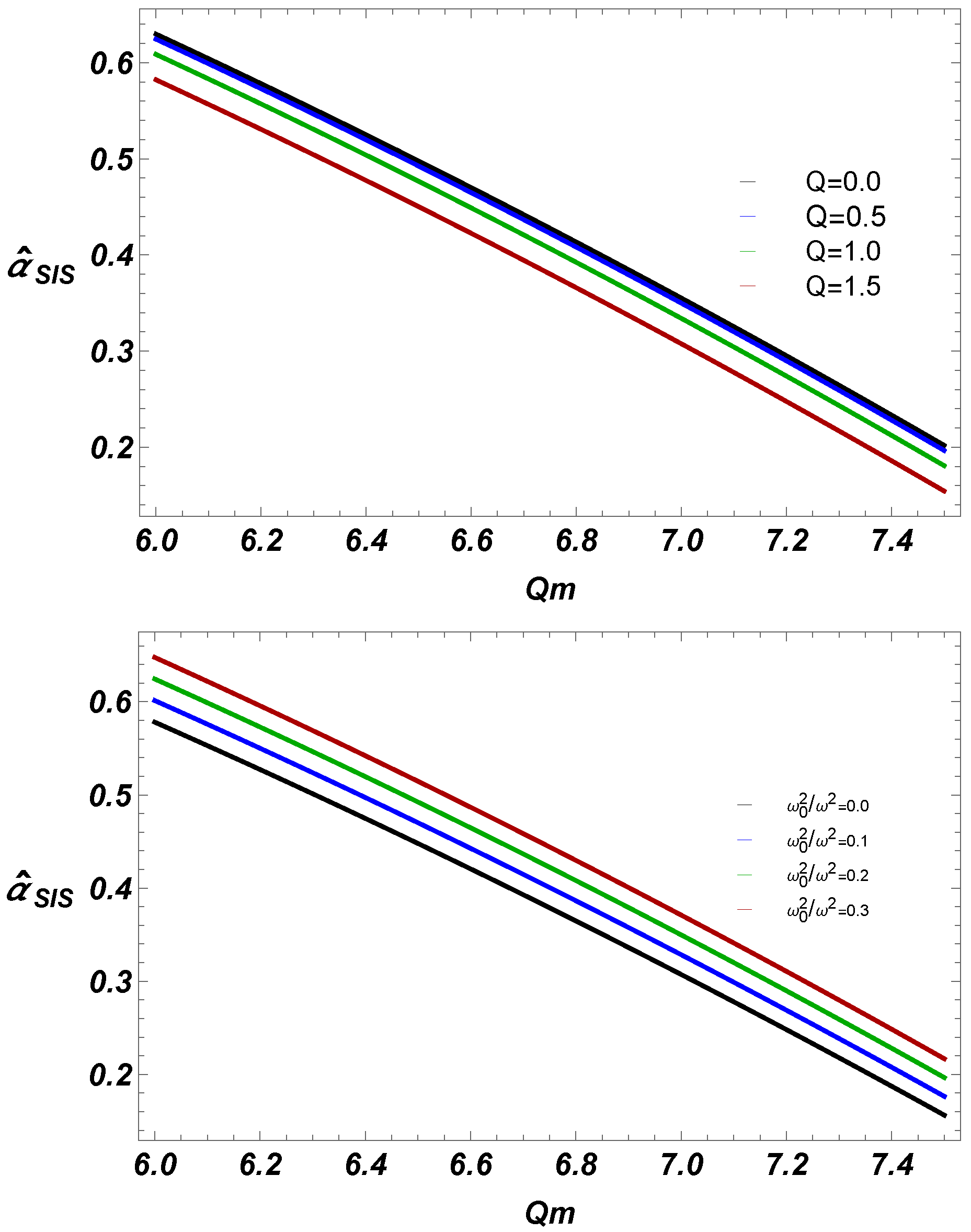
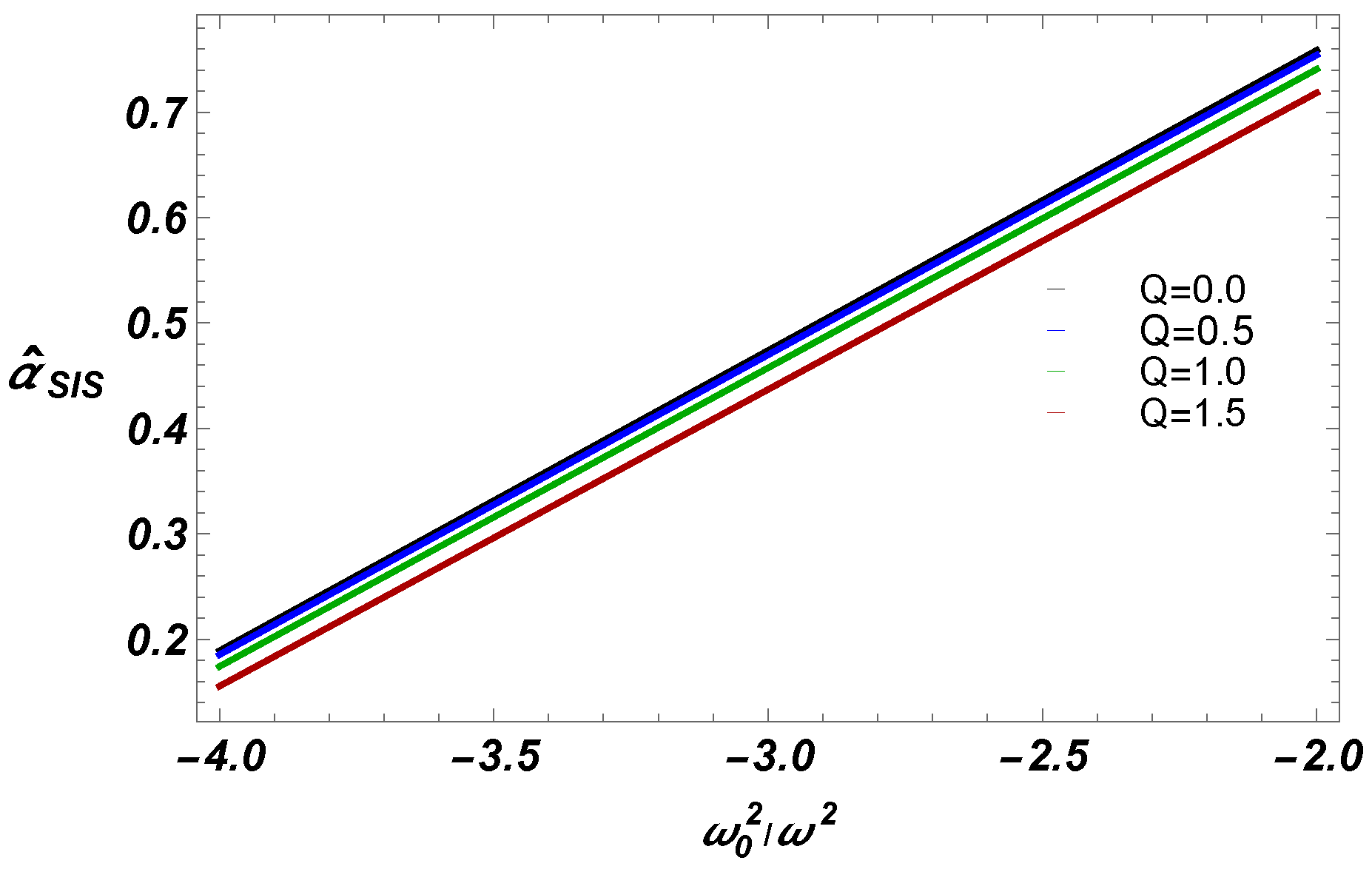
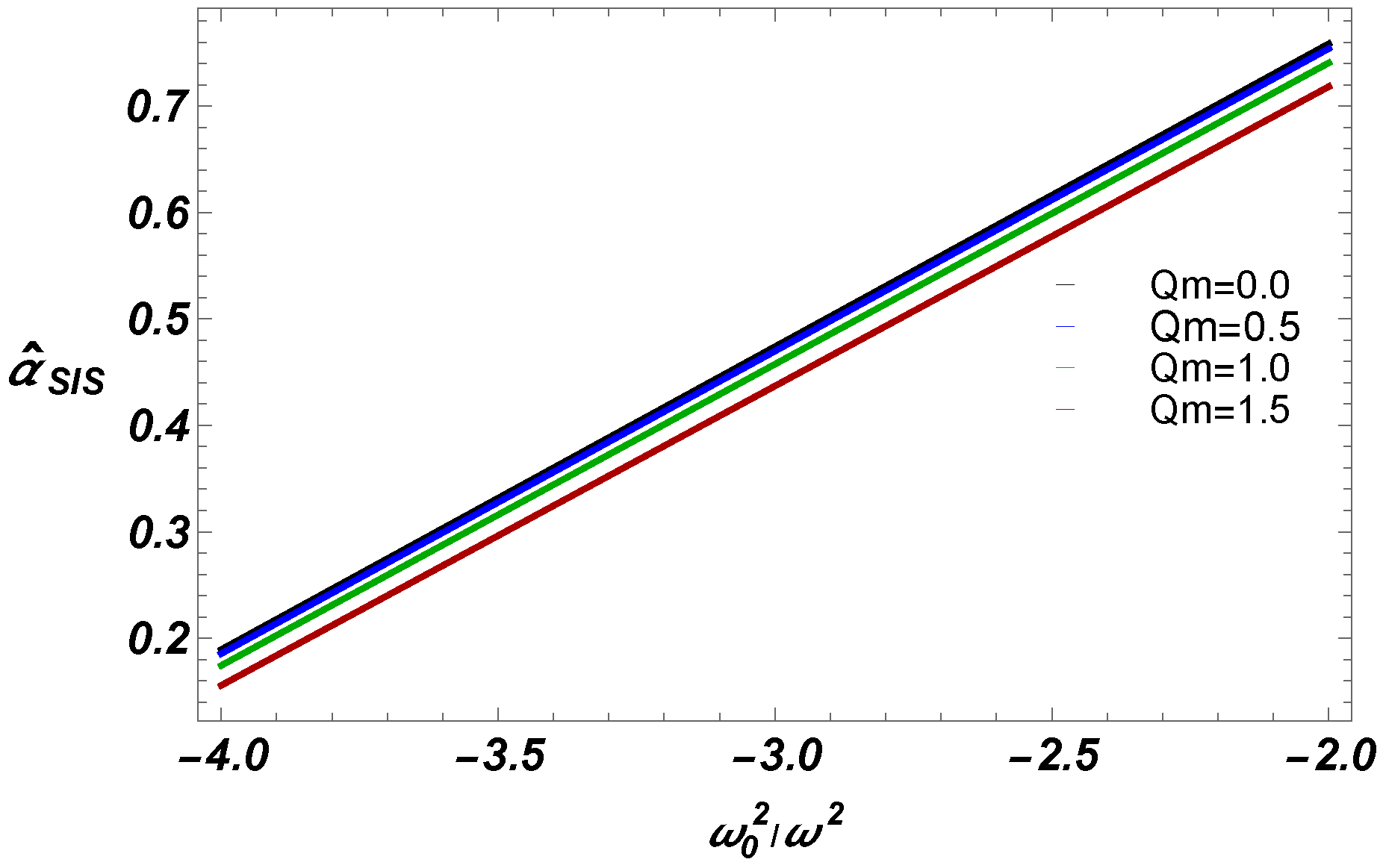
- We have also studied deflection angle near EEH BH with plasma (homogeneous, and non-homogeneous fields). Our work shows that for fixed BH parameters, uniform plasma has the greater impact on deflection angle than non-uniform plasma.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Addesso, P.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; et al. First M87 event horizon telescope results. VI. The shadow and mass of the central black hole. Astrophys. J. Lett. 2019, 875, L6. [Google Scholar] [CrossRef]
- Will, C.M. The confrontation between general relativity and experiment. Living Rev. Relativ. 2014, 17, 4. [Google Scholar] [CrossRef]
- Born, M.; Infeld, L. Foundations of the new field theory. Proc. R. Soc. A 1934, 144, 425–451. [Google Scholar] [CrossRef]
- Hoffmann, B. Gravitational and electromagnetic mass in the Born-Infeld electrodynamics. Phys. Rev. 1935, 47, 877–880. [Google Scholar] [CrossRef]
- Hoffmann, B.; Infeld, L. On the choice of the action function in the new field theory. Phys. Rev. 1937, 51, 765–773. [Google Scholar] [CrossRef]
- Fradkin, E.S.; Tseytlin, A.A. Non-linear electrodynamics from quantized strings. Phys. Lett. B 1985, 163, 123–130. [Google Scholar] [CrossRef]
- Abouelsaood, A.; Callan, C.G.; Nappi, C.R.; Yost, S.A. Open strings in background gauge fields. Nucl. Phys. B 1987, 280, 599–624. [Google Scholar] [CrossRef]
- Tseytlin, A.A. On non-abelian generalisation of the Born-Infeld action in string theory. Nucl. Phys. B 1997, 501, 41–52. [Google Scholar] [CrossRef]
- Garcia, A.; Salazar, H.; Plebanski, J.F. Type-D solutions of the Einstein and Born-Infeld nonlinear-electrodynamics equations. Il Nuovo C. B 1984, 84, 65–90. [Google Scholar] [CrossRef]
- Demianski, M. Static electromagnetic geon. Found. Phys. 1986, 16, 187–190. [Google Scholar] [CrossRef]
- Fernando, S.; Krug, D. Charged black hole solutions in Einstein-Born-Infeld gravity with a cosmological constant. Gen. Relativ. Gravit. 2003, 35, 129–137. [Google Scholar] [CrossRef]
- Dey, T.K. Born–Infeld black holes in the presence of a cosmological constant. Phys. Lett. B 2004, 595, 484–490. [Google Scholar]
- Diaz-Alonso, J.; Rubiera-Garcia, D. Electrostatic spherically symmetric configurations in gravitating nonlinear electrodynamics. Phys. Rev. D 2010, 81, 064021. [Google Scholar] [CrossRef]
- Diaz-Alonso, J.; Rubiera-Garcia, D. Asymptotically anomalous black hole configurations in gravitating nonlinear electrodynamics. Phys. Rev. D 2010, 82, 085024. [Google Scholar] [CrossRef]
- Diaz-Alonso, J.; Rubiera-Garcia, D. Black holes from generalized gauge field theories. J. Phys. Conf. Ser. 2011, 283, 012014. [Google Scholar] [CrossRef]
- Diaz-Alonso, J.; Rubiera-Garcia, D. Electrically charged black hole solutions in generalized gauge field theories. J. Phys. Conf. Ser. 2011, 314, 012065. [Google Scholar] [CrossRef]
- Soleng, H.H. Charged black points in general relativity coupled to the logarithmic U (1) gauge theory. Phys. Rev. D 1995, 52, 6178–6181. [Google Scholar] [CrossRef] [PubMed]
- de Oliveira, H.P. Non-linear charged black holes. Class. Quantum Gravity 1994, 11, 1469–1482. [Google Scholar] [CrossRef]
- Heisenberg, W.; Euler, H. Folgerungen aus der diracschen theorie des positrons. Z. Phys. 1936, 98, 714–732. [Google Scholar] [CrossRef]
- Yajima, H.; Tamaki, T. Black hole solutions in Euler-Heisenberg theory. Phys. Rev. D 2001, 63, 064007. [Google Scholar] [CrossRef]
- Ayón-Beato, E.; García, A. Regular black hole in general relativity coupled to nonlinear electrodynamics. Phys. Rev. Lett. 1998, 80, 5056–5059. [Google Scholar] [CrossRef]
- Ayón-Beato, E.; García, A. New regular black hole solution from nonlinear electrodynamics. Phys. Lett. B 1999, 464, 25–29. [Google Scholar] [CrossRef]
- Cirilo Lombardo, D.J. Charge without charge, regular spherically symmetric solutions and the Einstein-Born-Infeld theory. Int. J. Theor. Phys. 2009, 48, 2267–2285. [Google Scholar] [CrossRef]
- Burinskii, A.; Hildebrandt, S.R. New type of regular black holes and particlelike solutions from nonlinear electrodynamics. Phys. Rev. D 2002, 65, 104017. [Google Scholar] [CrossRef]
- Hendi, S.H. Rotating black string with nonlinear source. Phys. Rev. D 2010, 82, 064040. [Google Scholar] [CrossRef]
- Novello, M.; Bergliaffa, S.E.P.; Salim, J.M. Singularities in general relativity coupled to nonlinear electrodynamics. Class. Quantum Gravity 2000, 17, 3821–3832. [Google Scholar] [CrossRef]
- Bronnikov, K.A. Regular magnetic black holes and monopoles from nonlinear electrodynamics. Phys. Rev. D 2001, 63, 044005. [Google Scholar] [CrossRef]
- Hassaïne, M.; Martínez, C. Higher-dimensional black holes with a conformally invariant Maxwell source. Phys. Rev. D 2007, 75, 027502. [Google Scholar] [CrossRef]
- Hassaïne, M.; Martínez, C. Higher-dimensional charged black hole solutions with a nonlinear electrodynamics source. Class. Quantum Gravity 2008, 25, 195023. [Google Scholar] [CrossRef]
- González, H.A.; Hassaïne, M.; Martínez, C. Thermodynamics of charged black holes with a nonlinear electrodynamics source. Phys. Rev. D 2009, 80, 104008. [Google Scholar] [CrossRef]
- Mazharimousavi, S.H.; Halilsoy, M.; Gurtug, O. Theorem to generate Einstein–nonlinear Maxwell fields. Class. Quantum Gravity 2010, 27, 205022. [Google Scholar] [CrossRef][Green Version]
- Dehghani, M.H.; Rastegar Sedehi, H.R. Thermodynamics of rotating black branes in (n+1)-dimensional Einstein-Born-Infeld gravity. Phys. Rev. D 2006, 74, 124018. [Google Scholar] [CrossRef]
- Dehghani, M.H.; Hendi, S.H.; Sheykhi, A.; Rastegar Sedehi, H. Thermodynamics of rotating black branes in Einstein–Born–Infeld-dilaton gravity. J. Cosmol. Astropart. Phys. 2007, 2, 020. [Google Scholar] [CrossRef]
- Schwinger, J. On gauge invariance and vacuum polarization. Phys. Rev. 1951, 82, 664–679. [Google Scholar] [CrossRef]
- Sauter, F. On the behavior of an electron in a homogeneous electric field in Dirac’s relativistic theory. Z. Phys. 1931, 69, 742–764. [Google Scholar] [CrossRef]
- Ruffini, R.; Vereshchagin, G.; Xue, S.-S. Electron–positron pairs in physics and astrophysics: From heavy nuclei to black holes. Phys. Rep. 2010, 487, 1–140. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series and Products, 5th ed.; Academic Press: New York, NY, USA, 1994. [Google Scholar]
- Gutiérrez, S.A.; Dudley, A.L.; Plebañski, J.F. Signals and discontinuities in general relativistic nonlinear electrodynamics. J. Math. Phys. 1981, 22, 2835–2848. [Google Scholar] [CrossRef]
- Bisnovatyi-Kogan, G.S.; Tsupko, O.Y. Gravitational lensing in a non-uniform plasma. Mon. Not. R. Astron. Soc. 2010, 404, 1790–1800. [Google Scholar] [CrossRef]
- Babar, G.Z.; Atamurotov, F.; Babar, A.Z. Gravitational lensing in 4-D Einstein–Gauss–Bonnet gravity in the presence of plasma. Phys. Dark Universe 2021, 32, 100798. [Google Scholar] [CrossRef]
- Atamurotov, F.; Abdujabbarov, A.; Rayimbaev, J. Weak gravitational lensing Schwarzschild-MOG black hole in plasma. Eur. Phys. J. C 2021, 81, 118. [Google Scholar] [CrossRef]
- Amaro, D.; Breton, N.; Lämmerzahl, C.; Macías, A. Thermodynamics of the Einstein-Euler-Heisenberg rotating black hole. Phys. Rev. D 2024, 110, 124020. [Google Scholar] [CrossRef]
- Atamurotov, F.; Shaymatov, S.; Sheoran, P.; Siwach, S. Charged black hole in 4D Einstein-Gauss-Bonnet gravity: Particle motion, plasma effect on weak gravitational lensing and centre-of-mass energy. J. Cosm. Astr. Phys. 2021, 8, 045. [Google Scholar] [CrossRef]
- Duan, Z.Q.; Zhao, J.Y.; Yang, K. Electrically charged black holes in gravity with a background Kalb-Ramond field. arXiv 2024, arXiv:2310.13555. [Google Scholar] [CrossRef]
- Ditta, A.; Tiecheng, X.; Atamurotov, F.; Mustafa, G.; Aripov, M.M. Particle dynamics and weak gravitational lensing around nonlinear electrodynamics black hole. Chin. J. Phys. 2023, 83, 664–679. [Google Scholar] [CrossRef]
- Amaro, D.; Lämmerzahl, C.; Macías, A. Particle motion in the Einstein-Euler-Heisenberg rotating black hole spacetime. Phys. Rev. D 2023, 107, 084040. [Google Scholar] [CrossRef]


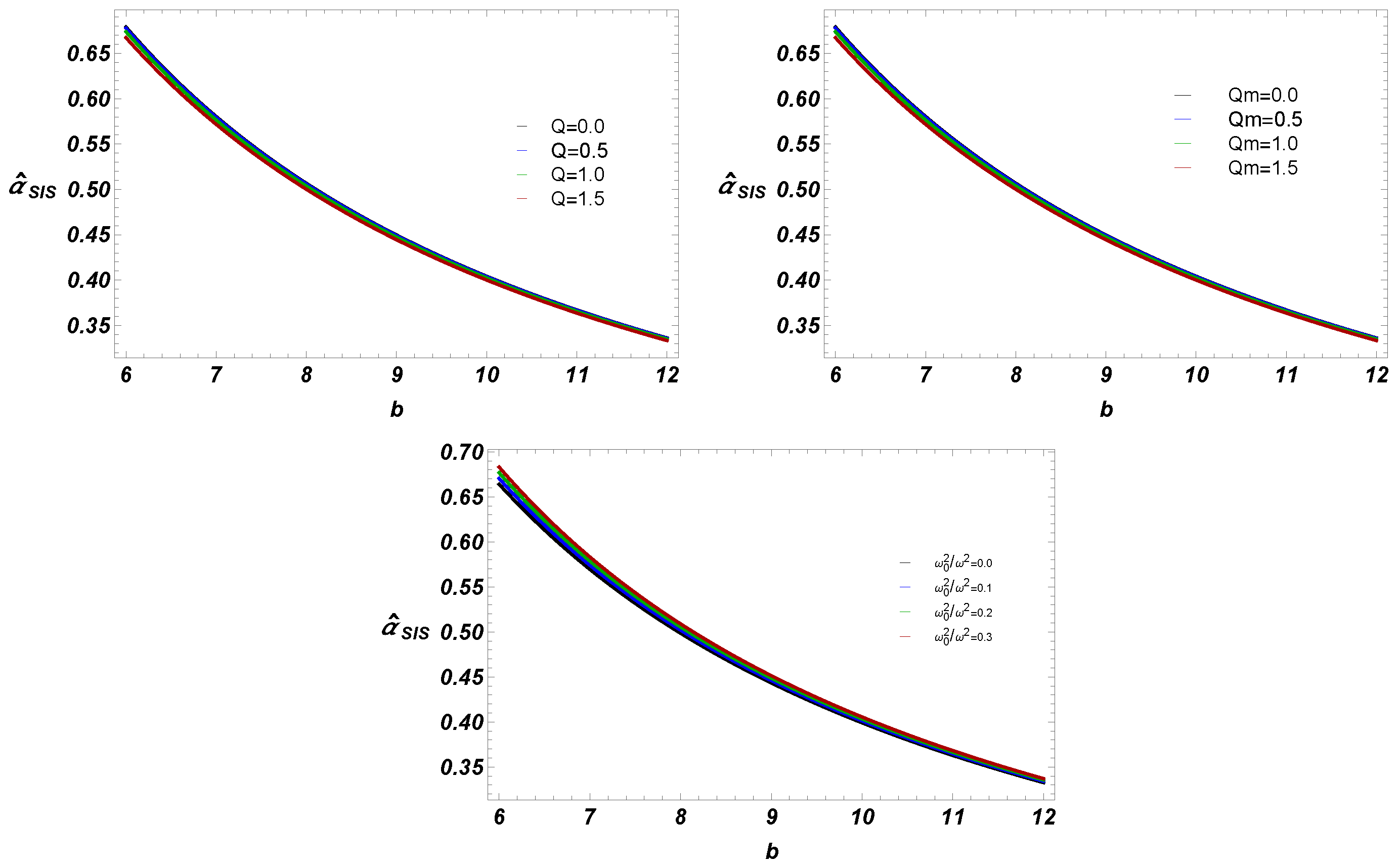

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ditta, A.; Mehmood, R.S.; Fiaz, M.; Bibi, B.; Deen, S.; Jaffar, R.; Mahmood, A. Exploring the Enigma of Particle Dynamics and Plasma Lensing Using Einstein–Euler–Heisenberg Black Hole Geometry. Universe 2025, 11, 19. https://doi.org/10.3390/universe11010019
Ditta A, Mehmood RS, Fiaz M, Bibi B, Deen S, Jaffar R, Mahmood A. Exploring the Enigma of Particle Dynamics and Plasma Lensing Using Einstein–Euler–Heisenberg Black Hole Geometry. Universe. 2025; 11(1):19. https://doi.org/10.3390/universe11010019
Chicago/Turabian StyleDitta, Allah, Raja Sikander Mehmood, Muhammad Fiaz, Bismillah Bibi, Sana Deen, Rimsha Jaffar, and Asif Mahmood. 2025. "Exploring the Enigma of Particle Dynamics and Plasma Lensing Using Einstein–Euler–Heisenberg Black Hole Geometry" Universe 11, no. 1: 19. https://doi.org/10.3390/universe11010019
APA StyleDitta, A., Mehmood, R. S., Fiaz, M., Bibi, B., Deen, S., Jaffar, R., & Mahmood, A. (2025). Exploring the Enigma of Particle Dynamics and Plasma Lensing Using Einstein–Euler–Heisenberg Black Hole Geometry. Universe, 11(1), 19. https://doi.org/10.3390/universe11010019







