Abstract
We have derived the tensor amplitudes for partial wave analysis of , within the helicity frame, as well as the amplitudes for the other decay sequences with same final states. These formulae are practical for the experiments measuring decaying into final states, such as BESIII with its recently collected huge and data samples.
PACS:
13.20.Gd; 13.30.Eg; 14.40.-n
1. Introduction
Recently, many measurements of or decays into baryon pairs have been reported by BESIII collaboration, such as [1], [2], [3], [4], [5], [6], [7] etc. These measurements are based on the huge or samples collected at the BESIII detector, which is operating at the electron position collider BEPCII. Taking advantage of the improved statistics, more precise measurements have been achieved, and some insights on the physics have been provided, such as the polarization parameters of baryons, relative phase between electric–magnetic and strong amplitudes, decay mechanism of decaying into baryon pairs, and search for excited baryon states, etc. However, there is no measurement of among these new exciting experimental results. A single will represent both and states later in this paper if not specified. The latest measurement of was conducted by BESII about 20 years ago [8]. The lack of a study does not mean this channel is not essential. In contrast, a careful analysis of would provide a lot of important information on the decay mechanism of the vector charmonia to the pair of , the first discovered resonance in particle physics, as well as the line shape of the invariant mass of the final states of this resonance. The main difficulty of this measurement is that has a much broader width than other baryon states. From PDG [9], the Breit–Wigner width of the is about 117 MeV, and the widths of other excited states are at the same level. It makes the interference effect significant in the measurement, but that has been ignored in previous measurements [8,10]. When we try to measure via final states protons and pions, which are the products of the strong decays of , the interference between and , as well as the excited states and even (excited-)nucleons, is expected to be large. This large interference makes a simple measurement of a two-body decay impossible since the signal yield cannot be extracted by a naive fit with only signal and background components, and needs to be considered carefully.
A partial wave analysis (PWA) is necessary to consider this interference correctly, while suitable formulae to describe these complex processes are still in short supply. Till now, most studies of have been based on N or scattering [11,12,13,14,15], where the PWA is applied but not suitable for studies since there are sequential decaysin the latter case. Compared with the abundant PWA formulae on the or heavy vectors decaying into final meson states [16,17], including radiative decays [18], similar results on the baryons are relatively rare. To the best of our knowledge, there are only two papers that have discussed the decays containing final baryon states. One has studied [19], and the other one has studied [20], but none of them can satisfy our request completely. This situation encourages us to write down the PWA formulae ourselves.
While there are many frames and formalisms in PWA, we choose to derive our formulae within the helicity frame with the covariant tensor formalism [21,22,23,24]. This choice is based on the following considerations. Firstly, the helicity frame is suitable for processes of sequential decays. In this frame, all the helicity states are defined in the rest frame of the mother particles, and the whole amplitude is a product of the amplitudes of sequentialprocesses. It reduces the complexity of the derivation of the formulae compared with the PWA based on canonical forms, where an L-S coupling method is used, such as that in [19,20,25]. Secondly, the advantage of the tensor formalism, compared to the helicity formalism, is that a spin tensor can couple to any four-momentum or another spin tensor to form the Lorentz invariant amplitudes, and the momentum dependence is separated explicitly from couplings. The momentum independence is important since it distinguishes the kinematics of an interaction from the dynamics that is really crucial. On the other hand, the helicity formalism takes simpler formulae by hiding this dependence in the so-called couplings, actually form factors. This paper is organized as follows. After this introduction, we discuss all the possible processes, i.e, the intermediate resonances involved in our partial wave analysis in Section 2. Then, we give the Lorentz invariant amplitudes in Section 3, composed of the constructions of each state’s wave function, concerns of the parity and charge conjugation translations, and the explicit covariant tensor formulae. Finally, we discuss some validations of these formulae and their possible applications on the present and future electron–positron colliding experiments.
2. Intermediate Resonances and Their
We only consider two kinds of first level decays of , which are and . Since our original physics motivation is to measure with decaying with almost 100% branching fraction to p and , the suitable final states in experiments are . The final states determine that there are three possible decay chains, that are , , , , , and , , as shown in Figure 1, Figure 2 and Figure 3. The reason why we do not consider the process of , is that the mass of is near the threshold of the invariant mass spectrum. Then, the relevant events can be removed easily during the data analysis. In the present and later descriptions, we shall omit the discussion on the charge-conjugated modes for compactness when no ambiguity is caused. Notice there are many possible combinations even in the first-level decays. For example, can decay into the following pairs if the phase space allows: , , , with representing both and here. will not be considered since it cannot decay into both charged p and . For the mode, the decay product at the first level can be, for example, , , , etc. Notice that we only consider the relevant nucleon and anti-nucleon pairs that are necessary for the analysis, not including all possible nucleon and anti-nucleon pairs.
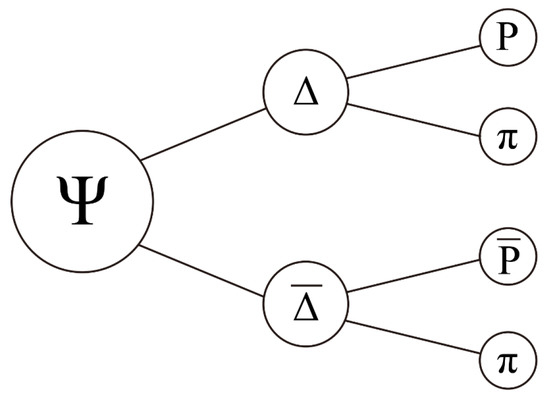
Figure 1.
Illustration of decay , .
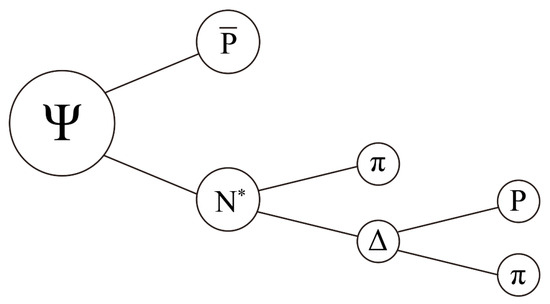
Figure 2.
Illustration of decay , , .
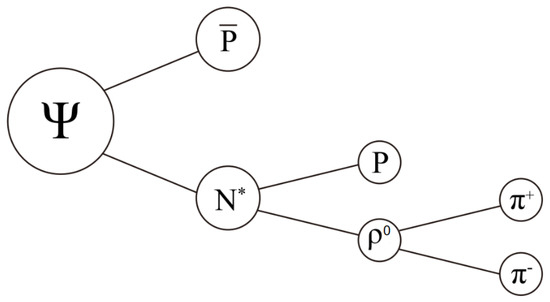
Figure 3.
Illustration of decay , , .
From the physical consideration, complex spin and parity combination sets are obtained. At the first level, decaying from a vector mother particle, i.e., , the of the decay products could be , , , , , , , , , , , and ; at the second level, if the decays are from , the final states are always , while the of the can be , , , , , , , and ; if a decay chain contains then there is another decay mode with final states , i.e., , while the of the initial can be , , , , , , and . In the processes involving the combination sets mentioned above, the orbital momenta should take all possible values to ensure conservation of the total angular momentum and parity.
3. Preparations
3.1. Wave Functions
To construct the covariant tensor amplitudes, we need the tensor wave functions describing relativistic particles with arbitrary spin (helicity) and satisfying the Rarita–Schwinger formalism [26]. We will follow the method proposed by Auvil and Brehm [27] to write down these wave functions explicitly. The wave function of a scalar particle is constant. We start with a particle of spin-1 at rest, whose wave functions may be expressed explicitly as column vectors:
Since a particle at rest cannot have the energy component if the spin (helicity) wave function is presented in the momentum space, the four-vector describing a spin-1 particle at rest is defined as
Then, the general helicity state vector with four-momentum p can be obtained by performing a Lorentz boost in the z direction and a proper rotation:
where m, E, p, and are the invariant mass, energy, momentum, and helicity (polar and azimuthal) angles of the particle, respectively, and satisfy with the natural unit. The wave function describing spin-2 particles can be constructed out of the wave functions of spin-1 via C-G coefficients as follows:
Then, the wave function of spin-n () particles can be derived in a cumulative way as tensor [28]:
Therefore, the wave functions should satisfy the Rarita–Schwinger conditions:
We shall turn to the Fermion particles now. Consider a spin- particle at rest and its basis vectors may be given by the spinors or two-dimensional column vectors:
We adopt the four-component Dirac spinor to describe the relativistic spin particles. Then, the two-component spinors are generalized to the four-component spinors :
where . After a boost, the helicity wave functions’ explicit expressions can be cast into the form
The “adjoint” spinor is defined as
The helicity wave functions for the anti-Fermion can be written down similarly as
Following Auvil and Brehm, wave functions corresponding to particles of spin can be constructed by the spin- wave functions and spin-n wave functions with C-G coefficients as the following:
The spin-j wave function Equation (14) is a four-component spinor with the four-vector indices . Since it describes a state of spin j, it can have only independent components. The desired supplementary conditions are just the Rarita–Schwinger equations:
where m is the mass of the spin-j particle and p is its four momentum.
3.2. Effective Vertices
We also need effective vertices to construct various partial wave amplitudes. The principle idea is that the decay mechanism has been considered an effective interaction. Then, all the loops in the Feynman diagrams are absorbed into the effective vertices [29]. A general form of any amplitude in a single decay chain can be expressed as
in which , , and e are wave functions of two baryons and a meson, respectively; B is considered the kernel of the propagator and usually parameterized as a Breit–Wigner function; and s are tensors representing effective vertices, which are composed by , , , , , , . The main target of this paper is to find all the independent effective vertices. Before that, it is worth taking some time to consider the constraints on them due to symmetry. Since, in these decays, the strong interaction is dominant, the conservation is expected under the transformation of parity P and charge conjugate C, respectively [30]. However, and do not correspond to precisely a particle and its anti-particle, and the charged particles do not have determined C-parity, so we only consider the symmetry of parity, and its conservation requires
where is the transformation property of different tensors, and , , and are the parities of the two baryons and one meson, respectively. The properties of different tensors under the P transformation are listed in Table 1. And we also notice the transformation property of wave function will be as and since each of them only takes Lorentz indexes without the Dirac ones.

Table 1.
The parity transformation properties of some tensors, the shorthand for while for is used as in [31].
4. Decay Amplitudes in Tensor Formalism
Now we are ready to derive the covariant invariant amplitudes in the tensor formalism for resonance decays. Let us consider a resonance of spin parity and mass m, decaying into two particles 1 and 2:
In the rest frame of the mother resonance, let p be the momentum of particle 1 with helicity angles . Usually, the amplitude A describing the decay process as two particles with helicity and may be written as
in the helicity formalism, where is the normalization factor, is the helicity coupling, and is the D function, with M being the z-component of the mother’s spin. However, with the explicit wave functions and effective vertices, we can construct the independent covariant invariant amplitudes in the tensor formalism:
4.1.
4.2.
4.3.
This type of partial wave formula for where the spin of is has been included in and will not be repeated.
4.4.
4.5.
4.6. The Formula of
4.7.
For completeness of the given formulae, we give the amplitudes of and . The amplitude formula of is 1. The amplitude formula of is
5. Discussion
5.1. Comparison to Helicity Formalism
Compared with the amplitudes in helicity formalism Equation (22), it is obvious that the helicity coupling ought to have momentum dependence but not expressed explicitly as that in the tensor formalism. When the measurements deal with narrow resonances such as and , this momentum dependence can be safely ignored. However, when the target resonance is the broad , separating the momentum dependence, i.e., the kinematic effect, from the dynamic part is crucial for the study of the line shape that reflects the internal interactions. As a cross check, we also calculate the number of considering the relevant symmetry, and it is found to be consistent with the number of in the tensor formalism.
5.2. Amplitude for Sequential Decays
In the previous section, we gave the sub-amplitudes for each interaction vertex. The whole amplitude of a decay chain then can be obtained in a straightforward way by the product of each sub-amplitude in the cascading decays. Thus, the cross-section can be written as
with
where and indicate collectively all angular and helicity variables of decay chains and of the intermediate and final states. are the propagators describing the dynamic interactions of each decay process, usually expressed in a Breit–Wigner form. Notice that in the helicity frame, the direction of the polarization of a state would be different when this state is in different decay chains. So an alignment, usually a rotation, is required to align the directions. This kind of alignment has been handled by experimentalists already [32,33] and been discussed further by new means in [34,35,36].
6. Summary
In this paper, we have derived the helicity amplitudes in the tensor formalism needed for the measurement of , , as well as the formulae for the sequential decaysof the other processes with the same final states. The covariant tensor formalism is adopted instead of the helicity formalism to make the momentum dependence explicit then more suitable to the measurements with broad resonances such as and its excited states. The number of independent terms in each decay chain has been checked and confirmed to be the same as the number of helicity amplitudes, and of course, the same as the number of partial waves in the decay too. These formulae are prepared for the measurements of decaying into final states, and also can be extended to the final states, such as since their spins and parities are same. Experiments which collected large and data samples, such as BESIII, would benefit from this study. Furthermore, as soon as the transitions of into nucleon and pion are well known phenomenologically and experimentally, some numerical analyses of the cascade decay of the charmonia states will be useful for readers.
It should be noticed only P-parity but not C-parity conservation is considered during the formula derivation since the fermions do not have certain C-parity. But in some special cases, where the daughter states are particles and anti-particles to each other, the C-parity is determined to be . It means if the L-S coupling scheme has been adopted, there is a chance to check the C violation by measuring the amplitude of the corresponding wave. However, the construction of pure spin wave functions based on high-fractional spin states such as two -spin states is beyond our ability. It also should be noticed that sometimes, the momentum notations P, , and are replaceable in the formulae since the constructed terms are dependent on each other, so the choice between them is somewhat just arbitrary. Breit–Wigner functions and projection operators are important in the experimental measurements too. But the projection operators can be obtained by the construction of wave functions mentioned in this paper straightforwardly. So we ignore a discussion of them. Furthermore, a complete discussion of the Breit–Wigner functions is beyond this paper’s scope, and their choices are left to experimentalists for when some specific forms are needed for specific resonances or decay channels.
Author Contributions
Conceptualization, K.Z.; formal analysis, K.S.; writing—original draft preparation, X.D. and K.S.; writing—review and editing, K.Z. and H.C.; visualization, X.D.; project administration, H.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Science Foundation of China (Nos. 11735010, U1932108, U2032102, and 12061131006). The numerical calculations in this paper were performed on the supercomputing system at the Supercomputing Center of Wuhan University.
Data Availability Statement
The original contributions presented in the study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
We would like to thank Yonggui Gao, Gang Li, ZhenTian Sun, JiaoJiao Song for useful discussion.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ablikim, M. et al. [BESIII Collaboration] Model-Independent Determination of the Spin of the Ω− and Its Polarization Alignment in ψ(3686)→Ω−. Phys. Rev. Lett. 2021, 126, 092002. [Google Scholar] [CrossRef] [PubMed]
- Ablikim, M. et al. [BESIII Collaboration] Observation of ψ(3686)→n and improved measurement of ψ(3686)→p. Phys. Rev. D 2018, 98, 032006. [Google Scholar] [CrossRef]
- Ablikim, M. et al. [BESIII Collaboration] Σ+ and polarization in the J/ψ and ψ(3686) decays. Phys. Rev. Lett. 2020, 125, 052004. [Google Scholar] [CrossRef] [PubMed]
- Ablikim, M. et al. [BESIII Collaboration] Study of J/ψ and ψ(3686)→Σ(1385)0(1385)0 and Ξ00. Phys. Lett. B 2017, 770, 217–225. [Google Scholar] [CrossRef]
- Ablikim, M. et al. [BESIII Collaboration] Study of ψ decays to the Ξ−+ and Σ(1385)∓(1385)± final states. Phys. Rev. D 2016, 93, 072003. [Google Scholar] [CrossRef]
- Ablikim, M. et al. [BESIII Collaboration] Measurement of J/ψ→Ξ(1530)−+ and evidence for the radiative decay Ξ(1530)−→γΞ−. Phys. Rev. D 2020, 101, 012004. [Google Scholar] [CrossRef]
- Ablikim, M. et al. [BESIII Collaboration] Observation of ψ(3686)→Ξ(1530)−(1530)+ and Ξ(1530)−+. Phys. Rev. D 2019, 100, 051101. [Google Scholar] [CrossRef]
- Bai, J.Z. et al. [BES Collaboration] Measurement of psi(2S) decays to baryon pairs. Phys. Rev. D 2001, 63, 032002. [Google Scholar] [CrossRef]
- Zyla, P.A. et al. [Particle Data Group Collaboration] Review of Particle Physics. PTEP 2020, 2020, 083C01. [Google Scholar]
- Eaton, M.W.; Goldhaber, G.; Abrams, G.S.; Blocker, C.A.; Carithers, W.C.; Chinowsky, W.; Coles, M.W.; Cooper, S.; Dieterle, W.E.; Dillon, J.B.; et al. Decays of the ψ(3097) to Baryon - Anti-baryon Final States. Phys. Rev. D 1984, 29, 804. [Google Scholar] [CrossRef]
- Hunt, B.C.; Manley, D.M. Updated determination of N∗ resonance parameters using a unitary, multichannel formalism. Phys. Rev. C 2019, 99, 055205. [Google Scholar] [CrossRef]
- Gridnev, A.B.; Horn, I.; Briscoe, W.J.; Strakovsky, I.I. The K-matrix approach to the Delta-resonance mass splitting and isospin violation in low-energy pi-N scattering. Phys. Atom. Nucl. 2006, 69, 1542–1551. [Google Scholar] [CrossRef]
- Koch, R.; Pietarinen, E. Low-Energy pi N Partial Wave Analysis. Nucl. Phys. A 1980, 336, 331–346. [Google Scholar] [CrossRef]
- Švarc, A.; Hadžimehmedović, M.; Omerović, R.; Osmanović, H.; Stahov, J. Poles of Karlsruhe-Helsinki KH80 and KA84 solutions extracted by using the Laurent-Pietarinen method. Phys. Rev. C 2014, 89, 045205. [Google Scholar] [CrossRef]
- Bernicha, A.; Lopez Castro, G.; Pestieau, J. Pion—proton scattering and isospin breaking in the Delta0-Delta++ system. Nucl. Phys. A 1996, 597, 623–635. [Google Scholar] [CrossRef]
- Zou, B.S.; Bugg, D.V. Covariant tensor formalism for partial wave analyses of psi decay to mesons. Eur. Phys. J. A 2003, 16, 537–547. [Google Scholar] [CrossRef]
- Dulat, S.; Zou, B.S. Covariant tensor formalism for partial wave analyses of ψ decays into γB, γγV and ψ(2S)→γχc0,1,2 with χc0,1,2→Kπ+π− and 2π+2π−. Eur. Phys. J. A 2005, 26, 125–134, Erratum in Eur. Phys. J. A 2020, 56, 275. [Google Scholar] [CrossRef]
- Wu, N.; Ruan, T.N. Covariant Helicity Amplitude Analysis for J/ψ→γPP*. Commun. Theor. Phys. 2001, 35, 547. [Google Scholar]
- Liang, W.H.; Shen, P.N.; Wang, J.X.; Zou, B.S. Theoretical formalism and Monte Carlo study of partial wave analysis for J/psi –> p anti-p omega. J. Phys. G 2002, 28, 333–343. [Google Scholar] [CrossRef]
- Zou, B.S.; Hussain, F. Covariant L-S scheme for the effective N*NM couplings. Phys. Rev. C 2003, 67, 015204. [Google Scholar] [CrossRef]
- Chung, S.U. Helicity coupling amplitudes in tensor formalism. Phys. Rev. D 1993, 48, 1225–1239, Erratum in Phys. Rev. D 1997, 56, 4419. [Google Scholar] [CrossRef] [PubMed]
- Chung, S.U. A General formulation of covariant helicity coupling amplitudes. Phys. Rev. D 1998, 57, 431–442. [Google Scholar] [CrossRef]
- Chung, S.U. Spin Formalisms; BNL Preprint; BNL-QGS-02-0900; CERN 71-8; Brookhaven National Laboratory: Upton, NY, USA, 2008. [Google Scholar]
- Hara, Y. Analyticity Properties of Helicity Amplitudes and Construction of Kinematical Singularity-Free Amplitudes for Any Spin. Phys. Rev. 1964, 136, B507–B514. [Google Scholar] [CrossRef]
- Filippini, V.; Fontana, A.; Rotondi, A. Covariant spin tensors in meson spectroscopy. Phys. Rev. D 1995, 51, 2247–2261. [Google Scholar] [CrossRef]
- Rarita, W.; Schwinger, J. On a theory of particles with half integral spin. Phys. Rev. 1941, 60, 61. [Google Scholar] [CrossRef]
- Auvil, P.R.; Brehm, J.J. Wave Functions for Particles of Higher Spin. Phys. Rev. 1966, 145, 1152. [Google Scholar] [CrossRef]
- Zhu, J.J.; Yan, M.L. Covariant amplitudes for mesons. arXiv 1999, arXiv:hep-ph/9903349. [Google Scholar]
- Scadron, M.D. Covariant Propagators and Vertex Functions for Any Spin. Phys. Rev. 1968, 165, 1640–1647. [Google Scholar] [CrossRef]
- Stapp, H.P. Derivation of the CPT Theorem and the Connection between Spin and Statistics from Postulates of the S-Matrix Theory. Phys. Rev. 1962, 125, 2139. [Google Scholar] [CrossRef]
- Peskin, M.E.; Schroeder, D.V. An Introduction to Quantum Field Theory; World Publishing Corporation: Beijing, China, 2011; pp. 64–71. [Google Scholar]
- Mizuk, R. et al. [Belle Collaboration] Observation of two resonance-like structures in the pi+ chi(c1) mass distribution in exclusive anti-B0 —> K- pi+ chi(c1) decays. Phys. Rev. D 2008, 78, 072004. [Google Scholar] [CrossRef]
- Aaij, R. et al. [LHCb Collaboration] Observation of J/ψp Resonances Consistent with Pentaquark States in →J/ψK−p Decays. Phys. Rev. Lett. 2015, 115, 072001. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Ping, R.G. Coherent helicity amplitude for sequential decays. Phys. Rev. D 2017, 95, 076010. [Google Scholar] [CrossRef]
- Marangotto, D. Helicity Amplitudes for Generic Multibody Particle Decays Featuring Multiple Decay Chains. Adv. High Energy Phys. 2020, 2020, 6674595. [Google Scholar] [CrossRef]
- Wang, M.; Jiang, Y.; Liu, Y.; Qian, W.; Lyu, X.; Zhang, L. A novel method to test particle ordering and final state alignment in helicity formalism. Chin. Phys. C 2021, 45, 063103. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).