Exploring New Physics with Deep Underground Neutrino Experiment High-Energy Flux: The Case of Lorentz Invariance Violation, Large Extra Dimensions and Long-Range Forces
Abstract
1. Introduction
2. The DUNE Experiment and the High-Energy Flux
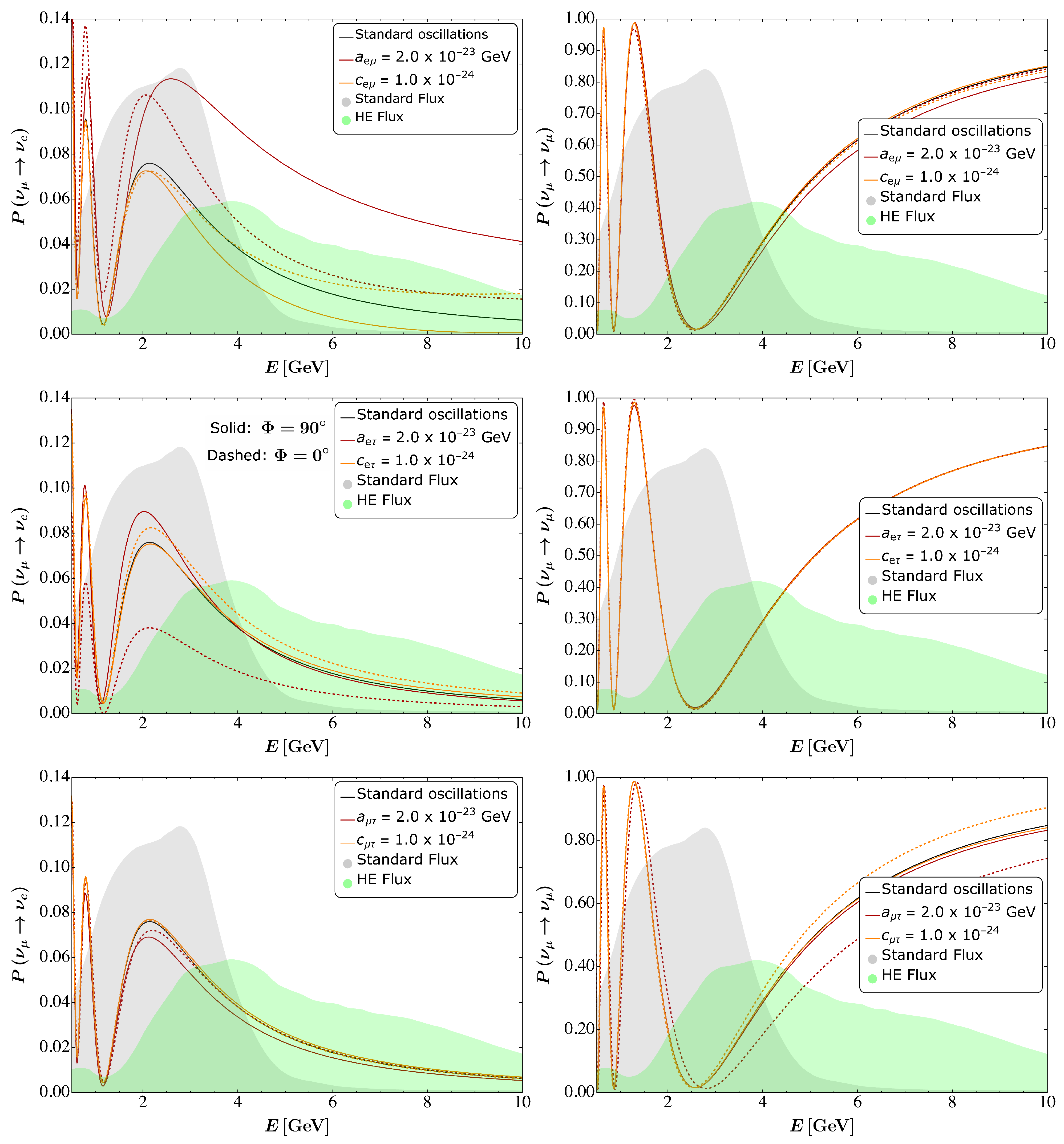
3. The Lorentz Invariance Violation Case
3.1. Theoretical Framework
3.2. HE-DUNE Results
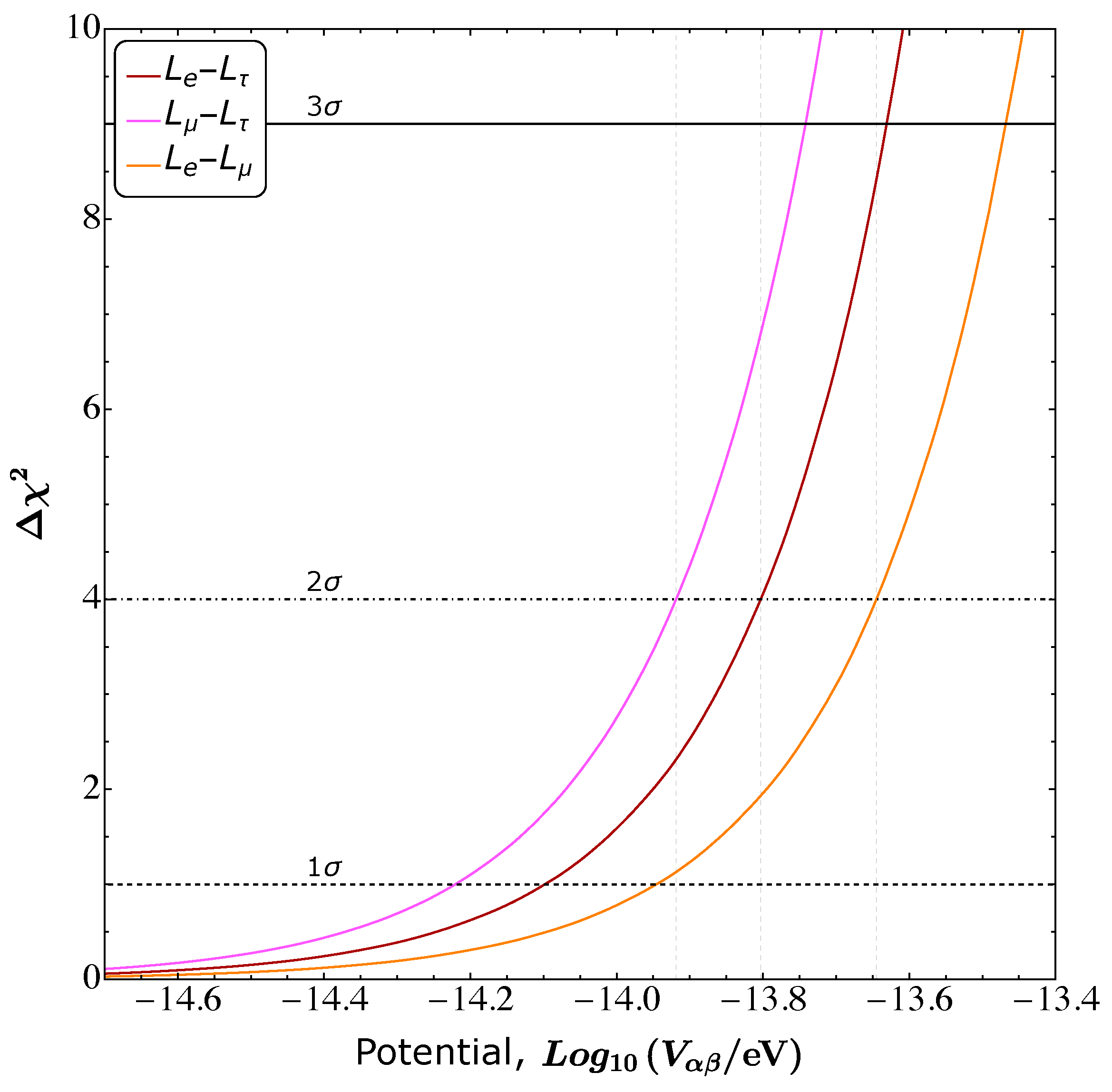
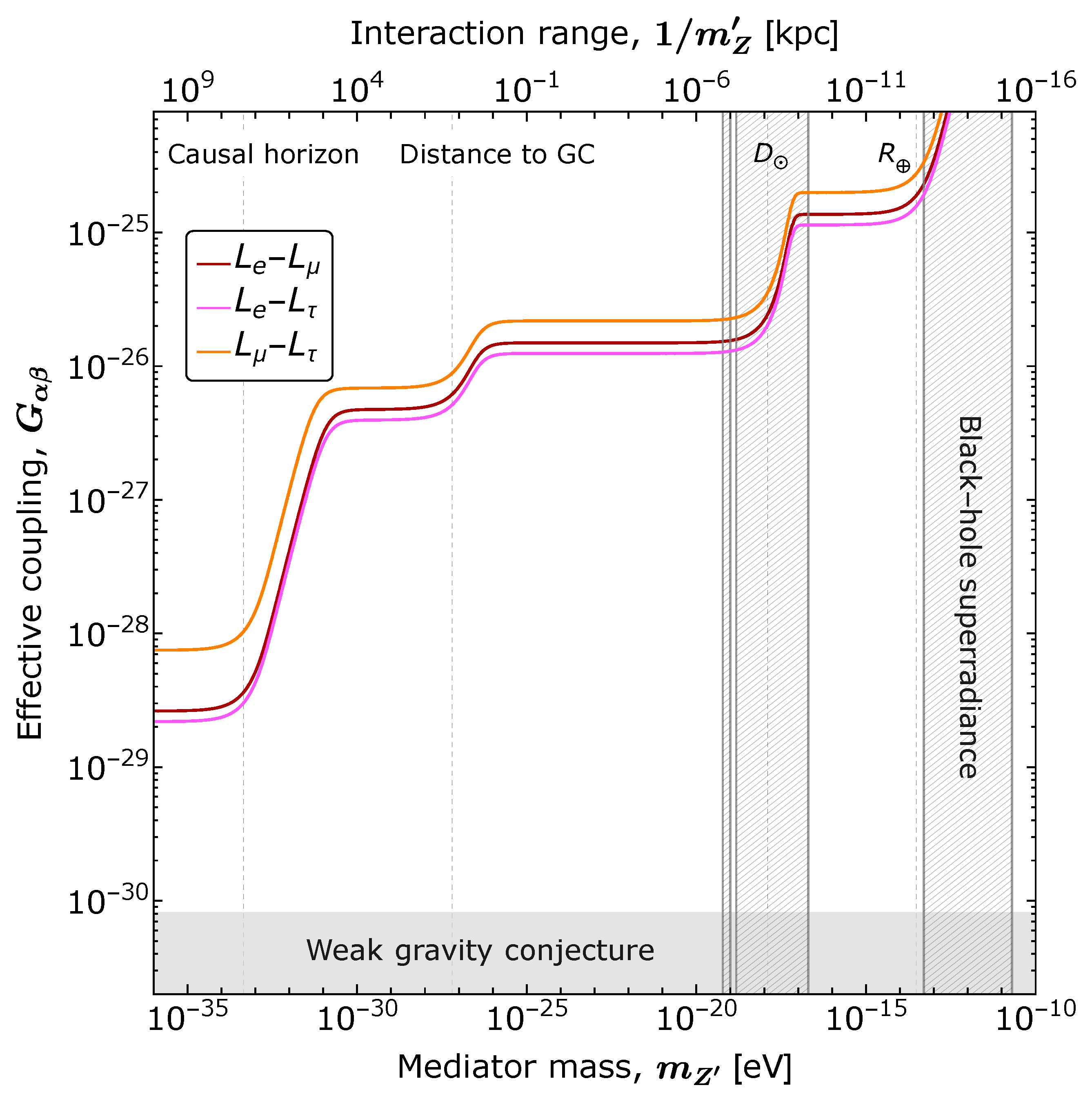
4. The Long-Range Forces Case
4.1. Theoretical Framework
4.2. HE-DUNE Results
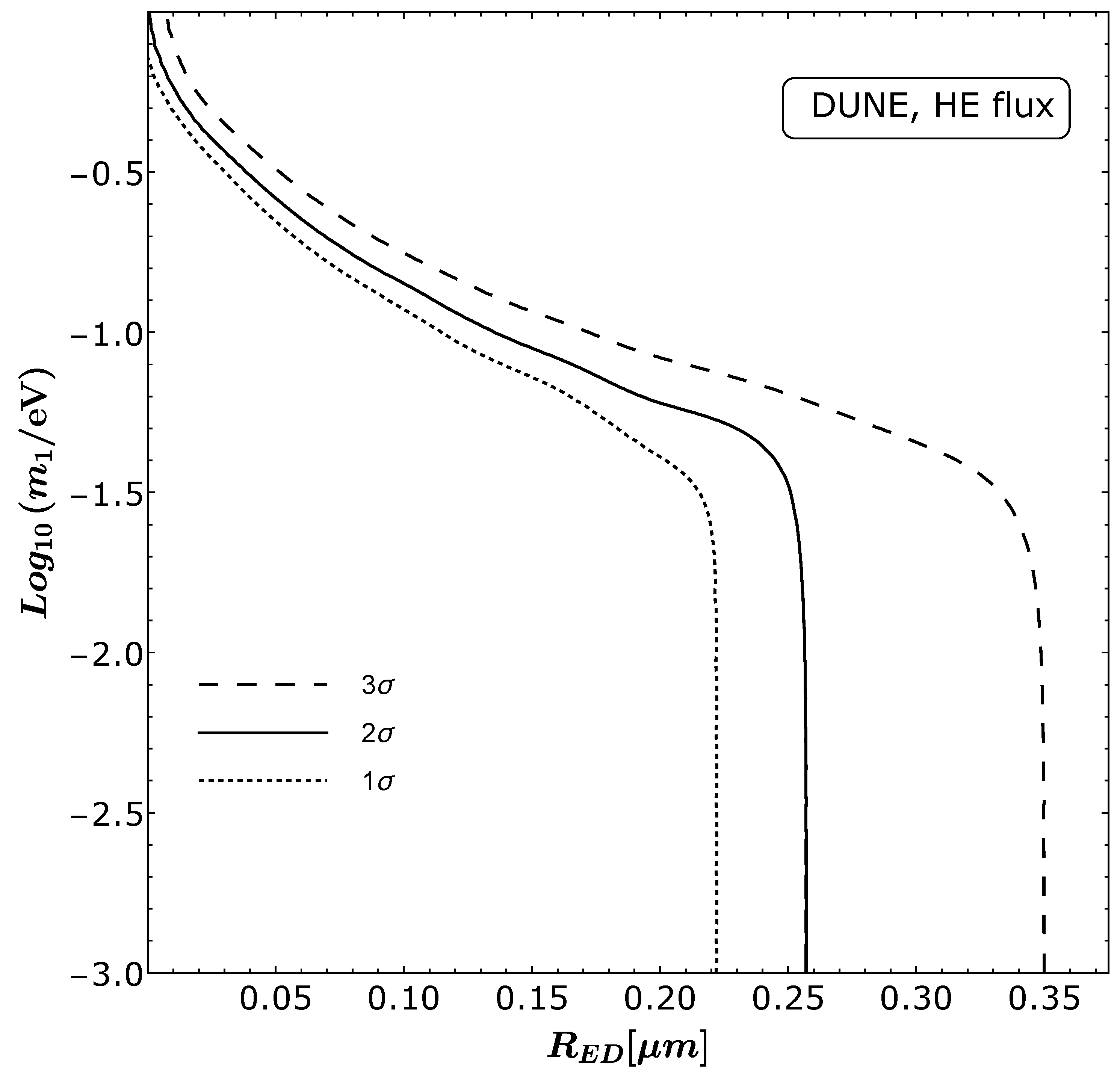
5. The Large Extra Dimensions Case
5.1. Theoretical Framework
5.2. HE-DUNE Results
6. Conclusions
- Lorentz Invariance Violation (LIV): in this model, the neutrino Lagrangian density is modified through several Lorentz-violating operators, both CPT-even and CPT-odd. The presence of such operators modifies the neutrino propagation Hamiltonian with the addition of two Hermitian matrices (CPT-violating) and (CPT-conserving). The effects of the second matrix increase linearly with the neutrino energy. We studied in Section 3.2 the sensitivity of HE-DUNE to the off-diagonal LIV parameters. We found that the limits on the moduli of CPT-violating parameters are worse than the ones that the standard DUNE is expected to set. On the other hand, HE-DUNE capabilities should exceed the standard DUNE ones in constraining energy-enhanced effects of CPT-conserving LIV parameters .
- Long-Range Forces (LRFs): in this model, we expect that new interactions with an ultra-light mediator, with a very long interaction length, arise from a gauge symmetry of the form . These interactions can modify the matter potential term in the neutrino oscillation Hamiltonian. We showed that the limits from HE-DUNE on this new potential are rather stringent but not enough to overcome the standard DUNE ones. We also computed the limits on the coupling of the new interaction as well as on the mass of the new mediator. These are correlated with the interaction length since, depending on that, neutrinos might experience the potential generated from various astrophysical matter densities.
- Large Extra Dimensions (LEDs): if right-handed neutrinos are singlets under the SM group, but they can propagate in space-time with more than four dimensions, the smallness of neutrino masses can be naturally explained. In the case in which one of the new dimensions is compactified in a sphere with a relatively large radius, the Kaluza–Klein excitations of the neutrino states can be treated as sterile neutrinos involved in the oscillation. In this approach, the transition probabilities depend not only on the standard mixing parameters but also on the smallest Dirac neutrino mass and on the compactification radius of the large extra dimension. We showed that the limit that HE-DUNE might set on , for small enough lightest neutrino mass, is better than the standard DUNE one. This is because the fast active–sterile oscillations coming from the Kaluza–Klein states might be resolved better at high energies than at lower ones.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
| 1 | For the other two oscillation channels, namely appearance and disappearance, the collaboration suggested 2% and 5%, respectively. |
| 2 | In Quantum Field Theory the CPT theorem states that the combination of the discrete transformations “Chargeconjugation” (C), “Parity” (P) and “Timereversal” (T) must be a symmetry of the theory. |
| 3 | The LIV probabilities shown here have been obtained in [41] neglecting also terms proportional to and where . |
| 4 | The appearance probability can be obtained from unitarity and the leading term will be the one depending again on (). |
| 5 | Notice that limits from the more energetic atmospheric and astrophysical neutrinos on CPT-even LIV parameters are more stringent than the DUNE ones due to the dependence on the neutrino energy of their effect on the oscillation probabilities. |
| 6 | |
| 7 | |
| 8 | |
| 9 |
References
- Fukuda, Y.; Hayakawa, T.; Ichihara, E.; Inoue, K.; Ishihara, K.; Ishino, H.; Itow, Y.; Kajita, T.; 554 Kameda, J.; Kasuga, S.; et al. Evidence for oscillation of atmospheric neutrinos. Phys. Rev. Lett. 1998, 81, 1562–1567. [Google Scholar] [CrossRef]
- Xu, X.J.; Wang, Z.; Chen, S. Solar neutrino physics. Prog. Part. Nucl. Phys. 2023, 131, 104043. [Google Scholar] [CrossRef]
- Choubey, S. Atmospheric neutrinos: Status and prospects. Nucl. Phys. B 2016, 908, 235–249. [Google Scholar] [CrossRef]
- Wen, L.J.; Cao, J.; Wang, Y.F. Reactor Neutrino Experiments: Present and Future. Ann. Rev. Nucl. Part. Sci. 2017, 67, 183–211. [Google Scholar] [CrossRef][Green Version]
- Mezzetto, M.; Terranova, F. Three-flavour oscillations with accelerator neutrino beams. Universe 2020, 6, 32. [Google Scholar] [CrossRef]
- Gando, A.; Gando, Y.; Ichimura, K.; Ikeda, H.; Inoue, K.; Kibe, Y.; Kishimoto, Y.; Koga, M.; Minekawa, Y.; Mitsui, T.; et al. Precision Measurement of Neutrino Oscillation Parameters with KamLAND. Phys. Rev. Lett. 2008, 100, 221803. [Google Scholar] [CrossRef]
- Gando, A.; Gando, Y.; Ichimura, K.; Ikeda, H.; Inoue, K.; Kibe, Y.; Kishimoto, Y.; Koga, M.; Minekawa, Y.; Mitsui, T.; et al. Constraints on θ13 from A Three-Flavor Oscillation Analysis of Reactor Antineutrinos at KamLAND. Phys. Rev. D 2011, 83, 052002. [Google Scholar] [CrossRef]
- Gando, A.; Gando, Y.; Hanakago, H.; Ikeda, H.; Inoue, K.; Ishidoshiro, K.; Ishikawa, H.; Koga, M.; Matsuda, R.; Matsuda, S.; et al. Reactor On-Off Antineutrino Measurement with KamLAND. Phys. Rev. D 2013, 88, 033001. [Google Scholar] [CrossRef]
- An, F.P.; Bai, J.Z.; Balantekin, A.B.; Band, H.R.; Beavis, D.; Beriguete, W.; Bishai, M.; Blyth, S.; Boddy, K.; Brown, R.L.; et al. Observation of electron-antineutrino disappearance at Daya Bay. Phys. Rev. Lett. 2012, 108, 171803. [Google Scholar] [CrossRef]
- Esteban, I.; Gonzalez-Garcia, M.C.; Maltoni, M.; Schwetz, T.; Zhou, A. The fate of hints: Updated global analysis of three-flavor neutrino oscillations. J. High Energy Phys. 2020, 9, 178. [Google Scholar] [CrossRef]
- Abe, K.; Abe, K.; Aihara, H.; Aimi, A.; Akutsu, R.; Andreopoulos, C.; Anghel, I.; Anthony, L.H.V.; Antonova, M.; Ashida, Y.; et al. Hyper-Kamiokande Design Report. arXiv 2018, arXiv:1805.04163. [Google Scholar]
- Acciarri, R.; Acero, M.A.; Adamowski, M.; Adams, C.; Adamson, P.; Adhikari, S.; Ahmad, Z.; Albright, C.H.; Alion, T.; Amador, E.; et al. Long-Baseline Neutrino Facility (LBNF) and Deep Underground Neutrino Experiment (DUNE): Conceptual Design Report, Volume 2: The Physics Program for DUNE at LBNF. arXiv 2015, arXiv:1512.06148. [Google Scholar]
- Himmel, A. New Oscillation Results from the NOvA Experiment. 2020. Available online: https://www.osti.gov/biblio/1640225/ (accessed on 15 March 2024).
- Batkiewicz-Kwasniak, M. The Latest T2K Neutrino Oscillation Results and the Future of the T2K and Hyper-Kamiokande Experiments. Acta Phys. Polon. Supp. 2022, 15, 23. [Google Scholar] [CrossRef]
- Rahaman, U.; Raut, S. On the tension between the latest NOvA and T2K data. arXiv 2021, arXiv:2112.13186. [Google Scholar]
- Ghoshal, A.; Giarnetti, A.; Meloni, D. On the role of the ντ appearance in DUNE in constraining standard neutrino physics and beyond. J. High Energy Phys. 2019, 12, 126. [Google Scholar] [CrossRef]
- Masud, M.; Bishai, M.; Mehta, P. Extricating New Physics Scenarios at DUNE with Higher Energy Beams. Sci. Rep. 2019, 9, 352. [Google Scholar] [CrossRef]
- De Gouvêa, A.; Kelly, K.J.; Stenico, G.V.; Pasquini, P. Physics with Beam Tau-Neutrino Appearance at DUNE. Phys. Rev. D 2019, 100, 016004. [Google Scholar] [CrossRef]
- De Romeri, V.; Giunti, C.; Stuttard, T.; Ternes, C.A. Neutrino oscillation bounds on quantum decoherence. J. High Energy Phys. 2023, 9, 97. [Google Scholar] [CrossRef]
- Mammen Abraham, R.; Alvarez-Muñiz, J.; Argüelles, C.A.; Ariga, A.; Ariga, T.; Aurisano, A.; Autiero, D.; Bishai, M.; Bostan, N.; Bustamante, M.; et al. Tau neutrinos in the next decade: From GeV to EeV. J. Phys. G 2022, 49, 110501. [Google Scholar] [CrossRef]
- Giarnetti, A.; Meloni, D. New Sources of Leptonic CP Violation at the DUNE Neutrino Experiment. Universe 2021, 7, 240. [Google Scholar] [CrossRef]
- Acciarri, R.; Acero, M.A.; Adamowski, M.; Adams, C.; Adamson, P.; Adhikari, S.; Ahmad, Z.; Albright, C.H.; Alion, T.; Amador, E.; et al. Long-Baseline Neutrino Facility (LBNF) and Deep Underground Neutrino Experiment (DUNE): Conceptual Design Report, Volume 1: The LBNF and DUNE Projects. arXiv 2016, arXiv:1601.05471. [Google Scholar]
- Abi, B.; Acciarri, R.; Acero, M.A.; Adamov, G.; Adams, D.; Adinolfi, M.; Ahmad, Z.; Ahmed, J.; Alion, T.; Monsalve, S.A.; et al. Long-baseline neutrino oscillation physics potential of the DUNE experiment. Eur. Phys. J. C 2020, 80, 978. [Google Scholar] [CrossRef]
- Abi, B.; Acciarri, R.; Acero, M.A.; Adamov, G.; Adams, D.; Adinolfi, M.; Ahmad, Z.; Ahmed, J.; Alion, T.; Monsalve, S.A.; et al. Deep Underground Neutrino Experiment (DUNE), Far Detector Technical Design Report, Volume II: DUNE Physics. arXiv 2020, arXiv:2002.03005. [Google Scholar]
- Abud, A.A.; Abi, B.; Acciarri, R.; Acero, M.A.; Adamov, G.; Adams, D.; Adinolfi, M.; Aduszkiewicz, A.; Ahmad, Z.; Ahmed, J.; et al. Deep Underground Neutrino Experiment (DUNE) Near Detector Conceptual Design Report. Instruments 2021, 5, 31. [Google Scholar] [CrossRef]
- Fermilab. Available online: http://home.fnal.gov/~ljf26/DUNEFluxes/ (accessed on 15 March 2024).
- Bishai, M.; Dolce, M. Optimization of the LBNF/DUNE Beamline for Tau Neutrinos. Available online: http://docs.dunescience.org/cgi-bin/RetrieveFile?docid=2013&filename=DOLCE_M_report.pdf&version=1 (accessed on 15 March 2024).
- DUNE Neutrino Flux Files Generated with G4LBNF. Available online: https://glaucus.crc.nd.edu/DUNEFluxes/ (accessed on 15 March 2024).
- Alion, T.; Back, J.J.; Bashyal, A.; Bass, M.; Bishai, M.; Cherdack, D.; Diwan, M.; Djurcic, Z.; Evans, J.; Fernandez-Martinez, E.; et al. Experiment Simulation Configurations Used in DUNE CDR. arXiv 2016, arXiv:1606.09550. [Google Scholar]
- Abi, B.; Acciarri, R.; Acero, M.A.; Adamov, G.; Adams, D.; Adinolfi, M.; Ahmad, Z.; Ahmed, J.; Alion, T.; Monsalve, S.A.; et al. Experiment Simulation Configurations Approximating DUNE TDR. arXiv 2021, arXiv:2103.04797. [Google Scholar]
- Colladay, D.; Kostelecky, V.A. CPT violation and the standard model. Phys. Rev. D 1997, 55, 6760–6774. [Google Scholar] [CrossRef]
- Colladay, D.; Kostelecky, V.A. Lorentz violating extension of the standard model. Phys. Rev. D 1998, 58, 116002. [Google Scholar] [CrossRef]
- Diaz, J.S.; Kostelecky, A. Lorentz- and CPT-violating models for neutrino oscillations. Phys. Rev. D 2012, 85, 016013. [Google Scholar] [CrossRef]
- Greenberg, O.W. CPT violation implies violation of Lorentz invariance. Phys. Rev. Lett. 2002, 89, 231602. [Google Scholar] [CrossRef]
- Kostelecky, V.A.; Potting, R. CPT and strings. Nucl. Phys. B 1991, 359, 545–570. [Google Scholar] [CrossRef]
- Kostelecky, V.A.; Potting, R. CPT, strings, and meson factories. Phys. Rev. D 1995, 51, 3923–3935. [Google Scholar] [CrossRef]
- Kostelecky, V.A.; Potting, R. Expectation values, Lorentz invariance, and CPT in the open bosonic string. Phys. Lett. B 1996, 381, 89–96. [Google Scholar] [CrossRef]
- Kostelecky, V.A.; Mewes, M. Lorentz and CPT violation in neutrinos. Phys. Rev. D 2004, 69, 016005. [Google Scholar] [CrossRef]
- Kostelecký, V.A.; Samuel, S. Spontaneous breaking of Lorentz symmetry in string theory. Phys. Rev. D 1989, 39, 683–685. [Google Scholar] [CrossRef] [PubMed]
- Kostelecký, V.A.; Samuel, S. Phenomenological gravitational constraints on strings and higher-dimensional theories. Phys. Rev. Lett. 1989, 63, 224–227. [Google Scholar] [CrossRef]
- Agarwalla, S.K.; Das, S.; Sahoo, S.; Swain, P. Constraining Lorentz invariance violation with next-generation long-baseline experiments. J. High Energy Phys. 2023, 7, 216. [Google Scholar] [CrossRef]
- Kumar Agarwalla, S.; Masud, M. Can Lorentz invariance violation affect the sensitivity of deep underground neutrino experiment? Eur. Phys. J. C 2020, 80, 716. [Google Scholar] [CrossRef]
- Kostelecky, A.; Mewes, M. Neutrinos with Lorentz-violating operators of arbitrary dimension. Phys. Rev. D 2012, 85, 096005. [Google Scholar] [CrossRef]
- Wolfenstein, L. Neutrino oscillations in matter. Phys. Rev. D 1978, 17, 2369–2374. [Google Scholar] [CrossRef]
- Barenboim, G.; Ternes, C.A.; Tórtola, M. New physics vs. new paradigms: Distinguishing CPT violation from NSI. Eur. Phys. J. C 2019, 79, 390. [Google Scholar] [CrossRef]
- Diaz, J.S. Correspondence between nonstandard interactions and CPT violation in neutrino oscillations. arXiv 2015, arXiv:1506.01936. [Google Scholar]
- Barenboim, G.; Masud, M.; Ternes, C.A.; Tórtola, M. Exploring the intrinsic Lorentz-violating parameters at DUNE. Phys. Lett. B 2019, 788, 308–315. [Google Scholar] [CrossRef]
- Fiza, N.; Khan Chowdhury, N.R.; Masud, M. Investigating Lorentz Invariance Violation with the long baseline experiment P2O. J. High Energy Phys. 2023, 1, 76. [Google Scholar] [CrossRef]
- Adamson, P.; Andreopoulos, C.; Arms, K.E.; Armstrong, R.; Auty, D.J.; Ayres, D.S.; Baller, B.; Barr, G.; Barrett, W.L.; Becker, B.R.; et al. Testing Lorentz Invariance and CPT Conservation with NuMI Neutrinos in the MINOS Near Detector. Phys. Rev. Lett. 2008, 101, 151601. [Google Scholar] [CrossRef]
- Adamson, P.; Andreopoulos, C.; Arms, K.E.; Armstrong, R.; Auty, D.J.; Ayres, D.S.; Baller, B.; Barr, G.; Barrett, W.L.; Becker, B.R.; et al. A Search for Lorentz Invariance and CPT Violation with the MINOS Far Detector. Phys. Rev. Lett. 2010, 105, 151601. [Google Scholar] [CrossRef] [PubMed]
- Adamson, P.; Andreopoulos, C.; Arms, K.E.; Armstrong, R.; Auty, D.J.; Ayres, D.S.; Baller, B.; Barr, G.; Barrett, W.L.; Becker, B.R.; et al. Search for Lorentz invariance and CPT violation with muon antineutrinos in the MINOS Near Detector. Phys. Rev. D 2012, 85, 031101. [Google Scholar] [CrossRef]
- Dighe, A.; Ray, S. CPT violation in long baseline neutrino experiments: A Three flavor analysis. Phys. Rev. D 2008, 78, 036002. [Google Scholar] [CrossRef]
- Barenboim, G.; Lykken, J.D. MINOS and CPT-violating neutrinos. Phys. Rev. D 2009, 80, 113008. [Google Scholar] [CrossRef]
- Rebel, B.; Mufson, S. The Search for Neutrino-Antineutrino Mixing Resulting from Lorentz Invariance Violation using Neutrino Interactions in MINOS. Astropart. Phys. 2013, 48, 78–81. [Google Scholar] [CrossRef]
- de Gouvêa, A.; Kelly, K.J. Neutrino vs. Antineutrino Oscillation Parameters at DUNE and Hyper-Kamiokande. Phys. Rev. D 2017, 96, 095018. [Google Scholar] [CrossRef]
- Barenboim, G.; Ternes, C.A.; Tórtola, M. Neutrinos, DUNE and the world best bound on CPT invariance. Phys. Lett. B 2018, 780, 631–637. [Google Scholar] [CrossRef]
- Majhi, R.; Chembra, S.; Mohanta, R. Exploring the effect of Lorentz invariance violation with the currently running long-baseline experiments. Eur. Phys. J. C 2020, 80, 364. [Google Scholar] [CrossRef]
- Majhi, R.; Singha, D.K.; Ghosh, M.; Mohanta, R. Distinguishing nonstandard interaction and Lorentz invariance violation at the Protvino to super-ORCA experiment. Phys. Rev. D 2023, 107, 075036. [Google Scholar] [CrossRef]
- Abe, K.; Amey, J.; Andreopoulos, C.; Antonova, M.; Aoki, S.; Ariga, A.; Assylbekov, S.; Autiero, D.; Ban, S.; Barbato, F.C.T.; et al. Search for Lorentz and CPT violation using sidereal time dependence of neutrino flavor transitions over a short baseline. Phys. Rev. D 2017, 95, 111101. [Google Scholar] [CrossRef]
- Aguilar-Arevalo, A.A.; Anderson, C.E.; Bazarko, A.O.; Brice, S.J.; Brown, B.C.; Bugel, L.; Cao, J.; Coney, L.; Conrad, J.M.; Cox, D.C.; et al. Test of Lorentz and CPT violation with Short Baseline Neutrino Oscillation Excesses. Phys. Lett. B 2013, 718, 1303–1308. [Google Scholar] [CrossRef]
- Giunti, C.; Laveder, M. Hint of CPT Violation in Short-Baseline Electron Neutrino Disappearance. Phys. Rev. D 2010, 82, 113009. [Google Scholar] [CrossRef]
- Abe, Y.; Aberle, C.; dos Anjos, J.C.; Bergevin, M.; Bernstein, A.; Bezerra, T.J.C.; Bezrukhov, L.; Blucher, E.; Bowden, N.S.; Buck, C.; et al. First Test of Lorentz Violation with a Reactor-based Antineutrino Experiment. Phys. Rev. D 2012, 86, 112009. [Google Scholar] [CrossRef]
- Diaz, J.S.; Schwetz, T. Limits on CPT violation from solar neutrinos. Phys. Rev. D 2016, 93, 093004. [Google Scholar] [CrossRef]
- Hooper, D.; Morgan, D.; Winstanley, E. Lorentz and CPT invariance violation in high-energy neutrinos. Phys. Rev. D 2005, 72, 065009. [Google Scholar] [CrossRef]
- Tomar, G.; Mohanty, S.; Pakvasa, S. Lorentz Invariance Violation and IceCube Neutrino Events. J. High Energy Phys. 2015, 11, 22. [Google Scholar] [CrossRef]
- Liao, J.; Marfatia, D. IceCube’s astrophysical neutrino energy spectrum from CPT violation. Phys. Rev. D 2018, 97, 041302. [Google Scholar] [CrossRef]
- Abbasi, R.; Abdou, Y.; Abu-Zayyad, T.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Andeen, K.; Auffenberg, J.; Bai, X.; Baker, M.; et al. Search for a Lorentz-violating sidereal signal with atmospheric neutrinos in IceCube. Phys. Rev. D 2010, 82, 112003. [Google Scholar] [CrossRef]
- Chatterjee, A.; Gandhi, R.; Singh, J. Probing Lorentz and CPT Violation in a Magnetized Iron Detector using Atmospheric Neutrinos. J. High Energy Phys. 2014, 6, 45. [Google Scholar] [CrossRef][Green Version]
- Sahoo, S.; Kumar, A.; Agarwalla, S.K. Probing Lorentz Invariance Violation with atmospheric neutrinos at INO-ICAL. J. High Energy Phys. 2022, 3, 50. [Google Scholar] [CrossRef]
- Datta, A.; Gandhi, R.; Mehta, P.; Sankar, S.U. Atmospheric neutrinos as a probe of CPT and Lorentz violation. Phys. Lett. B 2004, 597, 356–361. [Google Scholar] [CrossRef][Green Version]
- Abe, K.; Haga, Y.; Hayato, Y.; Ikeda, M.; Iyogi, K.; Kameda, J.; Kishimoto, Y.; Miura, M.; Moriyama, S.; Nakahata, M.; et al. Test of Lorentz invariance with atmospheric neutrinos. Phys. Rev. D 2015, 91, 052003. [Google Scholar] [CrossRef]
- Argüelles, C.A.; Aurisano, A.J.; Batell, B.; Berger, J.; Bishai, M.; Boschi, T.; Byrnes, N.; Chatterjee, A.; Chodos, A.; Coan, T.; et al. New opportunities at the next-generation neutrino experiments I: BSM neutrino physics and dark matter. Rept. Prog. Phys. 2020, 83, 124201. [Google Scholar] [CrossRef]
- Argüelles, C.A.; Barenboim, G.; Bustamante, M.; Coloma, P.; Denton, P.B.; Esteban, I.; Farzan, Y.; Martínez, E.F.; Forero, D.V.; Gago, A.M.; et al. Snowmass white paper: Beyond the standard model effects on neutrino flavor: Submitted to the proceedings of the US community study on the future of particle physics (Snowmass 2021). Eur. Phys. J. C 2023, 83, 15. [Google Scholar] [CrossRef]
- NuFit 5.2. 2022. Available online: www.nu-fit.org (accessed on 15 March 2024).
- Huber, P.; Lindner, M.; Winter, W. Simulation of long-baseline neutrino oscillation experiments with GLoBES (General Long Baseline Experiment Simulator). Comput. Phys. Commun. 2005, 167, 195. [Google Scholar] [CrossRef]
- Huber, P.; Kopp, J.; Lindner, M.; Rolinec, M.; Winter, W. New features in the simulation of neutrino oscillation experiments with GLoBES 3.0: General Long Baseline Experiment Simulator. Comput. Phys. Commun. 2007, 177, 432–438. [Google Scholar] [CrossRef]
- Kopp, J.; Lindner, M.; Ota, T.; Sato, J. Non-standard neutrino interactions in reactor and superbeam experiments. Phys. Rev. D 2008, 77, 013007. [Google Scholar] [CrossRef]
- Huber, P.; Lindner, M.; Winter, W. Superbeams versus neutrino factories. Nucl. Phys. B 2002, 645, 3–48. [Google Scholar] [CrossRef]
- Fogli, G.L.; Lisi, E.; Marrone, A.; Montanino, D.; Palazzo, A. Getting the most from the statistical analysis of solar neutrino oscillations. Phys. Rev. D 2002, 66, 053010. [Google Scholar] [CrossRef]
- Abi, B.; Acciarri, R.; Acero, M.A.; Adamov, G.; Adams, D.; Adinolfi, M.; Ahmad, Z.; Ahmed, J.; Alion, T.; Monsalve, S.A.; et al. Prospects for beyond the Standard Model physics searches at the Deep Underground Neutrino Experiment. Eur. Phys. J. C 2021, 81, 322. [Google Scholar] [CrossRef]
- Singh, M.; Bustamante, M.; Agarwalla, S.K. Flavor-dependent long-range neutrino interactions in DUNE & T2HK: Alone they constrain, together they discover. J. High Energy Phys. 2023, 8, 101. [Google Scholar] [CrossRef]
- Berryman, J.M.; de Gouvêa, A.; Kelly, K.J.; Peres, O.L.G.; Tabrizi, Z. Large, Extra Dimensions at the Deep Underground Neutrino Experiment. Phys. Rev. D 2016, 94, 033006. [Google Scholar] [CrossRef]
- Agarwalla, S.K.; Das, S.; Giarnetti, A.; Meloni, D.; Singh, M. Enhancing sensitivity to leptonic CP violation using complementarity among DUNE, T2HK, and T2HKK. Eur. Phys. J. C 2023, 83, 694. [Google Scholar] [CrossRef]
- Denton, P.B.; Gehrlein, J.; Pestes, R. CP -Violating Neutrino Nonstandard Interactions in Long-Baseline-Accelerator Data. Phys. Rev. Lett. 2021, 126, 051801. [Google Scholar] [CrossRef]
- de Gouvêa, A.; Kelly, K.J. Non-standard Neutrino Interactions at DUNE. Nucl. Phys. B 2016, 908, 318–335. [Google Scholar] [CrossRef]
- Neutrino Non-Standard Interactions: A Status Report. SciPost Phys. Proc. 2019, 2, 1. [CrossRef]
- Bakhti, P.; Rajaee, M. Sensitivities of future reactor and long-baseline neutrino experiments to NSI. Phys. Rev. D 2021, 103, 075003. [Google Scholar] [CrossRef]
- Ge, S.F.; Parke, S.J. Scalar Nonstandard Interactions in Neutrino Oscillation. Phys. Rev. Lett. 2019, 122, 211801. [Google Scholar] [CrossRef] [PubMed]
- Denton, P.B.; Giarnetti, A.; Meloni, D. How to identify different new neutrino oscillation physics scenarios at DUNE. J. High Energy Phys. 2023, 2, 210. [Google Scholar] [CrossRef]
- Aguilar, J.; Anastasopoulos, M.; Baussan, E.; Bhattacharyya, A.K.; Bignami, A.; Blennow, M.; Bogomilov, M.; Bolling, B.; Bouquerel, E.; Bramati, F.; et al. Study of non-standard interaction mediated by a scalar field at ESSnuSB experiment. arXiv 2023, arXiv:2310.10749. [Google Scholar]
- Gupta, A.; Majumdar, D.; Prakash, S. Neutrino oscillation measurements with JUNO in the presence of scalar NSI. arXiv 2023, arXiv:2306.07343. [Google Scholar]
- Sarker, A.; Medhi, A.; Bezboruah, D.; Devi, M.M.; Dutta, D. Impact of scalar NSI on the neutrino mass hierarchy sensitivity at DUNE, T2HK and T2HKK. arXiv 2023, arXiv:2309.12249. [Google Scholar]
- Grifols, J.A.; Masso, E.; Peris, S. Supernova neutrinos as probes of long range nongravitational interactions of dark matter. Astropart. Phys. 1994, 2, 161–165. [Google Scholar] [CrossRef]
- Grifols, J.A.; Masso, E.; Toldra, R. Majorana neutrinos and long range forces. Phys. Lett. B 1996, 389, 563–565. [Google Scholar] [CrossRef]
- Grifols, J.A.; Masso, E. Neutrino oscillations in the sun probe long range leptonic forces. Phys. Lett. B 2004, 579, 123–126. [Google Scholar] [CrossRef]
- Mishra, P.; Majhi, R.; Pusty, S.K.; Ghosh, M.; Mohanta, R. Study of Long Range Force in P2SO and T2HKK. arXiv 2024, arXiv:2402.19178. [Google Scholar]
- Agarwalla, S.K.; Bustamante, M.; Singh, M.; Swain, P. A plethora of long-range neutrino interactions probed by DUNE and T2HK. arXiv 2024, arXiv:2404.02775. [Google Scholar]
- Agarwalla, S.K.; Bustamante, M.; Das, S.; Narang, A. Present and future constraints on flavor-dependent long-range interactions of high-energy astrophysical neutrinos. J. High Energy Phys. 2023, 8, 113. [Google Scholar] [CrossRef]
- Chatterjee, S.S.; Dasgupta, A.; Agarwalla, S.K. Exploring Flavor-Dependent Long-Range Forces in Long-Baseline Neutrino Oscillation Experiments. J. High Energy Phys. 2015, 12, 167. [Google Scholar] [CrossRef]
- Coloma, P.; Gonzalez-Garcia, M.C.; Maltoni, M. Neutrino oscillation constraints on U(1)’ models: From non-standard interactions to long-range forces. J. High Energy Phys. 2021, 1, 114, Erratum in: J. High Energy Phys. 2022, 11, 115. [Google Scholar] [CrossRef]
- Smirnov, A.Y.; Xu, X.J. Wolfenstein potentials for neutrinos induced by ultra-light mediators. J. High Energy Phys. 2019, 12, 46. [Google Scholar] [CrossRef]
- Chauhan, G.; Xu, X.J. Impact of the cosmic neutrino background on long-range force searches. J. High Energy Phys. 2024, 7, 255. [Google Scholar] [CrossRef]
- He, X.G.; Joshi, G.C.; Lew, H.; Volkas, R.R. New-Z′ phenomenology. Phys. Rev. D 1991, 43, R22–R24. [Google Scholar] [CrossRef]
- He, X.G.; Joshi, G.C.; Lew, H.; Volkas, R.R. Simplest Z′ model. Phys. Rev. D 1991, 44, 2118–2132. [Google Scholar] [CrossRef]
- Foot, R.; He, X.G.; Lew, H.; Volkas, R.R. Model for a light Z-prime boson. Phys. Rev. D 1994, 50, 4571–4580. [Google Scholar] [CrossRef]
- Asai, K.; Hamaguchi, K.; Nagata, N.; Tseng, S.Y.; Tsumura, K. Minimal Gauged U(1)Lα-Lβ Models Driven into a Corner. Phys. Rev. D 2019, 99, 055029. [Google Scholar] [CrossRef]
- Asai, K.; Hamaguchi, K.; Nagata, N. Predictions for the neutrino parameters in the minimal gauged U(1)Lμ-Lτ model. Eur. Phys. J. C 2017, 77, 763. [Google Scholar] [CrossRef]
- Lou, Y.; Nomura, T. Neutrino observables in gauged U(1)Lα-Lβ models with two Higgs doublet and one singlet scalars. arXiv 2024, arXiv:2406.01030. [Google Scholar]
- Bustamante, M.; Agarwalla, S.K. Universe’s Worth of Electrons to Probe Long-Range Interactions of High-Energy Astrophysical Neutrinos. Phys. Rev. Lett. 2019, 122, 061103. [Google Scholar] [CrossRef] [PubMed]
- Wise, M.B.; Zhang, Y. Lepton Flavorful Fifth Force and Depth-dependent Neutrino Matter Interactions. J. High Energy Phys. 2018, 6, 53. [Google Scholar] [CrossRef]
- Khatun, A.; Thakore, T.; Kumar Agarwalla, S. Can INO be Sensitive to Flavor-Dependent Long-Range Forces? J. High Energy Phys. 2018, 4, 23. [Google Scholar] [CrossRef]
- Agarwalla, S.K.; Das, S.; Masud, M.; Swain, P. Evolution of neutrino mass-mixing parameters in matter with non-standard interactions. J. High Energy Phys. 2021, 11, 94. [Google Scholar] [CrossRef]
- Joshipura, A.S.; Mohanty, S. Constraints on flavor dependent long range forces from atmospheric neutrino observations at super-Kamiokande. Phys. Lett. B 2004, 584, 103–108. [Google Scholar] [CrossRef]
- Bandyopadhyay, A.; Dighe, A.; Joshipura, A.S. Constraints on flavor-dependent long range forces from solar neutrinos and KamLAND. Phys. Rev. D 2007, 75, 093005. [Google Scholar] [CrossRef]
- Gonzalez-Garcia, M.C.; Maltoni, M. Determination of matter potential from global analysis of neutrino oscillation data. J. High Energy Phys. 2013, 9, 152. [Google Scholar] [CrossRef]
- Honda, M.; Kao, Y.; Okamura, N.; Pronin, A.; Takeuchi, T. Constraints on New Physics from Long Baseline Neutrino Oscillation Experiments. arXiv 2007, arXiv:0707.4545. [Google Scholar]
- Farzan, Y.; Palomares-Ruiz, S. Flavor of cosmic neutrinos preserved by ultralight dark matter. Phys. Rev. D 2019, 99, 051702. [Google Scholar] [CrossRef]
- Aartsen, M.G.; Abbasi, R.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Alispach, C.; Allison, P.; Amin, N.M.; et al. IceCube-Gen2: The window to the extreme Universe. J. Phys. G 2021, 48, 060501. [Google Scholar] [CrossRef]
- Heeck, J.; Rodejohann, W. Gauged Lμ-Lτ and different Muon Neutrino and Anti-Neutrino Oscillations: MINOS and beyond. J. Phys. G 2011, 38, 085005. [Google Scholar] [CrossRef]
- McMillan, P.J. Mass models of the Milky Way. Mon. Not. R. Astron. Soc. 2011, 414, 2446–2457. [Google Scholar] [CrossRef]
- Miller, M.J.; Bregman, J.N. The Structure of the Milky Way’s Hot Gas Halo. Astrophys. J. 2013, 770, 118. [Google Scholar] [CrossRef]
- Baryakhtar, M.; Lasenby, R.; Teo, M. Black Hole Superradiance Signatures of Ultralight Vectors. Phys. Rev. D 2017, 96, 035019. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Motl, L.; Nicolis, A.; Vafa, C. The String landscape, black holes and gravity as the weakest force. J. High Energy Phys. 2007, 6, 60. [Google Scholar] [CrossRef]
- de Gouvêa, A. Neutrino Mass Models. Ann. Rev. Nucl. Part. Sci. 2016, 66, 197–217. [Google Scholar] [CrossRef]
- King, S.F. Neutrino mass models. Rept. Prog. Phys. 2004, 67, 107–158. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Dimopoulos, S.; Dvali, G.R.; March-Russell, J. Neutrino masses from large extra dimensions. Phys. Rev. D 2001, 65, 024032. [Google Scholar] [CrossRef]
- Dienes, K.R.; Dudas, E.; Gherghetta, T. Neutrino oscillations without neutrino masses or heavy mass scales: A Higher dimensional seesaw mechanism. Nucl. Phys. B 1999, 557, 25. [Google Scholar] [CrossRef]
- Dvali, G.R.; Smirnov, A.Y. Probing large extra dimensions with neutrinos. Nucl. Phys. B 1999, 563, 63–81. [Google Scholar] [CrossRef]
- Mohapatra, R.N.; Perez-Lorenzana, A. Three flavor neutrino oscillations in models with large extra dimensions. Nucl. Phys. B 2001, 593, 451–470. [Google Scholar] [CrossRef]
- Barbieri, R.; Creminelli, P.; Strumia, A. Neutrino oscillations from large extra dimensions. Nucl. Phys. B 2000, 585, 28–44. [Google Scholar] [CrossRef]
- Davoudiasl, H.; Langacker, P.; Perelstein, M. Constraints on large extra dimensions from neutrino oscillation experiments. Phys. Rev. D 2002, 65, 105015. [Google Scholar] [CrossRef]
- Antoniadis, I.; Arkani-Hamed, N.; Dimopoulos, S.; Dvali, G.R. New dimensions at a millimeter to a Fermi and superstrings at a TeV. Phys. Lett. B 1998, 436, 257–263. [Google Scholar] [CrossRef]
- Antoniadis, I.; Kiritsis, E.; Rizos, J.; Tomaras, T.N. D-branes and the standard model. Nucl. Phys. B 2003, 660, 81–115. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Dimopoulos, S.; Dvali, G.R. The Hierarchy problem and new dimensions at a millimeter. Phys. Lett. B 1998, 429, 263–272. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Dimopoulos, S.; Dvali, G.R. Phenomenology, astrophysics and cosmology of theories with submillimeter dimensions and TeV scale quantum gravity. Phys. Rev. D 1999, 59, 086004. [Google Scholar] [CrossRef]
- Esmaili, A.; Peres, O.L.G.; Tabrizi, Z. Probing Large Extra Dimensions with IceCube. J. Cosmol. Astropart. Phys. 2014, 12, 2. [Google Scholar] [CrossRef]
- Machado, P.A.N.; Nunokawa, H.; Zukanovich Funchal, R. Testing for Large Extra Dimensions with Neutrino Oscillations. Phys. Rev. D 2011, 84, 013003. [Google Scholar] [CrossRef]
- Machado, P.A.N.; Nunokawa, H.; dos Santos, F.A.P.; Funchal, R.Z. Bulk Neutrinos as an Alternative Cause of the Gallium and Reactor Anti-neutrino Anomalies. Phys. Rev. D 2012, 85, 073012. [Google Scholar] [CrossRef]
- Basto-Gonzalez, V.S.; Esmaili, A.; Peres, O.L.G. Kinematical Test of Large Extra Dimension in Beta Decay Experiments. Phys. Lett. B 2013, 718, 1020–1023. [Google Scholar] [CrossRef]
- Girardi, I.; Meloni, D. Constraining new physics scenarios in neutrino oscillations from Daya Bay data. Phys. Rev. D 2014, 90, 073011. [Google Scholar] [CrossRef]
- Rodejohann, W.; Zhang, H. Signatures of Extra Dimensional Sterile Neutrinos. Phys. Lett. B 2014, 737, 81–89. [Google Scholar] [CrossRef]
- Carena, M.; Li, Y.Y.; Machado, C.S.; Machado, P.A.N.; Wagner, C.E.M. Neutrinos in Large Extra Dimensions and Short-Baseline νe Appearance. Phys. Rev. D 2017, 96, 095014. [Google Scholar] [CrossRef]
- Stenico, G.V.; Forero, D.V.; Peres, O.L.G. A Short Travel for Neutrinos in Large Extra Dimensions. J. High Energy Phys. 2018, 11, 155. [Google Scholar] [CrossRef]
- Basto-Gonzalez, V.S.; Forero, D.V.; Giunti, C.; Quiroga, A.A.; Ternes, C.A. Short-baseline oscillation scenarios at JUNO and TAO. Phys. Rev. D 2022, 105, 075023. [Google Scholar] [CrossRef]
- Forero, D.V.; Giunti, C.; Ternes, C.A.; Tyagi, O. Large extra dimensions and neutrino experiments. Phys. Rev. D 2022, 106, 035027. [Google Scholar] [CrossRef]
- Roy, S. Capability of the proposed long-baseline experiments to probe large extra dimension. Phys. Rev. D 2023, 108, 055015. [Google Scholar] [CrossRef]



| Oscillation Parameters () | Normal Ordering (NO) |
|---|---|
| () | |
| () |
| 95% CL limit () | 95% CL limit () | ||
|---|---|---|---|
| <5.1 | <0.43 | ||
| <9.3 | <2.23 | ||
| <1.12 (<1.0) | <0.66 (<0.64) |
| 95% CL limit | < eV | < eV | < eV |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giarnetti, A.; Marciano, S.; Meloni, D. Exploring New Physics with Deep Underground Neutrino Experiment High-Energy Flux: The Case of Lorentz Invariance Violation, Large Extra Dimensions and Long-Range Forces. Universe 2024, 10, 357. https://doi.org/10.3390/universe10090357
Giarnetti A, Marciano S, Meloni D. Exploring New Physics with Deep Underground Neutrino Experiment High-Energy Flux: The Case of Lorentz Invariance Violation, Large Extra Dimensions and Long-Range Forces. Universe. 2024; 10(9):357. https://doi.org/10.3390/universe10090357
Chicago/Turabian StyleGiarnetti, Alessio, Simone Marciano, and Davide Meloni. 2024. "Exploring New Physics with Deep Underground Neutrino Experiment High-Energy Flux: The Case of Lorentz Invariance Violation, Large Extra Dimensions and Long-Range Forces" Universe 10, no. 9: 357. https://doi.org/10.3390/universe10090357
APA StyleGiarnetti, A., Marciano, S., & Meloni, D. (2024). Exploring New Physics with Deep Underground Neutrino Experiment High-Energy Flux: The Case of Lorentz Invariance Violation, Large Extra Dimensions and Long-Range Forces. Universe, 10(9), 357. https://doi.org/10.3390/universe10090357






