On Quark–Lepton Mixing and the Leptonic CP Violation
Abstract
1. Introduction
2. Corrections to BM, TBM and GR
2.1. Notation
2.2. Corrections from the (13)-Sector to BM, TBM and GR
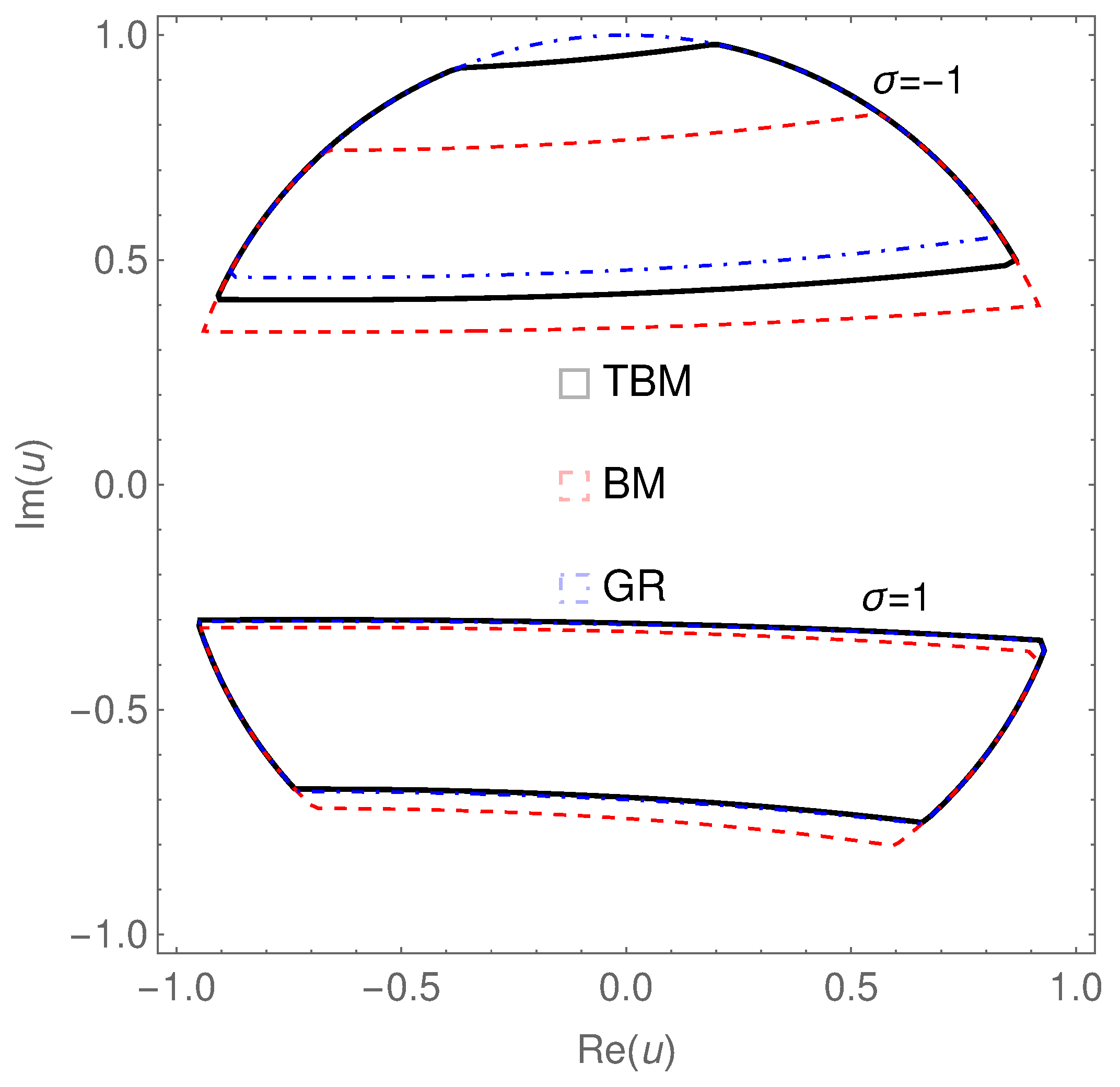
- In the limit of exact TBM, BM and GR, the invariant J reduces towhich all lead to a suppressed CP violation in the lepton sector, in agreement with Table 2 for an appropriate choice of .
- Retaining terms proportional to (and setting ) does not cure the previous problem since they appear only to .
- To reconcile our prediction with the experimental value, we need to allow for a deviation from exact TBM, BM and GR forms provided by . The degeneracy between and will allow the latter to assume both positive and negative values.
2.3. Perturbation on the (23)-Sector
2.4. The Full Glory: Perturbation on the (12)-Sector
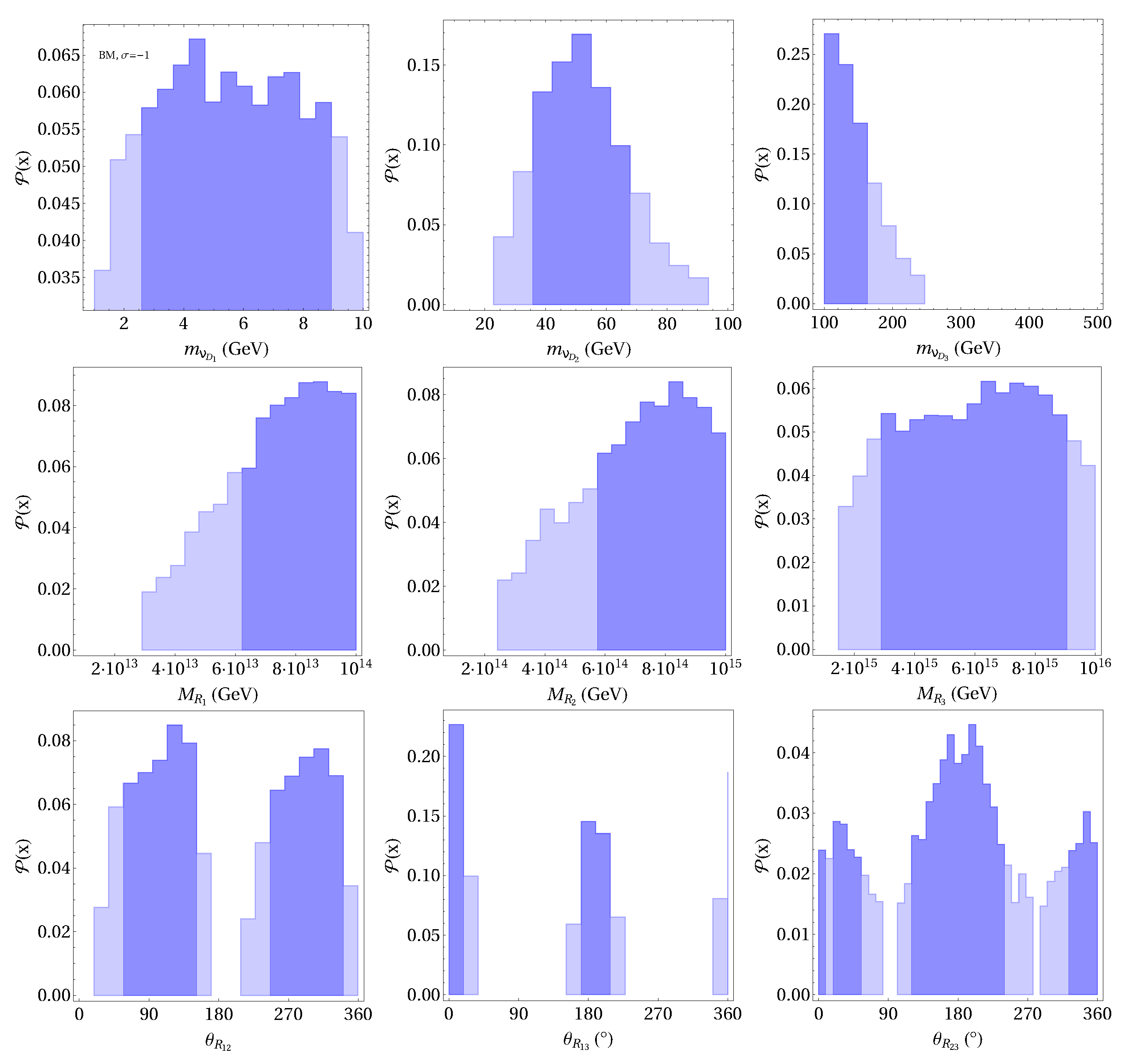
3. On the Neutrino Masses
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Full (λ3) Formulae
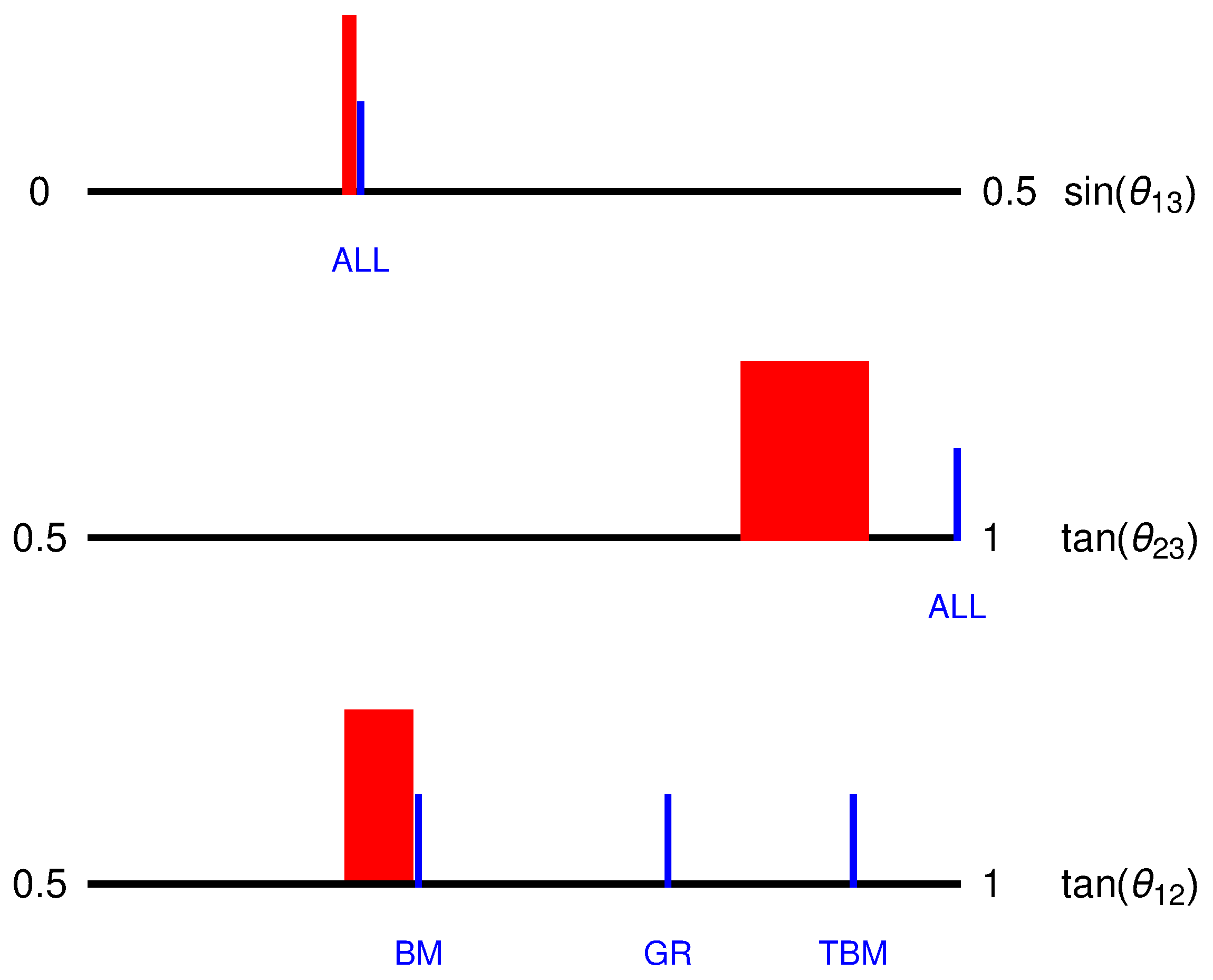
| 1 | For our purposes, it is enough to consider the normal hierarchy only, as the only significant difference with respect to the inverted ordering case is a slight preference for the opposite octant. |
| 2 | We do not report the spread of as, for any pattern, its absolute value is around two orders of magnitude smaller than the experimental best-fit. |
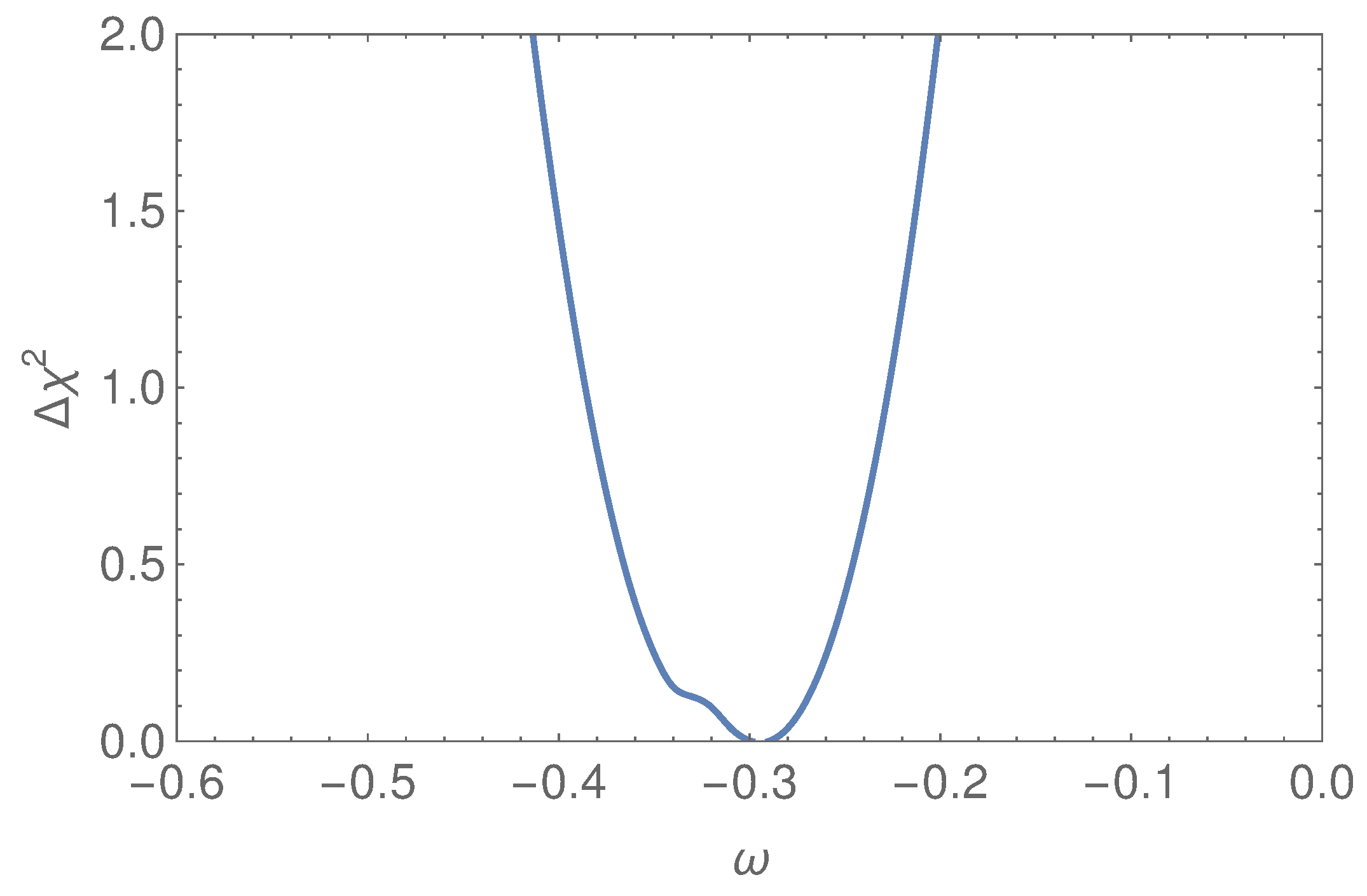
| 3 | Since the complex variable u was already enough to guarantee the correct amount of leptonic CP violation, we prefer to reduce the number of free parameters by choosing a real correction . |
| 4 | |
| 5 | If, instead, we prefer to deal with complex matrices, phases must thus be added to to help in vanishing all imaginary parts of Equation (33). |
References
- Minakata, H.; Smirnov, A.Y. Neutrino mixing and quark-lepton complementarity. Phys. Rev. D 2004, 70, 073009. [Google Scholar] [CrossRef]
- Georgi, H.; Jarlskog, C. A New Lepton-Quark Mass Relation in a Unified Theory. Phys. Lett. B 1979, 86, 297–300. [Google Scholar] [CrossRef]
- Raidal, M. Relation Between the Neutrino and Quark Mixing Angles and Grand Unification. Phys. Rev. Lett. 2004, 93, 161801. [Google Scholar] [CrossRef] [PubMed]
- Frampton, P.H.; Mohapatra, R.N. Possible Gauge Theoretic Origin for Quark-Lepton Complementarity. J. High Energy Phys. 2005, 2005, 025. [Google Scholar] [CrossRef]
- Antusch, S.; King, S.; Mohapatra, R. Quark–lepton complementarity in unified theories. Phys. Lett. B 2005, 618, 150–161. [Google Scholar] [CrossRef]
- Xing, Z.Z. Nontrivial correlation between the CKM and MNS matrices. Phys. Lett. B 2005, 618, 141–149. [Google Scholar] [CrossRef]
- Datta, A.; Everett, L.; Ramond, P. Cabibbo haze in lepton mixing. Phys. Lett. B 2005, 620, 42–51. [Google Scholar] [CrossRef][Green Version]
- Patel, K.M. An SO(10)XS4 Model of Quark-Lepton Complementarity. Phys. Lett. B 2011, 695, 225–230. [Google Scholar] [CrossRef]
- Picariello, M.; Chauhan, B.C.; Pulido, J.; Torrente-Lujan, E. Predictions from non-trivial quark-lepton complementarity. Int. J. Mod. Phys. A 2007, 22, 5860–5874. [Google Scholar] [CrossRef]
- Chauhan, B.; Picariello, M.; Pulido, J.; Torrente-Lujan, E. Quark–lepton complementarity with lepton and quark mixing data predict . Eur. Phys. J. C 2007, 50, 573–578. [Google Scholar] [CrossRef][Green Version]
- Harada, J. Neutrino mixing and CP violation from Dirac-Majorana bimaximal mixture and quark-lepton unification. Europhys. Lett. (EPL) 2006, 75, 248–253. [Google Scholar] [CrossRef][Green Version]
- Zhukovsky, K.; Davydova, A.A. CP violation and quark-lepton complementarity of the neutrino mixing matrix. Eur. Phys. J. C 2019, 79, 385. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, X.; Ma, B.Q. Quark-lepton complementarity and self-complementarity in different schemes. Phys. Rev. D 2012, 86, 093019. [Google Scholar] [CrossRef]
- Zhang, X.; Zheng, Y.j.; Ma, B.Q. Quark-lepton complementarity revisited. Phys. Rev. D 2012, 85, 097301. [Google Scholar] [CrossRef]
- Barranco, J.; Gonzalez Canales, F.; Mondragon, A. Universal Mass Texture, CP violation and Quark-Lepton Complementarity. Phys. Rev. D 2010, 82, 073010. [Google Scholar] [CrossRef]
- Cheung, K.; Kang, S.K.; Kim, C.S.; Lee, J. Lepton flavor violation as a probe of quark-lepton unification. Phys. Rev. D 2005, 72, 036003. [Google Scholar] [CrossRef]
- Hochmuth, K.A.; Rodejohann, W. Low and high energy phenomenology of quark-lepton complementarity scenarios. Phys. Rev. D 2007, 75, 073001. [Google Scholar] [CrossRef]
- Plentinger, F.; Seidl, G.; Winter, W. The Seesaw mechanism in quark-lepton complementarity. Phys. Rev. D 2007, 76, 113003. [Google Scholar] [CrossRef]
- Kang, S.K. Revisiting the Quark-Lepton Complementarity and Triminimal Parametrization of Neutrino Mixing Matrix. Phys. Rev. D 2011, 83, 097301. [Google Scholar] [CrossRef]
- Ke, H.W.; Liu, T.; Li, X.Q. Determination of the mixing between active neutrinos and sterile neutrino through the quark-lepton complementarity and self-complementarity. Phys. Rev. D 2014, 90, 053009. [Google Scholar] [CrossRef]
- Ferrandis, J.; Pakvasa, S. Quark-lepton complenmentarity relation and neutrino mass hierarchy. Phys. Rev. D 2005, 71, 033004. [Google Scholar] [CrossRef]
- Kang, S.K.; Kim, C.; Lee, J. Importance of threshold corrections in quark–lepton complementarity. Phys. Lett. B 2005, 619, 129–135. [Google Scholar] [CrossRef][Green Version]
- Schmidt, M.A.; Smirnov, A.Y. Quark Lepton Complementarity and Renormalization Group Effects. Phys. Rev. D 2006, 74, 113003. [Google Scholar] [CrossRef]
- Dighe, A.; Goswami, S.; Roy, P. Quark-lepton complementarity with quasidegenerate Majorana neutrinos. Phys. Rev. D 2006, 73, 071301. [Google Scholar] [CrossRef]
- Ferrandis, J.; Pakvasa, S. A Prediction for |U(e3)| from patterns in the charged lepton spectra. Phys. Lett. B 2004, 603, 184–188. [Google Scholar] [CrossRef]
- Meloni, D. Bimaximal mixing and large theta13 in a SUSY SU(5) model based on S4. J. High Energy Phys. 2011, 2011, 10. [Google Scholar] [CrossRef]
- Harada, J. Non-maximal θ23, large θ13 and tri-bimaximal θ12 via quark-lepton complementarity at next-to-leading order. Europhys. Lett. 2013, 103, 21001. [Google Scholar] [CrossRef]
- Sharma, G.; Chauhan, B.C. Quark-lepton complementarity predictions for and CP violation. J. High Energy Phys. 2016, 2016, 75. [Google Scholar] [CrossRef]
- Harrison, P.F.; Perkins, D.H.; Scott, W.G. Tri-bimaximal mixing and the neutrino oscillation data. Phys. Lett. B 2002, 530, 167. [Google Scholar] [CrossRef]
- Feruglio, F.; Paris, A. The golden ratio prediction for the solar angle from a natural model with A 5 flavour symmetry. J. High Energy Phys. 2011, 2011, 101. [Google Scholar] [CrossRef]
- Jarlskog, C. Commutator of the Quark Mass Matrices in the Standard Electroweak Model and a Measure of Maximal CP Nonconservation. Phys. Rev. Lett. 1985, 55, 1039–1042. [Google Scholar] [CrossRef] [PubMed]
- UTfit Collaboration; Bona, M.; Ciuchini, M.; Franco, E.; Lubicz, V.; Martinelli, G.; Parodi, F.; Pierini, M.; Roudeau, P.; Schiavi, C.; et al. The unitarity triangle fit in the standard model and hadronic parameters from lattice QCD: A reappraisal after the measurements of Δms and BR(B→τυτ). J. High Energy Phys. 2006, 2006, 081. [Google Scholar]
- Esteban, I.; Gonzalez-Garcia, M.C.; Maltoni, M.; Schwetz, T.; Zhou, A. The fate of hints: Updated global analysis of three-flavor neutrino oscillations. J. High Energy Phys. 2020, 2020, 178. [Google Scholar] [CrossRef]
- NuFIT 5.3. 2024. Available online: http://www.nu-fit.org/sites/default/files/v53.fig-chisq-dma.pdf (accessed on 11 August 2024).
- Abe, K. et al. [Super-Kamiokande Collaboration] Atmospheric neutrino oscillation analysis with external constraints in Super-Kamiokande I-IV. Phys. Rev. D 2018, 97, 072001. [Google Scholar] [CrossRef]
- Farzan, Y.; Smirnov, A.Y. Leptonic CP violation: Zero, maximal or between the two extremes. J. High Energy Phys. 2007, 2007, 59. [Google Scholar] [CrossRef]
- Altarelli, G.; Feruglio, F. Models of neutrino masses and mixings. New J. Phys. 2004, 6, 106. [Google Scholar] [CrossRef]
- de Salas, P.F.; Forero, D.V.; Gariazzo, S.; Martínez-Miravé, P.; Mena, O.; Ternes, C.A.; Tórtola, M.; Valle, J.W.F. 2020 global reassessment of the neutrino oscillation picture. J. High Energy Phys. 2021, 2021, 71. [Google Scholar] [CrossRef]
- Capozzi, F.; Di Valentino, E.; Lisi, E.; Marrone, A.; Melchiorri, A.; Palazzo, A. Unfinished fabric of the three neutrino paradigm. Phys. Rev. D 2021, 104, 083031. [Google Scholar] [CrossRef]
- Feroz, F.; Hobson, M.P. Multimodal nested sampling: An efficient and robust alternative to MCMC methods for astronomical data analysis. Mon. Not. R. Astron. Soc. 2008, 384, 449. [Google Scholar] [CrossRef]
- Feroz, F.; Hobson, M.P.; Bridges, M. MultiNest: An efficient and robust Bayesian inference tool for cosmology and particle physics. Mon. Not. R. Astron. Soc. 2009, 398, 1601–1614. [Google Scholar] [CrossRef]
- Feroz, F.; Hobson, M.P.; Cameron, E.; Pettitt, A.N. Importance Nested Sampling and the MultiNest Algorithm. Open J. Astrophys. 2019, 2, 10. [Google Scholar] [CrossRef]
- Harrison, P.F.; Perkins, D.H.; Scott, W.G. A Redetermination of the neutrino mass squared difference in tri-maximal mixing with terrestrial matter effects. Phys. Lett. B 1999, 458, 79–92. [Google Scholar] [CrossRef]
| Parameter | Best-Fit Value and Range |
|---|---|
| A | |
| T | |||||
|---|---|---|---|---|---|
| 1 | 2715 | ||||
| 1 | 2500 | ||||
| 1 | 2580 |
| Parameter | Best-Fit Value and Range |
|---|---|
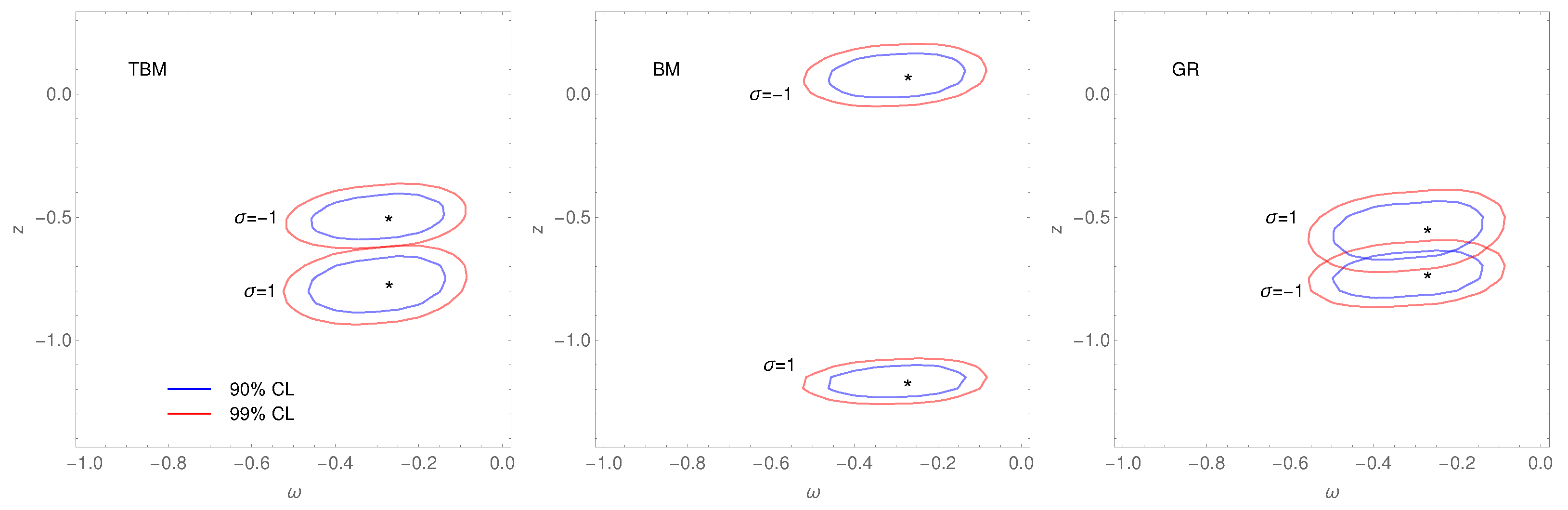
| Pattern | Re | Im | z | |
|---|---|---|---|---|
| TBM | −0.27 (−0.27) | 0.57 (−0.55) | −0.27 (−0.27) | −0.50 (−0.77) |
| BM | −0.27 (−0.29) | 0.57 (−0.56) | −0.27 (−0.27) | 0.08 (−1.17) |
| GR | −0.27 (−0.27) | 0.57 (−0.54) | −0.27 (−0.27) | −0.73 (−0.55) |
| (GeV) | ( GeV) | () | |||
|---|---|---|---|---|---|
| BM | 0.42 | (9.35, 55.35, 117.70) | (4.0, 70.10, 297.51) | (145.80, 195.44, 162.01) | |
| 0.44 | (9.98, 36.84, 111.52) | (3.59, 67.78, 708.16) | (122.88, 12.88, 112.59) | ||
| TBM | 0.31 | (9.38, 58.54, 130.56) | (3.41, 93.21, 794.35) | (331.00, 347.73, 317.70) | |
| 0.34 | (9.66, 34.52, 159.29) | (2.09, 55.69, 485.30) | (321.58, 354.03, 221.83) | ||
| GR | 0.19 | (9.83, 80.88, 201.77) | (3.55, 86.014, 728.73) | (341.65, 171.70, 188.76) | |
| 0.45 | (9.26, 42.48, 156.88) | (2.97, 38.95, 268.45) | (145.00, 8.15, 341.63) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giarnetti, A.; Marciano, S.; Meloni, D. On Quark–Lepton Mixing and the Leptonic CP Violation. Universe 2024, 10, 345. https://doi.org/10.3390/universe10090345
Giarnetti A, Marciano S, Meloni D. On Quark–Lepton Mixing and the Leptonic CP Violation. Universe. 2024; 10(9):345. https://doi.org/10.3390/universe10090345
Chicago/Turabian StyleGiarnetti, Alessio, Simone Marciano, and Davide Meloni. 2024. "On Quark–Lepton Mixing and the Leptonic CP Violation" Universe 10, no. 9: 345. https://doi.org/10.3390/universe10090345
APA StyleGiarnetti, A., Marciano, S., & Meloni, D. (2024). On Quark–Lepton Mixing and the Leptonic CP Violation. Universe, 10(9), 345. https://doi.org/10.3390/universe10090345







