Abstract
Solar energetic particles (SEPs) are bursts of high-energy particles that originate from the Sun and can last for hours or even days. The aim of this study is to understand how the characteristics of energetic particles ware affected by the characteristic parameters of corotating interaction regions (CIRs). In particular, the particle intensity distribution with time and space in CIRs with different characteristics were studied. The propagation and acceleration of particles were described by the focused transport equation (FTE). We used a three-dimensional magnetohydrodynamic (MHD) model to simulate the background solar wind with CIRs. By changing the inner boundary conditions, we constructed CIRs with different solar wind speeds, angles between the polar axis and rotation axis, and the azimuthal widths of the fast streams. Particles were impulsively injected at the inner boundary of the MHD model. We then studied the particle propagation and compression acceleration in different background solar wind. The results showed that the CIR widths are related to the solar wind speed, tilt angles, and the azimuthal widths of the fast stream. The acceleration of particles in the reverse and forward compression regions are mainly influenced by the solar wind speed difference and the slow solar wind speed, respectively. Particles with lower energy (sub-MeV) are more sensitive to the solar wind speed difference and the tilt angle. The particle intensity variation with time and the radial distance is mainly influenced by the solar wind speed. The longitudinal distribution of particle intensity is affected by the solar wind speed, tilt angles, and the azimuthal widths of the fast stream.
1. Introduction
Recent years, solar energetic particles (SEPs) have attracted much attention since more and more space missions have been conducted. They can damage not only spacecraft, but also astronauts’ health in the human space activities.
It is now generally accepted that particle events can be roughly classified into two types based on the characteristics of the event: impulsive SEP events and gradual SEP events. A recent work [1] has subdivided particle events further. Impulsive SEP events are composed of either pure “impulsive” SEPs generated by magnetic reconnection in solar jets (SEP1), or ambient ions and SEP1 ions reaccelerated by the shock wave driven by the narrow coronal mass ejection (CME) from the same jet (SEP2). A gradual SEP event is produced when a moderately fast, wide CME-driven shock wave preferentially accelerates accumulated remnant SEP1 ions from an active region fed by multiple jets (SEP3), or when a very fast, wide CME-driven shock wave is completely dominated by ambient coronal seed population (SEP4).
There are many factors affecting the characteristics of SEPs. Besides the seed populations and the turbulence, energetic particles can be greatly affected by background solar wind structure. A typical large-scale background structure is the corotation interaction region (CIR), formed when fast solar wind catches up slow solar wind. Moreover, these CIRs are sometimes associated with suprathermal particle populations, which are typically believed to be accelerated by the compression waves bounding the CIR [2]. In previous works, the parameters describing the CIRs were found to be statistically correlated to the characteristics of energetic particles. The speed difference between fast and slow solar wind showed a good correlation with proton peak intensity during the solar quiet periods [3]. The peak ion intensity [4] and spectral index [5] were found to be statistically correlated to the compression region widths for CIRs with shocks. The peak He intensities showed a positive correlation with magnetic compression ratios for the events with intensity peak time near the CIR trailing edge [6]. The He ion intensity was positively correlated with the tilt angle during periods of a highly inclined current sheet [7]. The particles’ characteristics in different CIR structures have also been studied by simulations. Fraction of trapped particles was found to be a function of compression width in the analytical model [8]. The power law above the injection speed of pickup ions was sensitive to the velocity gradient in CIRs [9].
However, in addition to suprathermal particle populations, it is not clear how energetic particles from different seed populations, such as impulsive SEP events, are modulated by CIRs with varying parameters. It is difficult for the observations to distinguish the role of a particular parameter of the background structure from other factors. While numerous numerical simulation studies have been conducted to examine the modulation effect of solar wind structure on particles [8,9,10,11,12], few have addressed the relationship between energetic particles and the characteristic parameters of CIRs in consideration of three-dimensional topology, so that the specific effect of different structures has not yet been revealed.
In this work, we aim to study how an (impulsive) SEP event can be modified by the presence of a CIR. Our study focuses on the propagation and the compression acceleration of particles in CIRs. We coupled the CIRs constructed with a 3D magnetohydorodynamic (MHD) model with the particle transport model described by the focused transport equation (FTE) [13,14,15,16]. We changed the solar wind speed, the angles between polar axis and rotation axis, and the azimuthal width of the fast streams in the backgrounds by changing the inner boundary conditions [17]. We impulsively injected protons at the inner boundary of the 3D MHD model. Our results showed how the particles are affected by parameters characterizing background solar wind structures.
The article is organized as follows: Section 2.1 provides a brief description of background solar wind structures calculated using the 3D MHD model. Section 2.2 describes the particle transport model. Section 3.1 explains the relationship between the CIR widths and parameters controlling the widths. Section 3.2 demonstrates the acceleration effect on particles with different energies in different compression regions. Section 3.3 presents the variations of particle intensity with different parameters of CIRs. Finally, Section 4 provides a summary.
2. Methods
2.1. MHD Model
The background solar wind structure was obtained by solving the ideal MHD equations [18,19,20]. The MHD equations are as followed:
where is the mass density, is the solar wind velocity, is the magnetic field vector, is the thermal pressure, and is the ratio of specific heats. Since the calculations are performed in a frame of reference corotating with the Sun, the additional fictitious force densities, , is introduced. is the sidereal angular velocity of the rotation. As the solution area changes from 0.1 AU to 10.0 AU, the radial grid resolution changes from 0.35 to 6.19 ( is the solar radius). The angular resolution of the mesh is .
In this work, we assumed that the large-scale coronal magnetic structure is in the tilted-dipole configuration, following the setup of Pizzo (1991) [21]. we constructed four sets of CIR backgrounds shown in Table 1. In the table, is the tilt angle. The tilt angle is the angle between the solar rotation axis and the magnetic dipole axis of the sun. and is the minimum and the maximum solar wind speed at the inner boundary (0.1 AU), respectively. It is assumed that the slow wind originates from a region centered on the magnetic equator. and is the minimum and the maximum solar wind speed at 1 AU, respectively. is longitudinal angular width of the fast streams (where the speed is larger than 500 km) at the solar equator. We set cases in Set A with the same and , Set B with the same and , and Set C with the same and . The speed difference between the maximum and minimum solar wind is not constant at different radial distances. Nevertheless, as is shown in Table 1, both the difference in for cases in Set A and for cases in Set B is less than 15 km. Referring to 151 stream interaction regions (SIRs) observed by both STEREO-A and STEREO-B in March 2007–August 2014 in [22], is between 250 km and 500 km and is between 300 km and 850 km. The of case 1 to 4 in Set A is within the observed range. Case 5 in Set A is an extreme case. The of cases 2, 3, and 4 in Set B is within the observed range and case 1 and 5 in Set B are extreme cases. The cases in Set D have the same , , and with case 5 in Set C, but have different widths of the fast streams. The radial solar wind speed at the inner boundary of the cases in Set A, B, C, and D is shown in Figure 1. The other parameters of the inner boundary are shown in Appendix A.

Table 1.
The parameter sets of the background solar wind.

Figure 1.
The radial solar wind speed at the inner boundary of the cases in Set A–D. The cases in Set A have the same . The cases in Set B have the same . The cases in Set C have the same and , but different . The cases in Set D have the same , , and , but different . From panel (D1–D3), is , , and , respectively.
2.2. Particle Transport Model
We described the particles with the phase-space distribution function and solved their evolution using the FTE.
The full FTE for the particle distribution function can be written as (without the stochastic diffusion , cross-field diffusion and the drift velocity ) [13,14,15,16]:
where,
where . , p and are the particle spatial location, momentum and cosine of pitch-angle respectively. is the particle speed. is the pitch-angle diffusion coefficient. is the unit vector of magnetic field. is the solar wind velocity.
The form of is chosen as [16,23]:
where . We set h = 0.05, q = 5/3.
The parallel mean free path is related to through [23]:
Similar to Dröge et al. (2010) [24] and Wijsen et al. (2019) [10], we set constant radial mean free path AU for 4 MeV particles. We considered neither the cross-field diffusion nor the drift velocity in our model.
We injected the protons from 0.5 MeV to 20 MeV at 0.1 AU in the latitude range and to longitude range. The particles were uniformly injected. The injection time profile was assumed to be [25]
where and are the rise and decay timescales of the injection time profile, respectively. is the normalization constant. The was assumed to be 0.21 days and the was assumed to be 0.08 days [26]. The spectral index for the power-law fits was assumed to be −4.4, based on the event Parker Solar Probe (PSP) observed at 0.17 AU on DOY 094 of 2019 [27]. About ∼ 5 particles were traced.
We then solved the FTE by the time-forward stochastic difference equation (SDE) [28,29,30].
The corresponding forward SDEs are
We averaged the results over a time period to increase the statistics, where is the time resolution in the binning procedure [29]. is the time resolution of the results. M is an arbitrary positive integer.
After the phase-space distribution function was obtained, the particle differential intensity (per unit of kinetic energy) was calculated by
where
The anisotropy was calculated by
3. Results and Discussion
3.1. Different Definitions of CIR width and Parameters Controlling Their Widths
In this subsection, we discussed different definitions of CIR width and how other parameters of CIR control the widths.
In the observation, assuming that the solar wind propagates predominantly radially, the actual CIR width can be estimated as . is given by the product of the measured duration of the event and the mean of maximum and minimum solar wind speed across the compression region [7,31]. The compression region boundaries were selected where the pressure starts increasing from and returns to the background. The width gives an estimate of the width of the CIR perpendicular to the average magnetic field direction in the CIR. is approximately the product of duration, mean velocity, and , where is the spiral angle [32]. In our model, the compression region boundaries were selected where the total perpendicular pressure is higher than the background. at 1 AU was calculated by , where W is a constant speed at which the compression moves radially outward in the inertial (not rotating) frame of reference, is an azimuthal width of the compression region, and is the solar rotation rate. W was calculated by the mean of maximum and minimum solar wind speed across the compression region in the solar equatorial plane at 1 AU. was calculated by the longitude difference between the compression region boundaries at 1 AU. was then calculated by . The spiral angle is , where r is the heliocentric distance (1 AU). Moreover, the width perpendicular to the stream interface (SI) in the 3-D geometry () was calculated. was calculated by the distance between the compression region boundaries perpendicular to the SI at 1 AU. The SI was determined where peaks at the same heliospheric radial distance and latitude. The SIs at all radii and latitudes form a surface. We then calculated the vertical vector of this surface at 1 AU on the solar equatorial plane, from which we determined the normal direction.
Figure 2 shows the CIR widths at 1 AU. The blue asterisks are . The red ones are . The yellow asterisks are .
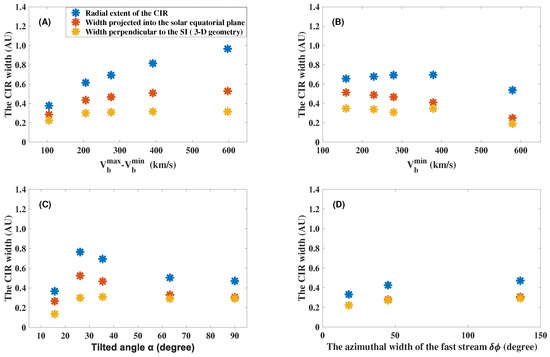
Figure 2.
The CIR width of the selected cases. The blue, red and yellow asterisks indicate the CIR radial extent, width projected into the solar equatorial plane and CIR width considering 3D geometry, respectively. Panels (A–D) are for cases in Set A–D, respectively.
As is shown in panel (A), for the cases in Set A, the increases as increases. The compression region expands to a greater width with a larger compression ratio. and are more sensitive to the than the . As the varies from 105 km to 597 km, varies from 0.22 AU to 0.31 AU, while varies from 0.29 AU to 0.53 AU and varies from 0.38 AU to 0.97 AU. For the cases in Set B, decreases as the increases. As varies from 159 km to 579 km, varies from 0.35 AU to 0.19 AU. Unlike Set A, the change in (0.12 AU) with is similar to (0.16 AU), while the change in (0.26 AU) is larger. For the cases in Set C, as increases, on the one hand, increases and then remains almost constant, and on the other hand, the ratio of the projection on the equatorial plane to decreases. Thus and increase and then decrease, peaking at a tilt angle of about . The variation of , , and with is 0.17 AU, 0.25 AU, and 0.39 AU, respectively. has little effect on the with of CIRs. decrease slightly with .
Our results indicate that different criteria lead to different CIR widths. We need to pay attention to the definitions when discussing them. Jian (2008) [32] found that, during 1979–1988, the SIR duration and width were smaller around solar minimum. The SIR width in their results correspond to in our results. Around solar minimum, the solar wind speed difference is smaller [32] and the tilted angle is smaller [33]. decreases as the solar wind difference decreases (Set A) and decreases when the tilt angle decreases from (Set C). This can explain the observation. Jian (2019) [22] reported that the SIRs are moderately wider in Solar Cycle 24 than in Solar Cycle 23. Although the mean solar wind speed difference is similar in these two cycles, the mean minimum solar wind speed and the mean maximum solar wind speed are both slower in Cycle 24 than in Cycle 23. According to our results in Set B, increases as decreases when remains the same. Our results are consistent with the observations.
3.2. Particle Acceleration in Various Compression Regions
This section explores the acceleration effect on particles in different compression regions and the impact of acceleration on particles with varying energy levels. Our work aims to study the CIR effect on particles when compressional acceleration dominates. Particles can cross the shock many times to gain energy systematically by diffusive shock acceleration (DSA). DSA operates because of the convergence of the flow of scattering centers at the shock. Therefore, compressional acceleration can work also in presence of compressions of non-shock type. Other acceleration effect, such as shock drift acceleration (SDA), is considered relatively insignificant.
Figure 3 displays the ratio of the maximum energy to the original energy ( = 5 MeV) at 1 AU after 60 h versus the CIR parameters. The red asterisks and blue circles are for the reverse and the forward compression regions, respectively.

Figure 3.
The ratio of the maximum energy to the original energy ( = 5 MeV) at 1 AU after 60 h versus the CIR parameters. The red asterisks and blue circles are for the reverse and the forward compression regions, respectively. Panels (A–D) are for cases in Set A–D, respectively.
As is shown in panel (D), the acceleration effect is similar with different azimuthal widths of the fast streams. However, the acceleration effect is affected by the solar wind speed and tilt angle. As is shown in panel (A), the acceleration effect of both reverse and forward compression region increases as increases. In the case with of 105 km, the forward compression region is not formed. As the varies from 206 to 391 km, the value of varies from 0.91 to 1.07 in the reverse compression regions and from 0.79 to 0.95 in the forward compression regions. The magnitude of change is similar in this range. However, the value of increases respectively by 0.32 and 0.14 in the reverse and forward compression region as varies from 391 to 597 km. Panel (B) shows that the acceleration effect decreases as increases. As the varies from 229 to 579 km, the value of varies from 1.01 to 0.55 in the reverse compression regions and from 1.01 to 0.63 in the forward compression regions. In these cases, the value difference of the is less than 0.1 between the forward and reverse region. However, in the case with of 159 km, the value of the in the forward compression region (1.27) is much larger than in the reverse compression region (1.05). The acceleration effect increases and then stays almost constant as increases (panel (C)). In the case with , both reverse and forward compression region are not formed. As varies from to , the value of varies from 0.87 to 1.03 in the reverse compression regions and from 0.75 to 0.97 in the forward compression regions. When and , the value of is almost the same.
In general, the particle acceleration effect in the reverse compression region is primarily affected by , especially when is larger than 390 km. However, the acceleration effect in the forward compression region is mainly influenced by , especially when is smaller than 300 km. The reverse compression regions could accelerate protons to higher energies than the forward compression regions in most cases. However, if is small or large (Case 1 and Case 5 in Set B), the forward compression region could accelerate particles more strongly than the reversed compression region (for the protons with 5 MeV). Figure 4 shows the divergence of the background solar wind velocity of Case 1 (panel (a)), Case 3 (panel (b)), and Case 5 (panel (c)) in Set B. The values of are extracted along the magnetic field lines with footpoints at the solar equator. The points with the same horizontal scale are in the same magnetic field line. The blue areas are the regions where , indicating converging (compressional) flows where particles can be accelerated. As shown in the panel (a), when is small, the values of are similar in the reverse and forward compression waves. However, the magnetic filed line across the forward compression wave (the right blue area) spans a larger radial extent within the compression wave than that across the reverse compression wave. Therefore, particles in the forward compression regions can be accelerated to higher energies. When is large (panel (c)), the compression waves are at larger radial distances. The acceleration effect is small and the particles are mainly affected by the adiabatic cooling effect. The particles suffer less from the adiabatic cooling effect within 2 AU in the forward compression region. In panel (b), the values of in the reverse compression wave are smaller than those in the forward wave. Therefore, particles can be accelerated more effectively in the reverse regions in this case. The of the SIRs usually varies between 200 km and 500 km in the observation [22]. Therefore, the particle acceleration efficiency observed in the reverse compression is expected to be usually higher than in the forward compression region.
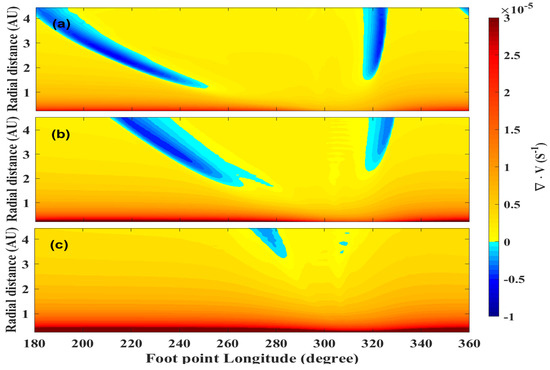
Figure 4.
The divergence of the background solar wind velocity of Case 1 (panel (a)), Case 3 (panel (b)), and Case 5 (panel (c)) in Set B.
Figure 5 shows the maximum ratio of the maximum energy in the reversed compression region to that in the approximated Parker field at 1 AU in the first 60 h versus the CIR parameters. The approximated Parker field is the region outside the CIR boundaries where there is no solar wind compression, approximating the Parker field. The blue asterisks, red circles, and yellow squares are for protons with original energy of 0.5 MeV, 5 MeV, and 20 MeV, respectively. As can be seen from panel (D), for particles with different energies, has similar effects on their acceleration. In all the panels, the values of for 20 MeV particles are similar to those for 5 MeV particles. However, the acceleration of 0.5 MeV particles varies more with (Set A), (Set B), and (Set C) than particles with higher energy. Therefore, more attention must be paid to the influence of background parameters when studying particles at lower energies (sub-MeV particles), especially the fast solar wind speed and the tilt angle.

Figure 5.
The maximum ratio of the maximum energy in the reversed compression region to that in the approximated Parker region at 1 AU in the first 60 h versus the CIR parameters. The blue asterisks, red circles, and yellow squares are for protons with original energy of 0.5 Mev, 5 MeV, and 20 MeV, respectively. Panels (A–D) are for cases in Set A–D, respectively.
It is worth noting that the numerical simulation results of particle acceleration are related to the numerical scheme and grid resolution of the MHD model [34]. The results may be different for different underlying MHD simulations. However, since the simulation methods used in different cases are the same, the resolution does not affect the regularity of the trend of particle acceleration with different CIR parameters or particle energies. The aim of our study is to compare the results for different CIR parameters, and a discussion of the simulation methods is beyond the scope of our study.
3.3. The Particle Intensity and the Parameters of CIRs
We then examined how different parameters affect particle intensities. Particles with energies ranging from 5 to 15 MeV were impulsively injected within of latitude of the inner. The particles injected are described in Section 2.2. The intensity distribution of 6.7–11.4 MeV particles in the solar equatorial plane was measured.
3.3.1. Peak Intensity of Particles and CIR Width
In this subsection, we investigated how the peak intensity of particles related to the CIR width.
Figure 6 shows peak intensity of particles versus at 1 AU. The blue asterisks, red circles, yellow squares, and purple crosses indicate cases in Set A, Set B, Set C, and Set D, respectively.
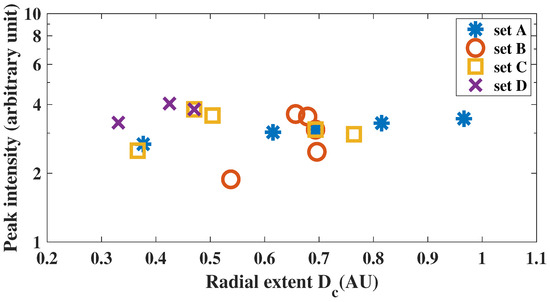
Figure 6.
The peak intensity of particles versus the CIR radial extent at 1 AU. The blue asterisks, red circles, yellow squares, and purple crosses indicate cases in Set A, Set B, Set C, and Set D, respectively.
Bucík et al. (2011) [7] analysed the observed events and found no relationship between the peak intensity (for 0.189 MeV/n He) and compression width for CIRs not bounded by reverse shocks. They interpreted that the compression is weak and therefore the acceleration could not operate. The compression width in their study corresponds to in our results. Our results in Figure 6 show that the peak intensity does not correlate well with when a compressional mechanism dominates. The peak intensity is not sensitive to the CIR parameters and varies within one order of magnitude in different cases. The seed populations in our models are different from those in the statistical study of [7]. Nevertheless, our findings indicate that, in the absence of shock waves, the impact of the CIR parameter on peak intensity is not significant when compression acceleration dominates.
3.3.2. The Temporal-Spatial Particle Intensity Distribution in Different CIRs
In this subsection, we investigated how the particle intensity varying with time and space related to the CIR parameters.
The distribution of particle intensity (6.7–11.4 MeV) with time, longitude, and radial distance for different cases is illustrated in Figure 7. The rows from top to bottom display the cases in Set A, B, C, and D, respectively. The columns from left to right represent the distribution of particle intensity varying with time, longitude, and radial distance, respectively.
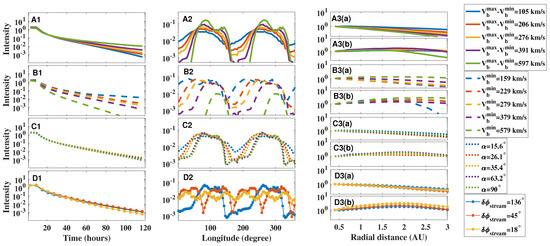
Figure 7.
The variations of particle intensity (6.7–11.4 MeV) with time, longitude, and radial distance for different cases. The rows from top to bottom display the cases in Set A–D, respectively. The columns from left to right represent the variations of particle intensity with time, longitude, and radial distance, respectively. Panels A3(a)–D3(a) and panels A3(b)–D3(b) show the distribution after 30 h and 120 h since the injection, respectively.
Panels A1, B1, C1, and D1 show the variation of longitudinally averaged particle intensity with time at 1 AU. As shown in the panels, the background parameters have little effect on the temporal peak intensity (longitudinally averaged). The intensity variation with time was little affected by (panel C1) and (panel D1). During the initial 30 h of the event, the intensity is mainly affected by (panel B1). The adiabatic cooling is stronger in the faster solar wind. As the event continues, the impact of (panel A1) increases. This is mainly due to the acceleration effect. By 120 h, the particle intensity difference in cases with different solar wind speeds has already exceeded one order of magnitude.
Panels A2, B2, C2, and D2 display the longitudinal distribution of particle intensity at 1 AU after 60 h since the injection. The longitudinal peak intensity is mainly influenced by (panel A2), since the acceleration effect on the particles is stronger when is larger. The intensity variation in the longitudinal direction is also dominated by . On the one hand, the larger , the stronger the acceleration effect in the compressed region. On the other hand, the larger , the stronger the adiabatic cooling effect in the fast solar wind. The intensity variation is secondarily affected by (panel D2). This is due to the fact that more compactly arranged CIRs weaken the effect in the rarefaction region and thus reduce the longitudinal intensity variation. (panel B2) also affects the longitudinal variation. The adiabatic cooling effect is weaker in the slower solar wind and therefore the particle intensity decreases less outside the compression region. (panel C2) has a slight effect on the amplitude, and only the case with a small () has a slighter longitudinal intensity variation.
The width of the longitudinal distribution of particle intensity (hereafter referred to as ), i.e., the longitudinal extension of particle intensity (above a certain value, say ), is also affected by the background parameters. (panel D2) affects . The smaller , the smaller will be. has the least effect on , e.g. the difference in is at most between cases in panel A2. The effect of (panel B2) on seems to be large. The smaller , the wider . The difference between different cases in panel B2 can be more than . However, are not that extreme in actual observations. The difference of is about between the cases with of 229 km and 379 km. also has a significant effect. The smaller the , the larger the . The difference in between the cases with of and is about . It is important to note that also depends on the chosen threshold (here ). The differs from the CIR width discussed earlier (see red asterisks in Figure 2). The will be influenced by other effects, such as the focusing effect and the adiabatic cooling effect. In addition, also varies with time.
Column 3 in Figure 7 displays the distribution of the the longitudinally averaged particle intensity with radial distance after 30 h (panels A3(a)–D3(a)) and 120 h (panels A3(b)–D3(b)) since the injection, normalized by the intensity at 0.3 AU.
After 30 h, the radial distribution of the particle intensity is mainly influenced by and (panel A3 (a) and panel B3 (a)). The larger and the smaller , the faster the particle intensity decreases with the radial distance. On the one hand, particles in the larger experience more adiabatic cooling effect and therefore decrease more quickly with the radial distance. On the other hand, particles in the smaller need to travel a longer distance to reach a certain radial distance due to the stronger curvature of the magnetic field lines. These propagation effects combined affect the variation of the particle intensity with radius at this time. The effects of and are small.
After 120 h, the distribution of particle intensity with radial distance is flatter, since particles have sufficient time to propagate and particles are accelerated at larger radial distances. Also for these reasons, the effect of the solar wind speed on the radial distribution of particles is reduced, except for a few extreme cases. The case with of 597 km in Set A (green solid line in panel A3(b)) and the case with the of 159 km in Set B (blue dotted line in panel B3(b)) have a roll-over of the particle intensities at larger radial distance. This is mainly due to the extension of the magnetic field lines to higher latitudes. For larger compression ratios, the magnetic field lines are more strongly bent towards the north and south. Since the particles are only injected within of latitude, the more the magnetic lines bend toward higher latitudes, the more particles leave the solar equatorial plane at smaller radial distances, resulting in a sudden drop in particle intensity with radius. At this time, the effect of is still small, but the effect of is slightly increased.
4. Summary and Conclusions
Prior works have investigated the modulation of SEP by a certain CIR structure [35,36], or the ensemble averaging of SEP modulation by multiple CIRs [12]. Nevertheless, the impact of the CIR parameters on SEPs requires further investigation.
A 3D MHD model was utilized to simulate the background solar wind structure with CIRs. The FTE describes the propagation and acceleration of particles. By modifying the inner boundary conditions, we were able to create CIRs with varying solar wind speeds, angles between the polar and rotation axes, and the azimuthal widths of the fast stream. Particles were impulsively injected at the inner boundary. We studied the particle propagation in various backgrounds.
It was found that the CIR widths, which vary depending on the criteria used, are correlated with background parameters such as the solar wind speed ( and ), tilt angle (), and the width of the fast streams (). The acceleration effect of particles in the reverse compression region is primarily influenced by , while the acceleration effect in the forward compression region is mainly affected by . The acceleration effect of particles with lower energies (sub-MeV) are more sensitive to the CIR parameters, especially and , than those with higher energies.
The CIR parameters also affect the spatial and temporal distribution of particle intensities. The speed of the solar wind significantly affects the radial distribution of the particle intensity during the early event (∼30 h). The time profile of the particle intensity is mainly affected by the solar wind speed. Solar wind speed also affects the longitudinal intensity distribution. The amplitude of the longitudinal variation of the particle intensity is affected by , while the width of the longitudinal extension of the particle intensity is affected by . primarily affects the width of the longitudinal extension of the particle intensity (). Once exceeds , variation on the particle modulation is minimal. primarily affects the longitudinal distribution of particles, both in terms of amplitude and width.
Our study provides insight into the effect of CIR parameters on particles, extending prior work on modeling CIR modulations on SEPs. This is the first study to our knowledge to investigate the effect of large-scale parameters of 3D CIRs on the propagation and compression acceleration of particles in simulations. Our study informs which parameters in the background to pay more attention to when predicting SEPs. Specifically, our results can be applied in setting the seed populations for coronal mass ejection (CME) events when predicting mixed events including both flares and CMEs (i.e., SEP3 mentioned in Section 1).
There are, however, some limitations that are worth noting. We mainly considered the compression acceleration mechanism in CIRs in this study. Other processes such as drift effects [37], the cross-field diffusion [38,39], stochastic diffusion, and magnetic reconnection acceleration were not taken into account. Moreover, the variation of CIR parameters with time was not considered. Future work should therefore establish background fields that change over time and include more particle processes.
Author Contributions
Methodology, Y.Z.; Software, Y.Z.; Validation, Y.Z. and F.S.; Formal analysis, Y.Z.; Investigation, Y.Z.; Resources, Y.Z.; Data curation, Y.Z.; Writing—original draft, Y.Z.; Writing—review & editing, F.S.; Visualization, Y.Z.; Supervision, F.S. Project administration, F.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China (42330210 and 41974202), the National Key RD Program of China (grant Nos. 2022YFF0503800 and 2021YFA0718600) and the Strategic Priority Research Program of the Chinese Academy of Sciences (grant No. XDB 41000000).
Data Availability Statement
No publicly achieved datasets were used in this work.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
We chose the potential field source surface (PFSS) model to describe the corona magnetic field [40,41]. The polarity of interplanetary magnetic field can be predicted reasonably well by the PFSS model. Subsequent magnetic field models are improved on this basis. In the PFSS model, we assumed that there are no currents above the photosphere, therefore . The magnetic field can be written as . Since , the Laplace equation is obtained. The solution in the spherical coordinates for the domain ( is the solar radius) is
where is Legendre Polynomials, and are harmonic coefficients. are dipole terms. is the axial dipole term and are equatorial dipole terms. We chose different harmonic coefficients to construct the coronal magnetic field. In this work, in order to obtain a dipole field with different tilt angles between solar rotation axis and dipole axis, we set ( and when ) and changed the coefficient of . Additionally, the background field with varying width (numbers) of the fast streams can be obtained by adjusting the value of either or .
We then use a simplified Wang–Sheeley–Arge (WSA) coronal solar wind model to set the radial velocity at inner boundary [42]:
where is the corona magnetic field expansion factor, is the minimum angular distance that an open field foot point lies from a coronal hole boundary. We calculated and from the coronal magnetic field we chose. adjusts the effect of and determines the width of the low speed flow. is the minimum possible speed and determines the maximum speed. We set , .
The radial magnetic field is assumed to be uniform at the inner boundary. To avoid magnetic field numerical reconnection which may affect our analysis, we set all the magnetic field line outward at inner boundary. We did not consider the influence of the current sheet on particles in this work. The radial magnetic field is [17]
We set . The proton temperature is [17,43]
where is the adiabatic index. is inner boundary radius. Suppose that the proton temperature is equal to the electron temperature . The number density is [17]
where km, G is the gravitational constant, is solar mass, is solar radius. We set . The latitudinal and longitudinal solar wind speeds are
where W is the solar rotation rate, is the radial distance of inner boundary. The latitudinal and longitudinal magnetic fields are set as
References
- Reames, D.V. Four Distinct Pathways to the Element Abundances in Solar Energetic Particles. Space Sci. Rev. 2020, 216, 20. [Google Scholar] [CrossRef]
- Richardson, I.G. Energetic particles and corotating interaction regions in the solar wind. Space Sci. Rev. 2004, 111, 267–376. [Google Scholar] [CrossRef]
- Kobayashi, M.N.; Doke, T.; Kikuchi, J.; Hayashi, T.; Itsumi, K.; Takashima, T.; Takehana, N.; Shirai, H.; Yashiro, J.; Hasebe, N.; et al. The correlation between CIR ion intensity and solar wind speed at 1 AU. Coupling High Low Latit. Heliosphere Relat. Corona 2000, 26, 861–864. [Google Scholar] [CrossRef]
- Buík, R.; Mall, U.; Korth, A.; Mason, G.M. On acceleration of <1 MeV/n He ions in the corotating compression regions near 1 AU: STEREO observations. Ann. Geophys. 2009, 27, 3677–3690. [Google Scholar]
- Filwett, R.J.; Desai, M.I.; Ebert, R.W.; Dayeh, M.A. Spectral Properties and Abundances of Suprathermal Heavy Ions in Compression Regions near 1 AU. Astrophys. J. 2019, 876, 88. [Google Scholar] [CrossRef]
- Ebert, R.W.; Dayeh, M.A.; Desai, M.I.; Mason, G.M. Corotating Interaction Region Associated Suprathermal Helium Ion Enhancements at 1 AU: Evidence for Local Acceleration at the Compression Region Trailing Edge. Astrophys. J. 2012, 749. [Google Scholar] [CrossRef]
- Bučík, R.; Mall, U.; Korth, A.; Mason, G.M. STEREO observations of the energetic ions in tilted corotating interaction regions. J. Geophys. Res. Space Phys. 2011, 116. [Google Scholar] [CrossRef]
- Giacalone, J.; Jokipii, J.R.; Kota, J. Particle acceleration in solar wind compression regions. Astrophys. J. 2002, 573, 845–850. [Google Scholar] [CrossRef]
- Chen, J.H.; Schwadron, N.A.; Möbius, E.; Gorby, M. Modeling interstellar pickup ion distributions in corotating interaction regions inside 1 AU. J. Geophys. Res. Space Phys. 2015, 120, 9269–9280. [Google Scholar] [CrossRef]
- Wijsen, N.; Aran, A.; Pomoell, J.; Poedts, S. Modelling three-dimensional transport of solar energetic protons in a corotating interaction region generated with EUHFORIA. AStronomy Astrophys. 2019, 622, A28. [Google Scholar] [CrossRef]
- Wijsen, N.; Samara, E.; Aran, À.; Lario, D.; Pomoell, J.; Poedts, S. A Self-consistent Simulation of Proton Acceleration and Transport Near a High-speed Solar Wind Stream. Astrophys. J. 2021, 908, L26. [Google Scholar] [CrossRef]
- Wijsen, N.; Li, G.; Ding, Z.; Lario, D.; Poedts, S.; Filwett, R.J.; Allen, R.C.; Dayeh, M.A. On the seed population of solar energetic particles in the inner heliosphere. J. Geophys. Res. Space Phys. 2023, 128, e2022JA031203. [Google Scholar] [CrossRef]
- Skilling, J. Cosmic Rays in Galaxy: Convection or Diffusion. Astrophys. J. 1971, 170, 265. [Google Scholar] [CrossRef]
- Isenberg, P.A. A hemispherical model of anisotropic interstellar pickup ions. J. Geophys.-Res.-Space Phys. 1997, 102, 4719–4724. [Google Scholar] [CrossRef]
- le Roux, J.A.; Webb, G.M. Time-Dependent Acceleration of Interstellar Pickup Ions at the Heliospheric Termination Shock Using a Focused Transport Approach. Astrophys. J. 2009, 693, 534–551. [Google Scholar] [CrossRef]
- Zhang, M.; Qin, G.; Rassoul, H. Propagation of Solar Energetic Particles in Three-Dimensional Interplanetary Magnetic Fields. Astrophys. J. 2009, 692, 109–132. [Google Scholar] [CrossRef]
- Shen, F.; Yang, Z.; Zhang, J.; Wei, W.; Feng, X. Three-dimensional MHD Simulation of Solar Wind Using a New Boundary Treatment: Comparison with In Situ Data at Earth. Astrophys. J. 2018, 866, 1–15. [Google Scholar] [CrossRef]
- Feng, X.S.; Wu, S.T.; Wei, F.S.; Fan, Q.L. A class of TVD type combined numerical scheme for MHD equations with a survey about numerical methods in solar wind simulations. Space Sci. Rev. 2003, 107, 43–53. [Google Scholar] [CrossRef]
- Shen, F.; Feng, X.; Song, W. An asynchronous and parallel time-marching method: Application to three-dimensional MHD simulation of solar wind. Sci. China Ser. Technol. Sci. 2009, 52, 2895–2902. [Google Scholar] [CrossRef]
- Shen, F.; Feng, X.; Wu, S.T.; Xiang, C. Three-dimensional MHD simulation of CMEs in three-dimensional background solar wind with the self-consistent structure on the source surface as input: Numerical simulation of the January 1997 Sun-Earth connection event. J. Geophys. Res. Space Phys. 2007, 112, 2006JA012164. [Google Scholar] [CrossRef]
- Pizzo, V.J. The Evolution of Corotating Stream Fronts near the Ecliptic Plane in the Inner Solar System: 2. Three-dimensional Tilted-dipole Fronts. J. Geophys. Res. Space Phys. 1991, 96, 5405–5420. [Google Scholar] [CrossRef]
- Jian, L.K.; Luhmann, J.G.; Russell, C.T.; Galvin, A.B. Solar Terrestrial Relations Observatory (STEREO) Observations of Stream Interaction Regions in 2007–2016: Relationship with Heliospheric Current Sheets, Solar Cycle Variations, and Dual Observations. Sol. Phys. 2019, 294, 31. [Google Scholar] [CrossRef]
- Qin, G.; Zhang, M.; Dwyer, J.R.; Rassoul, H.K.; Mason, G.M. The model dependence of solar energetic particle mean free paths under weak scattering. Astrophys. J. 2005, 627, 562–566. [Google Scholar] [CrossRef]
- Dröge, W.; Kartavykh, Y.Y.; Klecker, B.; Kovaltsov, G.A. Anisotropic Three-Dimensional Focused Transport of Solar Energetic Particles in the Inner Heliosphere. Astrophys. J. 2010, 709, 912–919. [Google Scholar] [CrossRef]
- Reid, G.C. A Diffusive Model for the Initial Phase of a Solar Proton Event. J. Geophys. Res. 1964, 69, 2659–2667. [Google Scholar] [CrossRef]
- Zhao, L.; Zhang, M.; Lario, D. Modeling the Transport Processes of a Pair of Solar Energetic Particle Events Observed by Parker Solar Probe Near Perihelion. Astrophys. J. 2020, 898, 16. [Google Scholar] [CrossRef]
- Leske, R.A.; Christian, E.R.; Cohen, C.M.S.; Cummings, A.C.; Davis, A.J.; Desai, M.I.; Giacalone, J.; Hill, M.E.; Joyce, C.J.; Krimigis, S.M.; et al. Observations of the 2019 April 4 Solar Energetic Particle Event at the Parker Solar Probe. Astrophys. J. Suppl. Ser. 2020, 246, 35. [Google Scholar] [CrossRef]
- Bobik, P.; Boschini, M.J.; Della Torre, S.; Gervasi, M.; Grandi, D.; La Vacca, G.; Pensotti, S.; Putis, M.; Rancoita, P.G.; Rozza, D.; et al. On the forward-backward-in-time approach for Monte Carlo solution of Parker’s transport equation: One-dimensional case. J. Geophys. Res. Space Phys. 2016, 121, 3920–3930. [Google Scholar] [CrossRef]
- Kopp, A.; Büsching, I.; Strauss, R.D.; Potgieter, M.S. A stochastic differential equation code for multidimensional Fokker–Planck type problems. Comput. Phys. Commun. 2012, 183, 530–542. [Google Scholar] [CrossRef]
- Strauss, R.D.T.; Effenberger, F. A Hitch-hiker’s Guide to Stochastic Differential Equations. Space Sci. Rev. 2017, 212, 151–192. [Google Scholar] [CrossRef]
- Jian, L.; Russell, C.T.; Luhmann, J.G.; Skoug, R.M. Properties of Interplanetary Coronal Mass Ejections at One AU During 1995–2004. Sol. Phys. 2006, 239, 393–436. [Google Scholar] [CrossRef]
- Jian, L.K.; Russell, C.T.; Luhmann, J.G.; Skoug, R.M.; Steinberg, J.T. Stream Interactions and Interplanetary Coronal Mass Ejections at 0.72 AU. Sol. Phys. 2008, 249, 85–101. [Google Scholar] [CrossRef]
- Sheeley, N.R.; Howard, R.A.; Koomen, M.J.; Michels, D.J.; Schwenn, R.; Mühlhäuser, K.H.; Rosenbauer, H. Coronal Mass Ejections and Interplanetary Shocks. J. Geophys. Res. Space Phys. 1985, 90, 163–175. [Google Scholar] [CrossRef]
- Husidic, E.; Wijsen, N.; Baratashvili, T.; Poedts, S.; Vainio, R. Energetic Particle Acceleration and Transport with the Novel Icarus + PARADISE Model. J. Space Weather. Space Clim. 2024, 14, 11. [Google Scholar] [CrossRef]
- Kocharov, L. Modeling the propagation of solar energetic particles in corotating compression regions of solar wind. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Wijsen, N.; Aran, A.; Pomoell, J.; Poedts, S. Interplanetary Spread of Solar Energetic Protons near a High-Speed Solar Wind Stream. Astron. Astrophys. 2019, 624, A47. [Google Scholar] [CrossRef]
- Wijsen, N.; Aran, A.; Sanahuja, B.; Pomoell, J.; Poedts, S. The effect of drifts on the decay phase of SEP events. Astron. Astrophys. 2020, 634, 2–13. [Google Scholar] [CrossRef]
- Wijsen, N.; Aran, A.; Pomoell, J.; Poedts, S. Spreading protons in the heliosphere: A note on cross-field diffusion effects. J. Phys. Conf. Ser. 2019, 1332. [Google Scholar] [CrossRef]
- Ding, Z.; Li, G.; Wijsen, N.; Poedts, S.; Yao, S. Modeling Ion Acceleration and Transport in Corotating Interaction Regions: The Mass-to-charge Ratio Dependence of the Particle Spectrum. Astrophys. J. Lett. 2024, 964, L8. [Google Scholar] [CrossRef]
- Schatten, K.H.; Wilcox, J.M.; Ness, N.F. A Model of Interplanetary and Coronal Magnetic Fields. Sol. Phys. 1969, 6, 442–455. [Google Scholar] [CrossRef]
- Altschuler, M.D.; Newkirk, G. Magnetic fields and the structure of the solar corona. Sol. Phys. 1969, 9, 131–149. [Google Scholar] [CrossRef]
- Arge, C.N.; Odstrcil, D.; Pizzo, V.J.; Mayer, L.R. Improved Method for Specifying Solar Wind Speed Near the Sun. In Solar Wind Ten; Velli, M., Bruno, R., Malara, F., Bucci, B., Eds.; American Institute of Physics Conference Series; AIP Publishing: Melville, NY, USA, 2003; Volume 679, pp. 190–193. [Google Scholar] [CrossRef]
- Totten, T.L.; Freeman, J.W.; Arya, S. An Empirical Determination of the Polytropic Index for the Free-streaming Solar Wind Using Helios 1 Data. J. Geophys. Res. Space Phys. 1995, 100, 13–17. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).