Optical Quasi-Periodic Oscillation of Blazar PKS 1440-389 in the TESS Light Curve
Abstract
1. Introduction
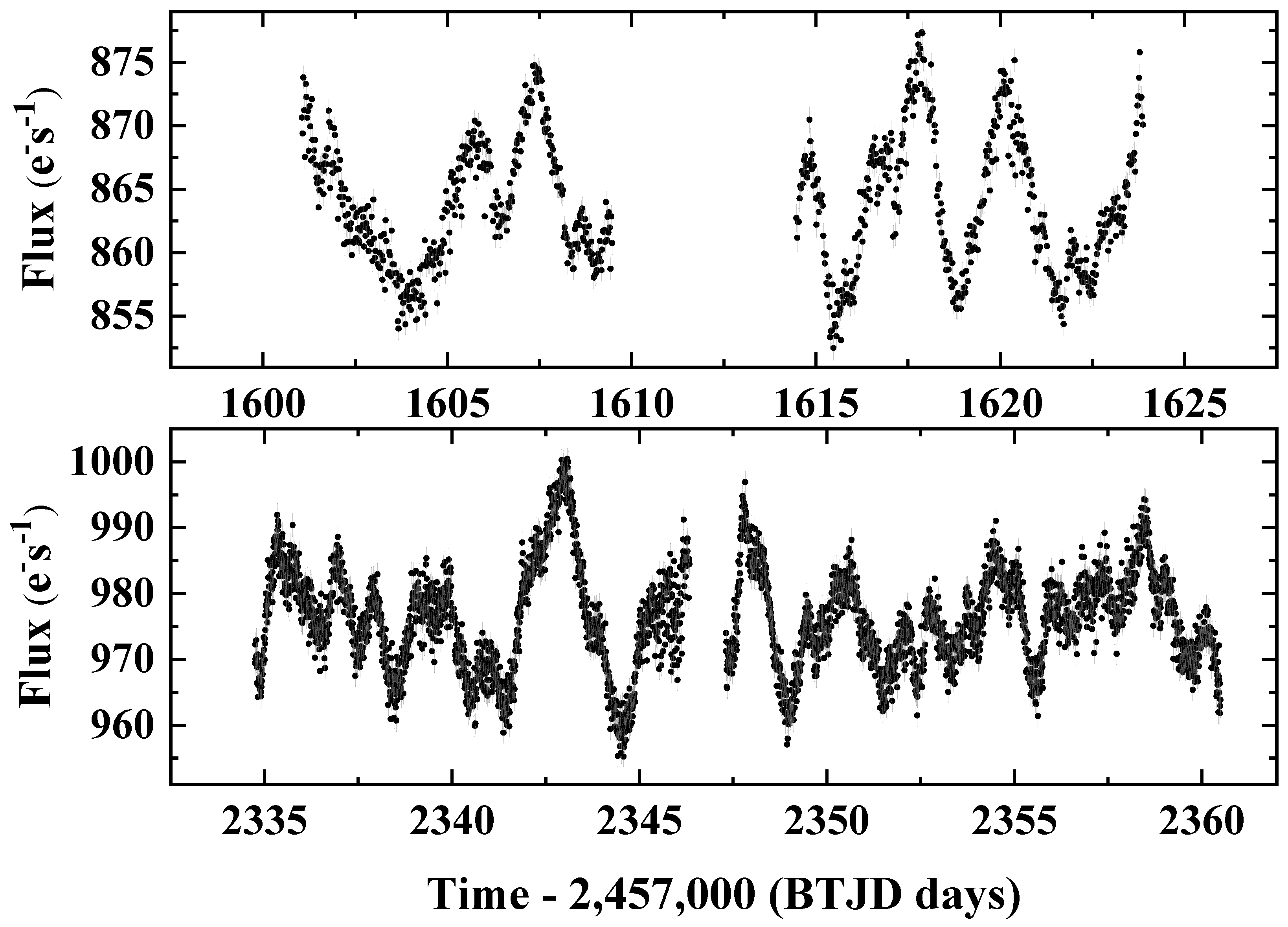
2. TESS Photometry
3. TESS Data Reduction
4. Data Analysis
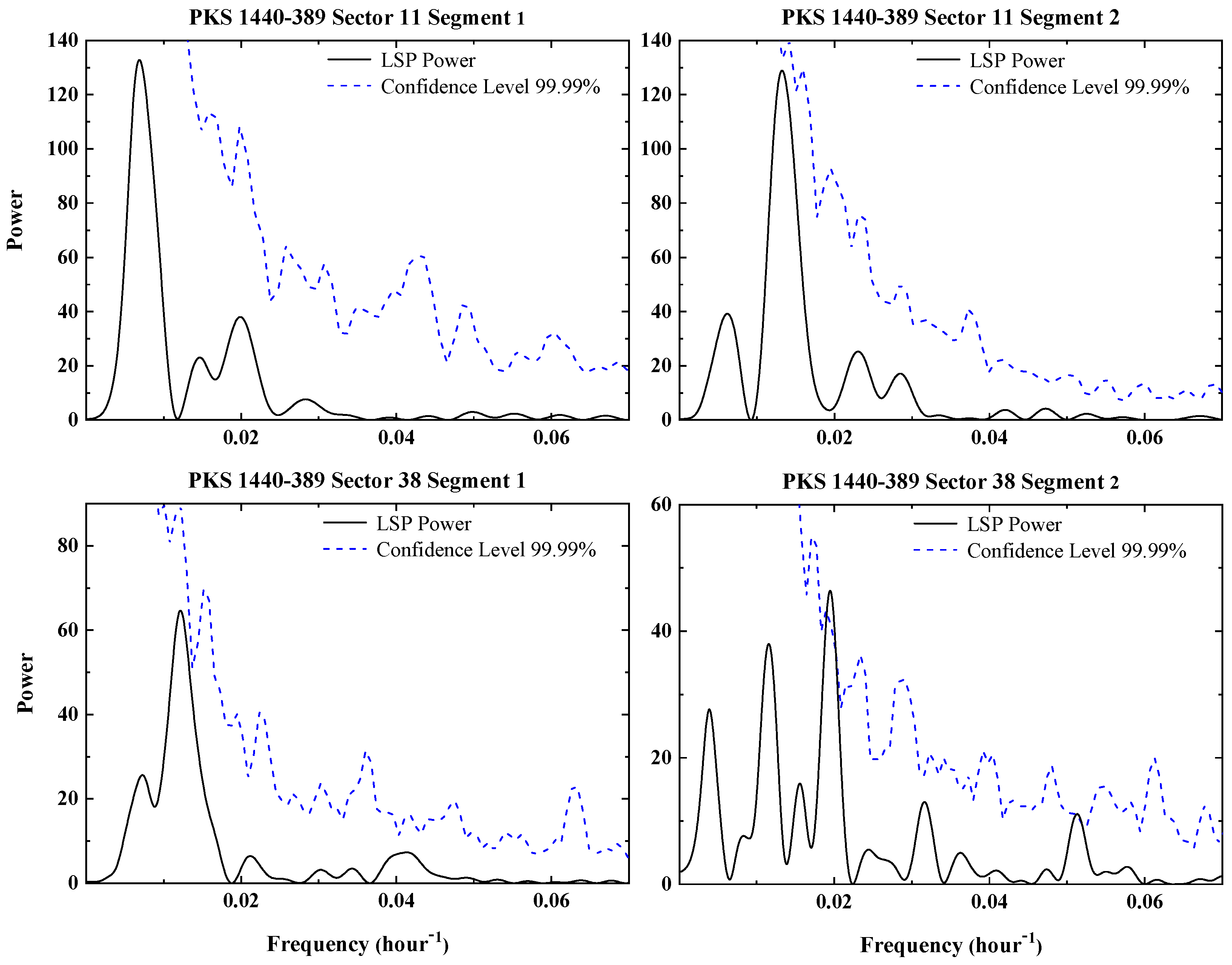
4.1. Lomb–Scargle Periodogram
4.2. Weighted Wavelet Z-Transform
4.3. Light-Curve Simulation and Confidence Evaluation
5. Results
6. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Padovani, P.; Alexander, D.M.; Assef, R.J.; Marco, B.D.; Giommi, P.; Hickox, R.C.; Richards, G.T.; Smolčić, V.; Hatziminaoglou, E.; Mainieri, V.; et al. Active galactic nuclei: What’s in a name? Astron. Astrophys. Rev. 2017, 107, 1–91. [Google Scholar] [CrossRef]
- Urry, C.M.; Padovani, P. Unified schemes for radio-loud active galactic nuclei. Publ. Astron. Soc. Pac. 1995, 25, 803–845. [Google Scholar] [CrossRef]
- Ghisellini, G.; Tavecchio, F.; Foschin, L.; Ghirlanda, G. The transition between BL Lac objects and flat spectrum radio quasars. Mon. Not. R. Astron. Soc. 2011, 414, 2674–2689. [Google Scholar] [CrossRef]
- Abdo, A.A.; Ackermann, M.; Agudo, I.; Agudo, I.; Aller, H.D.; Aller, M.F.; Angelakis, E.; Arkharov, A.A.; Axelsson, M.; Bach, U.; et al. The spectral energy distribution of Fermi bright blazars. Astrophys. J. 2010, 716, 30–70. [Google Scholar] [CrossRef]
- Sobolewska, M.A.; Siemiginowska, A.; Kelly, B.C.; Nalewajko, K. Stochastic Modeling of the Fermi/LAT γ-Ray Blazar Variability. Astrophys. J. 2014, 786, 143–156. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Albert, A.; Atwood, W.B.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Becerra Gonzalez, J.; Bellazzini, R.; et al. Multiwavelength Evidence for Quasi-periodic Modulation in the Gamma-Ray Blazar PG 1553+113. Astrophys. J. Lett. 2015, 813, L41–L48. [Google Scholar] [CrossRef]
- Li, X.-P.; Yang, H.-Y.; Cai, Y.; Song, X.-F.; Yang, H.-T.; Shan, Y.-Q. A Quasi-periodic Oscillation of 4.6 years in the Radio Light Curves of the Blazar PKS 0607–157. Res. Astron. Astrophys. 2023, 23, 095010–095018. [Google Scholar] [CrossRef]
- Gong, Y.-L.; Zhou, L.-C.; Yuan, M.; Zhang, H.-Y.; Yi, T.-F.; Fang, J. Quasiperiodic Behavior in the γ-Ray Light Curve of the Blazar PKS 0405-385. Astrophys. J. 2022, 931, 168–175. [Google Scholar] [CrossRef]
- Zhou, J.-N.; Wang, Z.-X.; Chen, L.; Wiita, P.J.; Vadakkumthani, J.; Morrell, N.; Zhang, P.-F.; Zhang, J.-J. A 34.5 day quasi-periodic oscillation in γ-ray emission from the blazar PKS 2247–131. Nat. Commun. 2018, 9, 4599. [Google Scholar] [CrossRef]
- Chen, J.-P.; Yi, T.-F.; Gong, Y.-L.; Yang, X.; Chen, Z.-H.; Chang, X.; Mao, L.-S. A 31.3 day Transient Quasiperiodic Oscillation in Gamma-ray Emission from Blazar S5 0716+714. Astrophys. J. 2022, 938, 8–16. [Google Scholar] [CrossRef]
- Roy, A.; Sarkar, A.; Chatterjee, A.; Gupta, A.C.; Chitnis, V.; Wiita, P.J. Transient quasi-periodic oscillations at γ-rays in the TeV blazar PKS 1510-089. Mon. Not. R. Astron. Soc. 2022, 510, 3641–3649. [Google Scholar] [CrossRef]
- Hong, S.-W.; Xiong, D.-R.; Bai, J.-M. Optical Quasi-periodic Oscillation of the BL Lacertae Object S5 0716+714 during the Faint State. Astron. J. 2017, 155, 31–39. [Google Scholar] [CrossRef]
- Mohan, P.; Gupta, A.C.; Bachev, R.; Strigachev, A. Kepler light-curve analysis of the blazar W2R 1926+42. Mon. Not. R. Astron. Soc. 2016, 456, 654–664. [Google Scholar] [CrossRef]
- Sarkar, A.; Kushwaha, P.; Gupta, A.C.; Chitnis, V.R.; Wiita, P.J. Multi-waveband quasi-periodic oscillations in the light curves of blazar CTA 102 during its 2016-2017 optical outburst. Astro. Astrophys. 2020, 642, A129–A137. [Google Scholar] [CrossRef]
- Vaughan, S.; Uttley, P.; Markowitz, A.G.; Huppenkothen, D.; Middleton, M.J.; Alston, W.N.; Scargle, J.D.; Farr, W.M. False periodicities in quasar time-domain surveys. Mon. Not. R. Astron. Soc. 2016, 461, 3145–3152. [Google Scholar] [CrossRef]
- Ricker, G.R.; Winn, J.N.; Vanderspek, R.; Latham, D.W.; Bakos, G.Á.; Bean, J.L.; Berta-Thompson, Z.K.; Brown, T.M.; Buchhave, L.; Butler, N.R.; et al. Transiting Exoplanet Survey Satellite. J. Astron. Telesc. Instrum. Syst. 2015, 1, 1–10. [Google Scholar] [CrossRef]
- Kishore, S.; Gupta, A.C.; Wiita, P.J. Detection of Quasiperiodic Oscillations in the Blazar S4 0954+658 with TESS. Astrophys. J. 2023, 943, 53–68. [Google Scholar] [CrossRef]
- Tripathi, A.; Smith, K.L.; Wiita, P.J.; Wagoner, R.V. Optical quasi-periodic oscillations in the TESS light curves of three blazars. Mon. Not. R. Astron. Soc. 2024, 527, 9132–9144. [Google Scholar] [CrossRef]
- Ricker, G.R.; Winn, J.N.; Vanderspek, R.; Latham, D.W.; Bakos, G.Á.; Bean, J.L.; Berta-Thompson, Z.K.; Brown, T.M.; Buchhave, L.; Butler, N.R.; et al. Transiting Exoplanet Survey Satellite (TESS). Proc. SPIE 2014, 9143, 914320–914334. [Google Scholar]
- Smith, K.L.; Sartori, L.F. The Rapid Optical Variability of the Nearby Radio-loud AGN Pictor A: Introducing the Quaver Pipeline for AGN Science with TESS. Astrophys. J. 2023, 2, 188–210. [Google Scholar] [CrossRef]
- Lomb, N.R. Least-Squares Frequency Analysis of Unequally Spaced Data. Astrophys. Space Sci. 1976, 39, 447–462. [Google Scholar] [CrossRef]
- Scargle, J.D. Studies in astronomical time series analysis. II. Statistical aspects of spectral analysis of unevenly spaced data. Astrophys. J. 1982, 263, 835–853. [Google Scholar] [CrossRef]
- VanderPlas, J.T. Understanding the Lomb-Scargle Periodogram. Astrophys. J. Suppl. Ser. 2018, 236, 16–43. [Google Scholar] [CrossRef]
- Wang, J.-Y.; An, T.; Baan, W.A.; Lu, X.-L. Periodic radio variabilities of the blazar 1156+ 295: Harmonic oscillations. Mon. Not. R. Astron. Soc. 2014, 443, 58–66. [Google Scholar] [CrossRef]
- Witt, A.; Schumann, A.Y. Holocene climate variability on millennial scales recorded in Greenland ice cores. Nonlin. Processes Geophys. 2005, 12, 345–352. [Google Scholar] [CrossRef]
- Grossmann, A.; Morlet, J. Decomposition of Hardy functions into square integrable wavelets of constant shape. SIAM J. Math. Anal. 1984, 12, 723–736. [Google Scholar] [CrossRef]
- Foster, G. Wavelets for period analysis of unevenly sampled time series. Astron. J. 1996, 112, 1709–1729. [Google Scholar] [CrossRef]
- Foster, G. Time series analysis by projection. I. statistical properties of Fourier analysis. Astron. J. 1996, 111, 541–554. [Google Scholar] [CrossRef]
- Emmanoulopoulos, D.; McHardy, I.M.; Papadakis, I.E. Generating artificial light curves: Revisited and updated. Mon. Not. R. Astron. Soc. 2013, 433, 907–927. [Google Scholar] [CrossRef]
- Valtonen, M.J.; Lehto, H.J.; Nilsson, K.; Heidt, J.; Takalo, L.O.; Sillanpää, A.; Villforth, C.; Kidger, M.; Poyner, G.; Pursimo, T.; et al. A massive binary black-hole system in OJ 287 and a test of general relativity. Nature 2008, 452, 851–853. [Google Scholar] [CrossRef] [PubMed]
- Li, X.-P.; Zhao, L.; Yan, Y.; Wang, L.-S.; Yang, H.-T.; Cai, Y.; Luo, Y.-H. Detection of quasi-periodic oscillations from the blazar PKS 1510-089. J. Astrophys. Astron. 2021, 42, 92–98. [Google Scholar] [CrossRef]
- Rieger, F.M. On the Geometrical Origin of Periodicity in Blazar-type Sources. Astrophys. J. 2004, 615, L5–L8. [Google Scholar] [CrossRef]
- Liska, M.; Hesp, C.; Tchekhovskoy, A.; Ingram, A.; van der Klis, M.; Markoff, S. Formation of precessing jets by tilted black hole discs in 3D general relativistic MHD simulations. Mon. Not. R. Astron. Soc. 2018, 474, L81–L85. [Google Scholar] [CrossRef]
- Stella, L.; Vietri, M. Lense-Thirring Precession and Quasi-periodic Oscillations in Low-Mass X-Ray Binaries. Astrophys. J. 1998, 492, L59–L62. [Google Scholar] [CrossRef]
- Chakrabarti, S.K.; Wiita, P.J. Spiral Shocks in Accretion Disks As a Contributor to Variability in Active Galactic Nuclei. Astrophys. J. 1993, 411, 602–609. [Google Scholar] [CrossRef]
- Mangalam, A.V.; Wiita, P.J. Accretion Disk Models for Optical and Ultraviolet Microvariability in Active Galactic Nuclei. Astrophys. J. 1993, 406, 420–429. [Google Scholar] [CrossRef]
- Espailat, C.; Bregman, J.; Hughes, P.; Lloyd-Davies, E. Wavelet Analysis of AGN X-Ray Time Series: A QPO in 3C 273? Astrophys. J. 2008, 679, 182–193. [Google Scholar] [CrossRef]
- Chang, X.; Yi, T.-F.; Xiong, D.-R.; Liu, C.-X.; Yang, X.; Li, H.-Z.; Gong, Y.-L.; Na, W.-W.; Li, Y.; Chen, Z.-H.; et al. Multicolour optical variability monitoring of blazars with high time resolution. Mon. Not. R. Astron. Soc. 2023, 520, 4118–4133. [Google Scholar] [CrossRef]
- Gupta, A.C.; Srivastava, A.K.; Wiita, P.J. Periodic Oscillations in the Intra-Day Optical Light Curves of the Blazar S5 0716+714. Astrophys. J. 2009, 690, 216–223. [Google Scholar] [CrossRef]
- Chang, Y.-L.; Arsioli, B.; Giommi, P.; Padovani, P.; Brandt, C.H. The 3HSP catalogue of extreme and high-synchrotron peaked blazars. Astro. Astrophys. 2019, 632, A77–A92. [Google Scholar] [CrossRef]
- Dong, L.-Y.; Zhang, H.-C.; Giannios, D. Kink instabilities in relativistic jets can drive quasi-periodic radiation signatures. Mon. Not. R. Astron. Soc. 2020, 494, 1817–1825. [Google Scholar] [CrossRef]
- Jorstad, S.G.; Marscher, A.P.; Raiteri, C.M.; Villata, M.; Weaver, Z.R.; Zhang, H.-C.; Dong, L.-Y.; Gómez, J.L.; Perel, M.V.; Savchenko, S.S.; et al. Rapid quasi-periodic oscillations in the relativistic jet of BL Lacertae. Nature 2022, 7926, 265–268. [Google Scholar] [CrossRef] [PubMed]
- Mizuno, Y.; Lyubarsky, Y.; Nishikawa, K.; Hardee, P.E. Three-Dimensional Relativistic Magnetohydrodynamic Simulations of Current-Driven Instability. I. Instability of a Static Column. Astrophys. J. 2009, 700, 684–693. [Google Scholar] [CrossRef]
- Tripathi, A.; Smith, K.L.; Wiita, P.J.; Wagoner, R.V. Search for quasi-periodic oscillations in TESS light curves of bright Fermi Blazars. Mon. Not. R. Astron. Soc. 2024, 528, 6608–6618. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, H.; Yi, T.; Tang, Y.; Wang, J.; Zhang, S.; Wang, L.; Chen, Y.; Shen, Y.; Dong, L.; Zhang, Y. Optical Quasi-Periodic Oscillation of Blazar PKS 1440-389 in the TESS Light Curve. Universe 2024, 10, 242. https://doi.org/10.3390/universe10060242
Lu H, Yi T, Tang Y, Wang J, Zhang S, Wang L, Chen Y, Shen Y, Dong L, Zhang Y. Optical Quasi-Periodic Oscillation of Blazar PKS 1440-389 in the TESS Light Curve. Universe. 2024; 10(6):242. https://doi.org/10.3390/universe10060242
Chicago/Turabian StyleLu, He, Tingfeng Yi, Yanke Tang, Junjie Wang, Shun Zhang, Liang Wang, Yutong Chen, Yuncai Shen, Liang Dong, and Yangwei Zhang. 2024. "Optical Quasi-Periodic Oscillation of Blazar PKS 1440-389 in the TESS Light Curve" Universe 10, no. 6: 242. https://doi.org/10.3390/universe10060242
APA StyleLu, H., Yi, T., Tang, Y., Wang, J., Zhang, S., Wang, L., Chen, Y., Shen, Y., Dong, L., & Zhang, Y. (2024). Optical Quasi-Periodic Oscillation of Blazar PKS 1440-389 in the TESS Light Curve. Universe, 10(6), 242. https://doi.org/10.3390/universe10060242





