Abstract
We investigate the stochastic version of the paradigmatic model of magnetohydrodynamic turbulence. The model can be interpreted as an active vector admixture subject to advective processes governed by turbulent flow. The back influence on fluid dynamics is explicitly taken into account. The velocity field is generated through a fully developed turbulent flow taking into account the violation of spatial parity, which is introduced through the helicity parameter . We consider a generalized setup in which parameter A is introduced in model formulation, which is associated with the interaction part of the model, and its actual value represents different physical systems. The model is analyzed by means of the field-theoretic renormalization group. The calculation is performed using -expansion, where is the deviation from the Kolmogorov scaling. Two-loop numerical calculations of the renormalization constant associated with the renormalization of the magnetic field are presented.
1. Introduction
Numerous important natural phenomena, spanning a wide range of spatial scales from microscopic to cosmological, are associated with hydrodynamic flows [1,2,3,4]. At all these scales, fluids can exist in a wide variety of states, each presenting an important challenge from both an experimental and a theoretical point of view. Especially intriguing behavior is observed for turbulent flows [5,6], which are generally considered rather a rule than an exception in nature [3]. Their study represents an exceptionally important task both from a theoretical perspective and from the standpoint of applications. It is noteworthy to mention several important areas where turbulence plays a pivotal role, including diverse challenges in fluid dynamics (such as turbulence in boundary layers [7], atmospheric turbulence [8,9], etc.), issues related to turbulent mixing and homogenization [10], the study of fusion plasma [11], and various astrophysical phenomena [12,13], among others. However, despite the enormous efforts that have been made to study turbulence for more than a century, the problem remains unsolved.
The modern theoretical approach to turbulence is grounded on the statistical analysis of the solutions to the Navier–Stokes (NS) equation, which is generally accepted as describing the motion of viscous (nonrelativistic) media [1]. As already noted, the medium during its movement can exist in various states depending on the flow parameters, for which the Reynolds number is typically introduced for classification. Defined as , where V is the typical average flow velocity, L is a typical macroscopic scale, and is the kinematic viscosity of the medium, represents the ratio between inertial and dissipative forces. At low values, , a regular (laminar) flow is observed. With an increase in , phenomena ranging from periodic, such as von Kármán vortices, to highly chaotic and irregular motion at very high values of (practically, is considered large enough) occur. The latter state of fluid is known as fully developed turbulence. In this state, the so-called inertial interval exhibits a transfer of kinetic energy from macroscopic L to microscopic (dissipative) ld scales. For fully developed turbulence, the symmetry and dimension arguments have led to important conclusions about the scaling behavior of velocity correlation functions, primarily through the famous Kolmogorov’s K41 theory. However, more detailed statistical descriptions of both the fully developed turbulence regime and its onset in laminar flow are still needed. Mathematically, this research gap stems from the well-known blow-up problem: the existence of a strong instability inherent in solutions of the NS equations at high Reynolds numbers. Generally speaking, for this equation, even the existence of a global smooth solution is in question at present [14]. Moreover, both mentioned problems are still unsolved not only for the Navier–Stokes equation but even for the simpler Euler equation (inviscid fluid).
Traditionally, the physical theory of developed turbulence models this instability effect by the addition of a suitably chosen random force to the NS equation. This addition also simulates the continuous input of mechanical energy necessary to sustain the turbulent cascade. The selection of the structure and statistics of this random force is the most critical aspect of the theory. Typically, random forces concentrated at large spatial scales are used to model large-scale effects on the scale-invariant behavior predicted by Kolmogorov’s theory. The standard stochastic problem formulation also assumes rotational symmetry of force correlations but can be expanded by varying the symmetry properties of force correlations (e.g., anisotropy and reflection asymmetry), to explore the impact of large-scale properties on velocity correlation scaling behavior [15].
In the context of developed turbulence studies, investigating the advection of specific quantities (such as temperature fields, concentration fields, or tracers) [4,16] by the turbulent field is paramount. The solution to this problem should shed light on the extent of turbulence intermittency [5], i.e., its fractal nature. In this case, the Prandtl number is often used to succinctly describe the flow’s quantitative characteristics [8,17]. For all types of admixtures, is defined as the dimensionless ratio of the kinematic viscosity coefficient to the corresponding diffusion coefficient D of a given admixture. Since both the kinematic viscosity and the diffusion coefficient are material- and flow-specific, resulting Prandtl numbers have to be specified under conditions characterizing the flow, hence are often found in property tables along with other material-specific properties [18,19]. Yet, in the limit of high Reynolds numbers, fully developed turbulence manifests through effective values of kinematic viscosity and the corresponding diffusion coefficient, rendering the turbulent Prandtl number independent of material and flow specifics. In what follows, we call such a turbulent Prandtl number [6,8].
Among general turbulence theory issues, describing fully developed turbulence in an electrically conducting fluid occupies a special place. The system of equations of motion for an electrically conducting fluid is known as the magnetohydrodynamics (MHD) equation system (see, e.g., [1,10,17,20]). For the first time, this system (in the case of an inviscid fluid) was investigated by Hannes Alfvén. For the subsequent fruitful application of it to problems in plasma physics, Alfvén was awarded the Nobel Prize in 1970. Nowadays, there are many theoretical methods for studying this system of equations, which constitute the golden fund of theoretical and mathematical physics. As is well known, in electrically conducting fluids, turbulent motions are accompanied by magnetic field fluctuations. However, such conducting fluids, exemplified by ionized gas (plasma) or magma, are rare under typical laboratory conditions. Conversely, astrophysical or geophysical settings, such as the solar wind or turbulent dynamo mechanisms generating large-scale magnetic fields, underscore the enduring interest in MHD turbulence studies [12,21,22].
From a chronological perspective, the Kazantsev–Kraichnan kinematic model holds paramount importance in magnetohydrodynamics [23,24,25]. The main idea of this model is the assumption that while the magnetic field is passively advected by the hydrodynamic flow, the reciprocal effect on the main flow from the magnetic field is negligible. However, this assumption falls short in describing realistic flows. A genuine model of magnetohydrodynamics must account for the interplay between the magnetic and velocity fields. Incorporating this interaction, along with spatial parity nonconservation, suggests the possibility of generating a uniform large-scale magnetic field within the system—a mechanism known as the turbulent dynamo [20]. Many studies have focused on this phenomenon, and here, we provide references only to those that are close in language to this paper [26,27,28].
As well as Kraichnan-like models, the MHD model should reveal scaling behavior for accompanying quantitative parameters such as correlation or structure functions. A quantitative description of these characteristics poses a natural challenge for the theory to explain and construct reliable approximation schemes for their calculation. As demonstrated by Kolmogorov’s theory, scaling invariance naturally emerges in turbulent flows [5]. However, exploring behaviors such as anomalous scaling demands extensive, meticulous analysis. This phenomenon is characterized by singular (arguably, powerlike) behavior of some statistical quantities (correlation functions, structure functions, etc.) in the inertial–convective range in the fully developed turbulence regime [3,5]. Moreover, it is worth noting that scaling properties manifest themselves more clearly at higher values of Reynolds number [29], making the limit critically important. Thus, employing the well-established renormalization group (RG) theory tools for analytical results on turbulent flows is prudent. Unlike numerical approaches, where achieving the limit is difficult, the RG method allows for analytical calculations, ultimately allowing for the examination of universal turbulent phenomena, i.e., independent of material microstructure and macroscopic flow conditions [15]. Additionally, the RG framework readily accommodates various scenarios, including the advection of different admixtures [29].
The renormalization group approach was previously applied to the kinematic MHD at the level of one-loop approximation in quantum field perturbation theory [27]. The authors also considered the case of so-called chiral or gyrotropic turbulent media, when the corresponding magnetic fields and velocity fields lack defined spatial parity. Technically, the presence of chirality means that all correlation functions’ transverse structures (assuming the medium is incompressible and magnetic field transversality is ensured by Maxwell’s equations) become a mixture of two quantities: tensor and pseudotensor (with respect to the three-dimensional rotation group ). It has been shown that spatial parity nonconservation, even without magnetic fluctuations, leads to spontaneous symmetry breaking tied to the instability of linearized MHD and the emergence of a large-scale homogeneous mean magnetic field . This field potentially stabilizes the system in its new “vacuum state”, acting through the turbulent dynamo mechanism. From a technical standpoint, spontaneous symmetry breaking generates new counterterms of mass renormalization type (here, a homogeneous magnetic field gradient plays the mass role) in a form , nontrivially arising during the ultraviolet (UV) renormalization procedure, starting from one-loop diagrams. Here, ld represents the naturally available cutoff scale in the theory. However, as demonstrated in [30,31], the appearance of these counterterms does not compromise the theory’s multiplicative renormalizability, in a sense that their contribution can always (at least at the one-loop level) be mitigated by an appropriate choice of , presumably stabilizing the system. Beyond merely positing a stabilizing magnetic field, the paper [30] predicts a new physical effect: the emergence of disturbances in Alfvén waves perpendicular to the spontaneous field , leading to their linear temporal growth. This results in long-lived pulses , , akin to the massless bosons in the Goldstone model.
In essence, numerous vector impurity models bear similarities to kinematic MHD to varying degrees. As repeatedly noted, the tensor nature of considered impurities significantly influences diffusion and advection processes [31,32,33,34]. For instance, as has been shown in [33], introducing spatial parity violation (helicity) into the turbulent flow not only offers a highly realistic physical scenario but also uniquely highlights the studied model’s specific tensorial and interactive properties. Consequently, the authors infer that interaction structures impact diffusion and advection processes more than the tensor nature of the advected field itself. To extend these findings beyond a few selected models, examining the general A model of passive vector advection, initially defined in [35], proves useful. To prevent confusion, it should be emphasized that the current general A model exclusively pertains to passive vector advection and should not be confused with the model A according to the classification of Halperin and Hohenberg [36] or with the A model of the forced Navier–Stokes equation presented in [37,38]. The model’s name stems from the widely accepted notation for the A parameter [28,31,39], which appears in its definition (refer to Section 2 for details). The A parameter plays a central role in the appropriate definition of a unified description of a wide range of vector admixture models. Given its requirement to be real without explicit restrictions, it can adopt values , , and , correlating to the kinematic MHD model, the model for passively advected vector fields, and the scenario of the so-called linearized Navier–Stokes equation [39], respectively. Thus, the general A model serves as a tool to unite several distinct but physically important cases into a single model. Overall, for this model, a comprehensive generalization to all physically permissible values of A (including beyond the boundaries of the interval ) was conducted by the authors of [28]. However, the impact of helical effects in a fully turbulent environment was confined to what was necessary for calculating the turbulent Prandtl number. Therefore, to obtain a comprehensive picture of MHD, it seems highly desirable to calculate the full set of renormalization constants for the general parametric A model considering the effects of spatial parity violation up to the two-loop order in perturbation theory.
To conduct the above-discussed studies, this endeavor employs quantum field theory methods alongside the established renormalization group technique tools (for instance, see [15,29,40]). The RG method has found extensive application in fully developed turbulence research without admixtures [30,41,42,43], as well as in studying advection–diffusion processes involving various admixtures, including passive scalar admixtures [35,43,44,45,46,47], magnetic admixtures [27,45,48], and also vector admixtures [33,39,45]. Highlighting the nuances of applying standard quantum field techniques to stochastic hydrodynamics issues is also pertinent. Among various regularization techniques in field theory, a distinguished role is played by dimensional regularization accompanied with -expansion [29,40]. This approach directly yields regularized counterparts for divergent Feynman diagrams, with the associated -expansion serving as a valuable perturbative method for calculating universal quantities in critical phenomena and stochastic dynamics theory [29,40]. It is worth mentioning that the parameter’s interpretation within stochastic turbulence theory differs from its role in critical phenomena models (e.g., well-known -theory), where the small -expansion parameter is usually determined by a difference from the upper critical dimension [29,40]. In the stochastic theory of developed turbulence, its definition has no relation to the dimension of space. Most studies integrate into the scaling behavior of random forces, strictly considering a three-dimensional context [5,15]. The parameter thus derives from the logarithmic theory where , aligning with the ideal scenario of (delta-shaped) energy infusion into the system from infinitely vast spatial scales [15,41]. Once a model undergoes correct renormalization, perturbative results for universal quantities, such as critical (scaling) exponents, become attainable. These invariably take the form of asymptotic series. Despite the existence of impressive multiloop outcomes in critical and stochastic dynamics [49,50,51], the developed turbulence RG theory predominantly limits analytical calculations to two-loop approximations [29,52,53]. In fact, it might be argued [42] that the complexity of such endeavors is arguably an order of magnitude greater than first-order analyses. Not only is the number of Feynman diagrams much higher but there are also intrinsic numerical problems with the correct extraction of divergent parts of Feynman diagrams. Therefore, any attempt that might help to make two-loop calculations feasible seems worthwhile to undertake.
A comprehensive two-loop calculation for the dynamo effect in stochastic MHD has not yet been finished. Our goal herein is to make progress in this direction and present particular results of two-loop approximation. In particular, we present details on the two-loop calculation of a three-point interaction vertex, which, by itself, presents quite demanding technical problems. To make the problem tractable, it is necessary to rely on powerful algorithmic and numerical approaches [54,55,56].
This paper is structured as follows. Section 2 defines the A model of passive advection of a vector admixture as a generalization of the stochastic MHD and introduces its field theoretical counterpart. Section 3 is devoted to a detailed renormalization group analysis. The final Section 4 is devoted to concluding remarks and plans for the future.
2. Formulation of the Quantum Field Model
It is well-known [1] that the hydrodynamics of a nonrelativistic incompressible viscous fluid is described by the Navier–Stokes equation
Here, represents the velocity field, stands for the (transverse) random force exerted per unit density, and scalar function denotes the pressure per unit density. Throughout the text, the argument of all field functions is defined as , where is a d-dimensional spatial vector and t is the time. The parameter represents the kinematic viscosity, the symbol ∇ is the spatial gradient, is the time derivative, is the Laplace operator, and parentheses indicate the standard dot product of three-dimensional vectors. Let us also stress that for possible verification and transparency in intermediate calculations, we retain general dimension d in actual expressions, although in the end, we are mainly interested in arguably the most relevant three-dimensional case . In other space dimensions, the used approach, strictly speaking, will not work.
In the approximation of an incompressible fluid (low Mach number), the explicit dependence on the pressure in (1) can be simply eliminated by taking the divergence of (1). The result is the following elliptic equation,
from which it follows that the pressure can be formally represented in terms of the fundamental solution of Equation (2). The symbol ⊗ here represents the outer product. Substituting this solution into (1), it is easy to see that the purely longitudinal contribution of pressure reduces the longitudinal part of the value . Therefore, the pressure term in (1) can be eliminated by discarding the contribution and at the same time placing a transverse projector in front of .
In the conventional field theory setting, the problem in (1) is analyzed throughout the entire space and along the whole time axis, which requires zero divergence-free boundary conditions and the implementation of a retardation condition, which entails that the velocity field vanishes as . Note that, generally speaking, these assumptions do not fix either the existence or the uniqueness of the solution of (1). A comprehensive overview of the current developments in the mathematical theory of the Navier–Stokes equations can be found, e.g., in [57].
Particularly, developed turbulence across a sufficiently broad range of parameters is described within the approximation of an incompressible fluid. This is adequate as long as the flow velocity is much less than the speed of sound [58,59]. As already noted in the introductory Section 1, investigating the turbulent regime at the level of numerical solutions of Equation (1) is extremely complicated by the fact that in this regime, all scales (mixing lengths) are interconnected in a cascade-like manner. Consequently, the flow in the boundary layer (the scale at which the pressure gradient becomes comparable to the viscous term) affects everything up to the overall scale of the system. This “entanglement of scales” implies that inevitable tiny errors at the smallest scales of the approximation grid will ultimately have a huge impact on the overall structure of the solution. For example, in the simplest idealized model of the atmosphere (considered as a two-dimensional ideal fluid on the surface of a torus), deviations increase by times in two months. Clearly, this fact alone renders dynamic weather forecasting for such a duration practically impossible, regardless of the computational power or the density of the data network employed. Therefore, in practical calculations, people often entirely forego solving the NS equation, describing the fluid flow not hydrodynamically but kinetically, i.e., through an ensemble of interacting particles with the same statistics as the real medium (see, for example, the lattice Boltzmann method [60,61]). By averaging such a lattice system over all particles in the continuum limit, the Navier–Stokes equations are obtained. However, the ensemble itself can be modeled without any approximations, which yields the correct fluid flow without solving any equations.
Taking these difficulties into account, the physical theory of developed turbulence follows a different route based on the stochastic version of Equation (1) (see, e.g., [3,5,8,15]). More specifically, in this approach, in Equation (1) is generalized to the random variable with prescribed stochastic properties. This modification aims to simulate physical processes, such as the injection of energy into the system and the influence of boundaries. Consequently, the theory’s main objective shifts to identifying the statistical characteristics of the (stochastic) velocity field .
Let us turn our attention to magnetohydrodynamics [12,21,22], where, as is known, any movement of a conducting fluid in a magnetic field generates an electromotive force, inducing electric currents. Due to the presence of the magnetic field, these currents create mechanical forces that alter the state of motion of the fluid. Accordingly, when examining the hydrodynamics of an electrically conducting fluid, Equation (1) has to be suitably modified to incorporate the interaction between the velocity field and the magnetic field and complemented by an appropriate equation of motion for the magnetic field. More specifically, a hydrodynamic description here implies the adoption of three fundamental assumptions: firstly, the fluid should be considered highly conductive; secondly, its motion is nonrelativistic; and finally, the bulk variables must change slowly over time compared to all relevant characteristic time scales. Summarizing the above, magnetohydrodynamics is the simplest sufficient approximation to describe many large-scale low-frequency phenomena. Experience shows that MHD is applicable across a vast range of spatial scales, from nanometer ( m) scales in, e.g., physics of semiconductors, to interstellar and galactic ( m) scales, e.g., galactic arms.
Let us clarify here the theoretical setup needed to write the system of MHD equations in the case of a viscous liquid with finite conductivity. In general, magnetohydrodynamics studies the interaction of the electromagnetic field with a liquid or gaseous moving conductor, treated as a continuous medium. The MHD equations are a combination of Maxwell’s equations for the electromagnetic field and the conventional hydrodynamic equations that describe the motion of the continuous medium. The hydrodynamic equations of an electrically conductive fluid are valid under the conditions of the so-called MHD limit. Broadly speaking, this corresponds to the limit in which the charge and volume densities are obtained from the fluid equations rather than from the Boltzmann equation [12]. Assuming this limit to be fulfilled, let us derive the equation of motion for the magnetic field in the MHD system. When the fluid is moving at the velocity , the corresponding electric current density is connected with the electromagnetic fields through generalized Ohm’s law [22]. Following [27], we use its simplest form here, omitting the Hall term and others:
Here, and are the electric and magnetic fields in the “laboratory” system of coordinates, where we measure the velocity , and is the electrical conductivity, which is assumed to be finite but large enough, i.e., the electromagnetic processes are not very fast. The last assumption regarding the value of allows us to omit displacement currents (and convection currents) compared to conduction currents; therefore, in Formula (3) denotes precisely the conduction current [12,22]. Then, taking the curl of Equation (3) using the Maxwell–Faraday equation , one can obtain
Utilizing another of Maxwell’s equations, , with c representing the speed of light and denoting the vacuum magnetic permeability, and noting that in the case of nonrelativistic motion, the time derivative of the electric field is much smaller than the spatial derivative of the magnetic field, we can eliminate in favor of and finally derive the governing dynamic equation for the magnetic field in the form
Here, the parameter is introduced, which has the meaning of the magnetic diffusion (or magnetic viscosity) coefficient. By elementary manipulations, Equation (5) can be reduced to the form
which presents a starting point for a majority of studies in the MHD area. For a more detailed exposition, the interested reader is referred to the literature [12,20].
Let us now go back to the dynamics of the velocity field in the presence of a magnetic field. To describe it, we will use the Navier–Stokes equation (1), where the Lorentz force contribution (per unit density) is explicitly allocated in the force term . Applying further reasoning similar to that used to obtain Equation (5), we obtain
Rewriting the first term on the right side of (7), we arrive at the final desired generalization of the Navier–Stokes equation:
where the second term on the right side is the total pressure, consisting of two terms: gas (or thermal) pressure p and the so-called magnetic pressure .
A stochastic version of the MHD model is obtained by generalizing the external force term in the Navier–Stokes equation (8) to a random variable , as well as adding the corresponding random force term modeling a magnetic noise to Equation (6). Stochastic random forces and serve to mimic microscopic effects such as the presence of boundaries or interactions between the mean velocity flow and its fluctuating part [29]. Notwithstanding their obvious physical relevance, it is widely believed that their actual form is unimportant for interesting universal quantities. Note that from now on, variables and in Equations (6) and (8) should already be understood as the fluctuation parts of the corresponding total magnetic field and velocity field [26,44]. Furthermore, as has been pointed out in introductory Section 1, here we will consider a generalization of Equation (6) by introducing a new parameter A into the nonlinear term . Such a generalization corresponds to the transition to the general model A [28,31]. Note that the conventional formulation of MHD corresponds to the value [26,27]. Eventually, the stochastic MHD can be formulated by two intercoupled stochastic differential equations [28,31]
with material (covariant) derivative , complemented by transversality conditions for all vector fields
In Equations (9)–(11), fields and are the stochastic magnetic and velocity fields, , where is a reciprocal magnetic Prandtl number (by definition, magnetic Prandtl number ). The scalar functions and have the meaning of total pressure (see Equation (8)) and have no significance for further analysis for reasons similar to the text after Formula (2) and will be omitted. In general, within the framework of homogeneous and isotropic developed turbulence, the random velocity field in Equation (8) is represented as , where is the constant mean flow velocity and is a relatively small stochastic (fluctuating) component. The statistical characteristics of the latter are the subject of our study, since can always be eliminated by transitioning to a moving reference frame through an appropriate Galilean transformation . Given the smallness of compared to , any explicit dependence on t in is neglected in comparison to . In terms of the correlators , this means that the average value of the corresponding dynamic correlator over time is nothing other than the value of the static (simultaneous) correlator for the distance . For brevity, we will henceforth denote as , always understanding it to refer specifically to the fluctuating component. In contrast to , the average value of the random field is usually assumed to be zero, and the corresponding uniform magnetic field required for mass applications is introduced as an additive to the source .
The influence of Galilean symmetry in the model governed by Equations (9) and (10) extends beyond the aspects previously discussed. This symmetry encapsulates the foundational physics of the model and has significant implications for the RG analysis (see Section 3 and [31]). Moving forward, we interpret the Galilean invariance of Models (9) and (10) in a broader context, specifically, as symmetry under what we term the generalized Galileo transformation (see, e.g., [15,31]). This concept goes beyond a mere constant speed transformation to include transformations with an arbitrarily variable speed that rapidly diminishes as . Being essentially similar to gauge transformations, the generalized Galilean transformation is structured as follows:
Hereinafter, denotes the Heaviside step function. Transformations (12) are considered here as an independent Lie group and not as a representation of the corresponding group of coordinate transformations. They generalize the usual Galilean transformations [1], in which the velocity is constant and .
Let us briefly discuss the physical relevance of the parameter A [28,31]. First, we note that the aforementioned Galilean symmetry (12) demands A only to be real, yet the interval already includes quite diverse, physically significant models. As already mentioned in Section 1, choosing leads us to the kinematic MHD model [27]. On the other hand, the choice leads to passive advection of a vector field in turbulent environments [35,39], and finally yields the model of the linearized Navier–Stokes equations [39]. Thus, the parameter A stands in front of the stretching term, and, due to its continuous nature, represents a measure of specific interactions allowed by Galilean symmetry. Varying A allows for the investigation of many passively advected vector admixtures with different interaction properties. Although A can take any real value, it is often discussed only within the smallest possible continuous interval that encompasses these three mentioned distinguished cases. However, as shown in [28], in cases where spatial parity conservation is violated in the model, in general, there are conditions under which it can be considered for all real A, without restrictions. The general conclusion is that adopting A as a general parameter of the theory allows for the simultaneous investigation of a multitude of diverse diffusion–advection processes. Particularly intriguing behavior is observed in processes occurring in MHD () that possess additional instability in helical environments, which can be stabilized on large scales by the emergence of a macroscopic field [28,30].
The cornerstone of the stochastic theory of developed turbulence is the choice of the random force correlator, along with the corresponding dynamic equations that define the model [29]. In the general case, in the system under consideration, all elements of the correlator matrix , , and are different from zero. In particular, this situation was considered in [27], applicable to magnetohydrodynamics. Let us start with the correlation function of a magnetic noise , which is assumed to be a transverse Gaussian random vector with zero mean
where is an integral scale related to the stirring of the magnetic field and function is finite in the asymptotic limit , while in the limit , it should rapidly decrease. As noted above, the requirement of time decorrelation in and other correlators is necessary to ensure the Galilean invariance of the model. A detailed form of is not relevant for the actual RG analysis [15]. In a physically more realistic formulation, the noise term could be substituted by something like , where represents a strong (≈– G), large-scale magnetic field [45,62].
Let us stress that, in contrast to the original work [27], our study explicitly omits both the correlators and . Here, we refer to a more general formulation of the problem considered previously in [27], which shows that both and can be discarded as they are zero at the kinetic (Kolmogorov’s) fixed point which we are interested in.
Our primary interest lies in the correlator . The transverse random force describes the injection of kinetic energy into the turbulent system on a large spatial scale. Therefore, the actual form of its correlator should match the expected behavior of energy injection, which is supposed to be concentrated in the infrared (IR) region. It turns out that this choice can be reconciled with the RG approach [29]. It is important to note that the universality of fully developed turbulence is not confined to the specific statistical properties of the random force, including the case with broken spatial parity. Hence, without loss of generality, we prescribe the pair correlation function of zero-mean Gaussian statistics
where the function of is the so-called pumping function and represents the pumping rate, and ld (ld is the dissipative length) is a typical ultraviolet turbulence scale. The tensor quantity will be specified later. Let us also note that in stochastic turbulence theory, we also require that correctly models the physical injection of energy (IR injection). Since for the problems of the theory, the exact macroscopic structure of a turbulent flow is negligible, the simplest cutoff can be taken as the corresponding IR regularization. Technically, this can be implemented by introducing the step function into the pumping function , where the parameter , and L is the integral scale of turbulence (size of the system). Thus, by adopting such a sharp IR cutoff, we effectively regularize the model in the IR region. It is also worth noting that regularization by cutoff in our case does not break the global symmetry group of Model (12), unlike in relativistic field theory models.
To apply the standard RG technique effectively, it is crucial for the function to exhibit a power-law behavior as k becomes large [29]. In particular, this requirement is fulfilled when acquires the specific power-law dependence
Here, is a coupling constant of the theory, m represents IR cutoff, and is the model parameter characterizing the type of pumping. For generality, we write expressions everywhere for an arbitrary dimension of space d, but we are mainly interested in the case . It is also worth mentioning that, strictly speaking, such a representation is valid only in the limit (see, e.g., [15]). Let us also stress that Formula (14) represents the correlator in a kind of natural condition: there are two direct physical cutoff scales L and ld. Such a form is convenient for the correct setting of the problem (so-called -renormalization of the model) but not for practical purposes. In practice, when calculating all necessary quantities, the limit of is always taken, transferring the regularization function to the parameter .
In a normal fluid (i.e., fluid invariant under Galilean transformations), to each quantity we can assign a specific spatial parity: and are vectors, whereas and are pseudovectors, and correlator is a tensor. Due to the additional requirement of transversality (11), any tensor is necessarily proportional to the transverse projector , and any pseudotensor is proportional to the structure , where is the Levi-Civita tensor. The transition to a helical fluid corresponds to the abandonment of spatial parity conservation and technically implies that the correlator (13) should be given by a sum of a true tensor and a pseudotensor, i.e., the tensor quantity in correlator (13) corresponds to the sum of the transverse projection operator and a so-called helical term (summation over repeated index l is implied) [30]. Hence, we choose the quantity in the following form:
Here, the helicity parameter is constrained within the range , expressing the positive definiteness of the correlator (13). It can be naturally interpreted as the amount of reflection symmetry breaking: the case corresponds to the nonhelical case, and is a state with maximal broken spatial parity.
Nonlinear stochastic differential equations (9) and (10) are notorious for their mathematical complexity. However, their behavior in specific circumstances can be effectively analyzed by methods of quantum field theory. In particular, the RG method provides a natural framework for the analysis of macroscopic behavior, i.e., the behavior of various correlation functions in the infrared limit. In order to apply the RG method, it is advantageous to recast the Langevin-like formulation of the model in terms of path integrals. Following the well-known Janssen–De Dominicis procedure [29,53], stochastic equations (9) and (10) are fully equivalent to the field-theoretic model of a double set of (unrenormalized) fields , where and are Martin–Siggia–Rose (MSR) response fields [63]. For the ensuing application of the RG method, it is necessary to distinguish between bare (unrenormalized) and renormalized parameters [29,40]. Therefore, we denote the bare fields with a circle on top “˚”, and later on, we write renormalized parameters and fields without any symbol whatsoever.
The field-theoretic model is then given by the De Dominicis–Janssen–Martin–Siggia–Rose (unrenormalized) action functional [28], which takes the compact form:
Hereinafter, we employed a condensed notation, in which all integrals over space-time are not explicitly written, and summations over repeated Latin indices are implicitly assumed. Thus, for instance, the expression in the action (16) actually stands for
where denotes the i-th component of the gradient.
The starting point of perturbation methods in quantum field theory is to express Green functions in terms of a corresponding sum of Feynman diagrams, whose relevance is controlled by interaction parameters (coupling constants). Throughout this text, by Green functions, we mean both correlation and response functions of the fields. These functions are derived from the functional averages of specific field products, weighted by the exponential of the action . In graphical terms, these objects can be represented by Feynman diagrams constructed according to the standard diagrammatic rules of quantum field theory. The Feynman diagram technique serves as a convenient graphical tool for organizing various algebraic structures that arise from the basic perturbation theory elements (propagators and interaction vertices) [29]. The graphical representation of these elements can be straightforwardly obtained. For completeness, we also present the necessary expressions here. In the frequency–momentum representation, the nonvanishing propagators of the model are expressed as
and are illustrated in Figure 1.
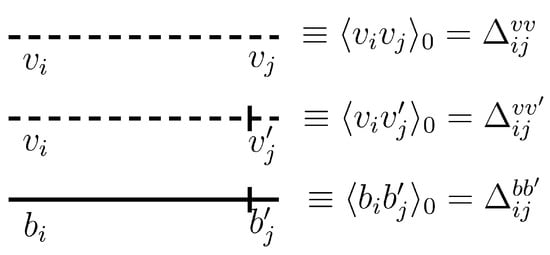
Figure 1.
Graphical representation of all propagators corresponding to the action (16).
The interaction part in (16) gives rise to three interaction vertices: , and , depicted in Figure 2, where
and stands for the momentum entering the vertex via the auxiliary field ( for and for and ).
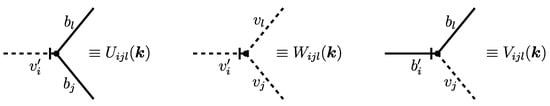
Figure 2.
Graphical representation of all interaction vertices of the model-related velocity nonlinearities of the action (16).
In actual calculations, it is often more suitable to work preferably with so-called connected Feynman diagrams, i.e., those diagrams that remain connected even if one of the internal lines is cut [29,40]. They can be obtained from the generating functional defined as
by taking the corresponding number of functional derivatives with respect to external sources J and then substituting . For dynamic models, the symbol , where is the complete set of fields of the model and are their MSR-conjugated analogs.
For translationally invariant theories, additional simplification consists of introducing functional for one-particle irreducible (1PI or vertex) functions [29,40]. This is an even more restricted class than that of connected Feynman diagrams since they are obtained from all possible diagrams by throwing away those Feynman graphs which fall into disjoint parts when one internal line is cut. Then, for each external leg in a diagram, we divide out one factor of the propagator. In this way, we arrive at so-called proper vertices [40,64] that are convenient for the RG analysis. It can be shown that [29] the corresponding functional for 1PI diagrams can be obtained by means of functional Legendre transform with respect to external sources
where x denotes the set of all discrete and continuous arguments of the field. Within the framework of the approach used, the set of independent variables for the functional is conveniently divided as follows: . Then, the 1PI functions are obtained by differentiation with respect to fields
Let us also note that for reasons of causality, all 1PI Green functions of the form vanish [29]. In the next section, we are primarily interested in the quantities of (for velocity fields and magnetic fields, respectively), as well as for the vertex U in Figure 2, since they are the only ones responsible for the renormalization of the model.
3. Renormalization and Results
To obtain relevant information about the macroscopic behavior of solutions to the stochastic problem obeying Equations (9) and (10), we adopt the field-theoretic RG method [29]. This approach utilizes powerful quantum field theory techniques such as Feynman diagrams and RG resummation, among others. The starting point of RG analysis involves determining canonical dimensions and identifying all permissible structures (conveniently represented through Feynman diagrams) that exhibit superficial ultraviolet divergences [40], as determined by their respective canonical dimensions. Typically, dynamical models like (16) exhibit two independent scaling dimensions [29,53], implying that each field quantity Q is assigned two independent canonical dimensions: the momentum dimension and the frequency dimension . These dimensions are individually determined based on standard normalization conditions and the requirement that each term in the action must be dimensionless (momentum and frequency separately) [29,40]. As in most models of critical dynamics, in the model under consideration, one can introduce the total canonical dimension for a given quantity Q, expressing invariance with respect to some “cumulative” transformation of coordinates and time. Since in linearized dynamic Equations (9) and (10), the operations and ∇ are included in the combination common to all fields, the total canonical dimension in our case is determined by the relation
By direct calculation from the action (16), the canonical dimensions of all relevant parameters are computed. In fact, the obtained values reproduce the result found in [27]. For the reader’s convenience, we also list it here in Table 1. From this table, we infer that Model (16) is logarithmic at and there is just one coupling constant .

Table 1.
Canonical dimension of the bare fields and parameters of the model (16).
A detailed analysis of all relevant UV-divergent parts and related technical details can be found in previous papers [27,28]. Here, it is only noted that in our case, in addition to the 1PI functions and of the general A-model considered in [28], an additional vertex is added. The counterterms to it have the structure of the bare vertex and define the renormalization constant . Furthermore, as a direct consequence of Galilean invariance (12) (the derivative enters (16) only in the form of ), the terms and do not renormalize [27]. However, it is important to understand that we have no renormalization of the vertex only for the trivial case and for . For the case , this statement relies on the antisymmetry of the corresponding vertex with [27], which obviously does not exist, e.g., for . Thus, further, we present expressions for all quantities in the form of expansions by the parameter A, not explicitly fixing its value but always keeping in mind the two cases and , where the latter corresponding to MHD is of primary interest to us in the context of RG analysis.
Thus, taking into account the comments made above, the model is multiplicatively renormalizable, and its action (16) can be written in the form
where only renormalized parameters and fields appear. The parameters of action are associated with the corresponding parameters of by multiplicative UV renormalization transformations of the following form:
where the whole set of the renormalization constants of the fields and parameters is determined from the relations
At this step, we have introduced the so-called renormalization mass parameter [29,40].
The renormalization constants , are calculated using the ultraviolet renormalization procedure, which can be vividly described as follows. To make sense of the diverging Feynman integrals, some intermediate regularization is introduced (in our case, it is the natural ultraviolet cutoff ). Simultaneously, the bare parameters of the model are replaced with their renormalized counterparts by introducing -dependent counterterms into the action. Renormalizability, then, means that with a special choice of the dependence of on (the requirement to cancel the UV-divergent parts of the diagrams), the limit exists, at least for all integrals necessary for calculating all observables. This limit is defined up to a finite number of constants that can be fixed by setting the values of observables and the normalization of fields. In statistical field theory, the so-called minimal subtraction scheme (MS) is considered the most convenient, where only the divergent parts of the diagrams are subtracted [29,40].
As noted in Section 2, from a technical perspective, the natural cutoff regularization is not very convenient for multiloop calculations, so usually, another step is taken: transitioning to the limit along with the introduction of a new type of regularization like dimensional, in which singularities are presented as poles by the regulator and the corresponding Green functions are understood as corresponding meromorphic functions. In our case, such a regularization parameter is , previously introduced in the correlator (13), which parameterizes the energy pumping into the system. In this setting, the renormalization constants of Model (24) are simply the principal parts of the Laurent series in the parameter , whose coefficients, being polynomials in g, can also parametrically depend on the space dimension d (however, in this work, we assume ), the gyrotropy parameter , the parameter A, and the renormalized magnetic Prandtl number u. Thus, a unified representation for these constants takes the form
For convenience, we assign specific notation to the sets of coefficients for each constant: for , for , and for . In what follows, to simplify the notation, we do not explicitly indicate the dependence on these parameters in the arguments of the corresponding renormalization constants.
The constants , and are determined from the condition of UV finiteness for the corresponding vertex functions, each obviously associated with its own set of diagrams. The last fact proves useful when verifying results with existing special cases. We are already familiar with the one-loop calculation results for specific cases [27], [44], and [65]. Our further goal is to complete the full two-loop calculation for all renormalization constants. In this regard, we present here details of the corresponding calculation for the renormalization constant .
Let us begin the description of the renormalization constants’ calculation process from the constant . Here, the previously noted issue regarding each renormalization constant corresponding to its own subclass of Feynman diagrams immediately becomes apparent. As can be directly inferred from the action functional (24), the constant corresponds to the pure Navier–Stokes equation (without the inclusion of the magnetic field) and can be calculated from Feynman diagrams constructed solely by propagators and vertices containing the fields and [27]. As a consequence, it cannot depend on parameters A and u, but it may depend on the gyrotropy parameter . Directly, the constant can be determined through the corresponding Dyson Equation [40] of the following form
where represents the renormalized self-energy operator defined as a sum containing all permissible 1PI Feynman diagrams. Hereinafter, all quantities where all variables are replaced by renormalized ones are marked with a subscript “R”.
The coefficient representing the one-loop contribution to was calculated for the first time in the work [41]. Subsequently, the corresponding two-loop contributions for both the nonhelical () and helical cases were detailed in [42] and [34], respectively. In addition, in ref. [42], it was shown that the coefficient is exactly related to the coefficient through the relation . The explicit expression for the coefficient is rather long and we shall not rewrite it here explicitly (see [34] for the details). Its value for the most physically important case , along with the exact value of the coefficient , is given in
Here, we introduce a typical geometric factor , where is the surface of the d-dimensional unit sphere, and is the Euler gamma function. At this point, it is important to note that the presence of a spiral contribution in the turbulent system not only does not destroy the stability of the Kolmogorov scaling regime determined by the coefficients indicated in (29) but also has no impact on its properties at all [34]. Additionally, it is worth mentioning that this parameter naturally arises when the magnetic field is included. From RG analysis of the three-dimensional MHD problem with a general correlator matrix, it is clear that in our case plays a role similar to the gauge parameter in QED [27].
The RG constant is calculated in the same vein as . Direct inspection of Feynman diagrams reveals that only those for which the vertex is not present contribute to . This omitting in action (24) is equivalent to moving to the passive admixture model [28,65]. The corresponding Dyson equation in the frequency–momentum representation for the renormalized 1PI Green function takes a similar (28) form
Note that from the last relation (26), it follows that the product of fields in is not renormalized: . The coefficient representing the one-loop contribution to , is given by
Corresponding two-loop expressions for coefficients can be found in [28,65] for the nonhelical term and the helical term, respectively. Since they are generally rather technical and not very illuminating, we shall not reproduce them here.
The renormalization constant is up to now known in the perturbation theory only for the MHD problem in the leading one-loop approximation [27]. For the two-loop calculation, the procedure follows similar steps to the previous cases. However, from a technical point of view, it poses a more challenging task. We determine RG constants from the three-point 1PI Green function . The needed perturbative relation can be formally expressed in the form
The subclass of Feynman diagrams that contribute to vertex can be defined simply as an absolute complement to the two subclasses already discussed, defining and . Using (32), the renormalization constant is determined from the UV finiteness condition for , which is more preferable to formulate in terms of a scalar quantity
Here, we take advantage of the fact that has the bare vertex index structure. The limit in Expression (33) does exist, provided the IR regularization of the graphs has been properly taken care of. In terms of quantity , Equation (32) can be reorganized as follows:
where is the loopless (tree) approximation, denotes scalarized contributions from the one-loop diagrams, represents the scalarized total contribution from the two-loop diagrams, etc. In diagram language, this equation then takes the form
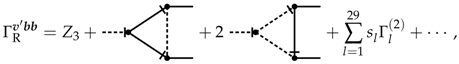 where the diagrams depicted represent the one-loop contribution , diagrams are shown in Figure 3, and are their symmetry factors. The symmetry factors , , and other two-loop diagrams have symmetry factor equal to 2. Then, the UV finiteness condition for may be cast in the form
where only the pole contributions to are meant.
where the diagrams depicted represent the one-loop contribution , diagrams are shown in Figure 3, and are their symmetry factors. The symmetry factors , , and other two-loop diagrams have symmetry factor equal to 2. Then, the UV finiteness condition for may be cast in the form
where only the pole contributions to are meant.
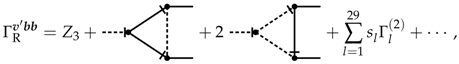
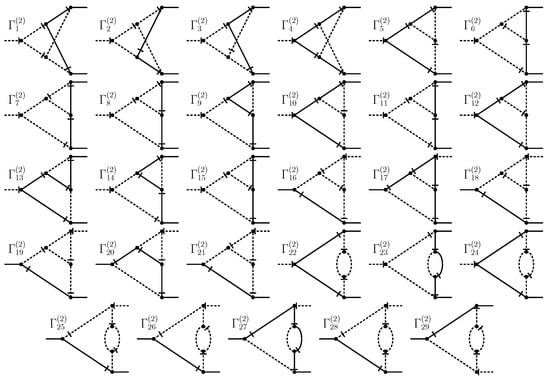
Figure 3.
Two-loop diagrams contributing to the renormalization constant through the operator defined in Equation (34).
By direct calculation, it is not difficult to obtain the pole contribution to in the following form:
from which we immediately obtain a one-loop contribution to in the form
Formula (38) generalizes the expression obtained in [27] to the case . From (37), one can see that the contribution singular in of the correction vanishes at . This is a general property due to the fact that the model with a passively advected vector field (case ) does not contain divergence in [33]. From this observation, it directly follows that for the case .
Calculating of the two-loop correction turns out to be a significantly more complex task. Compared to and , not only does the number of Feynman diagrams increase (twenty-nine versus eight diagrams) but also their structure is considerably more complicated. The diagrams are computed in the frequency–momentum representation, and, after analytic integration over frequencies, the remaining expressions can only be examined numerically in the same manner as in [43]. The integrals remaining after frequency integration contain parameters such as the reciprocal Prandtl number u, whose value in [28] was determined to the two-loop precision. Note that within the framework of the -expansion, for the second-order calculation, it suffices to compute the two-loop Feynman integrals at the value of determined at the one-loop fixed point. This is so because the integrals themselves are already proportional to , which is of order . Finally, the general pole part of can be formally expressed through the following structures:
where the coefficients C, , and are functions of d, u, and A and are to be further computed. The nonzero value of the coefficient C arises specifically in cases where the diagram contains one of the two divergent subgraphs represented in Equation (35). Its independence from the chirality parameter stems from the model’s multiplicative renormalizability and the fact that the one-loop contribution does not depend on . The values of the coefficients C, , and for each specific diagram in Figure 3 can be found in Appendix A. In addition, to explain intermediate steps in the aforementioned described calculational procedure, we briefly elaborate in Appendix B on the used methodology in the analysis of a particular two-loop Feynman diagram.
From Expression (39), it follows in a straightforward manner that the two-loop contributions and to constant have the form
The coefficient C at the second-order pole is not of particular interest to us because it does not contribute to the RG analysis. Its value is only needed to verify calculations through cancellation with corresponding one-loop contributions. The corresponding expressions are given in Appendix A. Therefore, we limit ourselves to presenting the value of the coefficient for the most physically interesting case of three-dimensional MHD
The RG analysis for all 1PI Green functions is based on the fundamental differential equation [29,40] expressing the independence of the renormalized functionals from the finite renormalization transformation parameter at the fixed model’s bare parameters . The equation can be presented in the following form:
Here, we have slightly abused the notation and returned to the terminology of Section 2 for 1PI functions. The gamma functions, namely, , , and are commonly defined through the following relations: , , where , i.e., the logarithmic derivative is taken at the constant bare parameters. Concurrently, the beta functions and expressing the change in the charges g and u under the renormalization group flow are defined as follows
The RG functions and are associated with the calculated two-loop constant . The direct calculation yields two relations,
where the former one is a consequence of the equation given in (26).
In MHD, as in the theory of homogeneous and isotropic turbulence, the nontrivial asymptotic large-scale behavior of Green functions is governed by anomalous dimensions (exponents) , which are determined by corresponding gamma functions taken at an IR stable fixed point of the corresponding RG equation (42). In its turn, coordinates of fixed points in the plane of renormalized couplings are determined from the requirement that all beta functions simultaneously vanish: and . The stability of the found fixed point is determined by the positive definiteness of the real part of the matrix , in the vicinity of .
In our model, there is one nontrivial stable fixed point – the so-called kinetic point [29]. With two-loop accuracy, its coordinates are determined by the following relations: and , where the corresponding coefficients of -expansions were calculated in general form in [28]. In the case of the three-dimensional MHD, they take the following form:
An important difference between MHD and ordinary hydrodynamic turbulence is the presence of a nontrivial anomalous dimension (exponent) of the magnetic field, calculated perturbatively. Let us recall that due to the absence of renormalization of the velocity field, the corresponding anomalous exponent of the velocity field is exactly equal to zero: . The two-loop anomalous exponent at the kinetic point has the form
which, along with the well-known exact (lacking corrections of order or higher) values of the anomalous dimensions and [29], completes the set of two-loop anomalous exponents in the model under consideration.
Along with the canonical dimensions given by (23), the large-scale behavior of Green functions (critical scaling in the language of RG) is also characterized by the corresponding critical dimensions
where and are the corresponding canonical dimensions listed in Table 1. Therefore, the critical dimensions in MHD are determined by the following relations:
Note that the absence of entails the fact that the second condition in (49) includes only exact . This precisely determines the Kolmogorov spectrum “” for the statistics of the velocity field correlations at the “physical” . In its turn, the presence of a nontrivial anomalous exponent of the magnetic field can have a significant influence on the scaling behavior of the statistical correlations of the magnetic field.
In what follows, we finally restrict ourselves to considering only the case of three-dimensional MHD. Thus, using Expression (47), one obtains the critical dimension of the magnetic field
For the physical setting where , the critical dimension manifests as . This dimension peaks at and and reaches a minimum of for . This observation underscores the significant influence of helicity on the scaling behavior within at least the regime governed by a kinetic fixed point.
4. Conclusions
In this study, we performed a two-loop calculation of the constant in the paradigmatic model of three-dimensional magnetohydrodynamic turbulence in a chiral medium. Conceptually, we followed the same calculation procedure previously applied to constants [65] and [28]. For the most interesting special case of stochastic MHD, corresponding to the value , RG analysis was performed, within which the dimension of the magnetic field was calculated. A strong influence of the effect of spatial parity violation on scaling behavior was discovered: the value of the critical dimension of the magnetic field in the absence of parity violation () differs by times from its value in the state with maximally violated mirror symmetry ().
It should be emphasized here that the main motivation for this study was a desire to more thoroughly investigate the statistical properties of magnetic fluctuations in magnetohydrodynamics, which are precisely determined by the anomalous dimension . At first glance, it may seem that even such a complex model as the one we employ here for this task is unsuitable, due to the absence of a magnetic field correlator in it. However, this is not the case. The reason is that even in the absence of a magnetic correlator in the Model (24), the normal state with in a chiral medium turns out to be unstable and stabilizes in a more “low-energy” state due to the spontaneous emergence of a uniform large-scale magnetic field [30]. Re-expansion (24) in the vicinity of this new ground state entails the appearance of the correlator , as well as and others. The corresponding scaling behavior in this case becomes nontrivial and will be described using the anomalous dimension obtained in this work. An article that will provide a detailed analysis of helical MHD with a spontaneously generated homogeneous magnetic field is reserved for future publication.
Author Contributions
Conceptualization, M.H. and T.L.; methodology, M.H. and T.L.; software, L.M., A.O. and Y.M.; validation, M.H., T.L., L.M., Y.M. and A.O.; investigation, M.H., T.L., L.M., Y.M. and A.O.; writing—original draft preparation, T.L., L.M. and A.O.; writing—review and editing, M.H., T.L. and A.O.; visualization, L.M.; supervision, M.H. and T.L.; project administration, M.H. and T.L.; funding acquisition, M.H. and T.L. All the authors contributed equally to all remaining parts of this work. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by VEGA grant №1/0535/21 of the Ministry of Education, Science, Research and Sport of the Slovak Republic and by VVGS grant 2023-2024 №2566 provided by the Faculty of Science at Pavol Jozef Šafárik University in Košice.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| 1PI | One-particle irreducible |
| RG | Renormalization group |
| IR | Infrared |
| MHD | Magnetohydrodynamic |
| MSR | Martin–Siggia–Rose (formalism) |
| MS | Minimal subtraction |
| NS | Navier–Stokes |
| UV | Ultraviolet |
Appendix A. Coefficients C, B(0), and B(ρ)
Let us now present the results on coefficients C, , and from Equation (39), which correspond to contributions of the graphs shown in Figure 3. All the graphs , were calculated using the technique presented in ref. [43]. In this appendix, we present numerical results for and , alongside analytical results for C, in the spatial dimension at , relevant to helical stochastic MHD. Additionally, we include parameter values for for illustrative purposes. It is noteworthy that for , all the contributions from the corresponding diagrams vanish. The numerical estimates for and are calculated at the one-loop kinetic point value of [29], ensuring two-loop precision. Each diagram’s numerical precision reaches six decimal places, with negligible errors not exceeding the tenth decimal place, hence not detailed here. All results obtained are collected in Table A1.

Table A1.
The results on coefficients , , and , from Equation (39), which correspond to contributions of graphs depicted in Figure 3 and are multiplied by the appropriate symmetry factors. The zeros in the column for at are explained by the vanishing of the corresponding tensor structure and in the column for values by the absence of a divergent subgraph in the diagram.
Table A1.
The results on coefficients , , and , from Equation (39), which correspond to contributions of graphs depicted in Figure 3 and are multiplied by the appropriate symmetry factors. The zeros in the column for at are explained by the vanishing of the corresponding tensor structure and in the column for values by the absence of a divergent subgraph in the diagram.
| 0 | ||||
| 0 | 0 | |||
| 0 | ||||
| 0 | ||||
| 0 | 0 | |||
| 0 | ||||
| 0 | ||||
| 0 | 0 | |||
| 0 | ||||
| 0 | ||||
| 0 | ||||
| Equation (A3) | ||||
| Equation (A4) | ||||
| 0 | ||||
| Equation (A5) |
We did not provide in Table A1 the values for the coefficients in the case , because their total sum, in fact, exactly equals zero. To clarify this point, let us consider the total contribution to the sum of coefficients from all Feynman diagrams. It has the form of the following integral
where and function is given by
Directly from (A2), it is clear that is symmetric with respect to the replacement , which ensures that the integral (A1) is zero. Thus, the renormalization constant does not depend on the for model at the level of two-loop approximation.
Furthermore, we present here the cumbersome expressions for the coefficients and :
The total value of the coefficient finally takes the form
There are certain cancelations in the given sum of . Let us consider a group of diagrams enumerated by indices 16, 18, and 21 in Figure 3. Each of them has a divergent subgraph , but in total sum, these divergences are canceled
Generally speaking, this fact is a corollary of the absence of divergences in the 1PI Green function . Another cancelation is observed for the diagrams containing a subgraph . In Figure 3, diagrams containing subgraph numbered 6, 7, 10, 12, 13, and 14, collectively, give zero contribution to C in this case:
Note that in magnetohydrodynamics (case ), such contributions do not arise at all, because all corresponding coefficients contain a factor . This is a general consequence of the fact that the vertex is not renormalized in MHD (see text after Equation (23)). It is worth mentioning that the given observation aligns with the analysis of the constant in the stochastic Navier–Stokes equation [42].
Let us write condition (36) at order for . With the use of the corresponding terms of the one-loop contribution (37), the summed two-loop contributions (39), and expression for the renormalization constant
we obtain
Taking into account relations (40), we see that the terms with in Equation (A9) are automatically canceled (as a consequence of renormalizability of the model), whereas for the coefficient of the second-order pole, we obtain
where one-loop coefficients , , and are given by (29), (31), and (38), respectively. The verification of the results given in this section consists of the coincidence of the expressions for from (A10) based on one-loop results and obtained using the first relation in (40) and the value of C in (A5) calculated directly from the two-loop diagrams.
Appendix B. Calculation of Feynman Diagram
In this section, we briefly discuss the two-loop calculation of Feynman diagrams , using one particular diagram as an example. The diagram with the distribution of momenta and vector indices is shown in Figure A1. We are interested in the asymptotic behavior of as . After standard integration over frequencies and scalarizing the diagram, according to condition (33), we obtain
where is a scalar function depending only on , and . It is defined through the relation
where the expression is obtained as a result of frequency integration and computing all tensor convolutions in the diagram. Finally, the explicit form of the function is given by
Note that for this particular diagram, the entire dependence on turned out to be pulled out from the function and collected before the integral sign.
The representations similar to (A11) are derived for all remaining diagrams, with specific functions . For detailed instructions on executing integrals of this form, refer to sources such as [42,43]. In our case, the methodology remains largely unchanged, involving first the isolation of poles followed by the computation of the integral’s residual part. Calculating contribution for the pole is straightforward and can be performed for arbitrary values of parameters. The numerical integration for the pole component was executed using the Wolfram Mathematica software [66], specifically for and , and employing the one-loop kinetic point value of . This process achieved high precision swiftly and concluded without issues. The outcomes for the segment of the diagram are documented in Table A1, detailing both helical (proportional to ) and nonhelical contributions.
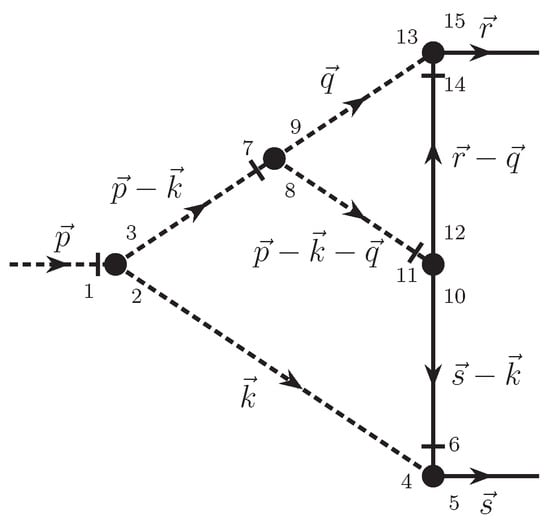
Figure A1.
The diagram with momenta and indices distribution. We use digit notation for vector indices instead of letters. For convenience, here denotes the momentum flowing into the diagrams through the field ,and , are momenta flowing out through fields .
References
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics, 2nd ed.; Pergamon: Oxford, UK, 1987. [Google Scholar]
- White, F.M. Fluid Mechanics, 7th ed.; McGraw-Hill: New York, NY, USA, 2011. [Google Scholar]
- Davidson, P.A. Turbulence: An Introduction for Scientists and Engineers; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Falkovich, G.; Gawȩdzki, K.; Vergassola, M. Particles and fields in fluid turbulence. Rev. Mod. Phys. 2001, 73, 913–975. [Google Scholar] [CrossRef]
- Frisch, U. Turbulence: The Legacy of A. N. Kolmogorov; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- McComb, W.D. The Physics of Fluid Turbulence; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Schlichting, H.; Gersten, K. Boundary-Layer Theory; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Monin, A.; Iaglom, A.; Lumley, J. Statistical Fluid Mechanics: Mechanics of Turbulence; Dover Publications: Mineola, NY, USA, 2007. [Google Scholar]
- Wyngaard, J. Turbulence in the Atmosphere; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Yoshizawa, A.; Itoh, S.I.; Itoh, K. Plasma and Fluid Turbulence: Theory and Modelling; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Horton, W. Turbulent Transport in Magnetized Plasmas, 2nd ed.; World Scientific: Singapore, 2017. [Google Scholar]
- Shore, S.N. Astrophysical Hydrodynamics: An Introduction; Wiley-VCH Verlag GmbH& KGaA: Weinheim, Germany, 2007. [Google Scholar]
- Zhou, Y.; Matthaeus, W.H.; Dmitruk, P. Colloquium: Magnetohydrodynamic turbulence and time scales in astrophysical and space plasmas. Rev. Mod. Phys. 2004, 76, 1015–1035. [Google Scholar] [CrossRef]
- Carlson, J.A.; Jaffe, A.; Wiles, A. The Millennium Prize Problems; AMS: Cambridge, MA, USA, 2006. [Google Scholar]
- Adzhemyan, L.T.; Antonov, N.V.; Vasiliev, A.N. Field Theoretic Renormalization Group in Fully Developed Turbulence; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Antonov, N. Anomalous scaling regimes of a passive scalar advected by the synthetic velocity field. Phys. Rev. E 1999, 60, 6691. [Google Scholar] [CrossRef]
- Biskamp, D. Magnetohydrodynamic Turbulence; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Chua, L.P.; Antonia, R.A. Turbulent Prandtl number in a circular jet. Int. J. Heat Mass Transf. 1990, 33, 331–339. [Google Scholar] [CrossRef]
- Coulson, J.M.; Richardson, J.F. Chemical Engineering; Elsevier: Amsterdam, The Netheralnds, 1999; Volume 1. [Google Scholar]
- Moffatt, H.K. Magnetic Field Generation in Electrically Conducting Fluids; Cambridge University Press: Cambridge, UK, 1978. [Google Scholar]
- Jones, C.A. Course 2 Dynamo theory. In Dynamos; Cardin, P., Cugliandolo, L., Eds.; Les Houches; Elsevier: Amsterdam, The Netheralnds, 2008; Volume 88, pp. 45–135. [Google Scholar] [CrossRef]
- Wald, R. Advanced Classical Electromagnetism; Princeton University Press: Princeton, NJ, USA, 2022. [Google Scholar]
- Kazantsev, A.P. Enhancement of a Magnetic Field by a Conducting Fluid. J. Exp. Theor. Phys. 1968, 26, 1031. [Google Scholar]
- Kraichnan, R.H. Anomalous scaling of a randomly advected passive scalar. Phys. Rev. Lett. 1994, 72, 1016–1019. [Google Scholar] [CrossRef] [PubMed]
- Antonov, N.V. Renormalization group, operator product expansion and anomalous scaling in models of turbulent advection. J. Phys. A 2006, 39, 7825. [Google Scholar] [CrossRef]
- Fournier, J.D.; Sulem, P.L.; Pouquet, A. Infrared properties of forced magnetohydrodynamic turbulence. J. Phys. A 1982, 15, 1393. [Google Scholar] [CrossRef]
- Adzhemyan, L.T.; Vasil’ev, A.N.; Gnatich, M. Quantum-field renormalization group in the theory of turbulence: Magnetohydrodynamics. Theor. Math. Phys. 1985, 64, 777–785. [Google Scholar] [CrossRef]
- Hnatič, M.; Zalom, P. Helical turbulent Prandtl number in the A model of passive vector advection. Phys. Rev. E 2016, 94, 053113. [Google Scholar] [CrossRef]
- Vasil’ev, A.N. The Field Theoretic Renormalization Group in Critical Behavior Theory and Stochastic Dynamics; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Adzhemyan, L.T.; Vasil’ev, A.N.; Gnatich, M. Turbulent dynamo as spontaneous symmetry breaking. Theor. Math. Phys. 1988, 72, 369–383. [Google Scholar] [CrossRef]
- Hnatič, M.; Honkonen, J.; Lučivjanský, T. Symmetry Breaking in Stochastic Dynamics and Turbulence. Symmetry 2019, 11, 1193. [Google Scholar] [CrossRef]
- Antonov, N.V.; Gulitskiy, N.M. Passive advection of a vector field: Anisotropy, finite correlation time, exact solution, and logarithmic corrections to ordinary scaling. Phys. Rev. E 2015, 92, 043018. [Google Scholar] [CrossRef] [PubMed]
- Jurčišinová, E.; Jurčišin, M.; Zalom, P. Turbulent Prandtl number of a passively advected vector field in helical environment: Two-loop renormalization group result. Phys. Rev. E 2014, 89, 043023. [Google Scholar] [CrossRef] [PubMed]
- Jurčišinová, E.; Jurčišin, M.; Remecký, R. Influence of helicity on the Kolmogorov regime in fully developed turbulence. Phys. Rev. E 2009, 79, 046319, Erratum in Phys. Rev. E 2012, 86, 049902. [Google Scholar] [CrossRef] [PubMed]
- Adzhemyan, L.T.; Antonov, N.V.; Mazzino, A.; Muratore-Ginanneschi, P.; Runov, A.V. Pressure and intermittency in passive vector turbulence. Europhys. Lett. 2001, 55, 801. [Google Scholar] [CrossRef]
- Hohenberg, P.C.; Halperin, B.I. Theory of dynamic critical phenomena. Rev. Mod. Phys. 1977, 49, 435–479. [Google Scholar] [CrossRef]
- Forster, D.; Nelson, D.R.; Stephen, M.J. Long-Time Tails and the Large-Eddy Behavior of a Randomly Stirred Fluid. Phys. Rev. Lett. 1976, 36, 867–870. [Google Scholar] [CrossRef]
- Forster, D.; Nelson, D.R.; Stephen, M.J. Large-distance and long-time properties of a randomly stirred fluid. Phys. Rev. A 1977, 16, 732–749. [Google Scholar] [CrossRef]
- Arponen, H. Anomalous scaling and anisotropy in models of passively advected vector fields. Phys. Rev. E 2009, 79, 056303. [Google Scholar] [CrossRef]
- Zinn-Justin, J. Quantum Field Theory and Critical Phenomena; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Adzhemyan, L.T.; Vasil’ev, A.N.; Pis’mak, Y.M. Renormalization-group approach in the theory of turbulence: The dimensions of composite operators. Theor. Math. Phys. 1983, 57, 268–281. [Google Scholar] [CrossRef]
- Adzhemyan, L.T.; Antonov, N.; Kompaniets, M.; Vasil’ev, A. Renormalization-group approach to the stochastic Navier–Stokes equation: Two-loop approximation. Int. J. Mod. Phys. B 2003, 17, 2137–2170. [Google Scholar] [CrossRef]
- Adzhemyan, L.T.; Honkonen, J.; Kim, T.; Sladkoff, L. Two-loop calculation of the turbulent Prandtl number. Phys. Rev. E 2005, 71, 056311. [Google Scholar] [CrossRef]
- Adzhemyan, L.T.; Vasil’ev, A.N.; Gnatich, M. Renormalization-group approach to the theory of turbulence. Inclusion of a passive admixture. Teor. Math. Phys. 1984, 58, 72–78. [Google Scholar] [CrossRef]
- Antonov, N.V.; Kostenko, M.M. Anomalous scaling of passive scalar fields advected by the Navier–Stokes velocity ensemble: Effects of strong compressibility and large-scale anisotropy. Phys. Rev. E 2014, 90, 063016. [Google Scholar] [CrossRef]
- Novikov, S. Transfer of a Passive Vector Admixture by a Two-Dimensional Turbulent Flow. Theor. Math. Phys. 2003, 136, 936–950. [Google Scholar] [CrossRef]
- Pagani, C. Functional renormalization group approach to the Kraichnan model. Phys. Rev. E 2015, 92, 033016. [Google Scholar] [CrossRef] [PubMed]
- Jurčišinová, E.; Jurčišin, M.; Remecký, R.; Zalom, P. Turbulent magnetic Prandtl number in helical kinematic magnetohydrodynamic turbulence: Two-loop renormalization group result. Phys. Rev. E 2013, 87, 043010. [Google Scholar] [CrossRef] [PubMed]
- Adzhemyan, L.T.; Antonov, N.V.; Gol’din, P.B.; Kim, T.L.; Kompaniets, M.V. Renormalization group in the infinite-dimensional turbulence: Third-order results. Phys. A Stat. 2008, 41, 495002. [Google Scholar] [CrossRef]
- Adzhemyan, L.; Evdokimov, D.; Hnatič, M.; Ivanova, E.; Kompaniets, M.; Kudlis, A.; Zakharov, D. Model A of critical dynamics: 5-loop ε expansion study. Phys. Stat. Mech. Its Appl. 2022, 600, 127530. [Google Scholar] [CrossRef]
- Adzhemyan, L.T.; Hnatič, M.; Ivanova, E.V.; Kompaniets, M.V.; Lučivjanský, T.; Mižišin, L. Field-theoretic analysis of directed percolation: Three-loop approximation. Phys. Rev. E 2023, 107, 064138. [Google Scholar] [CrossRef] [PubMed]
- Täuber, U.C.; Howard, M.; Vollmayr-Lee, B.P. Applications of field-theoretic renormalization group methods to reaction–diffusion problems. J. Phys. A Math. Gen. 2005, 38, R79. [Google Scholar] [CrossRef]
- Täuber, U.C. Critical Dynamics: A Field Theory Approach to Equilibrium and Non-Equilibrium Scaling Behavior; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Adzhemyan, L.T.; Ivanova, E.V.; Kompaniets, M.V.; Vorobyeva, S.Y. Diagram reduction in problem of critical dynamics of ferromagnets: 4-loop approximation. J. Phys. A Math. Theor. 2018, 51, 155003. [Google Scholar] [CrossRef]
- Binoth, T.; Heinrich, G. An automatized algorithm to compute infrared divergent multi-loop integrals. Nucl. Phys. B 2000, 585, 741–759. [Google Scholar] [CrossRef]
- Hahn, T. Cuba—A library for multidimensional numerical integration. Comput. Phys. Commun. 2005, 168, 78–95. [Google Scholar] [CrossRef]
- Lemarie-Rieusset, P. The Navier–Stokes Problem in the 21st Century, 2nd ed.; Chapman and Hall/CRC: Amsterdam, The Netheralnds, 2023. [Google Scholar]
- Batchelor, G. An Introduction to Fluid Dynamics; Cambridge Mathematical Library, Cambridge University Press: Cambridge, UK, 1967. [Google Scholar]
- Falkovich, G. Fluid Mechanics: A Short Course for Physicists; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Chen, S.; Doolen, G.D. Lattice Boltzmann Method for Fluid Flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Krüger, T.; Kusumaatmaja, H.; Kuzmin, A.; Shardt, O.; Silva, G.; Viggen, E. The Lattice Boltzmann Method: Principles and Practice; Graduate Texts in Physics; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Antonov, N.V.; Lanotte, A.; Mazzino, A. Persistence of small-scale anisotropies and anomalous scaling in a model of magnetohydrodynamics turbulence. Phys. Rev. E 2000, 61, 6586–6605. [Google Scholar] [CrossRef]
- Martin, P.C.; Siggia, E.D.; Rose, H.A. Statistical Dynamics of Classical Systems. Phys. Rev. A 1973, 8, 423–437. [Google Scholar] [CrossRef]
- Vasil’ev, A.N. Functional Methods in Quantum Field Theory and Statistical Physics; Gordon and Breach: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Jurčišinová, E.; Jurčišin, M.; Remecký, R. Turbulent Prandtl number in the A model of passive vector admixture. Phys. Rev. E 2016, 93, 033106. [Google Scholar] [CrossRef]
- Wolfram Research, Inc. Wolfram Programming Lab; Version 12.2; Wolfram Research, Inc.: Champaign, IL, USA, 2021. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).