An Investigation of the Loop Oscillations after a Solar Flare
Abstract
1. Introduction
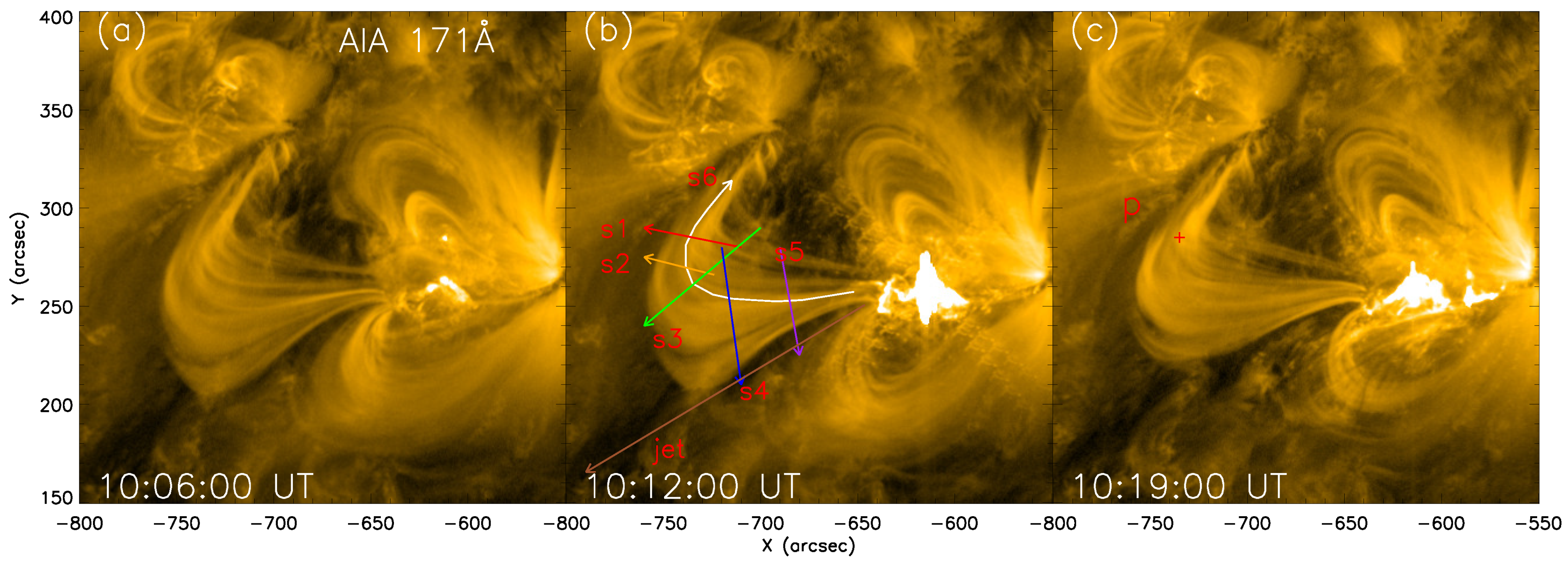
2. Observations and Measurements
3. Data Analysis and Results
3.1. Position Oscillations in Coronal Loops
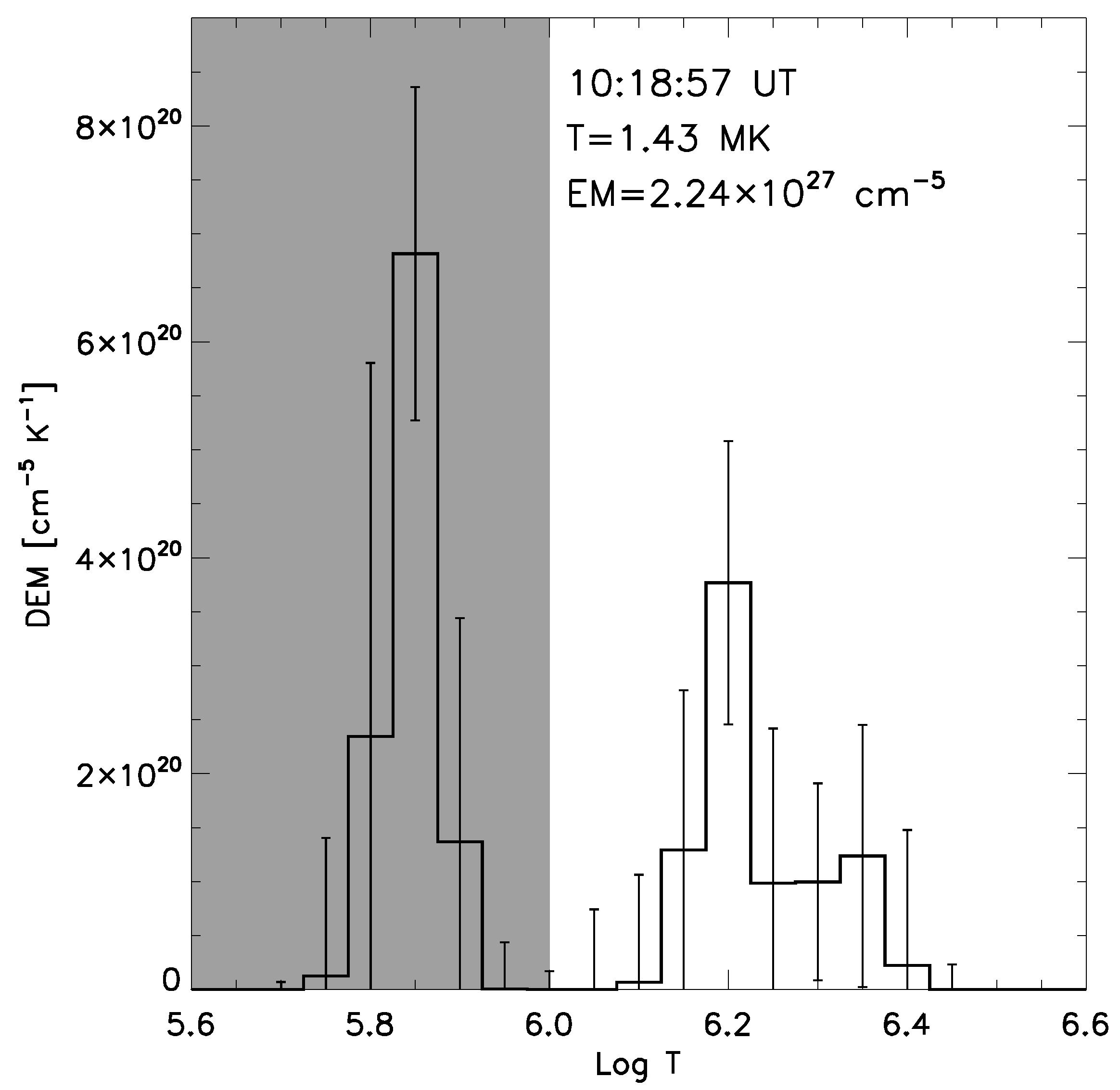
3.2. DEM Analysis
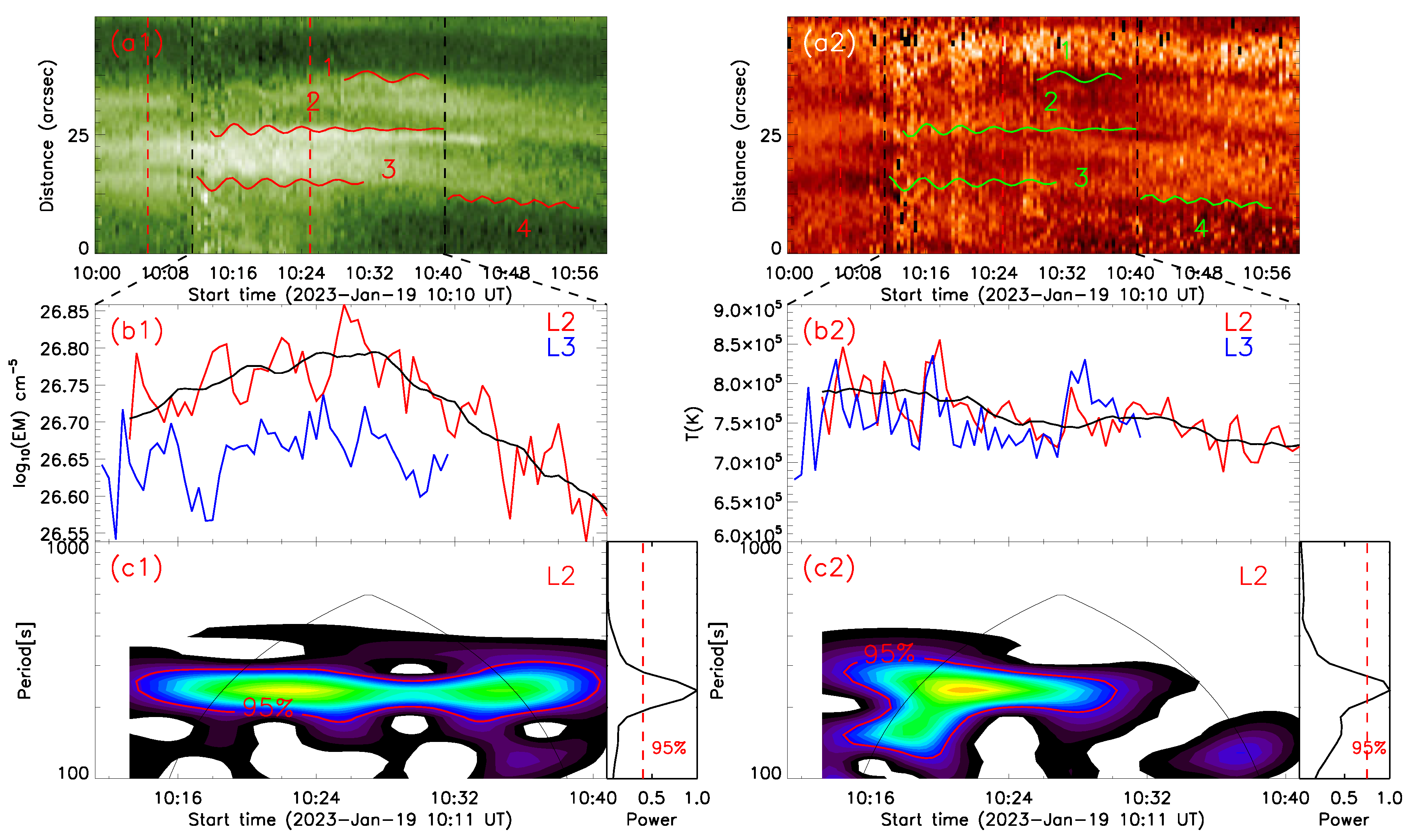
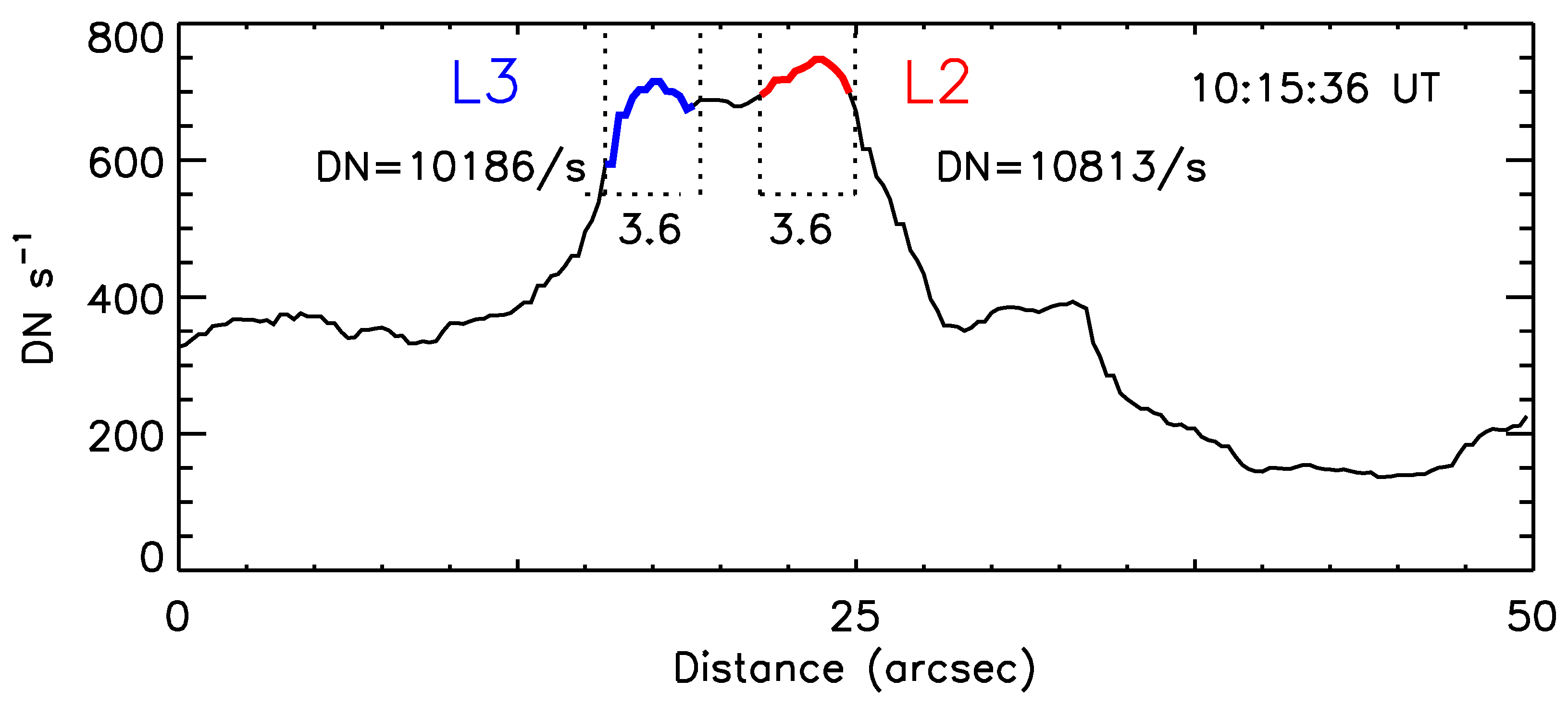
3.3. Brightness Oscillations
4. Discussions and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Reale, F. Coronal loops: Observations and modeling of confined plasma. Living Rev. Sol. Phys. 2014, 11, 4. [Google Scholar] [CrossRef]
- Mac Cormack, C.; Fuentes, M.L.; Mandrini, C.; Lloveras, D.; Poisson, M.; Vásquez, A. Scaling Laws of Quiet-Sun Coronal Loops. arXiv 2022, arXiv:2206.09921. [Google Scholar] [CrossRef]
- Ji, H.; Cao, W.; Goode, P.R. Observation of ultrafine channels of solar corona heating. Astrophys. J. Lett. 2012, 750, L25. [Google Scholar] [CrossRef]
- Aschwanden, M.J.; Boerner, P. Solar corona loop studies with the atmospheric imaging assembly. I. Cross-sectional temperature structure. Astrophys. J. 2011, 732, 81. [Google Scholar] [CrossRef]
- Peter, H.; Bingert, S.; Klimchuk, J.; de Forest, C.; Cirtain, J.; Golub, L.; Winebarger, A.; Kobayashi, K.; Korreck, K. Structure of solar coronal loops: From miniature to large-scale. Astron. Astrophys. 2013, 556, A104. [Google Scholar] [CrossRef]
- Gupta, G.R.; Del Zanna, G.; Mason, H. Exploring the damping of Alfvén waves along a long off-limb coronal loop, up to 1.4 R⊙. Astron. Astrophys. 2019, 627, A62. [Google Scholar] [CrossRef]
- Nakariakov, V.M.; Kolotkov, D.Y. Magnetohydrodynamic waves in the solar corona. Annu. Rev. Astron. Astrophys. 2020, 58, 441–481. [Google Scholar] [CrossRef]
- Nakariakov, V.; Ofman, L.; Deluca, E.; Roberts, B.; Davila, J. TRACE observation of damped coronal loop oscillations: Implications for coronal heating. Science 1999, 285, 862–864. [Google Scholar] [CrossRef]
- Aschwanden, M.J.; De Pontieu, B.; Schrijver, C.J.; Title, A.M. Transverse oscillations in coronal loops observed with TRACE–II. Measurements of geometric and physical parameters. Sol. Phys. 2002, 206, 99–132. [Google Scholar] [CrossRef]
- Goddard, C.; Nisticò, G.; Nakariakov, V.; Zimovets, I. A statistical study of decaying kink oscillations detected using SDO/AIA. Astron. Astrophys. 2016, 585, A137. [Google Scholar] [CrossRef]
- Anfinogentov, S.; Nakariakov, V.; Nisticò, G. Decayless low-amplitude kink oscillations: A common phenomenon in the solar corona? Astron. Astrophys. 2015, 583, A136. [Google Scholar] [CrossRef]
- Karampelas, K.; Van Doorsselaere, T. Transverse loop oscillations via vortex shedding: A self-oscillating process. Astrophys. J. Lett. 2021, 908, L7. [Google Scholar] [CrossRef]
- Mandal, S.; Chitta, L.P.; Antolin, P.; Peter, H.; Solanki, S.K.; Auchère, F.; Berghmans, D.; Zhukov, A.N.; Teriaca, L.; Cuadrado, R.A.; et al. What drives decayless kink oscillations in active-region coronal loops on the Sun? Astron. Astrophys. 2022, 666, L2. [Google Scholar] [CrossRef]
- Zimovets, I.; Nakariakov, V. Excitation of kink oscillations of coronal loops: Statistical study. Astron. Astrophys. 2015, 577, A4. [Google Scholar] [CrossRef]
- Shen, Y.; Liu, Y.; Tian, Z.; Qu, Z. On a small-scale EUV wave: The driving mechanism and the associated oscillating filament. Astrophys. J. 2017, 851, 101. [Google Scholar] [CrossRef]
- Shen, Y.; Tang, Z.; Li, H.; Liu, Y. Coronal EUV, QFP, and kink waves simultaneously launched during the course of jet–loop interaction. Mon. Not. R. Astron. Soc. Lett. 2018, 480, L63–L67. [Google Scholar] [CrossRef]
- Reeves, K.K.; Polito, V.; Chen, B.; Galan, G.; Yu, S.; Liu, W.; Li, G. Hot plasma flows and oscillations in the loop-top region during the 2017 September 10 X8. 2 solar flare. Astrophys. J. 2020, 905, 165. [Google Scholar] [CrossRef]
- Zhang, Q. Simultaneous transverse oscillations of a coronal loop and a filament excited by a circular-ribbon flare. Astron. Astrophys. 2020, 642, A159. [Google Scholar] [CrossRef]
- Nechaeva, A.; Zimovets, I.V.; Nakariakov, V.M.; Goddard, C. Catalog of decaying kink oscillations of coronal loops in the 24th solar cycle. Astrophys. J. Suppl. Ser. 2019, 241, 31. [Google Scholar] [CrossRef]
- Hui, T.; McIntosh, S.W.; Wang, T.; Ofman, L.; De Pontieu, B.; Innes, D.E.; Peter, H. Persistent doppler shift oscillations observed with Hinode/EIS in the solar corona: Spectroscopic signatures of Alfvenic waves and recurring upflows. Astrophys. J. 2012, 759, 144. [Google Scholar]
- Nakariakov, V.M.; Anfinogentov, S.; Nisticò, G.; Lee, D.H. Undamped transverse oscillations of coronal loops as a self-oscillatory process. Astron. Astrophys. 2016, 591, L5. [Google Scholar] [CrossRef]
- Guo, X.; Liang, B.; Feng, S.; Dai, W.; Yang, Y. Simultaneous Detection of Flare-related Decaying and Decayless Kink Oscillations Using Jerk-aware Motion Magnification. Res. Astron. Astrophys. 2022, 22, 115012. [Google Scholar] [CrossRef]
- Pascoe, D.J.; Goddard, C.R.; Nakariakov, V.M. Spatially resolved observation of the fundamental and second harmonic standing kink modes using SDO/AIA. Astron. Astrophys. 2016, 593, A53. [Google Scholar] [CrossRef]
- Mandal, S.; Tian, H.; Peter, H. Flare-induced decay-less transverse oscillations in solar coronal loops. Astron. Astrophys. 2021, 652, L3. [Google Scholar] [CrossRef]
- Zhong, S.; Nakariakov, V.M.; Kolotkov, D.Y.; Verbeeck, C.; Berghmans, D. Two-spacecraft detection of short-period decayless kink oscillations of solar coronal loops. Mon. Not. R. Astron. Soc. 2022, 516, 5989–5996. [Google Scholar] [CrossRef]
- Hindman, B.W.; Jain, R. An interpretation of flare-induced and decayless coronal-loop oscillations as interference patterns. Astrophys. J. 2014, 784, 103. [Google Scholar] [CrossRef][Green Version]
- Antolin, P.; De Moortel, I.; Van Doorsselaere, T.; Yokoyama, T. Modeling observed decay-less oscillations as resonantly enhanced Kelvin–Helmholtz vortices from transverse MHD waves and their seismological application. Astrophys. J. Lett. 2016, 830, L22. [Google Scholar] [CrossRef]
- Karampelas, K.; Van Doorsselaere, T.; Antolin, P. Heating by transverse waves in simulated coronal loops. Astron. Astrophys. 2017, 604, A130. [Google Scholar] [CrossRef]
- Karampelas, K.; Van Doorsselaere, T. Generating transverse loop oscillations through a steady-flow driver. Astrophys. J. Lett. 2020, 897, L35. [Google Scholar] [CrossRef]
- Afanasyev, A.; Van Doorsselaere, T.; Nakariakov, V. Excitation of decay-less transverse oscillations of coronal loops by random motions. Astron. Astrophys. 2020, 633, L8. [Google Scholar] [CrossRef]
- Ruderman, M.; Petrukhin, N. Excitation of decayless kink oscillations by random motion. Mon. Not. R. Astron. Soc. 2021, 501, 3017–3029. [Google Scholar] [CrossRef]
- Goossens, M.; Van Doorsselaere, T.; Soler, R.; Verth, G. Energy content and propagation in transverse solar atmospheric waves. Astrophys. J. 2013, 768, 191, Erratum in Astrophys. J. 2013, 771, 74. [Google Scholar] [CrossRef]
- Zaitsev, V.V.; Stepanov, A.V. Coronal magnetic loops. Physics-Uspekhi 2008, 51, 1123. [Google Scholar] [CrossRef]
- Stepanov, A.V.; Zaitsev, V.V.; Nakariakov, V.M. Coronal seismology. Physics-Uspekhi 2012, 55, 929. [Google Scholar] [CrossRef]
- Nakariakov, V.M.; Ofman, L. Determination of the coronal magnetic field by coronal loop oscillations. Astron. Astrophys. 2001, 372, L53–L56. [Google Scholar] [CrossRef]
- Andries, J.; Arregui, I.; Goossens, M. Determination of the coronal density stratification from the observation of harmonic coronal loop oscillations. Astrophys. J. 2005, 624, L57. [Google Scholar] [CrossRef]
- Van Doorsselaere, T.; Brady, C.S.; Verwichte, E.; Nakariakov, V.M. Seismological demonstration of perpendicular density structuring in the solar corona. Astron. Astrophys. 2008, 491, L9–L12. [Google Scholar] [CrossRef]
- Ruderman, M.S.; Verth, G.; Erdélyi, R. Transverse oscillations of longitudinally stratified coronal loops with variable cross section. Astrophys. J. 2008, 686, 694. [Google Scholar] [CrossRef]
- Verth, G.; Erdélyi, R. Effect of longitudinal magnetic and density inhomogeneity on transversal coronal loop oscillations. Astron. Astrophys. 2008, 486, 1015–1022. [Google Scholar] [CrossRef]
- Antolin, P.; Yokoyama, T.; Van Doorsselaere, T. Fine strand-like structure in the solar corona from magnetohydrodynamic transverse oscillations. Astrophys. J. Lett. 2014, 787, L22. [Google Scholar] [CrossRef]
- Pesnell, W.D.; Thompson, B.J.; Chamberlin, P. The Solar Dynamics Observatory (SDO); Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Boerner, P.; Edwards, C.; Lemen, J.; Rausch, A.; Schrijver, C.; Shine, R.; Shing, L.; Stern, R.; Tarbell, T.; Title, A.; et al. Initial calibration of the atmospheric imaging assembly (AIA) on the solar dynamics observatory (SDO). Sol. Phys. 2012, 275, 41–66. [Google Scholar] [CrossRef]
- Lemen, J.R.; Title, A.M.; Akin, D.J.; Boerner, P.F.; Chou, C.; Drake, J.F.; Duncan, D.W.; Edwards, C.G.; Friedlaender, F.M.; Heyman, G.F.; et al. The atmospheric imaging assembly (AIA) on the solar dynamics observatory (SDO). Sol. Phys. 2012, 275, 17–40. [Google Scholar] [CrossRef]
- Wang, T.; Ofman, L.; Davila, J.M.; Su, Y. Growing transverse oscillations of a multistranded loop observed by SDO/AIA. Astrophys. J. Lett. 2012, 751, L27. [Google Scholar] [CrossRef]
- Gao, Y.; Tian, H.; Van Doorsselaere, T.; Chen, Y. Decayless oscillations in solar coronal bright points. Astrophys. J. 2022, 930, 55. [Google Scholar] [CrossRef]
- Su, W.; Guo, Y.; Erdélyi, R.; Ning, Z.; Ding, M.; Cheng, X.; Tan, B. Period increase and amplitude distribution of kink oscillation of coronal loop. Sci. Rep. 2018, 8, 4471. [Google Scholar] [CrossRef]
- Zhong, Y.; Kolotkov, D.Y.; Zhong, S.; Nakariakov, V.M. Comparison of damping models for kink oscillations of coronal loops. Mon. Not. R. Astron. Soc. 2023, 525, 5033–5040. [Google Scholar] [CrossRef]
- Nakariakov, V.; Anfinogentov, S.; Antolin, P.; Jain, R.; Kolotkov, D.; Kupriyanova, E.; Li, D.; Magyar, N.; Nistico, G.; Pascoe, D.; et al. Kink oscillations of coronal loops. Space Sci. Rev. 2021, 217, 73. [Google Scholar] [CrossRef]
- Cheung, M.C.; Boerner, P.; Schrijver, C.; Testa, P.; Chen, F.; Peter, H.; Malanushenko, A. Thermal diagnostics with the atmospheric imaging assembly on board the solar dynamics observatory: A validated method for differential emission measure inversions. Astrophys. J. 2015, 807, 143. [Google Scholar] [CrossRef]
- Su, Y.; Veronig, A.M.; Hannah, I.G.; Cheung, M.C.; Dennis, B.R.; Holman, G.D.; Gan, W.; Li, Y. Determination of differential emission measure from solar extreme ultraviolet images. Astrophys. J. Lett. 2018, 856, L17. [Google Scholar] [CrossRef]
- Van Doorsselaere, T.; Gijsen, S.; Andries, J.; Verth, G. Energy propagation by transverse waves in multiple flux tube systems using filling factors. Astrophys. J. 2014, 795, 18. [Google Scholar] [CrossRef]
- Yuan, D.; Van Doorsselaere, T. Forward modeling of standing kink modes in coronal loops. I. Synthetic views. Astrophys. J. Suppl. Ser. 2016, 223, 23. [Google Scholar] [CrossRef]
- Long, D.M.; Valori, G.; Pérez-Suárez, D.; Morton, R.J.; Vásquez, A.M. Measuring the magnetic field of a trans-equatorial loop system using coronal seismology. Astron. Astrophys. 2017, 603, A101. [Google Scholar] [CrossRef]
- Yang, Z.; Tian, H.; Tomczyk, S.; Morton, R.; Bai, X.; Samanta, T.; Chen, Y. Mapping the magnetic field in the solar corona through magnetoseismology. Sci. China Technol. Sci. 2020, 63, 2357–2368. [Google Scholar] [CrossRef]
- Li, D.; Bai, X.; Tian, H.; Su, J.; Hou, Z.; Deng, Y.; Ji, K.; Ning, Z. Traveling kink oscillations of coronal loops launched by a solar flare. Astron. Astrophys. 2023, 675, A169. [Google Scholar] [CrossRef]
- Li, D.; Long, D.M. A Statistical Study of Short-period Decayless Oscillations of Coronal Loops in an Active Region. Astron. Astrophys. 2023, 944, 8. [Google Scholar] [CrossRef]
- Verwichte, E.; Aschwanden, M.J.; Van Doorsselaere, T.; Foullon, C.; Nakariakov, V.M. Seismology of a Large Solar Coronal Loop from EUVI/STEREO Observations of its Transverse Oscillation. Astron. Astrophys. 2009, 698, 397–404. [Google Scholar] [CrossRef]
- White, R.S.; Verwichte, E. Transverse coronal loop oscillations seen in unprecedented detail by AIA/SDO. Astron. Astrophys. 2012, 537, A49. [Google Scholar] [CrossRef]
- Cooper, F.C.; Nakariakov, V.M.; Tsiklauri, D. Line-of-sight effects on observability of kink and sausage modes in coronal structures with imaging telescopes. Astron. Astrophys. 2003, 397, 765–770. [Google Scholar] [CrossRef]

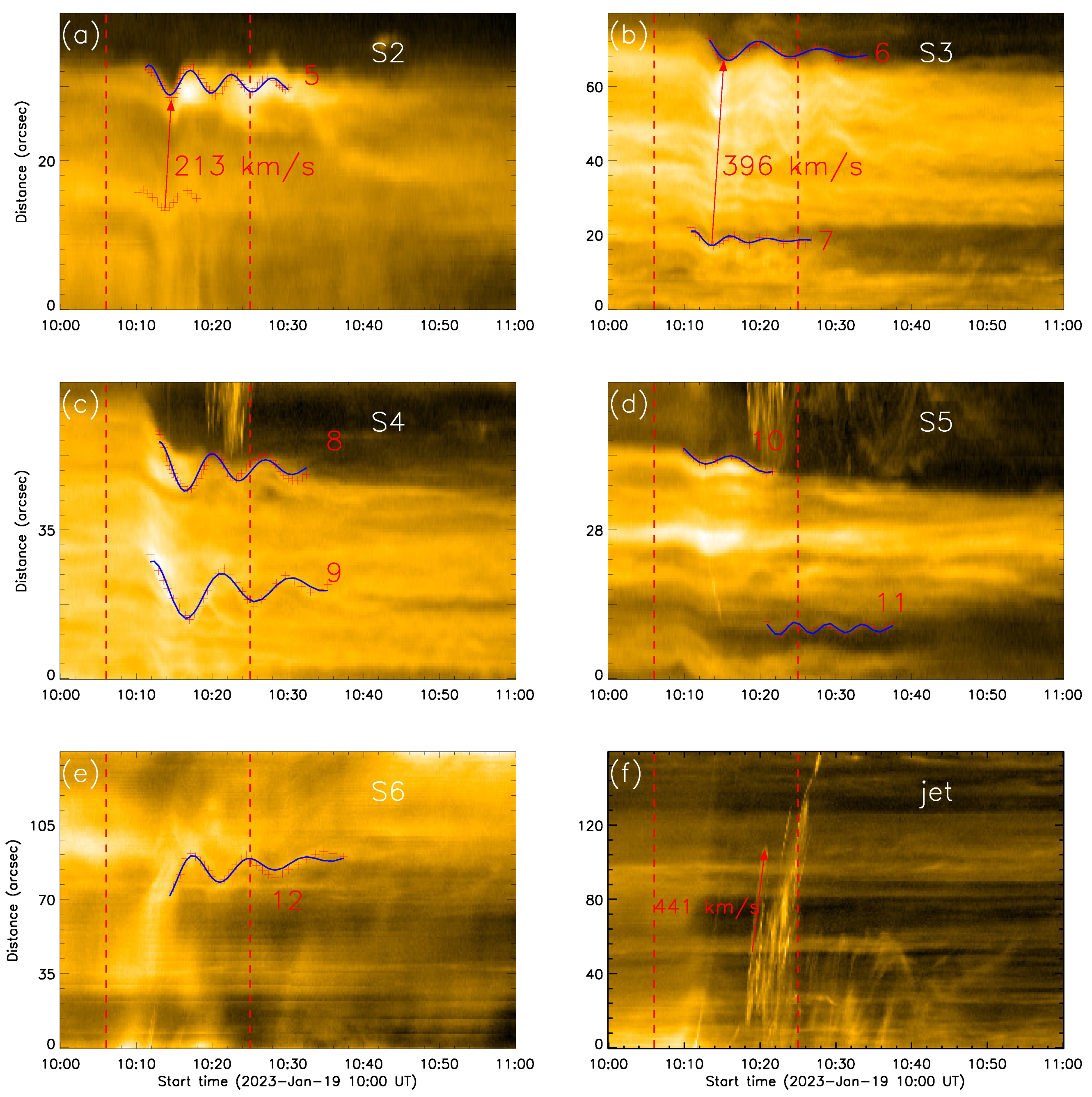
| Slit | Loops | P (min) | (Mm) | (min) | (km/s) | (min) | Duration (min) |
|---|---|---|---|---|---|---|---|
| S1 | 1 | 5.79 | 0.84 | 1027.70 | 15.17 | 1.62 | 9.91 |
| 2 | 3.93 | 1.30 | 11.98 | 34.65 | 1.95 | 27.33 | |
| 3 | 4.18 | 1.33 | 15.61 | 33.30 | 0.87 | 19.55 | |
| 4 | 3.08 | 0.58 | 551.09 | 19.65 | 1.13 | 14.49 | |
| S2 | 5 | 5.43 | 1.56 | 19.37 | 30.16 | 1.45 | 18.82 |
| S3 | 6 | 8.03 | 3.20 | 10.55 | 41.70 | 1.79 | 20.82 |
| 7 | 4.91 | 1.94 | 6.31 | 41.50 | 1.04 | 15.89 | |
| S4 | 8 | 7.04 | 5.34 | 11.85 | 79.44 | 1.56 | 19.42 |
| 9 | 9.10 | 6.65 | 13.62 | 76.49 | 2.26 | 23.47 | |
| S5 | 10 | 7.91 | 1.21 | 20.19 | 16.08 | 1.76 | 11.77 |
| 11 | 4.43 | 1.06 | 21.96 | 25.05 | 0.74 | 16.62 | |
| S6 | 12 | 7.41 | 8.79 | 10.50 | 124.29 | 1.47 | 22.94 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Ning, Z.; Li, D.; Shi, F.; Song, Y.; Yang, Y. An Investigation of the Loop Oscillations after a Solar Flare. Universe 2024, 10, 201. https://doi.org/10.3390/universe10050201
Xu J, Ning Z, Li D, Shi F, Song Y, Yang Y. An Investigation of the Loop Oscillations after a Solar Flare. Universe. 2024; 10(5):201. https://doi.org/10.3390/universe10050201
Chicago/Turabian StyleXu, Jun, Zongjun Ning, Dong Li, Fanpeng Shi, Yuxiang Song, and Yuzhi Yang. 2024. "An Investigation of the Loop Oscillations after a Solar Flare" Universe 10, no. 5: 201. https://doi.org/10.3390/universe10050201
APA StyleXu, J., Ning, Z., Li, D., Shi, F., Song, Y., & Yang, Y. (2024). An Investigation of the Loop Oscillations after a Solar Flare. Universe, 10(5), 201. https://doi.org/10.3390/universe10050201







