Abstract
Recent measurements on heavy-flavour production as a function of charged-particle multiplicity at the LHC are discussed. Focus is given to quarkonium results in small (pp or pPb) collision systems. The measurements of relative yields, i.e., the ratio of the particle yields in given multiplicity intervals to the multiplicity integrated yield are presented and compared to model calculations from Monte Carlo event generators as well as to models considering effects at play in the initial and/or final state of the collision. The absolute inclusive J/ yield as a function of the absolute charged-particle multiplicity is evaluated; a smooth behaviour of the absolute yield is observed across collision systems, from pp to pPb and PbPb collisions. Analogous measurements of the excited-to-ground state quarkonium ratios as a function of charged-particle multiplicity are also reviewed. Finally, the study of exotic particle production as a function of charged-particle multiplicity is introduced as a complementary tool to investigate the nature of the hadron.
1. Introduction
Heavy flavours are key observables of hadronic collisions. Their large mass allows evaluating their production cross-section with perturbative QCD calculations down to low momenta [1]. Their production cross-section is sensitive to the gluon and heavy-quark content of the colliding hadrons and thus to the parton distributions of the incoming proton (PDF) or nucleus (nPDF) [2,3]. The eventual binding of heavy quarks into a quarkonium pair () involves long distances, i.e., non-perturbative calculations, and is assumed to factorise with the other terms in most models. Quarkonium production in collisions involving heavy nuclei (pA collisions) might also be affected by interactions with the final-state comoving particles [4] or by coherent gluon radiation of the heavy quark pair while traversing the nucleus [5], both effects causing an effective reduction in quarkonium yields. It is crucial to control these phenomena to properly interpret the measurements of quarkonium production in heavy-ion collisions (AA collisions), where a high temperature and energy density partonic medium, the quark-gluon plasma (QGP), is expected to be formed. The short production time of heavy flavours (shorter than the QGP formation time) makes them excellent probes of the QGP as they probe the whole evolution of the system. At LHC energies, the dominant effects on the production of quarkonia in the QGP are expected to be the suppression caused by the medium colour screening [6] and the regeneration of bound states [7], which do partly compensate. Contemporary theoretical studies of quarkonium behaviour under extreme conditions extend towards a real-time dynamic picture, describing quarkonium production in thermal and out-of-equilibrium scenarios [8].
The measurement of particle production yields and their evolution as a function of the impact parameter of collision (or collision centrality), as well as their evolution with kinematic variables such as the transverse momentum () or (pseudo)rapidity ( or y), are the common basis for such studies. Often, the ratio of these measurements in heavy-ion collisions (for a given centrality class) and pp collisions, or the ratio of the results in different collision centralities, are built to disentangle possible QGP effects from those present in pp data, considered as a reference. An alternative observable that has recently raised the interest of the community is the representation of particle yields as a function of the collision charged-particle multiplicity. Both quantities (the centrality of the collision and the charged-particle multiplicity) are connected with the energy density of the interaction region, according to the naive Bjorken model [9]. Charged particle multiplicity measurements are then complementary to the measurements as a function of collision centrality, with the advantage that multiplicity can be evaluated experimentally in all collision systems from pp to pA, as well as to AA, whereas the centrality of collision is usually deduced based on Glauber model estimates [10], requires a good knowledge of the nuclear density function of the colliding particles and might be affected by fluctuations in the initial state of collision when dealing with small (pp or pA) systems. As a consequence, the measurements of particle production as a function of charged-particle multiplicity have gained popularity in small systems. They provide a tool to observe the evolution of particle production from very low multiplicities, characteristic of pp collisions associated with low energy densities, up to the largest multiplicities attained in heavy-ion collisions which are associated with the largest energy densities attained in the laboratory. They also facilitate the scrutiny of high-multiplicity pp and pPb events where unexpected phenomena, usually attributed to QGP creation, have been observed; see Ref. [11]. Such observations are not understood in the scenario of free streaming partons in the final state of pp collisions, requiring further studies and raising many questions. What is the mechanism that originates collective behaviour in small systems? Is a large enough energy density attained in small systems to create QGP droplets? Do hard probes, being heavy objects such as quarkonia, interact with (small) QGP droplets in small systems? Can all hadronic collisions (be they small or large) be described within the same formalism? Are multiparton interactions the origin of these features?
In this report, we review recent measurements of quarkonium production as a function of charged-particle multiplicity in small systems at LHC energies and compare them against model predictions. Focus is given to charmonium and bottomonium yields (Section 2), the excited-to-ground state quarkonium yield ratios (Section 3) and to probing the nature of hadron production (Section 4).
2. Multiplicity Dependence of Quarkonium Yields
Event charged-particle multiplicity is the most common event classifier used experimentally. Most of the analyses of particle production as a function of charged-particle multiplicity in small systems report the results as relative (or self-normalised) quantities, i.e., as the ratio of the quantities in the given event class to those integrated over all event classes. The motivation to evaluate this ratio is that part of the experimental uncertainties cancel in the ratio, improving measurement precision. In addition, the ratio is independent of the absolute particle production yield, and is only sensitive to the possible variation of the particle yield as a function of charged-particle multiplicity.
The production of heavy-flavour yields (be it D mesons, heavy-flavour decay leptons, inclusive J/ or , or prompt J/) increases with charged-particle multiplicity measured at midrapidity in pp collisions at the LHC [12,13,14,15,16,17]. For illustration, Figure 1 presents the relative inclusive J/ yield at midrapidity as a function of the relative charged-particle multiplicity at midrapidity [16]. The yields of observables measured at midrapidity, i.e., in the same rapidity interval as that of multiplicity measurement, are found to increase faster than with the linear () approach with charged-particle multiplicity [15,16]. This behaviour is the expected one based on the naive association of events with larger multiplicities with events involving a larger momentum transfer and having a larger probability of creating harder (rarer) probes in the interaction. It is important to mention that the same behaviour is observed for both open and hidden heavy-flavour production, suggesting a common origin for the relative variation of the yields with charged-particle multiplicity, independent of the hadronisation process. In contrast, the yields of observables measured at large rapidity follow a less steep trend as a function of charged-particle multiplicity at midrapidity, closer to the linear approach [13,14]. It should be noted that most of the models can capture this variation of heavy-flavour yields with rapidity qualitatively, suggesting that this effect is under control by models, even though it remains difficult to disentangle its origin.
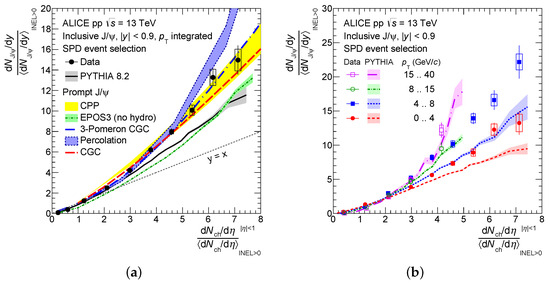
Figure 1.
Relative inclusive J/ yield at midrapidity as a function of the relative charged-particle multiplicity at midrapidity in pp collisions at TeV [16]. (a) Results are compared to PYTHIA 8.2 [18] and theoretical calculations from the coherent particle production model [19], the percolation model [20], the EPOS3 event generator [21], the CGC model [22], the 3-Pomeron CGC model [23]. (b) Results in intervals compared to PYTHIA 8.2 [18] calculations. PYTHIA 8.2 calculations refer to the inclusive (prompt and non-prompt) contributions.
Diverse model calculations are shown in Figure 1. Monte Carlo event generators are ideal tools to interpret these measurements, as they evaluate both the underlying event characteristics and the hard process yields by describing both the multiple scatterings via pQCD and the non-perturbative aspects with phenomenological models. PYTHIA 8 [18] calculations expect an increase in heavy-flavour yields as a function of charged-particle multiplicity, but are unable to describe the steep increase in heavy-flavour yields at midrapidity [15,16]. The trends depicted by PYTHIA 8 [18] and EPOS 3 [21] calculations are similar, despite the different implementation of the hard scattering and multiple scattering contributions in these models. It should be noted that the transverse momentum dependence of the yields is qualitatively (not quantitatively) described by both PYTHIA and EPOS calculations [14,15,16]; see also Figure 1. EPOS 3 calculations can also be performed considering that the density of charged particles in the system is large enough to undergo a collective expansion, which can be described in terms of hydrodynamics [24], as supported by LHC measurements [25]. The results of EPOS 3 assuming an hydrodynamic expansion of the system better describe the steeper increase in the yields at midrapidity, and have little influence on the observables at large rapidity [15,26].
The results are also compared to initial-state models in Figure 1. In the coherent particle production (CPP) model [27], high-multiplicity hadronic interactions are treated on equal footing regardless of the collision system, from pp to AA collisions. The model relies on parametrisation of the mean multiplicities of light and heavy particle production, assuming their linear dependence on binary nucleon–nucleon collisions in pA collisions. This model takes into consideration the possible mutual boosting of the gluon densities and saturation scales in colliding protons [28]. The model is defined for at least one nucleon–nucleon collision, i.e., relative charged-particle multiplicity . The uncertainties on the CPP model are those resulting from parametrisation of the measurements and their corresponding experimental uncertainties. CPP calculations describe J/ results.
High-energy hadronic collisions can also be simulated in the percolation framework [29]. The key ingredients of this model are the colour ropes or flux tubes (strings) that are formed in each parton–parton interaction and constitute the main source of particle production. The strings have non-negligible transverse size and can interact among each other. In particular, they can overlap, reducing their effective number and, consequently, particle production. In this string model [20], the number of heavy-flavour hadrons is assumed to be proportional to the number of partonic scatterings, which corresponds to the number of produced strings. Instead, charged-particle multiplicity scales with the number of participants due to the influence of shadowing [30], parton saturation [31], or percolation [29]. The behaviour of J/ relative yields is reproduced by the percolation calculation for both central and large rapidity.
Gluon saturation phenomena can also be studied via the colour glass condensate (CGC) effective field theory [32,33]. The CGC framework can be used to evaluate the short distance charmonium production cross-sections. It can be combined with the fragmentation functions of heavy quarks to D/B hadrons, or the non-relativistic (NRQCD) long-distance matrix (LDME) hadronisation for quarkonium production. The improved colour evaporation model (ICEM) [34] is used to evaluate the probability of a () pair to form a quarkonium state, considering that the transverse momentum of the quarkonia differs from that of the heavy-quark pair. This CGC+ICEM model predicts the rapid increase with charged-particle multiplicity for both D mesons and J/ at midrapidity [22], but cannot describe the less steep trend of J/ produced at large rapidity [14]. This picture assumes that gluon–gluon fusion is the dominant mechanism for heavy quark production. Another calculation in CGC saturation approach considers a sizeable contribution of multipomeron mechanisms, in particular of the higher-order three-pomeron term (three-pomeron CGC) [23]. This calculation describes the observed trend for J/ production both at central and large rapidity.
All models discussed above qualitatively describe the observed trend of heavy-flavour yields as a function of charged-particle multiplicity in pp collisions, but only the CPP, percolation and three-pomeron CGC qualitatively reproduce the observed features.
In the charmonia sector, the relative yields of inclusive J/ at large rapidity were evaluated as a function of the relative charged-particle multiplicity for all pp, pPb and PbPb collisions. The results were published in Ref. [26]. One observes a striking similarity of the trend for pp and PbPb data, as well as with the results for pPb data in the Pb-going direction. The difference in the trend observed for pPb results in the p- and Pb-going direction is attributed to the fact that the forward (p-going) rapidity region probes the Pb-nucleus low Bjorken-x regime ( in a naive two-body calculation for ), whereas the backward (Pb-going) rapidity is sensitive to intermediate-to-large values (). The trend for pPb data is described by EPOS 3 calculations [26].
To complete the picture and understand whether the yields present (or not) a uniform behaviour across collision systems, it is worth to draw these results in terms of absolute quantities in addition to relative ones. The calculation of absolute yields and charged-particle multiplicity was performed exploiting -integrated data from the ALICE Collaboration [13,14,26,35,36,37,38]. Figure 2 presents the results for inclusive J/ yields at large rapidity as a function of charged-particle multiplicity at midrapidity for various collision systems. The top figure evidences a smooth and continuous behaviour as a function of charged-particle multiplicity from pp to PbPb collisions, for J/ yields in the same rapidity range. This is in contrast with the naive expectations from the sequential colour screening scenario for heavy-ion collisions, from which one would expect to visualise an onset corresponding to bound state dissociation conditions. The most recent picture where the influence of sequential melting is balanced by the regeneration effect might conciliate this observation. However, the absence of onset in the distribution remains to be understood. The ratio of inclusive J/ yields at large rapidity to charged-particle multiplicity at midrapidity is also shown in Figure 2 as a function of charged-particle multiplicity at midrapidity for various collision systems. At low multiplicities, a hierarchy of yields is observed, larger for higher center-of-mass energies, as expected. For pp data, the deviation of the ratio from a flat behaviour suggests that a naive multiparton scenario where the correlation between the two quantities is expected to be linear is not sufficient to describe the results. PbPb data present a smooth continuous trend for GeV/c, while the distribution of the points for seems to change its slope for charged-particle multiplicity around 200. This difference is attributed to the contribution of J/ originated from photoproduction processes induced by the strong electromagnetic field generated in heavy-ion collisions [39], which is more important for peripheral (i.e., low-multiplicity) collisions. The precision of the measurements and the requirement of the GeV/c selection to remove contribution from photoproduction do not allow for us to conclude on a possible smooth behaviour from pp to PbPb data. The larger luminosities from the LHC Run 3 should allow reaching better precision, better quantification of the contribution from photon-induced processes and comparison of quarkonium yields across collision systems.
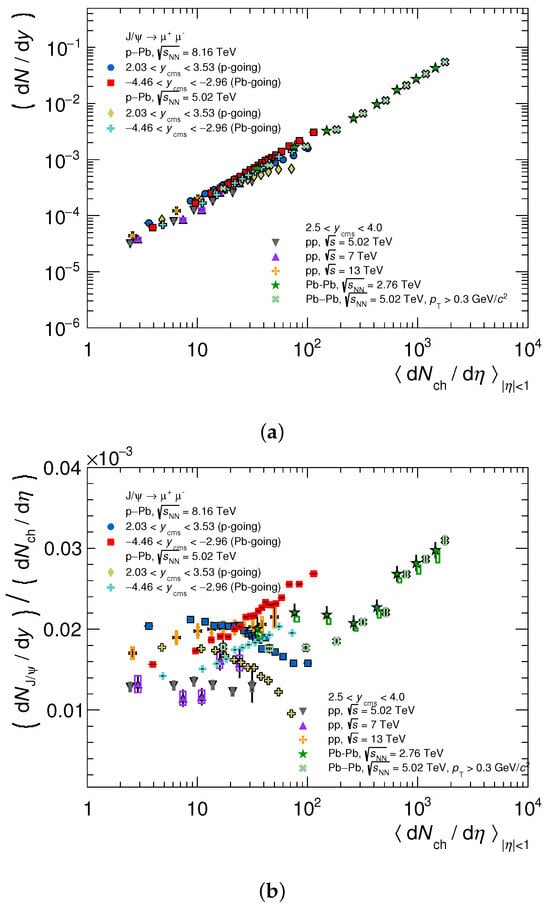
Figure 2.
(a) Inclusive J/ yield at large rapidity as a function of charged-particle multiplicity at midrapidity for various collision systems. (b) Ratio of inclusive J/ yield at large rapidity to the charged-particle multiplicity at midrapidity. Data collected from Refs. [13,14,26,35,36,37,38].
3. Excited-to-Ground State Ratios
The study of quarkonium ground and excited states is of particular interest, as excited states are characterised by a lower binding energy and a larger binding radius than the ground states [40]. Excited states are then more sensitive to effects at play in the-final state than ground-state quarkonia, be it dissociation by colour screening due to the formation of a QGP or QGP droplets [41] or the influence of interactions with the final state particles, such as assumed in the comover model [4]. Excited-to-ground state quarkonium ratios are frequently exploited in order to disentangle these final-state effects from those at play in the initial state of the interaction, which are similar for both ground and excited states and are assumed to cancel in excited-to-ground state ratios.
In the charmonium sector, recent results of (-integrated) relative yield ratio show an approximately flat trend as a function of relative charged-particle multiplicity [42]; see Figure 3. These results are consistent with none or small final-state effects, such as those predicted by the comover model [4]. Analogous measurements in pPb collisions present similar results [42].
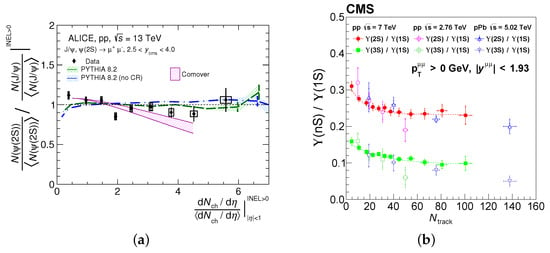
Figure 3.
(a) Ratio of relative yields at large rapidity as a function of the relative charged-particle multiplicity at midrapidity [42]. (b) and ratios at midrapidity as a function of the multiplicity of charged tracks at midrapidity [12,17]. The lines are fits to the data with an exponential function.
In the bottomonium sector, a decrease in yield ratios at midrapidity is observed as a function of the multiplicity of charged tracks at midrapidity [17]; see Figure 3. The results present a smooth behaviour from pp to pPb as a function of charged-particle multiplicity, which the authors did fit with an exponential function. PbPb data are missing in this comparison. A comparison of these results with model calculations is still missing, as the measurements were released as a function of the number of reconstructed tracks in the detector, and not corrected to that of a physics event class. The observed trend suggests a decrease, as expected by the comover model, but a quantitative comparison is missing.
Excited-to-ground state bottomonium ratios as a function of the local multiplicity or event shape in pp collisions evidence a connection of heavy-flavour production with the underlying event [17]. The ratios of bottomonium excited-to-ground states remain consistent, regardless of whether the multiplicity is measured within a cone around the upsilon momentum direction, in a cone opposite to the upsilon’s momentum, or the transverse region. This is in contrast with a possible bias caused by the hard scattering products or by feed-down contributions, which would only produce particles near the observable. In addition, a variation in the ratios with the transverse sphericity () of the event is observed. is defined in terms of the eigenvalues of the transverse momentum matrix of charged particles. The results with show a similar decrease with charged-particle multiplicity, while the ratios in the interval are nearly independent of multiplicity [17]. These results are interpreted as an influence of the underlying event. High multiplicity events with small values are explained by the presence of localized objects, such as jets, which have, on average, a higher .
4. Quarkonia as Tools to Study Exotica
The exotic hadron was first observed in 2003 by Belle in the exclusive decays, [43], and has been observed since in many experiments. This state, which decays into , has a mass of MeV, a value that is very near the mass threshold [43]. The exact nature of the state is still under intense scrutiny. Among the open possibilities are a tetraquark, composed of a diquark–antidiquark bound state [44,45]; a molecule, as suggested by the distance of its mass to the sum of and mass threshold [46,47,48]; or a mixture of them, a hadrocharmonium or adjoint charmonium state, where two light quarks orbit a charmonium core [49,50,51]. The size of the state would be of ∼1 fm for a compact tetraquark scenario [44,52,53,54], or of the order of 10 fm, or more, if the coupling to the closest channel is dominant, given the small binding energy in the molecular scenario [46,55,56]. It is then conjectured that studies in heavy-ion collisions could provide complementary information on its nature, as quarkonium yields in heavy-ion collisions are expected to vary with their binding energy.
The recent measurement of production as a function of charged-particle multiplicity in pp collisions at TeV by LHCb has attracted the interest of the community [57]. The to production cross-section ratio has been evaluated separately for the prompt and non-prompt contributions as a function of multiplicity for GeV/c; see Figure 4. The ratio decreases as a function of multiplicity for prompt contribution, while the non-prompt ratio does not present a significant variation with multiplicity. Different interpretations have been proposed and are still under debate; see Refs. [58,59]. Authors from Ref. [58] consider that if the structure of the hadron is that of a compact tetraquark, its evolution with multiplicity is governed by the interactions with comoving particles with similar rapidities, in the so-called comover interaction model (CIM), and that recombination influence is irrelevant. If the structure is that of a molecule, they consider either the same CIM scenario, with a breakup cross-section driven by a geometric one, or an alternative one, where coalescence plays the dominant role. Their calculation can be seen in the figure, and it concludes that the molecular component cannot dominate the wave function. Instead, the authors of Ref. [59] use the CIM with a different assumption for the breakup cross-section, and conclude that the results are compatible with a loosely bound molecule state.
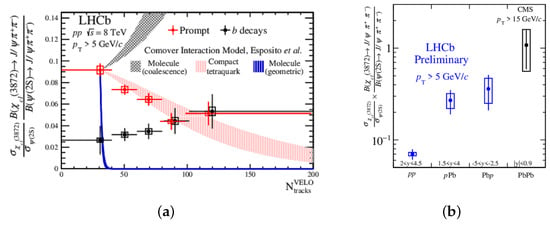
Figure 4.
Ratio of to production cross-section in decay. (a) Ratio as a function of charged-particle multiplicity in pp collisions at 8 TeV for both prompt and non-prompt components, at large rapidity for GeV/c [57]. (b) Ratio for prompt contribution in pp and pPb collisions (large rapidity, GeV/c ) and PbPb data (central rapidity, GeV/c [57,60,61].
Such results have motivated similar measurements in heavy-ion collisions, in particular those of Refs. [60,61] in pPb and PbPb collisions, which are especially challenging. Figure 4 summarises the results. The to production cross-section ratio increases from pp to pPb and to PbPb collisions. This trend seems in contradiction with the decreasing trend as a function of multiplicity observed in pp data. Different effects could be at play. On the one hand, it has been observed that production is suppressed in pPb and PbPb collisions, which might increase the ratio if there are no final-state effects at play for . On the other hand, the larger particle densities of heavy-ion collisions might allow for coalescence to become the dominant effect for . More precise and differential measurements are required to clarify the observed trends and improve our understanding of its nature.
5. Discussion
Data show that quarkonium yields increase as a function of charged-particle multiplicity in all collision systems at the LHC. A smooth increase in the absolute inclusive J/ yield is observed as a function of charged-particle multiplicity from pp to pA and to AA collisions. The results in pp collisions are qualitatively described by PYTHIA 8 and EPOS 3 Monte Carlo event generators as well as by initial-state models based on coherent particle production, parton percolation or parton saturation phenomena. A quantitative description of the measured trend is accomplished by these initial-state models. Excited-to-ground state quarkonium ratios are also studied, as they are sensitive to final-state effects. In pp and pPb collisions, the relative yield ratio does not present a significant trend as a function of relative charged-particle multiplicity, with values compatible with unity. In contrast, yield ratios show a decrease with charged-particle multiplicity. These results point to an influence of final-state effects, like the one expected by the comover model, but quantitative comparison is still missing. In addition, the multiplicity dependence of appears as a complementary tool to study its nature.
The improvements in both detector and collider capabilities for the LHC Run 3 will allow for us to collect larger data samples. The increased statistics will be materialised into high-precision measurements. In particular, a net amelioration is expected for rare probe measurements for which statistics are crucial. This will make possible precise differential measurements of multiple particle production, such as or as a function of their rapidity, to further constrain multiparton interactions. It will also facilitate the scrutiny of extremely-high-multiplicity events where the effects are expected to be more prominent. Altogether, these measurements will bring information on initial- and final-state effects at play in small collision systems.
Funding
This research received no external funding.
Data Availability Statement
Data used in this report can be found in the data bases provided in the cited publications.
Acknowledgments
The author would like to thank E. González Ferreiro, C. Cheshkov and R. Granier de Cassagnac for fruitful discussions and advices while preparing some of the figures of this review.
Conflicts of Interest
The author declares no conflict of interest.
References
- Bodwin, G.T.; Braaten, E.; Lepage, G.P. Rigorous QCD analysis of inclusive annihilation and production of heavy quarkonium. Phys. Rev. D 1995, 51, 1125–1171, Erratum in Phys. Rev. D 1997, 55, 5853. [Google Scholar] [CrossRef]
- Ma, Y.Q.; Venugopalan, R. Comprehensive Description of J/ψ Production in Proton-Proton Collisions at Collider Energies. Phys. Rev. Lett. 2014, 113, 192301. [Google Scholar] [CrossRef] [PubMed]
- Vogt, R. Shadowing and absorption effects on J/ψ production in dA collisions. Phys. Rev. C 2005, 71, 54902. [Google Scholar] [CrossRef]
- Ferreiro, E.G. Excited charmonium suppression in proton–nucleus collisions as a consequence of comovers. Phys. Lett. B 2015, 749, 98–103. [Google Scholar] [CrossRef]
- Arleo, F.; Peigné, S. Quarkonium suppression in heavy-ion collisions from coherent energy loss in cold nuclear matter. JHEP 2014, 10, 73. [Google Scholar] [CrossRef]
- Matsui, T.; Satz, H. J/ψ Suppression by Quark-Gluon Plasma Formation. Phys. Lett. B 1986, 178, 416–422. [Google Scholar] [CrossRef]
- Acharya, S. et al. [ALICE Collaboration] Centrality and transverse momentum dependence of inclusive J/ψ production at midrapidity in Pb–Pb collisions at sNN = 5.02 TeV. Phys. Lett. B 2020, 805, 135434. [Google Scholar] [CrossRef]
- Rothkopf, A. Heavy Quarkonium in Extreme Conditions. Phys. Rept. 2020, 858, 1–117. [Google Scholar] [CrossRef]
- Bjorken, J. Highly Relativistic Nucleus-Nucleus Collisions: The Central Rapidity Region. Phys. Rev. D 1983, 27, 140–151. [Google Scholar] [CrossRef]
- Glauber, R.; Matthiae, G. High-energy scattering of protons by nuclei. Nucl. Phys. B 1970, 21, 135–157. [Google Scholar] [CrossRef]
- Citron, Z.; Dainese, A.; Grosse-Oetringhaus, J.F.; Jowett, J.M.; Lee, Y.-J.; Wiedemann, U.A. Report from Working Group 5: Future physics opportunities for high-density QCD at the LHC with heavy-ion and proton beams. CERN Yellow Rep. Monogr. 2019, 7, 1159–1410. [Google Scholar] [CrossRef]
- Chatrchyan, S. et al. [CMS Collaboration] Event Activity Dependence of Y(nS) Production in = 5.02 TeV pPb and = 2.76 TeV pp Collisions. JHEP 2014, 4, 103. [Google Scholar] [CrossRef]
- Abelev, B. et al. [The ALICE collaboration] J/ψ Production as a Function of Charged Particle Multiplicity in pp Collisions at = 7 TeV. Phys. Lett. B 2012, 712, 165–175. [Google Scholar] [CrossRef]
- Acharya, S. et al. [ALICE Collaboration] Forward rapidity J/ψ production as a function of charged-particle multiplicity in pp collisions at = 5.02 and 13 TeV. JHEP 2022, 6, 15. [Google Scholar] [CrossRef]
- Adam, J. et al. [The ALICE Collaboration] Measurement of charm and beauty production at central rapidity versus charged-particle multiplicity in proton-proton collisions at = 7 TeV. JHEP 2015, 9, 148. [Google Scholar] [CrossRef]
- Acharya, S. et al. [ALICE Collaboration] Multiplicity dependence of J/ψ production at midrapidity in pp collisions at = 13 TeV. Phys. Lett. B 2020, 810, 135758. [Google Scholar] [CrossRef]
- Sirunyan, A.M. et al. [CMS Collaboration] Investigation into the event-activity dependence of Υ(nS) relative production in proton-proton collisions at = 7 TeV. JHEP 2020, 11, 1. [Google Scholar] [CrossRef]
- Sjostrand, T.; Mrenna, S.; Skands, P.Z. A Brief Introduction to PYTHIA 8.1. Comput. Phys. Commun. 2008, 178, 852–867. [Google Scholar] [CrossRef]
- Kopeliovich, B.Z.; Pirner, H.J.; Potashnikova, I.K.; Reygers, K.; Schmidt, I. J/ψ in high-multiplicity pp collisions: Lessons from pA collisions. Phys. Rev. D 2013, 88, 116002. [Google Scholar] [CrossRef]
- Ferreiro, E.G.; Pajares, C. High multiplicity pp events and J/ψ production at LHC. Phys. Rev. C 2012, 86, 34903. [Google Scholar] [CrossRef]
- Werner, K.; Guiot, B.; Karpenko, I.; Pierog, T. Analysing radial flow features in p-Pb and p-p collisions at several TeV by studying identified particle production in EPOS3. Phys. Rev. C 2014, 89, 64903. [Google Scholar] [CrossRef]
- Ma, Y.Q.; Tribedy, P.; Venugopalan, R.; Watanabe, K. Event engineering studies for heavy flavour production and hadronization in high multiplicity hadron-hadron and hadron-nucleus collisions. Phys. Rev. D 2018, 98, 74025. [Google Scholar] [CrossRef]
- Levin, E.; Schmidt, I.; Siddikov, M. Multiplicity dependence of quarkonia production in the CGC approach. Eur. Phys. J. C 2020, 80, 560. [Google Scholar] [CrossRef]
- Drescher, H.J.; Hladik, M.; Ostapchenko, S.; Pierog, T.; Werner, K. Parton based Gribov-Regge theory. Phys. Rept. 2001, 350, 93–289. [Google Scholar] [CrossRef]
- Khachatryan, V. et al. [CMS Collaboration] Observation of Long-Range Near-Side Angular Correlations in Proton-Proton Collisions at the LHC. JHEP 2010, 9, 91. [Google Scholar] [CrossRef]
- Acharya, S. et al. [ALICE Collaboration] J/ψ production as a function of charged-particle multiplicity in p-Pb collisions at = 8.16 TeV. JHEP 2020, 9, 162. [Google Scholar] [CrossRef]
- Kopeliovich, B.Z.; Pirner, H.J.; Potashnikova, I.K.; Reygers, K.; Schmidt, I. Heavy quarkonium in the saturated environment of high-multiplicity pp collisions. Phys. Rev. D 2020, 101, 54023. [Google Scholar] [CrossRef]
- Kopeliovich, B.Z.; Pirner, H.J.; Potashnikova, I.K.; Schmidt, I. Mutual boosting of the saturation scales in colliding nuclei. Phys. Lett. B 2011, 697, 333–338. [Google Scholar] [CrossRef]
- Armesto, N.; Braun, M.A.; Ferreiro, E.G.; Pajares, C. Percolation approach to quark - gluon plasma and J/ψ suppression. Phys. Rev. Lett. 1996, 77, 3736–3738. [Google Scholar] [CrossRef]
- Ferreiro, E.G.; Fleuret, F.; Lansberg, J.P.; Rakotozafindrabe, A. Cold nuclear matter effects on J/ψ production: Intrinsic and extrinsic transverse momentum effects. Phys. Lett. B 2009, 680, 50–55. [Google Scholar] [CrossRef]
- Kharzeev, D.; Levin, E.; Nardi, M.; Tuchin, K. Gluon saturation effects on J/ψ production in heavy ion collisions. Phys. Rev. Lett. 2009, 102, 152301. [Google Scholar] [CrossRef]
- Gelis, F.; Iancu, E.; Jalilian-Marian, J.; Venugopalan, R. The Color Glass Condensate. Ann. Rev. Nucl. Part. Sci. 2010, 60, 463–489. [Google Scholar] [CrossRef]
- Blaizot, J.P. High gluon densities in heavy ion collisions. Rept. Prog. Phys. 2017, 80, 32301. [Google Scholar] [CrossRef]
- Ma, Y.Q.; Vogt, R. Quarkonium Production in an Improved Color Evaporation Model. Phys. Rev. D 2016, 94, 114029. [Google Scholar] [CrossRef]
- Adam, J. et al. [The ALICE Collaboration] Differential studies of inclusive J/ψ and ψ(2S) production at forward rapidity in Pb-Pb collisions at = 2.76 TeV. JHEP 2016, 5, 179. [Google Scholar] [CrossRef]
- Acharya, S. et al. [ALICE Collaboration] Studies of J/ψ production at forward rapidity in Pb-Pb collisions at = 5.02 TeV. JHEP 2020, 2, 41. [Google Scholar] [CrossRef]
- Adamová, D. et al. [ALICE Collaboration] J/ψ production as a function of charged-particle pseudorapidity density in p-Pb collisions at = 5.02 TeV. Phys. Lett. B 2018, 776, 91–104. [Google Scholar] [CrossRef]
- Acharya, S. et al. [ALICE Collaboration] Energy dependence of forward-rapidity J/ψ and ψ(2S) production in pp collisions at the LHC. Eur. Phys. J. C 2017, 77, 392. [Google Scholar] [CrossRef]
- Acharya, S. et al. [ALICE Collaboration] Photoproduction of low-pT J/ψ from peripheral to central Pb-Pb collisions at 5.02 TeV. Phys. Lett. B 2023, 846, 137467. [Google Scholar] [CrossRef]
- Kluberg, L.; Satz, H. Color Deconfinement and Charmonium Production in Nuclear Collisions. In Relativistic Heavy Ion Physics; Stock, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Satz, H. Color deconfinement in nuclear collisions. Rept. Prog. Phys. 2000, 63, 1511. [Google Scholar] [CrossRef]
- Acharya, S. et al. [ALICE Collaboration] Measurement of ψ(2S) production as a function of charged-particle pseudorapidity density in pp collisions at = 13 TeV and p-Pb collisions at = 8.16 TeV with ALICE at the LHC. JHEP 2023, 6, 147. [Google Scholar] [CrossRef]
- Choi, S.K. et al. [Belle Collaboration] Observation of a narrow charmonium-like state in exclusive B±→K±π+π−J/ψ decays. Phys. Rev. Lett. 2003, 91, 262001. [Google Scholar] [CrossRef]
- Maiani, L.; Piccinini, F.; Polosa, A.D.; Riquer, V. Diquark-antidiquarks with hidden or open charm and the nature of X(3872). Phys. Rev. D 2005, 71, 14028. [Google Scholar] [CrossRef]
- ’t Hooft, G.; Isidori, G.; Maiani, L.; Polosa, A.D.; Riquer, V. A Theory of Scalar Mesons. Phys. Lett. B 2008, 662, 424–430. [Google Scholar] [CrossRef]
- Tornqvist, N.A. Isospin breaking of the narrow charmonium state of Belle at 3872-MeV as a deuson. Phys. Lett. B 2004, 590, 209–215. [Google Scholar] [CrossRef]
- Braaten, E.; Lu, M. The Effects of charged charm mesons on the line shapes of the X(3872). Phys. Rev. D 2008, 77, 14029. [Google Scholar] [CrossRef]
- Chen, R.; Sun, Z.F.; Liu, X.; Zhu, S.L. Strong LHCb evidence supporting the existence of the hidden-charm molecular pentaquarks. Phys. Rev. D 2019, 100, 11502. [Google Scholar] [CrossRef]
- Dubynskiy, S.; Voloshin, M.B. Hadro-Charmonium. Phys. Lett. B 2008, 666, 344–346. [Google Scholar] [CrossRef]
- Dubynskiy, S.; Gorsky, A.; Voloshin, M.B. Holographic Hadro-Quarkonium. Phys. Lett. B 2009, 671, 82–86. [Google Scholar] [CrossRef]
- Hanhart, C.; Kalashnikova, Y.S.; Nefediev, A.V. Interplay of quark and meson degrees of freedom in a near-threshold resonance: Multi-channel case. Eur. Phys. J. A 2011, 47, 101–110. [Google Scholar] [CrossRef]
- Esposito, A.; Pilloni, A.; Polosa, A.D. Multiquark Resonances. Phys. Rept. 2017, 668, 1–97. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Hwang, D.S.; Lebed, R.F. Dynamical Picture for the Formation and Decay of the Exotic XYZ Mesons. Phys. Rev. Lett. 2014, 113, 112001. [Google Scholar] [CrossRef] [PubMed]
- Esposito, A.; Polosa, A.D. A bb di-bottomonium at the LHC? Eur. Phys. J. C 2018, 78, 782. [Google Scholar] [CrossRef] [PubMed]
- Guo, F.K.; Hanhart, C.; Meißner, U.G.; Wang, Q.; Zhao, Q.; Zou, B.S. Hadronic molecules. Rev. Mod. Phys. 2018, 90, 15004, Erratum in Rev. Mod. Phys. 2022, 94, 29901. [Google Scholar] [CrossRef]
- Braaten, E.; Kusunoki, M. Low-energy universality and the new charmonium resonance at 3870-MeV. Phys. Rev. D 2004, 69, 74005. [Google Scholar] [CrossRef]
- Aaij, R. et al. [LHCb Collaboration] Observation of Multiplicity Dependent Prompt χc1(3872) and ψ(2S) Production in pp Collisions. Phys. Rev. Lett. 2021, 126, 92001. [Google Scholar] [CrossRef] [PubMed]
- Esposito, A.; Ferreiro, E.G.; Pilloni, A.; Polosa, A.D.; Salgado, C.A. The nature of X(3872) from high-multiplicity pp collisions. Eur. Phys. J. C 2021, 81, 669. [Google Scholar] [CrossRef]
- Braaten, E.; He, L.P.; Ingles, K.; Jiang, J. Production of X(3872) at High Multiplicity. Phys. Rev. D 2021, 103, L071901. [Google Scholar] [CrossRef]
- Modification of χc1(3872) and ψ(2S) production in pPb collisions at = 8.16 TeV. In Proceedings of the 29th International Conference on Ultra-relativistic Nucleus-Nucleus Collisions, Krakow, Poland, 4–10 April 2022.
- Sirunyan, A.M. et al. [CMS Collaboration] Evidence for X(3872) in Pb-Pb Collisions and Studies of its Prompt Production at = 5.02 TeV. Phys. Rev. Lett. 2022, 128, 32001. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).