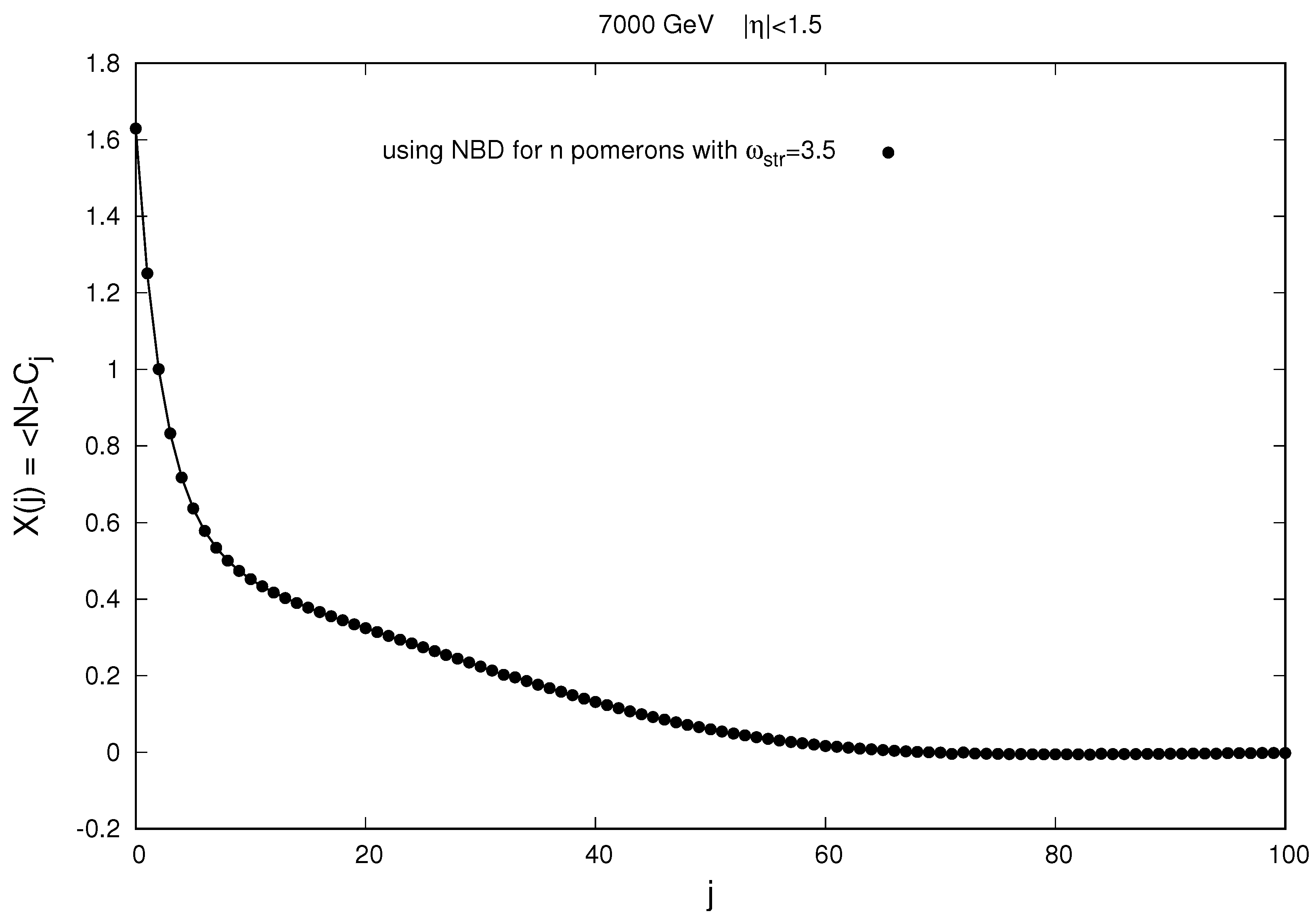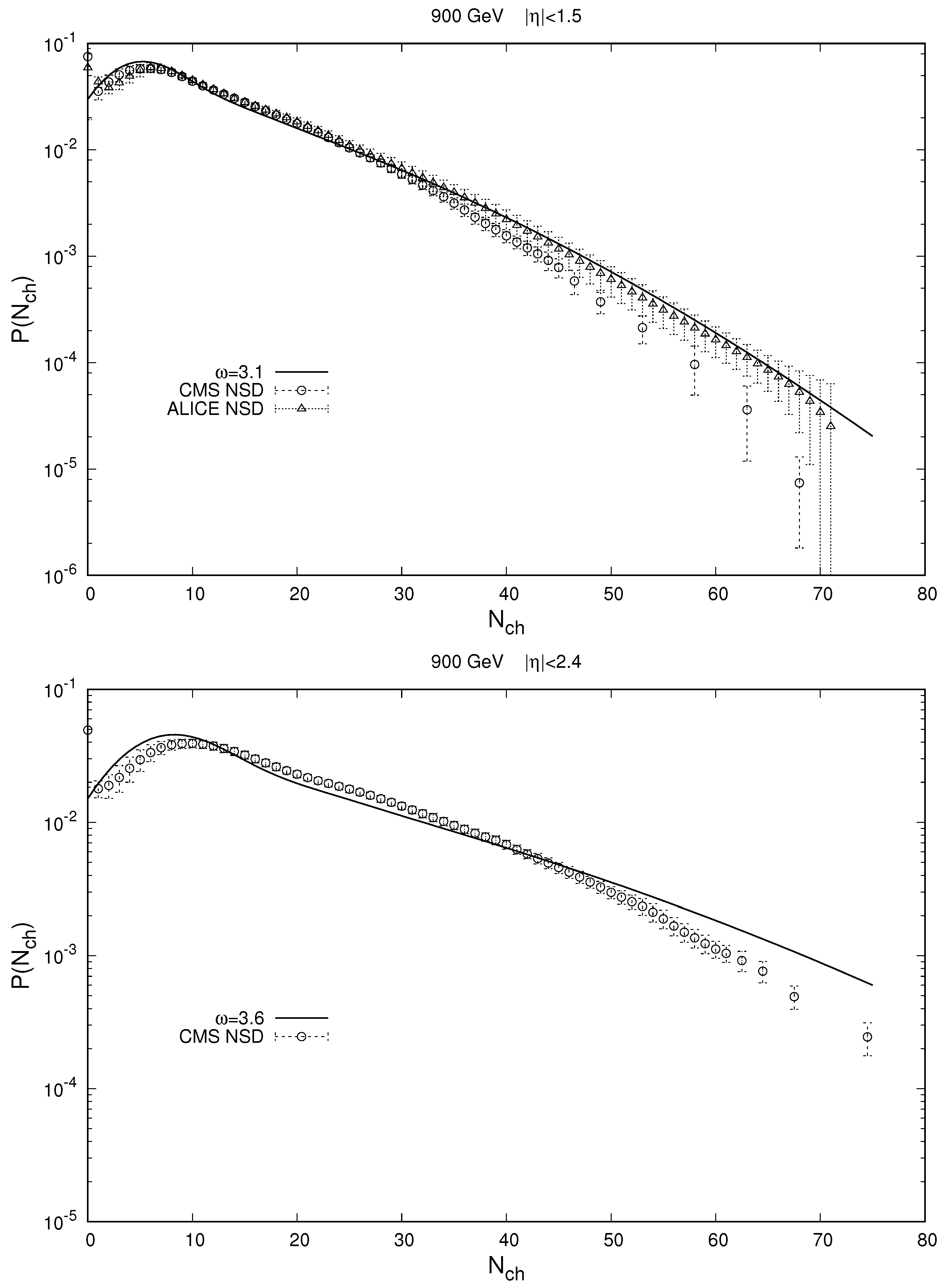Multiplicity Distributions and Modified Combinants in the Multipomeron Model of pp Interaction at High Energies

Abstract

The multiplicity distributions of charged particles and their combinants for pp collisions at LHC energies are studied within the Multipomeron Exchange Model (MEM) that takes into account the phenomenon of string fusion. It is shown that the use of Gaussian-type distributions for multiplicity distributions at a fixed number of pomerons allows, within the MEM framework, the reproduction of the resulting multiplicity distributions and the oscillatory behavior of combinants, found in the ALICE and CMS pp collision data at LHC energies. It is important that in the proposed approach, the parameters of these Gaussian-type distributions are not considered free, but are calculated from the two-particle correlation function of a single string.

1. Introduction

In recent years, in the ALICE and CMS experiments at the LHC, extensive information has been obtained on the processes of the multiple production of charged particles in the interaction of protons in the ultra-high-energy region. In particular, the multiplicity distributions of charged particles in pseudorapidity intervals of various widths for several initial energies of pp collision have been studied in detail [1,2,3,4]. Note that these experimental data also include information related to the rare, most central pp collisions, in which more than a hundred charged particles are produced [2,3,4].

The obtained multiplicity distributions, especially in wide rapidity observation windows, display rather complex behavior, which cannot be described by simple distributions such as the Negative Binomial Distribution (NBD) usually used in this case. As we will see below, the shape of these distributions, among other factors, also depends on the correlations between the production of individual particles and is therefore of undoubted interest as a tool that allows one to obtain information about the pp interaction, including its initial stage, at which quark–gluon strings arise in the interaction of partons.

The form of the obtained experimental distributions imposes serious constraints on the models used to describe the pp interaction process. Of particular interest are the regularities found when analyzing the behavior of the combinants of these multiplicity distributions [5,6,7,8,9,10,11,12].

For a given generating function $G\left(t\right)$ of the multiplicity distribution $P\left(N\right)$,

$$G\left(t\right)=\sum _{N=0}^{\infty }P\left(N\right)t^N$$

(1)

The combinants, $C^{*}\left(j\right)$, for this multiplicity distribution, $P\left(N\right)$, are defined as the expansion coefficients of the logarithm of the generating function $G\left(t\right)$:

$$F\left(t\right)=lnG\left(t\right)=\sum _{j=0}^{\infty }{C}^{*}\left(j\right)t^j.$$

(2)

It turned out [6,7,8], that the combinants extracted from the experimental distributions over the multiplicity of charged particles obtained in the ALICE and CMS experiments at the LHC [3,4] exhibited characteristic oscillations when studying their dependence on their order j. These oscillations cannot be reproduced in most models used to describe multiple production in high-energy pp interactions (see, for example, [6,8]).

Note also that a similar oscillatory pattern was found earlier in the so-called $H_q$ moments, the ratio of cumulant to factorial moments, which is also very sensitive to tiny details of the multiplicity distribution [13]. This allowed the study of parton correlations in quark and gluon jets, calculating the moments of their multiplicity distributions in fixed-coupling QCD. Later, it was also demonstrated that such sign-changing oscillations can also be well described by the H-function generalization of NBD [14,15].

In the present article, we analyze this problem within the framework of the Multipomeron Exchange Model (MEM) [16,17,18]. In this model, each cut pomeron corresponds to the formation of a pair of quark–gluon strings. An increase in the multiplicity of charged particles per unit of rapidity with increasing initial pp-collision energy is explained by both an increase in the average number of cut pomerons and an increase in the average multiplicity from a single string, which effectively takes into account string fusion processes [19,20,21,22,23,24,25,26,27,28]. The usual Regge dependence of the distribution over the number of cut pomerons in pp collisions on the initial energy with standard parameters [29] is used.

In the framework of the MEM, we find the multiplicity distributions of charged particles and their combinants in pp collisions at LHC energies and compare the calculation results with the experimental data obtained by the ALICE [3] and CMS [4] collaborations at CERN. We show that the original version of the MEM with a Poisson distribution of particles from a single cut pomeron cannot explain the experimental data. Replacing the Poisson distribution with a Negative Binomial Distribution (NBD), for which the scaled variance $\omega >1$, also does not allow one to obtain agreement between the results of model calculations and experimental data.

We demonstrate that the experimental data can be explained using the Gaussian distribution for non-negative integer values of the argument, normalized to 1, as the distribution over the multiplicity of charged particles for events with a given number of cut pomerons. To fix the value of the scaled variance $\omega$, we use the results of the papers [30,31,32,33,34], in which it was shown that $\omega -1$ is proportional to the width of the observation window and the integral of the two-particle correlation function of a single source (string) over the observation window. In these works, this allowed the extraction of the two-particle correlation function of a single string from ALICE data on forward–backward multiplicity correlations in pp collisions [35]. Using the values of the parameter $\omega$ obtained on the basis of these works for observation windows of various widths, we obtain a qualitative description of the experimental data from the ALICE and CMS collaborations at the LHC on the distribution of the multiplicity of charged particles in pp collisions in the energy range of 0.9–7 TeV.

Using the obtained multiplicity distributions, we also calculate the corresponding combinants. Indeed, they turn out to be very sensitive to the shape of the multiplicity distribution spectra, as noted in [6]. Even minor deviations between the ALICE and CMS data, within the experimental error, lead to considerable changes in the behavior of the combinants.

As a result, we show that the combinants calculated in the framework of the MEM, using the Gaussian distribution at non-negative integer values of the argument as the multiplicity distribution and fixing the value of the scaled variance $\omega$ based on [30,31,32,33,34], allow us to reproduce the behavior of combinants found in the experimental data of ALICE and CMS for pp collisions in the energy range of 0.9–7 TeV, in particular, the characteristic oscillations of their magnitude with an increase in the combinant order.

2. General Formulas, Combinants, and Modified Combinants

To find the values of combinants $C^{*}\left(j\right)$ for a given distribution over the multiplicity $P\left(N\right)$, it is convenient to use the recursive relation:

$$NP\left(N\right)=\sum _{j=1}^{N}j{C}^{*}\left(j\right)P(N-j),$$

(3)

directly following from their definition (see Formulas (1) and (2)). Often, instead of the combinants $C^{*}\left(j\right)$, the so-called modified combinants $C\left(j\right)$ are used:

$$C\left(j\right)\equiv \frac{j+1}{\langle N\rangle }{C}^{*}(j+1),\mathrm{where}\langle N\rangle =\sum _{N=1}^{\infty }NP\left(N\right).$$

(4)

For modified combinants, the recursive Relation (3) takes the following form:

$$(N+1)P(N+1)=\langle N\rangle \sum _{j=0}^{N}C\left(j\right)P(N-j).$$

(5)

A systematic analysis of combinants is of interest, because relations of this type, when the quantity $(N+1)P(N+1)$ is linearly expressed in terms of $P\left(N\right)$ with smaller values of the argument, are found in many phenomenological models, for example, in cascade and clans models [6,7]. Note that a similar relation arises when analyzing forward–backward multiplicity correlations in the framework of a two-stage scenario (see Formula (32) in [36]).

Below, to quantify the combinants, we will use the variables $X\left(j\right)$, which are the modified combinants multiplied by the average multiplicity:

$$X\left(j\right)\equiv \langle N\rangle C\left(j\right)=(j+1)C^{*}(j+1)$$

(6)

This was also the approach in other papers [6,8]. Then, using (5), we find the following explicit recurrence relation:

$$X\left(N\right)=(N+1)\frac{P(N+1)}{P\left(0\right)}-\sum _{j=0}^{N-1}X\left(j\right)\frac{P(N-j)}{P\left(0\right)},$$

(7)

which allows us to recursively calculate all $X\left(j\right)$ for a known multiplicity distribution $P\left(N\right)$. For example, for the first few $X\left(j\right)$, we have

$$X\left(0\right)=\overline{P}\left(1\right),X\left(1\right)=2\overline{P}\left(2\right)-{\overline{P}}^2\left(1\right),X\left(2\right)=3\overline{P}\left(3\right)-3\overline{P}\left(1\right)\overline{P}\left(2\right)+{\overline{P}}^3\left(1\right),$$

$$X\left(3\right)=4\overline{P}\left(4\right)-4\overline{P}\left(1\right)\overline{P}\left(3\right)-2{\overline{P}}^2\left(2\right)+4{\overline{P}}^2\left(1\right)\overline{P}\left(2\right)-{\overline{P}}^4\left(1\right).$$

(8)

Here,

$$\overline{P}\left(N\right)\equiv \frac{P\left(N\right)}{P\left(0\right)}.$$

In the numerical calculations, we use Formula (8) to control our code.

3. Multipomeron Exchange Model (MEM)

In the present work, calculations of multiplicity distributions and modified combinants were carried out using the Multipomeron Exchange Model (MEM) [16,17,18]. Within this model, the distribution over the number of charged particles, $N=N_{ch}$, is given by the sum of contributions from events with different numbers of cut pomerons, $n=n_{pom}$:

$$P\left(N\right)=\sum _{n=1}^{\infty }P\left(n\right)P_n\left(N\right).$$

(9)

In this formula, for the probability of the occurrence of an event with n cut pomerons in a given pp collision, the known distribution obtained in the framework of the quasi-eikonal Regge approach [37],

$$P\left(n\right)=\frac{A\left(z\right)}{n}\left[1-e^{-z}\sum _{l=0}^{n-1}{z}^l/l!\right],$$

(10)

is used, where

$$z=\frac{2\gamma C}{\lambda }{\xi }^{\Delta },\lambda =R^2+{\alpha }^{\prime }\xi ,\xi =ln(s/s_0).$$

(11)

Here, s is the square of the pp collision energy in the center-of-mass system, $s_0\simeq 1$ GeV², and $1+\Delta$ and ${\alpha }^{\prime }$ are the intercept and slope of the pomeron trajectory, respectively. The parameters $\gamma$ and R describe the vertex of the pomeron coupling to the scattering hadrons (the protons in our case). The quasi-eikonal parameter C effectively takes into account the contribution of diffraction processes to this vertex. The factor $A\left(z\right)$ provides the normalization condition

$$\sum _{n=1}^{\infty }P\left(n\right)=1,$$

(12)

which means that we consider only Non-Diffractive (ND) processes with at least one cut pomeron.

We use the standard set of Regge parameters [29]:

$$\Delta =0.139,{\alpha }^{\prime }=0.21{\mathrm{GeV}}^{-2},$$

(13)

$$\gamma ={\gamma }_{pp}=1.77{\mathrm{GeV}}^{-2},R^2=R_{pp}^2=3.18{\mathrm{GeV}}^{-2},C=1.5,$$

With this set of parameters, the distributions of events over the number of cut pomerons for the pp interaction at $\sqrt{s}=$ 0.9 and 7 TeV are shown in Figure 1.

In the MEM, it is assumed that each cut pomeron corresponds to the formation of a pair of quark–gluon strings [38,39]. An increase in the multiplicity of charged particles per unit of rapidity with an increasing initial pp collision energy is explained by both an increase in the average number of cut pomerons (see Figure 1) and an increase in the average multiplicity from a single string, which effectively takes into account string fusion processes [19,20,21,22,23]. Proceeding from this condition, in papers [16,17,18], the following dependence on the initial energy for the multiplicity of charged particles per unit of rapidity from the decay of a single string $k\left(s\right)$ was used:

$$k\left(s\right)=0.255+0.0653ln\sqrt{s/s_0}.$$

(14)

For n cut pomerons, this leads to the following average number of charged particles in the $\delta \eta$-wide rapidity interval:

$${\langle N\rangle }_n=2n{\mu }_{str}=2n\delta \eta k\left(s\right),$$

(15)

where we also introduce ${\mu }_{str}=\delta \eta k\left(s\right)$—the average number of charged particles produced in this rapidity interval from the decay of a single string.

In the original version of the model, for the distribution over the number of charged particles from a single string, the Poisson distribution with the average value ${\mu }_{str}$ was assumed,

$$P_{str}\left(N\right)=e^{-{\mu }_{str}}\frac{{\mu }_{str}^N}{N!},$$

(16)

which leads to the Poisson distribution with the average value, given by (15), for n cut pomerons:

$$P_n\left(N\right)=e^{-{\langle N\rangle }_n}\frac{{{\langle N\rangle }_n}^N}{N!}.$$

(17)

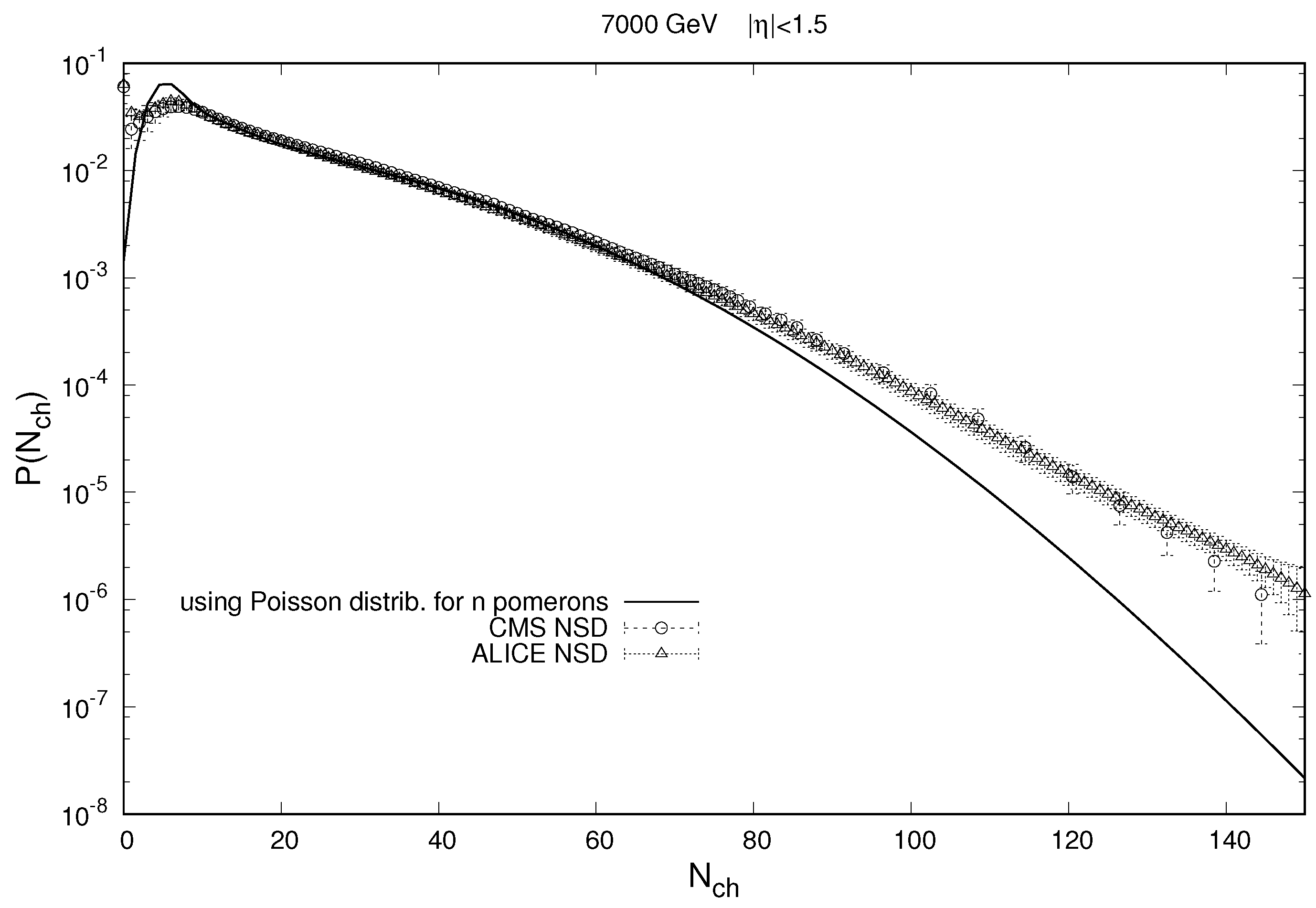
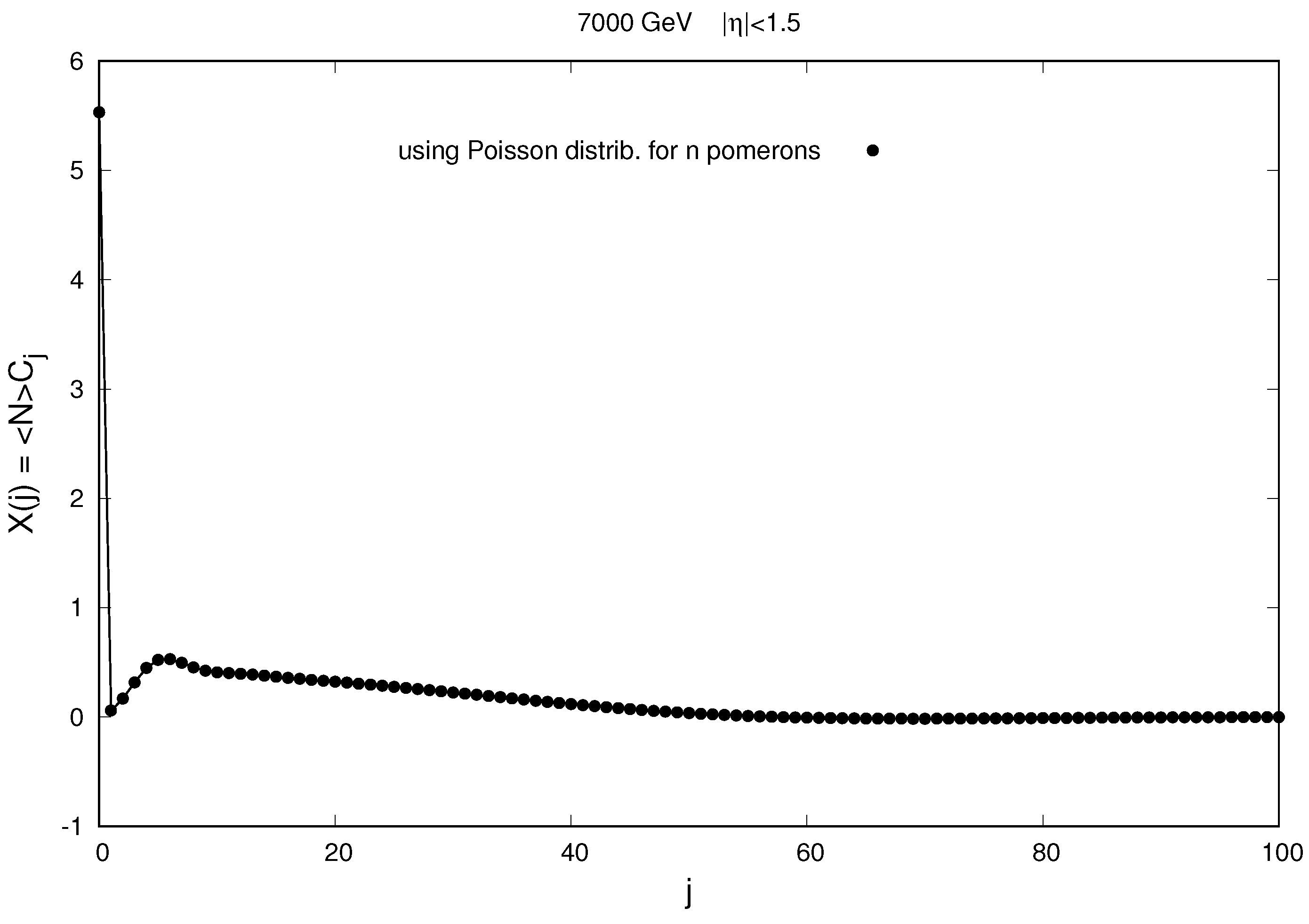
The charged particle multiplicity distribution calculated by (9) for this case, along with the corresponding experimental data of the ALICE [3] and CMS [4] collaborations at the LHC, is shown in Figure 2. In Figure 3, we see that, assuming a Poisson distribution of particles from a single string (or pomeron) (the original version of the MEM), it is not possible to describe the behavior of the distribution by the number of charged particles in the region of low multiplicities ($N<10$). This also leads to the absence of oscillations in the dependence of the modified combinants on their order (see Figure 3), which is observed when analyzing the experimental data (see [6,7,8] and Figure 9 below in Section 7).

Note also that the shape of the spectrum presented in Figure 2, calculated here within the framework of the original version of the MEM, agrees with the spectra given by the authors of the model for a narrower observational pseudo-rapidity window, $\delta \eta =1$ (see, for example, Figures 6 and 14 in [18]).

In the present work, we try to modify the original version of the MEM so that it provides a more adequate description of the distribution of charged particles by multiplicity, including the case of wider rapidity observation windows. This, in particular, makes it possible to obtain experimentally observed oscillations in the magnitude of modified combinants as their order increases.

4. Width of Multiplicity Distribution from String Fragmentation

Since we plan to use a more sophisticated distribution than the Poisson distribution, (16), for the multiplicity distribution of charged particles from the fragmentation of a single string, we need to know, in addition to the average value of the number of charged particles ${\langle N\rangle }_{str}={\mu }_{str}$ (see Formula (15)), the width of the distribution from one string. Conveniently, it is characterized by the scaled variance:

$${\omega }_{str}\equiv \frac{{\langle N^2\rangle }_{str}-{〈N〉}_{str}^2}{{\langle N\rangle }_{str}}.$$

(18)

(In the case of the Poisson distribution, ${\omega }_{str}=1$.)

The properties of any source, in particular a string, can be characterized by one- and two-particle pseudo-rapidity distributions of particles produced from the fragmentation of this source:

$$\lambda \left(\eta \right)\equiv \frac{dN}{d\eta },{\lambda }_2({\eta }_1,{\eta }_2)\equiv \frac{d^{2}N}{d{\eta }_{1}d{\eta }_2}.$$

(19)

For the production of N particles in a certain pseudo-rapidity interval $\delta \eta$ as a result of the decay of such a source, we have [40]

$${\int }_{\delta \eta }d\eta \lambda \left(\eta \right)=\langle N\rangle ,{\int }_{\delta \eta }d{\eta }_1{\int }_{\delta \eta }d{\eta }_2{\lambda }_2({\eta }_1,{\eta }_2)=\langle N(N-1)\rangle .$$

(20)

Instead of a two-particle pseudo-rapidity distribution, ${\lambda }_2({\eta }_1,{\eta }_2)$, it is convenient to use the two-particle correlation function $\Lambda ({\eta }_1,{\eta }_2)$, which describes the correlations between particles produced from the decay of a given string:

$$\Lambda ({\eta }_1,{\eta }_2)\equiv \frac{{\lambda }_2({\eta }_1,{\eta }_2)}{\lambda \left({\eta }_1\right)\lambda \left({\eta }_2\right)}-1.$$

(21)

If we have no correlation between the production of particles with ${\eta }_1$ and ${\eta }_2$, then ${\lambda }_2({\eta }_1,{\eta }_2)=\lambda \left({\eta }_1\right)\lambda \left({\eta }_2\right)$ and $\Lambda ({\eta }_1,{\eta }_2)=0$. Using the Formulas (18), (20) and (21), we can express ${\omega }_{str}$ through $\lambda \left(\eta \right)$ and $\Lambda ({\eta }_1,{\eta }_2)$ [30]:

$${\omega }_{str}=1+\frac{{\int }_{\delta \eta }d{\eta }_1{\int }_{\delta \eta }d{\eta }_2\lambda \left({\eta }_1\right)\lambda \left({\eta }_2\right)[1+\Lambda ({\eta }_1,{\eta }_2)]}{{\int }_{\delta \eta }d\eta \lambda \left(\eta \right)}-{\int }_{\delta \eta }d\eta \lambda \left(\eta \right).$$

(22)

From this formula, we see in particular that if there is no correlation between the production of particles from a given source, then $\Lambda ({\eta }_1,{\eta }_2)=0$, and we have ${\omega }_{str}=1$.

Formula (22) can be simplified in the region of central rapidities at LHC energies. In this region, the constant distribution in rapidity for particles produced from a string decay is a good approximation:

$$\lambda \left(\eta \right)=\frac{{\mu }_{str}}{\delta \eta },{\mu }_{str}\equiv \langle N\rangle .$$

(23)

It is also usually assumed that in this region there is translational invariance in rapidity, which leads to the dependence of the two-particle correlation function $\Lambda ({\eta }_1,{\eta }_2)$ only on the difference in the rapidities of the observed particles:

$$\Lambda ({\eta }_1,{\eta }_2)=\Lambda ({\eta }_1-{\eta }_2).$$

(24)

Under these assumptions, instead of (22), we find [31]

$${\omega }_{str}=1+{\mu }_{str}J,J\equiv \frac{1}{{\delta \eta }^2}{\int }_{\delta \eta }d{\eta }_1{\int }_{\delta \eta }d{\eta }_2\Lambda ({\eta }_1-{\eta }_2).$$

(25)

This formula was apparently used for the first time in [41]. It is important to note that, as is immediately clear from the connection (25), the Poisson form of the distribution over the number of particles produced from the decay of a string is possible only in the complete absence of correlations between them, i.e., when $\Lambda ({\eta }_1-{\eta }_2)=0$.

In paper [30], the two-particle correlation function $\Lambda (\Delta \eta ,\Delta \varphi )$ between particles separated in rapidity, $\Delta \eta ={\eta }_1-{\eta }_2$, and in azimuth, $\Delta \varphi ={\varphi }_1-{\varphi }_2$, was extracted from the ALICE experimental data on forward–backward multiplicity correlations in pp collisions at 0.9, 2.76, and 7 TeV [35]. In papers [31,32,33], it was shown that after integration over azimuthal angles

$$\Lambda \left(\Delta \eta \right)=\frac{1}{\pi }{\int }_0^{\pi }\Lambda (\Delta \eta ,\Delta \varphi )d\Delta \varphi ,$$

(26)

the resulting $\Lambda \left(\Delta \eta \right)$ is well approximated by the following exponential dependence:

$$\Lambda \left(\Delta \eta \right)={\Lambda }_0{e}^{-\frac{\left|\Delta \eta \right|}{{\eta }_{corr}}},$$

(27)

with parameters ${\Lambda }_0$ and ${\eta }_{corr}$ depending on the collision energy. For this simple form of $\Lambda ({\eta }_1-{\eta }_2)$, the integral J in (25) can be calculated explicitly [34]:

$$J=\frac{2{\Lambda }_0{\eta }_{corr}}{{\left(\delta \eta \right)}^2}\left[\delta \eta -{\eta }_{corr}\left(1-e^{-\delta \eta /{\eta }_{corr}}\right)\right].$$

(28)

Then, using in (28) the values of the parameters ${\Lambda }_0$ and ${\eta }_{corr}$ found in [31] for the initial energies of 0.9 and 7 TeV, we calculate by Formula (25) the values of the scaled variances ${\omega }_{str}$ for window widths of $\delta \eta =$ 3 and 4.8 units of rapidity. The results are presented in

Table 1. Scaled variance of multiplicity from a single string. ${\omega }_{str}$ (18), calculated using the string two-particle correlation function $\Lambda ({\eta }_1-{\eta }_2)$ from [31], according to Formulas (25) and (26)–(28) for two widths of rapidity windows $\delta \eta =$ 3 and 4.8 at initial energies of pp collision 0.9 and 7 TeV.

$\sqrt{s}$, TeV	0.9	7.0
$\delta \eta =3$	3.1	3.5
$\delta \eta =4.8$	3.6	4.0

.

5. MEM with the Negative Binomial Multiplicity Distribution from String Decay

In this section, instead of the Poisson distribution (16), we try to use the Negative Binomial Distribution (NBD) as the multiplicity distribution from a single string:

$$P_{str}^{NBD}\left(N\right)=\frac{p^N}{q^{N+{\kappa }_0}}\frac{\Gamma (N+{\kappa }_0)}{\Gamma \left({\kappa }_0\right)N!},$$

(29)

where $\Gamma (...)$ is the Gamma function, and the parameters p and q are connected by the relation $q=p+1$, with $p>0$ and ${\kappa }_0>0$. This distribution corresponds to the generating function

$$g_{NBD}\left(t\right)={(q-pt)}^{-{\kappa }_0}.$$

(30)

Distribution (29) leads to the NBD of multiplicity for events with n cut pomerons, in which $2n$ strings are formed:

$$P_n^{NBD}\left(N\right)=\frac{p^N}{q^{N+\kappa }}\frac{\Gamma (N+\kappa )}{\Gamma \left(\kappa \right)N!}.$$

(31)

The parameters p, q, and $\kappa$ are expressed through ${\mu }_{str}$ and ${\omega }_{str}$ as follows:

$$q=p+1={\omega }_{str},\kappa =2n{\kappa }_0,{\kappa }_0=\frac{{\mu }_{str}}{p}=\frac{{\mu }_{str}}{{\omega }_{str}-1}.$$

(32)

Note that the mean ${\langle N\rangle }_n$ and the scaled variance $\omega$ for distribution (31) are given by

$${\langle N\rangle }_n=\kappa p=2n{\kappa }_{0}p=2n{\mu }_{str},\omega \equiv \frac{{\langle N^2\rangle }_n-{〈N〉}_n^2}{{\langle N\rangle }_n}=q={\omega }_{str}.$$

(33)

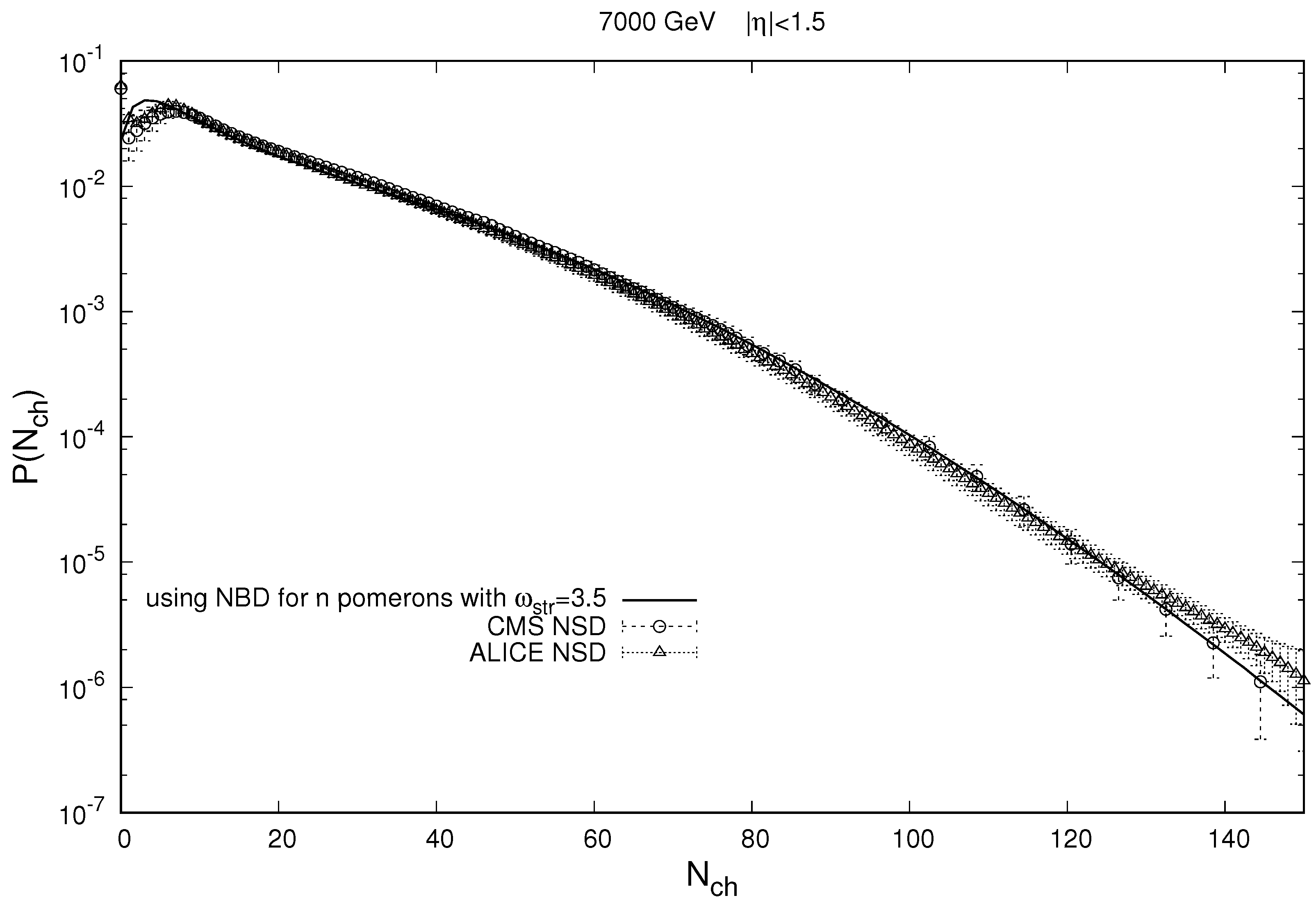
Using these formulas and the value of $\omega ={\omega }_{str}$ from Table 1 found in Section 4, we calculate the charged particle multiplicity distribution by (9) for this case. As an example, the calculation results of the multiplicity distribution in pp collisions for a window width $\delta \eta =$ 3 units of rapidity at an initial energy for the pp collision of 7 TeV are presented in Figure 4, along with the corresponding experimental data of the ALICE [3] and CMS [4] collaborations at the LHC.

In Figure 4, we see that using the NBD for the description of particle production from a single string, instead of the Poisson distribution used in the original version of the MEM, gives a better description of the multiplicity distribution in pp collisions. However, it is not yet possible to correctly describe the first few points ($N<5$). Nevertheless, these few starting points have a strong influence on the behavior of the combinants, since the combinants for a known multiplicity distribution $P\left(N\right)$ are calculated recursively using Relation (7). As can be seen from Figure 5, the oscillations of combinants with an increase in their order are still not observed when we use the NBD for the multiplicity from a single string. Conversely, for combinants calculated from experimentally measured multiplicity distributions $P\left(N\right)$, such oscillations take place (see [6,7,8] and Figure 9 below in Section 7).

6. MEM with Gaussian-Type Multiplicity Distributions

In this section, we will use Gaussian-type distributions to describe the production of particles from n pomerons. For this purpose, we will use the distributions

$$P_n\left(N\right)=Cexp\left[-\frac{{(N-2n{\mu }_{str})}^2}{2{\omega }_{str}2n{\mu }_{str}}\right],$$

(34)

limiting it to only non-negative integer values of N. This leads to a normalization condition fixing the normalization constant C:

$$\sum _{N=0}^{\infty }{P}_n\left(N\right)=1,C^{-1}=\sum _{N=0}^{\infty }exp\left[-\frac{{(N-2n{\mu }_{str})}^2}{2{\omega }_{str}2n{\mu }_{str}}\right].$$

(35)

Note that at $2n{\mu }_{str}\gg 1$ from (34), we have

$${\langle N\rangle }_n\equiv \sum _{N=1}^{\infty }N{P}_n\left(N\right)\to 2n{\mu }_{str}$$

(36)

and

$${\omega }_n\left[N\right]\equiv \frac{{\langle N^2\rangle }_n-{〈N〉}_n^2}{{\langle N\rangle }_n}\to {\omega }_{str}.$$

(37)

In distribution (34), we use the same values of the parameters: ${\mu }_{str}=k\left(s\right)\delta \eta$ is given by Formula (14), and ${\omega }_{str}$, which was calculated from the string two-particle correlation function $\Lambda ({\eta }_1-{\eta }_2)$, is given by Table 1.

The results of the calculation by Formula (9) of the resulting distribution over the multiplicity of charged particles using Gaussian distribution (34) over the multiplicity of particles for a fixed number of pomerons with the above parameters are presented in Figure 6 and Figure 7. From these figures, we see that the use of Gaussian distribution (34) for non-negative integer values of the argument gives a good (within the experimental error) description of the resulting distribution over the multiplicity of charged particles. 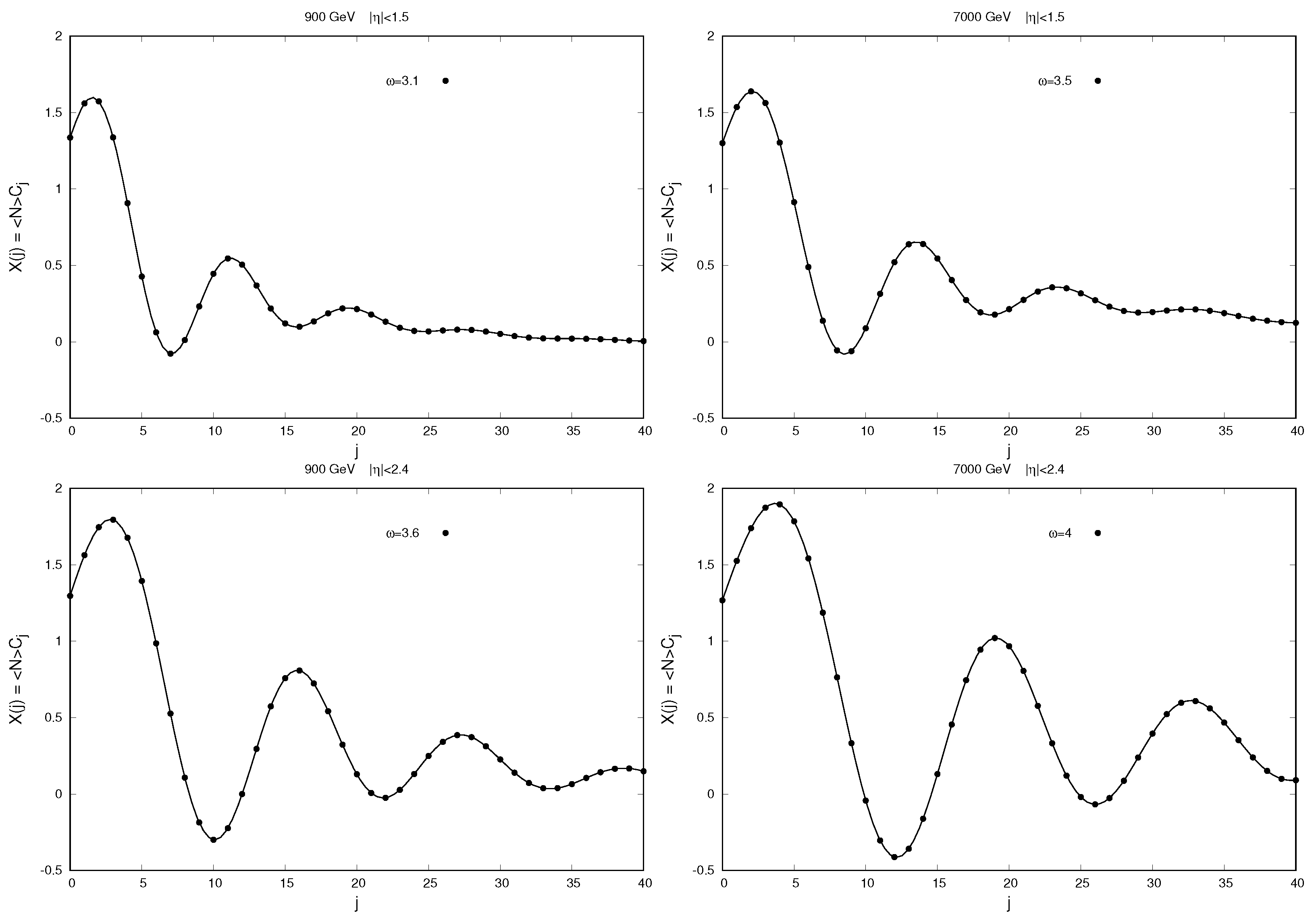This is also confirmed by the oscillatory behavior of the combinants of these distributions as functions of their numbers, as shown in Figure 8.

Analyzing the behavior of combinants as functions of their numbers, as presented in Figure 8, which was obtained in this version of the MEM, one can see the following characteristic features. The period and amplitude of the resulting oscillations increase with an increasing initial energy and increasing pseudo-rapidity observation window width. At the same time, they also become less damped.

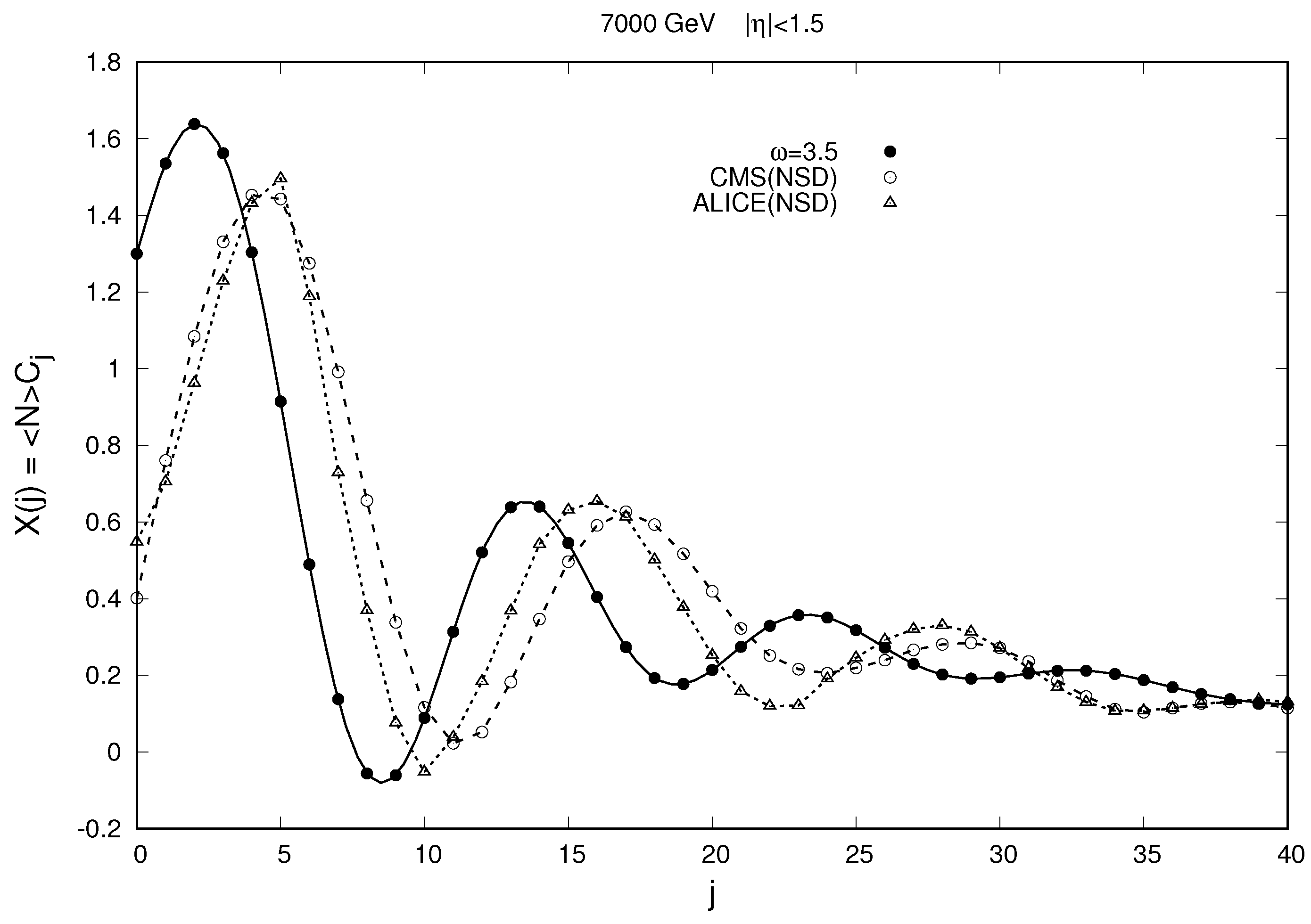
7. Comparison of Combinants with Experimental Data

A comparison of the behavior of combinants calculated using the MEM and Gaussian distribution for a multiplicity of particles from a fixed number of pomerons, (34), with experimental data from the ALICE [3] and CMS [4] collaborations at the LHC is shown in Figure 9. From this figure, it can be seen that the values of the calculated combinants demonstrate approximately the same oscillations with an increasing combinant number as the value of combinants extracted from the experimental data of the ALICE [3] and CMS [4] collaborations at the LHC, although with a certain phase shift.

Additional research showed that this phase shift in the oscillations of combinants compared to the experimental data in Figure 9 can be explained by the fact that model calculations using Formula (9) assume the presence of at least one cut pomeron (two strings) in each event. This means that the theoretical analysis corresponds to the case of so-called Non-Diffractive (ND) processes, which exclude the contribution of both Single Diffractive (SD) and Double Diffractive (DD) processes. Conversely, the experimental data used are related to the so-called NSD (Non-Single Diffractive) processes, which exclude SD processes but include DD processes.

It is clear that the main influence of DD processes on the studied multiplicity distributions in the region of central rapidities at high energies of the LHC is reduced only to the appearance of additional events with the absence of particles in the observation window at central rapidities, i.e., with an increased value of the zero bin, $P(N=0)$, due to the DD contribution. Indeed, in all the graphs in Figure 6 and Figure 7, we actually observe that for the NSD data all experimental values of $P\left(0\right)$ have a significant excess compared to the general course of the $P\left(N\right)$ dependencies at $N>0$. Therefore, it seems appropriate to eliminate the contribution of DD processes by adjusting the zero bin value, $P\left(0\right)$, of the data so that its value corresponds to the overall smooth behavior of $P\left(N\right)$ up to $N=0$.

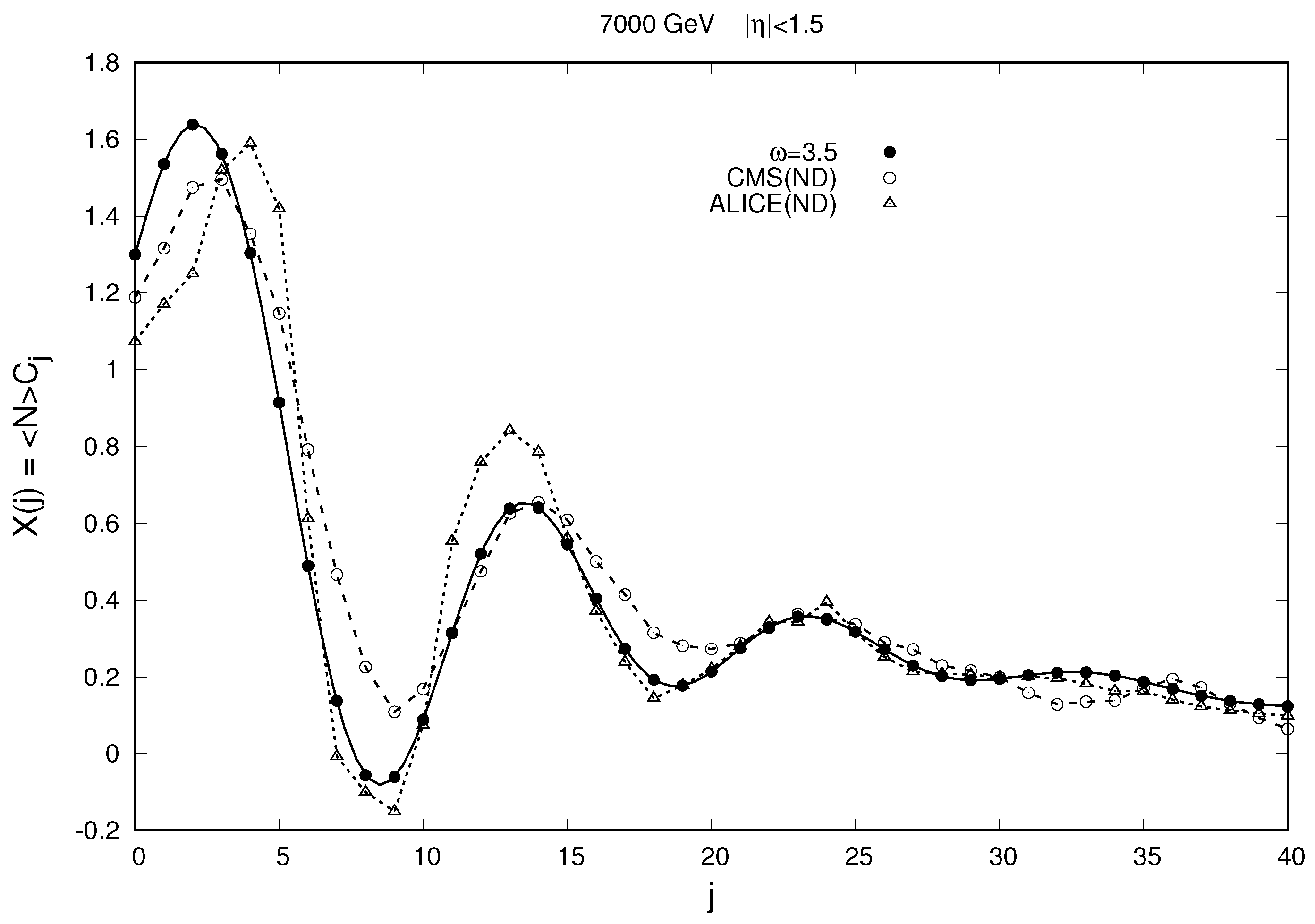
The results of comparing our model calculations of combinants with experimental data of the ALICE [3] and CMS [4] collaborations at the LHC, with the exclusion of the DD process contribution as indicated above, are presented in Figure 10. From this figure, we see that after eliminating the contribution of DD processes, the systematic phase shift observed in Figure 9 disappears. As a result, the agreement between the model calculations of the combinants and the experimental data is significantly improved—the deviations of the calculations from the experiment turn out to be approximately the same as the deviations between the results of the two experiments, ALICE [3] and CMS [4].

8. Discussion and Conclusions

Within the framework of the Multipomeron Exchange Model (MEM) [16,17,18], the distributions of the multiplicity of charged particles and their modified combinants in pp collisions at LHC energies were calculated, and the results were compared with experimental data obtained by the ALICE [3] and CMS [4] collaborations at CERN. It was found that the initial version of the MEM with a Poisson distribution of particles from a single pomeron, which corresponds to the scaled variance ${\omega }_{str}=1$ for string decay, cannot explain the experimental data (see Figure 2).

Replacing the Poisson distribution with a Negative Binomial Distribution (NBD) possessing a scaled variance ${\omega }_{str}>1$ improves the description of the multiplicity distribution in pp collisions (see Figure 4). However, it is not yet possible to correctly describe the first few points, which have a strong influence on the behavior of the combinants. Indeed, when calculating the combinants, we see in Figure 5 that this version of the MEM also cannot describe the oscillatory behavior of the combinants observed in the experimental data (see Figure 9)).

As a result, we showed that the experimentally observed dependences of the ALICE [3] and CMS [4] collaborations at the LHC can be explained when a Gaussian distribution limited to non-negative integer values of the argument, (34), is used to describe multiplicity distributions for a fixed number of pomerons. Note that in the presented approach, the value of the parameter ${\omega }_{str}$ in these distributions is not free, but is fixed based on our previous works [30,31,32,33,34], in which it was shown that ${\omega }_{str}-1$ is proportional (see Formula (25)) to the integral of the two-particle correlation function of a string, $\Lambda ({\eta }_1-{\eta }_2)$, over the observation window.

We calculated the values of the parameter ${\omega }_{str}$ from the two-particle correlation function $\Lambda ({\eta }_1-{\eta }_2)$ by Formulas (25) and (26–28) for observation windows of various widths (see Table 1). Using these values, we obtained a good description of the ALICE and CMS experimental data [3,4] on the multiplicity distributions of charged particles in pp collisions in the energy range of 0.9–7 TeV (see Figure 6 and Figure 7).

Using the obtained multiplicity distributions, we calculated the corresponding modified combinants. They turned out to be very sensitive to the shape of the spectra of multiplicity distributions, as noted in [6]. We also observed this in the experimental data (see Figure 9). Even minor deviations in the ALICE and CMS data, within the error bars, led to significant changes in the behavior of combinants, especially high-order combinants. We showed that the results of our calculations of combinants within the framework of the MEM, using Gaussian distributions for non-negative integer values of the argument as multiplicity distributions for a given number of pomerons and the values of the parameter ${\omega }_{str}$ obtained from the two-particle correlation function $\Lambda ({\eta }_1-{\eta }_2)$ of a single string (see Table 1), allowed us to also reproduce, qualitatively well, the oscillatory behavior of combinants for observation windows of different widths (see Figure 8 and Figure 10) discovered in the ALICE and CMS experimental data [3,4] for pp collisions in the energy range of 0.9–7 TeV.

9. Summary

It was found that the initial version of the Multipomeron Exchange Model (MEM) with a Poisson distribution of particles from a single pomeron cannot reproduce the multiplicity distributions observed in pp collisions by the ALICE and CMS collaborations at the LHC. Replacing the Poisson distribution with a Negative Binomial Distribution improved the agreement with the experimental data, excluding the region of low multiplicities, which did not enable us to obtain the oscillations of multiplicity distribution combinants observed in the data with an increase in their order.

It was shown that using Gaussian-type distributions as multiplicity distributions for a fixed number of pomerons within the MEM allowed us to reproduce both the resulting multiplicity distributions and the oscillatory behavior of combinants discovered in the ALICE and CMS pp collision data for observation windows of different widths in the energy range of 0.9–7 TeV. Here, the parameters of these Gaussian-type distributions are not free, but are calculated from the two-particle correlation function of a string.