Using the Difference of the Inclinations of a Pair of Counter-Orbiting Satellites to Measure the Lense–Thirring Effect
Abstract
1. Introduction
2. The General Expressions for the LT and Precessions of the Orbital Plane and Their Consequences
3. The Impact of the Unavoidable Departures of the Actual Orbits from the Ideal Ones
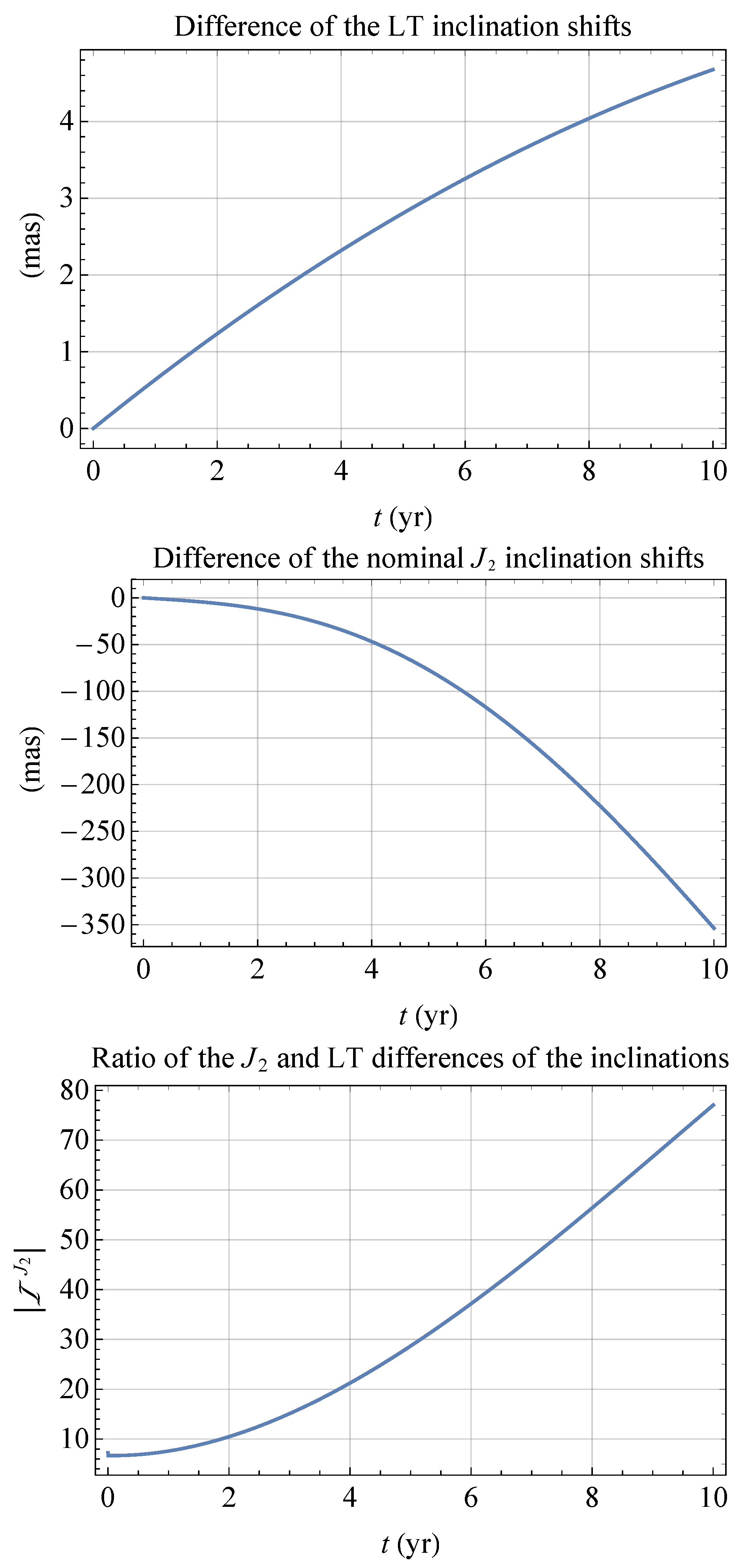
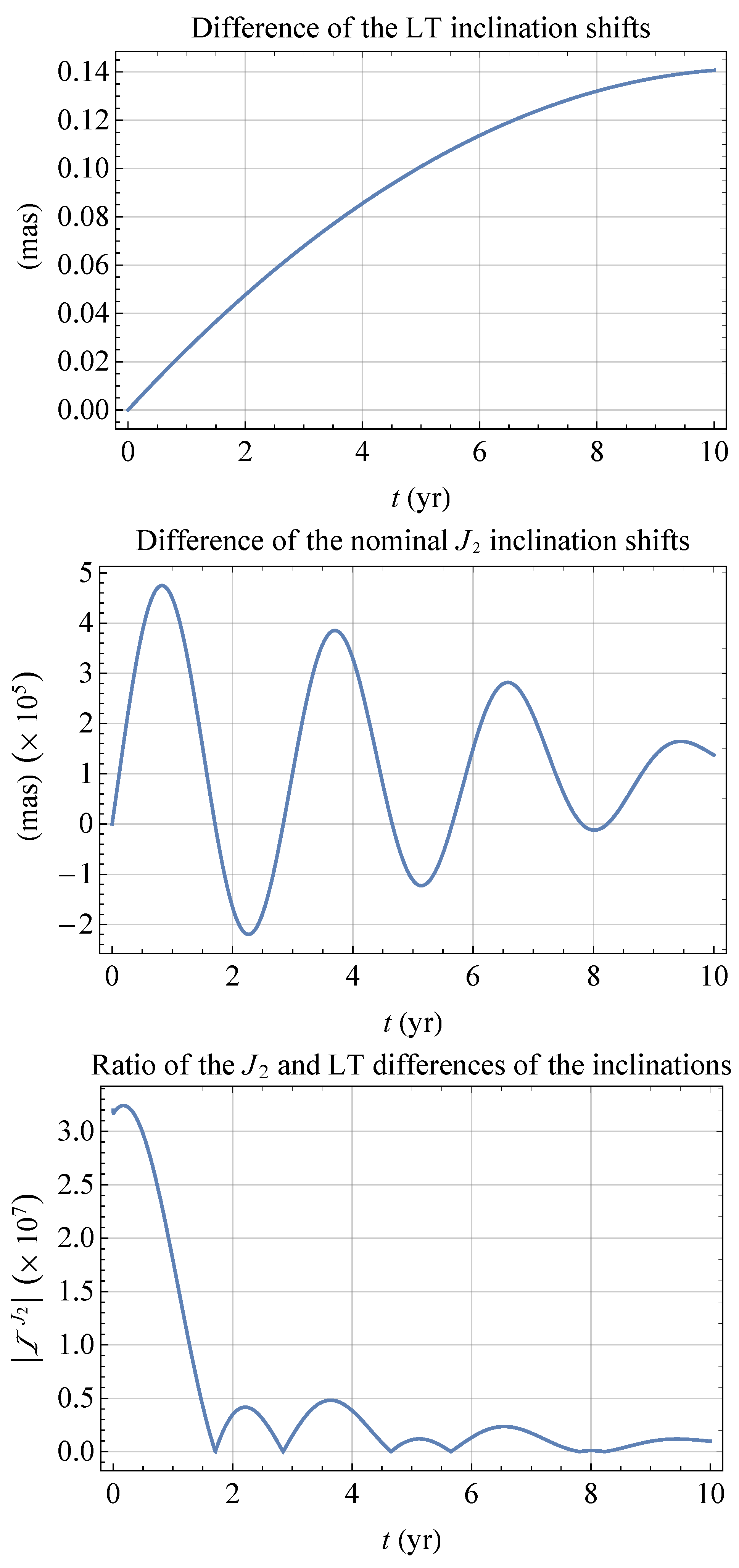
3.1. The Difference in the Inclinations
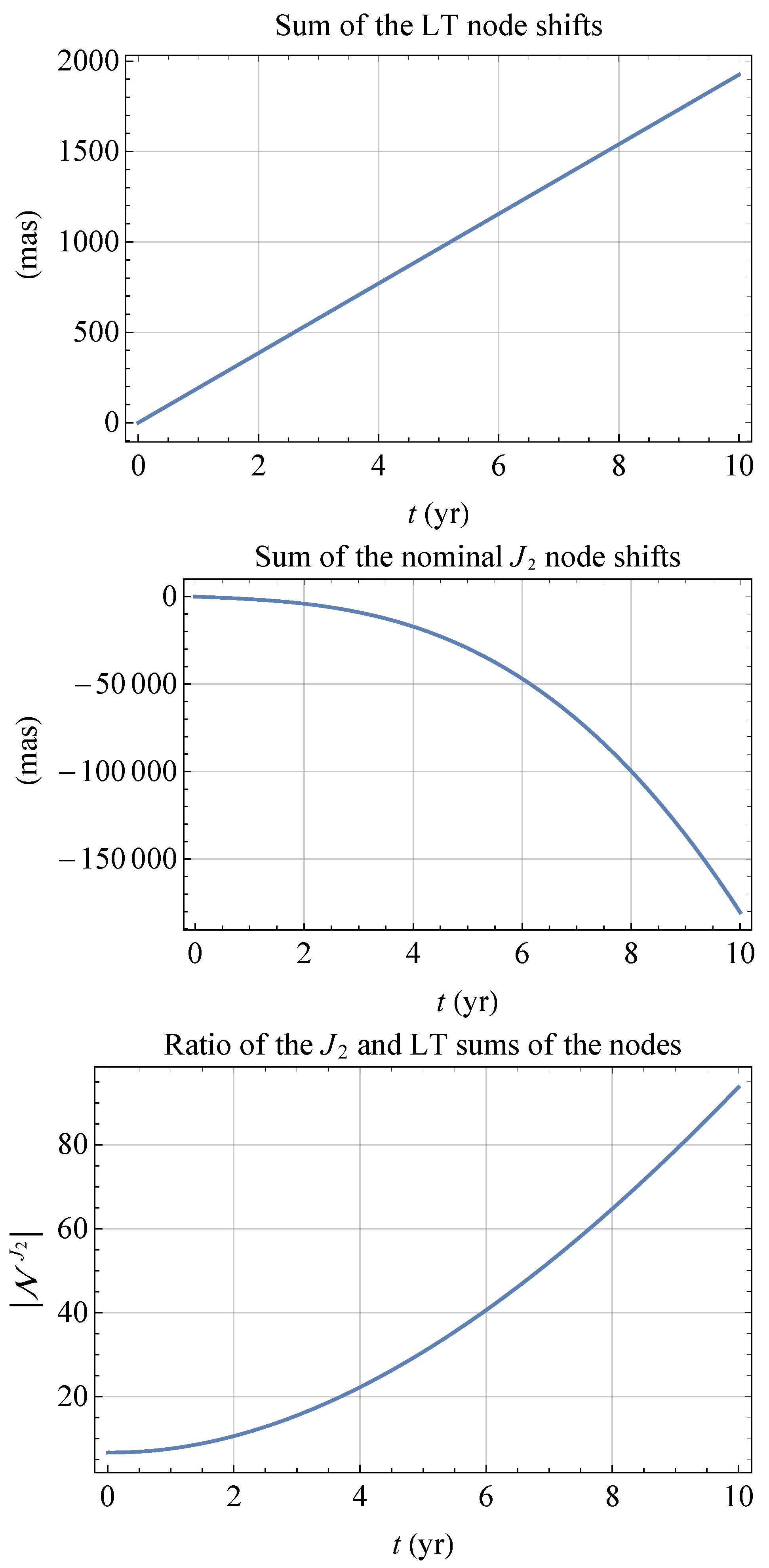
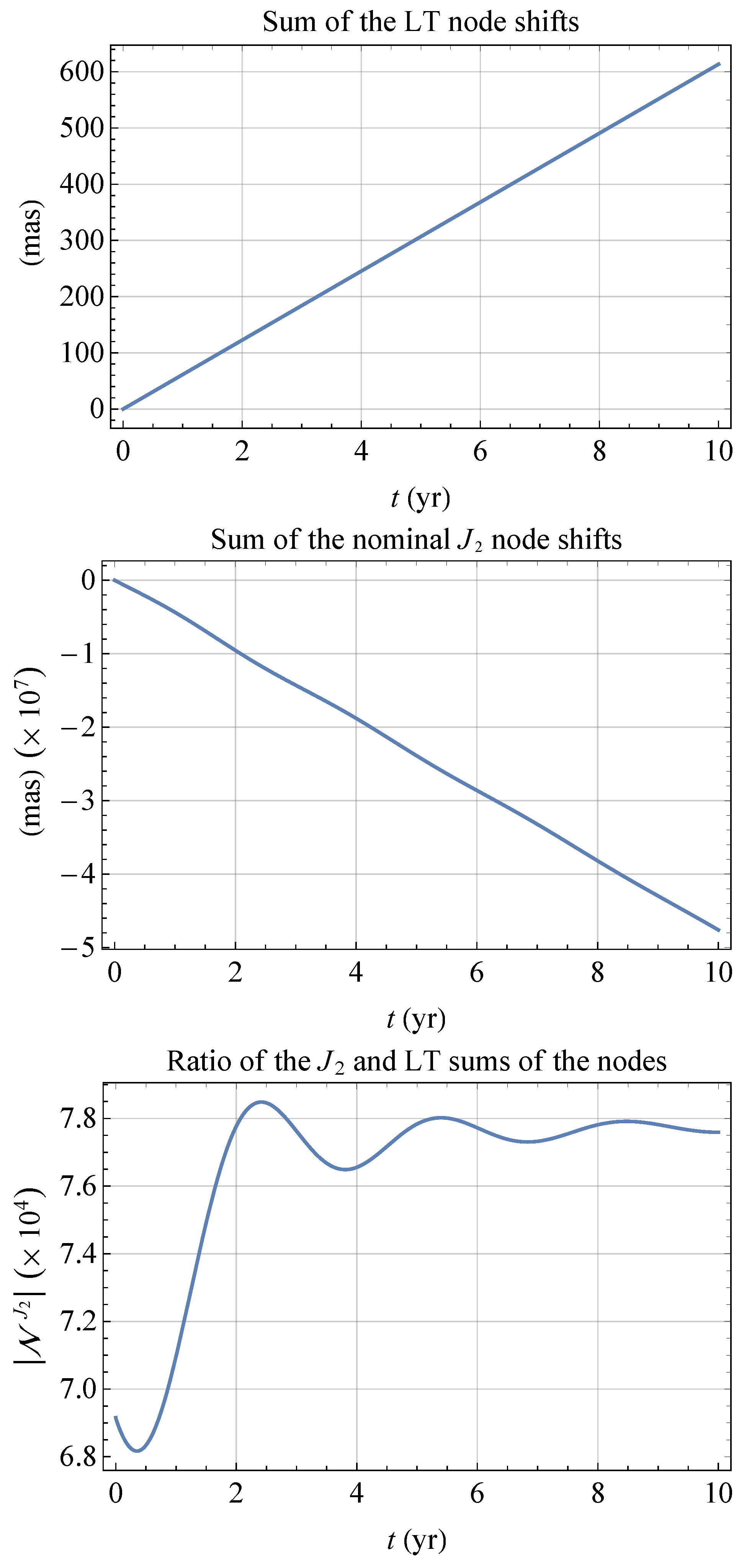
3.2. The Sum of the Nodes
4. The LAGEOS–LARES 2 Case
5. Summary and Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lense, J.; Thirring, H. Über den Einfluß der Eigenrotation der Zentralkörper auf die Bewegung der Planeten und Monde nach der Einsteinschen Gravitationstheorie. Phys. Z 1918, 19, 156–163. [Google Scholar]
- Mashhoon, B.; Hehl, F.W.; Theiss, D.S. On the gravitational effects of rotating masses: The Thirring–Lense papers. Gen. Relativ. Gravit. 1984, 16, 711–750. [Google Scholar] [CrossRef]
- Pfister, H. On the history of the so–called Lense–Thirring effect. Gen. Relativ. Gravit. 2007, 39, 1735–1748. [Google Scholar] [CrossRef]
- Pfister, H. The History of the So–Called Lense–Thirring Effect. In the Eleventh Marcel Grossmann Meeting on Recent Developments in Theoretical and Experimental General Relativity, Gravitation and Relativistic Field Theories; Kleinert, H., Jantzen, R.T., Ruffini, R., Eds.; World Scientific: Singapore, 2008; pp. 2456–2458. [Google Scholar] [CrossRef]
- Pfister, H. Gravitomagnetism: From Einstein’s 1912 Paper to the Satellites LAGEOS and Gravity Probe B. In Relativity and Gravitation; Bičák, J., Ledvinka, T., Eds.; Springer Proceedings in Physics; Springer: Cham, Switzerland, 2014; Volume 157, pp. 191–197. [Google Scholar] [CrossRef]
- Cohen, S.C.; Smith, D.E. LAGEOS Scientific results: Introduction. J. Geophys. Res. 1985, 90, 9217–9220. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Petterson, J.A. The Lense–Thirring Effect and Accretion Disks around Kerr Black Holes. Astrophys. J. Lett. 1975, 195, L65. [Google Scholar] [CrossRef]
- Rees, M.J. Relativistic jets and beams in radio galaxies. Nature 1978, 275, 516–517. [Google Scholar] [CrossRef]
- Rees, M.J. Black Hole Models for Active Galactic Nuclei. Annu. Rev. Astron. Astr. 1984, 22, 471–506. [Google Scholar] [CrossRef]
- Stone, N.; Loeb, A. Observing Lense-Thirring Precession in Tidal Disruption Flares. Phys. Rev. Lett. 2012, 108, 061302. [Google Scholar] [CrossRef]
- Franchini, A.; Lodato, G.; Facchini, S. Lense–Thirring precession around supermassive black holes during tidal disruption events. Mon. Not. Roy. Astron. Soc. 2016, 455, 1946–1956. [Google Scholar] [CrossRef]
- Pasham, D.R.; Zajaček, M.; Nixon, C.J.; Coughlin, E.R.; Śniegowska, M.; Janiuk, A.; Czerny, B.; Wevers, T.; Guolo, M.; Ajay, Y.; et al. Lense-Thirring precession after a supermassive black hole disrupts a star. Nature 2024, 630, 325–328. [Google Scholar] [CrossRef]
- Stella, L.; Vietri, M. Lense–Thirring Precession and Quasi–periodic Oscillations in Low-Mass X-Ray Binaries. Astrophys. J. Lett. 1998, 492, L59–L62. [Google Scholar] [CrossRef]
- Stella, L.; Possenti, A. Lense–Thirring Precession in the Astrophysical Context. Space Sci. Rev. 2009, 148, 105–121. [Google Scholar] [CrossRef]
- Braginsky, V.B.; Caves, C.M.; Thorne, K.S. Laboratory experiments to test relativistic gravity. Phys. Rev. D 1977, 15, 2047–2068. [Google Scholar] [CrossRef]
- Dymnikova, I.G. REVIEWS OF TOPICAL PROBLEMS: Motion of particles and photons in the gravitational field of a rotating body (In memory of Vladimir Afanas’evich Ruban). Sov. Phys. Usp. 1986, 29, 215–237. [Google Scholar] [CrossRef]
- Tartaglia, A. Angular–momentum effects in weak gravitational fields. Europhys. Lett. 2002, 60, 167–173. [Google Scholar] [CrossRef]
- Ruggiero, M.L.; Tartaglia, A. Gravitomagnetic effects. Nuovo Cim. B 2002, 117, 743. [Google Scholar] [CrossRef]
- Schäfer, G. Gravitomagnetic Effects. Gen. Relativ. Gravit. 2004, 36, 2223–2235. [Google Scholar] [CrossRef]
- Schäfer, G. Gravitomagnetism in Physics and Astrophysics. Space Sci. Rev. 2009, 148, 37–52. [Google Scholar] [CrossRef]
- Pugh, G.E. (Ed.) Proposal for a Satellite Test of the Coriolis Prediction of General Relativity. In Nonlinear Gravitodynamics: The Lense-Thirring Effect; Research memorandum; Weapons Systems Evaluation Group, The Pentagon: Washington, DC, USA, 1959; Reprinted in Ruffini, R.J.; Sigismondi, C. (Eds.) Nonlinear Gravitodynamics: The Lense-Thirring Effect; World Scientific: Singapore, 2003; pp. 414–426. [Google Scholar]
- Schiff, L. Possible new experimental test of general relativity theory. Phys. Rev. Lett. 1960, 4, 215–217. [Google Scholar] [CrossRef]
- Everitt, C.W.F.; Debra, D.B.; Parkinson, B.W.; Turneaure, J.P.; Conklin, J.W.; Heifetz, M.I.; Keiser, G.M.; Silbergleit, A.S.; Holmes, T.; Kolodziejczak, J.; et al. Gravity Probe B: Final Results of a Space Experiment to Test General Relativity. Phys. Rev. Lett. 2011, 106, 221101. [Google Scholar] [CrossRef]
- Everitt, C.W.F.; Muhlfelder, B.; Debra, D.B.; Parkinson, B.W.; Turneaure, J.P.; Silbergleit, A.S.; Acworth, E.B.; Adams, M.; Adler, R.; Bencze, W.J.; et al. The Gravity Probe B test of general relativity. Class. Quantum Gravit. 2015, 32, 224001. [Google Scholar] [CrossRef]
- Everitt, C.W.F. The Gyroscope experiment—I: General description and analysis of gyroscope performance. In Proceedings of the International School of Physics “Enrico Fermi”. Course LVI. Experimental Gravitation; Bertotti, B., Ed.; Academic Press: Cambridge, MA, USA, 1974; pp. 331–360. [Google Scholar]
- Everitt, C.W.F.; Buchman, S.; Debra, D.B.; Keiser, G.M.; Lockhart, J.M.; Muhlfelder, B.; Parkinson, B.W.; Turneaure, J.P.; Gravity Probe B team. Gravity Probe B: Countdown to Launch. In Gyros, Clocks, Interferometers…: Testing Relativistic Gravity in Space; Lämmerzahl, C., Everitt, C.W.F., Hehl, F.W., Eds.; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2001; Volume 562, pp. 52–82. [Google Scholar] [CrossRef]
- Park, R.S.; Folkner, W.M.; Konopliv, A.S. Estimation of Solar Angular Momentum from Lense–Thirring Precession of Mercury. Iau Gen. Assem. 2015, 22, 2227771. [Google Scholar]
- Pavlov, D.; Dolgakov, I. General relativity tests by the dynamics of the Solar system. In Journées 2023 “Systèmes de Rférénce Spatio-Temporels"; Bizouard, C., Fienga, A., Paganelli, F., Eds.; Observatoire de la Côte d’Azur, 2024; pp. 156–160. [Google Scholar]
- Pavlov, D.; Dolgakov, I. Studying the Properties of Spacetime with an Improved Dynamical Model of the Inner Solar System. Universe 2024, 10, 413. [Google Scholar] [CrossRef]
- Bolton, S.J.; Lunine, J.; Stevenson, D.; Connerney, J.E.P.; Levin, S.; Owen, T.C.; Bagenal, F.; Gautier, D.; Ingersoll, A.P.; Orton, G.S.; et al. The Juno Mission. Space Sci. Rev. 2017, 213, 5–37. [Google Scholar] [CrossRef]
- Finocchiaro, S.; Iess, L.; Folkner, W.M.; Asmar, S. The Determination of Jupiter’s Angular Momentum from the Lense-Thirring Precession of the Juno Spacecraft. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 5–9 December 2011; Volume 2011, p. P41B-1620. [Google Scholar]
- Durante, D.; Cappuccio, P.; di Stefano, I.; Zannoni, M.; Casajus, L.G.; Lari, G.; Falletta, M.; Buccino, D.R.; Iess, L.; Park, R.S.; et al. Testing General Relativity with Juno at Jupiter. Astrophys. J. 2024, 971, 145. [Google Scholar] [CrossRef]
- Ciufolini, I.; Lucchesi, D.M.; Vespe, F.; Mandiello, A. Measurement of dragging of inertial frames and gravitomagnetic field using laser–ranged satellites. Nuovo Cim. A 1996, 109A, 575–590. [Google Scholar] [CrossRef]
- Pearlman, M.; Arnold, D.; Davis, M.; Barlier, F.; Biancale, R.; Vasiliev, V.; Ciufolini, I.; Paolozzi, A.; Pavlis, E.C.; Sośnica, K.; et al. Laser geodetic satellites: A high-accuracy scientific tool. J. Geod. 2019, 93, 2181–2194. [Google Scholar] [CrossRef]
- Coulot, D.; Deleflie, F.; Bonnefond, P.; Exertier, P.; Laurain, O.; de Saint-Jean, B. Satellite Laser Ranging. In Encyclopedia of Solid Earth Geophysics; Gupta, H.K., Ed.; Encyclopedia of Earth Sciences Series; Springer: Berlin/Heidelberg, Germany, 2011; pp. 1049–1055. [Google Scholar] [CrossRef]
- Iorio, L.; Lichtenegger, H.I.M.; Ruggiero, M.L.; Corda, C. Phenomenology of the Lense–Thirring effect in the solar system. Astrophys. Space Sci. 2011, 331, 351–395. [Google Scholar] [CrossRef]
- Ciufolini, I.; Paolozzi, A.; Koenig, R.; Pavlis, E.C.; Ries, J.; Matzner, R.; Gurzadyan, V.; Penrose, R.; Sindoni, G.; Paris, C. Fundamental Physics and General Relativity with the LARES and LAGEOS satellites. Nucl. Phys. B Proc. Suppl. 2013, 243, 180–193. [Google Scholar] [CrossRef]
- Renzetti, G. History of the attempts to measure orbital frame–dragging with artificial satellites. Centr. Eur. J. Phys. 2013, 11, 531–544. [Google Scholar] [CrossRef]
- Lucchesi, D.M.; Anselmo, L.; Bassan, M.; Magnafico, C.; Pardini, C.; Peron, R.; Pucacco, G.; Visco, M. General Relativity Measurements in the Field of Earth with Laser–Ranged Satellites: State of the Art and Perspectives. Universe 2019, 5, 141. [Google Scholar] [CrossRef]
- Lucchesi, D.M.; Visco, M.; Peron, R.; Bassan, M.; Pucacco, G.; Pardini, C.; Anselmo, L.; Magnafico, C. A 1% Measurement of the Gravitomagnetic Field of the Earth with Laser–Tracked Satellites. Universe 2020, 6, 139. [Google Scholar] [CrossRef]
- Milani, A.; Nobili, A.; Farinella, P. Non–Gravitational Perturbations and Satellite Geodesy; Adam Hilge: London, UK, 1987. [Google Scholar]
- Lucchesi, D.M. Reassessment of the error modelling of non–gravitational perturbations on LAGEOS II and their impact in the Lense–Thirring determination. Part I. Planet. Space Sci. 2001, 49, 447–463. [Google Scholar] [CrossRef]
- Lucchesi, D.M. Reassessment of the error modelling of non–gravitational perturbations on LAGEOS II and their impact in the Lense–Thirring derivation–Part II. Planet. Space Sci. 2002, 50, 1067–1100. [Google Scholar] [CrossRef]
- Lucchesi, D.M. LAGEOS Satellites Germanium Cube–Corner-Retroreflectors and the Asymmetric Reflectivity Effect. Celest. Mech. Dyn. Astr. 2004, 88, 269–291. [Google Scholar] [CrossRef]
- Lucchesi, D.M.; Ciufolini, I.; Andrés, J.I.; Pavlis, E.C.; Peron, R.; Noomen, R.; Currie, D.G. LAGEOS II perigee rate and eccentricity vector excitations residuals and the Yarkovsky–Schach effect. Planet. Space Sci. 2004, 52, 699–710. [Google Scholar] [CrossRef]
- Van Patten, R.A.; Everitt, C.W.F. A Possible Experiment with Two Counter-Orbiting Drag-Free Satellites to Obtain a New Test of Einstein’s General Theory of Relativity and Improved Measurements in Geodesy. Celest. Mech. Dyn. Astr. 1976, 13, 429–447. [Google Scholar] [CrossRef]
- Van Patten, R.A.; Everitt, C.W.F. Possible experiment with two counter-orbiting drag-free satellites to obtain a new test of Einstein’s general theory of relativity and improved measurements in geodesy. Phys. Rev. Lett. 1976, 36, 629–632. [Google Scholar] [CrossRef]
- Ciufolini, I. Measurement of the Lense-Thirring drag on high-altitude, laser-ranged artificial satellites. Phys. Rev. Lett. 1986, 56, 278–281. [Google Scholar] [CrossRef]
- Ciufolini, I.; Paolozzi, A.; Pavlis, E.C.; Ries, J.C.; Matzner, R.; Paris, C.; Ortore, E.; Gurzadyan, V.; Penrose, R. The LARES 2 satellite, general relativity and fundamental physics. Eur. Phys. J. C 2023, 83, 87. [Google Scholar] [CrossRef]
- Iorio, L. Limitations in Testing the Lense–Thirring Effect with LAGEOS and the Newly Launched Geodetic Satellite LARES 2. Universe 2023, 9, 211. [Google Scholar] [CrossRef]
- Iorio, L. A new proposal for measuring the Lense-Thirring effect with a pair of supplementary satellites in the gravitational field of the Earth. Phys. Lett. A 2003, 308, 81–84. [Google Scholar] [CrossRef]
- Souchay, J.; Capitaine, N. Precession and Nutation of the Earth. In Tides in Astronomy and Astrophysics; Souchay, J., Mathis, S., Tokieda, T., Eds.; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2013; Volume 861, pp. 115–166. [Google Scholar] [CrossRef]
- Petit, G.; Luzum, B. (Eds.) IERS Conventions (2010); IERS Technical Note; Verlag des Bundesamts für Kartographie und Geodäsie: Frankfurt am Main, Germany, 2010; Volume 36. [Google Scholar]
- Capitaine, N.; Wallace, P.T. High precision methods for locating the celestial intermediate pole and origin. Astron. Astrophys. 2006, 450, 855–872. [Google Scholar] [CrossRef]
- Montenbruck, O.; Gill, E. Satellite Orbits; Spinger: Berlin/Heidelberg, Germany, 2000. [Google Scholar] [CrossRef]
- Ciufolini, I.; Paris, C.; Pavlis, E.C.; Ries, J.C.; Matzner, R.; Deka, D.; Ortore, E.; Kuzmicz-Cieslak, M.; Gurzadyan, V.; Penrose, R.; et al. On the high accuracy to test dragging of inertial frames with the LARES 2 space experiment. Eur. Phys. J. C 2024, 84, 998. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iorio, L. Using the Difference of the Inclinations of a Pair of Counter-Orbiting Satellites to Measure the Lense–Thirring Effect. Universe 2024, 10, 447. https://doi.org/10.3390/universe10120447
Iorio L. Using the Difference of the Inclinations of a Pair of Counter-Orbiting Satellites to Measure the Lense–Thirring Effect. Universe. 2024; 10(12):447. https://doi.org/10.3390/universe10120447
Chicago/Turabian StyleIorio, Lorenzo. 2024. "Using the Difference of the Inclinations of a Pair of Counter-Orbiting Satellites to Measure the Lense–Thirring Effect" Universe 10, no. 12: 447. https://doi.org/10.3390/universe10120447
APA StyleIorio, L. (2024). Using the Difference of the Inclinations of a Pair of Counter-Orbiting Satellites to Measure the Lense–Thirring Effect. Universe, 10(12), 447. https://doi.org/10.3390/universe10120447





