CESE Schemes for Solar Wind Plasma MHD Dynamics
Abstract
1. Introduction
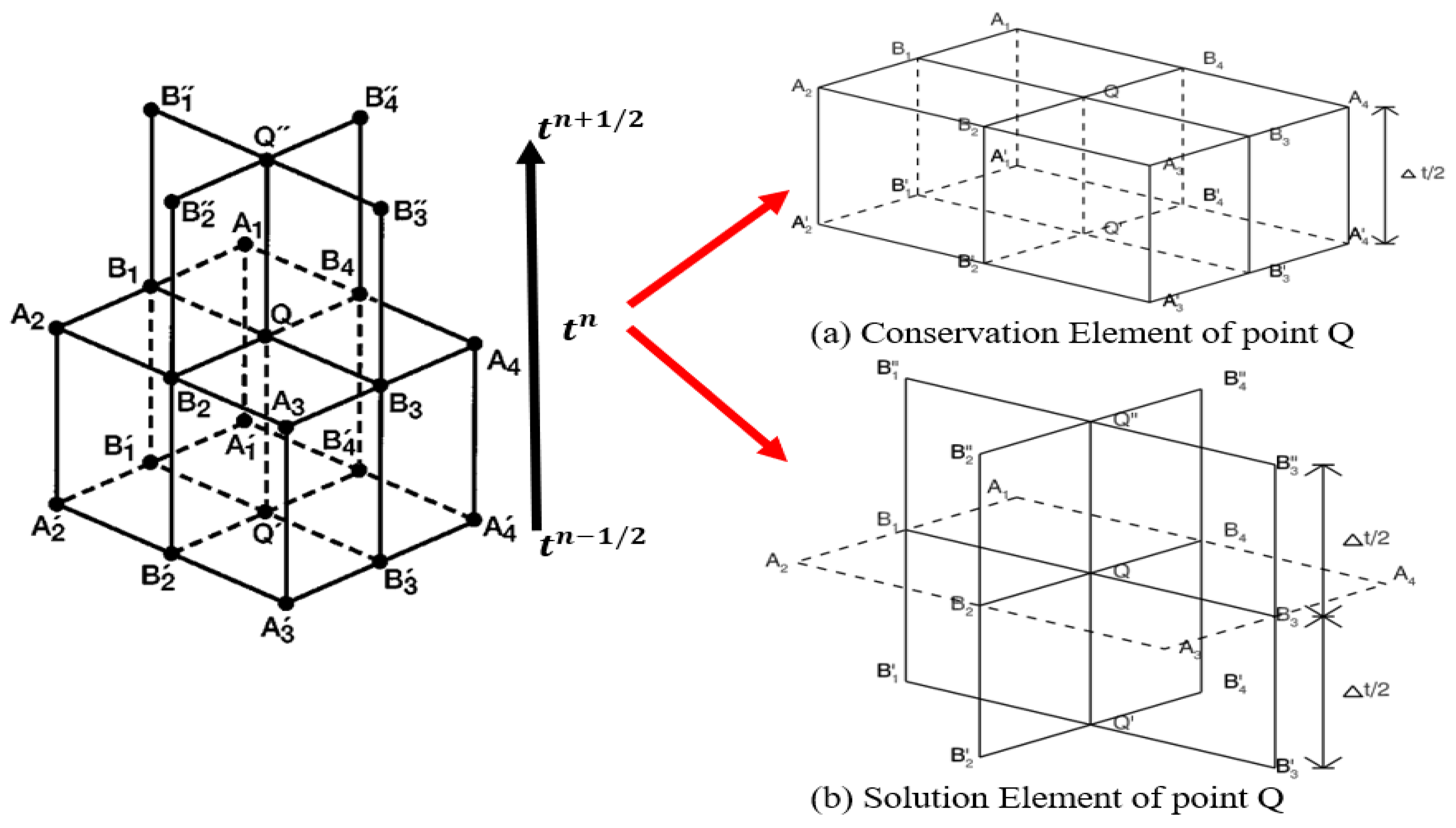
2. Brief Introduction to CESE Method
3. Development of CESE-MHD Models and Their Applications
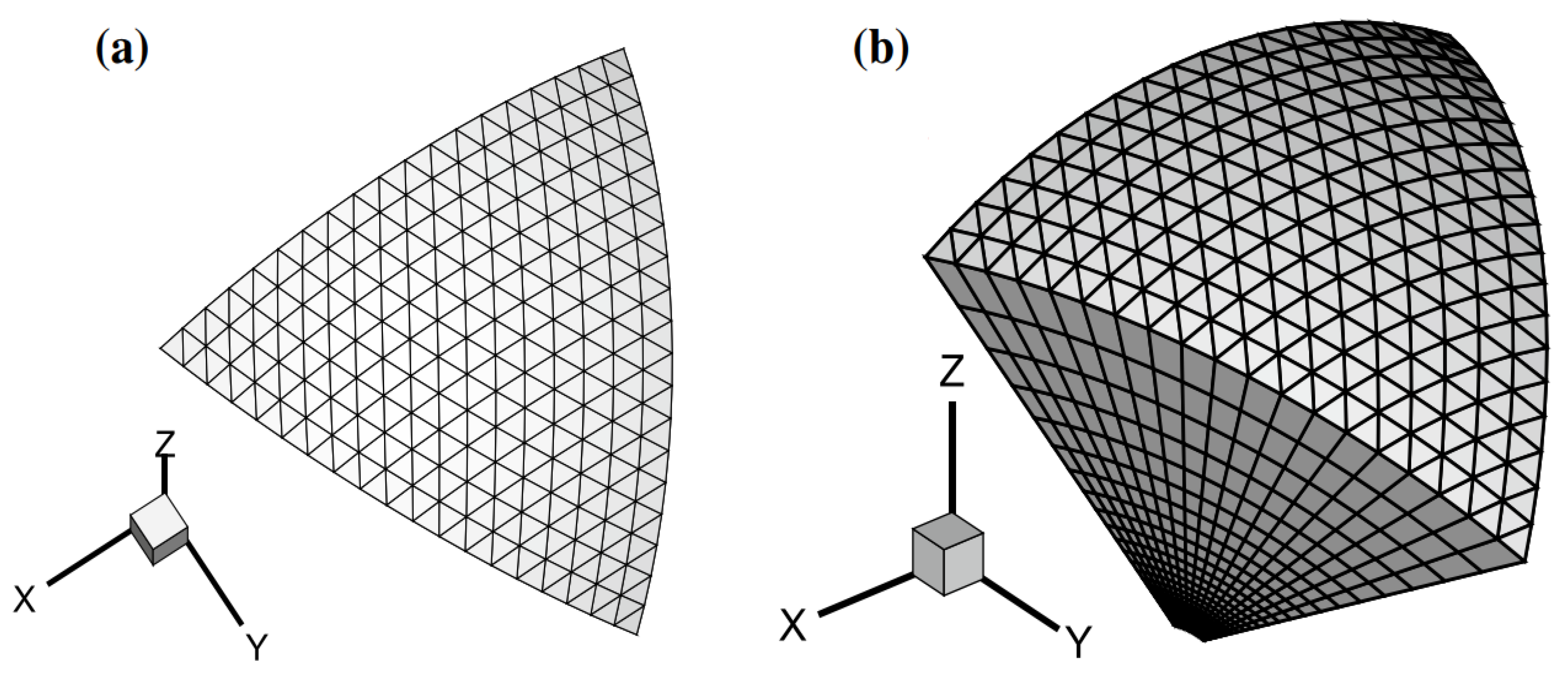
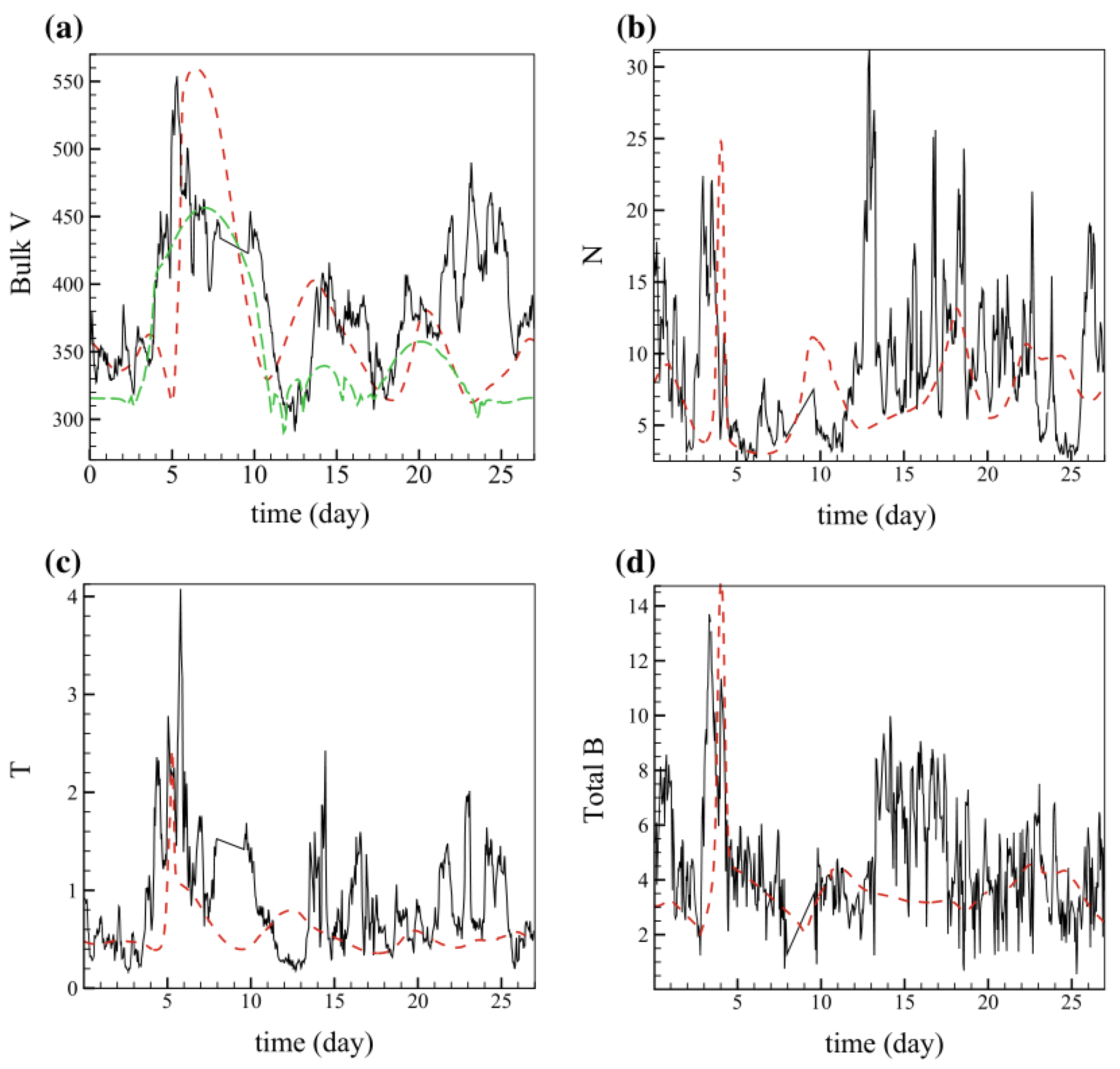
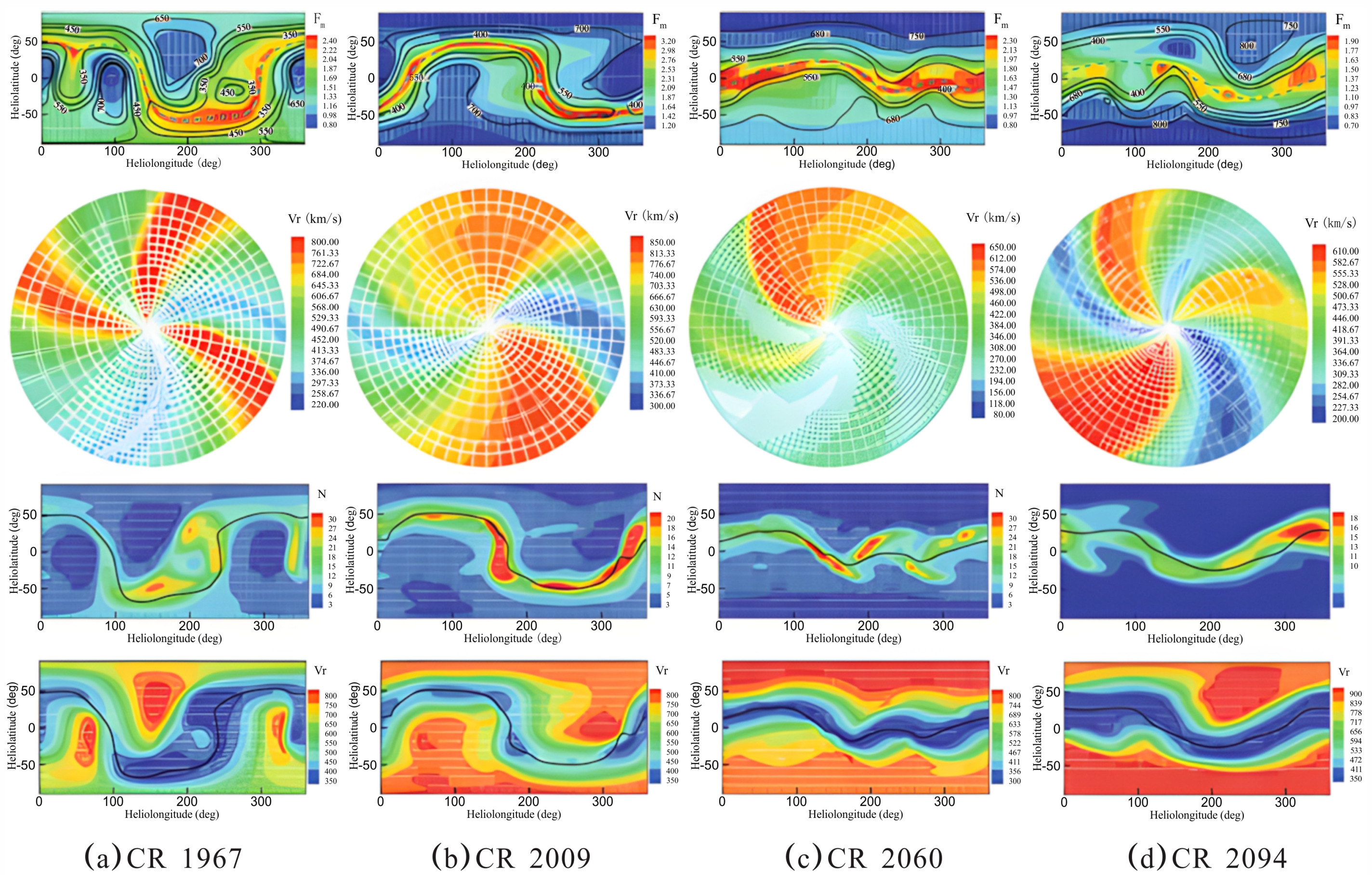
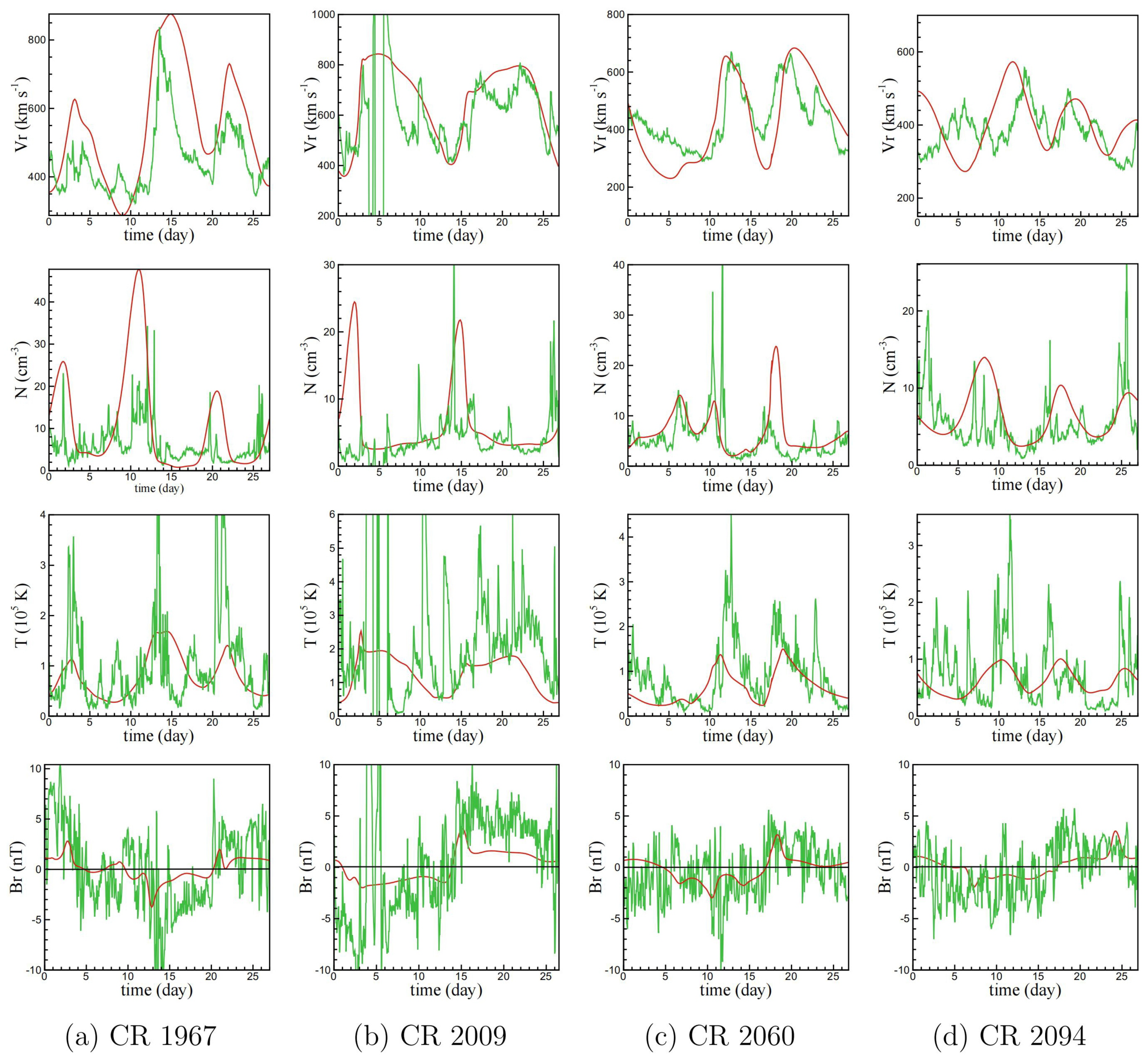
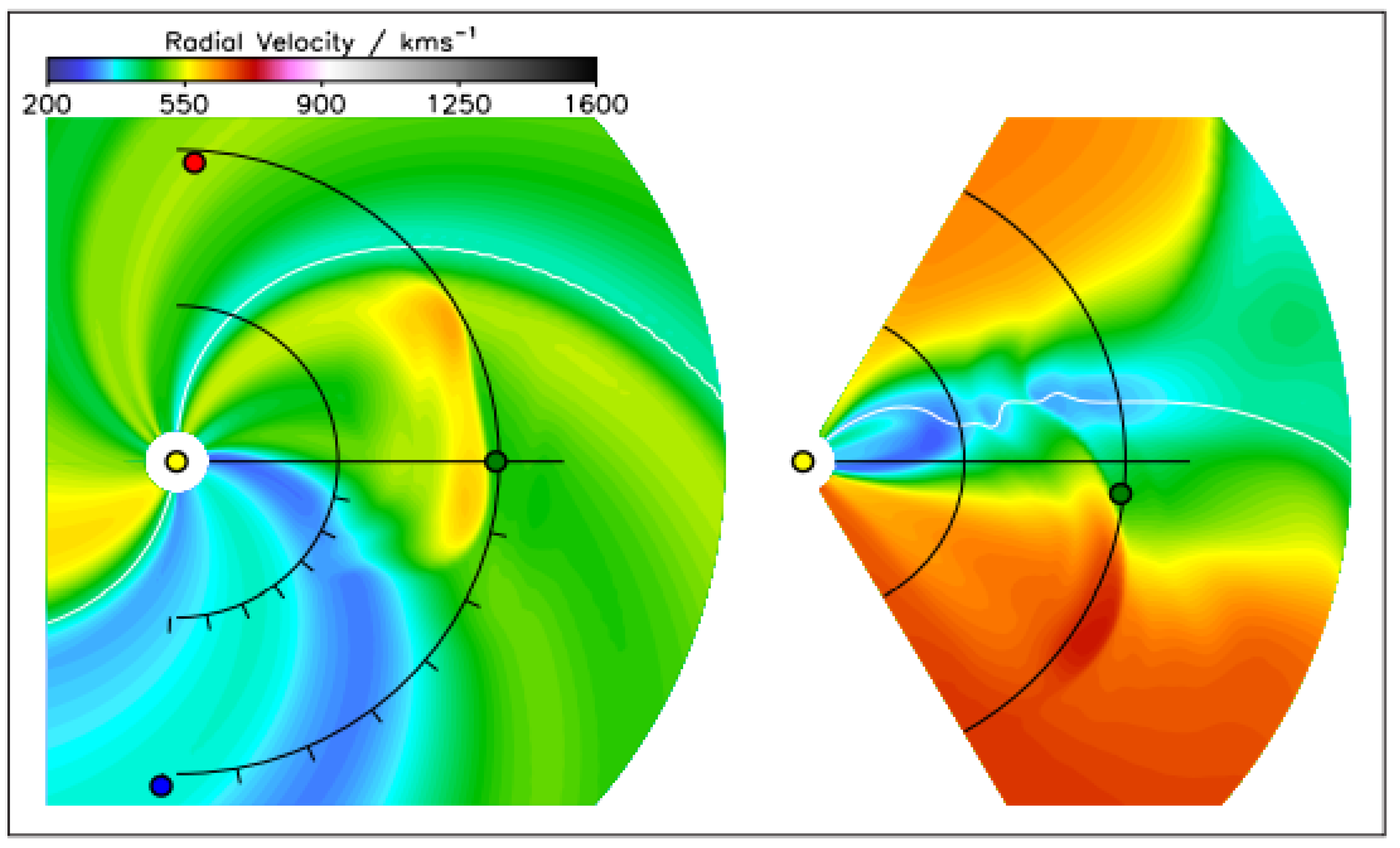
3.1. CESE-MHD Models Applied to Background Solar Wind
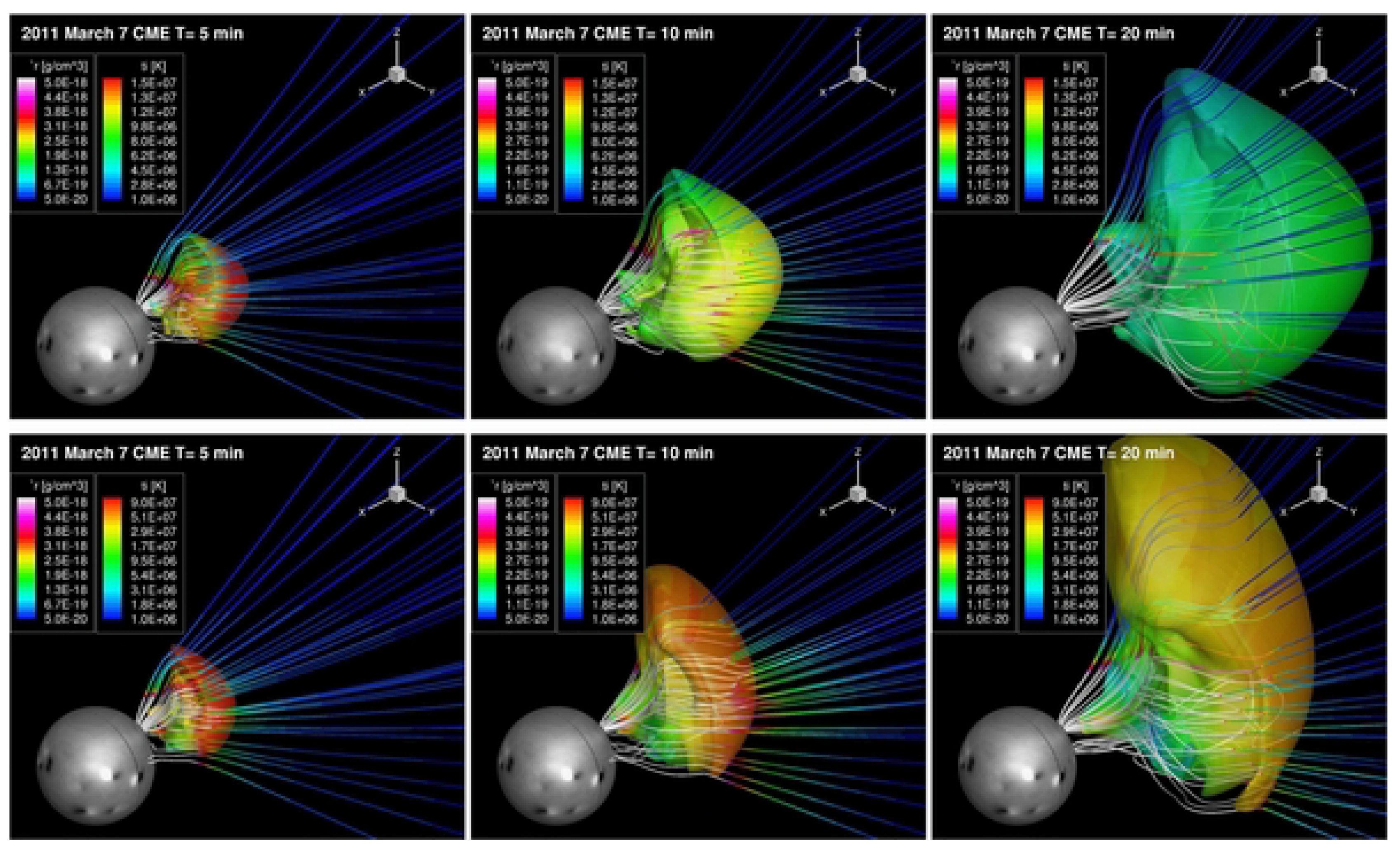
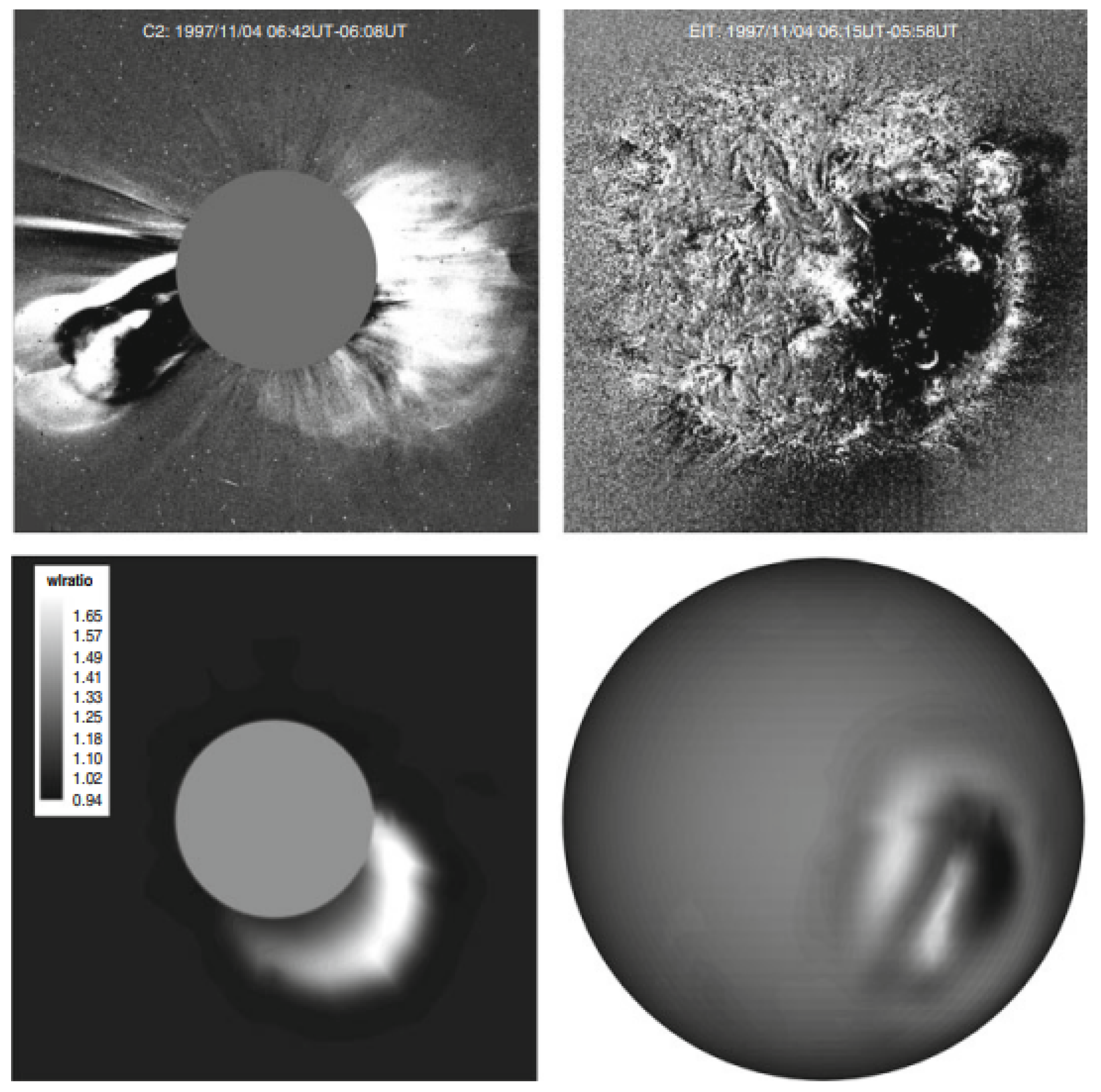
3.2. CESE-MHD Models Applied to Solar Eruptive Activities
3.3. CESE-MHD Models Applied to Magnetosphere
4. Conclusions and Future Avenues
Author Contributions
Funding
Conflicts of Interest
References
- Chang, S.C. The Method of Space-Time Conservation Element and Solution Element—A New Approach for Solving the Navier-Stokes and Euler Equations. J. Comput. Phys. 1995, 119, 295–324. [Google Scholar] [CrossRef]
- Feng, X. Magnetohydrodynamic Modeling of the Solar Corona and Heliosphere; Springer: Singapore, 2020; pp. 1–763. [Google Scholar]
- Chang, S.C.; Wang, X.Y.; Chow, C.Y. The Space-Time Conservation Element and Solution Element Method: A New High-Resolution and Genuinely Multidimensional Paradigm for Solving Conservation Laws. J. Comput. Phys. 1999, 156, 89–136. [Google Scholar] [CrossRef]
- Chang, S.C.; Wang, X.Y. A 2D Non-Splitting Unstructured Triangular Mesh Euler Solver Based on the Space-Time Conservation Element and Solution Element Method. Comput. Fluid Dyn. J. 1999, 8, 309–325. [Google Scholar] [CrossRef]
- Chang, S.C.; Wang, X.Y.; To, W.M. Application of the Space–Time Conservation Element and Solution Element Method to One-Dimensional Convection–Diffusion Problems. J. Comput. Phys. 2000, 165, 189–215. [Google Scholar] [CrossRef]
- Zhang, Z.C.; Yu, S.; Chang, S.C. A Space-Time Conservation Element and Solution Element Method for Solving the Two- and Three-Dimensional Unsteady Euler Equations Using Quadrilateral and Hexahedral Meshes. J. Comput. Phys. 2002, 175, 168–199. [Google Scholar] [CrossRef]
- Chang, S.C. A new approach for constructing highly stable high order, cese schemes. In Proceedings of the AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010. [Google Scholar]
- Wang, X.Y.J. A Summary of the Space-Time Conservation Element and Solution Element (CESE) Method. In Proceedings of the NASA/TM—2015-218743, Hampton, NY, USA, June 2015. [Google Scholar]
- Feng, X.; Hu, Y.; Wei, F. Modeling the Resistive MHD by the Cese Method. Sol. Phys. 2006, 235, 235–257. [Google Scholar] [CrossRef]
- Hu, Y.; Feng, X. Numerical Study for the Bursty Nature of Spontaneous Fast Reconnection. Sol. Phys. 2006, 238, 329–345. [Google Scholar] [CrossRef]
- Jiang, C.; Feng, X. Extrapolation of the solar coronal magnetic field from sdo/hmi magnetogram by a CESE–MHD–NLFFF code. Astrophys. J. 2013, 769, 144. [Google Scholar] [CrossRef]
- Feng, X.S.; Jiang, C.W.; Xiang, C.Q.; Zhao, X.P.; Wu, S.T. A data-driven model for the global coronal evolution. Astrophys. J. 2012, 758, 62. [Google Scholar] [CrossRef]
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics, 3rd ed.; A Practical Introduction; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Wen, C.Y.; Jiang, Y.; Shi, L. Space–Time Conservation Element and Solution Element Method; Springer: Singapore, 2023; p. 139. [Google Scholar]
- Yang, Y.; Feng, X.S.; Jiang, C.W. A high-order CESE scheme with a new divergence-free method for MHD numerical simulation. JCoPh 2017, 349, 561–581. [Google Scholar] [CrossRef]
- Zhou, Y.; Feng, X. A Two-Dimensional Third-Order CESE Scheme for Ideal MHD Equations. Commun. Comput. Phys. 2023, 34, 94–115. [Google Scholar] [CrossRef]
- Goodrich, C.; Sussman, A.; Lyon, J.; Shay, M.; Cassak, P. The CISM code coupling strategy. J. Atmos. Sol.-Terr. Phys. 2004, 66, 1469–1479. [Google Scholar] [CrossRef]
- Arge, C.N.; Pizzo, V.J. Improvement in the prediction of solar wind conditions using near-real time solar magnetic field updates. J. Geophys. Res. Atmos. 2000, 105, 0465–10480. [Google Scholar] [CrossRef]
- Linker, J.A.; Mikic, Z.; Biesecker, D.A.; Forsyth, R.J.; Gibson, S.E.; Lazarus, A.J.; Lecinski, A.; Riley, P.; Szabo, A.; Thompson, B.J. Magnetohydrodynamic modeling of the solar corona during Whole Sun Month. J. Geophys. Res. Space Phys. 1999, 104, 9809–9830. [Google Scholar] [CrossRef]
- Mikic, Z.; Linker, J.A.; Schnack, D.D.; Lionello, R.; Tarditi, A. Magnetohydrodynamic modeling of the global solar corona. Phys. Plasmas 1999, 6, 2217–2224. [Google Scholar] [CrossRef]
- Tóth, G.; van der Holst, B.; Sokolov, I.V.; De Zeeuw, D.L.; Gombosi, T.I.; Fang, F.; Manchester, W.B.; Meng, X.; Najib, D.; Powell, K.G.; et al. Adaptive numerical algorithms in space weather modeling. J. Comput. Phys. 2012, 231, 870–903. [Google Scholar] [CrossRef]
- Wu, S.; Dryer, M. Comparative analyses of current three-dimensional numerical solar wind models. Sci. China Earth Sci. 2015, 58, 839–858. [Google Scholar] [CrossRef]
- Feng, X.; Zhou, Y.; Wu, S.T. A Novel Numerical Implementation for Solar Wind Modeling by the Modified Conservation Element/Solution Element Method. Astrophys. J. 2007, 655, 1110. [Google Scholar] [CrossRef]
- Hu, Y.Q.; Feng, X.S.; Wu, S.T.; Song, W.B. Three-dimensional MHD modeling of the global coronal hroughout solar cycle 23. J. Geophys. Res. 2008, 113, A03106. [Google Scholar] [CrossRef]
- Feng, X.S.; Zhang, Y.; Yang, L.P.; Wu, S.T.; Dryer, M. An operational method for shock arrival time prediction by one-dimensional CESE-HD solar wind model. J. Geophys. Res. 2009, 114, A10103. [Google Scholar] [CrossRef]
- Zhou, Y.; Feng, X. Numerical study of successive CMEs during 4–5 November 1998. Sci. China E Technol. Sci. 2008, 51, 1600–1610. [Google Scholar] [CrossRef]
- Zhou, Y.; Feng, X.; Wu, S.T. Numerical Simulation of the 12 May 1997 CME Event. Chin. Phys. Lett. 2008, 25, 790–793. [Google Scholar]
- Chang, S.C.; Wang, X.Y. Multi-dimensional Courant number insensitive CE/SE Euler solvers for application involving highly non-uniform meshes. In Proceedings of the AIAA-2003-5280, Huntsville, AL, USA, 20–23 July 2003. [Google Scholar]
- Yen, J.C.; Duell, E.G.; Martindale, W. CAA using 3D CESE method with a simplified Courant number insensitive scheme. In Proceedings of the AIAA-2006-2417, Cambridge, MA, USA, 8–10 May 2006. [Google Scholar]
- Maurits, N.M.; van der Ven, H.; Veldman, A.E.P. Explicit multi-time stepping methods for convection-dominated flow problems. Comput. Methods Appl. Mech. Eng. 1998, 157, 133–150. [Google Scholar] [CrossRef]
- Van der Ven, H.; Niemann-Tuitman, B.E.; Veldman, A.E.P. An explicit multi-time-stepping algorithm for aerodynamic flows. J. Comput. Appl. Math. 1997, 82, 423–431. [Google Scholar] [CrossRef]
- Feng, X.; Yang, L.; Xiang, C.; Jiang, C.W.; Ma, X.; Wu, S.T.; Zhong, D.; Zhou, Y. Validation of the 3D AMR SIP–CESE Solar Wind Model for Four Carrington Rotations. Sol. Phys. 2012, 279, 207–229. [Google Scholar] [CrossRef]
- Feng, X.S.; Ma, X.P.; Xiang, C.Q. Data-driven modeling of the solar wind from 1 R s to 1 AU. JGRA 2015, 120, 159–174. [Google Scholar] [CrossRef]
- Feng, X.; Yang, L.; Xiang, C.; Wu, S.T.; Zhou, Y.; Zhong, D. Three-dimensional solar wind modeling from the sun to earth by a SIP-CESE mhd model with a six-component grid. Astrophys. J. 2010, 723, 300. [Google Scholar] [CrossRef]
- Balsara, D.S.; Kim, J. A comparison between divergence-cleaning and staggered-mesh formulations for numerical magnetohydrodynamics. Astrophys. J. 2004, 602, 1079–1090. [Google Scholar] [CrossRef]
- Tóth, G. The ∇·B = 0 constraint in shock-capturing magnetohydrodynamics codes. J. Comput. Phys. 2000, 161, 605–652. [Google Scholar] [CrossRef]
- Rider, W.J. Filtering non-solenoidal modes in numerical solutions of incompressible flows. Int. J. Numer. Methods Fluids 1998, 28, 789–814. [Google Scholar] [CrossRef]
- Holst, M.; Saied, F. Multigrid solution of the Poisson-Boltzmann equation. J. Comput. Chem. 1993, 14, 105–113. [Google Scholar] [CrossRef]
- Feng, X.; Xiang, C.; Zhong, D.; Zhou, Y.; Yang, L.; Ma, X. SIP-CESE MHD model of solar wind with adaptive mesh refinement of hexahedral meshes. Comput. Phys. Commun. 2014, 185, 1965–1980. [Google Scholar] [CrossRef]
- Jiang, C.; Feng, X.S.; Zhong, D.K. AMR simulations of magnetohydrodynamic problems by the CESE method in curvilinear coordinates. Sol. Phys. 2010, 267, 463–491. [Google Scholar] [CrossRef]
- Hayashi, K.; Hoeksema, J.T.; Liu, Y.; Bobra, M.G.; Sun, X.D.; Norton, A.A. The helioseismic and magnetic imager (HMI) vector magnetic field pipeline: Magnetohydrodynamics simulation module for the global solar corona. J. Geophys. Res. Space Phys. 2015, 290, 1507–1529. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Liu, Y.; Hoeksema, J.; Hayashi, K.; Zhao, X. A new method for polar field interpolation. Sol. Phys. 2011, 270, 9–22. [Google Scholar] [CrossRef]
- Gressl, C.; Veronig, A.M.; Temmer, M.; Odstrčil, D.; Linker, J.A.; Mikić, Z.; Riley, P. Comparative study of MHD modeling of the background solar wind. Sol. Phys. 2014, 289, 1783–1801. [Google Scholar] [CrossRef]
- Riley, P.; Linker, J.A.; Lionello, R.; Mikic, Z. Corotating interaction regions during the recent solar minimum: The power and limitations of global MHD modeling. J. Atmos. Sol.-Terr. Phys. 2012, 83, 1–10. [Google Scholar] [CrossRef]
- Riley, P.; Ben-Nun, M.; Linker, J.A.; Mikić, Z.; Svalgaard, L.; Harvey, J.; Bertello, L.; Hoeksema, T.; Liu, Y.; Ulrich, R.K. A Multi-Observatory Inter-Comparison of Line-of-Sight Synoptic Solar Magnetograms. Sol. Phys. 2014, 289, 769–792. [Google Scholar] [CrossRef]
- Feng, X.; Zhang, S.; Xiang, C.; Yang, L.; Jiang, C.; Wu, S.T. A Hybrid Solar Wind Model of the CESE+HLL Method with A Yin–Yang Overset Grid and an AMR Grid. Astrophys. J. 2011, 734, 50. [Google Scholar] [CrossRef]
- Li, H.; Feng, X. CESE-HLL Magnetic Field-Driven Modeling of the Background Solar Wind During Year 2008. J. Geophys. Res. Space Phys. 2018, 123, 4488–4509. [Google Scholar] [CrossRef]
- Li, H.; Feng, X.; Wei, F. Assessment of CESE-HLLD ambient solar wind model results using multipoint observation. J. Space Weather Space Clim. 2020, 10, 44. [Google Scholar] [CrossRef]
- Chen, P. Coronal Mass Ejections: Models and Their Observational Basis. Living Rev. Sol. Phys. 2011, 8, 1. [Google Scholar] [CrossRef]
- Webb, D.F.; Howard, T.A. Coronal Mass Ejections: Observations. Living Rev. Sol. Phys. 2012, 9, 3. [Google Scholar] [CrossRef]
- Yang, L.; Hou, C.; Feng, X.; He, J.; Xiong, M.; Zhang, M.; Zhou, Y.; Shen, F.; Zhao, X.; Li, H.; et al. Global Morphology Distortion of the 2021 October 9 Coronal Mass Ejection from an Ellipsoid to a Concave Shape. Astrophys. J. 2023, 942, 65. [Google Scholar] [CrossRef]
- Yang, L.P.; Feng, X.S.; Xiang, C.Q.; Liu, Y.; Zhao, X.; Wu, S.T. Time-dependent MHD modeling of the global solar corona for year 2007: Driven by daily-updated magnetic field synoptic data. J. Geophys. Res. 2012, 117, A08110. [Google Scholar] [CrossRef]
- Zhou, Y.F.; Feng, X.S.; Wu, S.T.; Du, D.; Shen, F.; Xiang, C.Q. Using a 3-D spherical plasmoid to interpret the Sun-to-Earth propagation of the 4 November 1997 coronal mass ejection event. J. Geophys. Res. Space Phys. 2012, 117, A01102. [Google Scholar] [CrossRef]
- Zhao, X.; Dryer, M. Current status of CME/shock arrival time prediction. Space Weather 2014, 12, 448–469. [Google Scholar] [CrossRef]
- Temmer, M.; Rollett, T.; Möstl, C.; Veronig, A.M.; Vršnak, B.; Odstrčil, D. Influence of the Ambient Solar Wind Flow on the Propagation Behavior of Interplanetary Coronal Mass Ejections. Astrophys. J. 2011, 743, 101. [Google Scholar] [CrossRef]
- Bain, H.M.; Mays, M.L.; Luhmann, J.G.; Li, Y.; Jian, L.K.; Odstrcil, D. Shock Connectivity in the 2010 August and 2012 July Solar Energetic Particle Events Inferred from Observations and Enlil Modeling. Astrophys. J. 2016, 825, 1. [Google Scholar] [CrossRef]
- Dewey, R.; Baker, D.; Anderson, B.; Benna, M.; Johnson, C.; Korth, H.; Gershman, D.; Ho, G.; McClintock, W.; Odstrcil, D. Improving solar wind modeling at Mercury: Incorporating transient solar phenomena into the WSA-ENLIL model with the Cone extension. J. Geophys. Res. Space Phys. 2015, 120, 5667–5685. [Google Scholar] [CrossRef]
- Dewey, R.M.; Baker, D.N.; Mays, M.L.; Brain, D.A.; Jakosky, B.M.; Halekas, J.S.; Connerney, J.E.P.; Odstrcil, D.; Luhmann, J.G.; Lee, C.O. Continuous solar wind forcing knowledge: Providing continuous conditions at Mars with the WSA-ENLIL + Cone model. J. Geophys. Res. Space Phys. 2016, 121, 6207–6222. [Google Scholar] [CrossRef]
- Taktakishvili, A.; Pulkkinen, A.; MacNeice, P.; Kuznetsova, M.; Hesse, M.; Odstrcil, D. Modeling of coronal mass ejections that caused particularly large geomagnetic storms using ENLIL heliosphere cone model. Space Weather 2011, 9, S06002. [Google Scholar] [CrossRef]
- Arge, C.N.; Odstrcil, D.; Pizzo, V.J.; Mayer, L.R. Improved Method for Specifying Solar Wind Speed Near the Sun. In Proceedings of the Solar Wind Ten; Velli, M., Bruno, R., Malara, F., Bucci, B., Eds.; American Institute of Physics Conference Series; AIP: Woodbury, NY, USA, 2003; Volume 679, pp. 190–193. [Google Scholar] [CrossRef]
- Parsons, A.; Biesecker, D.; Odstrcil, D.; Millward, G.; Hill, S.; Pizzo, V. Wang-Sheeley-Arge–Enlil Cone Model Transitions to Operations. Space Weather 2011, 9, S03004. [Google Scholar] [CrossRef]
- Schatten, K.H.; Wilcox, J.M.; Ness, N.F. A model of interplanetary and coronal magnetic fields. Sol. Phys. 1969, 6, 442–455. [Google Scholar] [CrossRef]
- Odstrcil, D. Modeling 3-D solar wind structure. Adv. Space Res. 2003, 32, 497–506. [Google Scholar] [CrossRef]
- Zhao, X.P.; Plunkett, S.P.; Liu, W. Determination of geometrical and kinematical properties of halo coronal mass ejections using the cone model. J. Geophys. Res. Space Phys. 2002, 107, SSH 13–1–SSH 13–9. [Google Scholar] [CrossRef]
- Manchester IV, W.B.; Vourlidas, A.; Tóth, G.; Lugaz, N.; Roussev, I.I.; Sokolov, I.V.; Gombosi, T.I.; De Zeeuw, D.L.; Opher, M. Three-dimensional MHD Simulation of the 2003 October 28 Coronal Mass Ejection: Comparison with LASCO Coronagraph Observations. Astrophys. J. 2008, 684, 1448–1460. [Google Scholar] [CrossRef]
- Manchester, W.B.I.; van der Holst, B.; Tóth, G.; Gombosi, T.I. The coupled evolution of electrons and ions in coronal mass ejection-driven shocks. Astrophys. J. 2012, 756, 81. [Google Scholar] [CrossRef]
- Jin, M.; Manchester, W.B.; van der Holst, B.; Oran, R.; Sokolov, I.; Tóth, G.Z.; Liu, Y.D.; Sun, X.; Gombosi, T.I.I. Numerical Simulations of Coronal Mass Ejection on 2011 March 7: One-Temperature and Two-Temperature Model Comparison. Astrophys. J. 2013, 773. [Google Scholar] [CrossRef]
- Jin, M.; Manchester, W.B.; van der Holst, B.; Sokolov, I.; Tóth, G.; Mullinix, R.E.; Taktakishvili, A.; Chulaki, A.; Gombosi, T.I. Data-Constrained Coronal Mass Ejections in a Global Magnetohydrodynamics Model. Astrophys. J. 2017, 834, 173. [Google Scholar] [CrossRef]
- Jin, M.; Schrijver, C.J.; Cheung, M.C.M.; DeRosa, M.L.; Nitta, N.V. A Numerical Study of Long-Range Magnetic Impacts During Coronal Mass Ejections. Astrophys. J. 2016, 820, 16. [Google Scholar] [CrossRef]
- Titov, V.S.; Démoulin, P. Basic topology of twisted magnetic configurations in solar flares. Astron. Astrophys. 1999, 351, 707–720. [Google Scholar]
- Gibson, S.E.; Low, B.C. A Time-dependent Three-dimensional Magnetohydrodynamic Model of the Coronal Mass Ejection. Astrophys. J. 1998, 493, 460. [Google Scholar] [CrossRef]
- Gosling, J.T.; Riley, P.; McComas, D.J.; Pizzo, V.J. Overexpanding coronal mass ejections at high heliographic latitudes: Observations and simulations. J. Geophys. Res. 1998, 103, 1941–1954. [Google Scholar] [CrossRef]
- Gopalswamy, N.; Hanaoka, Y.; Hudson, H.S. Structure and dynamics of the corona surrounding an eruptive prominence. Adv. Space Res. 2000, 25, 1851–1854. [Google Scholar] [CrossRef]
- Zhou, Y.F.; Feng, X.S. MHD numerical study of the latitudinal deflection of coronal mass ejection. J. Geophys. Res. Space Phys. 2013, 118, 6007–6018. [Google Scholar] [CrossRef]
- Zhou, Y.; Feng, X.; Zhao, X. Using a 3-D MHD simulation to interpret propagation and evolution of a coronal mass ejection observed by multiple spacecraft: The 3 April 2010 event. J. Geophys. Res. Space Phys. 2014, 119, 9321–9333. [Google Scholar] [CrossRef]
- Zhou, Y.; Feng, X. Numerical study of the propagation characteristics of coronal mass ejections in a structured ambient solar wind. J. Geophys. Res. Space Phys. 2017, 122, 1451–1462. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, J.J.; Feng, X.S.; Chen, P.F.; Zhang, B. Prediction of the Transit Time of Coronal Mass Ejections with an Ensemble Machine-learning Method. Astrophys. J. Suppl. Ser. 2023, 268, 69. [Google Scholar] [CrossRef]
- Pizzo, G.; Millward, A.; Parsons, D.; Biesecker, S.; Hill, D.O. Wang-Sheeley-Arge–Enlil Cone Model Transitions to Operations. J. Geophys. Res. Space Phys. 2000, 9, S03004. [Google Scholar] [CrossRef]
- Jiang, C.; Wu, S.T.; Yurchyshyn, V.; Wang, H.; Feng, X.; Hu, Q. How did a major confined flare occur in super solar active region 12192. Astrophys. J. 2016, 828, 62. [Google Scholar] [CrossRef]
- Jiang, C.W.; Feng, X.S.; Wu, S.T.; Hu, Q. Study of the three-dimensional coronal magnetic field of active region 11117 around the time of a confined flare using a data-driven CESE-MHD model. Astrophys. J. 2012, 759, 85. [Google Scholar] [CrossRef]
- Jiang, C.; Zou, P.; Feng, X.; Hu, Q.; Liu, R.; Vemareddy, P.; Duan, A.; Zuo, P.; Wang, Y.; Wei, F. Magnetohydrodynamic Simulation of the X9.3 Flare on 2017 September 6: Evolving Magnetic Topology. Astrophys. J. 2018, 869, 13. [Google Scholar] [CrossRef]
- Liu, C.; Shen, F.; Liu, Y.; Zhang, M.; Liu, X. Numerical Study of Divergence Cleaning and Coronal Heating/Acceleration Methods in the 3D COIN-TVD MHD Model. Front. Phys. 2021, 9, 705744. [Google Scholar] [CrossRef]
- Zhang, M.; Feng, X. A Comparative Study of Divergence Cleaning Methods of Magnetic Field in the Solar Coronal Numerical Simulation. Front. Astron. Space Sci. 2016, 3, 6. [Google Scholar] [CrossRef]
- Janhunen, P.; Palmroth, M.; Laitinen, T.; Honkonen, I.; Juusola, L.; Facskó, G.; Pulkkinen, T.I. The GUMICS-4 global MHD magnetosphere-ionosphere coupling simulation. J. Atmos. Sol.-Terr. Phys. 2012, 80, 48–59. [Google Scholar] [CrossRef]
- Miyoshi, T.; Terada, N.; Matsumoto, Y.; Fukazawa, K.; Umeda, T.; Kusano, K. The HLLD Approximate Riemann Solver for Magnetospheric Simulation. IEEE Trans. Plasma Sci. 2010, 38, 2236–2242. [Google Scholar] [CrossRef]
- Guo, X. An extended HLLC Riemann solver for the magneto-hydrodynamics including strong internal magnetic field. J. Comput. Phys. 2015, 290, 352–363. [Google Scholar] [CrossRef]
- Powell, K.G.; Roe, P.L.; Linde, T.J.; Gombosi, T.I.; De Zeeuw, D.L. A Solution-Adaptive Upwind Scheme for Ideal Magnetohydrodynamics. J. Comput. Phys. 1999, 154, 284–309. [Google Scholar] [CrossRef]
- Ogino, T.; Walker, R.J.; Kivelson, M.G. A global magnetohydrodynamic simulation of the Jovian magnetosphere. J. Geophys. Res. Space Phys. 1998, 103, 225–235. [Google Scholar] [CrossRef]
- Wang, J.; Du, A.M.; Zhang, Y.; Zhang, T.L.; Ge, Y.S. Modeling the Earth’s magnetosphere under the influence of solar wind with due northward IMF by the AMR-CESE-MHD model. Sci. China Earth Sci. 2015, 58, 1235–1242. [Google Scholar] [CrossRef]
- Tanaka, T. Generation mechanisms for magnetosphere-ionosphere current systems deduced from a three-dimensional MHD simulation of the solar wind-magnetosphere-ionosphere coupling processes. J. Geophys. Res. Space Phys. 1995, 100, 12057–12074. [Google Scholar] [CrossRef]
- Hu, Y.; Guo, X.; Li, G.; Wang, C.; Huang, Z. Oscillation of Quasi-Steady Earth’s Magnetosphere. Chin. Phys. Lett. 2005, 22, 2723. [Google Scholar] [CrossRef]
- Raeder, J. Global Magnetohydrodynamics—A Tutorial. In Space Plasma Simulation; Springer: Berlin/Heidelberg, Germany, 2003; pp. 212–246. [Google Scholar] [CrossRef]
- Wang, J.; Feng, X.; Du, A.; Ge, Y. Modeling the interaction between the solar wind and Saturn’s magnetosphere by the AMR-CESE-MHD method. J. Geophys. Res. Space Phys. 2014, 119, 9919–9930. [Google Scholar] [CrossRef]
- Raeder, J.; Berchem, J.; Ashour-Abdalla, M. The geospace environment modeling grand challenge: Results from a global geospace circulation model. J. Geophys. Res. 1998, 103, 14787–14797. [Google Scholar] [CrossRef]
- Wang, J.; Guo, Z.; Yasong, S.G.; Du, A.; Huang, C.; Qin, P. The responses of the Earth’s magnetopause and bow shock to the IMF Bz and the solar wind dynamic pressure: A parametric study using the AMR-CESE-MHD model. J. Space Weather Space Clim. 2018, 8, A41. [Google Scholar] [CrossRef]
- Yang, Y.; Manchester, W.B. Using a Higher-order Numerical Scheme to Study the Hall Magnetic Reconnection. Astrophys. J. 2020, 892, 61. [Google Scholar] [CrossRef]
- Yang, Y.; Feng, X.S.; Jiang, C.W. An upwind CESE scheme for 2D and 3D MHD numerical simulation in general curvilinear coordinates. JCoPh 2018, 371, 850–869. [Google Scholar] [CrossRef]
- Yu, S.T.; Chang, S.C. Treatment of stiff source terms in conservation laws by the method of space-time conservation element/solution element. In Proceedings of the 35th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1997. [Google Scholar]
- Patoul, J.; Foullon, C.; Riley, P. 3D Electron Density Distributions in the Solar Corona During Solar Minima: Assessment for More Realistic Solar Wind Modeling. Astrophys. J. 2015, 814, 68. [Google Scholar] [CrossRef]
- Owens, M.J.; Riley, P.; Horbury, T.S. Probabilistic Solar Wind and Geomagnetic Forecasting Using an Analogue Ensemble or “Similar Day” Approach. Sol. Phys. 2017, 292, 69. [Google Scholar] [CrossRef]
- Pesnell, W.D. Predictions of solar cycle 24: How are we doing? Space Weather 2015, 14, 10–21. [Google Scholar] [CrossRef]
- Angelopoulos, V.; Cruce, P.; Drozdov, A.; Grimes, E.W.; Hatzigeorgiu, N. The space physics environment data analysis system (SPEDAS). Space Sci. Rev. 2019, 215, 9. [Google Scholar] [CrossRef] [PubMed]
- Kuznetsov, V. Solar and heliospheric space missions. Adv. Space Res. 2015, 55, 879–885. [Google Scholar] [CrossRef]
- Ma, R.; Angryk, R.; Riley, P. A data-driven analysis of interplanetary coronal mass ejecta and magnetic flux ropes. In Proceedings of the 2016 IEEE International Conference on Big Data (Big Data), Washington, DC, USA, 5–8 December 2016; pp. 3177–3186. [Google Scholar] [CrossRef]
- McGranaghan, R.M.; Bhatt, A.; Matsuo, T.; Mannucci, A.J.; Semeter, J.L.; Datta-Barua, S. Ushering in a new frontier in geospace through data science. J. Geophys. Res. Space Phys. 2017, 122, 879–885. [Google Scholar] [CrossRef]
- Priest, E.R.; Forbes, T.G. The magnetic nature of solar flares. Astron. Astrophys. Rev. 2002, 10, 313–377. [Google Scholar] [CrossRef]
- Yang, L.; Wang, H.; Feng, X.; Xiong, M.; Zhang, M.; Zhu, B.; Li, H.; Zhou, Y.; Shen, F.; Zhao, X.; et al. Numerical MHD Simulations of the 3D Morphology and Kinematics of the 2017 September 10 CME-driven Shock from the Sun to Earth. Astrophys. J. 2021, 918, 31. [Google Scholar] [CrossRef]




| Model Name | Numerical Scheme | Scheme Precision (Order) | Divergence-Free Method | Reference |
|---|---|---|---|---|
| GUMICS-4 | Godunov-type scheme+HLL/Roe solver | 1 | Projection method | Janhunen et al. [84] |
| HLLD | Upwind FVM+Harten–Lax–van Leer Discontinuities (HLLD) | 2 | No | Miyoshi et al. [85] |
| HLLC | Upwind FVM+Harten–Lax–van Leer contact (HLLC) | 2 | Hyperbolic cleaning method | Guo [86] |
| BATS-RUS | TVD+Roe | 2 | 8-Wave | Powell et al. [87] |
| GEDAS | Modified leap-frog method | 2 | No | Ogino et al. [88] |
| AMR-CESE-MHD | Space–time conservation element and solution element | 2 | 8-Wave+diffusion | Wang et al. [89] |
| Tanaka | TVD+MUSCL | 3 | Projection method | Tanaka [90] |
| PPMLRMHD | PPMLR | 3 | 8-Wave | You-Qiu et al. [91] |
| Open GGCM | TVD | 4 | Constrained transport | Raeder [92] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Li, H. CESE Schemes for Solar Wind Plasma MHD Dynamics. Universe 2024, 10, 445. https://doi.org/10.3390/universe10120445
Yang Y, Li H. CESE Schemes for Solar Wind Plasma MHD Dynamics. Universe. 2024; 10(12):445. https://doi.org/10.3390/universe10120445
Chicago/Turabian StyleYang, Yun, and Huichao Li. 2024. "CESE Schemes for Solar Wind Plasma MHD Dynamics" Universe 10, no. 12: 445. https://doi.org/10.3390/universe10120445
APA StyleYang, Y., & Li, H. (2024). CESE Schemes for Solar Wind Plasma MHD Dynamics. Universe, 10(12), 445. https://doi.org/10.3390/universe10120445





