Decoding Quantum Gravity Information with Black Hole Accretion Disk
Abstract
:1. Introduction
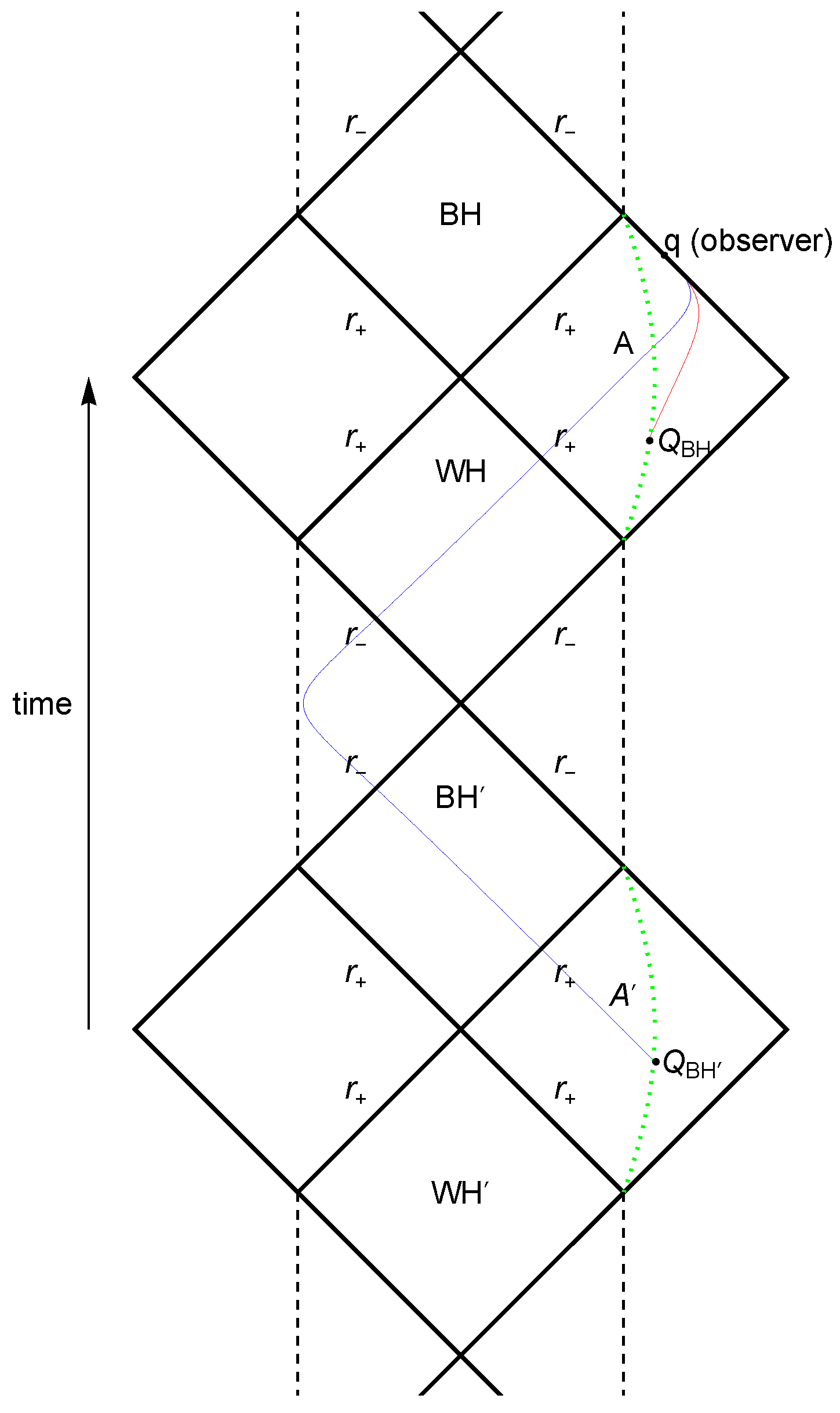
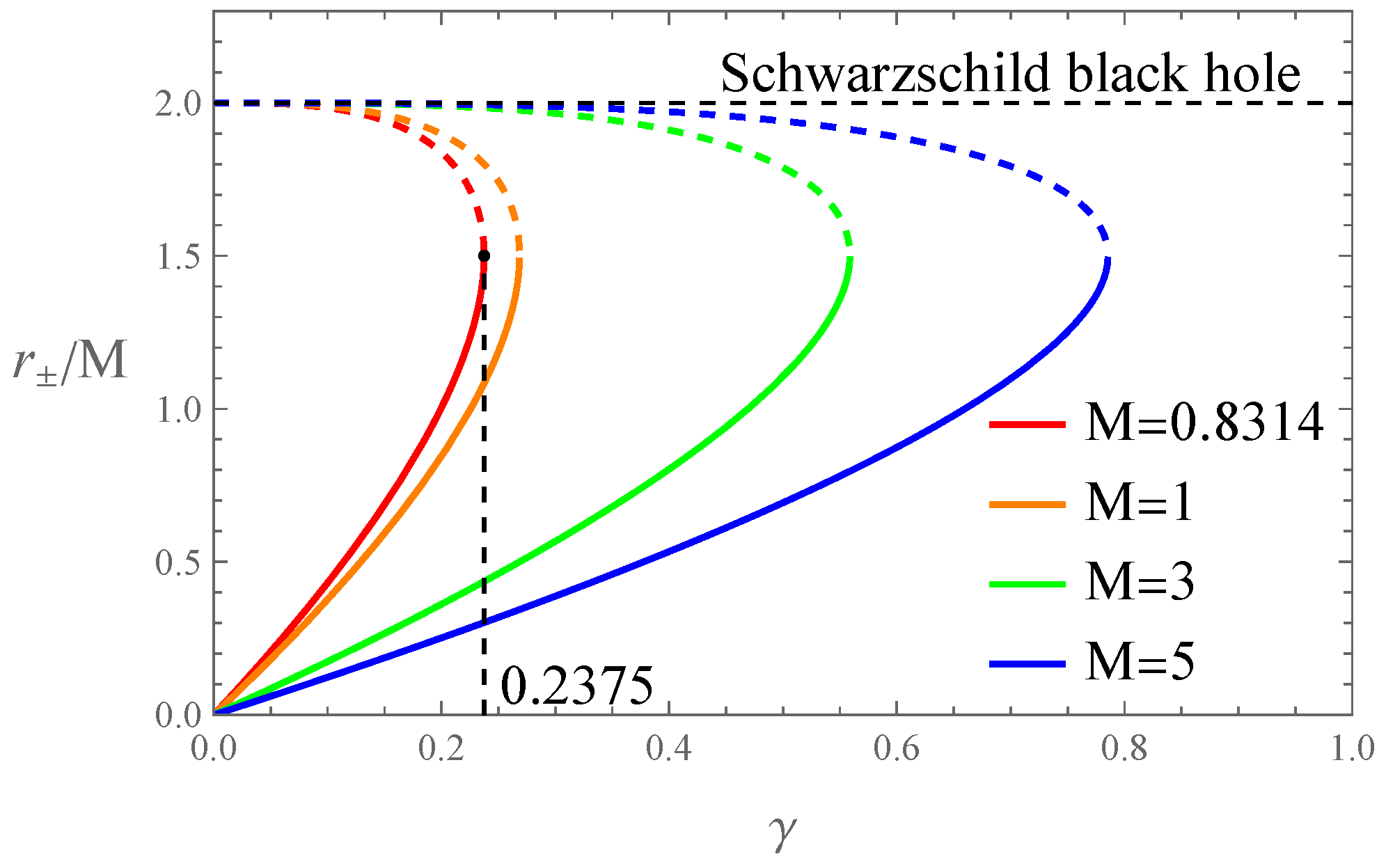
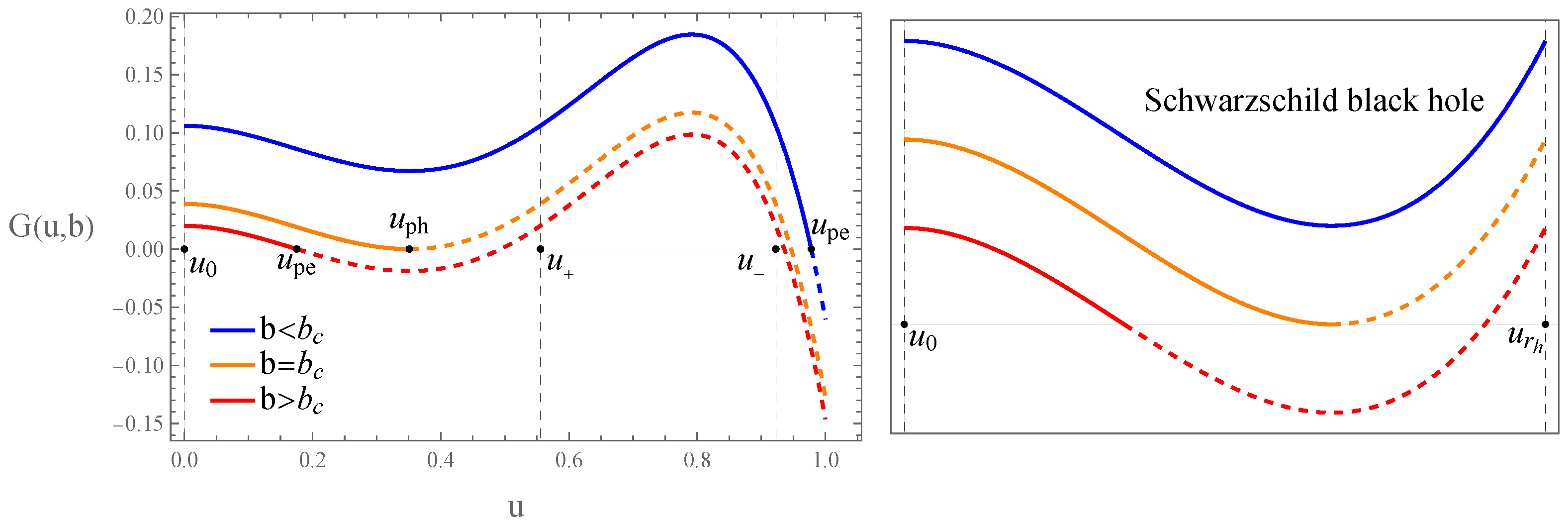
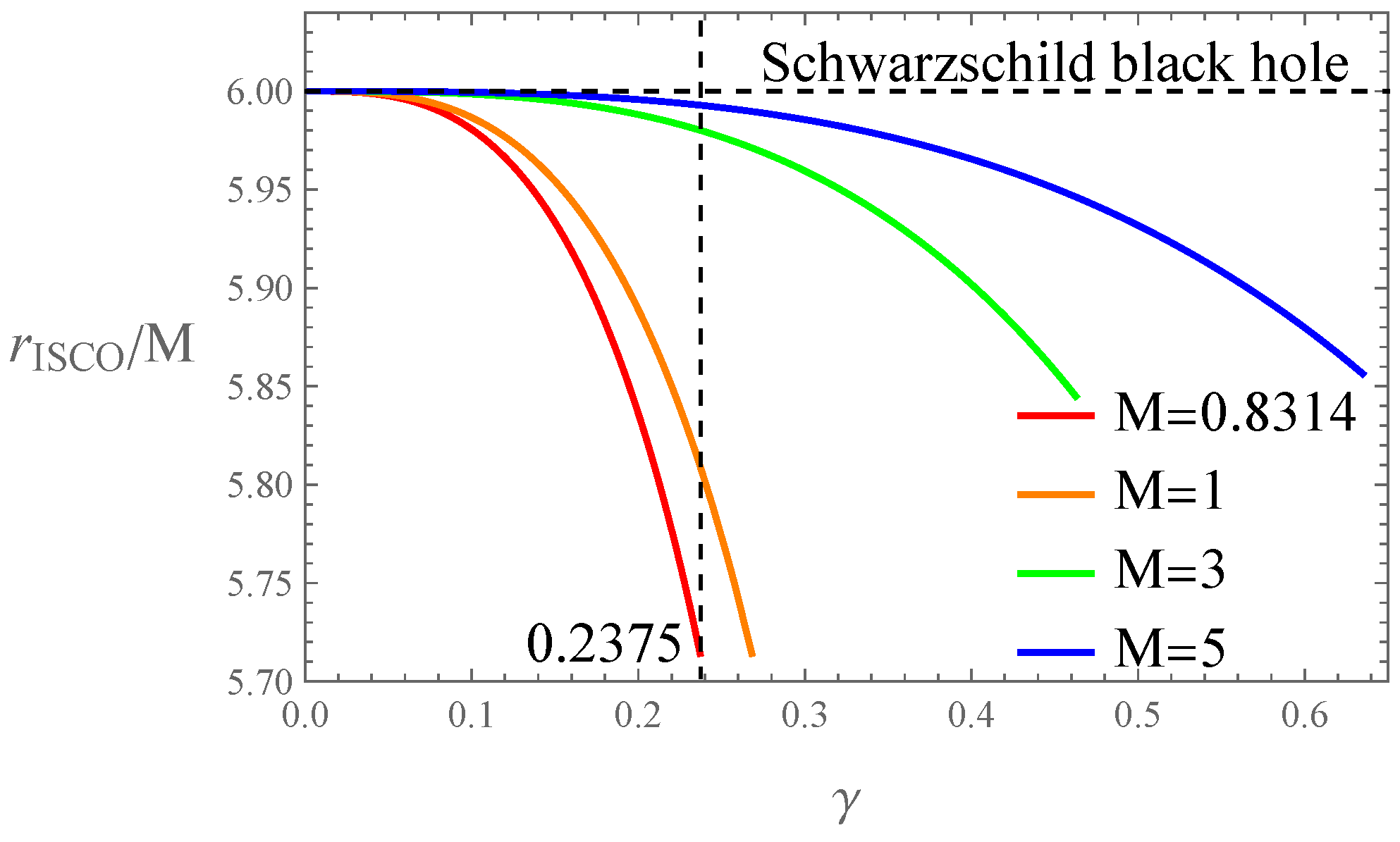
2. Null Geodesics in the Quantum-Corrected Spacetime
3. Image of a Thin Accretion Disk Produced by a White Hole
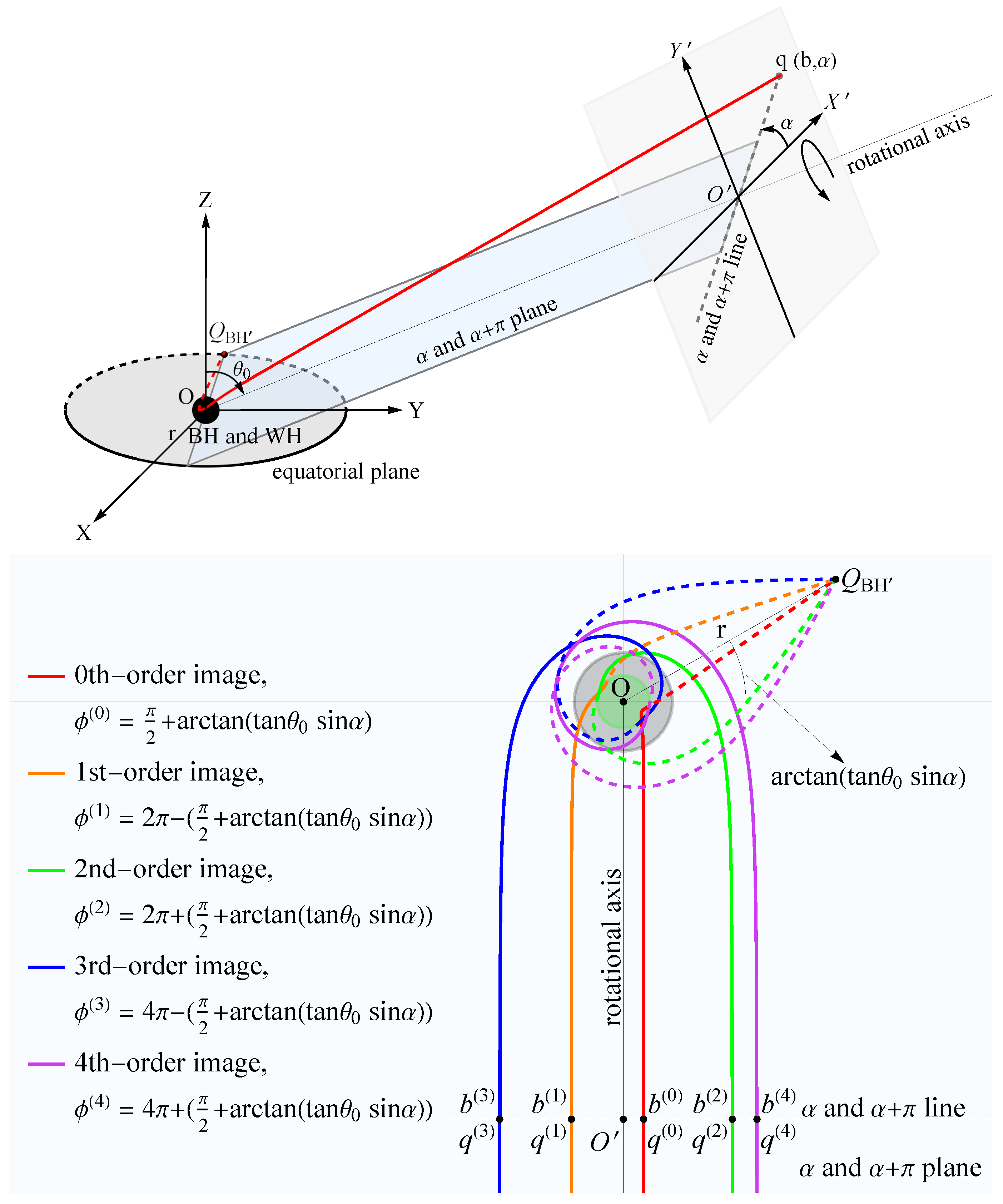
3.1. Observation Coordinate System
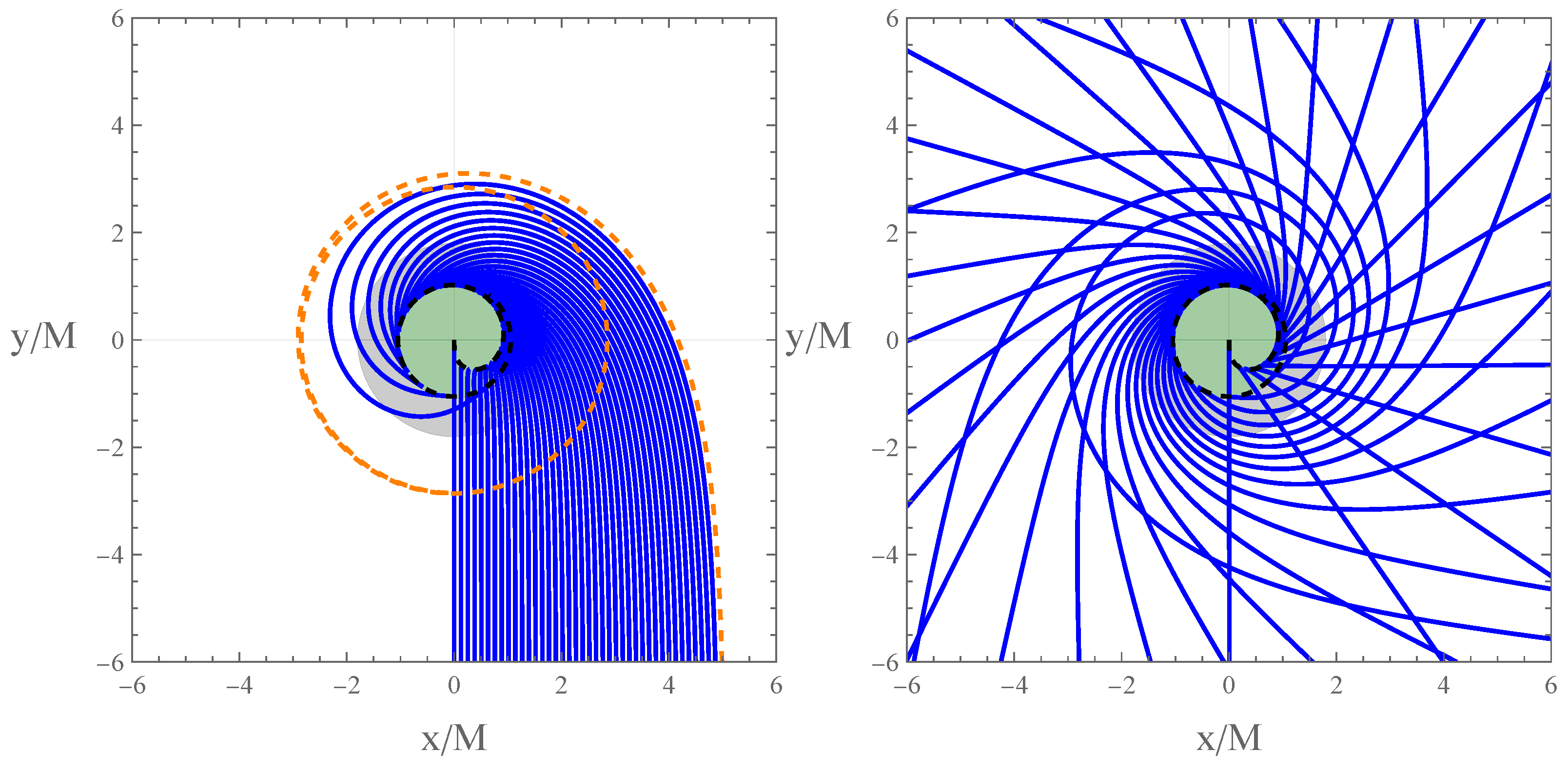
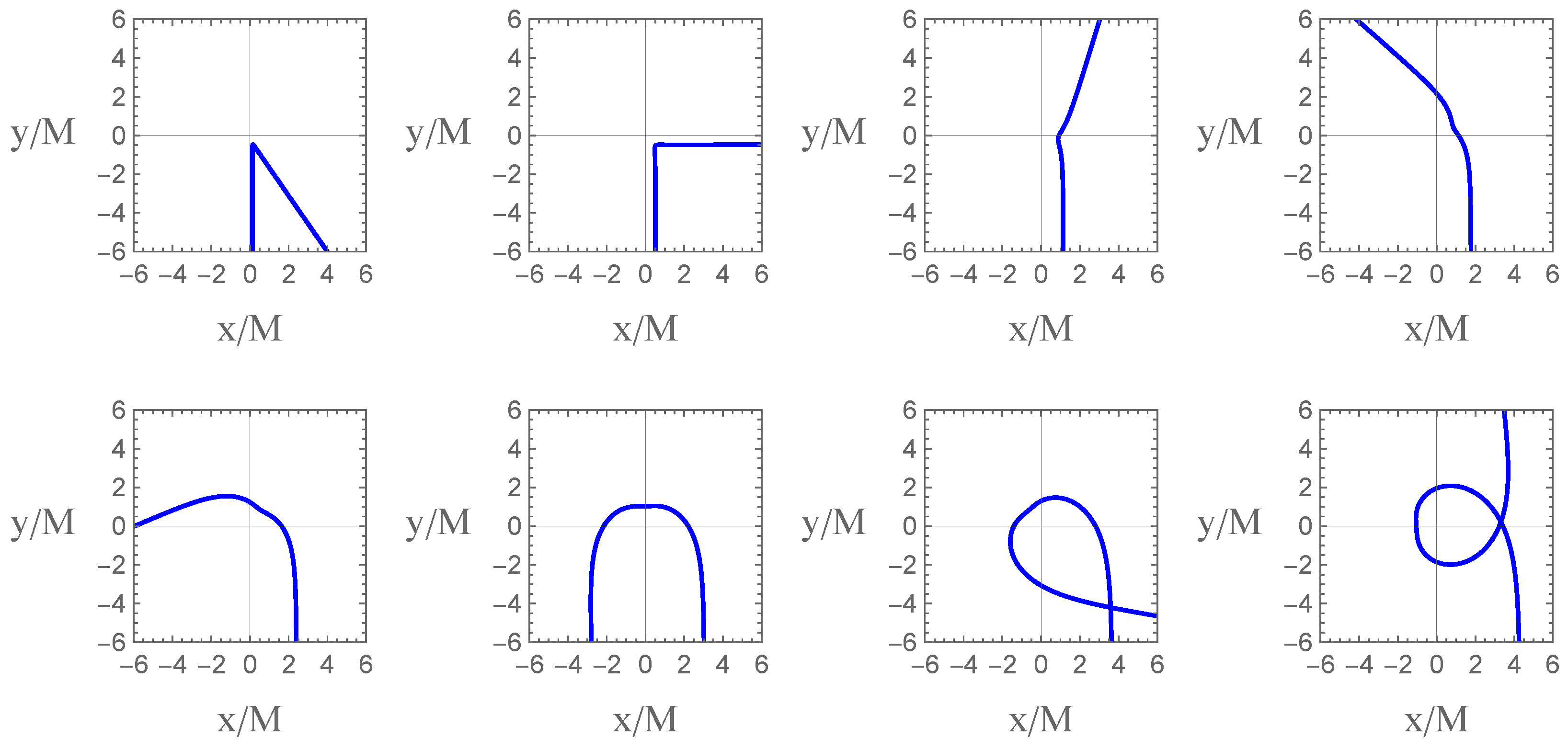
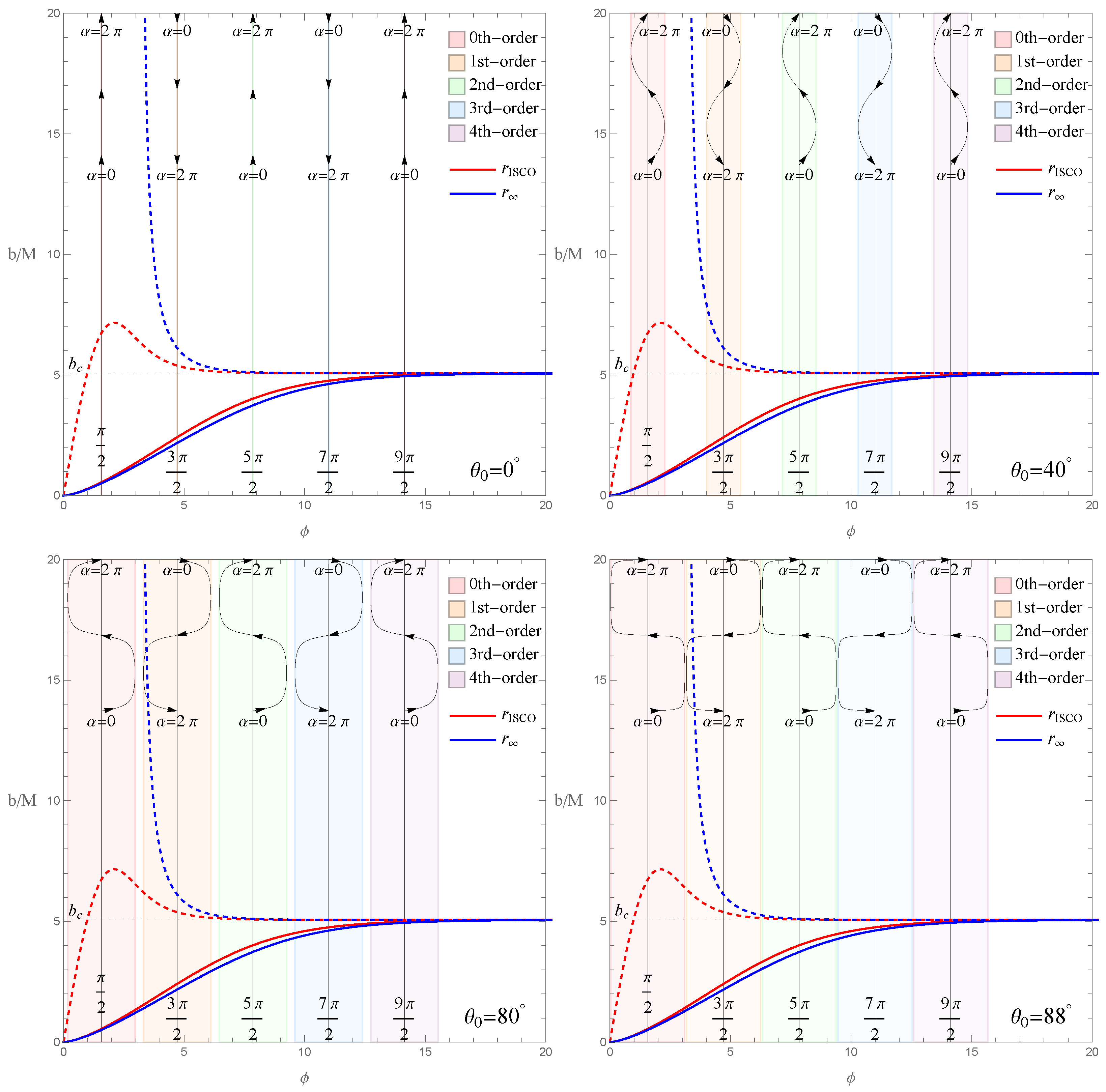
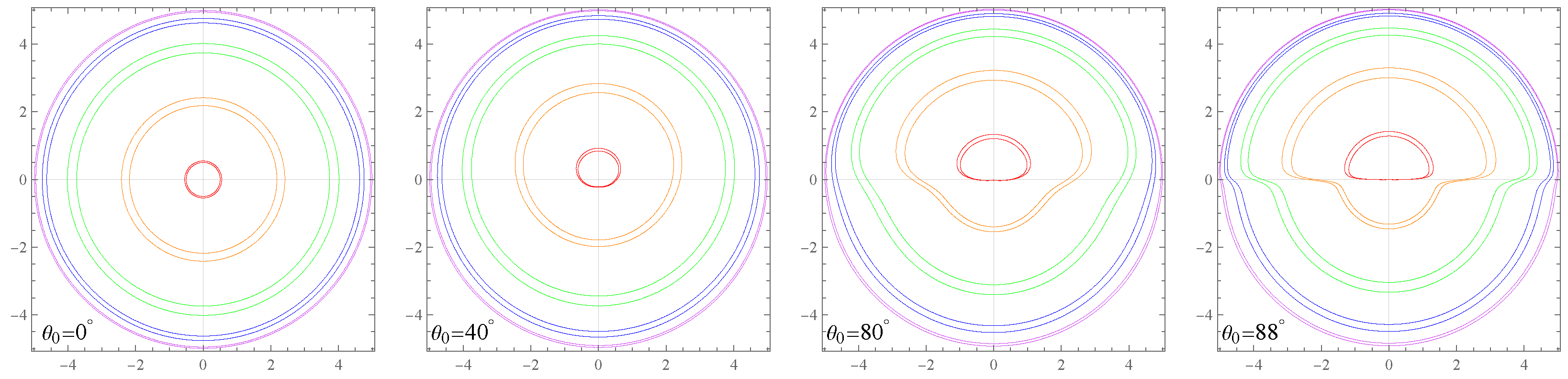
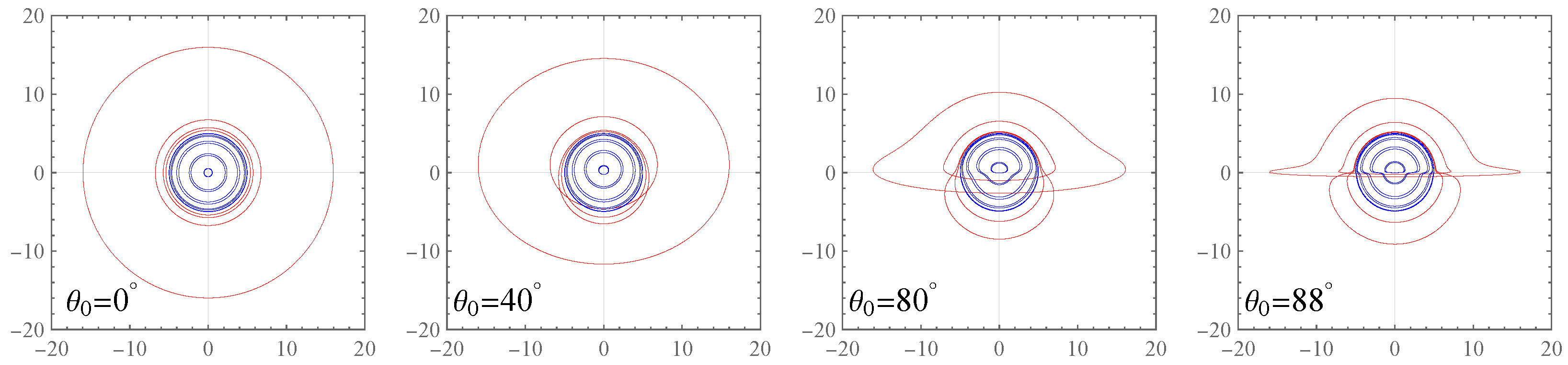
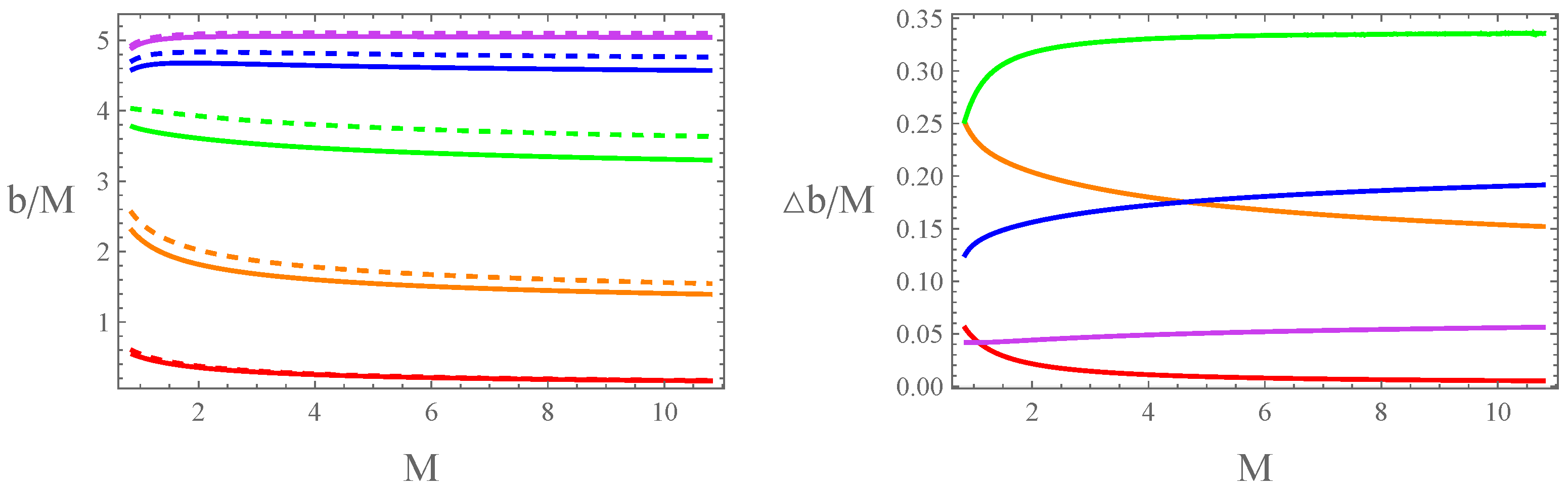
3.2. Image of a Thin Accretion Disk
- (a)
- All accretion disk images are confined within a circle of radius ;
- (b)
- Images corresponding to larger orbital radii have smaller b values and appear on the inner side of the image, which is the opposite of what occurs with traditional accretion disk images;
- (c)
- The 2nd-order image of the accretion disk is the widest, whereas the 0th-order image is very narrow. In contrast, in traditional accretion disk images, the 0th-order is the widest. Additionally, compared to traditional accretion disk images, even the widest image produced by the white hole remains relatively narrow. It is important to note that the blue curve plotted corresponds to the circular orbit at . Since the actual outermost circular orbit of the accretion disk has a finite radius, the disk image will be even narrower;
- (d)
- As increases, the value of b increases in , while it decreases in . This causes the upper part of the accretion disk image to enlarge and the lower part to shrink, resulting in a shell-like shape. This contrasts sharply with traditional accretion disk images beyond the 1st-order. Additionally, the variation in accretion disk image width with respect to differs from that of traditional accretion disks. For instance, in the 1st-order image, the traditional accretion disk is widest at , whereas the accretion disk image produced by the white hole is widest at ;
- (e)
- Other features of the accretion disk images are generally consistent with those of traditional accretion disk images, including the circular nature of the 0th-order image and the symmetry of the images about the -axis.
3.3. Light Intensity Distribution on Accretion Disk
4. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Penrose, R. Gravitational collapse and space-time singularities. Phys. Rev. Lett. 1965, 14, 57. [Google Scholar] [CrossRef]
- Hawking, S.; Penrose, R. Proceedings the royal-of-society. Proc. R. Soc. Lond. A 1970, 1970. [Google Scholar]
- Hawking, S.W. Particle creation by black holes. Commun. Math. Phys. 1975, 43, 199–220. [Google Scholar] [CrossRef]
- Ashtekar, A.; Bojowald, M. Quantum geometry and the Schwarzschild singularity. Class. Quantum Gravity 2005, 23, 391. [Google Scholar] [CrossRef]
- Modesto, L. Loop quantum black hole. Class. Quantum Gravity 2006, 23, 5587. [Google Scholar] [CrossRef]
- Cartin, D.; Khanna, G. Wave functions for the Schwarzschild black hole interior. Phys. Rev. D 2006, 73, 104009. [Google Scholar] [CrossRef]
- Boehmer, C.G.; Vandersloot, K. Loop quantum dynamics of the Schwarzschild interior. Phys. Rev. D 2007, 76, 104030. [Google Scholar] [CrossRef]
- Chiou, D.W. Phenomenological loop quantum geometry of the Schwarzschild black hole. Phys. Rev. D 2008, 78, 064040. [Google Scholar] [CrossRef]
- Campiglia, M.; Gambini, R.; Pullin, J. Loop quantization of spherically symmetric midi-superspaces: The interior problem. AIP Conf. Proc. 2007, 24, 3649–3672. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; et al. First M87 event horizon telescope results. VI. The shadow and mass of the central black hole. Astrophys. J. Lett. 2019, 875, L6. [Google Scholar]
- Giesel, K.; Thiemann, T. Algebraic quantum gravity (AQG): IV. Reduced phase space quantization of loop quantum gravity. Class. Quantum Gravity 2010, 27, 175009. [Google Scholar] [CrossRef]
- Gambini, R.; Pullin, J. Loop quantization of the Schwarzschild black hole. Phys. Rev. Lett. 2013, 110, 211301. [Google Scholar] [CrossRef]
- Bianchi, E.; Dona, P.; Speziale, S. Polyhedra in loop quantum gravity. Phys. Rev. D 2011, 83, 044035. [Google Scholar] [CrossRef]
- Gambini, R.; Olmedo, J.; Pullin, J. Quantum black holes in loop quantum gravity. Class. Quantum Gravity 2014, 31, 095009. [Google Scholar] [CrossRef]
- Hooft, G. How quantization of gravity leads to a discrete space-time. J. Phys. Conf. Ser. 2016, 701, 012014. [Google Scholar] [CrossRef]
- Ashtekar, A.; Bianchi, E. A short review of loop quantum gravity. Rep. Prog. Phys. 2021, 84, 042001. [Google Scholar] [CrossRef]
- McCabe, G. Loop Quantum Gravity and Discrete Space-Time. PhilSci Archive. 2018. Available online: http://philsci-archive.pitt.edu/14959/ (accessed on 8 October 2024).
- Wang, C.H.T.; Rodrigues, D.P. Closing the gaps in quantum space and time: Conformally augmented gauge structure of gravitation. Phys. Rev. D 2018, 98, 124041. [Google Scholar] [CrossRef]
- Kelly, J.G.; Santacruz, R.; Wilson-Ewing, E. Black hole collapse and bounce in effective loop quantum gravity. Class. Quantum Gravity 2020, 38, 04LT01. [Google Scholar] [CrossRef]
- Perez, A. Black holes in loop quantum gravity. Rep. Prog. Phys. 2017, 80, 126901. [Google Scholar] [CrossRef]
- Bouhmadi-López, M.; Brahma, S.; Chen, C.Y.; Chen, P.; Yeom, D.h. A consistent model of non-singular Schwarzschild black hole in loop quantum gravity and its quasinormal modes. J. Cosmol. Astropart. Phys. 2020, 2020, 066. [Google Scholar] [CrossRef]
- Ashtekar, A.; Olmedo, J.; Singh, P. Regular black holes from loop quantum gravity. In Regular Black Holes; Springer: Singapore, 2023; pp. 235–282. [Google Scholar]
- Olmedo, J.; Saini, S.; Singh, P. From black holes to white holes: A quantum gravitational, symmetric bounce. Class. Quantum Gravity 2017, 34, 225011. [Google Scholar] [CrossRef]
- Abedi, J.; Arfaei, H. Obstruction of black hole singularity by quantum field theory effects. J. High Energy Phys. 2016, 2016, 135. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Snyder, H. On continued gravitational contraction. Phys. Rev. 1939, 56, 455. [Google Scholar] [CrossRef]
- Bojowald, M.; Goswami, R.; Maartens, R.; Singh, P. Black hole mass threshold from nonsingular quantum gravitational collapse. Phys. Rev. Lett. 2005, 95, 091302. [Google Scholar] [CrossRef] [PubMed]
- Bojowald, M.; Reyes, J.D.; Tibrewala, R. Nonmarginal Lemaitre-Tolman-Bondi-like models with inverse triad corrections from loop quantum gravity. Phys. Rev. D 2009, 80, 084002. [Google Scholar] [CrossRef]
- Marto, J.; Tavakoli, Y.; Moniz, P.V. Improved dynamics and gravitational collapse of tachyon field coupled with a barotropic fluid. Int. J. Mod. Phys. D 2015, 24, 1550025. [Google Scholar] [CrossRef]
- Achour, J.B.; Brahma, S.; Uzan, J.P. Bouncing compact objects. Part I. Quantum extension of the Oppenheimer-Snyder collapse. J. Cosmol. Astropart. Phys. 2020, 2020, 041. [Google Scholar] [CrossRef]
- Achour, J.B.; Brahma, S.; Mukohyama, S.; Uzan, J.P. Towards consistent black-to-white hole bounces from matter collapse. J. Cosmol. Astropart. Phys. 2020, 2020, 020. [Google Scholar] [CrossRef]
- Münch, J. Effective quantum dust collapse via surface matching. Class. Quantum Gravity 2021, 38, 175015. [Google Scholar] [CrossRef]
- Münch, J. Causal structure of a recent loop quantum gravity black hole collapse model. Phys. Rev. D 2021, 104, 046019. [Google Scholar] [CrossRef]
- Husain, V.; Kelly, J.G.; Santacruz, R.; Wilson-Ewing, E. Quantum gravity of dust collapse: Shock waves from black holes. Phys. Rev. Lett. 2022, 128, 121301. [Google Scholar] [CrossRef] [PubMed]
- Lewandowski, J.; Ma, Y.; Yang, J.; Zhang, C. Quantum oppenheimer-snyder and swiss cheese models. Phys. Rev. Lett. 2023, 130, 101501. [Google Scholar] [CrossRef] [PubMed]
- Ashtekar, A.; Olmedo, J.; Singh, P. Quantum transfiguration of Kruskal black holes. Phys. Rev. Lett. 2018, 121, 241301. [Google Scholar] [CrossRef] [PubMed]
- Ashtekar, A.; Olmedo, J.; Singh, P. Quantum extension of the Kruskal spacetime. Phys. Rev. D 2018, 98, 126003. [Google Scholar] [CrossRef]
- Zhang, C.; Ma, Y.; Yang, J. Black hole image encoding quantum gravity information. Phys. Rev. D 2023, 108, 104004. [Google Scholar] [CrossRef]
- Meissner, K.A. Black-hole entropy in loop quantum gravity. Class. Quantum Gravity 2004, 21, 5245. [Google Scholar] [CrossRef]
- Domagala, M.; Lewandowski, J. Black-hole entropy from quantum geometry. Class. Quantum Gravity 2004, 21, 5233. [Google Scholar] [CrossRef]
- Novikov, I.D.; Thorne, K.S. Astrophysics of black holes. In Black Holes (Les Astres Occlus); Dewitt, C., Dewitt, B.S., Eds.; Gordon and Breach: New York, NY, USA, 1973; pp. 343–450. [Google Scholar]
- Ellis, G.F.; Maartens, R.; MacCallum, M.A.H. Relativistic Cosmology; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Luminet, J.P. Image of a spherical black hole with thin accretion disk. Astron. Astrophys. 1979, 75, 228–235. [Google Scholar]
- Huang, Y.X.; Guo, S.; Cui, Y.H.; Jiang, Q.Q.; Lin, K. Influence of accretion disk on the optical appearance of the Kazakov-Solodukhin black hole. Phys. Rev. D 2023, 107, 123009. [Google Scholar] [CrossRef]
- You, L.; Wang, R.b.; Ma, S.J.; Deng, J.B.; Hu, X.R. Optical properties of Euler-Heisenberg black hole in the Cold Dark Matter Halo. arXiv 2024, arXiv:2403.12840. [Google Scholar]


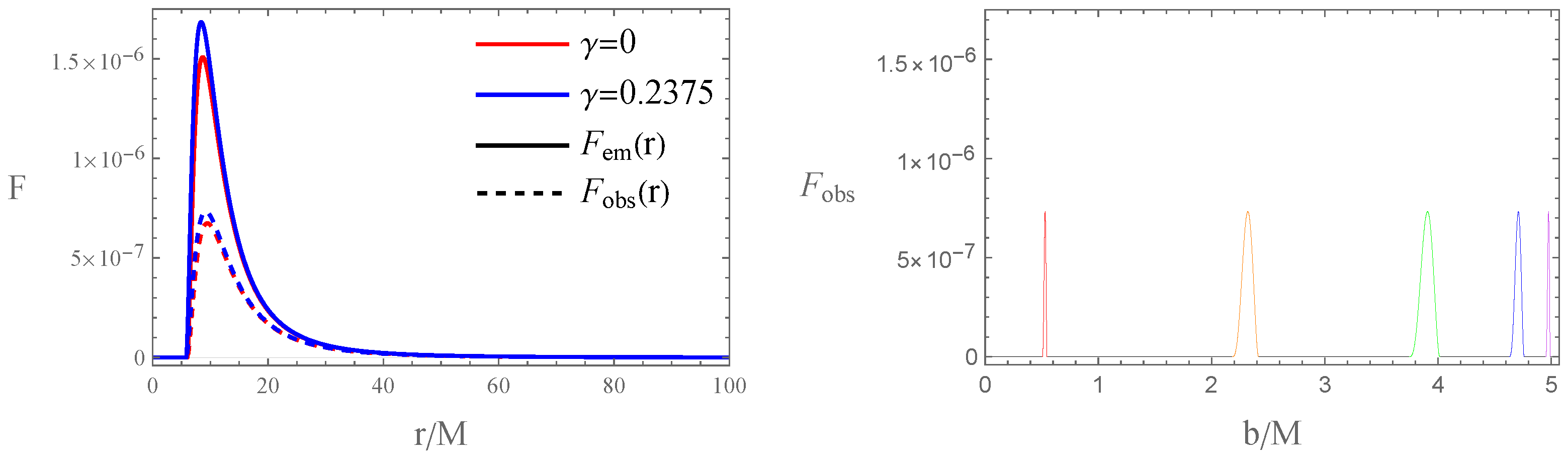

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, L.; Feng, Y.-H.; Wang, R.-B.; Hu, X.-R.; Deng, J.-B. Decoding Quantum Gravity Information with Black Hole Accretion Disk. Universe 2024, 10, 393. https://doi.org/10.3390/universe10100393
You L, Feng Y-H, Wang R-B, Hu X-R, Deng J-B. Decoding Quantum Gravity Information with Black Hole Accretion Disk. Universe. 2024; 10(10):393. https://doi.org/10.3390/universe10100393
Chicago/Turabian StyleYou, Lei, Yu-Hang Feng, Rui-Bo Wang, Xian-Ru Hu, and Jian-Bo Deng. 2024. "Decoding Quantum Gravity Information with Black Hole Accretion Disk" Universe 10, no. 10: 393. https://doi.org/10.3390/universe10100393
APA StyleYou, L., Feng, Y.-H., Wang, R.-B., Hu, X.-R., & Deng, J.-B. (2024). Decoding Quantum Gravity Information with Black Hole Accretion Disk. Universe, 10(10), 393. https://doi.org/10.3390/universe10100393





