Mass Distribution and Maximum Mass of Neutron Stars: Effects of Orbital Inclination Angle
Abstract
1. Introduction
2. Neutron Star Mass Measurements
2.1. Orbital Inclination Angle
2.2. Relativistic Binaries
- Orbital period decay, :
- Range of Shapiro delay, r:
- Shape of Shapiro delay, s:
- “Einstein delay”, :
- Advance of periastron, :
Shapiro Delay
2.3. Optical Spectroscopy
2.4. Gamma-Ray Pulsars
3. Analysis of the Mass Distribution
3.1. “Accuracy-Dependent” Model
3.2. “Accuracy-Independent” Model
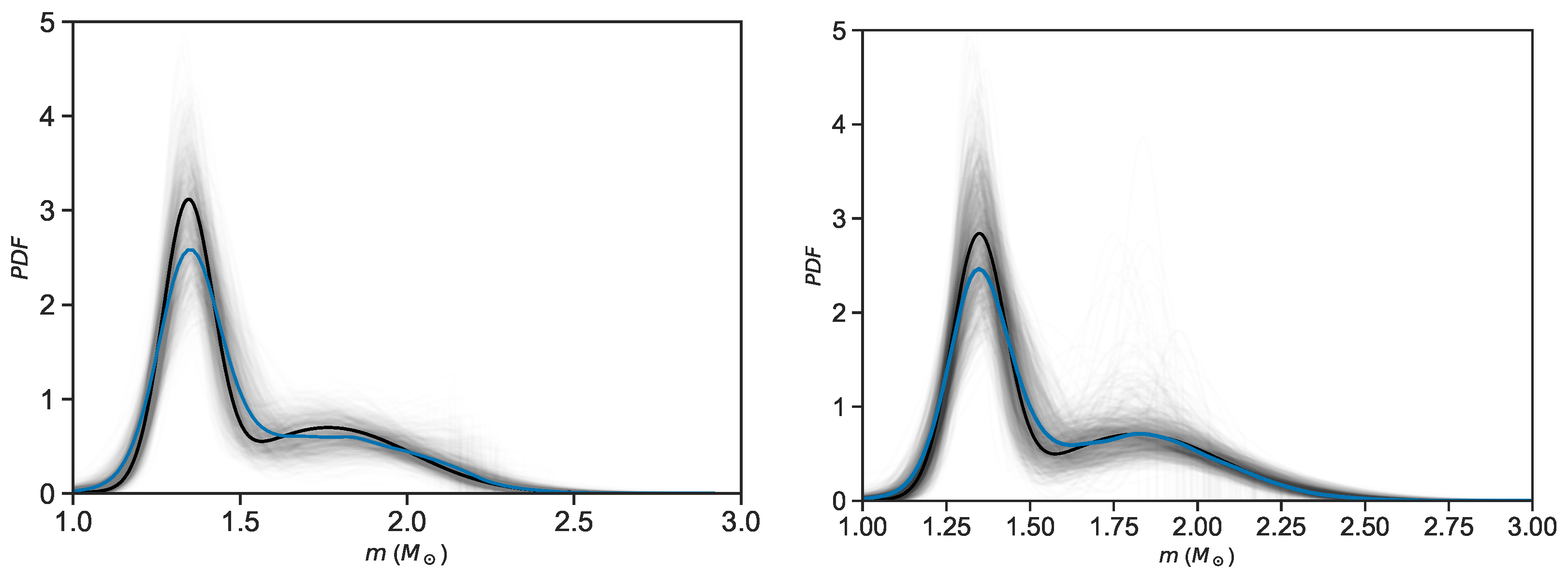
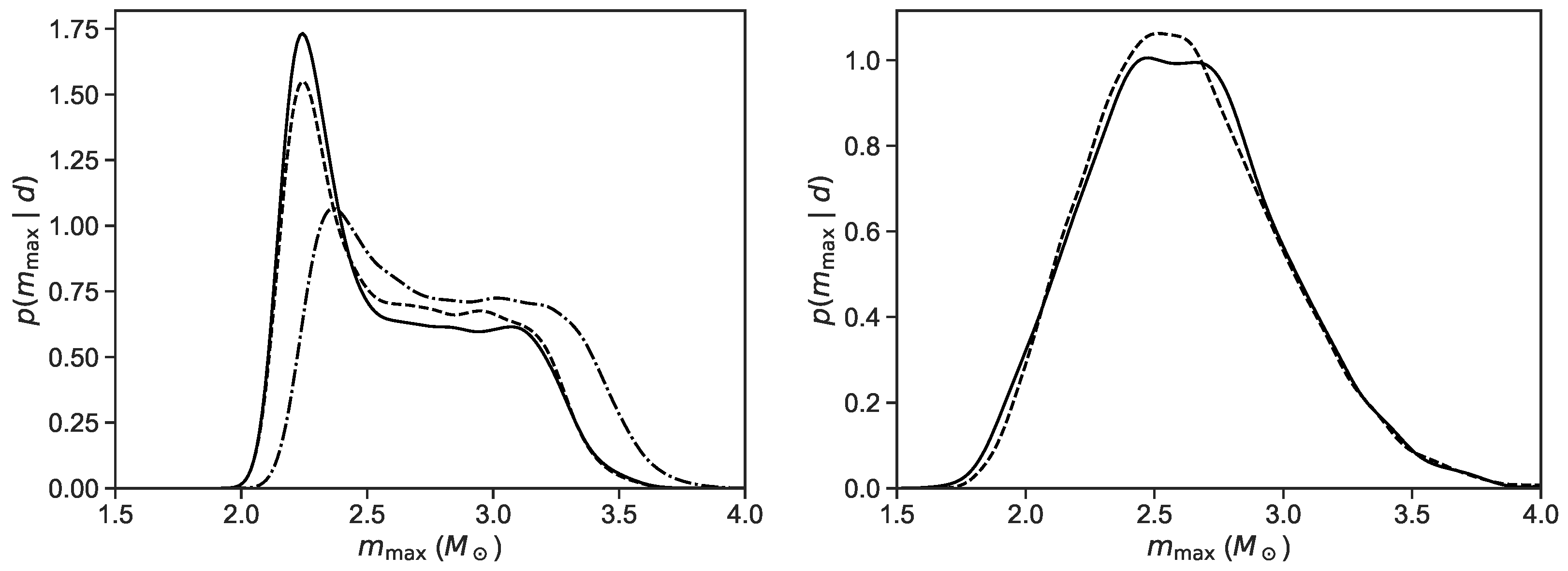
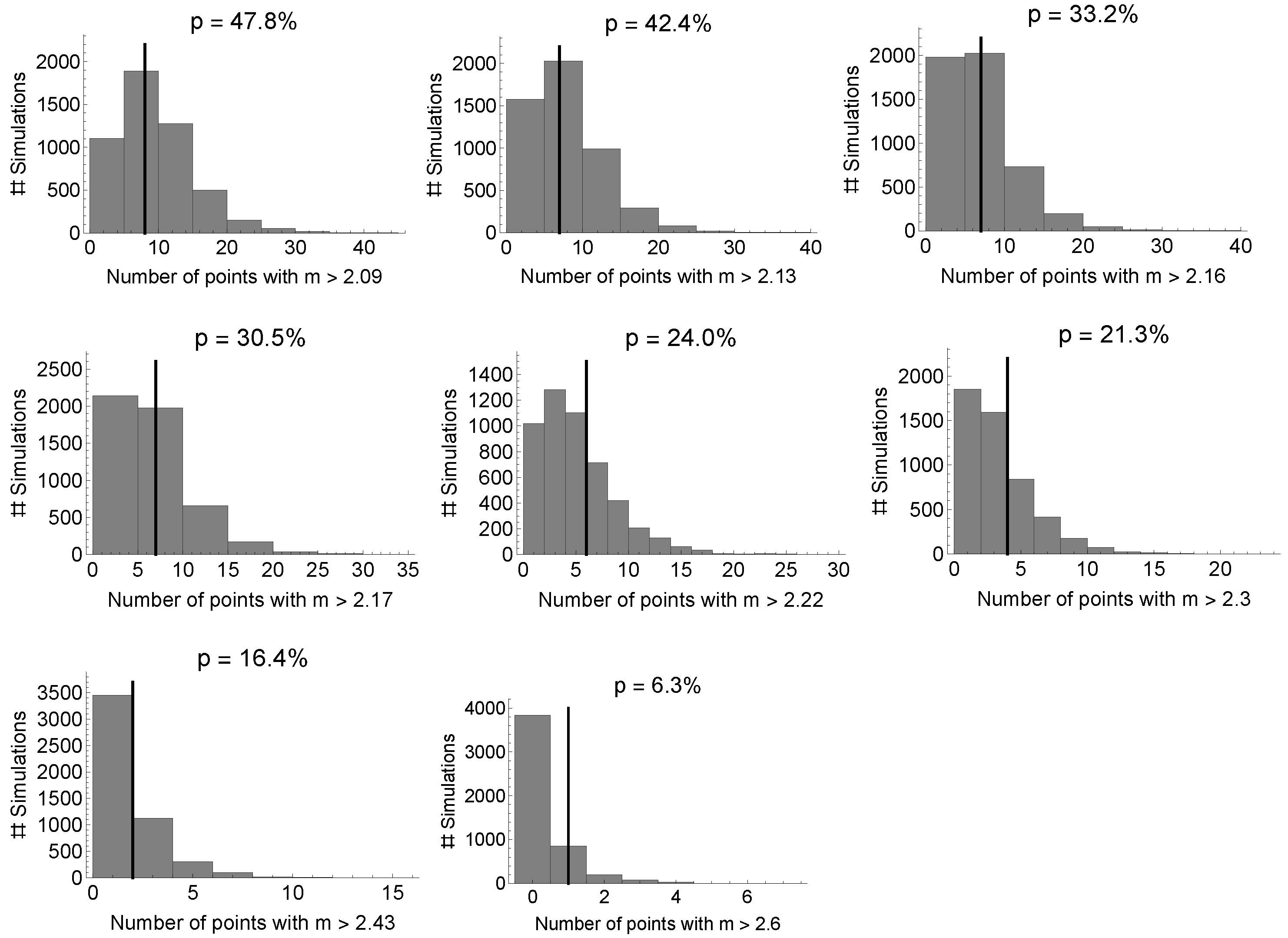
4. Results
4.1. Effects on Individual Masses
4.1.1. PSR B1957+20
4.1.2. PSR J1311-3430
4.1.3. PSR B1516+02B
4.1.4. PSR J1748-2021B
4.2. Effects on the Maximum Mass
4.3. Posterior Predictive Check
5. Discussions and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| NS | Neutron Star |
| GR | General Relativity |
| Fe | Iron |
| TOV | Tolman-Oppenheimer-Volkoff |
| EoS | Equation of state |
| BH | Black Hole |
| O-Ne-Mg | Oxygen-Neon-Magnesium |
| AIC | Accretion-Induced-Collapse |
| WD | White-Dwarf |
| GW | Gravitational Wave |
| LV | LIGO-Virgo |
| BBH | Binary Black Hole |
| ToA | Time of arrival |
| NICER | Neutron star Interior Composition ExploreR |
| pK | post-Keplerian |
| DNS | Double Neutron Star |
| MCMC | Markov Chain Monte Carlo |
| HPDI | Highest posterior density interval |
| MS | Main sequence |
| PPC | Posterior predictive check |
Appendix A. Sample of Neutron Stars
| Pulsar | Type | f [] | [] | q | [] | Reference |
|---|---|---|---|---|---|---|
| 2S 0921-630 | x-ray/optical | 1.44 ± 0.1 | [56] | |||
| 4U 1538-522 | x-ray/optical | 1.02 ± 0.17 | [63] | |||
| 4U 1608-52 | x-ray/optical | 1.57 ± 0.29 | [64] | |||
| 4U 1700-377 | x-ray/optical | 1.96 ± 0.19 | [63] | |||
| 4U 1702-429 | x-ray/optical | 1.9 ± 0.3 | [65] | |||
| 4U 1724-207 | x-ray/optical | 1.81 ± 0.31 | [64] | |||
| 4U 1820-30 | x-ray/optical | 1.77 ± 0.27 | [64] | |||
| 4U 1822-371 | x-ray/optical | 1.96 ± 0.36 | [66] | |||
| Cen X-3 | x-ray/optical | 1.57 ± 0.16 | [63] | |||
| Cyg X-2 | x-ray/optical | 1.71 ± 0.21 | [67] | |||
| EXO 0748-676 | x-ray/optical | 2.01 ± 0.21 | [68] | |||
| EXO 1722-363 | x-ray/optical | 1.91 ± 0.45 | [63] | |||
| EXO 1745-248 | x-ray/optical | 1.65 ± 0.26 | [64] | |||
| Her X-1 | x-ray/optical | 1.073 ± 0.358 | [69] | |||
| J013236.7+303228 | x-ray/optical | 2.0 ± 0.4 | [70] | |||
| J0212.1+5320 | x-ray/optical | 1.85 ± 0.29 | [71] | |||
| J0427.9-6704 | x-ray/optical | 1.86 ± 0.11 | [72] | |||
| J0846.0+2820 | x-ray/optical | 1.96 ± 0.41 | [72] | |||
| J0952-0607 | x-ray/optical | 2.35 ± 0.17 | [27] | |||
| J1023+0038 | x-ray/optical | 1.65 ± 0.16 | [72] | |||
| J1048+2339 | x-ray/optical | 1.96 ± 0.22 | [72] | |||
| J1301+0833 | x-ray/optical | 1.60 ± 0.23 | [24] | |||
| J1311-3430 | x-ray/optical | [24] | ||||
| J1417.7-4407 | x-ray/optical | 1.62 ± 0.3 | [72] | |||
| J1555-2908 | x-ray/optical | 1.67 ± 0.06 | [73] | |||
| J1653-0158 | x-ray/Optical | 2.15 ± 0.16 | [24] | |||
| J1723-2837 | x-ray/optical | [72] | ||||
| J1810+1744 | x-ray/Optical | 2.13 ± 0.04 | [24] | |||
| J2039.6-5618 | x-ray/optical | 2.04 ± 0.31 | [72] | |||
| J2129-0429 | x-ray/optical | 1.74 ± 0.18 | [72] | |||
| J2215+5135 | x-ray/optical | 2.28 ± 0.10 | [74] | |||
| J2339-0533 | x-ray/optical | 1.47 ± 0.09 | [75] | |||
| KS 1731-260 | x-ray/optical | 1.61 ± 0.37 | [64] | |||
| LMC X-4 | x-ray/optical | 1.57 ± 0.11 | [63] | |||
| OAO 1657-415 | x-ray/optical | 1.74 ± 0.3 | [63] | |||
| SAX 1748.9-2021 | x-ray/optical | 1.81 ± 0.31 | [64] | |||
| SAX J1802.7-2017 | x-ray/optical | 1.57 ± 0.25 | [63] | |||
| SMC X-1 | x-ray/optical | 1.21 ± 0.12 | [63] | |||
| Vela X-1 | x-ray/optical | 2.12 ± 0.16 | [63] | |||
| XTE J1855-026 | x-ray/optical | 1.41 ± 0.24 | [63] | |||
| XTE J2123-058 | x-ray/optical | 1.53 ± 0.36 | [76] | |||
| B1957+20 | x-ray/optical | 0.005 | 69.2 ± 0.8 | [49] | ||
| J1740-5350 | x-ray/optical | 0.002644 | 5.85 ± 0.13 | 1.6±0.3 | [77] | |
| J1816+4510 | x-ray/optical | 0.0017607 | 9.54 ± 0.21 | 1.45 ± 0.38 | [78] | |
| B1534+12 | NS-NS | 1.3332 ± 0.0010 | [79] | |||
| B1534+12 Cp | NS-NS | 1.3452 ± 0.0010 | [79] | |||
| B1913+16 | NS-NS | 1.438 ± 0.001 | [80] | |||
| B1913+16 Cp | NS-NS | 1.390 ± 0.001 | [80] | |||
| B2127+11C | NS-NS | 1.358 ± 0.010 | [81] | |||
| B2127+11C Cp | NS-NS | 1.354 ± 0.010 | [81] | |||
| J0453+1559 | NS-NS | 1.559 ± 0.004 | [82] | |||
| J0453+1559 Cp | NS-NS | 1.174 ± 0.004 | [82] | |||
| J0509+3801 | NS-NS | 1.34 ± 0.08 | [83] | |||
| J0509+3801 Cp | NS-NS | 1.46 ± 0.08 | [83] | |||
| J0514-4002A | NS-NS | 1.25 ± 0.05 | [84] | |||
| J0514-4002A Cp | NS-NS | 1.22 ± 0.05 | [84] | |||
| J0737-3039A | NS-NS | 1.338185 ± 0.000013 | [2] | |||
| J0737-3039B | NS-NS | 1.248868 ± 0.000012 | [2] | |||
| J1756-2251 | NS-NS | 1.341 ± 0.007 | [85] | |||
| J1756-2251 Cp | NS-NS | 1.230 ± 0.007 | [85] | |||
| J1757-1854 | NS-NS | 1.3406 ± 0.0005 | [86] | |||
| J1757-1854 Cp | NS-NS | 1.3922 ± 0.0005 | [86] | |||
| J1807-2500B | NS-NS | 1.3655 ± 0.0021 | [83] | |||
| J1807-2500B Cp | NS-NS | 1.2064 ± 0.0020 | [83] | |||
| J1829+2456 | NS-NS | 1.306 ± 0.007 | [87] | |||
| J1829+2456 Cp | NS-NS | 1.299 ± 0.007 | [87] | |||
| J1906+0746 | NS-NS | 1.291 ± 0.011 | [88] | |||
| J1906+0746 Cp | NS-NS | 1.322 ± 0.011 | [88] | |||
| J1913+1102 | NS-NS | 1.62 ± 0.03 | [89] | |||
| J1913+1102 Cp | NS-NS | 1.27 ± 0.03 | [89] | |||
| J1018-1523 | NS-NS | 0.238062 | 2.3 ± 0.3 | [90] | ||
| J1325-6253 | NS-NS | 0.1415168 | 2.57 ± 0.06 | 1.37 ± 0.27 | [91] | |
| J1411+2551 | NS-NS | 0.1223898 | 2.538 ± 0.022 | [92] | ||
| J1759+5036 | NS-NS | 0.081768 | 2.62 ± 0.03 | 1.52 ± 0.26 | [93] | |
| J1811-1736 | NS-NS | 0.128121 | 2.57 ± 0.10 | 1.34 ± 0.16 | [94] | |
| J1930-1852 | NS-NS | 0.34690765 | 2.54 ± 0.03 | [95] | ||
| J1946+2052 | NS-NS | 0.268184 | 2.50 ± 0.04 | 1.25 ± 0.15 | [96] | |
| J2140-2311B | NS-NS | 0.2067 | 2.53 ± 0.08 | 1.3 ± 0.2 | [97] | |
| B1855+09 | NS-WD | 1.54 ± 0.13 | [98] | |||
| J0337+1715 | NS-WD | 1.4401 ± 0.0015 | [99] | |||
| J0348+0432 | NS-WD | 2.01 ± 0.04 | [50] | |||
| J0437-4715 | NS-WD | 1.44 ± 0.07 | [100] | |||
| J0621+1002 | NS-WD | 1.53 ± 0.15 | [101] | |||
| J0740+6620 | NS-WD | 2.08 ± 0.07 | [102] | |||
| J0751+1807 | NS-WD | 1.64 ± 0.15 | [103] | |||
| J0955-6150 | NS-WD | 1.71 ± 0.03 | [104] | |||
| J1012+5307 | NS-WD | 1.72 ± 0.16 | [105] | |||
| J1017-7156 | NS-WD | [98] | ||||
| J1022-1001 | NS-WD | [98] | ||||
| J1125-6014 | NS-WD | 1.68 ± 0.16 | [106] | |||
| J1141-6545 | NS-WD | 1.27 ± 0.01 | [107] | |||
| J1528-3146 | NS-WD | 1.61 ± 0.14 | [108] | |||
| J1600-3053 | NS-WD | 2.06 ± 0.42 | [98] | |||
| J1614-2230 | NS-WD | 1.94 ± 0.03 | [106] | |||
| J1713+0747 | NS-WD | 1.28 ± 0.08 | [98] | |||
| J1738+0333 | NS-WD | 1.47 ± 0.07 | [109] | |||
| J1741+1351 | NS-WD | 1.14 ± 0.34 | [110] | |||
| J1748-2446am | NS-WD | 1.649 ± 0.074 | [111] | |||
| J1802-2124 | NS-WD | 1.24 ± 0.11 | [112] | |||
| J1811-2405 | NS-WD | 2.0 ± 0.65 | [113] | |||
| J1909-3744 | NS-WD | 1.45 ± 0.03 | [106] | |||
| J1910-5958A | NS-WD | 1.55 ± 0.07 | [114] | |||
| J1918-0642 | NS-WD | 1.29 ± 0.10 | [115] | |||
| J1933-6211 | NS-WD | 1.40 ± 0.25 | [116] | |||
| J1946+3417 | NS-WD | 1.828 ± 0.022 | [117] | |||
| J1949+3106 | NS-WD | 1.34 ± 0.16 | [118] | |||
| J1950+2414 | NS-WD | 1.496 ± 0.023 | [118] | |||
| J1959+2048 | NS-WD | 2.18 ± 0.09 | [74] | |||
| J2043+1711 | NS-WD | 1.38 ± 0.13 | [115] | |||
| J2045+3633 | NS-WD | 1.251 ± 0.021 | [119] | |||
| J2053+4650 | NS-WD | 1.40 ± 0.21 | [120] | |||
| J2222-0137 | NS-WD | 1.831 ± 0.010 | [121] | |||
| J2234+0611 | NS-WD | 1.353 ± 0.016 | [122] | |||
| B1516+02B | NS-WD | 0.000646723 | 2.29 ± 0.17 | [11] | ||
| B1802-07 | NS-WD | 0.00945034 | 1.62 ± 0.07 | [8] | ||
| B2303+46 | NS-WD | 0.246261924525 | 2.64 ± 0.05 | [8] | ||
| J0024-7204H | NS-WD | 0.001927 | 1.665 ± 0.007 | 1.41 ± 0.08 | [123,124] | |
| J1748-2021B | NS-WD | 0.0002266235 | 2.69 ± 0.071 | [12] | ||
| J1748-2446I | NS-WD | 0.003658 | 2.17 ± 0.02 | [20] | ||
| J1748-2446J | NS-WD | 0.013066 | 2.20 ± 0.04 | [20] | ||
| J1750-37A | NS-WD | 0.0518649 | 1.97 ± 0.15 | [11] | ||
| J1823-3021G | NS-WD | 0.0123 | 2.65 ± 0.07 | 2.1 ± 0.2 | [125] | |
| J1824-2452C | NS-WD | 0.006553 | 1.616 ± 0.007 | [126] | ||
| J0045-7319 | NS-MS | 1.58 ± 0.34 | [8] | |||
| J1903+0327 | NS-MS | 1.667 ± 0.016 | [115] |
| 1 | The equation of state needs to obey causality. The stiffest EoS is the one in which the sound speed in the medium equals the speed of light. |
| 2 | This is the reason why these systems are called spiders, in an analogy with the black widow and redback spiders, which are known to kill and devour their male partners. |
| 3 | The difference is irrelevant for the whole sample of 3000+ pulsars known today, which would need to rotate much faster to hold an excess of mass over the . |
References
- Hewish, A. Pulsars. Sci. Am. 1968, 219, 25–35. [Google Scholar] [CrossRef]
- Kramer, M.; Stairs, I.H.; Manchester, R.N.; Wex, N.; Deller, A.T.; Coles, W.A.; Ali, M.; Burgay, M.; Camilo, F.; Cognard, I.; et al. Strong-field gravity tests with the double pulsar. Phys. Rev. X 2021, 11, 041050. [Google Scholar] [CrossRef]
- Baade, W.; Zwicky, F. On super-novae. Proc. Natl. Acad. Sci. USA 1934, 20, 254–259. [Google Scholar] [CrossRef] [PubMed]
- Cameron, A.G. Neutron Star Models. Astrophys. J. 1959, 130, 884. [Google Scholar] [CrossRef]
- Nomoto, K. Evolution of 8–10 solar mass stars toward electron capture supernovae. I-Formation of electron-degenerate O+ NE+ MG cores. Astrophys. J. 1984, 277, 791–805. [Google Scholar] [CrossRef]
- Finn, L.S. Observational constraints on the neutron star mass distribution. Phys. Rev. Lett. 1994, 73, 1878. [Google Scholar] [CrossRef] [PubMed]
- Rhoades, C.E., Jr.; Ruffini, R. Maximum mass of a neutron star. Phys. Rev. Lett. 1974, 32, 324. [Google Scholar] [CrossRef]
- Thorsett, S.E.; Chakrabarty, D. Neutron star mass measurements. i. radio pulsars. Astrophys. J. 1999, 512, 288. [Google Scholar] [CrossRef]
- Barziv, O.; Kaper, L.; Van Kerkwijk, M.H.; Telting, J.H.; Van Paradijs, J. The mass of the neutron star in Vela X-1. Astron. Astrophys. 2001, 377, 925–944. [Google Scholar] [CrossRef]
- Nice, D.J.; Splaver, E.M.; Stairs, I.H.; Löhmer, O.; Jessner, A.; Kramer, M.; Cordes, J.M. A 2.1 M⊙ Pulsar Measured by Relativistic Orbital Decay. Astrophys. J. 2005, 634, 1242. [Google Scholar] [CrossRef]
- Freire, P.C.C.; Wolszczan, A.; van den Berg, M.; Hessels, J.W.T. A massive neutron star in the globular cluster M5. Astrophys. J. 2008, 679, 1433. [Google Scholar] [CrossRef]
- Freire, P.C.C.; Ransom, S.M.; Bégin, S.; Stairs, I.H.; Hessels, J.W.T.; Frey, L.H.; Camilo, F. Eight new millisecond pulsars in NGC 6440 and NGC 6441. Astrophys. J. 2008, 675, 670. [Google Scholar] [CrossRef]
- Demorest, P.B.; Pennucci, T.; Ransom, S.M.; Roberts, M.S.E.; Hessels, J.W.T. A two-solar-mass neutron star measured using Shapiro delay. Nature 2010, 467, 1081–1083. [Google Scholar] [CrossRef] [PubMed]
- Cromartie, H.T.; Fonseca, E.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Brook, P.R.; DeCesar, M.E.; Dolch, T.; Ellis, J.A.; et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. 2020, 4, 72–76. [Google Scholar] [CrossRef]
- Schwab, J.; Podsiadlowski, P.; Rappaport, S. Further evidence for the bimodal distribution of neutron-star masses. Astrophys. J. 2010, 719, 722. [Google Scholar] [CrossRef]
- Podsiadlowski, P.; Langer, N.; Poelarends, A.J.T.; Rappaport, S.; Heger, A.; Pfahl, E. The effects of binary evolution on the dynamics of core collapse and neutron star kicks. Astrophys. J. 2004, 612, 1044. [Google Scholar] [CrossRef]
- Hiramatsu, D.; Howell, D.A.; Van Dyk, S.D.; Goldberg, J.A.; Maeda, K.; Moriya, T.J.; Tominaga, N.; Nomoto, K.; Hosseinzadeh, G.; Arcavi, I.; et al. The electron-capture origin of supernova 2018zd. Nat. Astron. 2021, 5, 903–910. [Google Scholar] [CrossRef]
- Zhang, C.M.; Wang, J.; Zhao, Y.H.; Yin, H.X.; Song, L.M.; Menezes, D.P.; Wickramasinghe, D.T.; Ferrario, L.; Chardonnet, P. Study of measured pulsar masses and their possible conclusions. Astron. Astrophys. 2011, 527, A83. [Google Scholar] [CrossRef]
- Valentim, R.; Rangel, E.; Horvath, J.E. On the mass distribution of neutron stars. Mon. Not. R. Astron. Soc. 2011, 414, 1427–1431. [Google Scholar] [CrossRef]
- Kiziltan, B.; Kottas, A.; De Yoreo, M.; Thorsett, S.E. The neutron star mass distribution. Astrophys. J. 2013, 778, 66. [Google Scholar] [CrossRef]
- Özel, F.; Freire, P. Masses, radii, and the equation of state of neutron stars. Annu. Rev. Astron. Astrophys. 2016, 54, 401–440. [Google Scholar] [CrossRef]
- Burrows, A.; Vartanyan, D. Core-collapse supernova explosion theory. Nature 2021, 589, 29–39. [Google Scholar] [CrossRef]
- Suwa, Y.; Yoshida, T.; Shibata, M.; Umeda, H.; Takahashi, K. On the minimum mass of neutron stars. Mon. Not. R. Astron. Soc. 2018, 481, 3305–3312. [Google Scholar] [CrossRef]
- Kandel, D.; Romani, R.W. An Optical Study of the Black Widow Population. Astrophys. J. 2022, 942, 6. [Google Scholar] [CrossRef]
- Linares, M. Super-Massive Neutron Stars and Compact Binary Millisecond Pulsars. In Proceedings of the XIII Multifrequency Behaviour of High Energy Cosmic Sources Workshop, Palermo, Italy, 3 June 2019. [Google Scholar]
- Horvath, J.E.; Bernardo, A.; Rocha, L.S.; Valentim, R.; Moraes, P.H.R.S.; de Avellar, M.G.B. Redback/Black Widow Systems as progenitors of the highest neutron star masses and low-mass Black Holes. Sci. China Phys. Mech. Astron. 2020, 63, 129531. [Google Scholar] [CrossRef]
- Romani, R.W.; Kandel, D.; Filippenko, A.V.; Brink, T.G.; Zheng, W. PSR J0952-0607: The Fastest and Heaviest Known Galactic Neutron Star. Astrophys. J. Lett. 2022, 934, L18. [Google Scholar] [CrossRef]
- Wang, B.; Liu, D. The formation of neutron star systems through accretion-induced collapse in white-dwarf binaries. Res. Astron. Astrophys. 2020, 20, 135. [Google Scholar] [CrossRef]
- Zhong, S.Q.; Li, L.; Dai, Z.G. GRB 211211A: A Neutron Star–White Dwarf Merger? Astrophys. J. Lett. 2023, 947, L21. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of gravitational waves from a binary neutron star inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Margalit, B.; Metzger, B.D. Constraining the maximum mass of neutron stars from multi-messenger observations of GW170817. Astrophys. J. Lett. 2017, 850, L19. [Google Scholar] [CrossRef]
- Alsing, J.; Silva, H.O.; Berti, E. Evidence for a maximum mass cut-off in the neutron star mass distribution and constraints on the equation of state. Mon. Not. R. Astron. Soc. 2018, 478, 1377–1391. [Google Scholar] [CrossRef]
- Shibata, M.; Zhou, E.; Kiuchi, K.; Fujibayashi, S. Constraint on the maximum mass of neutron stars using GW170817 event. Phys. Rev. D 2019, 100, 023015. [Google Scholar] [CrossRef]
- Shao, D.-S.; Tang, S.-P.; Jiang, J.-L.; Fan, Y.-Z. Maximum mass cutoff in the neutron star mass distribution and the prospect of forming supramassive objects in the double neutron star mergers. Phys. Rev. D 2020, 102, 063006. [Google Scholar] [CrossRef]
- Shao, D.-S.; Tang, S.-P.; Sheng, X.; Jiang, J.-L.; Wang, Y.-Z.; Jin, Z.-P.; Fan, Y.-Z.; Wei, D.-M. Estimating the maximum gravitational mass of nonrotating neutron stars from the GW170817/GRB 170817A/AT2017gfo observation. Phys. Rev. D 2020, 101, 063029. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agathos, M.; et al. GW190814: Gravitational waves from the coalescence of a 23 solar mass black hole with a 2.6 solar mass compact object. Astrophys. J. Lett. 2020, 896, L44. [Google Scholar] [CrossRef]
- Nathanail, A.; Most, E.R.; Rezzolla, L. GW170817 and GW190814: Tension on the Maximum Mass. Astrophys. J. Lett. 2021, 908, L28. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C. Population properties of compact objects from the second LIGO–Virgo gravitational-wave transient catalog. Astrophys. J. Lett. 2021, 913, L7. [Google Scholar] [CrossRef]
- Ye, C.; Fishbach, M. Inferring the Neutron Star Maximum Mass and Lower Mass Gap in Neutron Star–Black Hole Systems with Spin. Astrophys. J. 2022, 937, 73. [Google Scholar] [CrossRef]
- Ai, S.; Gao, H.; Yuan, Y.; Zhang, B.; Lan, L. What constraints can one pose on the maximum mass of neutron stars from multi-messenger observations? Mon. Not. R. Astron. Soc. 2023, 526, 6260–6273. [Google Scholar] [CrossRef]
- Most, E.R.; Papenfort, L.J.; Weih, L.R.; Rezzolla, L. A lower bound on the maximum mass if the secondary in GW190814 was once a rapidly spinning neutron star. MNRAS Lett. 2020, 499, L82–L86. [Google Scholar] [CrossRef]
- Lorimer, D.R.; Kramer, M. Handbook of Pulsar Astronomy; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- The ATNF Pulsar Catalogue. Available online: https://www.atnf.csiro.au/research/pulsar/psrcat/ (accessed on 26 October 2023).
- Riley, T.E.; Watts, A.L.; Bogdanov, S.; Ray, P.S.; Ludlam, R.M.; Guillot, S.; Arzoumanian, Z.; Baker, C.L.; Bilous, A.V.; Chakrabarty, D.; et al. A NICER view of PSR J0030+ 0451: Millisecond pulsar parameter estimation. Astrophys. J. Lett. 2019, 887, L21. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Ray, P.S.; Bogdanov, S.; Guillot, S.; Morsink, S.M.; Bilous, A.V.; Arzoumanian, Z.; Choudhury, D.; Deneva, J.S.; et al. A NICER view of the massive pulsar PSR J0740+ 6620 informed by radio timing and XMM-Newton spectroscopy. Astrophys. J. Lett. 2021, 918, L27. [Google Scholar] [CrossRef]
- Kansabanik, D.; Bhattacharyya, B.; Roy, J.; Stappers, B. Unraveling the eclipse mechanism of a binary millisecond pulsar using broadband radio spectra. Astrophys. J. 2021, 920, 58. [Google Scholar] [CrossRef]
- Atwood, W.B.; Abdo, A.A.; Ackermann, M.; Althouse, W.; Anderson, B.; Axelsson, M.; Baldini, L.; Ballet, J.; Band, D.L.; Barbiellini, G.; et al. The large area telescope on the Fermi gamma-ray space telescope mission. Astrophys. J. 2009, 697, 1071. [Google Scholar] [CrossRef]
- Clark, C.J.; Kerr, M.; Barr, E.D.; Bhattacharyya, B.; Breton, R.P.; Bruel, P.; Camilo, F.; Chen, W.; Cognard, I.; Cromartie, H.T.; et al. Neutron star mass estimates from gamma-ray eclipses in spider millisecond pulsar binaries. Nat. Astron. 2023, 7, 451–462. [Google Scholar] [CrossRef] [PubMed]
- Van Kerkwijk, M.H.; Breton, R.P.; Kulkarni, S.R. Evidence for a Massive Neutron Star from a Radial-velocity Study of the Companion to the Black-widow Pulsar PSR B1957+ 20. Astrophys. J. 2011, 728, 95. [Google Scholar] [CrossRef]
- Antoniadis, J.; Tauris, T.M.; Ozel, F.; Barr, E.; Champion, D.J.; Freire, P.C.C. The millisecond pulsar mass distribution: Evidence for bimodality and constraints on the maximum neutron star mass. arXiv 2016, arXiv:1605.01665. [Google Scholar]
- Farrow, N.; Zhu, X.J.; Thrane, E. The mass distribution of galactic double neutron stars. Astrophys. J. 2019, 876, 18. [Google Scholar] [CrossRef]
- Stan Development Team. Stan Modeling Language Users Guide and Reference Manual. 2020. Available online: https://mc-stan.org/ (accessed on 26 October 2023).
- Farr, W.M.; Chatziioannou, K. A Population-Informed Mass Estimate for Pulsar J0740+ 6620. Res. Notes AAS 2020, 4, 65. [Google Scholar] [CrossRef]
- Rocha, L.S. The Masses of Neutron Stars. Doctoral Dissertation, Universidade de São Paulo, São Paulo, 2023. Available online: https://www.teses.usp.br/teses/disponiveis/14/14131/tde-04102023-161616/en.php (accessed on 26 October 2023).
- Horvath, J.E.; Rocha, L.S.; Bernardo, A.L.; de Avellar, M.G.; Valentim, R. Birth events, masses and the maximum mass of Compact Stars. In Astrophysics in the XXI Century with Compact Stars; World Scientific: Singapore, 2023; pp. 1–51. [Google Scholar]
- Steeghs, D.; Jonker, P.G. On the mass of the neutron star in v395 carinae/2s 0921–630. Astrophys. J. 2007, 669, L85. [Google Scholar] [CrossRef]
- Romani, R.W.; Filippenko, A.V.; Silverman, J.M.; Cenko, S.B.; Greiner, J.; Rau, A.; Elliott, J.; Pletsch, H.J. PSR J1311-3430: A Heavyweight Neutron Star with a Flyweight Helium Companion. Astrophys. J. Lett. 2012, 760, L36. [Google Scholar] [CrossRef]
- Rezzolla, L.; Most, E.R.; Weih, L.R. Using gravitational-wave observations and quasi-universal relations to constrain the maximum mass of neutron stars. Astrophys. J. Lett. 2018, 852, L25. [Google Scholar] [CrossRef]
- Ruiz, M.; Shapiro, S.L.; Tsokaros, A. GW170817, general relativistic magnetohydrodynamic simulations, and the neutron star maximum mass. Phys. Rev. D 2018, 97, 021501. [Google Scholar] [CrossRef] [PubMed]
- Ai, S.; Gao, H.; Zhang, B. What constraints on the neutron star maximum mass can one pose from GW170817 observations? Astrophys. J. 2020, 893, 146. [Google Scholar] [CrossRef]
- Fan, Y.-Z.; Han, M.-Z.; Jiang, J.-L.; Shao, D.-S.; Tang, S.-P. Maximum gravitational mass inferred at about 3% precision with multimessenger data of neutron stars. arXiv 2023, arXiv:2309.12644. [Google Scholar]
- de Sá, L.M.; Bernardo, A.; Bachega, R.R.A.; Rocha, L.S.; Moraes, P.H.R.S.; Horvath, J.E. An Overview of Compact Star Populations and Some of Its Open Problems. Galaxies 2023, 11, 19. [Google Scholar] [CrossRef]
- Falanga, M.; Bozzo, E.; Lutovinov, A.; Bonnet-Bidaud, J.M.; Fetisova, Y.; Puls, J. Ephemeris, orbital decay, and masses of ten eclipsing high-mass X-ray binaries. Astron. Astrophys. 2015, 577, A130. [Google Scholar] [CrossRef]
- Özel, F.; Psaltis, D.; Güver, T.; Baym, G.; Heinke, C.; Guillot, S. The dense matter equation of state from neutron star radius and mass measurements. Astrophys. J. 2016, 820, 28. [Google Scholar] [CrossRef]
- Nättilä, J.; Miller, M.C.; Steiner, A.W.; Kajava, J.J.E.; Suleimanov, V.F.; Poutanen, J. Neutron star mass and radius measurements from atmospheric model fits to X-ray burst cooling tail spectra. Astron. Astrophys. 2017, 608, A31. [Google Scholar] [CrossRef]
- Munoz-Darias, T.; Casares, J.; Martínez-Pais, I.G. The “k-correction” for irradiated emission lines in lmxbs: Evidence for a massive neutron star in x1822–371 (v691 cra). Astrophys. J. 2005, 635, 502. [Google Scholar] [CrossRef]
- Casares, J.; Hernández, J.G.; Israelian, G.; Rebolo, R. On the mass of the neutron star in Cyg X-2. Mon. Not. R. Astron. Soc. 2010, 401, 2517–2520. [Google Scholar] [CrossRef]
- Knight, A.H.; Ingram, A.; Middleton, M.; Drake, J. Eclipse mapping of EXO 0748–676: Evidence for a massive neutron star. Mon. Not. R. Astron. Soc. 2022, 510, 4736–4756. [Google Scholar] [CrossRef]
- Rawls, M.L.; Orosz, J.A.; McClintock, J.E.; Torres, M.A.P.; Bailyn, C.D.; Buxton, M.M. Refined neutron star mass determinations for six eclipsing x-ray pulsar binaries. Astrophys. J. 2011, 730, 25. [Google Scholar] [CrossRef]
- Bhalerao, V.B.; van Kerkwijk, M.H.; Harrison, F.A. Constraints on the Compact Object Mass in the Eclipsing High-mass X-Ray Binary XMMU J013236. 7+ 303228 in M 33. Astrophys. J. 2012, 757, 10. [Google Scholar] [CrossRef]
- Shahbaz, T.; Linares, M.; Breton, R.P. Properties of the redback millisecond pulsar binary 3FGL J0212. 1+ 5320. Mon. Not. R. Astron. Soc. 2017, 472, 4287–4296. [Google Scholar] [CrossRef]
- Strader, J.; Swihart, S.; Chomiuk, L.; Bahramian, A.; Britt, C.; Cheung, C.C.; Dage, K.; Halpern, J.; Li, K.-L.; Mignani, R.P.; et al. Optical spectroscopy and demographics of redback millisecond pulsar binaries. Astrophys. J. 2019, 872, 42. [Google Scholar] [CrossRef]
- Kennedy, M.R.; Breton, R.P.; Clark, C.J.; Mata Sánchez, D.; Voisin, G.; Dhillon, V.S.; Halpern, J.P.; Marsh, T.R.; Nieder, L.; Ray, P.S.; et al. Measuring the mass of the black widow PSR J1555-2908. Mon. Not. R. Astron. Soc. 2022, 512, 3001–3014. [Google Scholar] [CrossRef]
- Kandel, D.; Romani, R.W. Atmospheric circulation on black widow companions. Astrophys. J. 2020, 892, 101. [Google Scholar] [CrossRef]
- Kandel, D.; Romani, R.W.; Filippenko, A.V.; Brink, T.G.; Zheng, W. Heated Poles on the Companion of Redback PSR J2339–0533. Astrophys. J. 2020, 903, 39. [Google Scholar] [CrossRef]
- Casares, J.; Dubus, G.; Shahbaz, T.; Zurita, C.; Charles, P.A. VLT spectroscopy of XTE J2123-058 during quiescence: The masses of the two components. Mon. Not. R. Astron. Soc. 2002, 329, 29–36. [Google Scholar] [CrossRef]
- Ferraro, F.R.; Sabbi, E.; Gratton, R.; Possenti, A.; D’Amico, N.; Bragaglia, A.; Camilo, F. Accurate mass ratio and heating effects in the dual-line millisecond binary pulsar in NGC 6397. Astrophys. J. 2003, 584, L13. [Google Scholar] [CrossRef][Green Version]
- Kaplan, D.L.; Bhalerao, V.B.; van Kerkwijk, M.H.; Koester, D.; Kulkarni, S.R.; Stovall, K. A metal-rich low-gravity companion to a massive millisecond pulsar. Astrophys. J. 2013, 765, 158. [Google Scholar] [CrossRef]
- Fonseca, E.; Stairs, I.H.; Thorsett, S.E. A comprehensive study of relativistic gravity using PSR B1534+ 12. Astrophys. J. 2014, 787, 82. [Google Scholar] [CrossRef]
- Weisberg, J.M.; Huang, Y. Relativistic measurements from timing the binary pulsar PSR B1913+ 16. Astrophys. J. 2016, 829, 55. [Google Scholar] [CrossRef]
- Jacoby, B.A.; Cameron, P.B.; Jenet, F.A.; Anderson, S.B.; Murty, R.N.; Kulkarni, S.R. Measurement of orbital decay in the double neutron star binary PSR B2127+ 11C. Astrophys. J. Lett. 2006, 644, L113. [Google Scholar] [CrossRef]
- Martinez, J.G.; Stovall, K.; Freire, P.C.C.; Deneva, J.S.; Jenet, F.A.; McLaughlin, M.A.; Bagchi, M.; Bates, S.D.; Ridolfi, A. Pulsar J0453+ 1559: A double neutron star system with a large mass asymmetry. Astrophys. J. 2015, 812, 143. [Google Scholar] [CrossRef]
- Martinez, J.G.; Stovall, K.; Freire, P.C.C.; Deneva, J.S.; Jenet, F.A.; McLaughlin, M.A.; Bagchi, M.; Bates, S.D.; Ridolfi, A. The timing of nine globular cluster pulsars. Astrophys. J. 2012, 745, 109. [Google Scholar]
- Ridolfi, A.; Freire, P.C.C.; Gupta, Y.; Ransom, S.M. Upgraded Giant Metrewave Radio Telescope timing of NGC 1851A: A possible millisecond pulsar- neutron star system. Mon. Not. R. Astron. Soc. 2019, 409, 3860–3874. [Google Scholar] [CrossRef]
- Ferdman, R.D.; Stairs, I.H.; Kramer, M.; Janssen, G.H.; Bassa, C.G.; Stappers, B.W.; Demorest, P.B.; Cognard, I.; Desvignes, G.; Theureau, G.; et al. PSR J1756-2251: A pulsar with a low-mass neutron star companion. Mon. Not. R. Astron. Soc. 2014, 443, 2183–2196. [Google Scholar] [CrossRef]
- Cameron, A.D.; Bailes, M.; Balakrishnan, V.; Champion, D.J.; Freire, P.C.C.; Kramer, M.; Wex, N.; Johnston, S.; Lyne, A.G.; Stappers, B.W.; et al. News and views regarding PSR J1757-1854, a highly-relativistic binary pulsar. In Proceedings of the 16th Marcel Grossmann Meeting, Online, 5–10 July 2021. [Google Scholar]
- Haniewicz, H.T.; Ferdman, R.D.; Freire, P.C.C.; Champion, D.J.; Bunting, K.A.; Lorimer, D.R.; McLaughlin, M.A. Precise mass measurements for the double neutron star system J1829+ 2456. Mon. Not. R. Astron. Soc. 2021, 500, 4620–4627. [Google Scholar] [CrossRef]
- van Leeuwen, J.; Kasian, L.; Stairs, I.H.; Lorimer, D.R.; Camilo, F.; Chatterjee, S.; Cognard, I.; Desvignes, G.; Freire, P.C.C.; Janssen, G.H.; et al. The binary companion of young, relativistic pulsar J1906+ 0746. Astrophys. J. 2015, 798, 118. [Google Scholar] [CrossRef]
- Ferdman, R.D.; Freire, P.C.C.; Perera, B.B.P.; Pol, N.; Camilo, F.; Chatterjee, S.; Cordes, J.M.; Crawford, F.; Hessels, J.W.T.; Kaspi, V.M.; et al. Asymmetric mass ratios for bright double neutron-star mergers. Nature 2020, 583, 211–214. [Google Scholar] [CrossRef] [PubMed]
- Swiggum, J.K.; Pleunis, Z.; Parent, E.; Kaplan, D.L.; McLaughlin, M.A.; Stairs, I.H.; Spiewak, R.; Agazie, G.Y.; Chawla, P.; DeCesar, M.E.; et al. The Green Bank North Celestial Cap Survey. VII. 12 New Pulsar Timing Solutions. Astrophys. J. 2023, 944, 154. [Google Scholar] [CrossRef]
- Sengar, R.; Balakrishnan, V.; Stevenson, S.; Bailes, M.; Barr, E.D.; Bhat, N.D.R.; Burgay, M.; Bernadich, M.C.I.; Cameron, A.D.; Champion, D.J.; et al. The High Time Resolution Universe Pulsar Survey—XVII. PSR J1325-6253, a low eccentricity double neutron star system from an ultra-stripped supernova. Mon. Not. R. Astron. Soc. 2022, 512, 57–82. [Google Scholar] [CrossRef]
- Martinez, J.G.; Stovall, K.; Freire, P.C.C.; Deneva, J.S.; Tauris, T.M.; Ridolfi, A.; Wex, N.; Jenet, F.A.; McLaughlin, M.A.; Bagchi, M. Pulsar J1411+ 2551: A low-mass double neutron star system. Astrophys. J. Lett. 2017, 851, L29. [Google Scholar] [CrossRef]
- Agazie, G.Y.; Mingyar, M.G.; McLaughlin, M.A.; Swiggum, J.K.; Kaplan, D.L.; Blumer, H.; Chawla, P.; DeCesar, M.; Demorest, P.B.; Fiore, W.; et al. The Green Bank Northern Celestial Cap Pulsar Survey. VI. Discovery and Timing of PSR J1759+ 5036: A Double Neutron Star Binary Pulsar. Astrophys. J. 2021, 922, 35. [Google Scholar] [CrossRef]
- Corongiu, A.; Kramer, M.; Stappers, B.W.; Lyne, A.G.; Jessner, A.; Possenti, A.; D’Amico, N.; Löhmer, O. The binary pulsar PSR J1811-1736: Evidence of a low amplitude supernova kick. Astron. Astrophys. 2007, 462, 703–709. [Google Scholar] [CrossRef]
- Swiggum, J.K.; Rosen, R.; McLaughlin, M.A.; Lorimer, D.R.; Heatherly, S.; Lynch, R.; Scoles, S.; Hockett, T.; Filik, E.; Marlowe, J.A.; et al. PSR J1930–1852: A pulsar in the widest known orbit around another neutron star. Astrophys. J. 2015, 805, 156. [Google Scholar] [CrossRef]
- Stovall, K.; Freire, P.C.C.; Chatterjee, S.; Demorest, P.B.; Lorimer, D.R.; McLaughlin, M.A.; Pol, N.; van Leeuwen, J.; Wharton, R.S.; Allen, B.; et al. PALFA discovery of a highly relativistic double neutron star binary. Astrophys. J. Lett. 2018, 854, L22. [Google Scholar] [CrossRef]
- Balakrishnan, V.; Freire, P.C.C.; Ransom, S.M.; Ridolfi, A.; Barr, E.D.; Chen, W.; Krishnan, V.V.; Champion, D.; Kramer, M.; Gautam, T.; et al. Missing for 20 yr: MeerKAT Redetects the Elusive Binary Pulsar M30B. Astrophys. J. Lett. 2023, 942, L35. [Google Scholar] [CrossRef]
- Reardon, D.J.; Shannon, R.M.; Cameron, A.D.; Goncharov, B.; Hobbs, G.B.; Middleton, H.; Shamohammadi, M.; Thyagarajan, N.; Bailes, M.; Bhat, N.D.R.; et al. The Parkes pulsar timing array second data release: Timing analysis. Mon. Not. R. Astron. Soc. 2021, 507, 2137–2153. [Google Scholar] [CrossRef]
- Voisin, G.; Cognard, I.; Freire, P.C.C.; Wex, N.; Guillemot, L.; Desvignes, G.; Kramer, M.; Theureau, G. An improved test of the strong equivalence principle with the pulsar in a triple star system. Astron. Astrophys. 2020, 638, A24. [Google Scholar] [CrossRef]
- Reardon, D.J.; Hobbs, G.; Coles, W.; Levin, Y.; Keith, M.J.; Bailes, M.; Bhat, N.D.R.; Burke-Spolaor, S.; Dai, S.; Kerr, M.; et al. Timing analysis for 20 millisecond pulsars in the Parkes Pulsar Timing Array. Mon. Not. R. Astron. Soc. 2016, 455, 1751–1769. [Google Scholar] [CrossRef]
- Kasian, L.E.R. Observations of Two Binary Pulsars. Doctoral Dissertation. Available online: https://open.library.ubc.ca/soa/cIRcle/collections/ubctheses/24/items/1.0072639 (accessed on 26 October 2023).
- Fonseca, E.; Cromartie, H.T.; Pennucci, T.T.; Ray, P.S.; Kirichenko, A.Y.; Ransom, S.M.; Demorest, P.B.; Stairs, I.H.; Arzoumanian, Z.; Guillemot, L.; et al. Refined mass and geometric measurements of the high-mass PSR J0740+ 6620. Astrophys. J. Lett. 2021, 915, L12. [Google Scholar] [CrossRef]
- Desvignes, G.; Caballero, R.N.; Lentati, L.; Verbiest, J.P.W.; Champion, D.J.; Stappers, B.W.; Janssen, G.H.; Lazarus, P.; Osłowski, S.; Babak, S.; et al. High-precision timing of 42 millisecond pulsars with the European Pulsar Timing Array. Mon. Not. R. Astron. Soc. 2016, 458, 3341–3380. [Google Scholar] [CrossRef]
- Serylak, M.; Venkatraman Krishnan, V.; Freire, P.C.C.; Tauris, T.M.; Kramer, M.; Geyer, M.; Parthasarathy, A.; Bailes, M.; Bernadich, M.C.I.; Buchner, S.; et al. The eccentric millisecond pulsar, PSR J0955-6150—I. Pulse profile analysis, mass measurements, and constraints on binary evolution. Astron. Astrophys. 2022, 665, A53. [Google Scholar] [CrossRef]
- Mata Sánchez, D.; Istrate, A.G.; van Kerkwijk, M.H.; Breton, R.P.; Kaplan, D.L. PSR J1012+ 5307: A millisecond pulsar with an extremely low-mass white dwarf companion. Mon. Not. R. Astron. Soc. 2020, 494, 4031–4042. [Google Scholar] [CrossRef]
- Shamohammadi, M.; Bailes, M.; Freire, P.C.C.; Parthasarathy, A.; Reardon, D.J.; Shannon, R.M.; Venkatraman Krishnan, V.; Bernadich, M.C.I.; Cameron, A.D.; Champion, D.J.; et al. Searches for Shapiro delay in seven binary pulsars using the MeerKAT telescope. Mon. Not. R. Astron. Soc. 2022, 520, 1789–1806. [Google Scholar] [CrossRef]
- Bhat, N.D.R.; Bailes, M.; Verbiest, J.P.W. Gravitational-radiation losses from the pulsar–white-dwarf binary PSR J1141–6545. Phys. Rev. D 2008, 77, 124017. [Google Scholar] [CrossRef]
- Berthereau, A.; Guillemot, L.; Freire, P.C.C.; Kramer, M.; Venkatraman Krishnan, V.; Cognard, I.; Theureau, G.; Bailes, M.; i Bernadich, M.C.; Lower, M.E. Radio timing constraints on the mass of the binary pulsar PSR J1528-3146. Astron. Astrophys. 2023, 674, A71. [Google Scholar] [CrossRef]
- Antoniadis, J.; van Kerkwijk, M.H.; Koester, D.; Freire, P.C.C.; Wex, N.; Tauris, T.M.; Kramer, M.; Bassa, C.G. The relativistic pulsar–white dwarf binary PSR J1738+ 0333—I. Mass determination and evolutionary history. Mon. Not. R. Astron. Soc. 2012, 423, 3316–3327. [Google Scholar] [CrossRef]
- Kirichenko, A.Y.; Karpova, A.V.; Zyuzin, D.A.; Zharikov, S.V.; López, E.A.; Shibanov, Y.A.; Freire, P.C.C.; Fonseca, E.; Cabrera-Lavers, A. Searching for optical companions to four binary millisecond pulsars with the Gran Telescopio Canarias. Mon. Not. R. Astron. Soc. 2020, 492, 3032–3040. [Google Scholar] [CrossRef]
- Andersen, B.C.; Ransom, S.M. A Fourier domain “Jerk” search for binary pulsars. Astrophys. J. Lett. 2018, 863, L13. [Google Scholar] [CrossRef]
- Ferdman, R.D.; Stairs, I.H.; Kramer, M.; McLaughlin, M.A.; Lorimer, D.R.; Nice, D.J.; Manchester, R.N.; Hobbs, G.; Lyne, A.G.; Camilo, F.; et al. A Precise Mass Measurement of the Intermediate-Mass Binary Pulsar PSR J1802–2124. Astrophys. J. 2010, 711, 764. [Google Scholar] [CrossRef]
- Ng, C.; Guillemot, L.; Freire, P.C.C.; Kramer, M.; Champion, D.J.; Cognard, I.; Theureau, G.; Barr, E.D. A Shapiro delay detection in the pulsar binary system PSR J1811–2405. Mon. Not. R. Astron. Soc. 2020, 491, 1261–1267. [Google Scholar] [CrossRef]
- Corongiu, A.; Venkatraman Krishnan, V.; Freire, P.C.C.; Kramer, M.; Possenti, A.; Geyer, M.; Ridolfi, A.; Abbate, F.; Bailes, M.; Barr, E.D.; et al. PSR J1910–5959 A: A rare gravitational laboratory for testing white dwarf models. Astron. Astrophys. 2023, 671, A72. [Google Scholar] [CrossRef]
- Arzoumanian, Z.; Brazier, A.; Burke-Spolaor, S.; Chamberlin, S.; Chatterjee, S.; Christy, B.; Cordes, J.M.; Cornish, N.J.; Crawford, F.; Thankful Cromartie, H.; et al. The NANOGrav 11-year data set: High-precision timing of 45 millisecond pulsars. Astrophys. J. Suppl. Ser. 2018, 235, 37. [Google Scholar] [CrossRef]
- Geyer, M.; Venkatraman Krishnan, V.; Freire, P.C.C.; Kramer, M.; Antoniadis, J.; Bailes, M.; Bernadich, M.C.I.; Buchner, S.; Cameron, A.D.; Champion, D.J.; et al. Mass measurements and 3D orbital geometry of PSR J1933–6211. Astron. Astrophys. 2023, 674, A169. [Google Scholar] [CrossRef]
- Barr, E.D.; Freire, P.C.C.; Kramer, M.; Champion, D.J.; Berezina, M.; Bassa, C.G.; Lyne, A.G.; Stappers, B.W. A massive millisecond pulsar in an eccentric binary. Mon. Not. R. Astron. Soc. 2017, 465, 1711–1719. [Google Scholar] [CrossRef]
- Zhu, W.W.; Freire, P.C.C.; Knispel, B.; Allen, B.; Stappers, B.W.; Lyne, A.G.; Chatterjee, S.; Cordes, J.M.; Crawford, F.; Deneva, J.S.; et al. Mass measurements for two binary pulsars discovered in the PALFA survey. Astrophys. J. 2019, 881, 165. [Google Scholar] [CrossRef]
- McKee, J.W.; Freire, P.C.C.; Berezina, M.; Champion, D.J.; Cognard, I.; Graikou, E.; Guillemot, L.; Keith, M.J.; Kramer, M.; Lyne, A.G.; et al. A precise mass measurement of PSR J2045+ 3633. Mon. Not. R. Astron. Soc. 2020, 499, 4082–4096. [Google Scholar] [CrossRef]
- Berezina, M.; Champion, D.J.; Freire, P.C.C.; Tauris, T.M.; Kramer, M.; Lyne, A.G.; Stappers, B.W.; Guillemot, L.; Cognard, I.; Barr, E.D.; et al. The discovery of two mildly recycled binary pulsars in the Northern High Time Resolution Universe pulsar survey. Mon. Not. R. Astron. Soc. 2017, 470, 4421–4433. [Google Scholar] [CrossRef]
- Guo, Y.J.; Freire, P.C.C.; Guillemot, L.; Kramer, M.; Zhu, W.W.; Wex, N.; McKee, J.W.; Deller, A.; Ding, H.; Kaplan, D.L.; et al. PSR J2222–0137—I. Improved physical parameters for the system. Astron. Astrophys. 2021, 654, A16. [Google Scholar] [CrossRef]
- Stovall, K.; Freire, P.C.C.; Antoniadis, J.; Bagchi, M.; Deneva, J.S.; Garver-Daniels, N.; Martinez, J.G.; McLaughlin, M.A.; Arzoumanian, Z.; Blumer, H.; et al. PSR J2234+ 0611: A new laboratory for Stellar evolution. Astrophys. J. 2019, 870, 74. [Google Scholar] [CrossRef]
- Freire, P.C.C.; Ridolfi, A.; Kramer, M.; Jordan, C.; Manchester, R.N.; Torne, P.; Sarkissian, J.; Heinke, C.O.; D’Amico, N.; Camilo, F.; et al. Long-term observations of the pulsars in 47 Tucanae—II. Proper motions, accelerations and jerks. Mon. Not. R. Astron. Soc. 2017, 471, 857–876. [Google Scholar] [CrossRef]
- Freire, P.C.; Camilo, F.; Kramer, M.; Lorimer, D.R.; Lyne, A.G.; Manchester, R.N.; D’Amico, N. Further results from the timing of the millisecond pulsars in 47 Tucanae. Mon. Not. R. Astron. Soc. 2003, 340, 1359–1374. [Google Scholar] [CrossRef]
- Ridolfi, A.; Gautam, T.; Freire, P.C.C.; Ransom, S.M.; Buchner, S.J.; Possenti, A.; Venkatraman Krishnan, V.; Bailes, M.; Kramer, M.; Stappers, B.W.; et al. Eight new millisecond pulsars from the first MeerKAT globular cluster census. Mon. Not. R. Astron. Soc. 2021, 504, 1407–1426. [Google Scholar] [CrossRef]
- Bégin, S. A Search for Fast Pulsars in Globular Cluster. Doctoral Dissertation, University of British Columbia, Vancouver, BC, Canada, 2006. [Google Scholar]
| Pulsar | |
|---|---|
| B1957+20 | 1.81 ± 0.07 |
| J1048+2339 | 1.58 ± 0.07 |
| J1555−2908 | 1.65 ± 0.04 |
| J1816+4510 | 1.90 ± 0.13 |
| J2129−0429 | 1.70 ± 0.11 |
| Mean | SD | HPDI | |
|---|---|---|---|
| – | |||
| – | |||
| – | |||
| – | |||
| – | |||
| – | |||
| – |
| mean | SD | HPDI | |
|---|---|---|---|
| – | |||
| – | |||
| – | |||
| – | |||
| – | |||
| – | |||
| – |
| Pulsar | |||
|---|---|---|---|
| B1957+20 | - | 1.16–2.14 | |
| J1311-3430 | - | 1.17–2.14 | |
| B1516+02B | 1.26–2.15 | - | |
| J1748-2021B | 1.23–2.59 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rocha, L.S.; Horvath, J.E.; de Sá, L.M.; Chinen, G.Y.; Barão, L.G.; de Avellar, M.G.B. Mass Distribution and Maximum Mass of Neutron Stars: Effects of Orbital Inclination Angle. Universe 2024, 10, 3. https://doi.org/10.3390/universe10010003
Rocha LS, Horvath JE, de Sá LM, Chinen GY, Barão LG, de Avellar MGB. Mass Distribution and Maximum Mass of Neutron Stars: Effects of Orbital Inclination Angle. Universe. 2024; 10(1):3. https://doi.org/10.3390/universe10010003
Chicago/Turabian StyleRocha, Lívia S., Jorge E. Horvath, Lucas M. de Sá, Gustavo Y. Chinen, Lucas G. Barão, and Marcio G. B. de Avellar. 2024. "Mass Distribution and Maximum Mass of Neutron Stars: Effects of Orbital Inclination Angle" Universe 10, no. 1: 3. https://doi.org/10.3390/universe10010003
APA StyleRocha, L. S., Horvath, J. E., de Sá, L. M., Chinen, G. Y., Barão, L. G., & de Avellar, M. G. B. (2024). Mass Distribution and Maximum Mass of Neutron Stars: Effects of Orbital Inclination Angle. Universe, 10(1), 3. https://doi.org/10.3390/universe10010003







